Rotating single-shot acquisition (RoSA) with composite reconstruction for fast high-resolution diffusion imaging

Abstract

Purpose

To accelerate high-resolution diffusion imaging, rotating single-shot acquisition (RoSA) with composite reconstruction is proposed. Acceleration was achieved by acquiring only one rotating single-shot blade per diffusion direction, and high-resolution diffusion-weighted (DW) images were reconstructed by utilizing similarities of neighboring DW images. Parallel imaging technique was implemented in RoSA to further improve the image quality and acquisition speed. RoSA performance was evaluated by simulation and human experiments.

Methods

A brain tensor phantom was developed to determine an optimal blade size and rotation angle by considering similarity in DW images, off-resonance effects, and k-space coverage. With the optimal parameters, RoSA MR pulse sequence and reconstruction algorithm were developed to acquire human brain data. For comparison, multi-shot echo-planar imaging (EPI) and conventional single-shot EPI sequences were performed with matched scan time, resolution, FOV, and diffusion directions.

Results

The simulation indicated an optimal blade size of 48×256 and a 30° rotation angle. For 1×1 mm² in-plane resolution, RoSA was 12 times faster than the multi-shot acquisition with comparable image quality. With the same acquisition time as SS-EPI, RoSA provided superior image quality and minimum geometric distortion.

Conclusion

RoSA offers fast high-quality high-resolution diffusion images. The composite image reconstruction is model-free and compatible with various diffusion computation approaches including parametric and non-parametric analyses.

Introduction

Single-shot echo-planar imaging (SS-EPI) is the most common sequence for diffusion-weighted imaging (DWI), a powerful tool for assessing the neuronal microstructures in vivo [1–3]. Although SS-EPI has gained popularity due to its fast acquisition, its spatial resolution is often limited [4], making it difficult to measure accurate diffusion properties in fine structures that require high spatial resolution [5–7], such as gyral projections [6,7], or penetrating fibers between basal ganglia [8]. Even with advances in parallel imaging, SS-EPI at a high resolution is limited by geometric distortion and a low signal-to-noise ratio (SNR).

Multi-shot techniques have been developed to improve the resolution by filling in the k-space with multiple readouts at the expense of possible motion artifacts and phase inconsistencies between shots [9–19]. In this category, periodically rotated overlapping parallel lines with enhanced reconstruction (PROPELLER) is a robust technique that is particularly suitable for high-resolution DWI in the presence of patient motion [12,13]. It uses fast spin-echo (FSE) readouts, which are free from EPI artifacts. In addition, the motion artifacts may be corrected by its self-navigation property as the center of the k-space is repeatedly sampled in each echo train with a rotating blade trajectory. The drawbacks of PROPELLER are that it is much slower than EPI and is quite specific absorption rate (SAR)-intensive. Therefore, PROPELLER EPI sequences were proposed to improve upon PROPELLER FSE by replacing FSE readouts with EPI [14,15]. Unlike conventional SS-EPI, short-axis PROPELLER EPI features short echo spacing, which greatly alleviates all of the aforementioned issues in SS-EPI, including geometric distortion [15]. Although the imaging speed of PROPELLER EPI is faster than that of PROPELLER FSE, it is still much slower than SS-EPI due to its multi-shot nature. Imaging speed is a common limitation for extensive use of multi-shot techniques, especially in applications that require a large number of diffusion directions [20–24].

To increase imaging speed for multi-shot DWI, acquiring only a subset of PROPELLER FSE blades for each DW image and a tensor model based reconstruction was suggested in [25]. A similar idea was proposed with a different reconstruction scheme to accelerate PROPELLER EPI, in which 10 diffusion directions are acquired with one unique blade per direction, and a full resolution DW image is reconstructed using all of the blades [26]. Although both studies [25,26] reported encouraging results with reduced data acquisition, these approaches lack the flexibility for extension to arbitrary diffusion direction schemes larger than 10 direction or to diffusion models other than Diffusion Tensor Imaging (DTI). Moreover, both methods use data from all diffusion directions to reconstruct a single DW image. Therefore, the similarities of neighboring DW images are either not considered [25] or only partly considered [26]. DW images contain a similar diffusion contrast when their diffusion directions are close in a q-space sphere. To our knowledge, this similarity feature among neighboring diffusion directions has not yet been explored as a means to reduce data acquisition and to improve diffusion imaging speed.

By taking advantage of similarities in DW images, we propose a rotating single-shot acquisition (RoSA) approach with model-free reconstruction to accelerate data acquisition for high-resolution diffusion imaging. In the RoSA scheme, one single-shot blade is acquired per diffusion direction. Upon reconstruction of any DW image, only a subset of DW images whose diffusion directions are close to the current DW image on the q-space sphere is used. Neighboring DW images are expected to become highly correlated when the diffusion signals are finely sampled on the q-space sphere. An image reconstruction technique used in highly constrained back-projection (HYPR) was adapted to reconstruct the RoSA. HYPR is a conventional non-iterative reconstruction technique for undersampled radial acquisition in time-resolved MRI in which correlations exist in a one-dimensional time domain [27], whereas correlations in the RoSA occur in a three-dimensional q-space. Parallel imaging is implemented in RoSA to further accelerate its acquisition and improve image quality. Here we demonstrate the feasibility of RoSA based on evaluation of its performance in both simulations and human experiments.

Methods

RoSA acquisition

During data acquisition, one EPI blade with a short axis in the frequency encoding direction in k-space was acquired for each diffusion direction in q-space. The EPI blade rotated as diffusion direction changed in a sorted sequence (Figure 1A,B). Herein, we demonstrate an intuitive heuristic spiral ordering scheme. As illustrated in Figure 1A, for a given number of total diffusion directions, they were first sampled on the half sphere in q-space to maximize the angular sampling resolution. Then, diffusion directions were sorted into a sequence that was closest to an Archimedean spherical spiral curve with corresponding blades periodically rotating in this order. Figure 1B shows rotating blades in k-space and Figure 1C shows corresponding DW images. To avoid the edge effect around the equator where only the upper hemisphere has diffusion directions, we took advantage of the antipodal symmetry property of q-space, and mirrored the diffusion directions to create a whole sphere distribution (Figure 1D).

Figure 1.

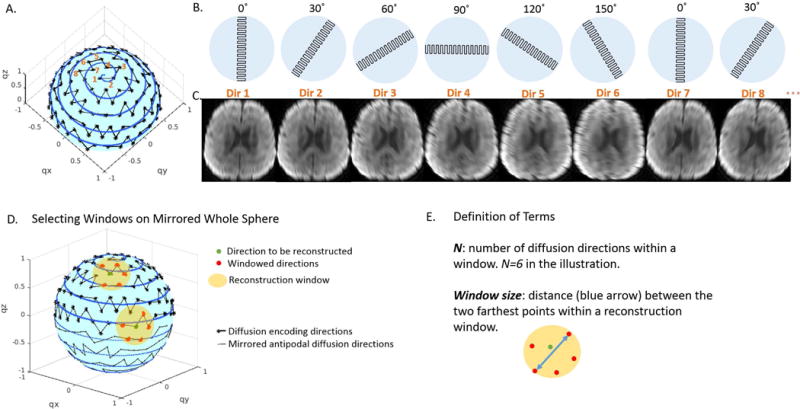
A. Diffusion directions on the half sphere of q-space were sorted according to the Archimedean spherical spiral curve. B. One EPI blade with a short axis in the frequency encoding direction was acquired for each diffusion direction. The EPI blade rotated periodically as the diffusion direction changed. C. DW images corresponding to blades in B. D. Two representative windows that comprise directions for reconstruction (green dots) and the neighboring directions (red dots, N=6) for reconstruction. One window is close to the pole and the other close to the equator where antipodally mirrored points (on dashed lines) were included. E. Definition of N and window size.

Reconstruction Window

For each diffusion direction to be reconstructed (green dot in Figure 1D), we searched its neighborhood to find a subset of DW blades each with a unique rotation angle (red dots in Figure 1D). Thus, on the q-space sphere each subset formed a reconstruction window (yellow discs in Figure 1D). Within the reconstruction window, “N” was defined as the number of diffusion directions, and “window size” as the distance between the two farthest points within the window (Figure 1E). The searching procedure was repeated till minimal window size was achieved for each diffusion direction, and high-resolution DW images were reconstructed with the windowed DW images through the composite reconstruction described below.

In theory, any diffusion direction in Figure 1A can be assigned with arbitrary rotating blade in Figure 1B. Such an assignment can be optimized to minimize the window size, therefore maximizing the similarity of DW images used for image reconstruction. To assess the goodness of the heuristic spiral-ordering scheme, we compared its averaged window size to those acquired from 1,000,000 trials of random assignments. Among the comparisons, the spiral-ordering scheme yielded the smallest overall window size (Supporting Figure S1).

Composite Reconstruction

The k-space blades within the reconstruction window were first combined to form a composite k-space data, which was then inversely Fourier-transformed (FT) to form a composite image. A final DW image was then reconstructed in the image space by constraining the composite image with the contrast provided by the current DW image. This reconstruction was adapted from HYPR [27] by replacing backprojection with FT. The full reconstruction comprised four computational steps that generated three intermediate images, I_i, I_C, $I_C^i$, and one final reconstructed image, $I_{\mathit{RoSA}}^i$, where i denotes the i^th target diffusion direction and C denotes the composite image (Figure 2). Note that prior to the composite reconstruction, the k-space data were centered, regridded, and Nyquist ghost corrected (see below sections In-line Reference Scan and Image Preprocessing).

Figure 2.

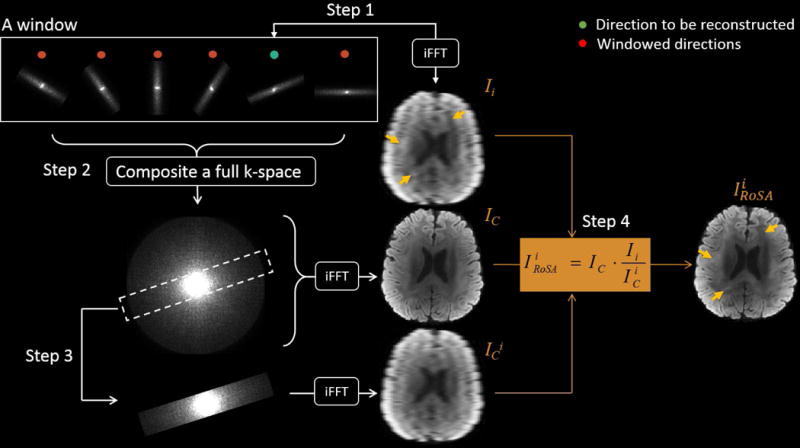
Schematic diagram of the RoSA reconstruction. Step1: Inverse fast Fourier transformation (iFFT) converts the target blade (green dot) to form the low-resolution DW image, I_i. Step2: All blades in the window are combined in the k-space and iFFT to form the composite image I_C. Step3: The composite k-space is cropped with the mask of the target blade to form the scaling image $I_C^i$. Step4: The composite image (I_C) is tuned by the contrast specific to the target diffusion direction (I_i) scaled by low-resolution profile ( $I_C^i$), as $I_{\mathit{RoSA}}^i=I_C·\frac{I_i}{I_C^i}$.

• Step 1: Generate low-resolution DW images (I_i). The k-space blade of the target diffusion direction i (green dot) was first inversely fast Fourier-transformed (iFFT) to form a low-resolution DW image, I_i, followed by motion correction to a reference image b₀ (i.e., b-value = 0 s/mm²) using a rigid body 6 DOF registration in FLIRT with correlation ratio as cost function (FSL).

• Step 2: Generate high-resolution composite images (I_C). The motion corrected k-space blades within the window were combined and density-corrected to form the composite k-space data followed by iFFT to yield the high-resolution composite image, I_C.

• Step 3: Generate scaling image ( $I_C^i$). The composite k-space data was cropped by the mask that matched the i^th k-space blade and iFFT to yield the scaling image $I_C^i$.

• Step 4: Generate reconstructed image ( $I_{\mathit{RoSA}}^i$). The high-resolution $I_{\mathit{RoSA}}^i$ was reconstructed by tuning the composite image I_C with the contrast specific to the target DW image. That is $I_{\mathit{RoSA}}^i=I_C·\frac{I_i}{I_C^i}$. As highlighted by arrows in Figure 2, the contrast that is unique to I_i is preserved in $I_{\mathit{RoSA}}^i$.

Simulations

To evaluate the RoSA approach, a high-quality, 1×1 mm² in-plane resolution brain tensor phantom was developed using a diffusion dataset acquired with multi-shot readout segmented EPI sequence (RESOLVE). The tensor matrix of the brain was derived and could be used as a phantom for generating DW images for an arbitrary direction scheme. In the simulations, we generated DW images at 60 directions and undersampled the k-space data to form rotating blades using the spiral ordering scheme described above. We performed three simulations:

• Simulation 1: The purpose of the first simulation was to demonstrate the performance of RoSA reconstruction in recovering full-resolution DW images and DTI fractional anisotropy (FA) without off-resonance effects. A blade size of 48×256 and 30 degree rotation angle for N=6 was used to generate the undersampled k-space. Full-resolution DW images were reconstructed with both RoSA reconstruction and simple zero-padding for comparison. The DTI metrics were estimated using a toolbox, DTIFIT, in FSL (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/) that fits a diffusion tensor model linearly at each voxel. Errors in FA and major eigenvector (EV1) were computed for quantitative comparisons. FA error was summarized as the 75^th percentile of absolute difference to the ground truth. EV1 error was summarized as the 75^th percentile of the angular difference (in degree) to the ground truth.

• Simulation 2: The second simulation was performed to investigate the image quality in the presence of off-resonance effects with and without the parallel imaging technique. Parallel imaging is expected to reduce the geometric distortion associated with the off-resonance effects via reducing the field of view (FOV). We used the field map acquired for the same subject to simulate distortions in DW images, and used an echo spacing of 0.36 ms based on our gradient system (80 mT/m maximum amplitude and 200 T/m/s slew rate) and a blade size of 48×256 (readout×phase). The distortion was simulated in the image domain using the FUGUE tool in FSL where voxels were displaced based on the given field map. To simulate the effects of parallel imaging, we artificially reduced the echo spacing by the reduction factor (R), which would achieve the same effect as reducing the FOV in SENSitivity Encoding (SENSE) or GeneRalized Autocalibrating Partial Parallel Acquisition (GRAPPA) approaches. The distorted DW images were then fed to the RoSA pipeline for reconstruction, and DTI results were compared.

• Simulation 3: The last simulation experiment was performed to investigate the optimal combination of blade width and N ranging from 2 to 12. In RoSA, the overall image quality is influenced by k-space coverage, and similarity among the DW images within the reconstruction window. The former is determined by blade width and N, and the latter is by N. We used FA error as a proxy for image quality to investigate combinations of blade width (32×256, 48×256, 64×256) and N. Similar to Simulation 2, the off-resonance effects were considered, and a reduction factor of R=3 was used for parallel imaging. Combinations with minimal FA errors were considered for subsequent human data acquisitions.

Human Experiments

A healthy volunteer was scanned at a 3 T system (MAGNETOM Prisma, Siemens Healthcare, Erlangen, Germany) with a 32-channel head coil. A prototype of RoSA sequence, combined with GRAPPA [28], was used for acquisition; Stejskal-Tanner pulsed-gradient spin-echo (PGSE) was used for diffusion weighting. The diffusion parameters were 4 b₀s and 60 diffusion directions at b-value = 1000 s/mm². RoSA parameters were: GRAPPA reduction factor R=3, matrix/blade size = 48×256, rotation angle = 30° (N=6), TE = 53 ms, FOV = 256 mm, 7/8 partial Fourier k-space sampling along the phase encoding (PE) direction, slice thickness = 2 mm, 10 slices, echo spacing = 0.36 ms, 2 averages. Total acquisition time was 2 min. The study was approved by our institutional review board, and informed consent was obtained for human studies.

For comparison, conventional SS-EPI diffusion data were acquired for the same volunteer at an in-plane resolution of 1×1 mm² and 2×2 mm² with a total acquisition time of 2 min and 1 min, respectively. Multi-shot sequence (RESOLVE) was performed at 1×1 mm² with 13 shots and a total acquisition time of 24 min. Echo spacing and TE are listed in Figure 7B. Other acquisition parameters were matched with RoSA including GRAPPA reduction factor, slice thickness, slice number, FOV, partial k-space coverage, and number of diffusion directions.

Figure 7.

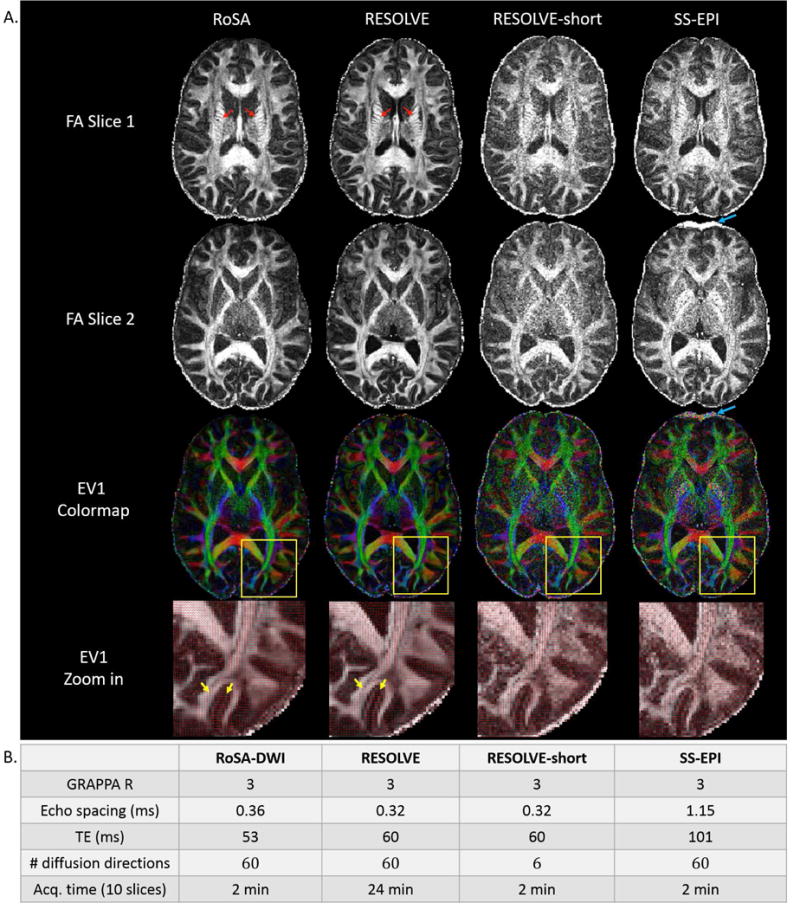
DTI metrics and sequence parameters of RoSA, RESOLVE, and SS-EPI. A. DTI metrics of RoSA, RESOLVE, and SS-EPI with matched image resolution (1×1×2mm³). RESOLVE-short with matched scan time of RoSA and SS-EPI was achieved by reducing diffusion direction from 60 to 6. Top two rows: FA of 2 different slices; 3^rd row: colormap of major eigenvectors (EV1); bottom row: EV1 overlaid on zoomed FA maps. The yellow squares indicate zoomed regions. RoSA and RESOLVE were able to show fine structures within the internal capsule (red arrows), and clear gyral stalks. RESOLVE-short and SS-EPI have excessive noise in the FA maps. The SS-EPI sequence demonstrated visible geometric distortions in the frontal lobes due to off-resonance effects of local field inhomogeneity (blue arrows). Orientations of major eigenvectors showed visible random variations using the RESOLVE-short and SS-EPI sequence (bottom zoomed-in view), whereas major eigenvectors using RoSA and RESOLVE showed ordered alignments along the gyral stalks and perpendicular projections inside grey matter (bottom row, yellow arrows). B. Critical imaging parameters: GRAPPA R denotes reduction factor for parallel imaging; TE denotes echo time; and Acq. denotes acquisition.

In-line Reference Scan and Nyquist Ghost Correction

Nyquist or FOV/2 ghosts commonly exist in EPI due to misalignment of the odd and even echoes caused by time delays, eddy currents, and static field inhomogeneity during EPI readout [29]. This problem was not fully addressed in previous PROPELLER EPI-based techniques [14,15]. In contrast to conventional single reference approaches [30,31], an in-line reference scan in the EPI pulse sequence was embeded immediately after every 90° excitation with only 3 readout lines (2 odds and 1 even) [32], which rotated the same way as the readout blade. Thus, the misalignment can be computed for each blade and the ghost can be corrected accordingly (Supporting Figure S2).

Image Preprocessing prior to RoSA reconstruction

Following Nyquist ghost correction, ramp-sampling correction was then carried out with sinc interpolation [33]. The Nyquist and ramp-sampling corrected k-space data were then GRAPPA reconstructed followed with homodyne reconstruction [34] to recover the partial k-space sampling along the PE direction and produce a full k-space blade (48×256). At this point, one can obtain an image at full resolution in the PE direction. Because the homodyne reconstruction clears the phase in the image domain, this procedure also centers the k-space peaks between the blades, a crucial step for subsequent data regridding [35]. According to the angulation of individual blades, the echo-centered full blades were regridded to Cartesian grid points using Kaiser-Bessel kernel [36] with an inherent post-compensation density correction [37]. The Kaiser–Bessel kernel is a smooth low-pass window function whose tradeoffs between main lobe width and side lobe levels of the spectral leakage can be controlled. Such characteristics have been shown to provide a good interpolation quality that is superior to both nearest-neighbor and linear interpolation and is computational inexpensive. The preprocessed low resolution DW images were then sent to the composite reconstruction. The apodization induced by the convolution kernel from regridding was corrected afterwards. In parallel, b₀ images were reconstructed similar to PROPELLER, as described in [15].

Results

Simulations

• Simulation 1: A tensor phantom without off-resonance effects was generated (Figure 3A). DW images and FA of the simple zero-padding approach and the RoSA reconstruction were compared with the ground truth in Figure 3A. With only 1/8 k-space data, the zero-padded images were blurred (Figure 3B). In the RoSA reconstruction, however, high-resolution DW images and FA were recovered and were similar to the ground truth (Figure 3C). The 75^th percentile of absolute FA error in the RoSA reconstruction was 0.02, which was six times smaller than 0.12 in zero-padding. In addition, the 75^th percentile of EV1 error was 8° in RoSA and 32° in zero-padding. In RoSA, EV1 had higher error mostly in the cerebrospinal fluid where water diffuses isotropically.

• Simulation 2: In the presence of off-resonance effects due to field inhomogeneity (ΔB₀), RoSA FA showed blurring in the tip of the frontal lobes as highlighted by the red circle in Figure 4. The off-resonance caused image distortions in the low-resolution DW images (I_i), and the rotation of blades produced blurring and image errors. The errors reduced significantly by using parallel imaging R=3 (Figure 4, right column, bottom), and gyral fiber stalks were better delineated (Figure 4, right column, middle).

• Simulation 3: The tradeoff between N and k-space coverage is shown in Figure 5 without off-resonance effects. For a fixed blade size (32×256), a reconstruction window comprising six blades (i.e., N=6) had a smaller window size compared to N=12 (Figure 5, yellow discs). Although with full k-space coverage, N=12 produced larger image errors than N=6 (Figure 5, DWI error and FA error). This demonstrates that a smaller window size, albeit partial k-space coverage, improves similarity among DW images within the reconstruction window; and hence, increases reconstructed image quality.

Figure 3.

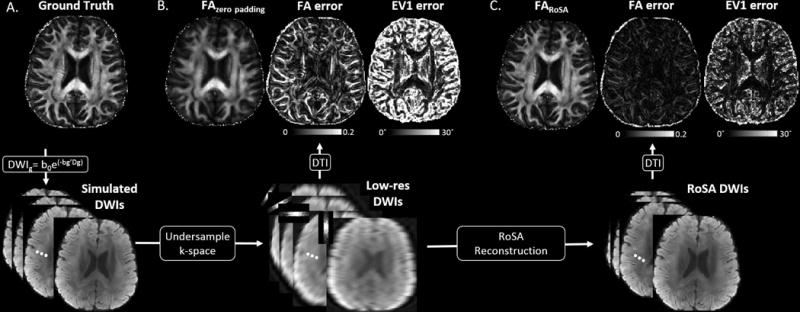
RoSA simulation without off-resonance effects. Column A. Phantom FA and simulated DW images. Column B. FA generated with the low-res DW images (bottom) via simple zero padding in k-space. Maps next to FA are FA errors and major eigenvector (EV1) errors (in degree). Column C. High-resolution FA generated with the RoSA reconstructed DW images in the bottom row. Maps next to FA are FA errors and EV1 errors.

Figure 4.

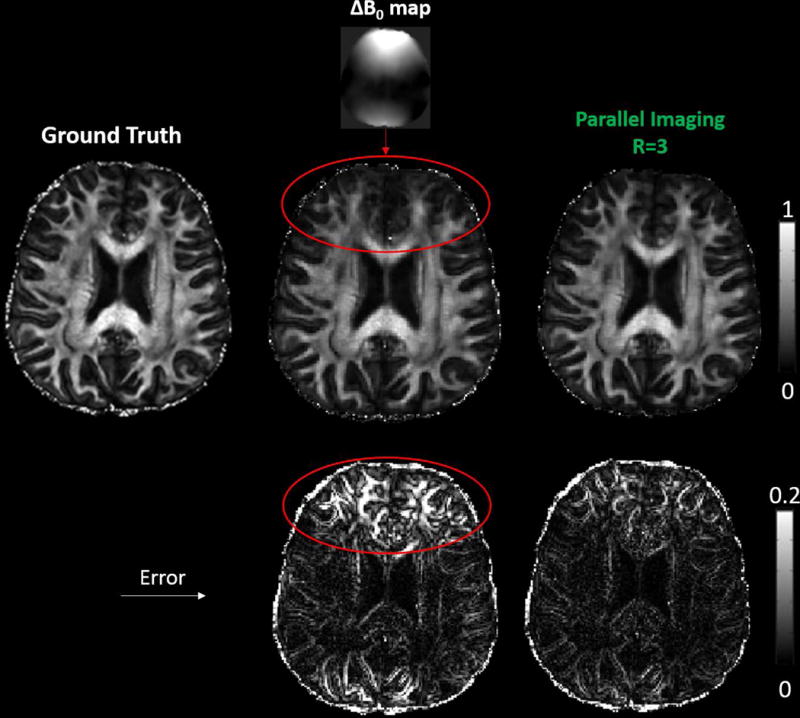
Simulated RoSA FA (middle row) and FA errors (bottom) in the presence of off-resonance effects with and without parallel imaging for a blade size of 48×256 and echo spacing of 0.36 ms. As highlighted by the red circles, the blurring in the tip of the frontal lobes arose from the rotating blades with off-resonance effects due to field inhomogeneity, ΔB₀ (fieldmap on top). With parallel imaging and a reduction factor of 3 (R = 3) (right column), the blurring artifact and FA errors were significantly reduced.

Figure 5.

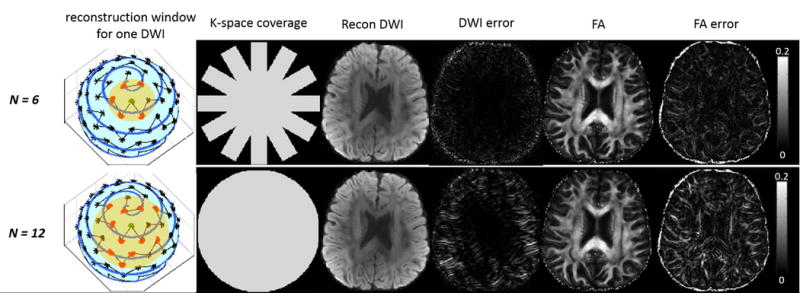
The tradeoff between N and k-space coverage without off-resonance effects. Yellow disc denotes reconstruction window. Recon DWI denotes reconstructed DW images. For a fixed blade size of 32×256, N=6 (partial k-space coverage) produced smaller reconstruction error than N=12 (full k-space coverage).

The optimal N for a given blade size can be identified via investigating image errors. FA errors are calculated for different combinations of blade size, number of blades in each reconstruction window (N), and the off-resonance effects (ΔB₀). While the smallest global error occurred at 64×256 blade with N=4, the smallest local error in high ΔB₀ region occurred at 48×256 with N=6 (Supporting Figure S3). Taking into account that TE was 9ms longer in a 64×256 blade, we moved forward with a blade size of 48×256 and N=6 for our human experiments.

Human Experiments

Rotating k-space blades (48×256) are shown in Figure 6A for six diffusion directions. The corresponding DW images via zero padding showed expected low resolution along the frequency encoding direction (Figure 6B). The RoSA reconstructed DW images (Figure 6C) not only recovered the image resolution along the frequency direction, but also maintained the diffusion contrast. Matching diffusion contrast can be appreciated in the RESOLVE DW images (Figure 6D) obtained with matched diffusion encoding scheme. While acquiring less k-space data by a factor of 5.3, RoSA produced comparable image quality, resolution, and diffusion contrast to that of RESOLVE by utilizing neighborhood similarities.

Figure 6.

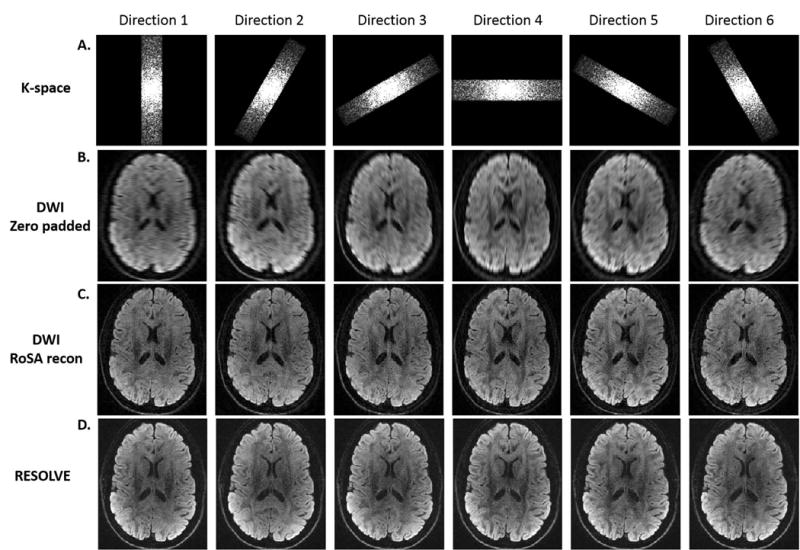
RoSA k-space blades and reconstructed DW images. A. Rotating k-space blade for 6 diffusion directions. B. The corresponding DW images with low-resolution along the frequency encoding directions. C. RoSA reconstructed DW images. D. DW images acquired by the multi-shot sequence, RESOLVE, with matched diffusion directions.

FA, EV1, and colormap are shown in Figure 7A for different methods: RoSA, RESOLVE, and conventional SS-EPI with matched resolution (1×1×2 mm³). Critical acquisition parameters are listed in Figure 7B. The DTI results from a shorter version of the RESOLVE sequence (i.e., RESOLVE-short) was added for comparisons with the matched scan time. RESOLVE-short was achieved by reducing the diffusion encoding directions from 60 to 6. Similar to Figure 6, RoSA produced comparable image quality in computed DTI metrics to RESOLVE. DTI images of SS-EPI and RESOLVE-short presented excessive noise due to long TE (101 ms) and severe undersampled q-space, respectively. With an advantage of shorter TE (~53 ms), RoSA and RESOLVE were able to show fine structures within the internal capsule (Figure 7A, top row, red arrows), and clear gyral stalks. In addition, images of RoSA, RESOLVE, and RESOLVE-short had minimum geometric distortions benefited from parallel imaging and very short echo spacing (~0.36 ms). In contrast, despite parallel imaging, long echo spacing (1.15 ms) in the SS-EPI sequence caused visible geometric distortions in the frontal lobes due to off-resonance effects of local field inhomogeneity (Figure 7A, 2^nd and 3^rd row, blue arrows). Further, orientations of major eigenvectors showed visible random variations using the RESOLVE-short and SS-EPI sequence (Figure 7A, bottom zoomed-in view), whereas major eigenvectors using RoSA and RESOLVE showed ordered alignments along the gyral stalks and perpendicular projections inside grey matter (Figure 7A, bottom row, yellow arrows). While RoSA and SS-EPI had same scan times, for the same brain coverage, the acquisition time of RESOLVE was 12 times longer.

Discussion

In this paper, we demonstrated the feasibility of RoSA, an innovative technique for fast high-resolution diffusion imaging. RoSA acquires one rotating blade per diffusion direction, and the high-resolution DW images are reconstructed with model-free composite reconstruction that takes advantage of the similarities between neighboring DW images. Similar to PROPELLER [12,38], RoSA has inherent navigation capabilities provided by the rotating blade trajectory that repeatedly samples the center of the k-space. As implemented with short-axis EPI readout, it also maintains the advantages of short-axis EPI over conventional SS-EPI in its reduced distortion, improved effective resolution in the phase-encoding direction associated with $T_2^{\ast }$ decay, and that geometric distortions do not scale with the target image resolution [15]. As a 2D acquisition technique, it can be easily combined with other fast-imaging techniques applied in the slice direction to further improve its imaging speed, such as the simultaneous multi-slice (SMS) [39] and generalized Slider method (gSlider-SMS) [40].

High-resolution diffusion imaging offers advantages in clinical diagnosis and basic research. For example, recurrent cholesteatoma may be detected earlier while the lesion is still small [41]; and small and short fibers may be detected to aid accuracy in white matter tractography: penetrating fibers between the space of extreme and external capsule [42], subcortical arcuate fibers [7], and gyral stalk projection fibers [5,6]. While conventional neuroimaging modalities such as T1-weighted and T2-weighted imaging routinely provide isotropic 1 mm resolution for whole-brain coverage, diffusion MRI is still restricted by coarse voxel sizes or very limited brain coverage. Compared to the low-resolution SS-EPI (2×2×2 mm³), the high-resolution FA map of RoSA (1×1×2 mm³) shows better separation between the external (Figure 8A, yellow arrows) and extreme capsules (Figure 8A, white arrows) and clearer fine structures in Figure 8B (white arrows). Such high-resolution images are currently available by the RESOLVE sequence in Siemens platforms, but with very limited brain coverage due to long scan time. With matched data quality shown in Figures 6–8, the RoSA approach provides 12 times faster imaging speed.

Figure 8.

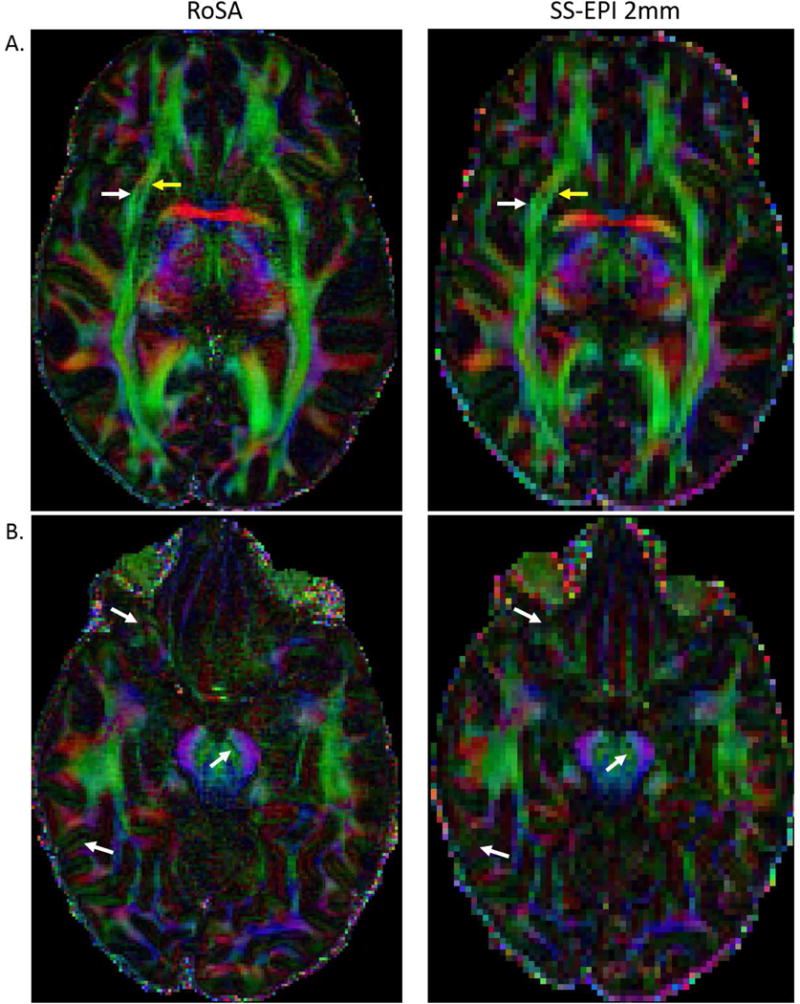
Comparison of high-resolution FA map of RoSA (1×1×2mm³) and low-resolution FA map of SS-EPI (2×2×2mm³). The external (yellow arrows in A) and extreme capsules (white arrows in A) can only be resolved in FA maps of high-resolution. Similarly, fine structures are only visible in high-resolution image in B.

The efficiency in RoSA is achieved by utilizing the similarity in DW images whose directions are close. The closeness of DW images in each sliding-window has a direct impact on the image quality. That is for each diffusion direction, its “unique neighbors” (neighbors with unique rotation blades) cannot be far away. However, finding the global optimal solution in pairing diffusion directions and rotating blades is computationally challenging. We proposed an intuitive heuristic spiral ordering scheme and assigned rotating blades to a diffusion direction in this order. A similar problem was previously proposed and set up as a traveling salesman problem [26]. Only 10 total diffusion directions, however, were considered in that study where the window length (i.e., N) was constrained to be the same as the total number of directions. Such a fixed reconstruction window is difficult to generalize to other direction schemes with a flexible N. While a better scheme may exist and has yet to be explored, the current RoSA scheme provides desired flexibility and demonstrates to achieve comparable data quality.

The composite image is a key component in HYPR, an imaging technique that explores temporal redundancy in time-resolved MRI with radial sampling [27]. The composite image comprises a set of correlated frames that provide high-resolution structural information, and is used to constrain the reconstruction of an undersampled frame. In RoSA, the q-space redundancy can be viewed as analogous to temporal redundancy as both have correlated information in the 4^th dimension (time domain vs. q-space). Therefore, the HYPR method can be readily adapted to reconstruct RoSA with a slight modification. In particular, as radial lines were replaced with rotating blades, we reconstruct the composite image by combining the data in k-space with density correction instead of filtered backprojection in image space. Projection reconstruction techniques have advantages over k-space methods with respect to diminished motion artifacts [43]. As rotating blades are self-navigating and a registration step is taken before combining in k-space, it is as robust to motion artifact as the PROPELLER technique [12]. Thus, by combining rotating blades with HYPR, RoSA preserves the merits of both.

The image quality of RoSA can be optimized by further improving k-space coverage and the off-resonance effects. As demonstrated in Simulation 3, wedges of k-space are not fully covered in order to guarantee a small window size (Figure 5,6). Although the effective resolution may be reduced due to the missing blades, a study showed that collecting every other blade only slightly decreases the SNR (from 18.5 to 18.2) with a mildly increased full-width half-maximum (FWHM) of the point spread function (PSF) (1.09 to 1.18) and non-significant artifacts [44]. Alternatively, an iterative reconstruction could be employed to further improve the situation [45].

Off-resonance artifact is a common problem in EPI-based acquisition techniques. Compared to conventional SS-EPI, echo spacing is reduced in RoSA and off-resonance artifacts are improved. In addition, parallel imaging was incorporated to further reduce the artifacts by a factor of R as has been implemented in the previous PROPELLER EPI-based techniques [46–47]. Note that depending on R and the geometric factor (g-factor), in parallel imaging, noise may be amplified. Because the HYPR reconstruction is a linear operation system ( $I_{\mathit{RoSA}}^i=I_C·\frac{I_i}{I_C^i}$), the noise amplification of parallel imaging in RoSA ( $I_{\mathit{RoSA}}^i$) is expected to be directly proportional to I_C, which is reconstructed similarly to PROPELLER. PROPELLER accelerated via parallel imaging, SENSE and GRAPPA, has been studied and documented in [48] and [49] respectively. Alternatively, ultimate image quality may be achieved by a post-processing approach. The off-resonance field ∆B₀ can be obtained via a set of reversed phase-encoding blades (i.e., an additional set of b₀s acquired with reversed phase-encoding) similar to that described in [50] as implemented in FSL TOPUP command [51]. Using the off-resonance fieldmap, the TOPUP command produces corrected images and the artifacts can be corrected at the blade level.

Other common artifacts in EPI-based imaging are eddy current and chemical shift artifacts. For RoSA, the eddy current arising from the diffusion gradients may produce eddy current artifacts/distortions in DW images of individual blades. Since diffusion directions within a reconstruction window are very close, the eddy current effect is expected to be very similar. Therefore, it could be corrected in the same way as correcting conventional Cartesian DW images. Minimal eddy current effects were observed in this study; thus, no correction was performed. In addition, while not observed in this study, ghosting artifact related to eddy current can be present and cannot be corrected with current Nyquist ghost correction method as reference lines precede the diffusion gradients. Such eddy-current related ghosting may be corrected at the level of image reconstruction described in [52]. The chemical shift may produce “fat-rim” artifacts in DW images when fat suppression pulses such as Spectral Attenuated Inversion Recovery (SPAIR) and Spectral Presaturation with Inversion Recovery (SPIR) fail. While fat rim is easier to detect in routine Cartesian encoding DW images, the presence of residual fat signal is a challenge for radially acquired sequences as the fat rim is shifted radially, leading to blurring in the reconstructed images. Alternatively, Dixon fat suppression can be applied at the cost of some increase in TR and scan time. Dixon is a robust fat suppression method that estimates the fat signal instead of suppressing it [53,54]. Specifically, in a recent work [55], Dixon is successfully combined with PROPELLER; thus, could be implemented to improve fat suppression in RoSA.

While the RoSA relies on the similarity feature in diffusion imaging, its image reconstruction is model-free, which is independent of diffusion models or underlying assumptions. Because of high popularity, DTI was presented in this work. Nevertheless, RoSA supports all diffusion analyses including parametric diffusion modeling [24,56–58] and non-parametric q-space approaches [22,23,59,60]. A feature in RoSA is that the more diffusion directions, the better the reconstruction, as a smaller window size can be achieved and DW images become more correlated. This feature is consistent with the current trend of diffusion MRI where larger numbers of directions are desired. Notably, 60–80 diffusion directions are recommended in [62], and the human connectome project (HCP) standardized 90-direction schemes [61].

Conclusion

RoSA offers high resolution and high image quality with more than a 10-fold improvement in imaging efficiency. The imaging speed is achieved by utilizing similarities in neighboring DW images, whereas the high image quality is achieved by the nature of short-axis EPI blade and composite reconstruction. The RoSA approach is versatile and compatible with various diffusion analyses or modeling approaches. In addition, as a 2D acquisition technique, it has the flexibility of being combined with simultaneous multi-slice acceleration approaches.