Applying allometric theory to fungi

Introduction

Fungi are prominent components of every ecosystem—in terms of biomass, diversity and functioning. However, in contrast to many other taxonomic groups, we have a poor mechanistic understanding of the patterns in fungal community organization and functioning. To address this gap, a growing number of researchers are beginning to characterize fungal diversity in terms of traits that explain how fungi respond to and influence the environment (Crowther et al., 2014; Aguilar-Trigueros et al., 2015).

In this paper, we argue that body size is a trait that, although historically ignored in mycology, could be a major axis for understanding the biology of fungi. Our argument is based on the fact that fungi vary considerably in size, ranging from single-celled microscopic organisms to one of the largest living organisms on earth (Smith et al., 1992). Thus the scaling of fungal traits to body size or its proxies is likely to capture a wealth of valuable baseline information about the ecology and functioning of those species.

To support our argument, we draw on advances in plant and animal ecology that apply allometric theory (that is, scaling relationships between traits and total body size) as a valuable conceptual framework. Allometric theory was originally used to understand developmental and evolutionary patterns (Bonner, 2011), but it has since been used to explain ecological phenomena (for example, Brown et al., 2004).

Although allometric theory has been applied to ecological phenomena, it has yet to be adopted in fungal biology. In this paper, we lay the foundations of the approach and point out how this theory could be adapted to understand the causes and consequences of size variation in the fungal kingdom, particularly to filamentous fungi. We do this by (i) outlining the conceptual basis behind allometric theory; (ii) addressing the methodological challenges as well as implications of applying such theory to fungi; and (iii) characterizing the allometric scaling of fungal metabolic rate to body size as a prominent example in allometric scaling. While we focus on the scaling of metabolic rate to body size because of its importance in predicting ecological relationships, we consider metabolic scaling as a springboard for that discussion that could lead to testing other scaling relationships in fungal biology in general.

Definition of allometry and the scaling of metabolic rate

In biology, allometry is traditionally understood as the scaling of trait variation to body size (Bonner, 2011). This emphasis on body size relies on two main observations: First, living organisms vary in total body size during their ontogeny as well as during their evolution, which has resulted in shifts in body size within each kingdom. Second, there is a strong correlation between body size and multiple relevant ecological and physiological traits. The mechanisms behind these relationships to body size depend on the trait, but they combine physical and biochemical constraints (Peters, 1983) as well as adaptive evolution (Glazier, 2010).

In most cases, traits change disproportionally to body size. This is expressed as

Power function of body size:

or equivalently as:

Body size specific trait:

or equivalently as:

where Y is the trait, M is the body size (usually in units of weight or volume), a is a coefficient of proportionality, and the power b is the scaling (allometric) factor (Niklas, 2004), which in many cases deviates from 1 (that is, disproportionality; see Supplementary Figure S1 for representation of each expression). Determining the value of this scaling factor represents the core of allometric research, as it reflects the physiological and ecological constraints to variation in body size in living organisms (Glazier, 2010). Traits that have been shown to scale allometrically to size in animals and plants include growth rate, metabolic rate, strength, life span, population density, competitive ability, and elemental incorporation rate, among others (Brown et al., 2004). Although many traits are likely to scale with organismal size, we consider determining metabolic scaling of fungi a first step in introducing allometric research to fungal biology, given its connections with many other performance characteristics.

Metabolic rate is expected to increase less proportionally to body size based on geometric arguments: metabolic rate depends on the surface area available to deliver nutrients and oxygen to each cell of an organism's body, but surface area increases only correspond to a two-thirds increase in size. In contrast to this geometric expectation, empirical tests of metabolic scaling on diverse organisms commonly report higher scaling factors. There have been numerous explanations for these deviations. For example, it has been proposed that as plant and animals increase in size, they achieve higher surface area than expected for their size, resulting from their developing complex respiratory and circulatory systems (Bonner, 2011).

Further, the metabolic theory of ecology proposes that as body size and metabolic rate account for the amount of resources and energy an organism needs, its scaling controls other ecological processes, from the individual to the ecosystem level (Brown et al., 2004). As initially formulated, this theory postulates that the metabolic scaling to body size should follow a common scaling factor of ¾.

Recent reviews have challenged some of the tenets of the metabolic theory of ecology. As more and better data are collected from a greater diversity of organisms, it has been shown that there is a large variation in scaling factors (for example, Makarieva et al., 2005; DeLong et al., 2010). It has also been pointed out that that metabolic rate may both affect and be affected by other biological and ecological processes, and thus causality cannot be determined (Glazier, 2015).

Fungi, a major group of eukaryotes, have not been considered in the development of metabolic theory of ecology, neither during its conception nor its later refinements over the last two decades (as Glazier (2010) points out). To address this important gap, in the next section, we develop a roadmap for applying allometric theory to fungi.

A roadmap for allometric scaling for fungi

Defining fungal size

Ideally, a measurement of size should capture the total amount of matter and space that the body of an organism occupies at a particular point in time. In allometric research, body size is usually measured as biomass, either directly or—for convenience—using different proxies for particular groups: biovolumes or protein contents for unicellular organisms (Makarieva et al., 2005), or length measurements of body axes (for example, diameter, height) in plants and animals (for example, Peters, 1983; Niklas, 2004). Given that most fungi display indeterminate growth, final body biomass can be methodologically challenging to ascertain. This challenge may have contributed to the failure to incorporate allometric theory into fungal ecology (and vice versa). A promising approach is to use determinate growth stages of fungi, such as sporocarp measurements (biomass, height, diameter) in a way analogous to plants and animals (Pringle et al., 2015). However, sporocarp formation (prevalent in a small group of fungal species), represents a very limited fungal life stage.

To address this shortcoming, we propose defining fungal body size using measurements of vegetative mycelial colonies. Although the hyphae are the basic units of filamentous fungi, we believe that a colony-level focus is useful because (i) the colony represents the most prevalent fungal body state because soon after an individual hypha forms, it branches profusely, then anastomoses and finally coordinates growth and flow of nutrients to form complex tissue (Moore et al., 2011); (ii) in many cases, fungal colonies can be distinguished from one another by observing them on the surface of substrates such as plant tissues, soil and litter layers, and wood, to name just a few. For example, colony biomass accumulated after a given amount of time represents the closest proxy of body size as it has been applied to other organisms (see Fuentes et al., 2015). In addition, we advocate scaling to other various measures of colony size such as ‘colony hyphal length’, ‘colony extension rate’ or ‘hyphal branching’, all of which represent valuable metrics to infer the ecology of fungi. For example, colony hyphal length (analogous to total root length in plants) better represents the earlier stages of the fungal body, and might be more representative of the type of growth observed in substrates like soils (sparse colony composed of connected hyphae). Colony extension rate represents a useful indication of how rapidly a fungal colony captures new space. Although it cannot provide information about biomass allocation per unit area, a species that extends at 1 mm per day necessarily has a greater potential to accumulate biomass and area than does a species that extends at 1 mm per year. Last, hyphal branching rate within a colony is generally a stronger predictor of biomass per unit area. Extensive hyphal proliferation within a colony generally represents a trade-off against mycelial extension within a colony (Moore et al., 2011), as the allocation of energy towards extending hyphal tips restricts the capacity for intra-colony growth. Therefore, although these growth metrics will have very different (even opposing) relationships with other functional traits, all of them are likely to provide viable options in the search for scaling relationships in fungal ecology.

Trait scaling to colony size measurements

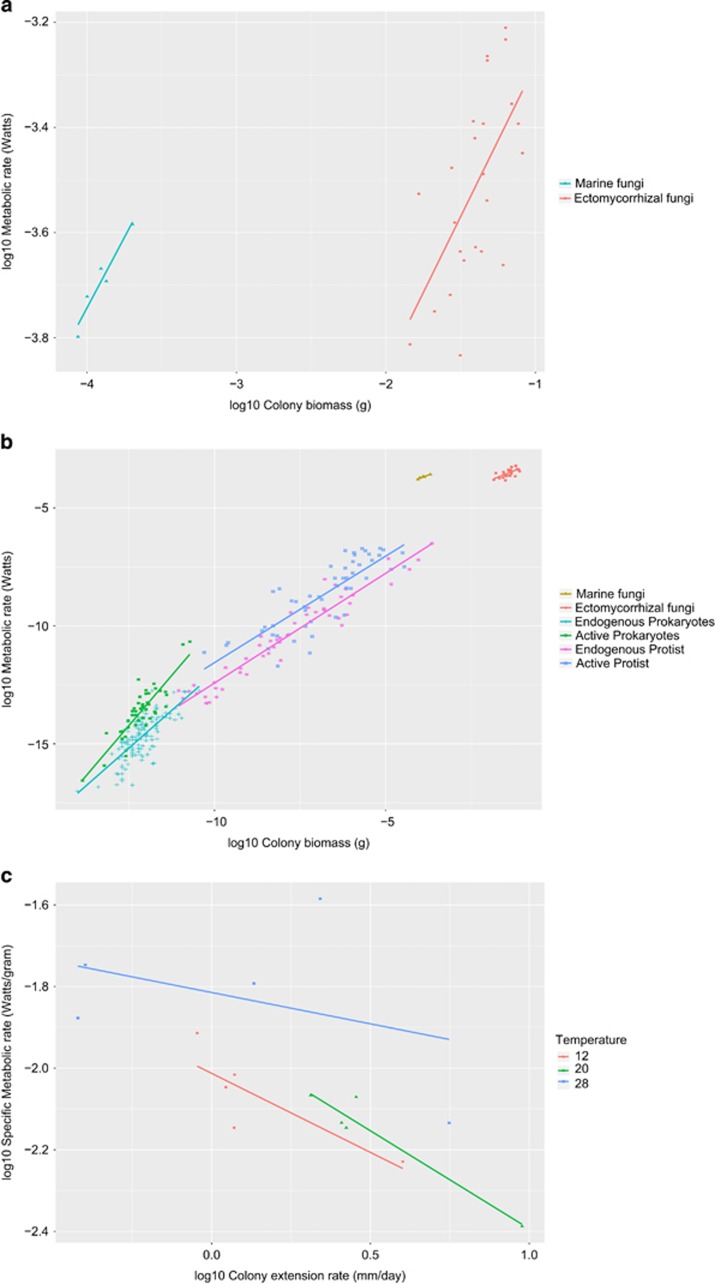
To illustrate how colony size measurements can be used in allometric research, we scaled metabolic rate to colony biomass accumulation and colony extension rate. Data for the scaling of metabolic rate to colony biomass were obtained from three studies: Fuentes et al. (2015) of five marine filamentous fungi; and two studies of ectomycorrhizal fungi: Wilkinson et al. (2012a) of eight species and Wilkinson et al. (2012b) with four species and four genotypes each (see Supplementary Material for details on data collection). These papers were chosen because they reported measures of metabolic rates (that is, respiration rates) and colony biomass of different fungal species on single individual colonies growing at constant temperature and with similar concentrations of glucose as a carbon source.

For visual comparison, we plotted the fungal data together with the data on metabolic scaling of bacteria and protozoa reported by DeLong et al. (2010). These data correspond to a synthesis of measurements of metabolic rates taken under laboratory conditions (such as the fungal data), and included metabolic rates of cells in starvation (known as ‘endogenous metabolism’, corresponding to maintenance energy expenditure using internal energy reserves), as well as cells in the presence of a nutrient source (referred as ‘active metabolism’, corresponding to growth energy expenditure), each of which are known to scale differently with size (Makarieva et al., 2005).

The scaling relationships we obtained were similar for both marine and ectomycorrhizal fungal data sets (b=0.58±0.15 for ectomycorrhizal fungi and 0.53±0.09 for marine fungi, P=0.001 and 0.009, respectively), as reported in Table 1 and Figures 1a and b. These values are very low when compared with those obtained by DeLong et al. (2010), who report supralinear relationships for endogenous and active metabolism for bacteria and nearly linear relationships for protists (both endogenous and active metabolism as well). These findings indicate that while bacteria and protists can simultaneously sustain larger size and higher metabolic rates, fungal colonies are more metabolically constrained (that is, metabolic rates increase very slowly compared with increases in colony size). This pattern is congruent with the growth kinetics of fungal colonies (Moore et al., 2011): metabolism is concentrated on the colony margin, meaning that the core (and older) sections of the colony slow their metabolism as they exhaust resources, expanding their search for nutrients to their surroundings.

Table 1. Scaling parameters between body mass and metabolic rate among different groups of fungi and other microorganisms.

Taxon group	Log(a) (±s.e.)	Scaling factor (b) (±s.e.)	r2	P-value	Sample size (number of species)	Data source
Scaling to biomass accumulation
Ectomycorrhizal fungi (20º)	−2.7 (0.21)	0.58 (0.15)	0.39	0.001	24	(Wilkinson et al., 2012a,2012b)
Marine fungi (20º)	−1.6 (0.35)	0.53 (0.09)	0.92	0.009	5	(Fuentes et al., 2015)
Endogenous protists (20 °C)	−3.12 (0.30)	0.93 (0.04)	0.92	2.2 × 10−16	52	(DeLong et al., 2010)
Active protists (20 °C)	−2.53 (0.59)	0.90 (0.08)	0.69	3.35 × 10−14	51	(DeLong et al., 2010)
Endogenous prokaryotes (20 °C)	0.76 (1.29)	1.27 (0.10)	0.55	2.2 × 10−16	121	(DeLong et al., 2010)
Active prokaryotes (20 °C)	7.02 (1.83)	1.7 (0.15)	0.75	2.91 × 10−14	44	(DeLong et al., 2010)
Scaling to radial extension rate
Saprotrophic fungi (12º)	−2.01 (0.04)	0.62 (0.15)	0.67	0.087	5	(Crowther and Bradford, 2013)
Saprotrophic fungi (20º)	−1.91348 (0.04)	0.53 (0.07)	0.92	8.96 × 10−3	5	(Crowther and Bradford, 2013)
Saprotrophic fungi (28º)	−1.81469 (0.09)	0.85 (0.21)	0.14	0.52	5	(Crowther and Bradford, 2013)

The proportionality constant ‘a’ and the scaling factor ‘b’ were calculated as the slope of the log–log relationship between body mass and metabolic rate for ectomycorrhizal and marine fungi, bacteria and, protozoa; or corresponding to the log–log relationship between metabolic rate and colony extension rate for saprotrophic fungi (using ordinary least square regression). Standard errors for each parameter are given in parenthesis. Data on ectomycorrhizal fungi were standardized to 20°C following DeLong et al. (2010) (The sample size of the ectomycorrhizal data also include different genotypes of the same species, see Supplementary Information for further details on data, transformations and calculation of parameters).

Figure 1.

Metabolic scaling to body size (biomass) of different groups of organisms. Scaling parameters for the regression lines are presented in Table 1. (a) Metabolic scaling to colony biomass for five species of marine fungi and 11 strains of ectomycorrhizal fungi; (b) comparison of the fungal metabolic scaling with the ones of bacteria and protists at two metabolic states; (c) scaling of specific metabolic rate to colony extension rate for a set of five species of saprotrophic fungi. Different colors and symbols represent different groups and metabolic states. Regression lines were fitted using ordinary least squares method.

We believe ours represents the first attempt to synthesize scaling relationships of metabolic rate to body size among groups of fungi and to directly compare these relationships to other taxonomic groups. We note, however, that the comparisons should be seen just as hypothesis generators as there are three major limitations in their interpretation. First, the fungal data sets are small (comprising relatively narrow body size range), which increases the error when calculating the scaling factor (White and Seymour, 2005). Second, the data sets correspond to different growing conditions: marine fungi were measured on liquid media, while ectomycorrhizal species were grown on a cellophane surface adjacent to nutrient source. Such differences in conditions can influence biomass production and metabolic rate and represent confounding factors in our analysis. Third, although fungal metabolic rate in the data sets was measured in older colonies that were likely not expanding, it cannot be ruled out that some growth was still taking place. Thus, the distinction between endogenous and active metabolism is unclear.

The metabolic scaling to colony extension rate of five saprotrophic fungi revealed the slightly higher allometric trends as observed in total colony biomass (Table 1). Scaling factors at the three temperatures varied from 0.62±(0.15) at 12 °C to 0.53±0.07 at 20 °C to 0.85±0.2 (±s.e., r²=0.67 P=0.08, r²=0.92, P<0.001, r²=0.14, P=0.52, respectively). The higher metabolic rates obtained could be due to the fact that these fungal colonies were only 10 days old at the time the biomass and respiration rates were measured (in contrast to 28-days old colonies for the ectomycorrhizal data set), or the use of highly nutritious media compared with the other studies, which, together with the narrow sample size, limits the interpretation of these results. However, when plotted as mass-specific metabolic rate, this scaling would suggest that fungi that capture a larger area in a given amount of time more efficiently consume resources than do fungi that are able to capture less area in the same amount of time. This makes intuitive sense, and considering that resources available for most fungi are ephemeral (for example, decaying matter), it showcases that, in principle, colony extension rate is a biologically relevant metric for allometric scaling in fungi, as it relates directly to the total amount of space and resources to which fungi can access in a short amount of time. Such patterns and rationale have parallels with traditional allometric theory and highlight the value of scaling relationships to colony extension rate.

Further steps: data collection and interpretation

As observed in the previous section, more data on larger sets of fungal diversity are greatly needed to determine scaling relationships in fungi. Colony size measurements from fungal culture collections represent a good starting point because they would allow for easier comparisons using standardized protocols. This lab-based approach is analogous to greenhouse studies for body size and dark-respiration for plants (Reich et al., 2006) and lab-based measurements of basal metabolic rate in animals (the metabolism of fasting, inactive animals), which have been used for years in allometric research (Peters, 1983, Kolokotrones et al., 2010). These data should include measures of active rates (that is, fungal colonies expanding through a given substrate), and endogenous rates (that is, fungal colonies that have ceased growth and exhausted nutrients).

These lab-based data could be directly used to understand the causes, mechanisms and consequences of variation in size among ecologically different sets of fungi. These data would allow us to determine the maximum size (for example, in terms of length or biomass) that a fungal colony can reach without losing its integrity; identify the major morphological–physiological challenges fungal colonies experience when attaining such size; or identify variation in metabolic scaling depending on fungal ontogeny or ecological guild. For example, (Glazier, 2010), argues that the metabolic rate of fungi is expected to scale proportionally (scaling factor of 1) with fungal size because of the high surface area that filamentous growth allows. We argue that such scaling is likely to happen in the initial stages of fungal development, when the surface area of single hypha is in direct contact with the environment, but as hyphae start to form dense and compact mycelia as a colony, deviations from proportionality are more likely.

We believe that measurements taken in the laboratory represent a solid foundation for understanding allometric relationship in fungi. Once these data are obtained, further studies could recalibrate the lab-based patterns to the real world. Then, these scaling patterns can be linked to measurements of fungal size in the field (as grams or centimeters of fungi per unit of substrate) to predict the energy consumption rates of fungi in nature. Smith et al. (1992) is a good example of size determination in the field, where measurements of grams of hyphae per volume of soil were used to estimate the biomass of fungal individuals (identified with genetic markers) occupying a given area. Thus, determining the predictive power of lab-based scaling to the real world requires combining multiple approaches from detailed observational studies to mathematical modeling, as is the case for any other successful attempt in ecology to link mechanistic laboratory studies to real ecological patterns.

Conclusion

It is intuitive that trait expression in fungi varies drastically at the largest scales of dissimilarity: massive, multicellular mycelia have a greater potential for resource capture, enzyme production, carbon mineralization and toxin production than do microscopic, single-celled yeasts. Thus, we argue that trait scaling to fungal body size represents a useful tool to understand trait variation in fungi. We believe that as more and better data on fungal size is produced, fungal scaling would allow us to infer a wide range of ecological characteristics that relate to the community ecology (for example, competitive ability) and functional capacity (for example, carbon mineralization rate) of fungi simply by estimating the growth rates or biomass production of those species relative to those of others. This might prove to be a valuable tool, with the potential to trigger a sea change in our understanding of fungi. Further exploration of these allometric relationships is essential to identify which functional characteristics show consistent scaling relationships—and at what scales. Ultimately, given the intrinsic linkages between fungal growth traits and overall metabolic rate, we propose that allometric scaling relationships might represent a promising platform to expand the use of trait-based approaches within fungal ecology. We hope we have provided a case for why size matters for fungi.