Distinct Protein Hydration Water Species Defined by Spatially Resolved Spectra of Intermolecular Vibrations

Abstract

In this molecular dynamics simulation study, we analyze intermolecular vibrations in the hydration shell of a solvated enyzme, the membrane type 1–matrix metalloproteinase, with high spatial resolution. Our approach allows us to characterize vibrational signatures of the local hydrogen bond network, the translational mobility of water molecules, as well as the molecular entropy, in specific local environments. Our study demonstrates the heterogeneity of water properties within the hydration shell of a complex biomolecule. We define a classification scheme based on the vibrational density of states that allows us to distinguish separate classes of hydration water species and facilitates the description of hydration water properties at distinct hydration sites. The results demonstrate that no single characteristic of the protein surface is sufficient to determine the properties of nearby water. The protein surface geometry, quantified here by the number of protein atoms in the vicinity of a hydration water molecule, as well as the chemical nature of a solvated protein functional group, influences dynamic and thermodynamic properties of solvating water molecules.

Introduction

The hydration of biomolecules is the subject of many experimental and theoretical studies, which aim to investigate the role of water for the stability and dynamics of enzymes, other proteins, nucleic acids, complexes, aggregates, and even lipid bilayers.¹⁻⁷ However, of particular interest are also the consequences of hydration for the properties of water molecules in the hydration layer itself.⁸⁻¹²

Hydration-induced changes in the aqueous solvent are manifold and occur on different length and time scales.^13,14 The structure of the hydrogen bond network has been shown to be affected by the solvation of a biomolecular interface only over short distances, corresponding roughly to a single hydration layer.¹⁵ Similarly, short-ranged effects are typically reported for so-called single particle dynamics, describing average dynamics of single water molecules, such as self-diffusion, rotational relaxation, and localized vibrational motion.^14,16 On the other hand, longer-ranged effects have been observed for collective properties, i.e., propagating vibrational modes in the hydrogen bond network, for which protein-induced effects have been observed on a 10 Å length scale.^17,18 Further, electrostatic interactions were observed to induce long-ranged orientational order of water molecules, in particular at low or zero ionic strength.^19,20

To some degree, it is justified to consider the hydration shell, in particular the first hydration layer, as part of a biomolecule.²¹ Many proteins or nucleic acids retain integral water molecules and parts of their first hydration layer even in dry environments, for example in crystals. The positions of the most strongly bound water molecules can then be observed by x-ray diffraction.^2,22,23 The importance of the first hydration layer is also evident when enzymes are transferred into non-native anhydrous environments, e.g., organic solvents, for industrial applications. For this purpose, the enzymes can be trapped kinetically in their natively folded structure.^24,25 In the anhydrous environment, the enzymatic activity is often observed to improve significantly if the remaining water content is sufficient to form a complete first hydration layer.²⁴

The temperature dependence of protein dynamics has also been shown to depend strongly on the surrounding hydration water. The so-called dynamical transition, as observed in quasi-elastic scattering experiments, dielectric spectroscopy, and in simulations, has been shown to occur only in the presence of water, and to occur simultaneously in the protein and its surrounding solvent.²⁶⁻³⁰

Further, hydration water is involved as a reacting species or catalyst in enzymatic reactions³¹ and it is generally involved in any biomolecular reaction that involves a binding event as an initial step. Binding requires the partial desolvation of the associating molecules and a corresponding change in the solvation free energy, which contributes to the thermodynamic driving force.

Predicting the properties of biomolecular hydration water without explicit simulation remains a challenge due to the very heterogeneous properties of the protein–water interface.²³ Known concepts for the solvation of small hydrophilic or hydrophobic solutes can be misleading, as very few portions of a protein surface are purely hydrophilic or hydrophobic.³² Large numbers of distinct functional groups are often found within a close range and the topological properties of the protein surface also play a significant role.¹⁴ Clefts and indentations are commonly found as well as protruding side chains or functional groups. However, relatively smooth planar surfaces persist as well. Therefore, hydration water properties are highly context dependent.

Here, we employ explicit solvent molecular dynamics simulations to study the hydration water of membrane type 1–matrix metalloproteinase (MT1-MMP), a proteolytic endopeptidase of the larger MMP family with proteolytic activity toward one or more extracellular matrix proteins, such as collagen, fibronectin, or laminin. MT1-MMP has been shown to promote cell migration,³³ as well as many pathological conditions, including arteriosclerosis, inflammations, rheumatoid arthritis, and cancer invasion/metastasis.³⁴⁻³⁶ It is therefore an important drug target, however, the systemic importance of enzymes in the MMP family and high structural similarities of their respective active sites, have impeded the design of effective, yet specific inhibitors without severe side effects.

Some natural and synthetic substrates have been found to inhibit the activity of MMP by binding to the active site,³⁷ but they all exhibit serious side effects due to insufficient selectivity.³⁸

A previous study indicated, that hydration water might play an important role for the enzymatic activity and/or molecular recognition at the MMP active site.^39,40 Further, the catalytic center includes a charged zinc ion, which is directly involved in the reaction mechanism and interacts with nearby water molecules.

This particular enzyme, therefore offers a variety of chemically distinct hydration sites, which we study in atomistic detail in our simulations. We utilize a spatially resolved analysis protocol, which allows us to study the properties of hydration water molecules in local environments. Our results show that the properties of hydration water vary significantly, even for hydration sites in very close proximity to each other. We characterize dynamic and thermodynamic properties of water in these hydration sites using expressions derived from the vibrational density of states (VDOS) of intermolecular vibrations, which provides rich information on the local chemical environment.

We use this information to identify distinct classes of water molecules in the hydration shell of the protein, which feature distinct dynamical and thermodynamical properties.

Our general insights, as well as the proposed classification scheme, may facilitate future studies of hydration water properties in heterogeneous solvation environments, as well as improve our general understanding of protein hydration.

Methods

Simulation Protocol

The MT1-MMP protein consists of 582 amino acid residues. The primary protein domains include the signal peptide (1–20), the pro–peptide (21–112), catalytic domain (114–287), hinge domain (285–318), and hemopexin-like domain (367–582).⁴¹ The inactive zymogen (proMT1-MMP) is activated by the removal of the pro–peptide, via proteolytic cleavage between TYR112 and ALA113.⁴² The hemopexin-like domain plays a functional role in substrate binding and in interactions with the tissue inhibitors of metalloproteinases (TIMPs).⁴³ In this study, we used the activated catalytic domain of MT1-MMP, whose structure was obtained from the protein databank (1BUV)⁴⁴ and contains coordinates from ILE114 up to SER287 at the C-terminus. The complexed TIMP inhibitor contained in this structure was removed prior to our simulations. The structure of the simulated MT1-MMP domain is shown in Figure 1. In addition to the 174 amino acids, the structure contains coordinates of two zinc ions (one of which is part of the catalytic center) and two calcium ions. The catalytic domain consists of three α-helices and a five-stranded mixed parallel and antiparallel β-sheet. The β-sheet is enveloped by three surface loops and two α-helices on its convex and concave sides, respectively. The active site of this enzyme contains a conserved zinc binding motif, HEXXHXXGXXH, where the catalytic zinc ion is coordinated by three histidines, i.e., HIS239, HIS243, and HIS249. The second zinc ion plays a role in stabilizing the native structure⁴⁵ and is tetrahedrally coordinated by residues HIS186, HIS201, HIS214, and ASP188. Further, the two noncovalently bound calcium ions are often considered essential for the folding and stability of the enzyme.⁴⁶

Figure 1.

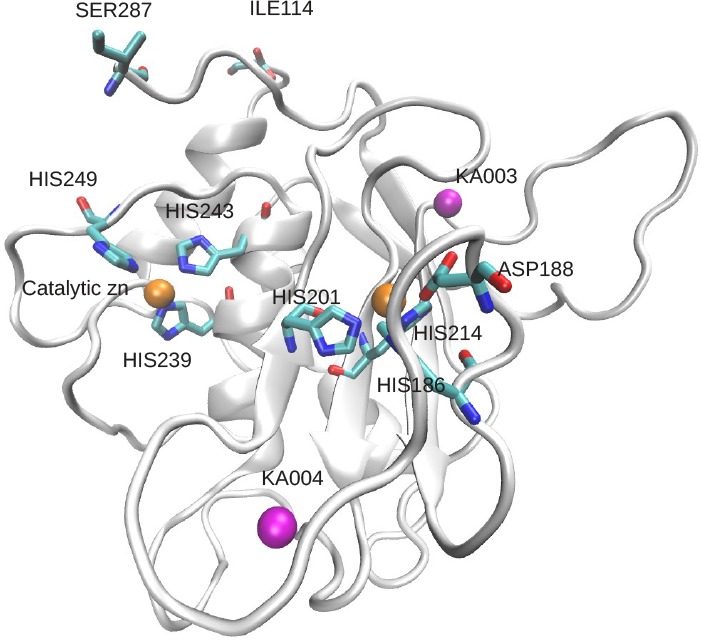
Catalytic domain of MT1-MMP. The side chains of histidines and aspartates complexing the two zinc ions are shown in a stick representation, as well as the C– and N–terminus (element color code: cyan for carbon, red for oxygen, and blue for nitrogen. The protein-bound ions are shown as solid colored spheres, the structural calcium ions in magenta, the catalytic and structural zinc ions is orange.

Prior to the simulation, the protonation states of titratable MT1-MMP residues were predicted for pH 7 based on continuum electrostatics⁴⁷ with the web-based tool H++.⁴⁸ The charge of the protein was then neutralized by the addition of 6 sodium ions within a cubic simulation box with 95 Å edges. Subsequently, the system was solvated with TIP3P water molecules.⁴⁹ The CHARMM-27 force field⁵⁰ was used as a starting point to describe the protein and the ions. Long-ranged electrostatics were treated using the particle mesh Ewald summation⁵¹ using a 1.2 Å real space grid. A 9.0 Å real-space cutoff was used for short-ranged interactions. Corresponding corrections for the energy and pressure were applied.

Molecular dynamics simulations of transition metal ions in enzyme catalytic centers with empirical force fields can provide challenges as the electronic structure of coordinated ions is not correctly represented by the parametrized potentials. The use of simple noncovalent Lennard-Jones and Coulomb interactions with atomic point charges results in an octahedral coordination of the zinc ions,⁴⁵ which contradicts experimental observations.³⁹

This can be circumvented by the inclusion of electronic degrees of freedom in QM/MM calculations,⁵² with accurate polarizable potentials⁴⁵ or via dummy particles carrying the ion charge.⁵³ Here, we followed previous work on the closely related MMP2 enzyme with a comparable catalytic center.⁵⁴

Based on this previous study, we implemented Lennard-Jones interaction parameters and geometric restraints for the first coordination shell of both zinc ions by including corresponding “covalent” terms in the topology of the protein. After a steepest descent energy minimization for 1000 steps, we performed a QM/MM calculation in which the two coordinated zinc ions, the side chains of coordinating protein residues, as well as one coordinating water molecule in case of the catalytic zinc ion, were included in the QM region containing 105 atoms in total. Electronic structure calculations were performed with the PBE0^55,56 density functional and a 6-31G**⁵⁷ basis set. The QM-region was electrostatically embedded into the surrounding environment described by point charges according to the employed force field. All protein atoms and water molecules within 6 Å from the protein were included in the MM-region. Protonation states of remote titratable side chains of the protein were adapted to ensure a neutral MM-region. Point charges for the QM-region were then determined by RESP⁵⁸ fitting based on 400 grid points in the environment of the QM atoms. TURBOMOLE 6.3^59,60 was used for the QM calculations and CHEMSHELL^61,62 for the QM/MM interface. Based on this model, we carried out a molecular dynamics equilibration with harmonic position restraints on the non-hydrogenprotein atoms for 2 ns, followed by an unrestrained simulation of 5 ns. These simulations were carried out in the isothermal–isobaric ensemble at 300 K and 1 bar using a Berendsen weak coupling algorithm⁶³ for the temperature and pressure with a time constant of 1.0 ps. The final structure of this simulation was then again subjected to the QM/MM calculation to determine an updated set of partial charges. This procedure was repeated 11 times to study the variations of the catalytic zinc ion charge for fluctuating geometries of the environment. Notably, we observe significant charge transfer between the nominally doubly charged catalytic zinc ion and its coordinating residues, which results in a fitted zinc ion point charge between +0.65 and +1.05. In Figure 2, we show that the magnitude of the fitted zinc ion charge is highly correlated to the coordination number observed in the following unrestrained 5 ns simulation (see above), obtained from the integral of the radial distribution function for the zinc ion and non-hydrogenatoms up to its first minimum.

Figure 2.

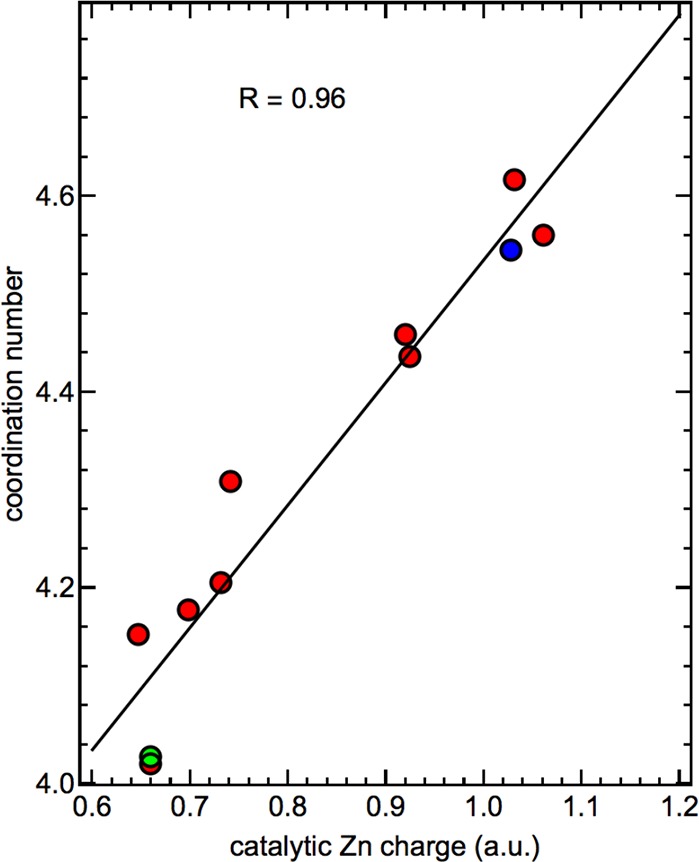
Correlation of the fitted point charge of the catalytic zinc ion based on the QM/MM calculation and the observed coordination number in the molecular dynamics simulation. The systems selected for the following simulations with approximately penta-coordinated (blue) and tetra-coordinated (green) catalytic sites are highlighted. The Pearson correlation coefficient R between the ion charge and its coordination number is 0.96.

We observed roughly two distinct populations within these 11 simulations, one with a very low point charge for the zinc ion between +0.65 and +0.75 and essentially tetrahedral coordination, as suggested by previous experimental studies on this protein prior to binding of a substrate in a time-resolved X-ray absorption (trXAS) experiment.^39,64 The other population is primarily penta-coordinated with a more oxidized charge state between +0.9 and +1.05. We note that equivalent charge fluctuations and correlations with the coordination number are observed experimentally in the aforementioned trXAS studies by a combined analysis of the absorption fine structure (EXAFS) and the zinc K-edge energy^39,64 during the catalytic action of the enzyme.

For our following simulations, we used charge distributions corresponding to both states described above, one with a tetra-coordinated catalytic zinc ion and a charge of +0.65 and one with an approximately penta-coordinated zinc ion and a fitted charge of +1.05. However, the results reported in this study, in particular the thermodynamic properties of water in the environment of the catalytic site, are identical within the statistical uncertainty. Therefore, we only report results for the system containing the tetra-coordinated catalytic zinc ion, which is in better agreement with the zinc coordination of the free enzyme (no substrate bound) obtained in the experiment. We note that penta-coordinated zinc ions have also been reported based on simulations of other enzymes in the MMP family, despite very similar structures of the catalytic site, indicating a delicate balance between both coordination states, which might play a crucial role for the catalytic mechanism.⁵⁴

The simulations of the chosen systems were extended by 100 ns using the Nose–Hoover⁶⁵ thermostat and the Parrinello–Rahman⁶⁶ barostat with time constants of 5 ps to allow for conformational sampling. The RMSD of non-hydrogen protein atoms did not exceed 3.0 Å for both systems indicating no substantial conformational changes. The 100 ns simulations were analyzed with an RMSD-based clustering algorithm to identify the most stable conformational state.⁶⁷ All backbone atoms were taken into account and an RMSD cut-off of 2.0 Å was used to identify distinct conformational substates. The most populated conformation was then used in subsequent simulations with a fixed protein conformation, using position restraints on protein atoms. This allowed for a detailed spatially resolved analysis of hydration water properties for selected regions of the protein–water interface (see below). The restrained simulations were carried out for 40 ns in the canonical ensemble using the Nose–Hoover thermostat as described above. Coordinates and velocities were stored every 8 fs. Trajectories were produced and analyzed in chunks of 2 ns fragments to reduce the amount of temporarily stored raw data.

Analysis

Three distinct cubic regions on the protein–water interface were defined to analyze, in detail, the vibrational and thermodynamic properties of water solvating distinct protein sites. For the analysis, three-dimensional cubic grids were defined and centered on the center-of-mass (COM) of the amino acids PRO220, HIS249, and ASP273. HIS249 is one of the side chains coordinating the catalytic zinc ion, PRO220 and ASP 273 are solvent exposed side chains and represent distinct parts of the protein–water interface. Each grid consisted of 32 × 32 × 32 cubic voxels with an edge length of 0.75 Å. The volume of these grids was chosen to include in addition to the respective central site, the hydration water environment of a representative fraction of the protein–water interface (see Figure 3).

Figure 3.

Representation of the analysis grids: The vertices of individual voxels of the three analysis grids are shown as green (environment of HIS249), red (environment of PRO220), and blue (environment of ASP273) points. The atoms corresponding to HIS249, PRO220, and ASP273 are shown as green, red, and blue spheres, respectively. The water molecules analyzed within the volume grids are shown for a snapshot of the simulations in a stick representation.

For each snapshot of the simulations, we computed the COM of each water molecule and determined whether it is located within the volume covered by one of the analysis grids. In that case, the water molecule was assigned to the voxel in which its COM was located at this time. It therefore contributed to the local number density n(r) in the respective voxel at coordinate r. In addition, its center of mass velocity and angular momenta, projected on each moment of inertia, were recorded for the following 200 snapshots of the trajectory, corresponding to a time window of 1.6 ps. This information was then used to compute the average translational and rotational vibrational density of states (VDOS) of a water molecule in each voxel of the analysis grids, describing the distribution of the kinetic energy of the respective degrees of freedom (DOF) in the frequency domain.

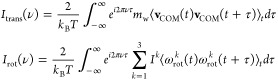1

Here, v_COM describes the velocity of the center of mass a water molecule with mass m_w, ω_rot^k the angular velocity of the molecule around the molecular axis k with corresponding moment of inertia I^k, k_B is Boltzmann’s constant, and T the temperature. The brackets ⟨⟩_t indicate ensemble averages over the simulation time. Integrating the respective VDOS over all frequencies results in the number of involved degrees of freedom, i.e., 3 per molecule.

A rigid water model was used in our simulations. Therefore, no intramolecular vibrations had to be considered. The VDOS includes information on the local short-time diffusion via the zero frequency response for the translational DOF, I_trans(ν = 0) . Likewise, the I_rot(ν = 0) provides information on the rotational diffusion. Further, the VDOS give detailed information on the intermolecular vibrational modes in which the water molecules participate, which include delocalized and collective hydrogen bond bending modes at frequencies below 100 cm^–1, stretch vibrations of the intermolecular hydrogen bond network around 200 cm^–1, and librations around the distinct rotational axes, between 300 and 1000 cm^–1.⁶⁸⁻⁷⁰

Here, we utilize this information in two distinct ways in order to characterize hydration sites at the protein–water interface and to identify distinct hydration water species. We integrate the combined intensities of the translational and orientational VDOS in the frequency windows from 0–100, 100–200, and 300–400 cm^–1 to describe the fraction of the total 6 DOF per molecule contributing to the respective intermolecular modes (DOF_0–100, DOF_100–200, and DOF_300–400, respectively). Hence, this simplified description allows us to quantify changes in the relative contribution of diffusive and delocalized modes, hydrogen bond stretch vibrations, as well as shifts in the libration band, due to interactions with the local environment of a water molecule.

In addition, we utilize a variation of the two-phase thermodynamics (2PT) approach proposed by Lin et al.^71,72 for bulk liquids to describe the average local molecular entropy of water molecules based on the VDOS.

In this approach, applied separately to the translational and rotational degrees of freedom, separate partition functions are constructed for diffusive and vibrational contributions to the molecular water entropy. Diffusive contributions to the translational and rotational VDOS are obtained via a comparison of the zero frequency response of the respective VDOS with the analytic expression for an abstract hard sphere (HS) fluid at the same particle density. Here, we employ the average bulk number density of water to describe the average packing of water molecules in the system, rather than the local number density in each voxel due to variations in the excess chemical potential. The 2PT procedure is a closed expression and free of adjustable parameters. Once the diffusive degrees of freedom are identified, their partition function is described based on analytic expressions for the HS fluid and the rigid rotor (RR) for translational and rotational degrees of freedom, respectively. These partition functions provide analytic expressions for the contribution of diffusive translational and rotational degrees of freedom to the molecular entropy. In addition, analytic VDOS contributions I_trans^HS(ν) and I_rot(ν) can be expressed and subtracted from the total translational and rotational VDOS. This eliminates any zero frequency contributions as well as low–frequency anharmonic relaxations. The VDOS for the remaining degrees of freedom are then described as a continuous distribution of harmonic oscillators (HO). This allows the construction of an analytic partition function and the computation of the corresponding molecular entropy contribution. We employ here the analytical expressions for the quantum mechanical HO model, which however only affects our reported results quantitatively, not qualitatively. This results in the total entropy expression

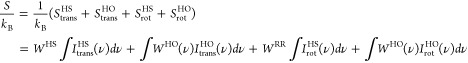2

We note that the 2PT approach does not provide a rigorous expression for the molecular entropy, but an estimation between the limiting cases of an actual HS fluid (high entropy) and a set of fully harmonic oscillators (low entropy). However, the approach has been shown to provide accurate results for several liquids.⁷³ We recently adapted the method as described here to allow for the description of local solvent entropies and found that it also allows accurate estimations of solvation entropies.

The described analysis is carried out for each voxel of the three analysis grids. The sampling time allows us to obtain statistically converged results for all reported properties, despite the high spatial resolution and resulting small volume of the 0.75 Å × 0.75 Å × 0.75 Å analysis voxels (≈1.4% of the volume of a water molecule). The high spatial resolution allows us to capture water properties also in highly localized hydration sites and provides a smooth spatial distribution of all analyzed properties: the local number density n(r), the number of DOF per molecule contributing to the local VDOS in the selected frequency ranges, DOF_0–100(r), DOF_100–200(r), and DOF_300–400(r), the full frequency–resolved VDOS and the local molecular entropy S(r).

Results and Discussion

In order to focus our analysis on water molecules located at favorable hydration sites, we select voxels in our analysis grid with a water number density n greater than 1.2 times the expected bulk value, which corresponds approximately to an excess chemical potential Δμ_ex = −k_BTln(n_local/n_bulk) lower than −0.5 kJ mol^–1.

In Figure 4, we show the distribution of average water entropies obtained from the local 2PT calculation within the studied set of hydration sites.

Figure 4.

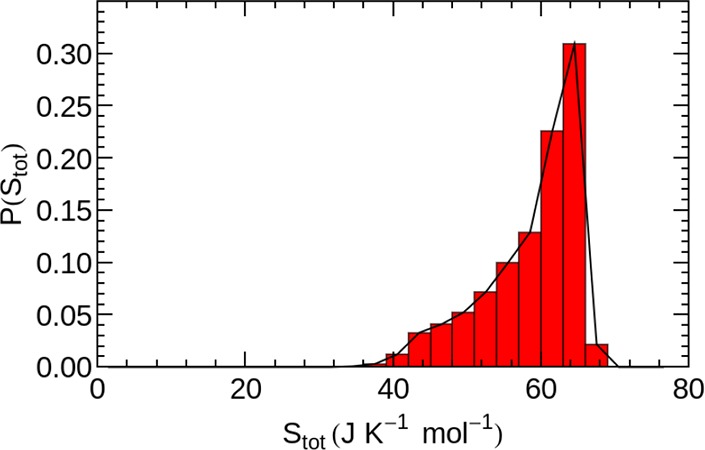
Histogram of the molecular water entropies in all analyzed hydration sites.

The bulk water entropy for the pure liquid has been determined previously using 2PT as 72.5 J mol^–1 K^–174 for the rigid TIP3P water model. Using the localized adaptation of the 2PT method, we identify bulk-like water with an average molecular entropy of ≈66 J mol^–1 K^–1 for distances larger than 7 Å from the closest protein atom.

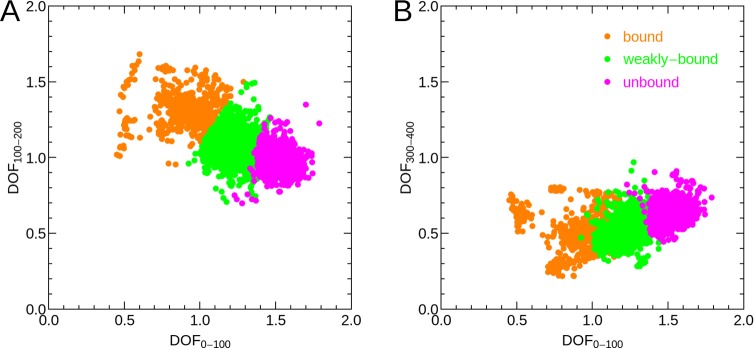
The nonsymmetric shape of the probability distribution of hydration water entropies in Figure 4, indicates the presence of several distinguishable hydration water species. In order to separate distinct hydration water species, contributing to the nonsymmetric distribution, we therefore utilize the information obtained from the partial integrals of the VDOS, i.e., the number of DOF involved in vibrations from 0–100, 100–200, and 300–400 cm^–1. In Figure 5, each VDOS corresponding to a high density hydration site is described by a single point in the 2-dimensional space spanned by two of the partial integrals, DOF_0–100 and DOF_100–200 in panel A and DOF_0–100 and DOF_300–400 in panel B. To separate distinguishable hydration water species, we utilized a k-means clustering algorithm in the 3-dimensional space spanned by the fractional VDOS integrals. The parameter k was set to 3, which resulted in hydration water species with clearly distinct vibrational features and associated entropies as shown below. Larger values for k resulted in pairs of hydration water species with qualitatively identical properties, which would not allow for an insightful interpretation. However, we note that our particular choice of distinguishing three distinct hydration water species is nevertheless an arbitrary one. The color code in Figure 5 indicates the cluster assignment of each individual hydration water site, which we name “bound”, “weakly bound”, and “unbound” water. The motivation for this categorization is described in the following.

Figure 5.

Scatter plots of partial VDOS integrals representing key vibrational features for the hydration water species and the number of degrees of freedom (DOF) per water molecule contributing to the vibrational spectrum in a given frequency range indicated by wavenumbers (cm^–1) as subscripts. (A) DOF_0–100 vs DOF_100–200; (B) DOF_0–100 vs DOF_300–400. Colors indicate the assignments based on a k-means clustering algorithm with k = 3 to “bound”, “weakly bound”, and “unbound” water.

Panel A of Figure 5 indicates that the largest separation between individual hydration water species is obtained by the number of DOF contributing to vibrations from 0–100 cm^–1, the frequency range including diffusion and low frequency vibrations. In addition, we observe a weak anti-correlation with the number of DOF involved in vibrations from 100 to 200 cm^–1, the typical frequency range for hydrogen bond stretch vibrations. This anti-correlation is not surprising, as a decreased VDOS at low frequencies below 100 cm^–1 must be compensated by an increased VDOS at higher frequencies to conserve the total number of DOF. In other words, the frequency of vibrational modes can shift up or down, but the total number of modes is constant. We identify some outliers from the general distribution, for example for DOF_0–100 ≤ 0.6, which may form a separate hydration species not considered here for simplicity.

Panel B of Figure 5 shows that monitoring DOF_300–400, which is expected to be anti-correlated to blue-shifts of low-frequency librations (i.e., librations relevant for the entropy), is not able to separate uniquely the individual hydration water species. This paramater is therefore less crucial to the separation of hydration water species compared to the integrated number of degrees of freedom at lower frequencies, DOF_0–100 and DOF_100–200.

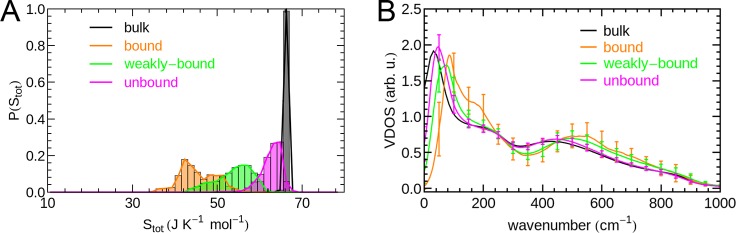
The performance of the separation scheme is indicated by the respective thermodynamic and vibrational properties of the individual hydration water species shown in Figure 6. The molecular entropies of each identified hydration water species result in partially separated distributions in panel A of Figure 6, which are describing the separate contributions to the asymmetric distribution of hydration water entropies in Figure 4. In addition, we observe distinct vibrational signatures in the VDOS averaged over the respective hydration water species in panel B of Figure 6.

Figure 6.

Properties of individual hydration water species. (A) Individual probability distributions of molecular entropies at hydration sites after separation into the individual hydration water species. These are compared to bulk-like water with a minimum distance of 7 Å to the closest protein atom. (B) VDOS of the individual hydration water species obtained from the k-means clustering in comparison to bulk-like water. “Error” bars describe the heterogeneity of vibrational signatures within a given hydration water species.

For the “bound” hydration water, we observe a significant suppression of diffusion and a reduction of low frequency modes below 50 cm^–1. The corresponding molecular entropies are describing the low-entropy tail of the hydration water entropy distribution in Figure 4. In addition, we find a pronounced shoulder in the 100–200 cm^–1 region and a significant blue-shift of librational modes with respect to bulk, which are both indicative of enhanced hydrogen bonding. Hence, the classification of this hydration water species as “bound” water. The standard deviations of VDOS intensities, obtained from averaging over hydration sites belonging to this hydration water species, indicate the heterogeneity of the underlying hydration water species.

For “weakly bound” water, we observe a less pronounced suppression of self-diffusion and low-frequency modes. The shift of these modes results in slightly increased intensities in the VDOS between 100 and 200 cm^–1. However, no additional shoulder indicating increased hydrogen bonding is observed. Compared to bulk-like water, we find a blue-shift of libration modes, which is only slightly less pronounced than for the “bound” water. The latter is described by both, a more pronounced minimum in the VDOS between 300 and 400 cm^–1 (i.e., DOF_300–400), as well as enhanced intensities relative to bulk-like water on the high-frequency tail of the VDOS between 500 and 900 cm^–1. This observation indicates that the libration modes might be more sensitive than the direct hydrogen bond stretch vibration signature between 100 and 200 cm^–1, if the entire shape of the libration band is considered. The increased binding can be the result of increased hydrogen bond strengths between water molecules or of direct binding to the protein surface.

The VDOS of “unbound” water largely resembles bulk water apart from decreased self-diffusion and a weak blue-shift of low-frequency modes. We note that the decrease in the apparent self-diffusion coefficient at zero frequency is also attributable to the presence of an impenetrable protein surface. This reduces the volume that can be explored by water molecules within a given time window, hence reducing the effective diffusion rate. This effect is also contributing to the reduced self-diffusion observed for the other water species, however, in their case also vibrational signatures indicating enhanced binding were observed. This is not the case here, hence the designation as “unbound” water. Not surprisingly, this “unbound” water species includes the high entropy tail of the hydration water entropy distribution in Figure 4 as is apparent from Figure 6A.

The main question we would like to address in this study is, which features of the protein surface determine the properties of solvating water molecules? To answer this question, we analyzed protein coordination numbers of the individual hydration water sites and the relative occurrence of the identified hydration water species in the environment of distinct functional groups of the protein. The results are displayed in Figure 7.

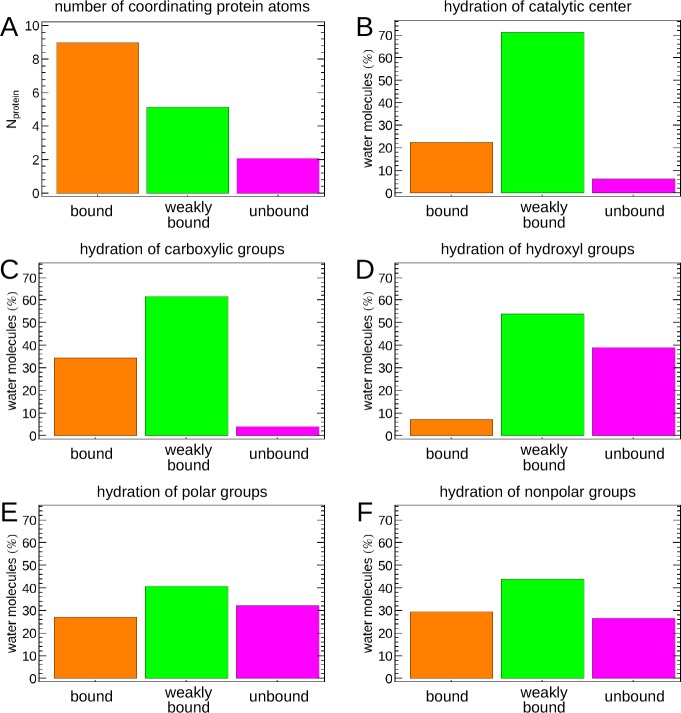
Figure 7.

Chemical context of distinct hydration water species. (A) Average number of non-hydrogen protein atoms within 3 Å of hydration sites corresponding the identified water species; relative abundance of the identified hydration water species within 3 Å of (B) the catalytic zinc ion, (C) carboxylic groups, (D) hydroxyl groups, (E) polar groups excluding carboxyl and hydroxyl groups, and (F) nonpolar groups.

In panel A, we count the number of (non-hydrogen) protein atoms within 3 Å of a given hydration site, described by the position of the corresponding voxel in the analysis grid, and average the result for the various hydration water species. The result clearly reveals that the average coordination by protein atoms is inversely proportional to the molecular entropy of water of the respective hydration water species. Consequently, “bound” water molecules featuring a low molecular entropy are surrounded by ≈9 protein atoms, indicating interactions with multiple functional groups. “Weakly bound” water molecules interact with approximately 5 protein atoms within a 3 Å distance, while “unbound” water molecules with an almost bulk-like entropy only interact with 2 to 3 protein atoms on average.

Based on the results shown in Figure 7A, one could draw the conclusion that the coordination by protein atoms, i.e., essentially the curvature of the hydrated protein surface (negative/concave curvature: indentations and cavities; positive/convex curvature: protuberances), is dominating the properties of hydration water molecules, such as the entropy and the spectrum of intermolecular vibrations studied here. To investigate this effect in more detail, we have studied the relative probability of finding each of the three distinct hydration water species within 3 Å of various protein functional groups in panels B–F of Figure 7. In addition, the spatial distributions of the respective hydration water species in the vicinity of the studied functional groups is illustrated in Figure 8.

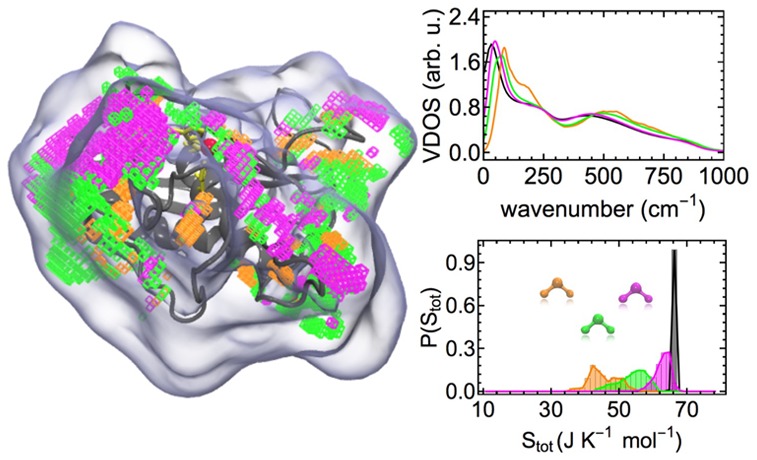
Figure 8.

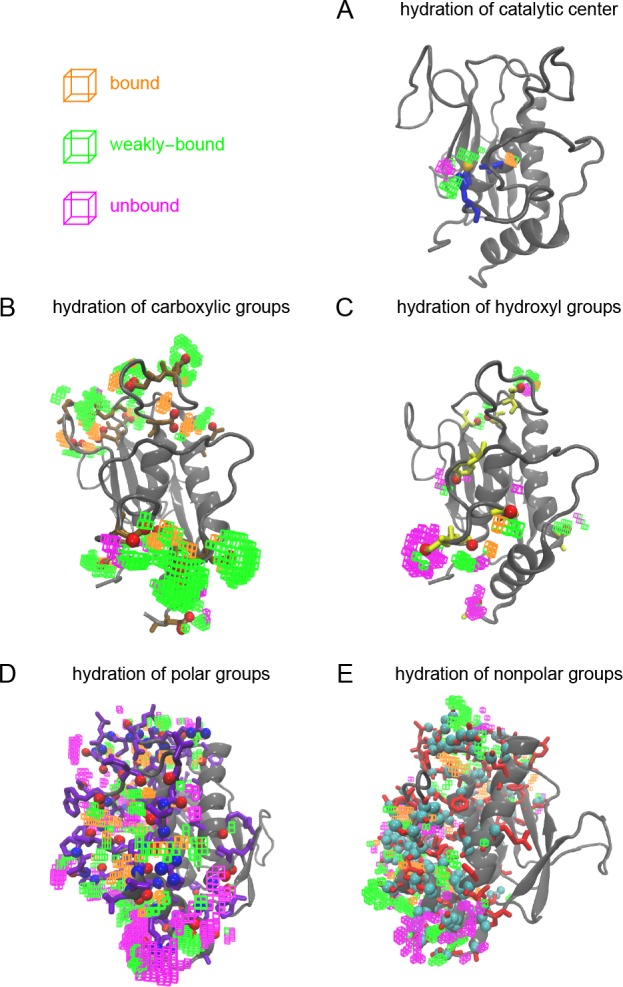
Hydration sites within 3 Å of distinct functional groups and their assignment to distinct hydration water species.

Our findings show that no hydration water species can be assigned to a single functional group. Instead, all three hydration water species are found in the vicinity of each protein functional group, albeit in varying relative amounts. The catalytic center of the MMP stands out with the largest relative abundance of “weakly bound” water. This finding may be surprising compared to previous simulation results that analyzed the dynamical properties of water solvating MT1-MMP.³⁹ In these earlier studies, the most pronounced slow-down of hydrogen bond rearrangement dynamics is found in the vicinity of the catalytic site due to strong ion–water binding.³⁹ However, we note that these earlier simulations did not account for charge transfer effects between coordinating histidines and the ion. In our present study, we observe a substantial decrease of the net zinc ion charge due to coordination by the surrounding histidines in Figure 2, which weakens the ion–water interactions. However, “unbound” water molecules are essentially absent in the catalytic site. The “bound” and “weakly bound” hydration sites that are found instead, share a reduced local entropy relative to bulk water. Upon binding of a substrate or inhibitor to the catalytic site, a large fraction of these water molecules will be released into the bulk resulting in an increase in entropy. However, at the same time they will lose favorable interactions with the protein and the zinc ion, which are responsible for the observed low entropies. Further, when discussing the role of water molecules for potential ligand binding free energies, it is relevant to distinguish solute–solvent and canceling solvent–solvent/solvent reorganization contributions to the enthalpy and entropy.^75,76 Therefore, we note that information on the entropy of water solvating the catalytic site of MMP is insufficient to determine their role for the binding affinity of substrates or ligands, despite the previously stated argument regarding the increase in entropy upon substrate binding and water repulsion.

The properties of hydration water in the environment of carboxylic groups are similar to water solvating the catalytic center. However, the fraction of “bound” water is significantly higher. Carboxylic groups form very strong hydrogen bonds with solvating water molecules, which result in the pronounced vibration at 200 cm^–1 observed in their respective VDOS, as well as low entropies. Both properties are characteristic for “bound” water as we define it here. Similar to the vicinity of the catalytic center, the “unbound” hydration water species is essentially absent close to carboxylic groups.

Interesting is the comparison of hydroxyl groups, polar groups (i.e., amino groups and carbonyls of the backbone, not including the separately analyzed carboxyl and hydroxyl groups), and nonpolar groups. In each case, substantial numbers of “unbound” water are observed, in addition to “bound” and “weakly bound” water molecules. The fraction of “bound” water is higher for polar (nonhydroxyl/noncarboxyl) groups compared to hydroxyl groups. We find these species primarily localized at hydrogen bonding sites of solvent-exposed backbone carbonyls, which form well-defined hydrogen bond acceptor sites. Only non-hydrogen atoms of the protein were restrained in our simulations. Hence, the O–H bonds of hydroxyl groups were allowed to rotate around the axis of the C–O bond. The optimal hydrogen bond acceptor and donor sites are hence less localized and water molecules in a respective volume will exhibit a mixed character, resulting in a more likely classification as a “weakly bound” species in average, explaining this observation.

However, also water in the vicinity of nonpolar functional groups features an increased fraction of “bound” water relative to hydroxyl groups, although nonpolar groups are not able to bind water molecules themselves. Naively, one would expect primarily “unbound” water molecules in the vicinity of such groups. Alternatively, one might assume the formation of clathrate structures around hydrophobic groups. However, we do not observe structural evidence for such an effect. Instead, the observation of “bound” water is the result of the location of these groups. Nonpolar groups are less likely to be found fully exposed to the aqueous solvent. Instead they are likely to be located in weakly solvated crevices of the protein surface, where hydrating water molecules are interacting with a multitude of additional functional groups. This is apparent in Figure 8, where “unbound” water is found in the environment of solvent-exposed nonpolar groups, however, various forms of bound water are found for hydrated, but buried nonpolar sites.

Conclusions

Our analysis highlights the heterogeneous character of the protein hydration shell, due to variations of the protein surface curvature and the different chemical nature of solvent-exposed functional groups. Nevertheless, we are able to identify distinct classes of hydration water species, based on their thermodynamic and vibrational signatures. Heterogeneity persists within some of these hydration water species, in particular for strongly bound species (“bound” water), as indicated by the standard deviations of VDOS intensities averaged over individual hydration sites in Figure 6B.

However, the distinct hydration water species exhibit unique vibrational signatures, which reflect the shape of their local potential energy surface and can be used to predict some of their properties. “Bound” water molecules feature essentially zero diffusion (i.e., I(ν = 0), Figure 6), a shoulder at 200 cm^–1 indicating increased hydrogen bonding and blue-shifted librations. The increased number of protein atoms in the environment of the “bound” water species (Figure 7A) limits the mobility of these water molecules and is therefore at least partially responsible for the absence of self-diffusion on time scales considered here. Consequently, molecular entropies are significantly reduced compared to bulk water with 40–50 J mol^–1 K^–1 (Figure 6) as determined within the spatially resolved 3D–2PT approach employed here.

For the “weakly bound” water species, we observe an onset of diffusivity and an increase of the molecular entropy relative to bound water to 50–60 J mol^–1 K^–1. No significant increase in intensity is observed for the 200 cm^–1 shoulder of the VDOS compared to bulk water, which is characteristic for hydrogen bond stretch vibrations. However, librational modes feature a significant blue-shift.

The highest entropy and diffusivity is observed in absence of both features. Diffusive translational motion in “unbound water” remains slowed down relative to bulk water due to the volume occupied by the protein, which is inaccessible for water diffusion. However, no vibrational signatures of increased binding interactions are observed in the VDOS of this water species. The entropy of “unbound” water molecules is found to be between 55–65 J mol^–1 K^–1, which is close to the bulk-like water entropy of ≈66 J mol^–1 K^–1 for water molecules >7 Å away from the protein.

Matching trends are observed for hydration water self-diffusion and the local molecular entropy, providing insights into the relationship between dynamics and thermodynamic properties, in particular entropy. The apparent correlation is not too surprising, as the diffusion coefficient, i.e., the intensity of the VDOS at zero frequency, plays an important role in the construction of the thermodynamic expression in the employed 2PT methodology. Beyond this fact, low-frequency vibrations are generally expected to provide a major contribution to the entropy due to the thermal accessibility of excited vibrational states (k_BT ≥ hν for T = 300 K and ν/c ≤ 200 cm^–1). Hence, it is clear that changes in the VDOS for the lowest-frequency intermolecular vibrations, including the zero-frequency response, must have a profound effect on the entropy. A relation between self-diffusion and entropy is also supported by previous work on bulk atomic liquids, for which even a quantitative universal scaling law has been derived that relates the diffusion coefficient to the excess entropy.⁷⁷

The identification of different classes of hydration water is an important step toward generalized descriptions of a protein hydration shell, which may allow improved predictions of hydration water properties without explicit simulation in the future.

Our results show, that individual hydration water species cannot be uniquely assigned to certain solvated functional groups on the protein surface. For example, we do not find unique features for water molecules solvating carboxylic groups or the catalytic center of the studied MT1-MMP protein, despite the presence of particularly attractive interactions of water with these groups due to their high charge density. Instead, we find varying distributions of all hydration water species in the vicinity of distinct functional groups. These distributions are understood as a combined result of interactions with one or more specific solvated functional groups and the geometrical constraints imposed by the solvated protein surface for the mobility of the water molecules and their hydrogen bond network. These geometrical constraints can be described qualitatively by the surface curvature or the number of coordinating protein atoms.

All factors are furthermore not independent from each other. Functional groups found at solvent-exposed sites with a positive surface curvature are more likely to be hydrophilic than nonpolar or hydrophobic. Hence, hydrophilic functional groups of a protein are more likely to feature hydration sites, whose properties are primarily determined by the interactions with them. Instead, nonpolar or hydrophobic groups are more likely to be less exposed to the solvent and to be part of concave sections of the protein surface. Hydration sites of nonpolar groups are therefore in average likely to interact also with other functional groups or to be geometrically trapped by surrounding protein atoms. In a reverse argument, areas of the protein surface with negative curvature (concave) are more likely to feature nonpolar groups than areas with a positive surface curvature (convex).

An additional factor regarding the solvation of functional groups of a protein is their propensity to be part of an intramolecular hydrogen bond network stabilizing secondary structure elements. This is in particular relevant for carbonyl and amine groups of the protein backbone, which are hydrophilic, but often secluded from the protein surface due to their role in secondary structure motifs. As a consequence, they are relatively inaccessible to the solvent or only partially solvated with the most favorable hydration sites being blocked. They become solvated primarily in unstructured loop regions of the protein.

These considerations are important when analyzing the average hydration properties of various functional groups, as we have done in this study. On the other hand, to predict properties of water at a given hydration site, it is clear that knowledge of the chemical nature of the closest solvated group is insufficient. In this case, the surface curvature, i.e., the number of other functional groups in the environment, needs to be considered, as well as potential interactions with them. Additional factors may include local electrostatic fields, determined by the charge distribution within the protein, which may affect water at a longer range. Quantifying these factors and their influence on hydration water properties, dynamical properties and entropy as studied here, as well as local potential energies and resulting free energies, will be the subject of future investigations.

The authors declare no competing financial interest.