Bayesian 2-Stage Space-Time Mixture Modeling With Spatial Misalignment of the Exposure in Small Area Health Data

Abstract

We develop a new Bayesian two-stage space-time mixture model to investigate the effects of air pollution on asthma. The two-stage mixture model proposed allows for the identification of temporal latent structure as well as the estimation of the effects of covariates on health outcomes. In the paper, we also consider spatial misalignment of exposure and health data. A simulation study is conducted to assess the performance of the 2-stage mixture model. We apply our statistical framework to a county-level ambulatory care asthma data set in the US state of Georgia for the years 1999–2008.

1. INTRODUCTION

Respiratory diseases such as asthma, chronic obstructive pulmonary disease (COPD), and bronchitis are important health problems in the United States. In 2008, it was estimated that more than 23 million Americans have asthma and approximately 13 million adults have COPD (Centers for Disease Control and Prevention 2008; Pleis, Lucas, and Ward 2009). In addition, respiratory diseases have a high cost in medical expenses. For example, the annual cost of asthma associated with medical expenses was estimated at about $50.1 billion in 2007 (Centers for Disease Control and Prevention 2011). Thus, finding the risk factors of respiratory diseases is important to policy-makers and program planners wishing to reduce incidence.

Numerous epidemiologic studies have found the risk factors that showed significant association with asthma, which is a common chronic disease in the US, about 1 % of all ambulatory visits (Dockery and Pope 1994; Ponka and Virtanen 1996; Eisner et al. 2001; Ellison-Loschmann et al. 2007). For example, socioeconomic and ethnic characteristics such as income and African–American race have been linked with greater risks of asthma (Eisner et al. 2001; Ellison-Loschmann et al. 2007). Elevated concentrations of air pollutants (e.g. particulate matter and ozone) have been shown to be associated with increased incidence of asthma (Stieb et al. 1996; Lin et al. 2002, 2008; Sheppard 2003).

Recently, the study of the association between PM_2.5 known as fine PM (ambient particles less than or equal to 2.5 μm in diameter) and asthma has received much attention in public health studies (e.g. Friedman et al. 2001; Sheppard 2003). However, most researches have been conducted using time-series analysis in specific locations because PM_2.5 data are available only in the limited locations. In addition, PM_2.5 concentrations and asthma data are collected over space and time so the relative risks of asthma may have space-time dependence structures and the association between PM_2.5 exposure and asthma may vary across space and time. Thus, spatiotemporal analysis of the association between PM_2.5 exposure and asthma is important and necessary.

In most environmental health effects studies, relative risk within the fixed space and time period is modeled using a linear function of air pollutants and covariates as well as space-time random effects. The coefficients of risk factors are constructed in various ways depending on the modeling approach (e.g. constant, space-varying, or space-time varying coefficients). Along with this coefficient structure, the relative risk model includes a function of space-time random effects (Bernardinelli et al. 1995; Xia, Carlin, and Waller 1997; Knorr-Held and Besag 1998; Knorr-Held 2000; Mugglin, Cressie, and Gemmell 2002; Richardson, Abellan, and Best 2006; Tzala and Best 2008). A commonly used approach (global modeling) has space, time, and space-time interaction random components in risk, and each random component explains the overall risk effect over their space-time domain (Knorr-Held 2000). However, temporal risk effects, for instance, can vary within the space-time domain, and a subset of spatial areas can have a homogeneous temporal profile in risk. In this situation, global modeling is not appropriate because it has the restrictive assumption of common risk effects across all areas.

Recently, Lawson et al. (2010) developed Bayesian space-time latent models using mixture structures in order to capture the heterogeneous temporal profiles of relative risks in space-time health data. They also proposed the use of entry parameters in the space-time mixture (STM) model for the estimation of the number of the underlying temporal risk patterns. Choi et al. (2011) evaluated the performance of STM models in terms of a range of measures and also compared space-time Dirichlet process mixture models with the STM models. They found that STM models are better than Dirichlet process mixture models in terms of recovery of spatial clustering of temporal profiles and how well they estimate the true number of latent temporal components.

When incorporating space-time varying risk factors such as air pollution and socioeconomic factors in space-time health modeling where space-time random effects are included, confounding bias problems may arise (Reich, Hodges, and Zadnik 2006; Ma, Lawson, and Liu 2007; Hodges and Reich 2010; Paciorek 2010). For example, air pollution varying spatiotemporally may be correlated with the space-time random effects so the confounding bias in estimating the effects of air pollution on health outcomes can appear in the model. However, there are a few statistical studies related to this bias problem in spatial models (Clayton, Bernardinelli, and Montomoli 1993; Hodges and Reich 2010; Paciorek 2010). In the STM models, space-time varying risk factors on health outcomes may be correlated with the locally varying temporal risk patterns so it can be difficult to exactly estimate both the effects of the risk factors on the outcomes and the underlying temporal components. This suggests that more studies are needed to better estimate the covariate effects and the space-time mixture structures.

In this paper, we introduce a new Bayesian 2-stage space-time mixture model to reduce confounding bias, which provides better estimates of the association between exposure to fine PM and health outcomes as well as the underlying temporal components. This method first obtains residuals from the covariates-only model and then using these residuals as input, a space-time mixture structure is fitted to find the locally different temporal components. From the estimation of the mixture structure and covariate information, the effects of covariates on health outcomes are finally estimated. We evaluate this approach using a simulation study in terms of recovering the coefficients of covariates and latent components. We also compare the 2-stage mixture model with the full space-time mixture model where relative risk is expressed as both a function of covariates and a space-time structure, in order to investigate how they bias the estimated health risks and they estimate the number of latent components. We conduct an analysis of the relationship between ambulatory care visits for asthma and exposure to PM_2.5 and socioeconomic factors. Since we have different sources of PM and health data, a “change of support” problem needs to be considered (Gotway and Young 2002; Banerjee, Carlin, and Gelfand 2004; Fuentes et al. 2006). Thus, we consider a space-time model for PM_2.5 to provide county-level estimates of PM_2.5, which allows for the estimation of the effects of fine PM on asthma outcomes. This work presented here is the first attempt to consider confounding bias problems in space-time models and then gain better estimates of the coefficients of space-time varying covariates and the true latent components, by introducing a 2-stage mixture model.

The remainder of this paper is organized as follows. In Section 2, we describe the asthma data, air pollution data, and socioeconomic data used in this study. In Section 3 we present the space-time PM_2.5 model and the 2-stage space-time mixture model. In Section 4 a simulation study is performed to verify the performance of the 2-stage space-time mixture model in comparison with the full space-time mixture model. In Section 5, the data analysis results from the 2-stage mixture model proposed are provided. Finally, a general discussion of our approach is provided in Section 6.

2. DATA DESCRIPTION

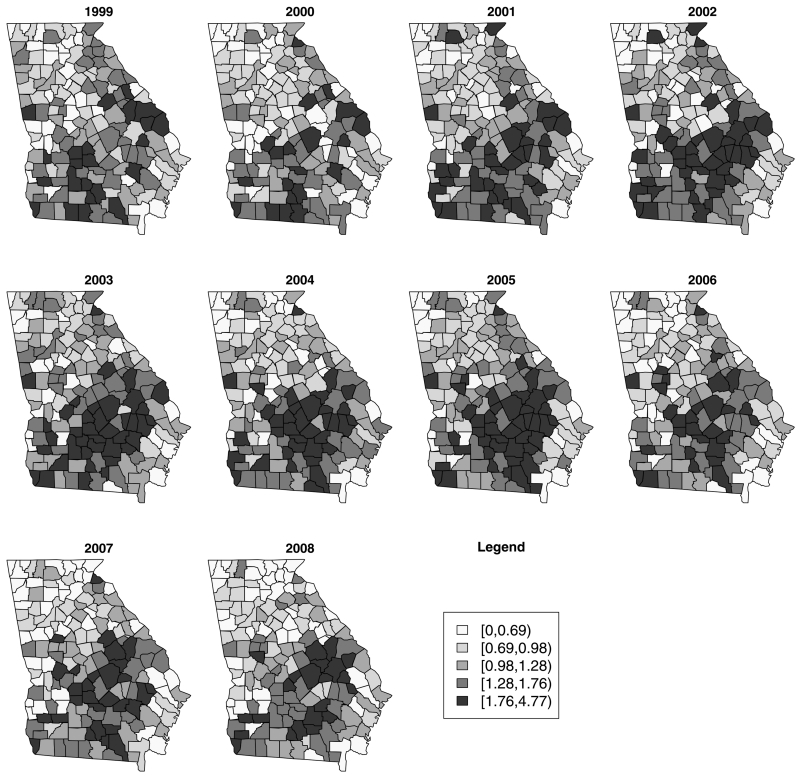
In the paper, we use county-level counts of ambulatory case sensitive asthma in the state of Georgia USA, for the year 1999 to 2008, which were obtained from the Georgia health information system OASIS (http://oasis.state.ga.us/), Georgia Division of Public Health. There are 159 counties and 10 time periods (years) in the available data. We used standardization to provide expected counts within counties for each time period. The expected count was calculated by using the internal standardization method (Banerjee, Carlin, and Gelfand 2004) based on the statewide population-based rate. Figure 1 displays the standardized incidence ratios for asthma for each year where the standardized incidence ratio is defined as the count of asthma divided by the expected count. Overall, the standardized incidence ratios are high in the south-east areas of Georgia over years.

Figure 1.

Standardized incidence maps for county-level ambulatory sensitive asthma in Georgia for individual year.

We use a PM_2.5 data set where PM_2.5 is the air quality standard set by the U.S. Environmental Protection Agency (EPA). The PM_2.5 data set from the Federal Reference Method (FRM) monitoring network was used. There are 31 monitoring stations in Georgia for the period 1999–2008. Originally, PM_2.5 concentrations were measured either every day, every third day, or every sixth day and the yearly averaged PM_2.5 values at each station were used in this study. Figure 2(a) presents the map of PM stations and Figure 2(b) shows the temporal plots of PM_2.5 for the selected two stations. Two stations have the decreasing temporal patterns of PM_2.5, but the station located in the urban area (A) has high PM_2.5 concentrations over time. As covariates in PM modeling, we also consider yearly averaged weather variables such as temperature (°F), dew point temperature (°F), and wind speed (miles per hour to tenths) from the U.S. National Climate Data Center. The coverage of th monitoring stations reflects the population concentrations and is relatively sparse in the more rural areas. This means that interpolation of effects will lead to less variation in estimated mean level in such areas.

Figure 2.

(a) Map of PM_2.5 monitoring stations. (b) Temporal trends of PM_2.5 for the selected locations (A and B).

County-level socioeconomic census data for year 2000 and estimated data for the other years are obtained from the Area Resource File (ARF) from the U.S. Department of Health and Human Services (http://arf.hrsa.gov). The ARF is a collection of county-level data sets from more than 50 sources such as American Hospital Association, American Medical Association, National Center for Health Statistics, and US Census Bureau. It contains a wide range of information and includes county level geographic information, socioeconomic, and environmental characteristics. Based on previous study and considering the availability of county-level data, the variables we considered as relevant predictors are: the proportion of black people (the black or African American population divided by total population), median household income (unit: $1000), and unemployment rate, as covariates in the health model (Castro et al. 2001; Eisner et al. 2001; Ellison-Loschmann et al. 2007). Unemployment rate data is also available at the US Bureau of Labor Statistics (http://www.bls.gov).

3. MODELS

Our environmental health framework has two main parts due to a “change of support” problem.

• (1)First part (space-time PM_2.5 model): we estimate the county-level PM_2.5 concentrations, which are used as the input for the health model in the next part.
• (2)Second part (2-stage space-time mixture model as a health model): we investigate the association between asthma and exposure to PM_2.5 as well as the estimation of temporal risk profiles.
  • (i)First-stage under the Second part: the covariate effects in the health model are only estimated.
  • (ii)Second-stage under the Second part: a space-time mixture structure in the residuals from the first-stage is estimated, and the covariate effects are re-estimated, allowing for the space-time random effects.

This two-part approach is the type of ‘Directional’ Bayesian approach (Fuentes and Raftery 2005), mainly used for computational reasons. Gelman (2004) presented the computational and practical benefits for this plug-in approach in comparison to a joint model. Unlike a joint model, the approach does not allow the health data to influence the air pollution modeling, which might be seen to be a reasonable approach. Therefore, the posterior distributions are obtained separately at each part. Of course, measurement error in the plug-in estimates can accommodate some of the biases. In addition, in the second part, a 2-stage space-time mixture model is proposed to gain better understanding about the covariate effects on asthma as well as space-time mixture structures.

3.1. Spatio-Temporal Model of Exposure

We consider a space-time model of PM_2.5 introduced by Fuentes et al. (2006) and Choi, Fuentes, and Reich (2009). We assume that PM_2.5(s_m, t_j) is the yearly averaged PM_2.5 concentration at station s_m (m = 1, …, M) and time t_j (j = 1, …, J) and is not the “true” PM value because of measurement error. Thus, the PM_2.5 model is given by

$${\mathrm{PM}}_{2.5}({\mathbf{s}}_m,t_j)=Z({\mathbf{s}}_m,t_j)+{ϵ}_1({\mathbf{s}}_m,t_j),$$

where Z(s_m, t_j) is the unobserved “true” PM process at space s_m and time t_j and ${ϵ}_1({\mathbf{s}}_m,t_j)\sim N(0,{\sigma }_1^2)$ is the measurement error. We model the true process Z(s_m, t_j) as

$$Z({\mathbf{s}}_m,t_j)={\mu }_z({\mathbf{s}}_m,t_j)+{ϵ}_2({\mathbf{s}}_m,t_j),$$

where μ_z(s_m, t_j) is the mean function and ${{ϵ}_2}^T=\left({ϵ}_2^T\right({\mathbf{s}}_1),\dots ,{ϵ}_2^T({\mathbf{s}}_M\left)\right)$, where ${ϵ}_2^T\left({\mathbf{s}}_m\right)=\left({ϵ}_2\right({\mathbf{s}}_m,t_1),\dots ,{ϵ}_2({\mathbf{s}}_m,t_J\left)\right)$, has a multivariate normal distribution with mean zero and space-time covariance function Σ_Z. The mean function μ_z(s_m, t_j) can be modeled with coordinates or meteorological variables. In this study, the mean function is assumed to be μ_z(s_m, t_j) = W^T (s_m, t_j)η_Z, where W(s_m, t_j) is a vector of coordinates (longitude and latitude) and meteorological variables (temperature, dew point temperature, and wind speed) with corresponding coefficient vector η_Z. Based on exploratory analysis and previous research (Choi, Fuentes, and Reich 2009), we use the separable space-time covariance ${\Sigma }_Z={\sigma }_e^2{H}_s\left(\varphi \right)\otimes H_t\left(\rho \right)$ where ⊗ denotes the Kronecker product. The matrix H_s(ϕ) is M × M with (H_s(ϕ))_mm′ = exp (−ϕ||s_m − s_m′||) and H_t(ρ) is J × J with ${\left(H_t\right(\rho \left)\right)}_{{\mathit{jj}}^{\prime }}={\rho }^{\mid t_j-t_{j^{\prime }}\mid }∕(1-{\rho }^2)$, where ϕ ~ Unif(0.01, 20) and ρ ~ Beta(1, 1), that is, uniform on (0,1).

The posterior estimate of true PM_2.5 at unobserved site s₀ and time t_j is calculated using Markov Chain Monte Carlo (MCMC) algorithms from the posterior predictive distribution of Z(s₀, t_j) given the observed information,

$$p\left(Z({\mathbf{s}}_0,t_j)\right)=\int p\left(Z({\mathbf{s}}_0,t_j)\mid {\mathrm{PM}}_{2.5},\mathbf{M},{ϴ}_z\right)p({ϴ}_z\mid {\mathrm{PM}}_{2.5},\mathbf{M})d{ϴ}_z,$$

where Θ_z is a set of all parameters included in the PM model, and ${\sigma }_1^2$ and ${\sigma }_e^2$ have uniform prior distributions (Gelman 2006). The “true” PM_2.5 of county i at time t_j of interest (Z_ij) is defined as

$$Z_{\mathit{ij}}=\frac{1}{\mid B_i\mid }{\int }_{B_i}Z({\mathbf{s}}_m,t_j)d\mathbf{s},$$ (3.1)

where B_i is the spatial domain within a county i. The estimate of Z_ij ($Z_{\mathit{ij}}^{\ast }$) is the average of estimates of true PM_2.5 at selected locations within a county i from a regular grid (about 2900 locations over the entire state of Georgia) at time t_j. We could consider block Kriging or MC integration for estimation of Z_ij. We have chosen the latter for convenience as this can be achieved by averaging simulated point level predictions at random locations within each county. We have found this approach to be reasonably accurate compared to block Kriging in preliminary evaluation studies.

3.2. Health Model: 2-Stage Space-Time Mixture Modeling

In space-time epidemiological studies, little is known about the impact of space-time random effects on the health effect of spatiotemporally varying covariates. Commonly used approach to the space-time association between covariates and human health outcomes is a Poisson regression model where risk is modeled as a linear function of covariates and space-time random effects. However, this full space-time modeling may cause confounding problems, not distinguishing the effects of covariates from unmeasured space-time random effects. In space-time mixture modeling, it is important to estimate the effects of covariates as well as the space-time mixture structure. Thus, we propose a 2-stage space-time mixture model. The value of this model lies in the ability to provide estimates of spatial disaggregation of risk while also providing good overall description of risk variation (Lawson et al. 2010).

Denote the count of disease in the ith area at the t_j th time period as y_ij, where i = 1, …, I and j = 1, …, J. We make the conventional assumption that y_ij follows a Poisson distribution as

$$y_{\mathit{ij}}\sim \mathrm{Pois}\left(e_{\mathit{ij}}{\theta }_{\mathit{ij}}\right),$$

where e_ij is the observed expected count and θ_ij is the relative risk.

In the first-stage, the effects of covariates (PM_2.5 and socioeconomic factors) are only considered in the log-relative risk model:

$$\log {\theta }_{\mathit{ij}}={\alpha }_0+Z_{\mathit{ij}}^{\ast }{\gamma }_{\mathit{ij}}+{\mathbf{X}}_{\mathit{ij}}^T{\beta }_{\mathit{ij}},$$ (3.2)

where α₀ is the intercept parameter. The value $Z_{\mathit{ij}}^{\ast }$ is the estimate of the “true” unobserved county-level PM_2.5 from the exposure model presented in Section 3.1 and the corresponding parameter γ_ij can be considered in various dependence structures. The vector X_ij includes p socioeconomic covariates of area i at time t_j with the corresponding parameter vector β_ij = (β_ij1, …, β_ijp)^T. The parameters γ_ij and β_ij, for example, can be assumed to be space-time-dependent structures as follows:

$$\begin{array}{cc}\hfill {\gamma }_{\mathit{ij}}& ={\gamma }_0+{\gamma }_i^1+{\gamma }_j^2,\hfill \\ \hfill {\beta }_{\mathit{ijp}}& ={\beta }_{0p}+{\beta }_{\mathit{ip}}^1+{\beta }_{\mathit{jp}}^2,\hfill \end{array}$$ (3.3)

where γ₀ and β_0p are the overall mean parameters of the coefficients over space and time, ${\gamma }_i^1$ and ${\beta }_{\mathit{ip}}^1$ are the spatially correlated components, and ${\gamma }_j^2$ and ${\beta }_{\mathit{jp}}^2$ are the temporally correlated components.

This covariates-only model provides the estimated relative risk ${\widehat{\theta }}_{\mathit{ij}}$ from the posterior distribution using a Bayesian approach. The residuals using these estimates and the data are calculated as

$${\widehat{r}}_{\mathit{ij}}=\log (y_{\mathit{ij}}∕e_{\mathit{ij}})-\log {\widehat{\theta }}_{\mathit{ij}}.$$

Since there could be greater variability such as space-time mixture structures over the fitted covariates-only model, these residuals are modeled for the overdispersion. In this article, they are used for the estimation of space-time mixture structures.

In the second-stage, we assume that the residual model is

$${\widehat{r}}_{\mathit{ij}}\mid {\widehat{\theta }}_{\mathit{ij}},y_{\mathit{ij}},e_{\mathit{ij}}\sim \mathrm{N}\left({\alpha }_r+{\Lambda }_{\mathit{ij}},{\sigma }_{r_{\mathit{ij}}}^2\right),$$ (3.4)

where ${\sigma }_{r_{\mathit{ij}}}^2$ is the variance and α_r is the intercept to explain the overall difference between the log(y_ij/e_ij) and the estimated log relative risk. The component Λ_ij represents a space-time random effect. Following Lawson et al. (2010) and Choi et al. (2011), the Λ_ij is modeled as a space-time mixture structure:

$$\begin{array}{cc}\hfill {\Lambda }_{\mathit{ij}}& =\sum _{l=1}^L{w}_{\mathit{il}}{\chi }_{\mathit{lj}},\hfill \\ \hfill w_{\mathit{il}}& =\frac{{\psi }_l{w}_{\mathit{il}}^{\ast }}{\sum _l{\psi }_l{w}_{\mathit{il}}^{\ast }},w_{\mathit{il}}^{\ast }\ge 0,\hfill \end{array}$$

where L is assumed to be a large value to estimate the “true” number of latent components. The latent component χ_lj represents the underlying temporal profile in relative risk by specifying a time-dependent structure, and w_il is the corresponding weight at area i. The weight w_il ≥ 0 is the proportion of component l at area i so the sum of all weights for each area should be one and the weight w_il is expressed using unstandardized weight $w_{\mathit{il}}^{\ast }\ge 0$. We model $w_{\mathit{il}}^{\ast }$ as a log-normal distribution with spatially dependent mean ξ_il and variance ${\sigma }_{w_l}^2$

$$\begin{array}{cc}\hfill w_{\mathit{il}}^{\ast }& \sim \mathrm{LN}({\xi }_{\mathit{il}},{\sigma }_{w_l}^2),\hfill \\ \hfill {\xi }_{\mathit{il}}& \sim \mathrm{MIAR}\left({\Sigma }_{\xi }\right).\hfill \end{array}$$

The mean ξ_il has a multivariate intrinsic autoregressive (MIAR) distribution (Gelfand and Vounatsou 2002) with cross-covariance function Σ_ξ, which is a relatively smooth spatial process:

$${\xi }_{\mathit{il}}\mid {\xi }_{i^{\prime }l,i^{\prime }\ne i}\sim \mathrm{N}\left(\frac{1}{N_i}\sum _{i^{\prime }\ne i}{G}_{{\mathit{ii}}^{\prime }}{\xi }_{i^{\prime }l},\frac{1}{N_i}{\Sigma }_{\xi }\right),$$

where G_ii′ = 1 if area i is adjacent to area i′, and G_ii′ = 0 otherwise. Also, N_i = Σ_i′≠i G_ii′ is the number of neighbors of area i. This multivariate spatial process allows for both the spatial dependence structure of the weights and the dependence structure between the different weights given neighboring sites.

The entry parameter ψ_l has a value of 0 or 1 and controls whether the lth temporal component is included in the model or not. If ψ_l = 1, then the łth temporal component is involved in the model. Otherwise, the lth temporal component is not involved in the model. In this study, the entry parameter is assumed to have a Bernoulli distribution, ψ_l ~ Bern(0.5), where 0.5 is a fair value (probability of the inclusion/exclusion of the entry parameter is 1/2).

By fitting the residual model in Equation (3.4) the estimated temporal components and weights (${\widehat{\chi }}_{\mathit{lj}}$ and ${\widehat{w}}_{\mathit{il}}$) are obtained. We adjust the temporal components using the intercept α_r, ${\widehat{\chi }}_{\mathit{lj}}^{\ast }={\widehat{\alpha }}_r+{\widehat{\chi }}_{\mathit{lj}}$, to improve the estimation performance. These estimates along with covariate information are used as the input in the final model expressed as

$$\log \left({\theta }_{\mathit{ij}}\right)={\alpha }_0+Z_{\mathit{ij}}^{\ast }{\gamma }_{\mathit{ij}}+{\mathbf{x}}_{\mathit{ij}}^T{\beta }_{\mathit{ij}}+\sum _{l=1}^L{\widehat{w}}_{\mathit{il}}{\widehat{\chi }}_{\mathit{lj}}^{\ast }+{\eta }_{\mathit{ij}},$$ (3.5)

where α₀, γ_ij, and β_ij are parameters for estimation and have the same structures as those of the covariates-only model in Equation (3.2). The random component ${\eta }_{\mathit{ij}}\sim \mathrm{N}(0,{\sigma }_{\eta }^2)$ is the uncorrelated space-time interaction term which is not captured by the estimated space-time mixture structure (${\widehat{\Lambda }}_{\mathit{ij}}$) presenting the locally varying temporal profiles in relative risk. This restricted Poisson regression model provides the final estimates for α₀, γ_ij, and β_ij, which are our main focus.

To conduct the spatial allocation of the temporal components in the 2-stage space-time mixture model, a post-processing method based on the posterior distributions of the weights is considered. The spatial cluster indicator C_i (= 1, …, L) is defined as

$$C_i=\arg \underset{l}{\max }\left\{w_{\mathit{il}}\right\}.$$ (3.6)

This indicator C_i has the label index of the temporal component with the largest weight value in area i. Thus, a subset of areas within the space-time domain is assigned to one of the temporal components included in the model, which represents the principal temporal profile of the area in relative risk.

In the covariates-only model in Equation (3.2) and the restricted regression model in Equation (3.5), the prior distributions of the intercept and the overall mean parameters in the coefficients are specified as ${\alpha }_0\sim \mathrm{N}(0,{\sigma }_{{\alpha }_0}^2)$, ${\gamma }_0\sim \mathrm{N}(0,{\sigma }_{{\gamma }_0}^2)$, and ${\beta }_{0p}\sim \mathrm{N}(0,{\sigma }_{{\beta }_{0p}}^2)$. We use an intrinsic autoregressive (IAR) distribution for the spatial components ${\gamma }_i^1$ and ${\beta }_{\mathit{ip}}^1$ (Besag, York, and Mollie 1991) that corresponds to a univariate spatial process (L = 1) in the MIAR distribution. The temporal components ${\gamma }_j^2$ and ${\beta }_{\mathit{jp}}^2$ are assigned to be random walk Gaussian distributions. All the standard deviation parameters in the models have uniform prior distributions (Gelman 2006). For both models, the likelihoods are defined as

$$\begin{array}{cc}\hfill p(\mathbf{y}\mid {ϴ}_1)& =\prod _{i=1}^I\prod _{j=1}^J\mathrm{Pois}(y_{\mathit{ij}}\mid e_{\mathit{ij}},{\alpha }_0,{\gamma }_{\mathit{ij}},{\beta }_{\mathit{ij}}),\hfill \\ \hfill p(\mathbf{y}\mid {ϴ}_3)& =\prod _{i=1}^I\prod _{j=1}^J\mathrm{Pois}(y_{\mathit{ij}}\mid e_{\mathit{ij}},{\alpha }_0,{\gamma }_{\mathit{ij}},{\beta }_{\mathit{ij}},{\eta }_{\mathit{ij}},{\widehat{w}}_{\mathit{il}},{\widehat{\chi }}_{\mathit{lj}}^{\ast }),\hfill \end{array}$$

where Θ₁ and Θ₃ are the sets of the parameters in the covariates-only model and the restricted regression model, respectively. Based on the likelihood and the prior distributions, the posterior distributions of the parameters Θ₁ and Θ₃ are obtained.

For the residual model in Equation (3.4), the likelihood is derived as

$$p({\widehat{r}}_{\mathit{ij}}\mid {ϴ}_2)=\prod _{i=1}^I\prod _{j=1}^J\mathrm{N}({\widehat{r}}_{\mathit{ij}}\mid {\alpha }_r,w_{\mathit{il}},{\chi }_{\mathit{lj}},{\sigma }_{r_{\mathit{ij}}}^2),$$

where ${\alpha }_r\sim \mathrm{N}(0,{\sigma }_{{\alpha }_r}^2)$ and σ_rij is assigned to be a uniform distribution. The covariance matrix of the MIAR distribution (Σ_ξ) is specified as an inverse Wishart prior distribution, Inv-Wishart((0.01I_L)⁻¹, L) and I_L is the L × L identity matrix. In this study, the temporal component χ_lj has an AR(1) model and each temporal parameter has a beta prior distribution, Beta(1, 1), that is, uniform on (0, 1). Similarly, the posterior distribution of all the parameters Θ₂ is obtained based on the likelihood and the prior distributions. For the estimation of all the parameters in these models, the Gibbs sampling algorithm and the Metropolis adaptive rejection sampling algorithm are implemented. The posterior means are used for the estimation of all the parameters except the cluster indicator C_i while the posterior mode is used for the estimation of C_i because C_i is the nominal value.

An identifiability problem of components in Bayesian space-time mixture modeling can appear because of the invariance of the likelihood under the permutation of the component labels (Stephens 2000; Jasra, Holmes, and Stephens 2005). We assume that the latent components in the proposed model follow temporally correlated structures while the corresponding weights follow spatially correlated structures. Moreover, during MCMC simulation, it could be possible that the components switch labels if multiple chains are used (Choi et al. 2011). In this study, a single chain is used to avoid the label switching problem. We also monitored output from initial runs to check for label switching and found that a single chain did not display switching.

4. SIMULATION STUDY

In this section we perform a simulation study to compare the 2-stage space-time mixture model proposed in the previous section with the full mixture model where risk is modeled as a linear function of covariates and a space-time mixture structure. We examine the performance of the 2-stage mixture model by investigating the capability of recovering the true coefficients and the true space-time mixture structure.

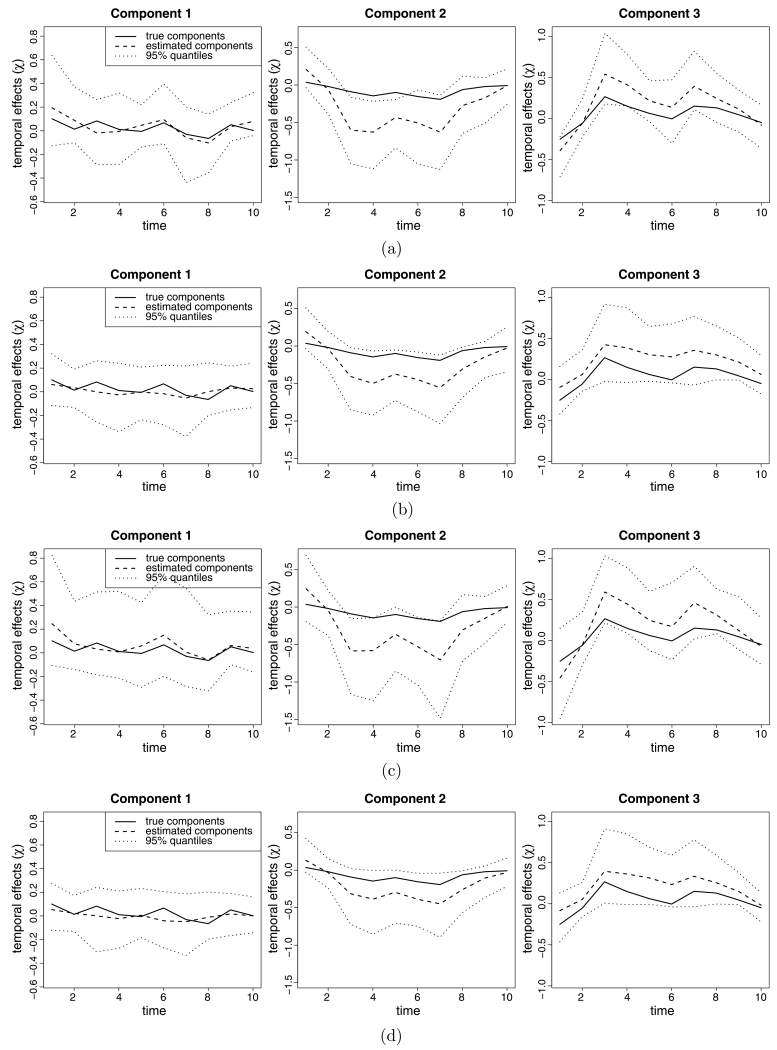
We simulate data under three designs. In all the designs, the 159 counties of the state of Georgia are used as a space domain because there are many counties with similar spatial shapes in Georgia and we conduct real data analysis within this spatial domain in Section 5. As the time domain, J = 10 time points are used. All the designs have L = 3 temporal components and the spatial design of the cluster indicator (C_i) created in Georgia (Figure 3). Each spatial cluster is assigned to one temporal component χ_lj that has an AR(1) structure with the temporal parameter ρ_l and the standard deviance 0.1. To make the components different, the temporal parameters are specified as ρ = (0.9, 0.7, 0.5) and the true temporal profiles are presented in Figure 4.

Figure 3.

Map of the spatial cluster indicator for simulation study.

Figure 4.

(a) Temporal plots from the full mixture model in Design 1. (b) Temporal plots from the 2-stage mixture model in Design 1. (c) Temporal plots from the full mixture model in Design 2. (d) Temporal plots from the 2-stage mixture model in Design 2.

In Design 1, two covariates (X_1ijk and X_2ijk) for county i and time j of the kth simulation data (k = 1, …, K) are considered, where X_1ijk is generated as X_1ijk ~ N(0, 1), independent over space, time, and simulation, and X_2ijk is generated from the IAR prior distribution with the overall variance 1, independent over time and simulation. Thus, X_2ijk has a spatial dependence structure while X_1ijk has no spatial dependence structure. We generate simulated count y_ijk as follows:

$$\begin{array}{cc}\hfill y_{\mathit{ijk}}& \sim \mathrm{Pois}\left(e_{\mathit{ijk}}{\theta }_{\mathit{ijk}}\right),k=1,\dots ,K,\hfill \\ \hfill \log \left({\theta }_{\mathit{ijk}}\right)& ={\beta }_0+{\beta }_1{X}_{1\mathit{ijk}}+{\beta }_2{X}_{2\mathit{ijk}}+{\chi }_{C_i,j}+{\eta }_{\mathit{ijk}},\hfill \end{array}$$

where β₀ = 1, β₁ = 0.05, and β₂ = 0.1. The expected count e_ijk is generated independently from the uniform distribution, Unif(15, 20), and the random effect η_ijk is generated as η_ijk ~ N(0, 0.01²).

For Designs 2 and 3, the true relative risks are assumed to be constant over simulations but the simulated counts are different

$$\begin{array}{cc}\hfill y_{\mathit{ijk}}& \sim \mathrm{Pois}\left(e_{\mathit{ij}}{\theta }_{\mathit{ij}}\right),k=1,\dots ,K,\hfill \\ \hfill \log \left({\theta }_{\mathit{ij}}\right)& ={\beta }_0+{\beta }_1{X}_{1\mathit{ij}}+{\beta }_2{X}_{2\mathit{ij}}+{\chi }_{C_i,j}+{\eta }_{\mathit{ij}},\hfill \end{array}$$

where β’s have the same values with the Design 1, and X_1ij and η_ij are generated from the same scheme as the Design 1. Here, we assume the second covariate X_2ij varies over space and time, and X_2ij is generated from the normal distribution with mean 0 and space-time covariance Σ_X2 = 0.1 Σ_S ⊗ Σ_T, where Σ_S and Σ_T are the covariance matrices of the IAR prior distribution and the AR(1) distribution. Designs 2 and 3 have values of 0.8 and 0.2 for the temporal parameter in Σ_T, respectively.

For each design we generate K = 200 data sets. For each simulated data, we fit two models: the full space-time mixture model and the 2-stage mixture model. We use L = 6 entry parameters in fitting the models because the true number of components is 3 and L = 6 is enough to estimate the true number of components. After fitting the models, we determine whether a temporal component is included in the model using the estimated corresponding entry parameter. If the estimated entry parameter is larger than 0.5, then the component is included in the model. Thus, the estimated number of components included in the model is computed. In addition, the identification of the estimated temporal components with the true temporal components is required when the estimated number of components is three, because the label switching problem can arise (Stephens 2000; Jasra, Holmes, and Stephens 2005). For the allocation of the estimated components and their labels, the mean square error method is used:

$$\widehat{\mathcal{C}}=\arg \underset{l^{\prime }}{\min }\sum _{l=1}^L\sum _{j=1}^J{({\widehat{\chi }}_{l^{\prime }j}-{\chi }_{\mathit{lj}})}^2,$$

where $\widehat{\mathcal{C}}$ includes the labels of the estimated components corresponding to the true components.

For each simulated data set and each model we compute posterior means as point estimates and 95 % intervals for β₀, β₁, and β₂. For the comparison, we use mean absolute error (MAE) and mean absolute error for β_p (p = 0, 1, 2) is calculated as

$$\mathrm{MAE}=\frac{1}{KIJ}\sum _{k=1}^K\sum _{i=1}^I\sum _{j=1}^J\mid {{\widehat{\beta }}_p}^{\left(k\right)}-{\beta }_p\mid$$

where ${{\widehat{\beta }}_p}^{\left(k\right)}$ is the estimate of the true β_p for the kth simulation.

Table 1 presents the results for the coefficients: the average of the estimates over simulation (mean), the 2.5th and 97.5th percentiles of the estimates, the averaged widths of 95 % intervals over simulation, the coverage probabilities for 95 % intervals, and MAE. Both models have similar results of β₁ associated with no space-time varying covariate. Overall, the averages of the estimates for β₀ and β₂ in the 2-stage mixture model are closer to the true values in comparison with the full mixture model, which means that the 2-stage mixture model has small biases of these estimates (β₀ and β₂). Also, the 2-stage models have the smallest MAE, which justifies that the 2-stage mixture models estimate the true coefficients very well. In the 2-stage model, the 2.5th and 97.5th percentiles of the estimates for β₀ and β₂ do not include the true coefficient values in some cases and the coverage probabilities of the intervals for the estimates are quite small. However, these results are because the averaged widths of 95 % intervals for the coefficients in the 2-stage model are much smaller than those in the full mixture model. Thus, in terms of the bias, the 2-stage mixture models are better than the full mixture models and especially, the 2-stage models dramatically improve the performance of the estimates of the intercept and coefficients associated with space (or space-time) varying covariates. But in terms of the intervals, the full mixture models are better than the 2-stage models.

Table 1.

Comparison of the estimation results from the full space-time mixture model (M1) and the 2-stage space-time mixture model (M2). True values: β₀ = 1.00, β₁ = 0.05, and β₂ = 0.10.

Design	Model	Parameter	mean	2.5 %	97.5 %	average width 95 % interval	coverage probability of 95 % interval	MAE
1	M1	β 0	0.929	0.600	1.116	0.340	0.895	0.097
		β 1	0.050	0.042	0.056	0.016	0.950	0.003
		β 2	0.101	0.091	0.113	0.014	0.885	0.004
	M2	β 0	0.965	0.948	0.985	0.018	0.005	0.035
		β 1	0.049	0.041	0.057	0.014	0.915	0.003
		β 2	0.100	0.096	0.104	0.002	0.400	0.002
2	M1	β 0	0.940	0.704	1.126	0.339	0.815	0.095
		β 1	0.050	0.042	0.056	0.015	0.965	0.003
		β 2	0.104	0.087	0.120	0.037	0.895	0.008
	M2	β 0	0.960	0.947	0.975	0.016	0.000	0.040
		β 1	0.050	0.043	0.056	0.014	0.945	0.003
		β 2	0.106	0.102	0.109	0.004	0.015	0.006
3	M1	β 0	0.964	0.744	1.122	0.322	0.950	0.069
		β 1	0.050	0.043	0.057	0.016	0.970	0.003
		β 2	0.101	0.084	0.124	0.048	1.000	0.007
	M2	β 0	0.964	0.951	0.977	0.015	0.000	0.036
		β 1	0.050	0.043	0.057	0.014	0.955	0.003
		β 2	0.100	0.095	0.106	0.007	0.795	0.002

Table 2 summarizes the estimated number of components included in the models by using a percentage table. Clearly, the 2-stage mixture models estimate the true number of components very well while the full mixture models estimate the small number of components. It is shown that 93 %, 87 %, and 94.5 % of the simulations in the 2-stage models estimate the exact true number of components in Designs 1–3, respectively. However, the full mixture models estimate the true number of components with less than 25 % of the simulations (10.5 % of the simulations in Designs 1 and 3, 23.0 % in Design 2). In estimating the true number of temporal components, the 2-stage mixture models are much better than the full mixture models.

Table 2.

Percentage table of the estimation of the number of components included in the model over simulation (%). The true number of components is three and the number of simulations is 200. (M1: the full space-time mixture model; M2: the 2-stage space-time mixture model).

		L
Design	Model	0	1	2	3	4	5	6	Total
1	M1	0.5	51.5	36.5	10.5	1.0	0	0	100
	M2	0	0	2.0	93.0	3.5	1.5	0	100
2	M1	0.5	19.0	55.5	23.0	2.0	0	0	100
	M2	1.0	0.5	4.5	87.0	5.5	1.5	0	100
3	M1	0	33.5	56.0	10.5	0	0	0	100
	M2	0	0	0.5	94.5	3.0	2.0	0	100

In Figure 4, the plots of the true temporal components and their estimates with 95 % credible intervals in Designs 1 and 2 are displayed using only the output when the models estimate the exact true number of components. As you can see the plots, all the intervals of the estimated temporal components from the 2-stage models contain the true profiles while the intervals for Component 2 from the full models do not include the true ones. Overall, the widths of the intervals in the 2-stage models are smaller than those in the full mixture models. Design 3 also has similar results. This suggests that the 2-stage mixture models fit the true temporal components well.

Finally, we examine the performance of spatial clustering in both models with the output when the estimated number of components is equal to the true number of components. To check the ability of the models in detecting the spatial clusters, we use the accuracy cluster rate, $A={\sum }_{i=1}^I{A}_i∕I$ and $A_i={\sum }_{k=1}^K\mathbf{I}(C_i^T={\widehat{C}}_{\mathit{ik}})∕K$, where I(·) is the indicator function, $C_i^T$ is the true spatial cluster indicator for county i and ${\widehat{C}}_{\mathit{ik}}$ is the estimated cluster indicator for the ith county at the kth simulation. This accuracy measure explains how well the model recovers the true spatial clusters over space and simulation. In Design 1, the 2-stage mixture models (0.59) provide higher A value than the full mixture model (0.55). In Designs 2 and 3, the full mixture models have a little bit higher A values than the 2-stage models, but a quite small output from the full mixture models is only used to compute the accuracy rate in comparison with the 2-stage mixture models. Thus, there is no big difference between both models in terms of recovering the true spatial clusters.

5. REAL DATA ANALYSIS

We apply our statistical framework to data in Georgia for the years 1999–2008 described in Section 2. We first analyze monitored PM_2.5 data using the space-time PM model proposed in Section 3.1 to produce the estimated county-level PM_2.5 concentrations. Using these PM_2.5 estimates and asthma data, the 2-stage mixture model is fitted to investigate the effects of air pollution on asthma and examine the space-time mixture structure.

For the PM model and the health model we use a single chain with a total of 70,000 iterations to satisfy convergence criteria. The number of iterations for the burnin period is 20,000, and the thinning rate is 10 so the number of samples used for the estimation of the parameters is 5000. MCMC convergence diagnostics using the Geweke convergence diagnostic (Geweke 1992), autocorrelation functions, and trace plots are conducted. The deviance and representative parameters met acceptable MCMC convergence. The computing time only to run the 2-stage mixture model as the health model is approximately 4 hours using a desktop PC with Intel Core 2 Duo process (3.16 GHz) and 4 GB RAM.

Figure 5 presents the maps of the estimated county-level PM_2.5 concentrations for the years 1999–2008. The estimated PM_2.5 concentrations for the first two years (1999 and 2000) are the highest values over the state of Georgia. For almost all areas, PM_2.5 concentrations tend to decrease from 1999 to 2008 (on average, the PM_2.5 concentration was 18.33 μg/m³ for 1999 and 13.08 μg/m³ for 2008). Also, the estimated PM_2.5 concentrations in the Atlanta areas were higher than the other areas for the years 2001–2006.

Figure 5.

Maps of the estimated PM_2.5 concentrations for the years 1999–2008 in Georgia.

To evaluate the prediction performance of the proposed PM_2.5 model, we conduct a calibration analysis. We randomly select 62 observations (1/5 of the data) and compare the 62 observed PM_2.5 values with the corresponding estimated PM_2.5 values. For each observation, we obtain a predicted value and its 95 % prediction intervals given the data, omitting the data we are predicting, and we repeat this process for the selected observations. The percentage of the observations that are outside the 95 % intervals is 1.61 %. This suggests that the PM_2.5 model considered here performs well in terms of the prediction.

To examine the performance of the 2-stage mixture model as the health model, we fit four different models:

• (1)Model 1: simple linear Poisson model in Equation (3.2)
• (2)
  Model 2: space-time random effect model proposed by Knorr-Held (2000)

  $$\log {\theta }_{\mathit{ij}}={\alpha }_0+Z_{\mathit{ij}}^{\ast }{\gamma }_{\mathit{ij}}+{\mathbf{X}}_{\mathit{ij}}^{\prime }{\beta }_{\mathit{ij}}+u_i+v_i+{\xi }_j+{\delta }_j+{\eta }_{\mathit{ij}},$$

  where u_i has an IAR distribution with the variance ${\sigma }_u^2$, ξ_j has an AR(1) with the temporal parameter ρ_ξ ~ Beta(1, 1), $v_i\sim \mathrm{N}(0,{\sigma }_v^2)$, ${\delta }_j\sim \mathrm{N}(0,{\sigma }_{\delta }^2)$, and ${\eta }_{\mathit{ij}}\sim \mathrm{N}(0,{\sigma }_{\eta }^2)$. All the standard deviances have uniform prior distributions.
• (3)
  Model 3: full space-time mixture model

  $$\log {\theta }_{\mathit{ij}}={\alpha }_0+Z_{\mathit{ij}}^{\ast }{\gamma }_{\mathit{ij}}+{\mathbf{X}}_{\mathit{ij}}^{\prime }{\beta }_{\mathit{ij}}+\sum _{l=1}^L{w}_{\mathit{il}}{\chi }_{\mathit{lj}}+{\eta }_{\mathit{ij}},$$

  where w_il, χ_lj, and η_ij have the same structures as in Section 3.2.
• (4)Model 4: 2-stage space-time mixture model proposed in Section 3.2.

For Models 3 and 4, we use L = 10 entry parameters because it seems to be large enough to find the true number of latent components. For all the models, we also consider three different structures for the coefficients (γ_ij and β_ij) in Equation (3.3):

• (i)Constant: The coefficients are constant over space and time (γ_ij = γ₀ and β_ijp = β_0p).
• (ii)Space-varying: The coefficients are constant over time but vary over space (${\gamma }_{\mathit{ij}}={\gamma }_0+{\gamma }_i^1$ and ${\beta }_{\mathit{ijp}}={\beta }_{0p}+{\beta }_{\mathit{ip}}^1$).
• (iii)Space-time varying: The coefficients vary over space and time, presented in Equation (3.3).

To assess how well the models considered fit the data and predicts, we use the DIC₃ measure proposed by Celeux et al. (2006) that uses a posterior estimate of likelihood in computing the effective number of parameters, pD. This measure is defined as ${\mathrm{DIC}}_3=\overline{D\left(ϴ\right)}+{\mathrm{pD}}_3=\overline{D\left(ϴ\right)}+[\overline{D\left(ϴ\right)}+2\log \widehat{p}(\mathbf{y}\mid ϴ\left)\right]$, where $\overline{D\left(ϴ\right)}$ is the posterior mean of the deviance. We use this DIC₃ measure instead of the standard DIC measure (Spiegelhalter et al. 2002) because DIC₃ is easily calculated by MCMC and it performs well in mixture models. It also provides stable and reliable evaluations. For the prediction performance, we consider the Marginal Predictive-likelihood (MPL) and the mean square prediction error (MSPE). The MPL computed using the Conditional Predictive Ordinate (CPO) (Dey, Chen, and Chang 1997) is specified as MPL = Σ_i,j log (CPO_ij), where CPO_ij is the marginal posterior predictive density of y_ij given the data omitting y_ij. Thus, the CPO represents a cross-validation measure, and the MPL explains a predictive measure for a future replication of the given data. The model with a larger value of MPL is better (Ibrahim, Chen, and Sinha 2001; Congdon 2005). The MSPE is given by $\mathrm{MSPE}=\frac{1}{IJ}{\sum }_{i,j}{(y_{\mathit{ij}}-{\widehat{y}}_{\mathit{ij}})}^2$, where ${\widehat{y}}_{\mathit{ij}}$ is the predicted value of the observed value y_ij from the posterior predictive distribution.

Table 3 reports these measures for the models considered and the estimated number of latent temporal components for Models 3 and 4. For each coefficient structure, the simple linear Poisson model (Model 1) has much larger DIC₃ and MSPE values and lower MPL values than the other models. Therefore, the simple linear Poisson model is not appropriate for this data set, and this implies that space, time, or space-time random effect needs to be considered in the model. In terms of DIC₃, MPL and MSPE, the constant coefficient structure over space and time in the space-time random effect model (Model 2) is much better than the other coefficient structures for that Model. Similarly, the 2-stage space-time mixture model (Model 4) with constant coefficients over space and time is better than the model with the other coefficient structures in terms of DIC₃ and MPL. The 2-stage mixture models with different coefficient structures provide similar MSPE values. In contrast, the full space-time mixture model (Model 3) with spatiotemporally varying coefficients has smaller DIC₃ and MPL than those with constant (or space-varying) coefficients. From these results, we can see that the 2-stage mixture model (Model 4) with constant coefficients over space and time has the smallest DIC₃ and MPL overall. Thus, this model is the best fit model among these models. Also, it appears that the 2-stage mixture models estimate four components included in the models while the full mixture models estimate the small number of components (1 or 2), which is consistent with the results obtained from the simulation study.

Table 3.

Comparison results from four models and three different coefficient structures for Asthma data in Georgia.

Coefficient structure	Model	DIC3	pD3	MPL	MSPE	$\widehat{L}$
Constant	Model 1	18977	45	−9490	708.5
	Model 2	10469	427	−5624	127.9
	Model 3	10551	487	−5846	127.9	1
	Model 4	10451	365	−5477	128.5	4
Space-varying	Model 1	11765	489	−6073	218.2
	Model 2	11221	521	−5788	171.4
	Model 3	10516	436	−5655	128.6	1
	Model 4	10500	432	−5650	128.2	4
Space-time varying	Model 1	11583	499	−6022	209.7
	Model 2	11150	423	−5754	169.7
	Model 3	10490	410	−5576	128.1	2
	Model 4	10453	422	−5621	127.6	4

In Table 4 the posterior means and 95 % credible intervals for the model parameters in the 2-stage mixture model with constant coefficients over space and time are presented. The proportion of black population and the unemployment rate are significant positive risk factors of the asthma while the PM_2.5 and the household median income are significant negative risk factors. For example, a higher proportion of black people or the unemployment rate is associated with increased risk of the asthma. The lower income is associated with increased risk of the asthma. The PM_2.5 parameter posterior mean is negative (−0.028) with a small 95 % credible interval (−0.034, −0.022). The full space-time mixture model showed little difference in the risk estimates of the socioeconomic covariates when compared to the 2-stage mixture model results. The posterior mean of PM_2.5 in the full space-time mixture model is also negative (−0.072) with a 95 % interval (−0.096, −0.049) and the intercept mean is 0.147 with a 95 % interval (0.027, 0.376). These interval widths are larger than those of PM_2.5 and the intercept in the 2-stage mixture model so these patterns follow those obtained in the simulation study. Here, our results for PM_2.5 are slightly surprising and inconsistent with some air pollution-related time-series studies (Tolbert et al. 2000; Sheppard 2003). However, all the other models (Models 1–3) including a simple linear Poisson model without space-time random effects also provide negative estimates for the PM_2.5 coefficient, adjusting for the socioeconomic covariates. We also estimate the effects of the 1-year lag PM instead of the effects of the current year PM because the previous year’s PM level could be associated with the current year’s health outcomes. We still have the negative effects of the 1-year lag PM on asthma (posterior mean = −0.035 with a 95 % interval (−0.042, −0.029) for the 2-stage model; posterior mean = −0.034 with a 95 % interval (−0.037, −0.030)). The PM effects conditional on possible subsets of the covariates in the 2-stage models are between −0.048 and −0.036, which are smaller than that of the 2-stage model with all the covariates. In this data set, adding the space-time mixture structure in the model provides no significant effect on the estimate of PM when comparing Model 1 and Model 4. These results seem to imply that the estimates of PM_2.5 are smoother, since PM_2.5 data in some areas are sparsely sampled. This may lead to less spatial variation in areas with high disease risk and may tend to produce the negative effects of PM_2.5 while controlling for the non-PM covariates and space-time mixture structures.

Table 4.

Parameter estimation in the best-fitted model (the 2-stage mixture model with constant coefficients over space and time).

covariates	mean	sd	2.50 %	97.5 %
intercept	0.197	0.0058	0.185	0.208
PM2.5	−0.028	0.0031	−0.034	−0.022
black proportion	0.004	0.0004	0.003	0.005
income	−0.019	0.0005	−0.020	−0.018
unemployment rate	0.024	0.0039	0.017	0.032

Figure 6 shows the plots for the temporal components included in the 2-stage mixture model after adjusting for the covariates. Component 1 has a stable increasing pattern and component 4 increases dramatically over year. On the other way, component 3 has a decreasing pattern. Component 2 tends to increase until 2002 and then decrease. In addition, component 2 has the largest relative risks over time while component 3 has the smallest relative risks. The maps of the estimated weights corresponding to the temporal components are displayed in Figure 7(a). Based on the allocation approach presented in Equation (3.6), the map of the spatial cluster indicator (C_i) is also displayed in Figure 7(b). Overall, the Atlanta areas and some of southern areas are assigned to component 2 (increasing and then decreasing from the year 2002) and some of central areas and southern-east areas are assigned to component 1 or 4. Northern areas and a few eastern or southern areas are assigned to component 3.

Figure 6.

Temporal plots for four estimated components from the 2-stage mixture model.

Figure 7.

(a) Maps of the estimated weights corresponding with the temporal components. (b) Map of the allocation using the weights.

As mentioned previously, it is possible to consider PM_2.5 estimated in counties with added measurement error. This could hope to partially address the issue of bias induced by using plug-in estimates. To explore the impact of adding PM_2.5 measurement error in the health model, we re-fit the full mixture model and the 2-stage mixture model with constant coefficients over space and time, with measure error added to the PM_2.5. We assume Berkson measurement error (Berkson 1950) in the PM_2.5 with ($Z_{\mathit{ij}}^{\ast }+{ϵ}_{\mathit{ij}}$) and ($Z_{\mathit{ij}}^{\ast }+\text{se}\left(Z_{\mathit{ij}}^{\ast }\right)\ast {ϵ}_{\mathit{ij}}$) replacing $Z_{\mathit{ij}}^{\ast }$, where ${ϵ}_{\mathit{ij}}\sim \mathrm{N}(0,{\sigma }_{ϵ}^2)$. The value of se($Z_{\mathit{ij}}^{\ast }$) was computed from the set of county prediction values used to estimate $Z_{\mathit{ij}}^{\ast }$. Table 5 displays the comparison of results from the 2-stage model with measurement error. As compared to the results from the 2-stage model without measurement error in Table 3, including the measurement error has an effect of reducing DIC₃ values and increasing MPL values. The models both including measurement error or not, have similar MSPE values. The DIC₃ and MPL measures favor the 2-stage mixture model with ($Z_{\mathit{ij}}^{\ast }+\text{se}\left(Z_{\mathit{ij}}^{\ast }\right)\ast {ϵ}_{\mathit{ij}}$) among these measurement error models. This model has DIC₃ = 10352 and MPL = −5432 although the MSPE is similar to that for the non measurement error version of this model. These results suggest that the measurement error models do provide a better fit overall to these data. However, the posterior mean estimate of PM_2.5 is −0.031 with 95 % interval (−0.038, −0.023) and the estimated number of temporal components is four, which is close to that for the 2-stage mixture model without measurement error. Thus, the models with measurement errors have little effect on the estimate of PM and the estimated number of components.

Table 5.

Comparison results from the 2-stage mixture model with constant coefficients over space and time and two different measurement error structures in the PM_2.5 for Asthma data in Georgia.

Measurement error structure	DIC3	pD3	MPL	MSPE	$\widehat{L}$
$Z_{\mathit{ij}}^{\ast }+{ϵ}_{\mathit{ij}}$	10366	399	−5463	128.4	4
$Z_{\mathit{ij}}^{\ast }+\text{se}\left(Z_{\mathit{ij}}^{\ast }\right)\ast {ϵ}_{\mathit{ij}}$	10352	378	−5432	128.7	4

We finally conduct a sensitivity analysis to examine whether there is any significant effect on the estimates of the covariate effects with using the hyperprior specification for the entry parameters (ψ_l). We assume ψ_l ~ Bern(p_ψ) and p_ψ ~ Beta(1, 1). Although two components are estimated as the number of latent components included in the 2-stage mixture model, the posterior means and 95 % credible intervals of the covariate effects are similar to those for the informative probability value (0.5) in the entry parameters. Thus, the estimates of the covariate effects have little effect on the use of a non-informative hyperprior in the entry parameters.

6. DISCUSSION

We have presented a novel approach to the incorporation of covariates within a space-time modeling framework. In particular, we have examined the use of space-time mixture models where covariates are to be introduced. A 2-stage procedure was proposed and applied both in simulations and real data. In simulated comparisons, the 2-stage model yielded lower error in the estimation of predictor parameters and also yielded much greater accuracy in the estimation of latent component numbers than other models, even though the coverage of its intervals was not good. There was little difference in the ability to detect spatial grouping or clustering of risk. In application to the ambulatory asthma data for 1999–2008 we found that we could model the data well with the 2-stage model approach and found four components to be optimal. In the real data analysis, we also found a small but negative posterior mean for the PM_2.5 parameter which is different from previously reported results based on time-series studies. The result holds across different space-time modeling scenarios and so we have concluded that it is substantive, but that the negative association could be partly contributed to by the smoothness of the interpolation in sparse areas. It is also an ecological finding. The socioeconomic covariates considered here were aggregated from individual level data and directly obtained from public websites. Although these factors at individual level are conventional predictors of asthma (e.g. race), they are significant risk factors at county level and these individual level properties should be considered as covariates at the individual level. Thus, the use of county level asthma data would lead to biased results (ecological inference) and so we cannot directly estimate the PM effects on asthma adjusting for the socioeconomic covariates. To better understand the PM effects on asthma, it would be useful to examine the individual level asthma data with the individual level risk factors.

We also explored the change of the coefficient estimates in covariates-only model and the two-stage model. We noticed that the estimates from both models were quite similar in the simulation study and the data analysis. But the coverage probabilities of the intervals for the estimates improved by adding the residual model and the SDs of the estimates in the 2-stage model were a little larger than those of the covariates-only model in the application.

In the simulation study and the application examined here, we found that the performance of the 2-stage mixture model and the full mixture model could have some patterns as the space-time dependence in the covariates and their coefficient structures would increase. Thus, we aim to examine their performance in-depth in the future.

In future analysis we would aim to consider the development of models that could combine predictor information with temporal components so that we could directly relate temporal effects to predictor temporal variation. We would want to consider directly modeling areas with higher densities of monitoring stations so that a more direct link with disease outcome could be examined.