Sample Size Calculations for Comparing Groups with Continuous Outcomes

Summary

Sample size justification is required for all clinical studies. However, to many biomedical and clinical researchers, power and sample size analysis seems like a magic trick of statisticians. In this note, we discuss power and sample size calculations and show that biomedical and clinical investigators play a significant role in making such analyses possible and meaningful. Thus, power analysis is really an interactive process and scientific researchers and statisticians are equal partners in the research enterprise.

1. Introduction

Sample size justification is required for all clinical studies. Although commercial and online statistical software have been developed to calculate sample sizes, for many biomedical and clinical researchers, the calculation of sample size seems like a magic trick of the statisticians. When their statisticians ask them for information pertaining to sample size calculations, many do not understand why statisticians ask them for such information.

Sample size, or power analysis, should be done at the design stage of a clinical study. In general, such calculations are based on statistical distributions of test statistics pertaining to study hypotheses. For adaptive designs ^[1], although sample size may be adjusted according to information accumulated after the study begins, the adjustment plan is pre-specified at the design stage.

Note that for some medical journals, editors often ask authors to calculate power of their completed studies and provide such information in their manuscripts. However, such post-hoc power analysis makes no statistical sense.^[2] This is because although outcomes of a real study, along with their associated test statistics, are random quantities in the design stage, they all become non-random once a study is completed and have no probabilistic interpretation. Of course, the information in a completed study can be used for designs of future relevant studies.

As study outcomes are random, what is actually observed after a study is completed may be quite different from what has been proposed in the design. However, this does not mean that the study design is wrong or the study was not executed correctly. For example, suppose X is a standard normal random variable with mean 0 and standard deviation 1. The probability that X > 1.96 or X < -1.96 is 0.05. Thus, although we usually get a value of X within the range -1.96 to 1.96 when sampling X, there is still a 5% chance that X is outside of this range. Thus, when values of X are observed outside of the range, it does not mean that our assumption about the distribution of X is wrong.

In this manuscript we discuss sample size and power calculations for continuous outcomes. We give the sample size formulas for one group, two independent groups, and two paired groups. We show how preliminary information can be used to power studies. Our paper can demystify sample size justification for biomedical and clinical researchers.

2. Sample size for one group

We first consider sample size calculations for one group. Although relatively simpler, it helps illustrate basic steps for sample size calculations.

Consider a continuous outcome X and assume it has a normal distribution (often called bell-shaped distribution) with mean µ and variance σ², denoted by X ~ N(µ,σ²). It is called the standard normal distribution if µ = 0 and σ = 1. For ease of exposition, we assume first that σ is a known constant.

Consider testing the hypothesis,

(1)

where µ₀ is a known constant, and H₀ and H₁ are called null and alternative hypotheses, respectively. Note that as two-sided alternatives as in (1) are the most popular in clinical research, we only focus on such hypotheses in what follows unless stated otherwise.

Let X₁, X₂, K, X_n be a random sample from X ~ N (µ, σ²) and 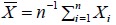be the sample mean. If the null H₀ is true, X̄ has a high probability of being close to µ₀. However, because X̄ is random, it is still possible for X̄ to be far away from µ₀, although such probabilities are small, especially for large n. The type I error α, a quantity introduced to indicate such an error rate, is the probability that measures the likelihood when X is too far from µ₀ under H₀. This error rate is typically set at α=0.05 for most studies and at α=0.01 for studies with large sample sizes. Given α, power is the probability that we reject H₀ when H₀ is false.

The decision to reject the null is based on the standardized difference between X̄ and µ₀, or the z -score ^[3]

(2)

We reject H₀ if |z|>z_α/2, where z_α/2 denotes the upper α/2 quantile of the standard normal distribution, i.e., Φ(z_α/2) = 1–α/2, with Φ denoting the cumulative distribution function of the standard normal distribution. For example, for α = 0.05, Z_α/2 = 1.96. If H₀: µ = µ₀ is true, the probability of rejecting H₀, therefore committing a type I error, is readily calculated as

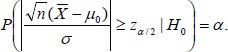(3)

In clinical studies, what we are really interested in is the opposite, i.e., how we can reject the null when theH₀ is false. This is because H₀ usually represents no treatment effect, i.e., a straw man. Statistical power allows one to quantify the chance of rejecting H₀ by specifying the mean µ under the alternative, i.e.,

(4)

Without loss of generality, we assume µ₁ > µ₀. Note that unlike the hypothesis stated in (1), we must specify a known value for µ under the alternative H_a if we wish to quantify our ability to reject H₀ when performing power analysis. Such explicit specification is not needed when we only test the null hypothesis after data is observed.

Given type I error α and a specific µ₁ in H_a, we then calculate power, or the probability that (the absolute value of) the standardized difference in (2) exceeds the threshold z_α/2, i.e.,

(5)

By comparing the above with (3), we see that the only difference in (5) is the change of condition from H₀ to H_a. The probability is again readily evaluated to yield:

(6)

As the above shows, the power, Power(n,α,H₀,H_a), is a function of sample size n, type I error α and values of µ specified in the null H₀ and alternative H_a.

In most clinical research studies, µ₀ and µ₁ are posited to reflect treatment effects. Thus, once α is selected, power is only a function of sample size n, which increases as n grows and approaches 1 as n grows unbounded. Thus, by increasing sample size, we can have more power to reject the null, or ascertaining treatment effect.

However, as increasing sample size implies higher cost for studies, power is generally set at some reasonable level such as 0.80. Also, although we can detect any small treatment effect, such statistical significance may have little clinical relevance. Thus, it is critical that we specify treatment effects that correspond to clinically meaningful differences.

Sample size justification works the opposite way. Given a type I error α, a pre-specified power 1 – β, and H₀ and H_a, we want to find the smallest n such that the test has the given power to reject H₀ under H_a

(7)

Although it is generally difficult to find an analytical formula for computing the smallest n satisfying (7), such an n is readily obtained by using statistical packages. Note that power in the literature is typically denoted by1 – β, where β denotes the probability that the null H₀ is rejected when H₀ is false, or type II error rate.

Although µ₁ – µ₀ measures treatment difference between the means of X under H, this difference depends on the scale of X and may change when different scales are used. For example, if X represents distance, µ₁ – µ₀ will have different values if different scales are used such as mile and kilometer. Thus, effect size is used to remove such dependency:

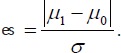(8)

The above is often referred to as Cohen’s d and is widely used in clinical research. In the example of distance, effect size is the same regardless of whether mile or kilometer is used.

Note that for simplicity, we have assumed that σ² is known. In practice, σ² is also unknown and is estimated by the sample variance, 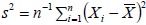. In this case, the above arguments still apply, but the cumulative normal distribution Φ will be replaced by the cumulative t distribution to account for sampling variability when estimating σ² by s².

3. Sample Size for Two Independent Groups

Now consider two independent samples and let X_ij (i = 0,1; j = 1,K,n_i) denote the random outcomes from the two samples. We assume that both group outcomes follow normal distributions, 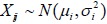, with unknown means µ_i and known variances .

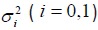Considering testing the hypothesis,

(10)

Let 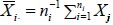denote the sample mean of the i th group (i = 0,1). As in the one-group case, the difference between the two sample means 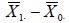should be close to d₀ if H₀ is true. Again, because 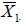and 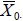. are random, it is still possible for 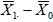to be very different from d₀, although such probabilities are small, especially for large n. The level of such type I error rate a is also set equal to 0.01 or 0.05 depending on sample size as discussed earlier.

Although most clinical trials allocate equal number of subjects into groups, some studies may assign more patients to a group^[4] We assume that the number of subjects in group 0 and group 1 are n₀ and n₁, respectively. If H₀: µ₁ – µ₀ = d₀ is true, the probability of rejecting H₀, therefore committing type I errors, is readily calculated as:

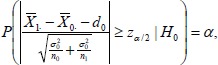(11)

where α is the type I error level set a priori and z_α/2 is the upper α/2 quantile of the standard normal distribution.

For power analysis, we again need to specify µ₁ – µ₀ under H_a to quantify the ability to reject the null when performing power analysis, i.e.,

(12)

Without loss of generality, we assume d₁ > d₀. Given a significance level α, H₀ and H_a, we then calculate power, or the probability that (the absolutely value of) the standardized difference in (11) exceeds the threshold Z_α/2, i.e.,

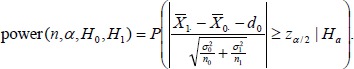As in the one-group case, we use effect size as a measure of treatment effect when calculating power. In this case, Cohen’s d is given by:

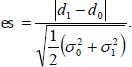In many studies, group variances are assumed the same, in which case the effect size reduces to

Given a type I error α, a power 1 – β, and H₀ and H_a, we can also find the smallest n such that the test has the given power to reject the null H₀ under H_a, i.e.,

Again, statistical packages are readily applied to find such an n.

Note that for simplicity, we have again assumed that the group variances 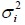are known. In practice, 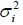are generally unknown and are estimated by the sample variance, 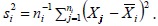In this case, the above arguments still apply, but the cumulative normal distribution Φ will be replaced by the cumulative t distribution to account for sampling variability when estimating 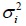by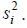

4. Sample Size for Paired Groups

In the last section, data from the two groups are assumed independent. When groups are formed by different subjects, they are generally independent. In practice, we may be interested in changes before and after an intervention. For example, suppose we are interested in the effect of a newly developed drug on high blood pressure. We measure blood pressure of each subject before and after administering the drug and compare mean blood pressure between the two assessments. Since subjects with their blood pressure above the mean before the intervention are likely to stay above the mean blood pressure after the intervention, the two measures of blood pressure are not independent. As a result, the two independent group t-test does not apply to this paired group, or prepost study, setting.

Let (X_0j,X_1j) denote the two paired outcomes from the j th pair. For each pair, treatment difference is D_j = X_1j -X_0j. If the difference D_j has a mean d = 0, then there is no treatment effect. In general, we are interested in testing the hypothesis

(13)

In the two independent group case, X_0j and X_1k are assumed to have their own means and the hypothesis (12) involves both group means. In the current paired-group case, it is not necessary to identify the means of X_0j and X_1j, since only the mean of difference D_j is of interest in the hypothesis (12). By comparing (4) and (13), it is readily seen that the sample size and power calculation is simply a special case of the one-group case with H₀: µ = 0.

5. Illustrations

In this section, we illustrate power and sample size calculations for the one group, two independent and two paired groups discussed using G*Power, a free program for power analysis, and R, a free package for statistical analysis, which also includes functions for power and sample size calculations for our current as well as more complex study settings.

Example 1. The mean weight of men aged 20-29 in a study population of interest in 1970 was µ₀ = 170 lbs with a standard deviation σ=40 lbs. A researcher proposes that the mean weight of this subpopulation has increased to µ₁ = 190 lbs in 2010 with the same standard deviation. The researcher wants to determine the sample size n so that there is 0.8 power to detect this difference.

The statistical hypotheses is

We set α=0.05. Although the alternative shows an increased weight, we compute power under a two-sided test. To compute power, we first convert the parameters into effect size:

When using the G*Power package, choose the following options (see Figure 1):

Figure 1.

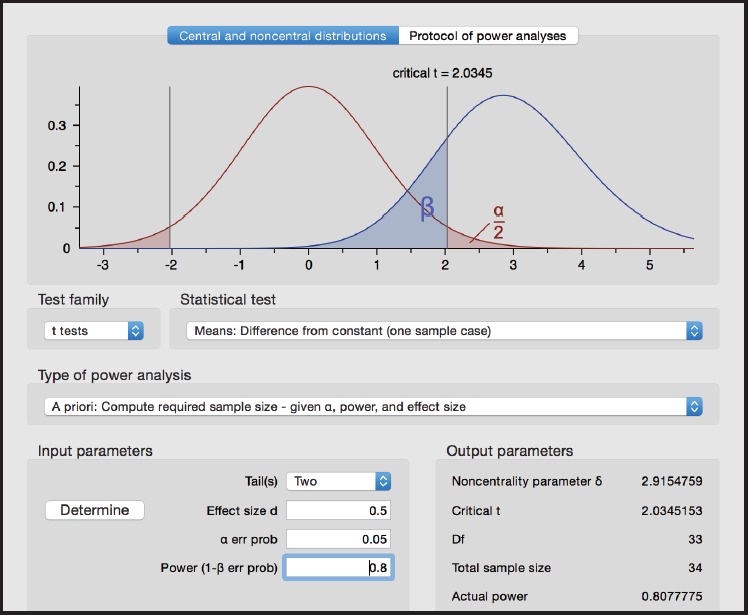
Screen shot from G*Power for Example 1

Test family > t tests

Statistical test > Means: Difference from constant (one sample case)

Type of power analysis > A priori: Compute required sample size

Tails > Two

Effect size d > 0.5

α err prob > 0.05

Power (1 - β err prob) 0.80

We obtain n=34 under Total sample size in the G*Power screen.

In R, we may use the pwr package to compute power. For t-tests, use the function:

pwr.t.test(n =, d =, sig.level =, power =, type = c(“two.sample”, “one.sample”, “paired”))

where n is the sample size, d is the effect size, and type indicates a two-sample t-test, one-sample t-test or paired t-test. For each function, entering any three of the four quantities (effect size, sample size, significance level, power) and the fourth is calculated.

Using the function pwr.t.test (d = 0.5, sig.level = 0.05, power = 0.8, type = “one.sample”), we obtain n = 33 after rounding to the nearest integer.

Example 2. A researcher, who wants to study the possible difference in hemoglobin between smokers µ₁ and non-smokers µ₀, would be interested to find any mean differences d₁ = |µ₁ – µ₀| ≥ 2 mmol/L between the two study populations, with 80% power. The standard deviation in each group is assumed to be σ = 5 mmol/L for both groups (from other published studies).

The statistical hypothesis is

Again, we set α=0.05 and compute power for a two-sided test. Under the assumptions, the effect size is

We also assume a common group size so that n₀ = n₁. In G*Power package, choose the following options (see Figure 2):

Figure 2.

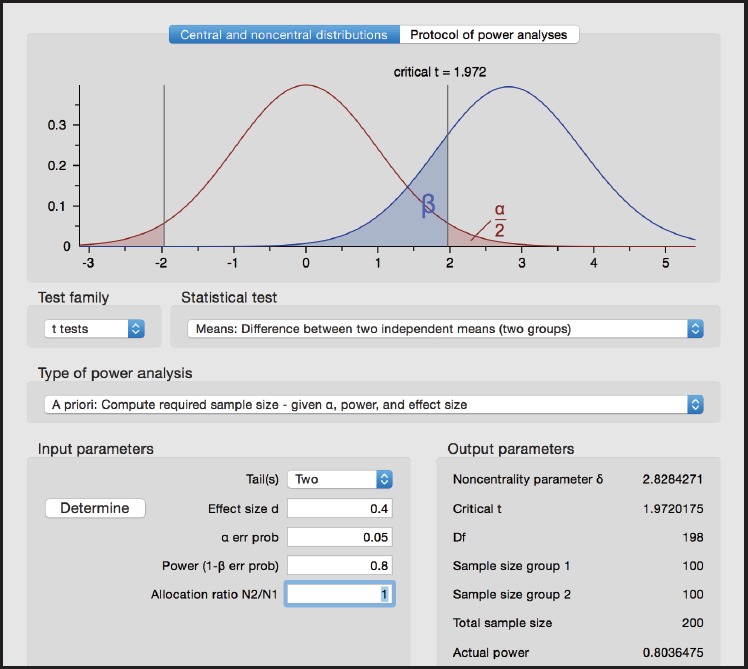
Screen shot from G*Power for Example 2

Test family > t tests

Statistical test > Means: Difference between two independent means (two groups)

Type of power analysis > A priori: Compute required sample size

Tails > Two

Effect size d > 0.4

α err prob > 0.05

Power (1 - β err prob) 0.80

Allocation ratio N2/N1 > 1

From G*Power, we obtain n₀ =n₁ =100 for each group or the total sample size n₀+n₁= 200.

Using the function pwr.t.test (d = 0.4, sig.level = 0.05, power = 0.8, type = “two.sample”) in R and rounding to the nearest integer, we obtain n₀ = n₁ = 99.

Example 3. A weight loss study using food diary wants to find a difference between pre- and post-intervention mean weight loss of d = 2 kg. The standard deviation of the difference d is assumed σ _d =5 kg.

The statistical hypotheses is

We set α=0.05 and compute power for a two-sided test. The effect size is

By viewing the paired-group setting as a special case of the one-group setting, we readily obtain sample size using the following options in G*Power (see Figure 3):

Figure 3.

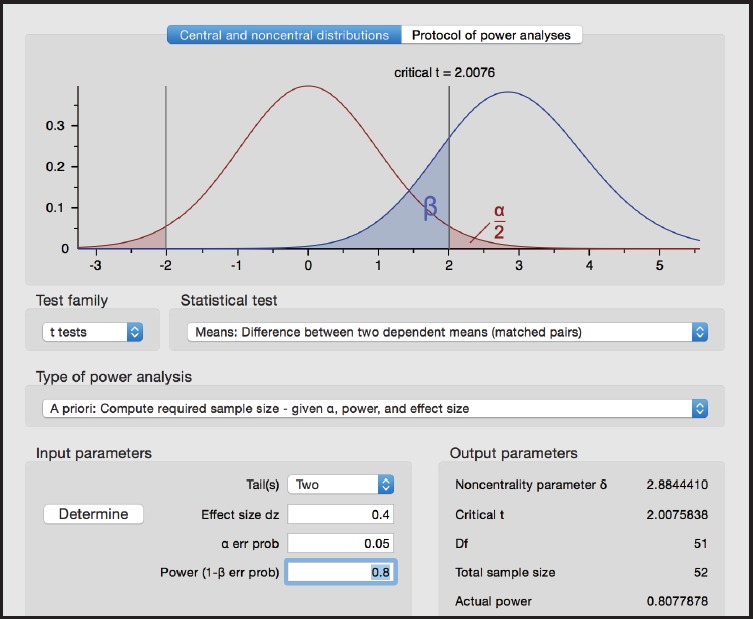
Screen shot from G*Power for Example 3

Test family > t tests

Statistical test > Means: Difference from constant (one sample case)

Type of power analysis > A priori: Compute required sample size

Tails > Two

Effect size d > 0.4

α err prob > 0.05

Power (1 - β err prob) 0.80

From G*Power, we obtain n=52.

Using the function pwr.t.test (d = 0.4, sig.level = 0.05, power = 0.8, type = “paired”) in R, we obtain n=51 after rounding to the nearest integer.

6. Conclusion

Sample size justification is an important consideration and a necessary component for clinical research studies. It provides critical information for assessing feasibility and clinical implications of such studies. Although power and sample size analysis relies on solid statistical theory and requires advanced computing methods, scientific investigators also play a critical role in this endeavor by providing relevant data. Without reliable input parameters, not only may power and sample size analysis be less informative, but more important potentially yield misleading information for study planning and execution.

Biography

Julia Zheng is currently completing her BS in Immunology and Microbiology at McGill University, Montreal, Canada. She is preparing to expand her interest in maths and computer science by pursuing a Bachelor’s in Computer Science at University of Windsor, Windsor, Canada. In the future, Julia hopes to engage in a Master or PhD in Biostatistics to pursue her research interests in the fields of life sciences, computing biology, and biostatistics.