Functional Connectivity Network Fusion with Dynamic Thresholding for MCI Diagnosis

Abstract

The resting-state functional MRI (rs-fMRI) has been demonstrated as a valuable neuroimaging tool to identify mild cognitive impairment (MCI) patients. Previous studies showed network breakdown in MCI patients with thresholded rs-fMRI connectivity networks. Recently, machine learning techniques have assisted MCI diagnosis by integrating information from multiple networks constructed with a range of thresholds. However, due to the difficulty of searching optimal thresholds, they are often predetermined and uniformly applied to the entire network. Here, we propose an element-wise thresholding strategy to dynamically construct multiple functional networks, i.e., using possibly different thresholds for different elements in the connectivity matrix. These dynamically generated networks are then integrated with a network fusion scheme to capture their common and complementary information. Finally, the features extracted from the fused network are fed into support vector machine (SVM) for MCI diagnosis. Compared to the previous methods, our proposed framework can greatly improve MCI classification performance.

1 Introduction

Alzheimer’s disease (AD) is an irreversible neurodegenerative disease resulting in progressive decline of memory and cognitive function. Mild cognitive impairment (MCI) is an intermediate stage between normal aging and AD. It is often misdiagnosed due to lacking of obvious clinical symptoms. Therefore, if MCI patients can be accurately diagnosed before the clinical onset of AD, treatments can be given in time to slow down the AD progress.

Recently, a variety of imaging modalities have been used for AD studies, such as structural MRI [1,2], diffusion MRI [3,4], and resting-state functional MRI (rs-fMRI) [5]. Different from structural and diffusion MRI that reveals brain morphological changes, rs-fMRI can examine both functional integration and segregation of brain networks that are undermined by MCI [6]. In previous studies, functional connectivity (FC) networks for characterizing pairwise correlation between different brain regions were constructed with rs-fMRI data and revealed the disrupted network topological properties in MCI [7].

Machine learning techniques are able to utilize features extracted from FC networks to identify MCI patients with a relatively high accuracy. Specifically, first, for reducing both the noise and unreliable connections, FC networks were often thresholded based on the connectivity strength, i.e., the FCs larger than a specific value were preserved and others were set to zero. Then, with a set of different threshold values, different topological views of the same original network can be derived to provide complementary information for enhancing the diagnosis. For example, Jie et al. [5] extracted features from multiple complementary thresholded networks and integrated them using multi-kernel learning for classification. Nevertheless, this method has two main drawbacks. (1) In terms of the thresholding strategy, they simply used a range of predetermined thresholds which might not be optimal. Thus, the classification performance often fluctuated greatly with a small change of threshold value, especially when the derived networks are very sparse. More importantly, all connections in the FC network are thresholded by the same unified threshold, which may be not reasonable since noise level in different brain regions could vary significantly. (2) In terms of the fusion strategy, searching for an optimal combination of the kernels, each designed for a derived network, becomes a daunting task, especially when the number of networks is large.

In this paper, we propose a novel classification framework with a dynamic thresholding strategy and then a network fusion scheme to address the above drawbacks. Specifically, for each subject, instead of thresholding all connections in its network by a set of predetermined values (i.e., network-wise thresholding), we propose to threshold each connection in the network (i.e., each element in the connectivity matrix) by a different threshold value (i.e., element-wise thresholding), which is randomly sampled from a distribution learned from all subject data. With this “element-wise” thresholding strategy, multiple FC networks can be dynamically constructed. To effectively integrate various information contained in these networks, we further adopt a novel network fusion method [8] to integrate these dynamic networks for capturing their common and complementary information. During the network fusion process, each thresholded network is iteratively updated under the interaction of two networks: a sparse network carrying the important strongest connectivity information of its own and the average of the other networks. Through such a fusion scheme, the full spectrum of complementary information can be integrated, without optimizing the weights of the kernels as in multi-kernel learning. After obtaining the fused network for each subject, we extract the local clustering coefficients (graph topological properties) of the network as features. Feature selection is then performed with the Least Absolute Shrinkage and Selection Operator (LASSO) [9] and the selected features are finally fed into support vector machine (SVM) for MCI classification. The performance of our proposed framework is evaluated with the Alzheimer’s Disease Neuroimaging Initiative Phase-2 (ADNI-2) database.

2 Method

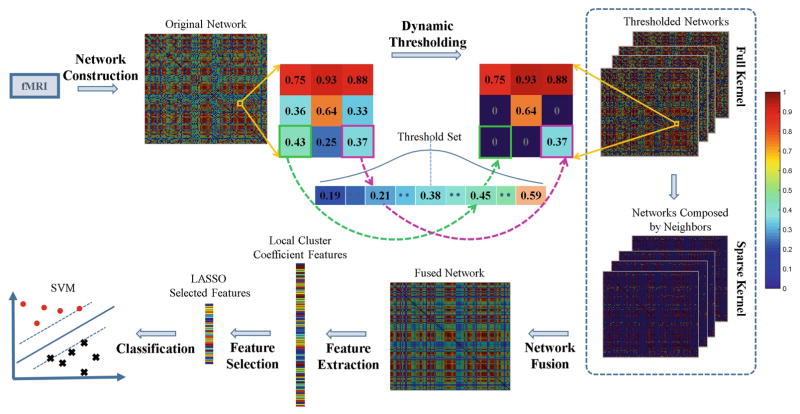
The overview of our method is illustrated in Fig. 1. The whole procedure can be divided into six steps: network construction, dynamic thresholding, network fusion, feature extraction, feature selection, and classification. Each step will be described in details below.

Fig. 1.

Overview of connectivity network fusion with dynamic thresholding.

2.1 Data Preprocessing and Network Construction

The dataset was downloaded from the ADNI-2 database (http://adni.loni.usc.edu/), which contained 30 normal controls (13M/17F; age: 74.3 ± 5.7) and 29 MCI subjects (16M/13F; age: 73.6 ± 4.8). Each subject was scanned with a 3.0T Philips Achieva scanner with the same protocol: a matrix size of 64 × 64 × 48 and an isotropic voxel size of 3.3 mm. Among the 140 collected rs-fMRI volumes, the first 10 volumes were discarded to ensure the magnetization equilibrium, and the remaining volumes were processed by SPM8 (http://www.fil.ion.ucl.ac.uk/spm/software/spm8). The data was slice-timing corrected, head motion corrected, normalized to the standard space, and parcellated into 116 regions of interest (ROIs) with the Automated Anatomical Labeling (AAL) atlas [10]. Then the mean rs-fMRI time series at each ROI was computed.

An original FC network can be represented by 116 nodes (i.e., 116 ROIs) and the edges connecting them (i.e., connections between each pair of 116 ROIs). The connection strength is computed by Pearson’s correlation between two mean time series between a pair of ROIs. Here, we only considered the magnitudes of correlation coefficients. Thus, we use their absolute values, i.e., the resultant connection strengths range from 0 to 1.

2.2 Dynamical Network Thresholding

The original FC network is usually dense and noisy. To better remove noise and also locate more biologically meaningful features for classification, the network needs to be sparse by proper thresholding. Previous methods for network-wise thresholding typically set up a set of unified thresholds for the entire network. However, for one thing, it is extremely difficult to find an optimal set of predetermined thresholds with brutal force; for another, it is not reasonable to use a uniform threshold for all connections, since correlation coefficients are often affected by different levels of noise.

Instead of using a unified threshold for the entire network, we used a dynamic threshold for each connection in the network. As the previous study had indicated that network sparsity between 25 % and 75 % was appropriate for MCI diagnosis [5], we recorded the thresholds corresponding to the 25 % and the 75 % network sparsity, respectively. Then, we generated the thresholds with a step size Δ between these two estimated thresholds. After finding thresholds across all subjects, we modeled the distribution of all these thresholds with a Gaussian function N(μ, σ), where μ was the mean of all the thresholds, and σ was the standard deviation. The rationale of using a Gaussian distribution was that the optimal threshold most likely appeared in the center of the Gaussian distribution based on previous studies [5] and the observation of our data. Then, for each connection element, we randomly sampled a value from the estimated Gaussian distribution and then used it to threshold this connection element in the original FC network. By implementing this element-specific thresholding for all elements, we obtained a new dynamically-thresholded network. For each subject, we repeated this for N times and constructed a set of dynamically-thresholded networks { ${\mathit{W}}_i^j$}, where j = 1, …, N for the subject i. An illustration of this procedure is shown in the Dynamic Thresholding step in Fig. 1.

Compared to the one-size-fits-all network-wise method [5], this element-wise dynamic strategy not only reduced the influence of threshold selection to the classification result, but also treated each connection separately. Besides, we obtained more different topological views of the original FC network for each subject.

2.3 Network Fusion

The dynamically-thresholded networks extracted in Sect. 2.2 provided complementary information for MCI classification. To leverage their common and complementary information, we adopted a recently developed Similarity Network Fusion (SNF) algorithm to fuse these networks [8].

To use SNF for our application, for each network ${\mathit{W}}_i^j$ of subject i, two kernel matrices were constructed: (1) a full kernel matrix, which was the network itself; (2) a sparse kernel matrix, which encoded the sparse yet strong connection information. Let N_u denote a set of k-nearest neighbors (the top k strongest connections) of the node u (including u itself) in ${\mathit{W}}_i^j$, then the sparse kernel ${\mathit{S}}_i^j$ could be represented as:

$${\mathit{S}}_i^j(u,v)=\{\begin{array}{cc}{\mathit{W}}_i^j(u,v)& v\in N_u\\ 0& \mathit{otherwise}\end{array}$$ (1)

where the connection between nodes v and u existed only if v was within the k-nearest neighbors of u. Based on these two kernel matrices, each network could be iteratively updated as follows:

$${({\mathit{W}}_i^j)}^{(m+1)}={\mathit{S}}_i^j\times \frac{{\sum }_{c\ne j}{({\mathit{W}}_i^c)}^{(m)}}{N-1}\times {({\mathit{S}}_i^j)}^T,c=1,\dots ,N$$ (2)

where ${({\mathit{W}}_i^c)}^{(m)}$ denotes the network ${\mathit{W}}_i^c$ for subject i at the m-th iteration and ${({\mathit{W}}_i^j)}^{(m+1)}$ is the updated ${\mathit{W}}_i^j$ after m + 1 iterations.

By interacting with other thresholded networks, ${\mathit{W}}_i^j$ can integrate the information provided by other topological views of the original network. Meanwhile, the sparse kernel matrix ${\mathit{S}}_i^j$ guides the iterative process through the strongest connections of ${\mathit{W}}_i^j$ and thus can suppress the noise effectively. From the perspective of matrix multiplication, Eq. (2) implies that the connection of any two nodes in ${\mathit{W}}_i^j$ also relies on the connections of their neighbors among other thresholded networks. In other words, if the respective neighbors of two nodes are strongly connected in other thresholded networks, their connection can be strengthened after the updates even though it may be weak itself and vice versa.

After the iterative process converged, we averaged the N networks to obtain our final fused dynamically dynamically-thresholded network for subject i:

$${\mathit{W}}_i=\frac{{\sum }_j{\mathit{W}}_i^j}{N},j=1,\dots ,N$$ (3)

Comparing to those thresholded networks ${\mathit{W}}_i^j$, the benefits of W_i are twofold. First, it doesn’t rely on any individual threshold as in ${\mathit{W}}_i^j$, and thus is less affected by noise; Second, it incorporates all the common and complementary information from all N networks ( ${\mathit{W}}_i^j$, j = 1, …, N) after SNF, so it can better represent the underlying ground truth of FC.

2.4 Classification

With the fused network W_i for each subject i, the local weighted clustering coefficients (LWCCs) x_i [11] were extracted as features. LWCCs are a the commonly used connectivity measures that compute the degree to which nodes in a graph tend to cluster together. Mathematically, for a subject i, let ${\mathit{x}}_{\mathit{i}}={[x_i^1,\dots ,x_i^L]}^T\in {ℝ}_{L\times 1}$, where L is the number of ROIs. Let d_l be the number of edges the node l connects and W_i(p, q) be the edge strength between any two nodes p and q in W_i, then $x_i^l$ can be computed as (l = 1, …, L):

$$x_i^l=\frac{2{\sum }_{p,q}{[{\mathit{W}}_i(l,p){\mathit{W}}_i(p,q){\mathit{W}}_i(q,l)]}^{1/3}}{d_l(d_l-1)}$$ (4)

Once the features were extracted, the LASSO feature selection scheme [9] was applied to select the most relevant features for MCI classification by minimizing the following objective function:

$$\underset{\mathit{a},b}{min}\frac{1}{2}\sum _{i=1}^N{(y_i-{\mathit{a}}^T{\mathit{x}}_i-b)}^2+\gamma {\Vert \mathit{a}\Vert }_1$$ (5)

where a denoted the weight coefficient vector and ||a||₁ is the l₁-norm of a. The regularization parameter γ balanced between the fitting error and the sparsity of solution; y_i and b were the class label of subject x_i and intercept, respectively. The corresponding features of non-zero components of a were selected and fed into SVM classifier for MCI classification.

3 Experimental Results

3.1 Experimental Setup

In our experiment, the step size for threshold selection is Δ = 0.01 and the number of dynamically-thresholded networks is N = 50 (Sect. 2.2). In network fusion (Sect. 2.3), k = 26 was set for the k-nearest neighbors of ${\mathit{S}}_i^j$, and the stopping criterion for iteration was $\Vert {(W_i^j)}^{(m+1)}-{(W_i^j)}^{(m)}\Vert \le 0.01$. The SLEP (http://www.yelab.net/software/SLEP/) was used for feature selection with LASSO, while the LIBSVM (https://www.csie.ntu.edu.tw/~cjlin/libsvm/) was utilized for SVM classification (Sect. 2.4).

To evaluate our proposed framework, dynamic thresholding with network fusion (DTN), we compared it with four other methods: the original Pearson’s correlation FC network (PCN), the network-wise thresholding with network fusion (NTN), the mean dynamic element-wise thresholding without fusion (MTN), and the traditional network-wise thresholding with multi-kernel learning (MKL). In PCN, we fed the original FC network directly to SVM for classification. In NTN, we generated 50 networks with the traditional network-wise thresholding and then fused them with our network fusion scheme. In MTN, we averaged over the 50 dynamic element-wise thresholded networks without network fusion for SVM classification. In MKL, 5 networks were randomly selected with network-wise thresholding and then fed into multi-kernel classification [5].

The classification performance was evaluated by the classical measures including accuracy (ACC), sensitivity (SEN), specificity (SPE), and area under the receiver operating characteristic curve (AUC). For all methods, the classification performance were evaluated through leave-one-out cross-validation.

3.2 Classification Performance

The classification results are reported in Table 1. Figure 2 plots the receiver operating characteristic (ROC) curves of all the methods. Our proposed framework outperforms all 4 comparison methods.

Table 1.

Classification performances of all methods in percentage.

Method	ACC	AUC	SEN	SPE
PCN	67.8	65.9	69.0	66.7
MKL	72.9	76.9	79.3	66.7
MTN	74.6	72.2	65.5	80.0
NTN	79.7	72.9	79.3	70.0
DTN	83.1	80.5	86.2	80.0

Fig. 2.

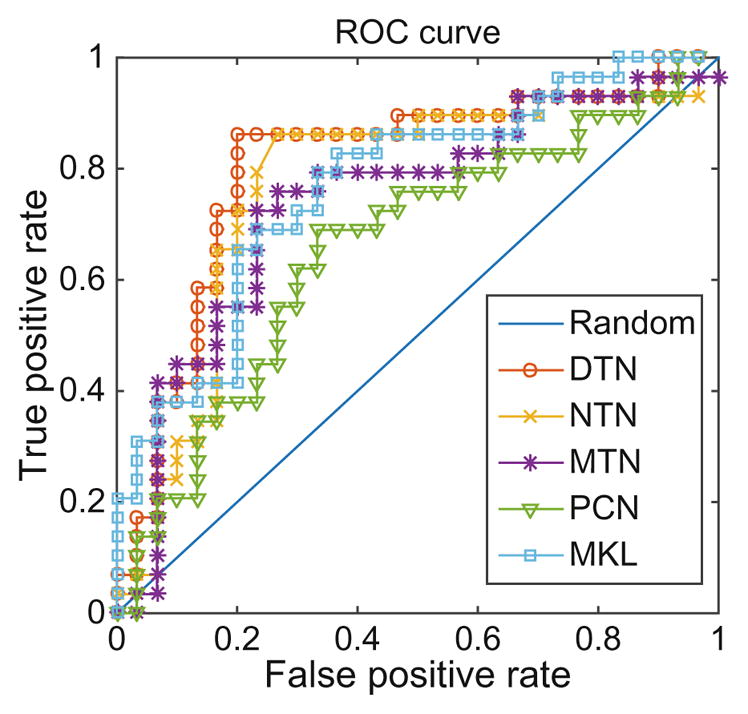
ROC curves of different methods.

Both MTN and NTN show better performance than PCN, which confirms that the two key steps, dynamic thresholding and network fusion, are both beneficial. Compared to MTN and NTN, the proposed framework DTN further improves the performance, which proves the effectiveness using the combination of both techniques. DTN achieves better performance than NTN because the dynamic element-wise thresholding, a more reasonable threshold selection scheme, which treats each connection individually and reduces the limitation of random threshold selection for the entire network. DTN outperforms MTN because the network fusion scheme can reveal the underlying topology closer to the ground truth than just simply averaging those networks. The fact that DTN acts better than MKL demonstrates that our method overcomes the drawbacks of the previous methods, and is indeed a better algorithm.

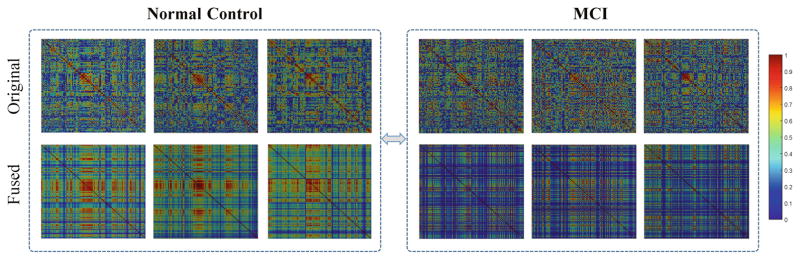
To further gain the insights of our algorithm, we randomly selected three normal controls and MCI patients from our dataset, respectively. Figure 3 illustrates their original FC networks and the dynamically-thresholded networks after fusion. Compared to the original networks, our fused networks show more block-like structures with more clear layouts. Besides, the original networks look similar between normal controls and MCI patients, while our fused networks show significant difference between the two groups. The MCI network connections seem to be much weaker, and this is consistent with the well-accepted FC breakdown concept in MCI.

Fig. 3.

Original networks and fused networks of three randomly selected normal controls (left) and MCI patients (right) respectively.

4 Conclusion

In this paper, we have proposed a novel classification framework for MCI identification with the FC networks constructed from rs-fMRI data. Unlike the previous network-wise thresholding algorithm that used a fixed value for the entire network, we developed an element-wise dynamic thresholding strategy to reduce the impact of threshold selection. The SNF fusion scheme further enhanced the FC structure by incorporating the complementary information contained in multiple dynamically-thresholded networks. The experimental results demonstrate the superior performance of our framework over other comparison methods, indicating that our method can be potentially used as a practical tool for rs-fMRI based studies.