The Robust EM-type Algorithms for Log-concave Mixtures of Regression Models

Abstract

Finite mixture of regression (FMR) models can be reformulated as incomplete data problems and they can be estimated via the expectation-maximization (EM) algorithm. The main drawback is the strong parametric assumption such as FMR models with normal distributed residuals. The estimation might be biased if the model is misspecified. To relax the parametric assumption about the component error densities, a new method is proposed to estimate the mixture regression parameters by only assuming that the components have log-concave error densities but the specific parametric family is unknown.

Two EM-type algorithms for the mixtures of regression models with log-concave error densities are proposed. Numerical studies are made to compare the performance of our algorithms with the normal mixture EM algorithms. When the component error densities are not normal, the new methods have much smaller MSEs when compared with the standard normal mixture EM algorithms. When the underlying component error densities are normal, the new methods have comparable performance to the normal EM algorithm.

1. Introduction

Suppose we have n subjects where the measurement of observation i is a d-dimensional vector x_i = (x_i1, …, x_id)^T for i = 1, …, n. Additionally, for a fixed finite integer k, x_i has a k-component mixture density of f : ℝ^d → ℝ:

$$f({\mathbf{x}}_i;\mathit{\psi })=\sum _{j=1}^k{\lambda }_j{g}_j({\mathbf{x}}_i;{\mathit{\theta }}_j),$$ (1.1)

where θ_j ∈ Θ_j ⊆ ℝ^q_j is the parameter corresponding to the component density g_j, λ_j ’s are the mixing proportions, λ_j ∈ (0, 1) for j = 1, …, k, ${\sum }_{j=1}^k{\lambda }_j=1$, and $\mathit{\psi }={({\lambda }_1,\dots ,{\lambda }_{k-1},{\mathit{\theta }}_1^T,\dots ,{\mathit{\theta }}_k^T)}^T\in {ℝ}^{{\sum }_{j=1}^k{q}_j+k-1}$. Model like (1.1) is called a finite mixture model, which provides a flexible methodology when the observations are from a number of classes with unknown class indicators.

Finite mixture models are widely used in econometrics, biology, genetics, and engineering; see, e.g. Frühwirth-Schnatter (2001), Grün & Hornik (2012), and Liang (2008) and Plataniotis (2000). For this reason, there is a rich history of studying mixture models both theoretically and practically. Everitt & Hand (1981), Lindsay (1995), and McLachlan & Peel (2000) provided great summaries of the theories, algorithms, and many technical details of mixture models.

When a random variable has a finite mixture density that depends on certain covariates, we obtain a finite mixture of regression (FMR) model. Suppose we observe univariate response y_i and p-dimensional covariate x_i, the FMR model can be written as follows:

$$f(y_i\mid {\mathbf{x}}_i;\mathit{\psi })=\sum _{j=1}^k{\lambda }_j{g}_j(y_i-{\mathbf{x}}_i^T{\mathit{\beta }}_j),$$ (1.2)

where β_j ⊆ ℝ^p, λ_j ∈ (0, 1), ${\sum }_{j=1}^k{\lambda }_j=1,\mathit{\psi }={({\lambda }_1,\dots ,{\lambda }_{k-1},{\mathit{\beta }}_1^T,\dots ,{\mathit{\beta }}_k^T)}^T\in {ℝ}^{kp+k-1}$, and g_j is a parametric distribution function, such as normal, for j-th component, j = 1, …, k.

The parametric FMR model (1.2) can be estimated through the maximum likelihood estimators. As there are usually no explicit solutions to the unknown parameters, it is natural to reformulate the likelihood as an incomplete data problem and apply the expectation-maximization (EM) algorithm for the FMR models; see, e.g. Dempster et al. (1977) and McLachlan & Krishnan (2007). Besides estimating the parameters in the FMR models, the EM algorithms also provide the probabilities that an observation belongs to certain classes. Consequently, FMR models can also be considered as unsupervised classification methods, even though clustering might not always be the goal.

Usually people assume that the densities g_j ’s belong to certain parametric families, e.g. normal distribution. These parametric assumptions are often too strong and restrictive. There exist some previous works for Model (1.1) and (1.2) with non-normal component error densities g_j ’s. Galimberti & Soffritti (2014), Song et al. (2014), Ingrassia et al. (2014), Punzo & McNicholas (2014), and Yao et al. (2014) discussed clustering and FMR model with heavy-trailed error distributions such as t or Laplace distributions. Liu & Lin (2014), Lin et al. (2007), Lin (2010), Zeller et al. (2011), and Lachos et al. (2011) explored the finite mixture models with skewed error distributions such as skewed-normal or skewed-t distribution. Verkuilen & Smithson (2012), Ingrassia et al. (2015), Punzo & Ingrassia (2016), and Bartolucci & Scaccia (2005) discussed the FMR model with other specific families such as beta or exponential distribution.

These previous works adjusted some certain model misspecification. However, most of the time, we are still not sure which parametric family we should apply, say error densities from logistic distribution vs Laplace distribution. Moreover, the parameter estimation may still be biased if the parametric model is misspecified. Another drawback is that each model requires a specific EM algorithm based on the parametric assumption. As a result, it would be valuable to have a universal EM algorithm for all, or at least some classes of the FMR models. Possible solutions include traditional nonparametric methods, e.g. Hunter & Young (2012) and Wu & Yao (2016), to adjust the parametric model mis-specification. These traditional nonparametric methods, e.g. kernel methods, bring new difficulties in selecting the tuning parameters.

To relax the parametric assumption, nonparametric shape constraints are becoming increasingly popular. In this paper, we make one shape constraint instead of a specific parametric assumption for each component density. We assume each component density g_j to be log-concave. A density g(x) is log-concave if its log-density, ϕ(x) = logg(x), is concave. Examples of log-concave densities include, but are not limited to normal, Laplace, chi-square, logistic, gamma with shape parameter greater than 1, and beta distribution with both parameters greater than 1. Log-concave densities are unimodal but unimodal densities are not necessarily log-concave. Log-concave densities have many favorable properties as described by Balabdaoui et al. (2009). To estimate the log-density ϕ(x), Dümbgen et al. (2011) proposed an estimator by maximizing a log-likelihood-type functional:

$$L(\varphi ,Q)=\int \varphi dQ-\int exp\{\varphi (x)\}dx+1,$$ (1.3)

where Q ∈ 𝒬, 𝒬 is the family of all d-dimensional distributions, ϕ ∈ Φ and Φ is the family of all concave function. For linear regression with log-concave error density, Dümbgen et al. (2011) proposed an estimator by maximizing:

$$\widehat{L}(\varphi ,\mathit{\beta },Q)=\frac{1}{n}\sum _{i=1}^n\varphi (y_i-{\mathbf{x}}_i^T\mathit{\beta })-\int exp\{\varphi (x)\}dx+1.$$ (1.4)

Such estimators, like the maximizers of (1.3) and (1.4), are called log-concave maximum likelihood estimators (LCMLEs), which were studied by, for example, Dümbgen & Rufibach (2009), Cule et al. (2010), Cule & Samworth (2010), Chen & Samworth (2013), and Dümbgen et al. (2011). Dümbgen et al. (2011) proved the existence, uniqueness, and consistency of LCMLEs for (1.3) and (1.4) under fairly general conditions. These estimators provide more generality and flexibility without any tuning parameter. For log-concave mixture models, Chang & Walther (2007) proposed a log-concave EM-type algorithm for mixture density estimation, along with the application in clustering. Hu et al. (2016) further proposed the LCMLE, which is the maximizer of a log-likelihood type functional, and proved the existence and consistency for the LCMLE for the log-concave mixture models. To the best of our knowledge, none of the existing works has studied the log-concave FMR models as well as their computational algorithms. This paper aims to fill in this gap.

In this paper, we adopt the idea of log-concave density estimation and combine it with the FMR models. The identifiability of the proposed model has been established by Wang et al. (2012), Balabdaoui & Doss (2014), and Wu & Yao (2016). We propose two EM-type algorithms, which aim at adjusting the model misspecification. The remainder of this paper is organized as follows. We introduce the basic setup, model details and notations in Section 2. We propose the EM-type algorithms for the log-concave mixtures of regression models in Section 3. Simulation studies and real data analysis are conducted in Sections 4 and 5. We end the paper with a short conclusion in Section 6.

2. Mixtures of Regression Models with Log-concave Error Densities

In this paper, we let Z be a latent variable with ℙ(Z = j) = λ_j, where λ_j ∈ (0, 1), and ${\sum }_{j=1}^k{\lambda }_j=1$ for j = 1, …, k. While given the latent variable Z = j, the response y_i has a linear relationship with x_i ∈ ℝ^p:

$$y_i={\mathbf{x}}_i^T{\mathit{\beta }}_j+{\epsilon }_j,$$ (2.1)

where β_j = (β_0,j, β_1,j, …, β_p−1,j)^T ∈ ℝ^p and ε_j is the error term with the distribution function g_j (j = 1, …, k). We assume that each component’s error distribution g_j is an unknown density function with the mean 0 for j = 1, …, k. If we do not assume a zero mean for g_j, β_j does not contain the intercept term accordingly. To relax the traditional parametric assumption about g_j, we only assume that g_j ’s are log-concave, i.e. log g_j is concave for j = 1, …, k. We define ${\mathit{\theta }}_j={({\lambda }_j,{\mathit{\beta }}_j^T)}^T$ for j = 1, …, k and $\mathit{\theta }={({\mathit{\theta }}_1^T,\dots ,{\mathit{\theta }}_k^T)}^T$. The likelihood function for the mixture of regressions model can be presented as:

$$f(y_i\mid {\mathbf{x}}_i,\mathit{\theta },\mathbf{g})=\sum _{j=1}^k{\lambda }_j{g}_j(y_i-{\mathbf{x}}_i^T{\mathit{\beta }}_j),$$ (2.2)

where $\mathit{\theta }\in \mathrm{\Theta }=\{\mathit{\theta }={({\mathit{\theta }}_1^T,\dots ,{\mathit{\theta }}_k^T)}^T\mid {\mathit{\beta }}_j\in {ℝ}^p,{\lambda }_j\in (0,1),{\sum }_{j=1}^k{\lambda }_j=1\}\subset {ℝ}^{k_p+k-1}$.

Let y = (y₁, …, y_n)^T ∈ ℝⁿ, x_i = (1, x_i,1, …, x_i,p−1)^T and X = (x₁, …, x_n)^T ∈ ℝ^n×p be the n observations for the mixture of regressions model, where n ≫ kp + k − 1. In order to estimate the model (2.2), it is natural to maximize the observed log-likelihood function:

$$\ell (\mathit{\theta },\mathbf{g}\mid \mathbf{X},\mathbf{y})=\sum _{i=1}^{n}log\sum _{j=1}^k{\lambda }_j{g}_j(y_i-{\mathbf{x}}_i^T{\mathit{\beta }}_j),$$ (2.3)

where g_j(x) = exp{ϕ_j(x)} for some unknown concave function ϕ_j(x).

3. The EM-type Algorithms for Log-concave FMR Models

We define the missing value Z = (z₁, …, z_n)^T ∈ ℝ^n×k, where z_i = (z_i1, …, z_ik)^T (i = 1, …, n ) is a k-dimensional indicator vector with its j-th element given by

$$z_{ij}=\{\begin{array}{ll}1\hfill & \text{if}({\mathbf{x}}_i,y_i)\text{belongs}\text{to}j\text{th}\text{group};\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$

Consequently, the complete log-likelihood for equation (2.3) is:

$${\ell }_c(\mathit{\theta },\mathbf{g}\mid \mathbf{X},\mathbf{y},\mathbf{Z})=\sum _{i=1}^n\sum _{j=1}^k{z}_{ij}\{log{\lambda }_j+log{g}_j(y_i-{\mathbf{x}}_i^T{\mathit{\beta }}_j)\}.$$ (3.1)

In the E-step, given the current estimate θ^(t) and $g_j^{(t)}$’s, we need to compute

$$Q(\mathit{\theta },\mathbf{g}\mid {\mathit{\theta }}^{(t)},{\mathbf{g}}^{(t)},\mathbf{X},\mathbf{y})=\mathbb{E}\{{\ell }_c(\mathit{\theta },\mathbf{g}\mid \mathbf{X},\mathbf{y},\mathbf{Z})\mid {\mathit{\theta }}^{(t)},{\mathbf{g}}^{(t)},\mathbf{X},\mathbf{y}\},$$

which is equivalent to computing

$$\begin{array}{l}{z}_{ij}^{(t+1)}=E(Z_{ij}\mid {\mathit{\theta }}^{(t)},{\mathbf{g}}^{(t)},\mathbf{X},\mathbf{y})=Pr(Z_{ij}=1\mid {\mathit{\theta }}^{(t)},{\mathbf{g}}^{(t)},\mathbf{X},\mathbf{y})\\ =\frac{{\lambda }_j^{(t)}{g}_j^{(t)}(y_i-{\mathbf{x}}_i^T{\mathit{\beta }}_j^{(t)})}{{\sum }_{h=1}^k{\lambda }_h^{(t)}{g}_h^{(t)}(y_i-{\mathbf{x}}_i^T{\mathit{\beta }}_h^{(t)})}.\end{array}$$ (3.2)

In M-step, we need to maximize the following Q function:

$$\begin{array}{l}Q(\mathit{\theta },\mathbf{g}\mid {\mathit{\theta }}^{(t)},\mathbf{X},\mathbf{y})=\sum _{i=1}^n\sum _{j=1}^k{z}_{ij}^{(t+1)}\{log{\lambda }_j+log{g}_j(y_i-{\mathbf{x}}_i^T{\mathit{\beta }}_j)\}\\ =\sum _{i=1}^n\sum _{j=1}^k{z}_{ij}^{(t+1)}log{\lambda }_j+\sum _{i=1}^n\sum _{j=1}^k{z}_{ij}^{(t+1)}log{g}_j(y_i-{\mathbf{x}}_i^T{\mathit{\beta }}_j).\end{array}$$ (3.3)

The first part of (3.3) is maximized by ${\lambda }_j^{(t+1)}=\frac{1}{n}{\sum }_{i=1}^n{z}_{ij}^{(t+1)}$, j = 1, …, k. However, for the second part, there is no explicit solution for β_j ’s and g_j ’s. Consequently, we propose to alternatively update g_j ’s and β_j ’s to maximize the second part of (3.3).

It is also well known that MLEs can be sensitive to outliers, see e.g. Yao et al. (2014) and García-Escudero et al. (2009). To overcome this problem, we further propose a robust technique, which adopts the idea of least trimmed squares (LTS), see e.g. Rousseeuw (1985) for a detailed description of LTS. For each algorithm, when updating λ_j ’s and β_j ’s in the t-th iteration (j = 1, …, k), we drop s observations with the least log-likelihood values. In that way, we sacrifice some efficiency to gain the robustness to the outliers. The number s is the trimming tuning parameter, which satisfies 0 < s < n/2. In this paper, we mainly use this trimmed idea to get a stable estimate of log-concave component error densities while enjoying its robustness when the component error densities are highly skewed or have heavy tails. Our empirical experience suggests that the choice of s = ⌊n/40⌋ works well. Note that a larger value of s would make our algorithms more robust if there are outliers in the data set and the sample size is not too small.

Our methodology is summarized as follows. First, we apply some stochastic search strategy, which will be addressed later, to create the initial value for normal mixtures of regression models from function regmixEM in R package mixtools, see Benaglia et al. (2009), until convergence. We treat the outcome of the normal mixture EM algorithm as the starting values for our EM-type algorithms, i.e. ${\mathit{\psi }}^{(0)}={({\widehat{\lambda }}_1^{(0)},\dots ,{\widehat{\lambda }}_k^{(0)},{\widehat{\mathit{\beta }}}_1^{(0)T},\dots ,{\widehat{\mathit{\beta }}}_k^{(0)T})}^T$. The normal mixture of regressions model usually provides good initial values and our proposed EM algorithm will further improve the estimate if the error density is not normally distributed. The initial estimated density g_j can be obtained by the function mlelcd in R package LogConcDEAD (Cule et al., 2009).

First, we propose the Algorithm 3.1 for the case that all components have the same error density g.

Algorithm 3.1

The EM-type algorithm when all g_j ’s are the same, i.e. g_j ≡ g. Initialize ψ⁽⁰⁾ and $z_{ij}^{(0)}$ from normal mixture EM algorithm with equal variances and initialize the trimmed index subset of size n − s, denoted by I⁽⁰⁾, which has the n − s largest log-likelihoods. Initialize g⁽⁰⁾ by the function mlelcd through fitted residuals $y_i-{\mathit{x}}_i^T{\mathit{\beta }}_j^{(0)}$ with weights $z_{ij}^{(0)}$ for i = 1, …, n, j = 1, …, k.

In t-th iteration, it consists of the following steps.

E-step

Given ψ^(t) and g^(t), we calculate

$$z_{ij}^{(t+1)}=E(Z_{ij}\mid \mathit{X},\mathit{y},{\mathit{\psi }}^{(t)},g^{(t)})=\frac{{\lambda }_j^{(t)}{g}^{(t)}(y_i-{\mathit{x}}_i^T{\mathit{\beta }}_j^{(t)})}{{\sum }_{h=1}^k{\lambda }_h^{(t)}{g}^{(t)}(y_i-{\mathit{x}}_i^T{\mathit{\beta }}_h^{(t)})},$$ (3.4)

for i = 1, …, n, j = 1, …, k.

M-step

1. Calculate the log-likelihood value for each observation:

   $${\ell }_i^{(t)}=\ell ({\mathit{x}}_i,y_i\mid g^{(t)},{\mathit{\psi }}^{(t)})=log\sum _{j=1}^k{\lambda }_j^{(t)}{g}^{(t)}(y_i-{\mathit{x}}_i^T{\mathit{\beta }}_j^{(t)}),$$

   from i = 1, …, n. Update the trimmed index subset of size n − s, denoted by I^(t+1), which has the n − s largest log-likelihoods.

2. Update λ simply through

   $${\lambda }_j^{(t+1)}=\frac{1}{n-s}\sum _{i\in I^{(t+1)}}{z}_{ij}^{(t+1)},j=1,\dots ,k.$$ (3.5)
3. Update β:

   $${\stackrel{\sim }{\beta }}_j^{(t+1)}\leftarrow arg\underset{{\mathit{\beta }}_j}{max}\sum _{i\in I^{(t+1)}}{z}_{ij}^{(t+1)}log{g}^{(t)}(y_i-{\mathit{x}}_i^T{\mathit{\beta }}_j),j=1,\dots ,k.$$ (3.6)
4. Shift the intercept of ${\stackrel{\sim }{\mathit{\beta }}}_j^{(t+1)}$ so that the residuals have a zero mean.

   $${\widehat{\mathit{\beta }}}_j^{(t+1)}=({\widehat{\beta }}_{j,0}^{(t+1)},{\stackrel{\sim }{\beta }}_{j,1}^{(t+1)}\dots ,{\stackrel{\sim }{\beta }}_{j,p-1}^{(t-1)}),$$
   where

   $${\widehat{\beta }}_{j,0}^{(t+1)}={\stackrel{\sim }{\beta }}_{j,0}^{(t+1)}+c_j^{(t+1)}\mathit{with}{c}_j^{(t+1)}=\frac{1}{n-s}\sum _{i\in I^{(t+1)}}{z}_{ij}^{(t+1)}(y_i-{\mathit{x}}_i^T{\stackrel{\sim }{\mathit{\beta }}}_j^{(t+1)}),$$

   for j = 1, …, k.

5. Update g by:

   $$g^{(t+1)}\leftarrow arg\underset{g\in \mathcal{G}}{max}\sum _{i=1}^n\sum _{j=1}^k{z}_{ij}^{(t+1)}logg(y_i-{\mathit{x}}_i^T{\widehat{\mathit{\beta }}}_j^{(t+1)}).$$ (3.7)

   where 𝒢 is the family of all log-concave densities.

In (3.6), β_j is updated through the function optim in R. The evaluation of $log{\widehat{g}}^{(t)}(y_i-{\mathit{x}}_i^T{\mathit{\beta }}_j^{(t+1)})$ is calculated through the function dlcd in R package LogConcDEAD. In (3.7), the error density g is updated through the function called mlelcd in the R package LogConcDEAD through kn fitted residuals $y_i-{\mathit{x}}_i^T{\mathit{\beta }}_j^{(t+1)}$ with weights $z_{ij}^{(t+1)}$, i = 1, …, n, j = 1, …, k. The algorithm is terminated if either t_max of iterations has been reached, or if ℓ^(t+1) − ℓ^(t) < 10⁻⁸, where ${\ell }^{(t)}={\sum }_{i\in I^{(t)}}{\ell }_{(i)}^{(t)}$ is the trimmed log-likelihood.

The algorithm usually converges after 10 iterations for p = 2 or 3. For each iteration, the most time consuming step is the (E) step for the density updating, which usually takes about 20 seconds for a sample size of 400. Consequently, the average computational time is about 3–5 minutes.

To avoid the local maximum, we follow the similar stochastic search strategy proposed by Dümbgen et al. (2013). We restart the entire algorithm 20 times. For each restart, we randomly sample ⌊αn⌋ (α ∈ (0, 1)) observations k times, fit k simple linear regressions, obtain the k groups of coefficients, and treat them as the starting values of β’s in the normal EM algorithm for k components. Additionally, we generate λ_j ’s from a Uniform(0,1) distribution, scale them so that their sum is one, and treat them as the starting values of the mixing proportions in the normal EM algorithm. We then fit a normal FMR model, obtain the estimated coefficients, and use them as the initial values for our algorithm. We repeat this procedure 20 times and select the solution with the highest trimmed likelihood to avoid getting stuck in a local maximum.

The LCMLEĝ has been studied by Walther (2002) and Rufibach (2007). Here, we briefly summarize the results. Given i.i.d. data X₁, …, X_n which follow a distribution g, the Log-concave Maximum Likelihood Estimator (LCMLE) ĝ exists uniquely and has support on the convex hull of the dataset (by Theorem 2 of Cule et al. (2010)). In addition, log ĝ is a piecewise linear function whose knots are a subset of {X₁, …, X_n}. Walther (2002) and Rufibach (2007) provided algorithms for computing ĝ(X_i), i = 1, …, n. The entire log-density log ĝ can be computed by linear interpolation between log ĝ(X_(i)) and log ĝ(X_(i+1)). Walther (2002) and Rufibach (2007) also pointed out that it is natural to apply weights in the density estimation step of the EM-type algorithms. The $z_{ij}^{(t+1)}$’s can be viewed as weights for the kn fitted residuals $y_i-{\mathbf{x}}_i^T{\mathit{\beta }}_j^{(t+1)}(i=1,\dots ,n,j=1,\dots ,k)$, while estimating the log-concave density g for M-step 3 in our algorithms.

A more general case is that the components’ error terms do not share a common distribution, i.e. at least one g_j is different. Consequently, we propose the following Algorithm 3.2. The main difference is that, in Algorithm 3.2, each component density g_j is estimated by the iterative residuals only from the according component class, instead of being estimated by the entire residuals from all components in Algorithm 3.1.

Algorithm 3.2

The EM-type algorithm when g_j ’s are different.

Initialize ψ⁽⁰⁾ and $z_{ij}^{(0)}$ from normal mixture EM algorithm with unequal variances and initialize the trimmed subset of size n − s, denoted by I⁽⁰⁾, which has the n − s largest log-likelihoods. For j ∈ {1, …, k}, initialize $g_j^{(0)}$ by the function mlelcd through fitted residuals $y_i-{\mathit{x}}_i^T{\mathit{\beta }}_j^{(0)}$ with weights $z_{ij}^{(0)}$ for i = 1, …, n.

In t-th iteration, it consists of the following steps.

E-step

Given ψ^(t) and g^(t), we calculate

$$z_{ij}^{(t+1)}=E(Z_{ij}\mid \mathit{X},\mathit{y},{\mathit{\psi }}^{(t)},g^{(t)})=\frac{{\lambda }_j^{(t)}{g}_j^{(t)}(y_i-{\mathit{x}}_i^T{\mathit{\beta }}_j^{(t)})}{{\sum }_{h=1}^k{\lambda }_h^{(t)}{g}_h^{(t)}(y_i-{\mathit{x}}_i^T{\mathit{\beta }}_h^{(t)})},$$ (3.8)

for i = 1, …, n, j = 1, …, k.

M-step

1. Calculate the log-likelihood value for each observation:

   $${\ell }_i^{(t)}=\ell ({\mathit{x}}_i,y_i\mid {\mathit{g}}^{(t)},{\mathit{\psi }}^{(t)})=log\sum _{j=1}^k{\lambda }_j^{(t)}{g}_j^{(t)}(y_i-{\mathit{x}}_i^T{\mathit{\beta }}_j^{(t)}),$$

   for i = 1, …, n. Update the trimmed subset of size n − s, denoted by I^(t+1), which has the n − s largest log-likelihoods.

2. Update λ simply through

   $${\lambda }_j^{(t+1)}=\frac{1}{n-s}\sum _{i\in I^{(t+1)}}{z}_{ij}^{(t+1)},j=1,\dots ,k.$$ (3.9)
3. Update β:

   $${\stackrel{\sim }{\mathit{\beta }}}_j^{(t+1)}\leftarrow arg\underset{{\mathit{\beta }}_j}{max}\sum _{i\in I^{(t+1)}}{z}_{ij}^{(t+1)}log{g}_j^{(t)}(y_i-{\mathit{x}}_i^T{\mathit{\beta }}_j),j=1,\dots ,k.$$ (3.10)
4. Shift the intercept of ${\stackrel{\sim }{\mathit{\beta }}}_j^{(t+1)}$ so that the residuals have a zero mean.

   $${\widehat{\mathit{\beta }}}_j^{(t+1)}=({\widehat{\beta }}_{j,0}^{(t+1)},{\stackrel{\sim }{\beta }}_{j,1}^{(t+1)}\dots ,{\stackrel{\sim }{\beta }}_{j,p-1}^{(t+1)}),$$
   where

   $${\widehat{\beta }}_{j,0}^{(t+1)}={\stackrel{\sim }{\beta }}_{j,0}^{(t+1)}+c_j^{(t+1)}\mathit{with}{c}_j^{(t+1)}=\frac{1}{n-s}\sum _{i\in I^{(t+1)}}{z}_{ij}^{(t+1)}(y_i-{\mathit{x}}_i^T{\stackrel{\sim }{\mathit{\beta }}}_j^{(t+1)}),$$

   for j = 1, …, k.

5. Update g_j by:

   $$g_j^{(t+1)}\leftarrow arg\underset{g_j\in \mathcal{G}}{max}\sum _{i=1}^n{z}_{ij}^{(t+1)}log{g}_j(y_i-{\mathit{x}}_i^T{\widehat{\mathit{\beta }}}_j^{(t+1)}).$$ (3.11)

   for j = 1, …, k, where 𝒢 is the family of all log-concave densities.

In (3.11), the j-th component density g_j is updated through the function called mlelcd in the R package LogConcDEAD through n fitted residuals $y_i-{\mathit{x}}_i^T{\mathit{\beta }}_j^{(t+1)}$ with weights $z_{ij}^{(t+1)}$, i = 1, …, n for j ∈ {1, …, k}. The algorithm is terminated if either the maximum number of iterations t_max has been reached, or if ℓ^(t+1) − ℓ ^(t) < 10⁻⁸, where ${\ell }^{(t)}={\sum }_{i\in I^{(t)}}{\ell }_i^{(t)}$ is the trimmed log-likelihood for t-th iteration.

4. Numerical Experiments

4.1. Simulation setup

In this section, we study the performance of our EM-type algorithms and compare them with the according EM algorithms for the normal FMR models. For the convenience purposes, in the following text and tables, we denote Algorithm 3.1 as “LCD-EM1” and compare it with the normal EM algorithm with equal variance and similar trimming techniques, denoted as “Normal-EM1”. We also denote Algorithm 3.2 as “LCD-EM2” and compare it with the normal EM algorithm with unequal variance and similar trimming techniques, denoted as “Normal-EM2”.

We generate data from 2-component log-concave FMR models:

$$y_i=\{\begin{array}{lll}{\mathit{\beta }}_1^T{\mathbf{x}}_i+e_{i,1}\hfill & \text{with}\text{probability}\hfill & \lambda ;\hfill \\ {\mathit{\beta }}_2^T{\mathbf{x}}_i+e_{i,2}\hfill & \text{with}\text{probability}\hfill & 1-\lambda .\hfill \end{array}$$ (4.1)

For Model I through Model VI, we set x_i = (1, x_1,i)^T, where x_1,i’s are independently generated from Uniform(−1, 3). We let λ = 0.3, β₁ = (β_0,1, β_1,1)^T = (0, 2)^T, and β₂ = (β_0,2, β_1,2)^T = (−2, 5)^T . For Model VII and Model VIII, we set x_i = (1, x_1,i, x_i,2)^T, where x_1,i’s and x_1,2’s are both independently generated from Uniform(−1, 3). We let λ = 0.3, β₁ = (β_0,1, β_1,1, β_2,1)^T = (0, 2, 1)^T, and β₂ = (β_0,2, β_1,2, β_2,2)^T = (−2, 5, 3)^T . We let e_i,1 = e_i,2 ≡ e_i, where e_i’s are independently and identically generated based on the parametric form from Table 1. For all eight models, we generate data for a finite sample size of n = 400.

Table 1.

The error densities for Model I to Model VIII and the summary of the according features.

	ei’s distribution	log-concave	symmetric
Model I	Standard Normal: N(0, 1)	Yes	Yes
Model II/VII	Centered Beta: 3(Beta(1, 2) − 1/3)	Yes	No
Model III/VIII	Centered Exponential: Exp(2) − 2	Yes	No
Model IV	Standard Laplace: Laplace(0, 1)	Yes	Yes
Model V	Centered Beta: 4(Beta(0.25, 0.75) − 1/4)	No	No
Model VI	Centered t: t4	No	Yes

For Model IX to Model XI, we let x_i = (1, x_1,i)^T, where x_1,i’s are independently generated as Uniform(−1, 3). We set n = 400, λ = 0.4, β₁ = (β_0,1, β_1,1)^T = (0, 1)^T, and β₂ = (β_0,2, β_1,2)^T = (−3, 4)^T . The component error densities are generated based on the parametric form of Model IX to Model XI in Table 2.

Table 2.

The error densities for Model IX, X, and XI.

	ei,1’s distribution	ei,2’s distribution
Model IX	N(0, 1)	N(0, 0.25)
Model X	3(Beta(1, 2) − 1/3)	N(0, 0.25)
Model XI	$\frac{2}{3}\mathit{Laplace}(0,1)$	$\frac{2}{3}(\mathit{Exp}(2)-2)$

For all nine models, we repeat the simulation N = 200 times. We visualize the generated data of Model III and IX for a single replicate in Figure 1. For both replicates, our proposed algorithm has monotone increasing log-likelihood.

Figure 1.

Generated data for Model III and XI (green and red line represent the true coefficients for the two components) and the monotone increasing log-likelihood value in each iteration.

It is also valuable to compare our proposed algorithm with some other parametric EM algorithms that are proposed in the literature. In this study, we select two popular ones, EM algorithm for Laplace-FMR models (denoted as “Laplace-EM”) and EM algorithm for t-FMR models (denoted as “t-EM”). We compare the same criteria in Model IV and Model VI.

There is a well-known label switching issue when sorting the labels for mixture models (Stephens, 2000; Yao & Lindsay, 2009). In this paper, we adopt the method of Yao (2015) to find the labels by minimizing the distance between the estimated classification probabilities and the true labels over different permutations. After sorting the labels, we compute the MSE of all parameters over the N replicates, i.e. $\mathit{MSE}=N^{-1}{\sum }_{h=1}^N{({\widehat{\mathit{\theta }}}_h-{\mathit{\theta }}_0)}^2$, where ${\widehat{\mathit{\theta }}}_h={({\widehat{\mathit{\beta }}}_1^T,{\widehat{\mathit{\beta }}}_2^T,\widehat{\lambda })}_h^T$ is the vector of parameter estimates of the h-th replicate and θ₀ is the true value for the vector of the parameters. As the mixtures of regression models serve as a methodology for classification, we compute the average of misclassification numbers (AMN) as well.

4.2. Selecting the trimming constant s and the stochastic search proportion α

One important key step for both algorithms is to select the appropriate trimming constant s and the stochastic search proportion α. Typically s is a relatively small positive constant. If s is too small (approaching zero), the algorithms do not have enough robustness powers against the outliers. If s is too large, we scarify too much on the efficiency. Choosing the trimming tuning parameters adaptively is not easy and has long been a challenging problem. One option is to choose s using the graphical way suggested by Neykov et al. (2007). In practice, we use s = 0.01–0.05. In our later simulation example, we choose s = 0.025, which means we drop 2.5% of the observations while updating the parameter. Table 3 shows the simulation results of MSE’s and AMN’s over N = 200 replicates for Model III with different trimming size. We observe that the trimming size between 0.01 or 0.05 is appropriate.

Table 3.

Simulation results for Model III with different trimming size.

Model	Method	β0,1	β1,1	β0,2	β1,2	λ	AMN
III	LCD-EM1(s=0)	0.01900	0.05215	0.02505	0.01878	0.00500	48.15
	LCD-EM1(s=0.01)	0.01770	0.05215	0.02474	0.01534	0.00307	48.02
	LCD-EM1(s=0.025)	0.01095	0.02746	0.02039	0.01676	0.00304	47.49
	LCD-EM1 (s=0.05)	0.01010	0.01910	0.02778	0.02018	0.00359	51.60
	LCD-EM1 (s=0.10)	0.01691	0.02437	0.02855	0.03010	0.00313	51.45

On the other hand, the selection of α is not that sensitive as long as α ≤ 0.5. We take Model II as an example. In Figure 2, we plot the R(β) vs different α’s, where $R(\mathit{\beta })=N^{-1}{\sum }_{h=1}^N{\Vert {\widehat{\mathit{\beta }}}_h-{\mathit{\beta }}_0\Vert }^2$, β₀ is the vector of true coefficient values, and β̂_h is the estimator for replicate h. We observe that R(β) are almost at the same level for α ∈ (0, 0.5). As α approaching 1, though not very frequently, the algorithm is more likely to get stuck in some local maximum estimator instead of the local maximum, as we are repeatedly using the same starting value. In practice, we choose α = 0.10, which usually works very well.

Figure 2.

Select Stochastic Search Proportion α

4.3. Simulation results

Table 4 displays the MSEs of parameter estimates (the value of Model IV and Model VI are multiplied by 10) and the average of misclassification numbers over N = 200 simulations for Algorithm 3.1. For the density which is not normally distributed, even is not log-concave (Model V and VI), Algorithm 3.1 demonstrates significant improvement over the traditional normal mixture EM algorithm in terms of much smaller MSE. Especially for Model II, III and V, many MSEs from LCD-EM1 are 30% less than those from the Normal-EM1. This phenomena is still true when we increase the dimensionality. Table 5 display the simulation results for p = 3. For Model VII and VIII, we still observe much smaller MSEs for LCD-EM1 when comparing with Normal-EM1.

Table 4.

Simulation results for Model I–VI.

Model	Method	β0,1	β1,1	β0,2	β1,2	λ	AMN
I	LCD-EM1	0.03096	0.01028	0.00874	0.00380	0.00081	41.55
	Normal-EM1	0.02671	0.00992	0.00819	0.00348	0.00072	41.43
II	LCD-EM1	0.00847	0.00273	0.00273	0.00051	0.00101	26.95
	Normal-EM1	0.01310	0.00341	0.00416	0.00134	0.00671	29.68
III	LCD-EM1	0.01095	0.02746	0.02039	0.01676	0.00304	47.49
	Normal-EM1	0.14997	0.04237	0.038357	0.03090	0.00402	62.17
IV	LCD-EM1	0.03794	0.01526	0.01304	0.00475	0.00152	54.25
	Normal-EM1	0.05371	0.01558	0.01538	0.00686	0.00146	55.86
	Laplace-EM	0.03314	0.02184	0.01404	0.00354	0.00102	54.08
V	LCD-EM1	0.01639	0.00317	0.00695	0.00031	0.00113	33.13
	Normal-EM1	0.05458	0.01504	0.02268	0.00480	0.00121	51.66
VI	LCD-EM1	0.01021	0.02783	0.01654	0.01300	0.00245	53.45
	Normal-EM1	0.01304	0.03233	0.02011	0.01813	0.00236	54.91
	t-EM	0.01421	0.01367	0.00816	0.01416	0.00257	52.08

Table 5.

Simulation results for Model VII–VIII.

Model	Method	β0,1	β1,1	β2,1	λ
VII	LCD-EM1	0.00001	0.00046	0.00224	0.00040
	Normal-EM1	0.00018	0.00589	0.00452	0.00158
VIII	LCD-EM1	0.04092	0.00027	0.01603	0.00037
	Normal-EM1	0.19841	0.00022	0.09888	0.00040
Model	Method	β0,2	β1,2	β2,2	AMN
VII	LCD-EM1	0.00163	0.00062	0.00051	22.32
	Normal-EM1	0.01002	0.00139	0.00247	24.38
VIII	LCD-EM1	0.00939	0.00009	0.00001	36.29
	Normal-EM1	0.03050	0.00440	0.00436	47.90

When the error density truly comes from the specific parametric family, the new algorithm still has comparable performance. The MSEs of LCD-EM1 is almost the same or only slightly worse than the according parametric EM algorithms for Model I/IV/VI. Notice that in most cases, we are unsure about the component densities and which parametric EM algorithm we should apply. In that case, our proposed algorithm shows great flexibility. After fitting this EM algorithm, one could characterize the component densities quite well and can further select the appropriate parametric EM algorithm to get further precisions.

To show the performance of Algorithm 3.2, we report the result over 200 replicates and compare the same criteria as we did for (4.1). Similar phenomena (shown in Table 6) are observed for Algorithm 3.2. For the component that truly comes from normal distribution (Model IX and Component 2 of Model X), our proposed algorithm has comparable performance to the normal EM algorithm with unequal variances and a similar trimming technique. For the components which are misspecified (Model XI and component 1 of Model X), potential improvements are gained if we apply LCD-EM2 instead of the Normal-EM2.

Table 6.

Simulation results for Model IX–XI.

Model	Method	β0,1	β1,1	β0,2	β1,2	λ	AMN
IX	LCD-EM2	0.01473	0.00700	0.00187	0.00088	0.00117	30.21
	Normal-EM2	0.01390	0.00551	0.00175	0.00081	0.00087	29.88
X	LCD-EM2	0.00543	0.00122	0.00199	0.00080	0.00084	26.97
	Normal-EM2	0.00633	0.00266	0.00183	0.00073	0.00075	27.89
XI	LCD-EM2	0.00658	0.00436	0.03836	0.00004	0.00022	49.20
	Normal-EM2	0.01943	0.01671	0.08099	0.00004	0.00185	61.28

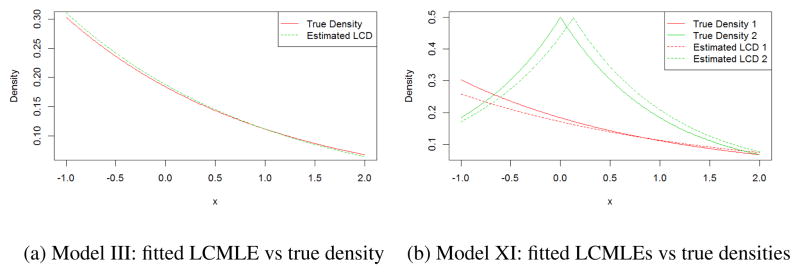
To further illustrate the performance of LCMLE for a single replicate, Figure 3a shows the fitted LCMLE for a single replicate of Model III’s simulation. The fitted error density by Algorithm 3.1 (green dashed line) approximates the true density (red solid line) well, even under a finite sample size of 400. Similar phenomena holds for Algorithm 3.2. The fitted log-concave error densities for the two components (red and green dashed lines) approximate the true densities (red and green solid line) for both two components well under a finite sample size of 400 for Model XI.

Figure 3.

Fitted LCMLE for Model III and XI vs the true densities.

4.4. Classification results

One important feature of the FMR model is that it serves as a tool of unsupervised learning. Consequently, we compare the average number of misclassifications (AMN’s) among the 200 replicates in Table 4 and Table 6. For Model I and Model VII, the average misclassification numbers for our EM-type algorithms are almost the same or only a little bit higher than the normal EM algorithm with similar trimming techniques. When the models are misspecified, the average misclassification numbers obtained from log-concave FMRs are smaller than those from the normal mixture EM algorithm with similar trimming techniques.

To further illustrate the classification result, we show the classification results for every replicate in Model I, III, IX and XI. In Figure 4, each point represents a single replicate. The x-axis represents the number of misclassifications by normal mixture EM algorithm. The y-axis represents the number of misclassifications by our log-concave mixture EM algorithm. We observe significant improvement in the sense of misclassification rates when the models are misspecified (in Figure 4b and 4d, the majority of points are under the identical line). When the component error densities are indeed normal, we observe no significant penalties if we apply the log-concave EM algorithm (Figure 4a and 4c).

Figure 4.

Numbers of misclassifications: normal mixture EM algorithm vs log-concave mixture EM algorithm for mixtures of regression models. The solid lines represents the identity.

4.5. Robustness to outliers

We artificially create Model XII, which has the setup of 4.1 with x_i = (1, x_1,i)^T, where x_1,i’s are independently generated as Uniform(−1, 3). We set λ = 0.3, β₁ = (β_0,1, β_1,1)^T = (0, 2)^T, and β₂ = (β_0,2, β_1,2)^T = (−1, 2)^T. We let e_i as Laplace(0,1) and artificially replace 10 observations (2.5%) with the extreme outliers. We generated five y values at x = −1 from a Uniform(−15, −10). We also generated another five y values at x = 2 from a Uniform(20, 25).

We report the similar criteria in Table 7. We observe that combining log-concave EM algorithm with trimming has the best robustness against the non-normal distributed density and outliers.

Table 7.

Simulation results for Model XII.

Model	Method	β0,1	β1,1	β0,2	β1,2	λ	AMN
XII	LCD-EM1(s=0)	0.12227	0.11354	0.02471	0.00086	0.00019	54.05
	LCD-EM1(s=0.01)	0.08403	0.01152	0.02666	0.00084	0.00009	53.80
	LCD-EM1 (s=0.025)	0.03180	0.00013	0.02359	0.00047	0.00001	53.35
	LCD-EM1 (s=0.05)	0.05297	0.00427	0.02595	0.00043	0.00015	53.35
	Normal-EM1 (s=0)	0.16953	0.22098	0.20755	0.17174	0.00423	66.35
	Normal-EM1 (s=0.025)	0.14019	0.04473	0.05549	0.16231	0.00459	65.35
	Normal-EM1 (s=0.05)	0.03666	0.02956	0.09437	0.02881	0.00348	64.75

5. Data Analysis

The tone dataset (from package mixtools) contains 150 trials from the same musician; see Cohen (1980) for a detailed description. In each trial, a fundamental tone, which was purely determined by a stretching ratio, was first provided to the musician. Then the musician tuned the tone one octave above. The tuning ratio, which was measured as the adjusted tone divided by the fundamental tone, was recorded. The purpose of this experiment was to demonstrate the “two musical perception theory”. We give the scatter plot of the data in Figure 5.

Figure 5.

Tone data from the tone perception study of Cohen (1980).

For the entire dataset, by applying Algorithm LCD-EM1 with k = 2, we obtain the fitted coefficients (shown as the solid lines in Figure 5) and the fitted log-likelihood value. We refit the data with Algorithm Normal-EM1, and report the same criteria as we did for Algorithm 3.1.

To further demonstrate the prediction power of Algorithms 3.1, we apply a 10-folder cross validation to the data set. Denote the full data set as 𝒟. We randomly partition 𝒟 into a training set ℛ_h and a testing set 𝒯_h with the property 𝒟 = ℛ_h + 𝒯_h for h = 1, …, H, where H = 10. For each folder h ∈ 1, …, H, we estimated the parameters ${\widehat{\lambda }}_j^h$’s and ${\widehat{\mathit{\beta }}}_j^h$’s, as well as the estimated log-concave density g^h through the training set ℛ_h. We then calculate the following two types of mean square errors:

• $E_1=H^{-1}{\sum }_{h=1}^H{\sum }_{i\in {\mathcal{T}}_h}{\sum }_{j=1}^k{\widehat{p}}_{ij}^h\{{(y_i-{\mathbf{x}}_i^T{\widehat{\mathit{\beta }}}_j^h)}^2\}$;

• $E_2=H^{-1}{\sum }_{h=1}^H{\sum }_{i\in {\mathcal{T}}_h}{min}_j\{{(y_i-{\mathbf{x}}_i^T{\widehat{\mathit{\beta }}}_j^h)}^2\}$;

  where ${\widehat{p}}_{ij}^h$ is the estimated probability that (x_i, y_i) is from j-th component for folder h:

  $${\widehat{p}}_{ij}^h=\frac{{\widehat{\lambda }}_j^h{g}^h(y_i-{\mathbf{x}}_i^T{\widehat{\mathit{\beta }}}_j^h)}{{\sum }_{m=1}^k{\widehat{\lambda }}_m^h{g}^h(y_i-{\mathbf{x}}_i^T{\widehat{\mathit{\beta }}}_m^h)},$$

  for i ∈ 𝒯_h and j ∈ {1, …, k}.

We report the same criteria based on the coefficients obtained by the Normal-EM1 algorithm. The results of fitting the log-concave FMR model and the normal FMR model are summarized in Table 8. The fitted result obtained by LCD-EM1 has a much larger log-likelihood. Additionally, Algorithm 3.1 provides much smaller mean square errors for both E₁ and E₂, which indicates that our proposed algorithm predicts the response more precisely than the traditional normal EM algorithm.

Table 8.

Estimated parameters and other characteristics of LCD-EM algorithm and Normal-EM algorithm for the tone dataset.

	LCD-EM1		Normal-EM1
	Comp 1	Comp 2	Comp 1	Comp 2
β0	−0.0143	1.9488	−0.0388	1.8924
β1	0.9968	0.0263	0.9989	0.0559
λ	0.4253	0.5747	0.3256	0.6744
ℓ	170.91		158.54
E1	0.0039		0.0105
E2	0.0033		0.0041

6. Conclusion and Discussion

This paper proposed two robust EM-type algorithms for the log-concave mixtures of regression models. These algorithms provide more flexibility, which allows a large family of error densities in the mixtures of regression models. By estimating the log-concave error density in every M-step of our algorithms, the log-concave maximum likelihood estimator corrects the model misspecification, e.g. adjusting skewness and heavy tails when the error distribution is not normal, in a nonparametric way without specifying the families of error densities.

Through numerical studies, our proposed algorithms have better performances than the parametric EM algorithms whose parametric families are misspecified. We also observe no significant penalties for applying our proposed algorithms instead of the according EM algorithms which correctly characterize the error densities in the FMR model.

Future work includes, but is not limited to the theoretical investigation of consistency and convergence properties for the log-concave FMR models, as an extension of Section 3 of Dümbgen et al. (2011). It would also be a challenging task to prove the ascending properties for these nonparametric EM algorithm.