Comparison of Planar, PET and Well-counter Measurements of Total Tumor Radioactivity in a Mouse Xenograft Model

Abstract

Introduction

Quantitative small animal radionuclide imaging studies are often carried out with the intention of estimating the total radioactivity content of various tissues such as the radioactivity content of mouse xenograft tumors exposed to putative diagnostic or therapeutic agents. We show that for at least one specific application, positron projection imaging (PPI) and PET yield comparable estimates of absolute total tumor activity and that both of these estimates are highly correlated with direct well-counting of these same tumors. These findings further suggest that in this particular application, PPI is a far more efficient data acquisition and processing methodology than PET.

Methods

Forty-one athymic mice were implanted with PC3 human prostate cancer cells transfected with PSMA (PC3 PSMA (+)) and one additional animal (for a total of 42) with a control blank vector (PC3 PSMA (−)). All animals were injected with [¹⁸F] DCFPyl, a ligand for the PC3 PSMA (+) receptor, and imaged for total tumor radioactivity with PET and PPI. The tumors were then removed, assayed by well counting for total radioactivity and the values between these methods intercompared.

Results

PET, PPI and well-counter estimates of total tumor radioactivity were highly correlated (R² > 0.98) with regression line slopes near unity (0.95 < slope ≤ 1.02) and intercepts near zero (−0.001 MBq ≤ intercept ≤ 0.004 MBq).

Conclusion

Total mouse xenograft tumor radioactivity can be measured with PET or PPI with an accuracy comparable to well counting if certain experimental and pharmacokinetic conditions are met. In this particular application, PPI is significantly more efficient than PET in making these measurements.

Animal Care

Animal care was provided in accordance with the procedures outlined in the “Guide for Care and Use of Laboratory Animals” (National Research Council; 1996; National Academy Press; Washington, D.C.)

Introduction

Small animal imaging studies with positron-emitting radionuclides are often carried out with multi-modality tomographic imaging devices that, in principle, provide the technical means for assaying any body organ for total radioactivity content without significant contamination from radioactivity in surrounding organs. While review articles are available that describe in detail virtually all confounding factors that can arise in general small animal imaging studies [1, 2], there is little direct, published experimental evidence regarding the accuracy of these methods when applied in actual small animal imaging experiments [3]. Moreover, PET imaging is also accompanied by practical complications that often slow data acquisition and analysis of these data, e.g. the need for CT imaging for attenuation correction, the need for tomographic image reconstruction and effective definition of many 2D ROIs to define an organ volume, etc. When the number of animals studied is large, as is often the case in mouse tumor imaging, this requirement alone can impose a significant time delay between study onset and final results.

Planar projection imaging of tumor-bearing mice is a potential alternative method for estimating total tumor radioactivity. Projection imaging takes advantage of the fact that gamma radiation from a low mass target volume passes largely unaffected through tissue and sums within the single ROI outlining that projected volume in 2D. As a result, total radioactivity in that target volume can, in principle, be obtained simply by scaling this summed ROI count rate by a factor that converts count rate to a unit of radioactivity, e.g. MBq. Image reconstruction and definition of many ROIs are thus avoided and the total radioactivity content of a tumor xenograft can, at least in principle, be determined immediately at the end of data acquisition.

However, there is a significant objection to quantitative planar projection imaging: the total raw tumor count rate must generally be corrected for an unknown “background” count rate that emanates from tissues surrounding the tumor and appears in the 2D tumor ROI. This complication can be mitigated in part by placing a tumor xenograft at a body location on the mouse favorable to planar projection imaging, a choice unavailable in a “general” radionuclide imaging study. Here, we sought to minimize this background contribution by placing the tumor on the right side of the chest of each animal just below the shoulder and away from the heart and as far from the kidneys (the excretion route for many drugs) and bladder as possible. When imaged in a standard posterior-anterior (PA) projection, a tumor with surrounding skin/tissue in this location can, depending on size, be largely surrounded by air and, as a result, background contamination should be reduced. It would be expected, therefore, that a simple background correction scheme (if needed) would suffice to correct for whatever background might remain. We also hypothesized that an attenuation correction could be implemented for planar imaging that depended on the tumor mass relative to the mass of a spherical calibration “phantom” imaged in the same physical environment as the animals.

If either PET or PPI imaging methods are to be considered reliable, both must yield accurate estimates of total tumor radioactivity and, arguably, the “gold standard” against which these methods are best judged is direct well-counting of these same excised tumors. Well-counting of these tumors is independent of all assumptions that are required by the imaging methods (although dependent on other conditions) and thus provides an independent estimator of total tumor radioactivity content. Accordingly, in order to test the hypothesis that both imaging methods would yield accurate measurements of total tumor radioactivity, we implanted nude mice with prostate specific membrane antigen (PSMA) (+) PC3 tumor cells strategically located as described above. After one to two week’s growth, we imaged these animals sequentially, first with the BioPET/CT [4] and then with the PPI [5]. After surgical excision, we compared well-counter estimates of total activity in these same tumors with total tumor activity calculated from these images. All animals were injected with 2-(3-{1-carboxy-5-[(6-[F]fluoro-pyridine-3-carbonyl)-amino]-pentyl}-ureido)-pentanedioic acid, ([¹⁸F] DCFPyL), a radiotracer ligand developed for prostate cancer imaging with high affinity for the PC3 PSMA (+) receptor [6, 7].

Methods and Materials

Animal Model

Forty-one athymic mice (nu/nu, 8 to 9 weeks old at the time of study, mean weight: 19.3 ± 2.2 g, Charles River Laboratories, Wilmington, MA) were implanted with 2 to 8 million PC3 human prostate cancer cells transfected with PSMA (PC3 PSMA (+)) [8]. One additional animal (for a total of 42) received PC3 cells transfected with a control blank vector (PC3 PSMA (−)). Importantly, all cells were injected below the right shoulder on the lateral chest region of each mouse. Injection of these cells was timed such that a different range of tumor sizes would be present on each of the three imaging days. The second group of 12 animals was imaged one week after the first (20 animals) and the third group of 10 animals one week after the second. This cell injection/growth schedule resulted in tumors weighing on average 0.96 ± 0.93 g.

Study Protocol

In addition to creating a range of tumor sizes, the time between injection of the tracer and the onset of imaging was 90 minutes for the first group of 20 animals and 30 minutes for the last two groups (22 animals). The intent of this difference in uptake time was to further alter the tumor-to-background ratio in the 30-minute animals compared to the 90-minute animals.

All animals were injected via tail vein (mean injected activity: 3.84 ± 0.24 MBq of [¹⁸F]DCFPyl) and imaged thereafter in pairs. The manner in which the animals were positioned for both the planar and tomographic imaging studies is shown in Figure 1A. PET and PPI imaging intervals and the counting interval for the well counter samples were such that for this injected activity, counting uncertainties in tumor count rates were less than 1% for all three devices at the time of measurement.

Figure 1.

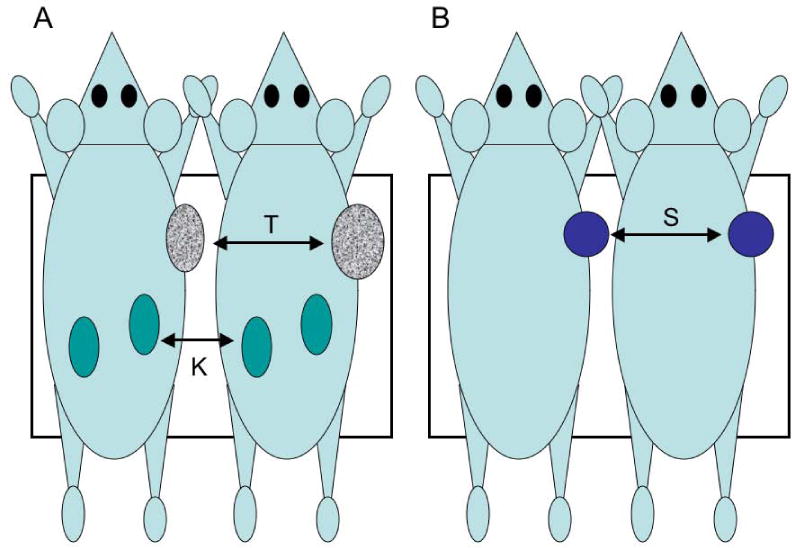
(A) Side-by-side positioning used for both tomographic PET and planar PPI imaging of the tumor-bearing mice shown in Figure 2; T = tumor, K = kidneys; (B) PET and PPI calibration geometry using a spherical source of F-18 and two non-radioactive mice. This same source was counted in a well counter the day following imaging. Black rectangles represent the approximate field of view of the PPI and a roughly equivalent portion of the whole-body tomographic field of view taken for analysis.

For tomographic imaging, the animal pair was placed side-by-side on a custom-made, 3D printed, forced-air heated imaging bed [9] and maintained during imaging with isoflurane/oxygen (1.5–2.0% v/v). Whole body imaging of the pair was then undertaken for 10 minutes (2 bed positions, 5 minutes/position) using an energy window of 250–700 keV. At the end of whole-body imaging, a CT scan of the pair was obtained to correct for attenuation caused by the animals and bed.

At the end of PET imaging, all pairs were immediately sacrificed by CO₂ inhalation and transported to a nearby location for projection imaging with the PPI. The animals were sacrificed at the end of PET imaging as a precaution against further accumulation of the tracer in the tumors between the end of PET imaging and the onset of PPI imaging and for logistical reasons unrelated to the experiment.

The PPI is an in-house developed imaging system designed to efficiently detect coincident annihilation radiation emanating from a mouse located midway between an opposed pair of planar LYSO-based imaging detectors. The field of view of the PPI is rectangular and large enough to “see” the whole body of a single mouse in a single projection. Conceptually, the PPI appears to be an electronically collimated, high-energy gamma camera with performance characteristics similar to gamma cameras of conventional design but at high photon energies. The PPI energy window for all studies was set to 400–620 keV to enhance rejection of scattered radiation and to eliminate the coincidence background from Lu-176. The cone angle for all studies was set to 5 degrees. The performance characteristics of the PPI are described in detail in [5].

The animal pair was arranged side-by-side in the PPI perpendicular to the long axis of the rectangular field of view of the scanner (Figure 1A) such that the tumors in both animals were visible in the same posterior-anterior (PA) projection image. The pair was then imaged for 10 minutes. Immediately after PPI imaging, the tumors in each pair were excised, weighed and placed in scintillation well counter vials. The samples accumulated during one day’s imaging were allowed to decay until tumor activity fell to within the linear counting range of the well counter (< 0.02 MBq) and then placed in the automatic sample changer of the well counter (Wizard 1480, PerkinElmer, Shelton, CT; energy window 400–1200 keV) and each counted for one minute.

Instrument Calibration

In order to calculate absolute tumor radioactivity in MBq, a calibration factor for each machine must be determined that scales tumor count rates to units of radioactivity. Moreover, since the absolute activity of each tumor was sought rather than some relative measure of activity, these calibration factors must be known with high accuracy if absolute activity measurements are to be meaningful. Accordingly, we made calibration measurements for all three machines using the same small spherical phantom (0.25 ml inner volume, Micro Hollow Sphere Phantom, Data Spectrum Corp., Durham, NC) filled with F-18 in water.

We first measured the activity in this sphere (6.29 MBq) with the dose calibrator and then imaged this sphere with the PET scanner. In the first scan, the sphere was tucked against the right hand side of the mouse shown on the left of Figure 1B, then again with the sphere tucked next to the right side of the mouse on the right side of Figure 1B. At the end of each of these imaging sessions, a CT scan was acquired for attenuation correction. Immediately following PET phantom imaging, this side-by-side imaging procedure was repeated with the PPI in exactly the same way (Figure 1B). That is, the two animals were placed side-by-side perpendicular to the long axis of the scanner and imaged first with the spherical source tucked against the right side of the animal on the left, then again with the source tucked against the right side of the animal on the right.

At the end of PPI imaging, the sphere was placed at the bottom and against the side of a standard well-counter vial (as with the tumors) and counted the next day to allow the activity in the sphere (as with the tumors) to fall to within the linear counting range of the well counter.

A calibration factor for each machine (in units of cps/MBq) was determined from these data by dividing the total sphere count rate decay corrected to the start time of that data acquisition, by imaging or counting, by the activity in the sphere determined by dose calibrator corrected to the start time of that same collection and by the positron branching ratio for F-18 (0.97). The same analytic methods (described below) applied to the mouse imaging data were applied to these phantom data to obtain these calibration factors. Note that this general method of image calibration approximately duplicates the physical environment of the actual mouse imaging studies and that only a single source of radioactivity is used for all three machine calibrations, in particular, without dilution for the well counter measurement.

Data Analysis

–General

All tumor activity measurements, whether by imaging or well counter, were decay corrected to the start time of the PPI imaging study in each animal. All imaging studies were analyzed by the same observer to avoid the additional variable of inter-observer bias. ROIs in all imaging studies, tomographic or planar, actual or calibration, were defined manually by this observer and no automated methods were employed. During image analysis, ROIs in a given study were defined by the observer without knowledge of, or reference to, any ROIs or results obtained in the same animal by another method including well counter results.

–Tomography

The tomographic PET image data acquired in each mouse pair (and phantom) were attenuation corrected and reconstructed with a 2D OSEM resolution recovery algorithm (16 subsets, 2 iterations) available on the PET scanner. These images were corrected for decay during data collection, scatter, random coincidences and dead time. The spatial resolution associated with this reconstruction method is approximately 1.3 mm. The tumor in each mouse was visualized in coronal section and ROIs were drawn by hand around the apparent tumor boundary in each slice. The total count rates occurring within each ROI were summed for all tumor slices to obtain the total tumor count rate. This rate was then divided by the (tomographic) calibration factor for the PET scanner (1,373 cps/MBq) to obtain total tumor radioactivity content.

In addition, the coronal image stack for each mouse pair was summed from anterior to posterior across the mouse thickness to create a single PA volume projection image. These volume projection images should approximate the planar projection images created with the PPI and thus, provide a different way of evaluating the accuracy of projection imaging in these animals. ROIs were drawn by hand around each tumor in the single volume projection image of a pair, the total count rate in these two ROIs determined and these rates divided by the (projection image) calibration factor (1,445 cps/MBq) to obtain an estimate of total tumor radioactivity for each animal. (It should be noted that the calibration factor for the PET volume projection images should be the same as for the coronal tomographic images (1,373 cps/MBq) but the small difference between the tomographic and volume projection factors was consistently observed on repeat analysis and is likely the result of observer bias in defining ROIs boundaries in images with very different contrasts).

–Positron Projection Imaging

An ROI was drawn around each apparent tumor in the side-by-side PA projection image of each mouse pair. The total count rate within each region was determined and these rates divided by the calibration factor for the PPI (315 cps/MBq). These values were then multiplied by the attenuation correction factor (see Appendix) calculated using the difference between the mass of each tumor and the spherical phantom mass to obtain the total tumor activity for each mouse. The relatively narrow energy window used for these measurements was chosen to improve rejection of scatter from within the animals and from surrounding structures and to effectively eliminate detection of coincidence events from the decay of Lu-176. The spatial resolution of the PPI [5] degrades with increasing cone angle and with increasing thickness of the target volume. In this study, we estimate that spatial resolution in the tumor volume averaged approximately 2 mm with the animal’s body axis aligned with the PPI image plane and with half the tumor above and half below the image plane. Under these conditions, average spatial resolution in the tumor volume will be higher (better) in small tumors and poorer in large tumors. A small tumor located exactly on the PPI image plane can be visualized with a maximum spatial resolution of approximately 1.7 mm.

In quantitative planar imaging studies it has been customary to define a second ROI thought to represent background radiation detected within the target ROI but not emanating from the target tissue and to use the counting information from this ROI to correct target activity for this background. In the present case, it was found that an explicit correction for this presumed background was not necessary. Accordingly, no background ROI was defined and only the count rate from within the tumor ROI was used in the calculation of total tumor radioactivity.

Well Counting

The well counter count rate for each excised tumor (and phantom) was divided by the (well counter) calibration factor (5.83 × 10⁵ cps/MBq) for the 400–1200 keV energy window to obtain the total tumor radioactivity content.

Imaging Calibration Factors

Tomographic and projection images of the spherical phantom were reconstructed and analyzed in the same way as the mice: tomographic ROIs were defined slice by coronal slice and the count rate in all slices summed to provide the total source count rate for the phantom; the coronal tomographic image stack spanning the sphere thickness in the PA direction was volume projected and the total count rate determined within the single ROI drawn around the projected spherical source; for the PPI an ROI was defined around each projected spherical source and the count rate from these regions taken to be the sphere count rate. In each of these analyses, the two count rate values, one from the left hand ROI and the other from the right, were averaged to obtain the calibration factor for that device and method.

Results

Representative coronal PET maximum intensity, PET volume projected and PPI planar projection images of the same pair of tumor-bearing mice are shown in Figure 2. Animals are arranged as shown in Figure 1A. An intense portion of a bladder originally visible in Figure 2A been masked out to allow proper display.

Figure 2.

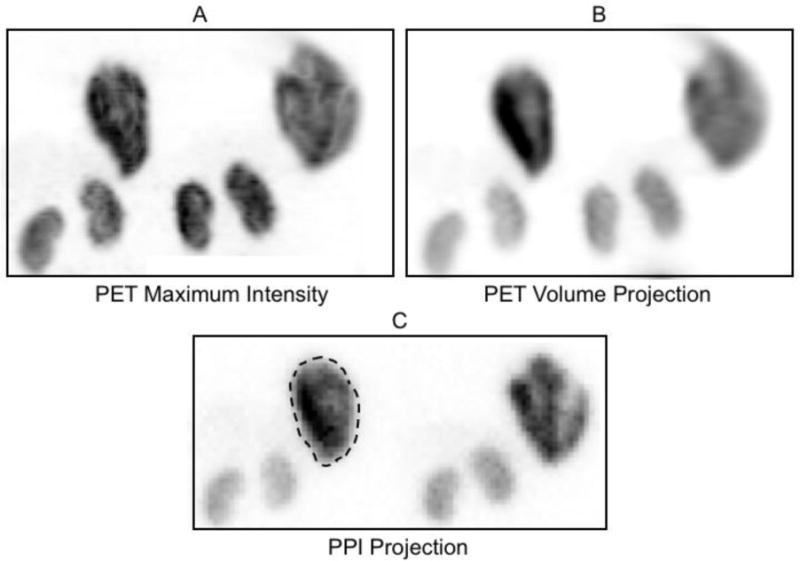
PPI and coronal PET images of the same mouse pair positioned as shown in Figure 1A: (A) maximum intensity projection image created from the coronal PET tomographic image stack, (B) volume projection image created by summing the coronal PET tomographic images spanning the mouse thickness and (C), PPI projection image acquired directly from the same mouse pair. A typical tumor region-of-interest is drawn around the tumor in the animal on the left. The physical orientation (separation, rotation around the body axis, tilt relative to the field-of-view, etc.) of the in pair in A and B are identical but differ slightly from that in C. The animal on the left in these images received 4.8 MBq of F-18 (tumor weight = 1.0 g) while the animal on the right received 3.8 MBq (tumor weight = 1.35 g). The PET whole body scans in these animals showed intense uptake in the tumor, kidneys and bladder (at, or just outside, the field of view in these projection images) and a faint, diffuse distribution of activity throughout the abdomen not visible on this brightness scale. No obvious differences to this overall pattern were evident in animals with a 30-minute or a 90-minute uptake period.

Total tumor radioactivity determined by PET tomographic imaging and by PPI planar imaging are compared to well counter measurements in Figure 3.

Figure 3.

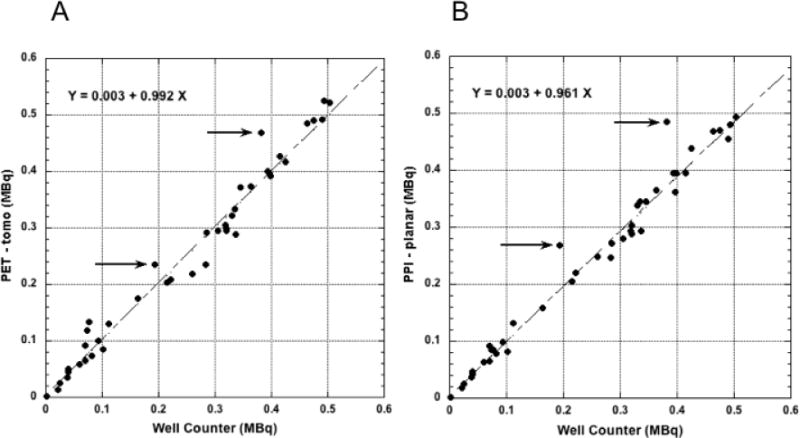
(A) Total tumor radioactivity determined by slice-by-slice analysis of the coronal PET tomographic image stack and (B), total radioactivity determined from the single tumor ROI defined for each mouse in the PPI images compared to well-counter radioactivity measurements of these same tumors; linear fits to these data do not include the points indicated by the arrows (discussed in text), i.e. N = 40, not 42.

PPI planar and PET volume projected imaging measurements of total tumor radioactivity are compared to the PET tomographic imaging measurements in Figure 4.

Figure 4.

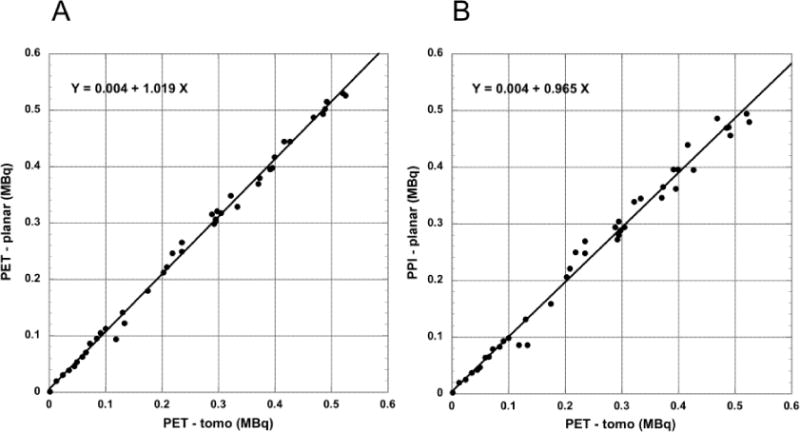
(A) Total tumor radioactivity determined from a single ROI defined in the coronal PET tomographic volume (planar) projection image and (B) from the single ROI defined in the PPI planar image compared to total radioactivity determined by slice-by-slice analysis of the coronal PET tomographic images (N = 42). Plots include points indicated by arrows in Figure 3.

Tumor activity determined with the two planar projection methods (PPI and PET volume projection) are compared in Figure 5.

Figure 5.

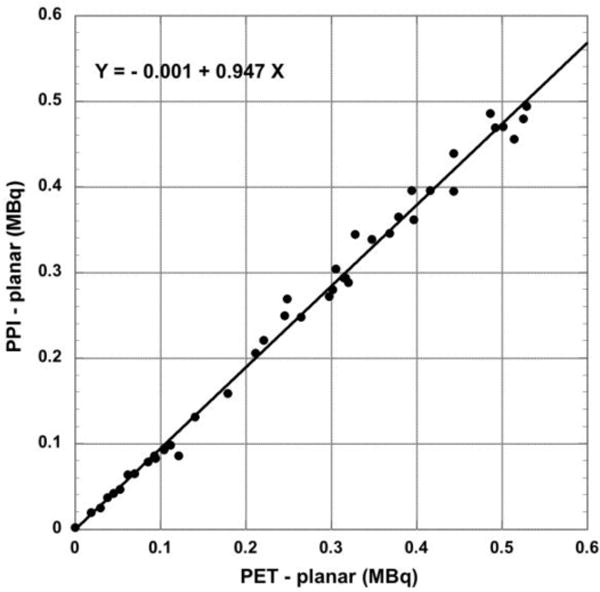
Total tumor radioactivity determined from planar PPI images compared to volume (planar) projections of the coronal PET tomographic images (N = 42). Plots include points indicated by arrows in Figure 3.

The statistical properties of these comparisons are summarized in Table 1.

Table 1.

Comparison	R2	Slope	Intercept MBq	RMS Error MBq
WC vs. PPI (S*) N = 40	0.99	0.96	0.003	0.020 (8.3%#)
WC vs PET (NS**) N = 40	0.98	0.99	0.003	0.021 (8.6%)
PET tomo vs. PPI (S) N = 42	0.99	0.97	0.004	0.017 (7.0%)
PET tomo vs. PET Projection (S) N = 42	0.99	1.02	0.004	0.010 (4.2%)
PET Projection vs. PPI (S) N = 42	0.99	0.95	−0.001	0.016 (6.7%)

WC: well counter.

PPI: positron planar projection imager.

PET tomo: positron emission tomography data analyzed slice by coronal slice.

PET projection: positron emission tomography data analyzed after volume projection of coronal images spanning the mouse thickness.

R: Linear correlation coefficient (squared).

^*S: Significantly different, two-tailed paired t-test, P < 0.05.

^**NS: Not significantly different, two tailed paired t-test, P > 0.05.

^#(RMS error/mean of ordinate values) × 100; ordinate is second entry in “comparison” column.

Discussion

While there are numerous reports describing the performance characteristics of small animal PET scanners [4, 10] and review articles [1,2] describing the many factors that affect small animal PET studies, there are surprisingly few [3] that describe the accuracy of actual measurements made with these machines in “real” small animal imaging experiments. Moreover, results from formal small animal scanner performance tests, even when available, do not provide a full picture of the kind and magnitude of errors that occur in actual imaging experiments. In “real” experiments, the accuracy of measurement of total tumor radioactivity depends on many factors that do not appear in performance tests, e.g. observer bias and variability in ROI definition of mouse tumor boundaries often in a “noisy” imaging environment, the effect of spatial variations in sensitivity on objects located at different places in the imaging field of view, effects of iteration and subset number and different forms of image reconstruction on apparent tumor count rate, physical differences between the tumor imaging environment and the calibration environment that cumulatively accentuate small differences in corrections for machine effects. In addition, any standards against which imaging estimates of tumor activity are judged are also subject to error. For example, the counting efficiency of a typical well counter depends, albeit relatively weakly, on the size of the counted sample and on the vertical and horizontal location of the sample in the well counter recess. Finally, all of these methods of measuring total tumor radioactivity are subject to errors due to counting fluctuations and such errors simply increase those from other sources. Given the number and complexity of these interactions, we sought to measure by experiment the cumulative error in imaging estimates of absolute total tumor radioactivity when many of these factors are controlled. We also sought to determine whether PPI projection imaging could replace PET in future studies with similar tracers in comparable animal models by also measuring the accuracy of this method.

The results portrayed in Figures 3–5 indicate that PET, PPI and well counter measurements of total tumor radioactivity are highly correlated and numerically similar to one other, but are identical (by two tailed paired t-test) in only one case (PET tomographic vs. well counter). This finding likely arises from small errors made in determining the calibration factors for each machine. The slope of the regression line in each of these figures is determined, in part, by the ratio of the calibration factors of the compared methods and small errors in either or both could easily combine to cause the slopes of these lines to differ from unity, e.g. by ~5% in Figure 5. The small absolute numerical differences between the various measurement are thus likely traceable to systematic errors in the calibration factors, values that affect all measurements made with a given machine. It should be noted that if “better” absolute agreement between methods is required, the regression relations for these comparisons could be used in reverse to eliminate (on average) such differences, e.g. use the regression relation in the PPI vs. well counter comparison to convert PPI values back to equivalent absolute well counter values.

The mean percent RMS uncertainties of the PET and PPI measurements when compared to the well counter (Table 1) are less than ± 9%. When the imaging methods are compared to one another, the RMS errors are somewhat less (≤ ± 7%). The smallest uncertainty (± 4.2%) is in the comparison of the PET tomographic values to the PET volume projection values. Collectively, these results suggest that PET and PPI generally yield similar, though not necessarily identical, estimates of total tumor activity compared to direct well counting of these same tumors. These results also imply that within these limits and for this particular application, PET and PPI imaging can act as surrogates for well counting of tumor samples.

The arrows inset in the graphs of Figure 3A and 3B identify (the same) two data points that differ substantially from both regression lines. These two points also contribute a majority to the RMS variation around the regression lines if these two points are included in the imaging vs. well counter analysis. However, when the imaging measurements are compared to each other with these data points included (Figures 4 and 5), no such deviations are observed. It is likely, therefore, that the well counter measurements are the source of these outliers, not the imaging measurements. In these two instances, residual tumor tissue could have been left behind after dissection thereby causing the well counter sample to contain less than the actual total tumor radioactivity. It should be noted that the imaging methods are also subject to similar partitioning errors from inaccurate ROI definition of the tumor boundary. It was found here, for example, that the very high biological contrast between tumor/kidneys and the rest of the body (Figure 2) occasionally decreased visual detection of small, peripheral lobular structures appended to the bulk tumor volume. To avoid this problem, and insure that ROIs actually encompassed the entire tumor, all images were “overexposed” during ROI creation to reveal and include these less intense appendages within the final ROI. Without such a display scheme, these appendages, when they exist, could be missed and total tumor radioactivity underestimated, particularly in the projection images. There are several other data points that might also represent tissue sampling or ROI identification errors, e.g. at well counter values near 0.07 MBq and between 0.25 and 0.30 MBq in Figure 3A.

The present work was undertaken not only to assess the accuracy of conventional PET relative to well counting for this particular drug/xenograft/geometry model, but also to determine if PPI imaging could be used as an alternative to PET for future investigations of this same compound and for other compounds with similar pharmacokinetics. The results shown in Figures 4 and 5 indicate that for this compound, tumor model and anatomical location of the tumor xenograft, PPI imaging can, in fact, make such measurements without significant loss of accuracy and without CT imaging. The usefulness of this finding lies in the fact that estimating total tumor activity by PPI imaging is much simpler than with PET. First, no image reconstruction is necessary and the image required for analysis is present at the end of data collection. Further, and more importantly, only a single ROI needs to be defined in this image to obtain total tumor activity. Conversely, tomographic slice-by-slice analysis of the equivalent PET data requires far more ROIs to define the tumor volume than the single ROI needed for PPI images (in this study, 22 times more tomographic ROIs on average per mouse). Unless an automatic or semi-automatic method could be devised to replace manual definition of ROIs with high confidence, this laborious analytic step remains a major obstacle to rapid analysis of PET tomographic image data. PPI imaging, where applicable, could significantly reduce this time, a not insignificant outcome for a laboratory engaged in multiple studies of large numbers of tumor-bearing animals for drug development purposes.

This same image projection strategy might also be applied to the analysis of tomographic PET data by volume projecting these data and creating a single ROI outlining the tumor in the resulting 2D image. Although image reconstruction would still be required, the time saved by reducing the number of ROIs from many to one might well be significant. Inspection of Figure 4A, shows that this scheme would not result in a significant loss in accuracy compared to slice by slice analysis of these same data.

The present work was appended to an ongoing study of the pharmacokinetic behavior of [¹⁸F]DCFPyl and the results portrayed in the Figures and Table and their interpretation depend directly on this behavior. As suggested in Figure 2, tumor uptake is high and blood/tissue clearance rapid so that by the time imaging began, 30 or 90 minutes post-injection, background from blood and surrounding tissue was minimal during both PET and PPI imaging. This result, while limiting extrapolation of these results to other studies, provides an opportunity to assess the accuracy of both methods under near ideal experimental circumstances. That is, factors that could affect PET imaging such as excessive (uncorrected) scatter from nearby high activity organs into the tumor ROIs is nearly non-existent because of tumor placement and the very favorable pharmacokinetic properties of the radiopharmaceutical. The very low blood/tissue background is even more important for PPI imaging since such activity could appear directly in the PPI projection image ROI and erroneously and variably increase the tumor count rate. Given these considerations, it would not be unreasonable to assume that the magnitudes of the “errors’ identified here, in both PET and PPI imaging, are likely smaller than would be encountered in other studies where conditions are less favorable.

However, while PET is resilient to increasingly unfavorable conditions (because of the various corrections that can be applied to these data) and PPI imaging is not, PPI imaging as implemented here offers the prospect of much more efficient imaging when conditions permit. We have, in fact, made similar PPI/PET and well counter comparisons with a different, much less favorable compound and tumor model (unpublished) but without the rigor employed here, and these results did suggest that PPI imaging may be more tolerant to deteriorating imaging conditions than might be imagined. Placing tumors on the animal’s lateral chest wall seems to reduce background effects substantially since the blood volume in tissues directly surrounding the tumor is small and this placement significantly reduces contamination from nearby organs. In any case, the potential for PPI imaging in any given instance could be tested by carrying out a small pilot study with a new compound to see if accuracy is preserved or by foreknowledge from the literature or previous studies indicating favorable pharmacokinetic behavior of the compound. If conditions were not favorable for PPI imaging, the study could be performed with PET.

Finally, we note that this PPI approach to tumor imaging is identical in concept to imaging single photon labeled compounds with a gamma camera equipped with parallel hole collimation. It would be expected that with the same tumor placement, similar tumor models and compounds meeting the same general conditions required by the PPI, single photon projection imaging of total tumor activity with devices like the MONICA portable dual gamma camera system [11] might also be performed with good accuracy when combined with model-based attenuation correction.

Conclusion

Total mouse xenograft tumor radioactivity can be measured with PET or positron projection imaging (PPI) with an accuracy comparable to well counting if certain tumor model, imaging geometry and pharmacokinetic conditions are met. In this particular application, the PPI imaging process is a substantially more efficient than PET in making these measurements.

Appendix

Approximate model-based correction for tumor attenuation in PPI images

We assume that tumors in these mice, like the spherical calibration phantom, are spherical and of density ρ. If so, the radius, R, of a sphere of mass M with these properties is given by:

$$\mathrm{R}={\left(3/\left(4\mathrm{\pi }\mathrm{\rho }\right)\right)}^{1/3}{\mathrm{M}}^{1/3}$$

The mean chord length, L, across a sphere of radius R is (4/3)R [12] so that:

$$\mathrm{L}=\left(4/3\right)\mathrm{R}=\left(4/3\right){\left(3/\left(4\mathrm{\pi }\mathrm{\rho }\right)\right)}^{1/3}{\mathrm{M}}^{1/3}$$

The fraction of radiation attenuated crossing this length relative to a reference sphere is:

$$\mathrm{\epsilon }=\text{exp}\left[-\mathrm{\mu }\left({\mathrm{L}}_0-\mathrm{L}\right)\right]$$

where L₀ is the mean chord length across the spherical phantom, L is the mean chord length across the (spherical) tumor and μ is the linear attenuation coefficient of tumor and spherical phantom (assumed to be the same) at 511 keV. Note that if the chord length across the tumor is greater than across the phantom, ε is greater than 1 and the tumor count rate will be increased by this factor. If the tumor chord length is less than the phantom chord length the opposite is the case and ε will be less than one and tumor count rate will be reduced by this factor.

Substitution gives an expression for ε in terms of tumor mass relative to phantom mass:

$$\mathrm{\epsilon }=\text{exp}\left[-\left(4/3\right){\left(3/\left(4\mathrm{\pi }\mathrm{\rho }\right)\right)}^{1/3}\mathrm{\mu }\left({\mathrm{M}}_0{ }^{1/3}-{\mathrm{M}}^{1/3}\right)\right]$$

For the attenuation correction applied in this work, we assume that μ = 0.096/cm, that ρ = 1g/cc and that M₀ equals the mass of the spherical portion of the Data Spectrum phantom when filled with water (outside radius of 0.493 cm and mass of 0.50 g). Under these conditions, the expression for ε becomes:

$$\mathrm{\epsilon }=\text{exp}\left[-0.0794\left(0.795-{\mathrm{M}}^{1/3}\right)\right]$$

For the tumor masses encountered here, the attenuation correction factors calculated from this equation ranged from 0.97 to 1.08 and, as would be expected, are modest corrections to the raw data. It should be borne in mind, however, that this correction model is a poor approximation to actual tumor geometry and could increase, rather than decrease, the difference between the PPI and tomographic/well counter measurements in any given animal. That no obvious distortions of the results are present in Figure 3B suggests that this correction does correctly compensate at least in part for this effect. Many other model-based methods can be envisioned that might improve on the present correction and/or dispense with the need for tumor weight. For example, an improved correction might be based on the dimensions of, and activity distribution within, the tumor ROI modified by direct caliper measurements of tumor size in the intact animal.

An improved, model-based correction might also be applied in single photon (projection) imaging of tumors with gamma camera-like devices such as MONICA [11]. An improved correction would likely be necessary since attenuation would be larger at (typically) lower single photon energies. In this case, however, it is not difficult to envision methods whereby tumor attenuation could be measured directly by transmission imaging. For example, a thin, small disc-shaped source of a long-lived gamma ray emitting isotope, larger in diameter than the largest expected tumor, could be placed over the tumor and the radiation passing through the tumor compared to radiation detected when the tumor (animal) was not present. If the gamma ray energy of the transmission source were higher than the isotope under study, energy windowing could be used to make transmission measurements at the same time that events were being recorded from the lower energy events associated with the tumor. An attenuation factor could then be determined from events in the high-energy window and scaled to correct for attenuation of events occurring in the low energy window.