A 3D Tissue-Printing Approach for Validation of Diffusion Tensor Imaging in Skeletal Muscle

Abstract

The ability to noninvasively assess skeletal muscle microstructure, which predicts function and disease, would be of significant clinical value. One method that holds this promise is diffusion tensor magnetic resonance imaging (DT-MRI), which is sensitive to the microscopic diffusion of water within tissues and has become ubiquitous in neuroimaging as a way of assessing neuronal structure and damage. However, its application to the assessment of changes in muscle microstructure associated with injury, pathology, or age remains poorly defined, because it is difficult to precisely control muscle microstructural features in vivo. However, recent advances in additive manufacturing technologies allow precision-engineered diffusion phantoms with histology informed skeletal muscle geometry to be manufactured. Therefore, the goal of this study was to develop skeletal muscle phantoms at relevant size scales to relate microstructural features to MRI-based diffusion measurements. A digital light projection based rapid 3D printing method was used to fabricate polyethylene glycol diacrylate based diffusion phantoms with (1) idealized muscle geometry (no geometry; fiber sizes of 30, 50, or 70 μm or fiber size of 50 μm with 40% of walls randomly deleted) or (2) histology-based geometry (normal and after 30-days of denervation) containing 20% or 50% phosphate-buffered saline (PBS). Mean absolute percent error (8%) of the printed phantoms indicated high conformity to templates when “fibers” were >50 μm. A multiple spin-echo echo planar imaging diffusion sequence, capable of acquiring diffusion weighted data at several echo times, was used in an attempt to combine relaxometry and diffusion techniques with the goal of separating intracellular and extracellular diffusion signals. When fiber size increased (30–70 μm) in the 20% PBS phantom, fractional anisotropy (FA) decreased (0.32–0.26) and mean diffusivity (MD) increased (0.44 × 10⁻³ mm²/s–0.70 × 10⁻³ mm²/s). Similarly, when fiber size increased from 30 to 70 μm in the 50% PBS diffusion phantoms, a small change in FA was observed (0.18–0.22), but MD increased from 0.86 × 10⁻³ mm²/s to 1.79 × 10⁻³ mm²/s. This study demonstrates a novel application of tissue engineering to understand complex diffusion signals in skeletal muscle. Through this work, we have also demonstrated the feasibility of 3D printing for skeletal muscle with relevant matrix geometries and physiologically relevant tissue characteristics.

Introduction

Skeletal muscle is a hierarchical tissue containing long contractile cells, bundled in extracellular matrix to form larger fascicles, which are then bundled to form whole muscle.¹ The microstructure of muscle is closely related to its performance capacity. For example, larger muscle fibers can produce greater contractile forces, and elevated extracellular matrix concentrations (fibrosis) result in increased passive stiffness.^2–4 With injury and disease, changes in muscle microstructure directly affect a muscle's performance capacity, so muscle biopsy and histopathological examination is the gold standard tool for diagnosis. However, biopsy/histology is highly invasive and often semiquantitative, so it is not conducive to longitudinal assessment of muscle health and recovery.

Diffusion tensor magnetic resonance imaging (DT-MRI) is a method that has been used to noninvasively measure the anisotropic restricted diffusion of water in tissue, which is related to its underlying microstructure.^5–7 For example, muscle cells are long columnar structures with a surrounding membrane (sarcolemma), which is believed to be the primary barrier to water diffusion.^8,9 Because of this geometry, diffusion is more restricted perpendicular to the membrane than along the longitudinal axis of the cell, yielding anisotropic diffusion in muscle. Thus the geometric anisotropy in the structure of the muscle tissue is expected to result in a measured anisotropy in the directional dependence of the diffusion signal. Fractional anisotropy (FA) is a key variable in DT-MRI and is believed to be most sensitive to changes in fiber size (larger fiber diameters = smaller anisotropy (FA)). However, the relationship between the DT-MRI signals and the tissue microstructure and physiology is exceedingly complex. Thus, while DT-MRI parameters have been shown to be sensitive to skeletal muscle changes associated with injury, age, and chronic pathology,⁷ these studies are nonspecific and, therefore, of limited clinical value. Microstructural and microfluidic changes associated with these conditions include fiber atrophy, fibrosis, edema, and increased sarcolemma permeability, all of which theoretically change diffusion of water in muscle.^7,10–13

In vivo, the presence of increased extracellular water due to edema/inflammation in injured muscle has been shown to strongly effect and may dominate the diffusion signal even when concurrent microstructural changes have an opposing diffusion profile.^10,12,14,15 Increased extracellular water content is normally observed on MRI as an increase in the T₂ relaxation value of the tissue. Multiecho DT-MRI techniques have been implemented to compartmentalize diffusion from intra- and extracellular water by combining traditional DT-MRI and T₂-relaxometry techniques.^16,17 This technique leverages the difference in T₂-relaxation of water in the intra- and extracellular space, theoretically limiting the parameter estimate errors found in traditional single-compartment (single-echo) diffusion techniques. However, uncoupling local inflammation/edema from the underlying microstructural changes in muscle is nearly impossible in vivo because multiple biological processes occur in parallel.

Nonphysiologically relevant anisotropic diffusion phantoms have been developed for DT imaging (DTI) reliability studies and to validate complex data analysis techniques.^18–21 However, no diffusion phantoms have been designed to systematically evaluate how muscle microstructure is related to the underlying diffusion profile. Recent developments in additive manufacturing technologies have enabled the construction of complex, precision-engineered 3D biomimetic scaffolds.²² These methods include two-photon laser direct writing,²³ inkjet 3D printing,²⁴ extrusion based 3D printing,²⁵ and digital light projection (DLP) based 3D printing.^26,27 Two-photon laser direct writing can achieve 100 nm resolution, yet this process would take days to fabricate a millimeter-size structure due to its point-by-point writing process. Both inkjet 3D printing and extrusion based 3D printing have a coarse spatial resolution, typically over 50 μm, rendering them impractical for fabricating skeletal muscle geometry, which is often smaller. DLP-based 3D printing, which is a mask-free, projection-style stereolithography technique, has the advantages of both high speed and high resolution: it takes seconds to photopolymerize a millimeter-size structure, and it has a micron scale resolution. Furthermore, unlike inkjet and extrusion based methods which give rise to interfaces between droplets or lines, DLP-based 3D projection printing yields smooth surfaces for superior structural integrity due to scanningless printing in the x-y plane and continuous polymerization in the z-direction. This technique has recently developed to fabricate various functional materials and devices^28–30 and tissue engineering scaffolds.^31–33 Therefore, DLP-based 3D printing is an attractive technique to fabricate anisotropic phantoms with skeletal muscle geometry for DT-MRI.

The focus of this study is to use new 3D printing strategies to develop a novel set of precision-engineered phantoms for characterizing the interrelationship between microstructural variables and MR-diffusion parameters in skeletal muscle. We hypothesize that physiologically relevant changes in muscle microstructure and microfluidics are separable and can be specifically identified using a novel application of multiecho DT-MRI experiments.

Methods

DLP-based 3D printing

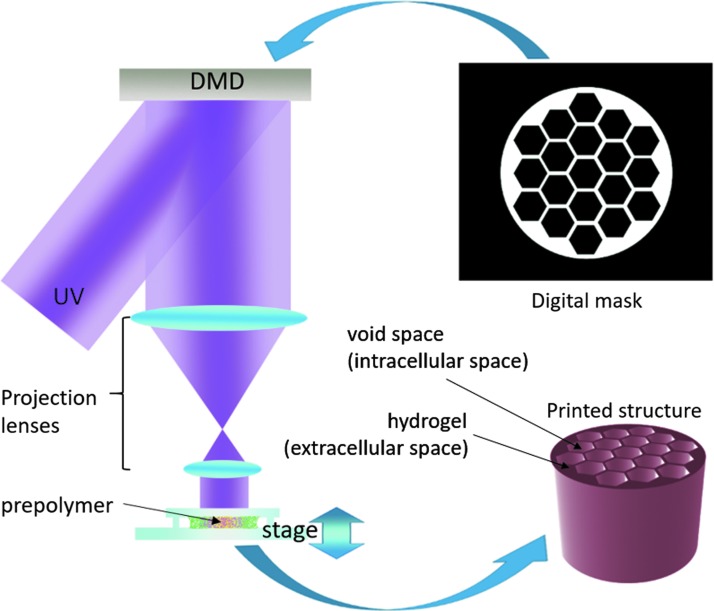
A DLP-based 3D printing system was used to fabricate all phantoms (Fig. 1).²⁶ Briefly, a collimated ultraviolet (UV) beam centered at 365 nm wavelength illuminates the digital micromirror device (DMD), which contains an array of 2 million micromirrors, and is reflected toward the prepolymer solution. Digital masks are continuously loaded to the DMD chip to control the on/off state of each single micromirror. The projection optics images the patterned UV light onto the prepolymer solution and polymerizes it as the pattern defined by the digital mask. By changing the digital masks and moving the stage in z direction simultaneously, a 3D structure can be printed within a few seconds. In the current setup, the overall size of the printed structure can be up to 4 × 6 mm in base area with a lateral resolution of 4 μm, and several millimeters in height.

FIG. 1.

Digital light projection based 3D printing system setup. A digital mask of the desired geometry is fed into a DMD. Digital masks control the on/off state of each mirror. A collimated UV beam at 365 nm wavelength is reflected off of the DMD chip, through a series of projection lenses into the prepolymer solution. Where the UV light strikes, the prepolymer cures into the desired geometry. Excess prepolymer solution is then washed away so that just the printed structure remains. The printed structure is designed to simulate the “extracellular” space in muscle, and the void space in the structure designed to simulate the “intracellular” space in muscle. DMD, digital micromirror device; UV, ultraviolet.

The prepolymer solution is a liquid state mixture of monomer or short-chain polymers, photoinitiators, and other additives. There are a large variety of photopolymerizable material that can be used for this DLP 3D printing system, such as polyethylene glycol diacrylate (PEGDA), poly-(methyl methacrylate), poly(acrylic acid), poly(lactic acid), and dipentaerythritol pentaacrylate.^30,31,34,35 Common photoinitiators include Irgacure 2959, Irgacure 651, Irgacure 819, 2-dimethoxy-2-phenylaceto-phenone, and lithium phenyl-2,4,6-trimethylbenzoylphosphinate (LAP).²⁷

Upon stimulation by UV light, the photoinitiator generates free radicals locally. Then the free radicals attack the C═C bonds and generate acrylic monomers with free electrons, which react with the monomers and cross-link them into polymer networks. This cures the places exposed to UV light. After exposure, the remaining liquid prepolymer is rinsed with phosphate-buffered saline (PBS), and a solid structure remains.

PEGDA (Sigma-Aldrich) was the main building material, and LAP was the photoinitiator chosen for the phantoms, as they can be combined with water to form hydrogel structures, ranging from 0% to 80% water content. The prepolymer solution is prepared as follows: The 50% PEGDA/50% PBS prepolymer solution contains 50% (v/v) PEGDA (700 Da), 50% (v/v) PBS (Life Technologies), 0.25% (w/v) LAP, and 0.001% (w/v) Tempo (Sigma-Aldrich) as a free radical quencher. The 80% PEGDA/20% PBS prepolymer solution contains 80% (v/v) PEGDA (700 Da), 20% (v/v) PBS, 0.25% (w/v) LAP, and 0.001% (w/v) Tempo.

Model overview

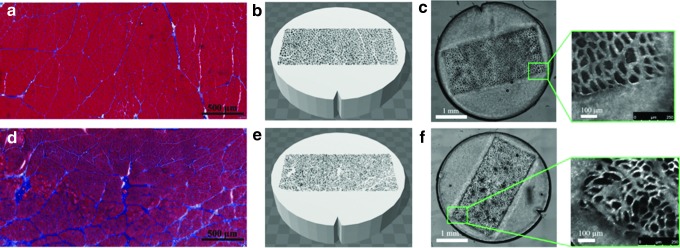
As a first step, the complex geometry of skeletal muscle was reduced to simple closely packed hexagons to systematically study the relationship between muscle microstructure and MR diffusion. Skeletal muscle structure was simplified into a two-compartment model: the intracellular space (the hexagons containing PBS only) and the sarcolemma + extracellular space (3D printed material; Fig. 1). Phantoms were printed in a 30, 50, or 70 μm diameter hexagon array to approximate atrophic, normal, and hypertrophic human skeletal muscle, respectively (Fig. 2). The effective extracellular spacing between fibers was 20 μm. To replicate skeletal muscle permeability, additional phantoms were printed in a 50 μm diameter hexagon array, with 40% of the fiber walls randomly deleted (Fig. 2). Solid phantoms with no geometry were also printed to assess the restricted diffusion profile of water within the extracellular material itself (Fig. 2). In addition, to model increased extracellular water volume fraction associated with edema, the concentration of water in the 3D printed hydrogel was printed with 20% or 50% PBS. To demonstrate the ability to 3D print geometrically complex phantoms, separate models were printed with histology informed geometry from normal rat muscle (tibialis anterior) and an atrophic rat muscle (30-day denervated tibialis anterior muscle; Fig. 3). Denervated skeletal muscle has smaller muscle fibers with increased fibrotic tissue deposition between fibers and is a common model of muscle atrophy.¹³ In these phantoms, histology images were imported into Blender (Stichting Blender Foundation, Amsterdam, Netherlands), the contours of the muscle fibers were manually segmented, and exported as a STereoLithography format (.stl) file. The outer dimensions of the phantoms were 3.8 mm wide and 1 mm tall.

FIG. 2.

Phantom designs (left column) and printed phantoms (right column). (a) and (b) 30 μm ideal geometry phantom. (c) and (d) 50 μm ideal geometry phantom. (e) and (f) 70 μm ideal geometry phantom. (g) and (h) phantom with no feature. (i) and (j) 50 μm ideal geometry phantom with 40% of walls randomly deleted.

FIG. 3.

Histology informed geometry in 3D printed diffusion phantoms. Histology from control (a) and 30-day denervated (d) skeletal muscle in rat tibialis anterior. 3D CAD reconstructions of skeletal muscle geometry for control (b) and denervated (e) samples. Light microscopy of control (c) and denervated (f) 3D printed diffusion phantoms.

Model validation

For each phantom, cross-sectional area of 20 “fibers” was randomly measured using ImageJ (NIH, Bethesda, MD). The mean absolute percent error was calculated between measured and expected “fiber” cross-sectional area of each set of phantoms to assess how similar the printed phantoms were to the original template.

MRI scanning

Phantoms were printed using the DLP-based 3D printing technique described above. After printing, phantoms were thoroughly rinsed with PBS to remove any remaining prepolymer solution, loaded in 4.3 mm diameter tubes, filled with PBS, and carefully capped to ensure no air bubbles were present. Five phantoms of each model were scanned at once. MR experiments were carried out using a 7T Bruker small animal imaging system (BioSpec 70/30; Bruker, Billerica, MA) with a 6 cm high-performance gradient insert capable of producing a maximum gradient amplitude of 1000 mT/m, maximum slew rate of 11,250 T/(m·s), and a 300 W quadrature transmit–receive volume coil. High-resolution structural scans of the samples were acquired using a 3D gradient recalled echo (FLASH) scan with the following parameters: echo time TE:7.3 ms, repetition time TR:15 ms, acquisition matrix: 450 × 450 × 66, voxel size:67 × 67 × 100μm³, number of averages nex = 4, bandwidth:50 kHz, and total acquistion time: 42:30. Then, samples underwent a series of diffusion weighted scans using a multishot spin-echo echo planar imaging (EPI) sequence with the following parameters: b = 500 s/mm², 15 diffusion encoding directions, diffusion gradient pulse width δ = 2 ms, diffusion gradient separation Δ = 9 ms, number of k-space segments = 4, 19 echo times at 10 ms interval (22.9–202.9 ms), and additional echoes at 252.9 ms and 302.9 ms, repetition time TR:5 s, matrix size:100 × 100, in-plane resolution: 300 × 300 μm², slice thickness: 400 μm, number of slices: 10, bandwidth 200 kHz, and total acquisition time: 1:52:00.

MRI analysis

Registered FLASH images were used to place regions of interest on each of the diffusion phantoms. For each voxel, the diffusion tensor was calculated using single-echo data (Eqn. 1) or as two compartments in slow exchange (Eqn. 2) from multiecho data using custom written software in Matlab (Mathworks, Natick, MA).

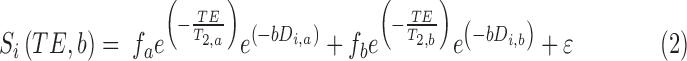Where 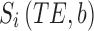is the signal along a certain gradient direction (S_i) at echo time (TE) and b-value (b) and f is the volume fraction of the short (a) and long (b) transverse relaxation (T₂) compartments of the apparent diffusion coefficient (D_i) along the same gradient direction, such that 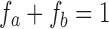. The MERA 2.03 toolbox was used to determine the number of T₂ components present in a voxel from each of the 16 sets of echo magnitudes.³⁶ If only a single T₂ component was present, the voxel was processed using single-echo data. If two T₂ components were found, the voxel was processed as two compartments in slow exchange, in which case, the MERA toolbox was used to solve for 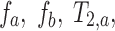and 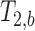. A nonlinear least square fit was used to solve D_i,a and D_i,b using the fit function in Matlab. The diffusion tensor was solved using AFNI.^37,38 Diagnolization of the diffusion tensor yields the eigenvalues (λ₁, λ₂, λ₃), which were used to calculate MD and FA (Eqns. 3 and 4). For single-echo analysis, data from the first recorded echo of the multiecho DTI sequence were used.

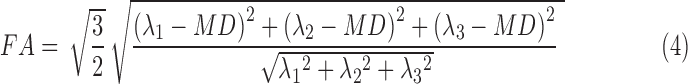FA is a normalized scalar measure of how anisotropic the diffusion profile is and varies from 0 (perfectly isotropic) to 1 (perfectly anisotropic). MD is a measure of the average overall diffusion. MD of unrestricted water is 2.5 × 10⁻³ mm²/s. Generally, as the restricted diffusion profile increases (increased FA), there is less overall diffusion (decreased MD) and vice versa.

Results

3D printed phantoms

We used 50% PEGDA/50% PBS and 80% PEGDA/20% PBS prepolymer solutions to successfully fabricate the five geometric designs (30 μm hexagons, 50 μm hexagons, 70 μm hexagons, 50 μm hexagon phantoms with 40% of walls randomly deleted, and phantoms with no geometry) and the two histology informed designs (control and 30-day denervation). Qualitatively, the five printed designs mimicked the input designs well based on microscopic image examination (Fig. 2 and 3). Quantitatively, mean percent error of the phantoms was largest (22.2%) for the 30 μm phantoms and 7–8% for all other phantoms. These microscopic images demonstrate the use of DLP-based 3D printing technology to fabricate phantoms of muscle tissue that reproduce the features of each muscle fiber.

Magnetic resonance imaging

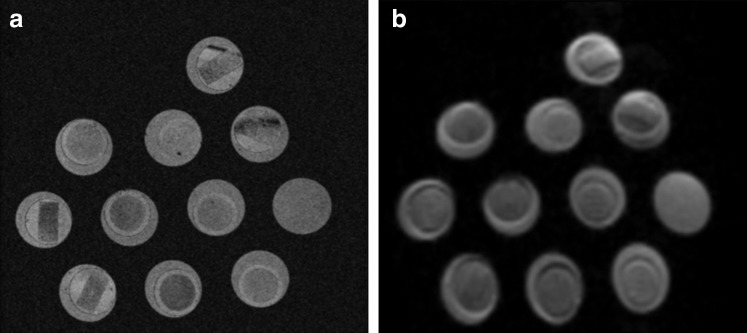
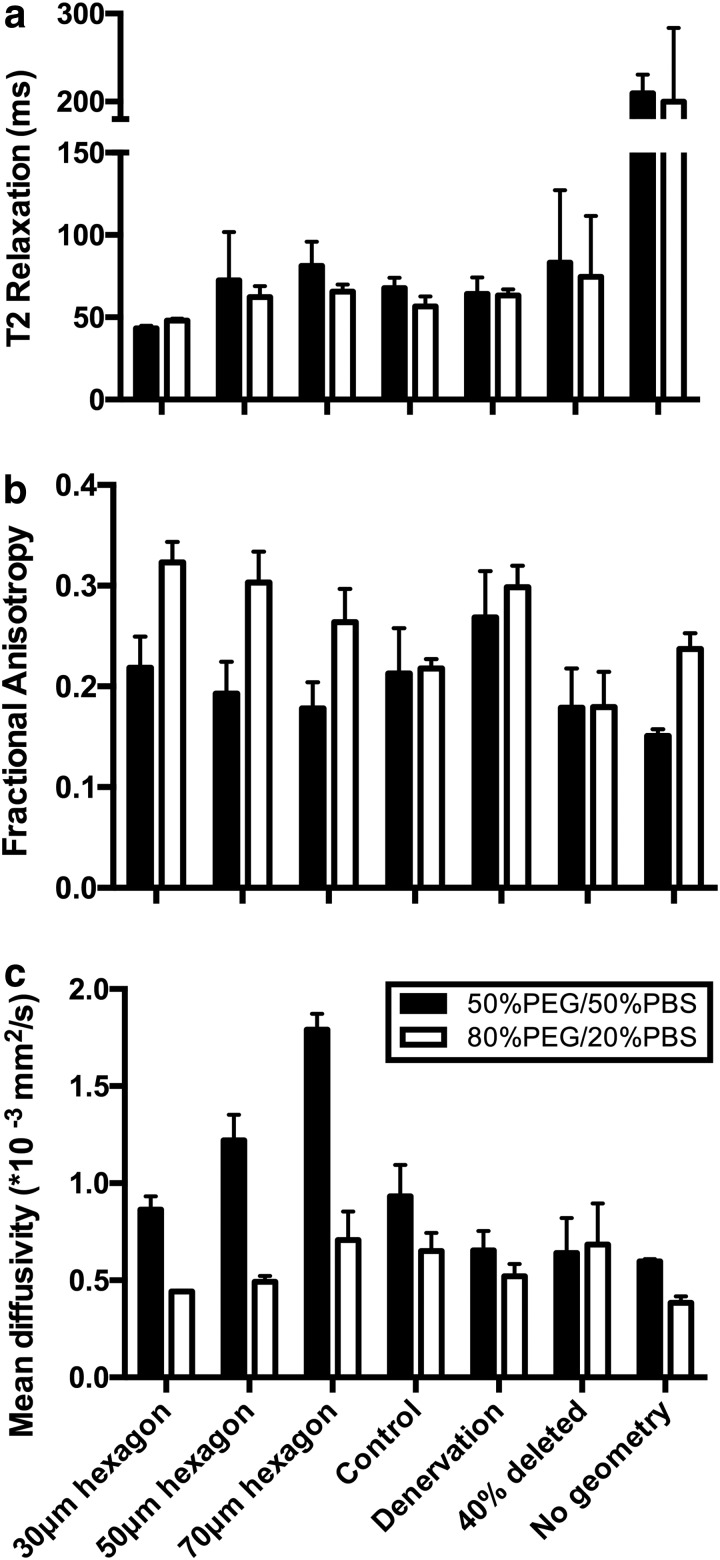
Structural MRI images (3D FLASH) were of sufficient resolution to identify phantom structure (Fig. 4a). The nondiffusion weighted EPI image (b = 0) demonstrated signal-to-noise (SNR) ratios (average 33.7 a.u.) above the minimum threshold for accurately calculating the diffusion tensor in skeletal muscle (Fig. 4b).^39,40 In general, the diffusion phantom with 50% PBS had effectively the same T₂ value as the phantoms with 20% PBS (Fig. 5a). However, the diffusion characteristics of the materials themselves had opposing diffusion characteristics; the diffusion phantom with 50% PBS had a lower FA and a higher MD than the phantoms with 20% PBS. FA decreased as the diameter of the hexagons increased for both phantoms (Fig. 5b). However, a FA of the 20% PBS phantoms was routinely higher than the 50% PBS phantoms, similar to the phantoms with no geometry. Interestingly, MD nearly doubled as fiber size increased for the 50% PBS phantoms, but only a slight difference was observed between 50 and 70 μm diameter hexagons in the 20% PBS phantoms (Fig. 5c). When 50 μm diameter hexagon models were printed with 40% of the walls deleted, decreased FA and slightly increased MD were observed only in the 20% PBS model. No decrease in MD was observed when 40% of walls were deleted for the 50% PBS model, which was unexpected. When comparing the histology informed muscle geometry models (normal and denervated), an increase in FA (Fig. 5b) and a decrease in MD (Fig. 5c) were observed in the denervation-based sample, which is consistent with previous findings from the literature. The multiecho DTI sequence was unable to define intra- and extracellular T₂ decay signals, indicating that the 20% and 50% PBS phantoms did not yield complex T₂ signals that would theoretically obscure underlying microstructural changes.

FIG. 4.

3D FLASH (a) and nondiffusion weighted (b = 0) (b) Diffusion tensor magnetic resonance imaging images of the diffusion phantoms.

FIG. 5.

The relationships between phantom microstructure and the diffusion tensor. Increasing fractional anisotropy (a) indicates more restricted diffusion. Increasing mean diffusivity (b) indicates increased magnitude of diffusion. Increasing T₂ relaxation (c) indicates increased water content. Mean ± standard deviation is shown for five phantoms with each geometry. PBS, phosphate-buffered saline; PEG, polyethylene glycol.

Discussion

This study demonstrated a technique to fabricate phantoms with physiologically relevant geometries. These phantoms were then used to explore the validity of DT-MRI as a method to measure microstructural changes in skeletal muscle. The FA and T₂ relaxation values of the phantoms were similar to what has previously been found in normal and edematous muscle, while MD was slightly below what has been previously reported (FA: 0.30 ± 0.08; MD: 1.52 ± 0.20*10⁻³ mm²/s; T₂: 28 ms-96 ms).^7,17,41 Our results demonstrate that as fiber size decreased, an increase in the FA and a decrease in MD were measurable, which is consistent with in vivo findings.¹³ Similarly, the differences in measured diffusion parameters between phantoms generated from normal and denervated muscle geometries are consistent with expected results from the literature and further support the idea that DLP-based 3D printing can be used to fabricate realistic skeletal muscle phantoms or constructs. However, although differences in T₂ relaxation and diffusion properties were found for the phantoms containing different concentrations of intra- and extracellular PBS, we were unable to identify differences in the regional diffusion of water.

The main goal in phantom design was to mimic the spectrum of structural and biophysical states possible in skeletal muscle. The relative distribution of intra- and extracellular water in real skeletal muscle is currently unknown. Due to histological limitations, the best method to measure water distribution in skeletal muscle is with MRI. However, measuring extracellular water volume fraction is extremely difficult when no edema is present. The best studies estimate extracellular water volume fraction to be around 5–20% in healthy muscle, to 45% in edematous muscle. However, these numbers have not been validated.

The 80% PEGDA/20% PBS was experimentally shown to be the phantom with the lowest overall volume fraction of PBS that resulted in adequate SNR (25) and exhibited a short T₂ relaxation time in the regions where geometry was printed. The 50% PEG/50% PBS models were deemed the largest volume fraction of water while still accurately being able to print accurate phantom geometries. As the overall volume fraction of PBS increases, there is a corresponding decrease in the structural stability of the models. Therefore, the different volume fractions of PBS and PEGDA were designed to replicate the minimum and the maximum extracellular water contents feasible to print with this method to simulate normal and edematous muscle, respectively.

In edematous skeletal muscle, increased MD and decreased FA are observed, regardless of other underlying fiber atrophy.¹¹ In the phantom with the larger fraction of water in the phantom material itself, this same pattern was similarly detected. These findings support the idea that in edematous skeletal muscle, the contribution of extracellular water may be dominating the overall diffusion signal. In real tissue, intra- and extracellular diffusions have been separated based on differences in T₂ relaxation between the two compartments using a multiecho DTI sequence.^16,17 In our study, we attempted to replicate these findings using a similar sequence, but were unsuccessful.

The different diameter sizes chosen for these models were designed to mimic a range of fiber sizes typically found in human muscles. Depending on the species, function, fiber type, age, and injury, muscle fiber diameters can range from 20 μm (mouse/human atrophic muscle) to 100 μm (normal frog/human hypertrophic muscle).¹ Average muscle fiber diameter is ∼40 to 60 μm; therefore, 50 μm diameter was chosen to be the average fiber diameter size. The atrophic (30 μm) and hypertrophic (70 μm) muscles were chosen to be out of the average range of a muscle fiber, but still in a relevant fiber diameter range of skeletal muscle.

The structural features responsible for permeability in skeletal muscle are currently not well understood. Moreover, the actual definition of the term “permeability” has been used inconsistently. Permeability can either be referred to as the normal passage of water molecules through the sarcolemma, between the intra and extracellular spaces, or as a structural defect in the sarcolemma itself. However, it is difficult to separate the contribution of either definition of permeability on the diffusion tensor as multiple microstructural changes are simultaneously occurring. Evans blue dye is commonly used to identify “permeable” fibers in histology of injured skeletal muscle.⁴² For example, in an acute cardiotoxin animal model, Evans Blue dye is observed in skeletal muscle and the diffusion profile is less restricted (decreased FA and increased MD).¹¹ The choice to represent permeability in our phantoms as randomly deleted walls is meant to represent a decreased overall diffusion environment. This was only observed for the phantoms printed with 20% PBS.

The development of 3D printed scaffolds to mimic realistic muscle architecture and physiology testing represents a major step forward in the validation and testing of the application of DT-MRI methods to muscle. Early diffusion phantoms were mainly fibrous vegetables.^43,44 These crude phantoms were used to measure variation in the direction of the diffusion tensor using different pulse sequences and image processing techniques. More complicated diffusion phantoms have been used to model diffusion in white matter tracts of nerve. Lorenz et al., used simple hydrophilic fibers, like hemp and linen, to study the relationship between diffusion and microstructure.²⁰ However, they used solid fibers with fluid surrounding it; therefore, diffusion measured was purely between fibers and would be inappropriate for skeletal muscle. Yanasak and Allison used circular glass capillaries with 23, 48, and 82 μm diameter that were filled with water as a model of nerve tissue to develop a diffusion phantom to test reproducibility of diffusion measurements.²¹ An increase in MD and a decrease in FA were found with increasing capillary size, which is consistent with changes in fiber size measured in vivo and this study. Similarly, hollow electrospun fibers have been used to simulate diffusion in nerve (∼10 μm diameter); however it is difficult to control the size, shape, and water properties of these fibers as they are being spun.¹⁸ In fairness, these phantoms were not engineered with skeletal muscle in mind.

One complication that we encountered in this study was the inability to separate diffusion from different compartments based on the estimated T₂ of the different tissue compartments. The multiexponential decay of skeletal muscle has been studied by several groups, and the consensus is that the short T₂ component can be attributed to intracellular diffusion and the long T₂ component can be attributed to extracellular diffusion.^45,46 We hypothesized that the water in the diffusion phantom would have a shorter T₂ decay due to interactions with the polymer substrate, which was observed (phantom T₂ ∼200 ms vs. free PBS ∼480 ms at 7T). One possible reason that we did not observe multiexponential decay in the 20% versus 50% PBS phantoms is that we did not manipulate the composition of intra- and extracellular water in a way that would mimic extracellular water in vivo. The net effect is that the intra- and extracellular water had the same T₂ values, making them inseparable with multiecho MRI, even though they were physically separated by the printed cell boundary.

This study demonstrated the fabrication and use of a precision-engineered phantom for DT-MRI. These constructs are especially attractive for tissue engineering as they can be used as 3D scaffolds for tissue-engineered muscle, with tight control over the geometry, mechanical properties, porosity, and biomimetic properties. Because muscle has such a strong structure–function relationship, having the ability to control geometry will be essential for designing muscle for future implantation. Furthermore, these scaffolds can be doped with cytokines, can be printed with different material properties (e.g., stiffness and chemical composition), and cells can be directly printed into the phantoms, which can provide more favorable environment for muscle cell proliferation. As these tissue-engineering constructs are developed, they have the potential to be used as tunable in vitro models for studying muscle injury and repair or in vivo as a personalized construct for regeneration.

There are several limitations to the phantoms demonstrated in this study. First, the maximum diameter of the phantoms made using this machine is 3.8 mm, which is close to the in-plane voxel dimension of a DTI sequence on a clinical scanner. Therefore, these phantoms would be inappropriate for validating DT-MRI at clinical imaging resolutions. However, with slight modification of the optical system, the DLP 3D printing system should be able to print larger scale phantoms (e.g., 5 cm tall scaffolds). In addition, with time, these hydrogel phantoms will begin to change shape due to swelling (∼4 days), creating variability in the geometry of the phantom if not scanned relatively soon after fabrication. However, as phantoms take a few seconds to fabricate, it is relatively easy to print phantoms immediately before MRI experiments to minimize the time allowed for samples to become deformed.

The goal of developing these phantoms was originally to validate DT-MRI as a technique to measure different microstructural features of skeletal muscle. Currently, it is believed that DT-MRI is sensitive to changes in fiber size associated with age, pathology, or injury. However, multiple microstructural changes occur simultaneously in muscle, which all have the potential to influence the diffusion of water. We have demonstrated that decreasing fiber diameter and increasing water content in the “extracellular” space affect the diffusion signal; decreasing fiber size increases FA and decreases MD; and increasing extracellular water content increases T₂ relaxation and results in more isotropic diffusion. However, in real muscle, permeability of the sarcolemma, fibrosis, and extracellular changes in fat fraction all contribute to the overall diffusion signal. Therefore, future iterations of these phantoms will investigate how these other structural features of muscle influence the DT-MRI signal individually and in combination with one another. While advanced simulation environments exist to model diffusion in 3D complex structures, these diffusion phantoms are necessary to translate in silico experiments to in vivo results.

Acknowledgments

The Digital Light Projection based 3D printing method was supported by grants from the National Institutes of Health (R01EB021857), the National Science Foundation (1547005 and 1644967), and California Institute for Regenerative Medicine (RT3-07899). L.R.F. is supported by grants from the National Institutes of Health (R01MH096100) and National Science Foundation (DBI-1147260, ACI-1550405, ACI-1440412, and AA013419-12). S.R.W. is supported by grants from the National Institutes of Health (HD073180) and Department of Defense (PR120576).

Disclosure Statement

No competing financial interests exist.