Abstract
Given a gene tree and a species tree, ancestral configurations represent the combinatorially distinct sets of gene lineages that can reach a given node of the species tree. They have been introduced as a data structure for use in the recursive computation of the conditional probability under the multispecies coalescent model of a gene tree topology given a species tree, the cost of this computation being affected by the number of ancestral configurations of the gene tree in the species tree. For matching gene trees and species trees, we obtain enumerative results on ancestral configurations. We study ancestral configurations in balanced and unbalanced families of trees determined by a given seed tree, showing that for seed trees with more than one taxon, the number of ancestral configurations increases for both families exponentially in the number of taxa n. For fixed n, the maximal number of ancestral configurations tabulated at the species tree root node and the largest number of labeled histories possible for a labeled topology occur for trees with precisely the same unlabeled shape. For ancestral configurations at the root, the maximum increases with 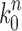 , where
, where 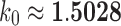 is a quadratic recurrence constant. Under a uniform distribution over the set of labeled trees of given size, the mean number of root ancestral configurations grows with
is a quadratic recurrence constant. Under a uniform distribution over the set of labeled trees of given size, the mean number of root ancestral configurations grows with 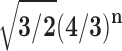 and the variance with ∼
and the variance with ∼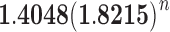 . The results provide a contribution to the combinatorial study of gene trees and species trees.
. The results provide a contribution to the combinatorial study of gene trees and species trees.
Keywords: : combinatorics, gene trees, phylogenetics, species trees
1. Introduction
Investigations of the evolution of genomic regions along species tree branches have generated new combinatorial structures that can assist in studying gene trees and species trees (Maddison, 1997; Degnan and Salter, 2005; Than and Nakhleh, 2009; Degnan et al., 2012; Wu, 2012). Among these structures are ancestral configurations, structures that for a given gene tree topology and species tree topology describe the possible sets of gene lineages that can reach a given node of the species tree (Wu, 2012).
Ancestral configurations represent the set of objects over which recursive computations are performed in a fundamental calculation for inference of species trees from information on multiple genetic loci: the evaluation of gene tree probabilities conditional on species trees (Wu, 2012). Because of the appearance of ancestral configurations in sets over which sums are computed [e.g., Eq. (7) of Wu (2012)], solutions to enumerative problems involving ancestral configurations contribute to an understanding of the computational complexity of phylogenetic calculations.
Under the assumption that a gene tree and a species tree have a matching labeled topology t, we examine the number of ancestral configurations that can appear at the nodes of the species tree. Extending results of Wu (2012), whose appendix reported the number of ancestral configurations for caterpillar species trees and established a lower bound for completely balanced species trees, we study the number of ancestral configurations when t belongs to families of trees characterized by a balanced or unbalanced pattern and a seed tree. As a special case, we derive upper and lower bounds on the number of ancestral configurations possessed by matching gene trees and species trees of given size. Finally, we study the mean and the variance of the number of ancestral configurations when t is a random labeled tree of given size selected under a uniform distribution.
2. Preliminaries
We study ancestral configurations for rooted binary labeled trees. We start with some definitions and preliminary results. In Section 2.1, we recall basic properties of rooted binary labeled trees. In Section 2.2, we recall properties of generating functions that will be used to derive some of our enumerative results. Following Wu (2012), in Section 2.3, we define ancestral configurations, and we determine a recursive procedure to compute their number for matching gene trees and species trees at a given species tree node. We then relate the total number of ancestral configurations in a tree to the number of ancestral configurations at the root of the tree.
2.1. Labeled topologies
A labeled topology, or tree for short, of size 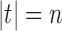 is a bifurcating rooted tree with n labeled taxa (Fig. 1A). We assume without loss of generality a linear (alphabetical) order
is a bifurcating rooted tree with n labeled taxa (Fig. 1A). We assume without loss of generality a linear (alphabetical) order 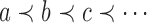 among the set
among the set 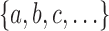 of possible labels for the taxa of a tree. A tree of size n has leaves labeled using the first n labels in the order
of possible labels for the taxa of a tree. A tree of size n has leaves labeled using the first n labels in the order 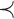 . Given two trees t1 and t2, we write
. Given two trees t1 and t2, we write 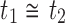 and say that t1 is isomorphic to t2 when, removing labels at their taxa, t1 and t2 share the same unlabeled topology. The set of trees of size n is denoted by Tn, and
and say that t1 is isomorphic to t2 when, removing labels at their taxa, t1 and t2 share the same unlabeled topology. The set of trees of size n is denoted by Tn, and 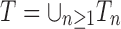 denotes the set of all trees of any size. The number of trees of size
denotes the set of all trees of any size. The number of trees of size 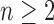 can be computed as
can be computed as 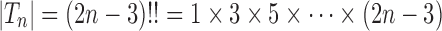 (Felsenstein, 1978), which can be rewritten for
(Felsenstein, 1978), which can be rewritten for 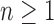 as
as
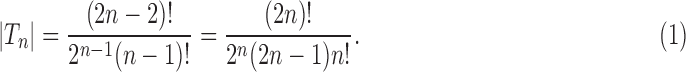 |
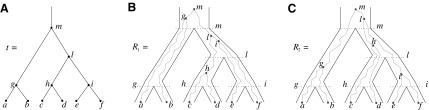
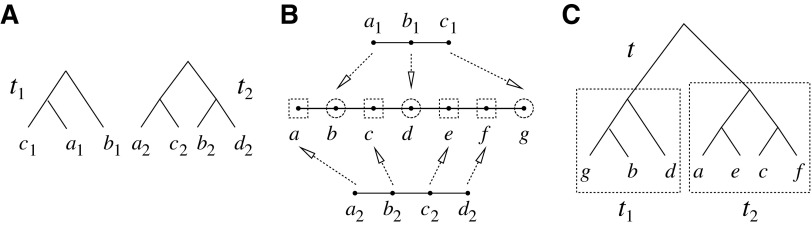
FIG. 1.
A gene tree and a species tree with a matching labeled topology t. (A) A tree t of size 6 isomorphic to the gene tree and species tree depicted in (B, C). Tree t is characterized by its shape and by the labeling of its taxa. It is convenient to label the internal nodes of t. We identify each lineage (edge) of t by its immediate descendant node, so, for example, lineage g results from the coalescence of lineages a and b. (B) A possible realization R1 of the gene tree in (A) (dotted lines) in the species tree with a matching topology (solid lines). The ancestral configuration at species tree node  is
is 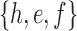 . The configuration at node m is
. The configuration at node m is 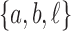 . (C) A different realization R2 of the gene tree in (A) in the matching species tree. The configurations at species tree nodes
. (C) A different realization R2 of the gene tree in (A) in the matching species tree. The configurations at species tree nodes 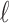 and m are
and m are 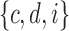 and
and 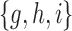 , respectively.
, respectively.
The exponential generating function associated with the sequence 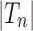 is defined as
is defined as
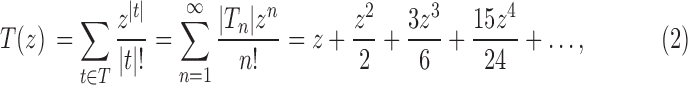 |
and it is given by (Flajolet and Sedgewick, 2009, Example II.19)
 |
Throughout the article, most of our results are purely combinatorial. Where a probability distribution on the set of labeled topologies of a given size is needed, we assume a uniform probability distribution over the set of trees of given size.
2.2. Exponential growth and analytic combinatorics
Following Flajolet and Sedgewick (2009), a sequence of non-negative numbers an is said to have exponential growth kn or, equivalently, to be of exponential order k when
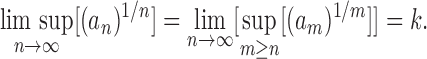 |
This relationship can be rephrased as 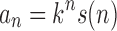 , where s is a subexponential factor, that is,
, where s is a subexponential factor, that is, 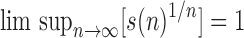 . By these definitions, a sequence an grows exponentially in n when its exponential order strictly exceeds 1.
. By these definitions, a sequence an grows exponentially in n when its exponential order strictly exceeds 1.
The exponential order of a sequence gives basic information about its speed of growth and enables comparisons with other sequences. In particular, from the definition, it follows that if 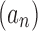 has exponential order ka and
has exponential order ka and 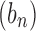 has exponential order
has exponential order 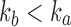 , then the sequence of ratios
, then the sequence of ratios 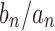 converges to 0 exponentially fast as
converges to 0 exponentially fast as 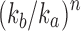 . If two sequences
. If two sequences 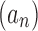 and
and 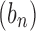 have the same exponential growth, then we write
have the same exponential growth, then we write 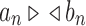 .
.
We are interested in the exponential growth of several increasing sequences of non-negative integers. Several results will be obtained through techniques of analytic combinatorics [see Sections IV and VI of Flajolet and Sedgewick (2009)]. The entries of a sequence of integers 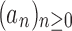 can be interpreted as the coefficients of the power series expansion
can be interpreted as the coefficients of the power series expansion 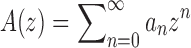 at
at 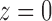 of a function
of a function 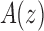 , the generating function of the sequence. Considering z as a complex variable, under suitable conditions, there exists a general correspondence between the singular expansion of the generating function
, the generating function of the sequence. Considering z as a complex variable, under suitable conditions, there exists a general correspondence between the singular expansion of the generating function 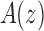 near its dominant singularity—the one nearest to the origin—and the asymptotic behavior of the associated coefficients an. In particular, the exponential order of the sequence
near its dominant singularity—the one nearest to the origin—and the asymptotic behavior of the associated coefficients an. In particular, the exponential order of the sequence 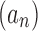 is given by the inverse of the modulus of the dominant singularity of
is given by the inverse of the modulus of the dominant singularity of 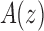 . For instance, the exponential order of the sequence
. For instance, the exponential order of the sequence  , with
, with 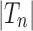 as in Equation (1), is 2 because
as in Equation (1), is 2 because 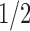 is the dominant singularity of the associated generating function [Eq. (3)]. In other words,
is the dominant singularity of the associated generating function [Eq. (3)]. In other words, 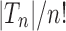 increases with a subexponential multiple of
increases with a subexponential multiple of 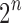 as n becomes large.
as n becomes large.
2.3. Gene trees, species trees, and ancestral configurations
In this section, we define the object on which our study focuses: the ancestral configurations of a gene tree G in a species tree S. Ancestral configurations have been introduced by Wu (2012). In our framework, where exactly one gene lineage has been selected from each species, we assume G and S to have the same labeled topology t.
2.3.1. Ancestral configurations
Suppose R is a realization of a gene tree G in a species tree S, where we focus on the case of 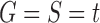 (Fig. 1). In other words, R is one of the evolutionary possibilities for the gene tree G on the matching species tree S. Viewed backward in time, for a given node k of t, consider the set
(Fig. 1). In other words, R is one of the evolutionary possibilities for the gene tree G on the matching species tree S. Viewed backward in time, for a given node k of t, consider the set 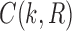 of gene lineages (edges of G) that are present in S at the point right before node k.
of gene lineages (edges of G) that are present in S at the point right before node k.
As in Wu (2012), the set 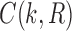 is called the ancestral configuration of the gene tree at node k of the species tree. Taking the tree t depicted in Figure 1A and considering the realization R1 of the gene tree
is called the ancestral configuration of the gene tree at node k of the species tree. Taking the tree t depicted in Figure 1A and considering the realization R1 of the gene tree 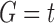 in the species tree
in the species tree 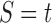 as given in Figure 1B, we see that the gene lineages a, b, and
as given in Figure 1B, we see that the gene lineages a, b, and 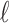 are those present in the species tree at the point right before the root node m. The set
are those present in the species tree at the point right before the root node m. The set 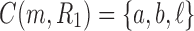 is thus the ancestral configuration of the gene tree at node m of the species tree. Similarly, the ancestral configuration of the gene tree at node
is thus the ancestral configuration of the gene tree at node m of the species tree. Similarly, the ancestral configuration of the gene tree at node 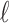 of the species tree is the set of gene lineages
of the species tree is the set of gene lineages  . In Figure 1C, where a different realization R2 of the same gene tree is depicted, the ancestral configuration at the root m of the species tree is the set of gene lineages
. In Figure 1C, where a different realization R2 of the same gene tree is depicted, the ancestral configuration at the root m of the species tree is the set of gene lineages 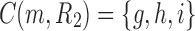 . The ancestral configuration at node
. The ancestral configuration at node 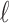 is
is 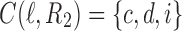 .
.
Let 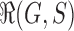 be the set of possible realizations of the gene tree
be the set of possible realizations of the gene tree 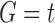 in the species tree
in the species tree 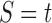 . For a given node k of t, by considering all possible elements
. For a given node k of t, by considering all possible elements 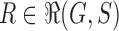 , we define the set
, we define the set
 |
and the number
 |
Thus, 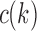 corresponds to the number of different ways the gene lineages of G can reach the point right before node k in S, when all possible realizations of the gene tree G in the species tree S are considered. For instance, taking t as in Figure 1A, we have
corresponds to the number of different ways the gene lineages of G can reach the point right before node k in S, when all possible realizations of the gene tree G in the species tree S are considered. For instance, taking t as in Figure 1A, we have 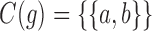 ,
, 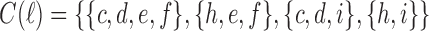 , and
, and
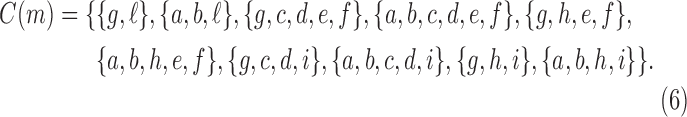 |
Note that for two different realizations  and an internal node k, we do not necessarily have
and an internal node k, we do not necessarily have  .
.
For each internal node k, our definition of ancestral configuration specifically excludes as a possibility the case in which all gene tree lineages descended from node k have coalesced at species tree node k so that 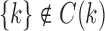 . Each configuration at node k is considered at the point right before node k in the species tree, and there is thus no time for the gene lineages from the left subtree of k to coalesce with those from the right subtree of k. Our definition is identical to that of Wu (2012), with the exception that we say that a leaf or 1-taxon tree has 0 ancestral configurations, whereas Wu assigns these cases 1 ancestral configuration.
. Each configuration at node k is considered at the point right before node k in the species tree, and there is thus no time for the gene lineages from the left subtree of k to coalesce with those from the right subtree of k. Our definition is identical to that of Wu (2012), with the exception that we say that a leaf or 1-taxon tree has 0 ancestral configurations, whereas Wu assigns these cases 1 ancestral configuration.
Because we assume gene tree G and species tree S have the same labeled topology t, the set 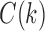 and the quantity
and the quantity 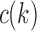 defined in Equations (4) and (5) depend only on node k and tree t. In what follows, we use the term configuration at node k of t to denote an element of
defined in Equations (4) and (5) depend only on node k and tree t. In what follows, we use the term configuration at node k of t to denote an element of 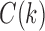 . The next result provides a recursive procedure for calculating the number
. The next result provides a recursive procedure for calculating the number 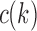 at a given node k of t.
at a given node k of t.
Proposition 1 Given a tree t with
 , the number
, the number
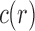 of possible configurations at the root r of t can be recursively computed as
of possible configurations at the root r of t can be recursively computed as
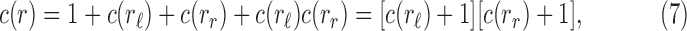 |
where
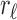 (resp. rr) denotes the left (resp. right) child of r and
(resp. rr) denotes the left (resp. right) child of r and
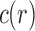 is set to 0 when
is set to 0 when
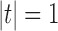 .
.
Proof. If A and B are two sets of sets, we define 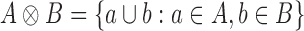 . The set
. The set 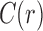 of configurations at internal node r can be decomposed as
of configurations at internal node r can be decomposed as
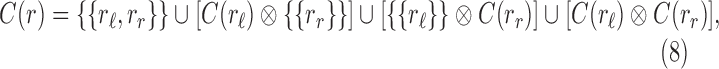 |
where the set unions are disjoint because, as already noted, 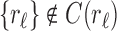 and
and 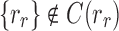 . We immediately obtain Equation (7), as
. We immediately obtain Equation (7), as 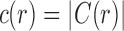 . ■
. ■
We reiterate that for Equation (7) to apply for all t with  , we must set to 0 the number of configurations at a species tree leaf and at the root of the 1-taxon tree. For the tree depicted in Figure 1A, each configuration in
, we must set to 0 the number of configurations at a species tree leaf and at the root of the 1-taxon tree. For the tree depicted in Figure 1A, each configuration in 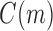 [Eq. (6)] can be obtained as described in Equation (8) from the configurations in
[Eq. (6)] can be obtained as described in Equation (8) from the configurations in 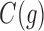 and
and 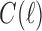 . Note indeed that
. Note indeed that 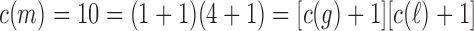 , as determined by Equation (7).
, as determined by Equation (7).
2.3.2. Total configurations and root configurations
Let 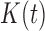 be the set of nodes of a tree t. The number of nodes
be the set of nodes of a tree t. The number of nodes 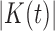 satisfies
satisfies 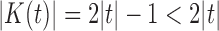 . Define the total number of configurations in t as the sum
. Define the total number of configurations in t as the sum
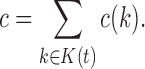 |
Let 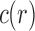 be the number of configurations at the root r of t, or root configurations for short. As is shown in Appendix 1,
be the number of configurations at the root r of t, or root configurations for short. As is shown in Appendix 1, 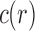 satisfies the bound
satisfies the bound
 |
Furthermore, because 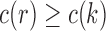 for each node k of t, we have
for each node k of t, we have
 |
This result indicates that the total number of configurations c and the number of root configurations 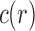 are equal up to a factor that is at most polynomial in the tree size
are equal up to a factor that is at most polynomial in the tree size 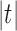 . A consequence is that in measuring
. A consequence is that in measuring 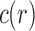 for a family
for a family 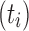 of trees of increasing size, an exponential growth of the form
of trees of increasing size, an exponential growth of the form 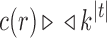 for the number of root configurations translates into the same exponential growth for the total number of configurations in t:
for the number of root configurations translates into the same exponential growth for the total number of configurations in t:
 |
where, by virtue of Equation (9),  .
.
An equivalent result holds when we consider the expected value of the total number of configurations 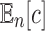 in a random labeled tree topology of given size n. Indeed, when a tree of size n is selected at random from the set of labeled topologies, Equation (10) gives
in a random labeled tree topology of given size n. Indeed, when a tree of size n is selected at random from the set of labeled topologies, Equation (10) gives 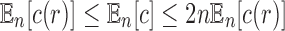 . Thus, the exponential growth of
. Thus, the exponential growth of 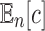 with respect to n can be recovered from the exponential growth of
with respect to n can be recovered from the exponential growth of 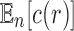 ,
,
 |
Similarly, for the second moment 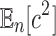 , we have
, we have 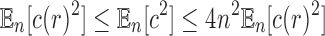 , and thus
, and thus
 |
Using these results, in Sections 3 and 5 we will determine the exponential growth of 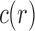 and c with respect to size
and c with respect to size  when t is considered in different settings. In Section 3, t belongs to families of unbalanced or balanced trees, whereas in Section 5, we perform our analysis considering t as a random labeled topology of given size.
when t is considered in different settings. In Section 3, t belongs to families of unbalanced or balanced trees, whereas in Section 5, we perform our analysis considering t as a random labeled topology of given size.
2.4. Root configurations in small trees
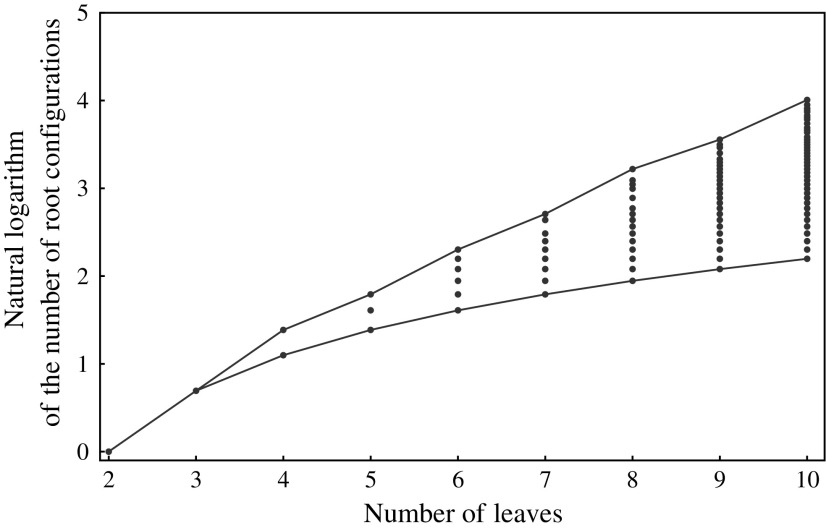
For small values of n, Equation (7) enables the exhaustive computation of the number of root configurations 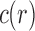 for representative labelings of each of the unlabeled topologies of size n. In Figure 2, each dot corresponds to the logarithm of the number of root configurations for a certain tree shape of size determined by its x-coordinate. The dots associated with the largest values of
for representative labelings of each of the unlabeled topologies of size n. In Figure 2, each dot corresponds to the logarithm of the number of root configurations for a certain tree shape of size determined by its x-coordinate. The dots associated with the largest values of 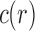 are connected by the top line, whose growth is linear in n. Indeed, as was shown by Wu (2012), there exist families of trees for which the growth of the number of root configurations is exponential in the tree size. From Equation (9), it follows that the growth of the sequence of the largest number of root configurations in trees of size n must be exponential in n as well.
are connected by the top line, whose growth is linear in n. Indeed, as was shown by Wu (2012), there exist families of trees for which the growth of the number of root configurations is exponential in the tree size. From Equation (9), it follows that the growth of the sequence of the largest number of root configurations in trees of size n must be exponential in n as well.
FIG. 2.
Natural logarithm of the number of root configurations for all possible tree shapes of size 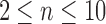 . The value for
. The value for 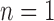 ,
,  , is omitted. Dots corresponding to the largest and smallest numbers of root configurations for each n are connected by the top and bottom lines, respectively.
, is omitted. Dots corresponding to the largest and smallest numbers of root configurations for each n are connected by the top and bottom lines, respectively.
The tree shapes whose labeled topologies possess the largest number of root configurations among trees of fixed size appear in Figure 3 together with their number of root configurations 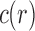 . Starting with
. Starting with 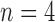 , each shape in the sequence can be seen to be produced by connecting two smaller shapes also in the sequence (possibly the same shape) to a shared root.
, each shape in the sequence can be seen to be produced by connecting two smaller shapes also in the sequence (possibly the same shape) to a shared root.
FIG. 3.
Tree shapes of size 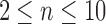 whose labeled topologies have the largest number of root configurations among trees of size n. The number of root configurations
whose labeled topologies have the largest number of root configurations among trees of size n. The number of root configurations 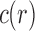 is indicated for each tree. In each tree displayed, the two root subtrees each maximize the number of root configurations among trees of their size.
is indicated for each tree. In each tree displayed, the two root subtrees each maximize the number of root configurations among trees of their size.
The tree shape that minimizes the number of root configurations is the caterpillar topology. The number of root configurations in the caterpillar of size n is 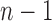 (Wu, 2012). The bottom line in Figure 2, which connects dots corresponding to the smallest number of root configurations for a tree with n taxa, grows with
(Wu, 2012). The bottom line in Figure 2, which connects dots corresponding to the smallest number of root configurations for a tree with n taxa, grows with 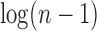 .
.
These observations show that tree topology can have a considerable impact on the number of ancestral configurations that are possible for a given tree size. Indeed, the next section investigates the effect of tree balance on the number of root configurations in a tree. Figure 2 suggests that for random labeled topologies of a specified size, we can expect the variance of the number of root configurations to be large. We will confirm this claim in Section 5. We will also show that although there exist tree families (e.g., caterpillars) for which the growth of the number of root configurations is polynomial in the tree size, the expected number of root configurations in a random labeled topology of given size n grows exponentially in n.
3. Root Configurations for Unbalanced and Balanced Families of Trees
In this section, we study the number of root configurations for particular families of trees, extending beyond two cases considered by Wu (2012): the caterpillar case, which was studied exactly, and the completely balanced case, for which a loose lower bound of 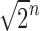 was reported. As balance is an important tree property that influences ancestral configurations, we study unbalanced and balanced families generated by different seed trees. Upper and lower bound results on the number of root configurations for trees of specified size appear in Section 4.
was reported. As balance is an important tree property that influences ancestral configurations, we study unbalanced and balanced families generated by different seed trees. Upper and lower bound results on the number of root configurations for trees of specified size appear in Section 4.
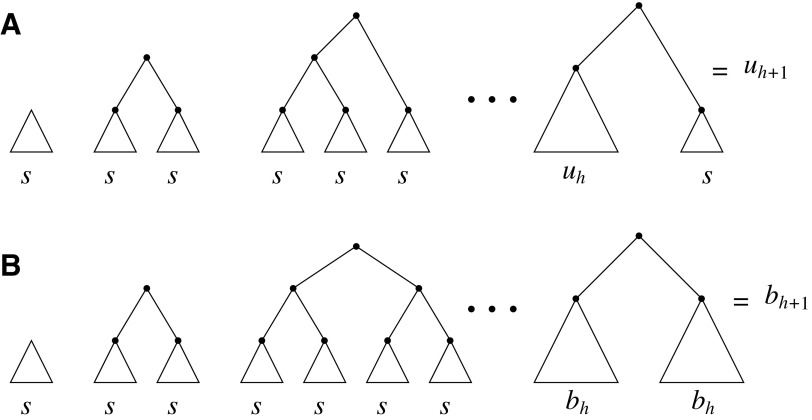
For a given seed tree s, we consider the unbalanced family 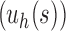 (Fig. 4A) and the balanced family
(Fig. 4A) and the balanced family 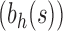 (Fig. 4B) defined as follows:
(Fig. 4B) defined as follows:
 |
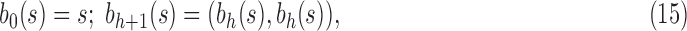 |
FIG. 4.
Unbalanced and balanced families of trees defined from a given seed tree s. (A) The unbalanced family 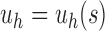 is defined by
is defined by  , setting
, setting  as the tree of size
as the tree of size 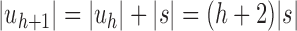 obtained by appending uh and s to a shared root node. (B) The balanced family
obtained by appending uh and s to a shared root node. (B) The balanced family  is defined by
is defined by 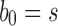 , setting
, setting 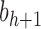 as the tree of size
as the tree of size 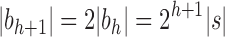 obtained by appending two copies of bh to a shared root node.
obtained by appending two copies of bh to a shared root node.
where 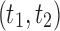 is the tree shape obtained by appending trees t1 and t2 to a shared root node. Note that the family of caterpillar trees is obtained as
is the tree shape obtained by appending trees t1 and t2 to a shared root node. Note that the family of caterpillar trees is obtained as 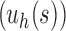 when
when 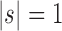 . For the same seed tree of size 1,
. For the same seed tree of size 1, 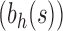 is the family of completely balanced trees. When
is the family of completely balanced trees. When 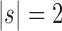 ,
, 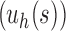 resembles the lodgepole family
resembles the lodgepole family 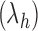 , which is defined recursively by setting
, which is defined recursively by setting 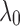 as the 1-taxon tree, and
as the 1-taxon tree, and 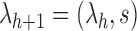 (Disanto and Rosenberg, 2015). The only difference is that in
(Disanto and Rosenberg, 2015). The only difference is that in  , each leaf is in a cherry, whereas
, each leaf is in a cherry, whereas 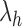 has a unique leaf that is not in a cherry. For each family, it is understood that we consider an arbitrary labeling of each unlabeled shape in the family.
has a unique leaf that is not in a cherry. For each family, it is understood that we consider an arbitrary labeling of each unlabeled shape in the family.
3.1. Unbalanced families
Fix a seed tree s and consider the family 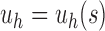 as defined in Equation (14). Let
as defined in Equation (14). Let 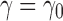 be the number of root configurations in
be the number of root configurations in 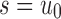 , and define
, and define 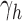 as the number of root configurations in uh. If s is the 1-taxon tree, then as noted earlier, the number of root configurations
as the number of root configurations in uh. If s is the 1-taxon tree, then as noted earlier, the number of root configurations 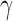 is set to 0. From Proposition 1, we obtain the recursion
is set to 0. From Proposition 1, we obtain the recursion
 |
starting with 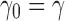 . As shown in Appendix 2, the generating function
. As shown in Appendix 2, the generating function
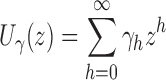 |
is described by
 |
For 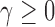 , the dominant singularity of
, the dominant singularity of 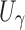 —the singularity nearest to the origin—is the solution
—the singularity nearest to the origin—is the solution 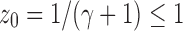 of the equation
of the equation 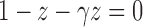 . Applying Theorem IV.7 of Flajolet and Sedgewick (2009) yields the exponential growth of the sequence
. Applying Theorem IV.7 of Flajolet and Sedgewick (2009) yields the exponential growth of the sequence 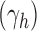 with respect to the index h as
with respect to the index h as
 |
Because uh has 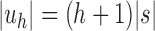 leaves, substituting
leaves, substituting 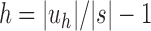 in Equation (18), we obtain the next proposition.
in Equation (18), we obtain the next proposition.
Proposition 2 In the unbalanced family
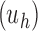 , the exponential growth of the number of root configurations in the size
, the exponential growth of the number of root configurations in the size
 is
is
 |
where
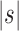 is the size of the seed tree and
is the size of the seed tree and
 is its number of root configurations. The total number of configurations in the family
is its number of root configurations. The total number of configurations in the family
 has the same exponential growth.
has the same exponential growth.
In other words, for values of the number of leaves n at which a member of the unbalanced family exists, the number of root configurations in the unbalanced family grows with 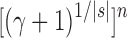 .
.
When the seed tree is the 1-taxon tree, so that 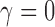 and
and 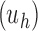 is the sequence of caterpillar trees, Equation (19) gives the exponential growth
is the sequence of caterpillar trees, Equation (19) gives the exponential growth 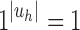 . Indeed, the number of root configurations in the caterpillar family grows like a polynomial function of the size, as immediately follows from Equation (16) [see also Wu (2012)]. Taking
. Indeed, the number of root configurations in the caterpillar family grows like a polynomial function of the size, as immediately follows from Equation (16) [see also Wu (2012)]. Taking  , the number of root configurations in
, the number of root configurations in 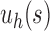 becomes exponential in the tree size. Table 1 illustrates that for unbalanced families defined by small seed trees of size greater than one, root configurations in n-taxon trees—provided that a tree with n taxa is in the family—have exponential growth in the range
becomes exponential in the tree size. Table 1 illustrates that for unbalanced families defined by small seed trees of size greater than one, root configurations in n-taxon trees—provided that a tree with n taxa is in the family—have exponential growth in the range 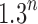 to
to 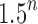 .
.
Table 1.
Approximate Values of the Constants That When Raised to the Power n Describe the Exponential Growth with the Number of taxa n of the Number of Ancestral Configurations in Unbalanced and Balanced Families For Small Seed Trees
| Seed tree s | 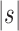 |
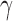 |
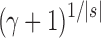 (unbalanced) (unbalanced)
|
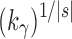 (balanced) (balanced)
|
Seed tree s | 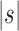 |
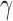 |
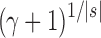 (unbalanced) (unbalanced)
|
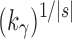 (balanced) (balanced)
|
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1.503 | 5 | 6 | 1.476 | 1.479 | ||
| 2 | 1 | 1.414 | 1.503 | 6 | 5 | 1.348 | 1.351 | ||
| 3 | 2 | 1.442 | 1.469 | 6 | 6 | 1.383 | 1.385 | ||
| 4 | 3 | 1.414 | 1.425 | 6 | 7 | 1.414 | 1.416 | ||
| 4 | 4 | 1.495 | 1.503 | 6 | 8 | 1.442 | 1.444 | ||
| 5 | 4 | 1.380 | 1.385 | 6 | 10 | 1.491 | 1.492 | ||
| 5 | 5 | 1.431 | 1.435 | 6 | 9 | 1.468 | 1.469 |
Each constant is obtained to three decimal places by numerically evaluating Equation (20).
3.2. Balanced families
The results change when we consider balanced families. For a fixed seed tree s, consider the family 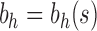 as defined in Equation (15). Let
as defined in Equation (15). Let 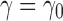 be the number of root configurations in seed tree
be the number of root configurations in seed tree 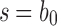 , and define
, and define 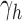 as the number of root configurations in bh. If
as the number of root configurations in bh. If 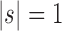 , then
, then 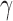 is 0. From Proposition 1, we obtain
is 0. From Proposition 1, we obtain
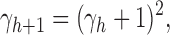 |
with 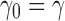 . Defining the sequence
. Defining the sequence 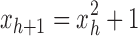 , with
, with 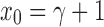 , it is straightforward to show that
, it is straightforward to show that 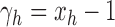 .
.
Sequence xh can be studied as in Aho and Sloane (1973, Section 3 and Example 2.2). For 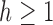 , a constant
, a constant 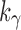 exists for which
exists for which
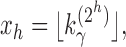 |
where 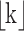 is the floor function for k. The constant
is the floor function for k. The constant 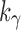 can be approximated using the recursive definition of xh, summing terms in a series:
can be approximated using the recursive definition of xh, summing terms in a series:
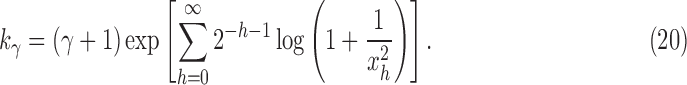 |
Switching back to 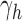 , for
, for 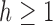 , we obtain
, we obtain
 |
Thus, because 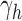 grows with
grows with 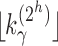 , to determine the exponential growth of the number of root configurations, it remains to evaluate the constant
, to determine the exponential growth of the number of root configurations, it remains to evaluate the constant 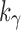 . Rescaling Equation (21) to consider the number of leaves
. Rescaling Equation (21) to consider the number of leaves 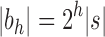 as a parameter, we obtain the next proposition.
as a parameter, we obtain the next proposition.
Proposition 3 In the balanced family
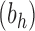 , the exponential growth of the number of root configurations in the size
, the exponential growth of the number of root configurations in the size
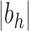 is
is
 |
where
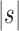 is the size of the seed tree. The constant
is the size of the seed tree. The constant
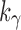 can be computed as in Equation (20) and bounded by
can be computed as in Equation (20) and bounded by
 |
The total number of configurations in the family
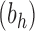 has the same exponential growth.
has the same exponential growth.
In other words, for values of the number of leaves n, at which a member of the balanced family exists, the number of root configurations in the balanced family grows with 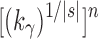 .
.
Proof. It remains only to prove the bound [Eq. (23)]. The lower bound follows quickly from Equation (20), as the exponent is positive. The upper bound is obtained by observing that the sequence 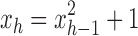 is increasing, and thus
is increasing, and thus 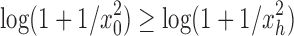 for each
for each 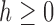 . Therefore, from Equation (20) and the fact that
. Therefore, from Equation (20) and the fact that 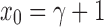 , we have
, we have
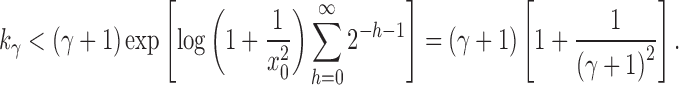 |
■
Comparing the number of root configurations in balanced families with those in unbalanced families (Table 1), we see that the exponential order for balanced families is greater than in unbalanced families, although typically still in the range 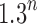 to
to 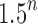 .
.
3.3. Comparing unbalanced and balanced families
For a given seed tree s, the quantities 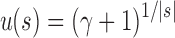 and
and  determine the exponential orders of the sequences considered in Propositions 2 and 3, respectively. We observe three facts.
determine the exponential orders of the sequences considered in Propositions 2 and 3, respectively. We observe three facts.
(i) Applying the lower bound in Equation (23), 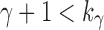 , for a fixed seed tree s, we always have
, for a fixed seed tree s, we always have
 |
Therefore, the growth of the number of ancestral configurations in the family 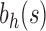 is exponentially faster than the growth in the family
is exponentially faster than the growth in the family 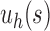 . When s is not small, however,
. When s is not small, however, 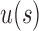 can become close to
can become close to 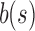 . For large s,
. For large s, 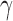 is also large. Owing to the upper bound in Equation (23), although
is also large. Owing to the upper bound in Equation (23), although 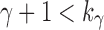 ,
, 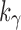 only slightly exceeds
only slightly exceeds 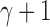 . Furthermore, the exponent
. Furthermore, the exponent 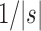 in the expressions for
in the expressions for 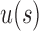 and
and 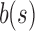 further reduces the difference between them.
further reduces the difference between them.
For instance, if s is the caterpillar tree with 10 leaves, we have 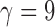 ,
, 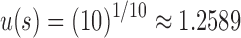 , and
, and 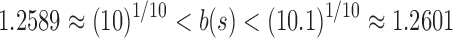 . In this case,
. In this case, 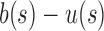 is bounded above by a constant near
is bounded above by a constant near  . The increasing similarity of
. The increasing similarity of  and
and 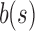 is already evident in Table 1, as their values for 6-taxon seed trees are substantially closer to each other than for the smaller 1-, 2-, and 3-taxon seed trees.
is already evident in Table 1, as their values for 6-taxon seed trees are substantially closer to each other than for the smaller 1-, 2-, and 3-taxon seed trees.
(ii) The choice of the seed tree can play an important role in the relative values of 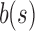 and
and 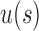 as taking two different seed trees can flip the inequality in Equation (24). In fact, if s1 and s2 are two seed trees of the same size
as taking two different seed trees can flip the inequality in Equation (24). In fact, if s1 and s2 are two seed trees of the same size 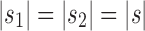 for which
for which 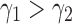 , then
, then
 |
To obtain this result, we note that 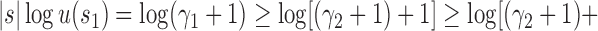
 , where the latter inequality follows from the upper bound [Eq. (23)]. The result is observable in Table 1, where at fixed
, where the latter inequality follows from the upper bound [Eq. (23)]. The result is observable in Table 1, where at fixed  of 4, 5, or 6,
of 4, 5, or 6, 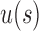 for some of the shapes exceeds
for some of the shapes exceeds 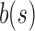 for other shapes.
for other shapes.
(iii) When the seed tree s is chosen as the 1-taxon tree with 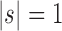 , the constant
, the constant 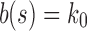 determines an upper bound for the number of root configurations that a tree of given size can have. This result is shown in more detail in the following section. The value of k0 can be computed numerically from Equation (20):
determines an upper bound for the number of root configurations that a tree of given size can have. This result is shown in more detail in the following section. The value of k0 can be computed numerically from Equation (20):
 |
This constant provides the exact value for which 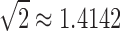 , reported by Wu (2012), provided a lower bound.
, reported by Wu (2012), provided a lower bound.
4. Smallest and Largest Numbers of Root Configurations for Trees of Fixed Size
We have seen that the number of root configurations for caterpillar trees grows polynomially and that the number of root configurations in unbalanced noncaterpillar families and balanced families grows exponentially. In the examples we have considered, the exponential growth proceeds with 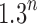 to
to 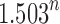 . We now show that the caterpillar trees have the smallest number of root configurations and that the constant k0 [Eq. (26)], in fact, provides an upper bound on the exponential growth of the number of root configurations as n increases. We characterize the labeled topologies that possess the largest number of root configurations at fixed n.
. We now show that the caterpillar trees have the smallest number of root configurations and that the constant k0 [Eq. (26)], in fact, provides an upper bound on the exponential growth of the number of root configurations as n increases. We characterize the labeled topologies that possess the largest number of root configurations at fixed n.
4.1. Smallest number of root configurations
For the caterpillar tree of size n, the number of root configurations is 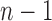 . We show that this value,
. We show that this value, 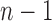 , is the smallest number of root configurations for a tree of size n.
, is the smallest number of root configurations for a tree of size n.
Let 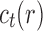 denote the number of root configurations of tree t. Let
denote the number of root configurations of tree t. Let 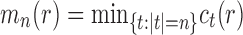 . Suppose we have shown for each i with
. Suppose we have shown for each i with 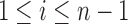 that
that
 |
The claim clearly holds for 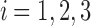 , for each of which the sole tree t has
, for each of which the sole tree t has 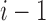 root configurations.
root configurations.
For 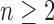 , we use induction to prove Equation (27) for
, we use induction to prove Equation (27) for 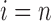 . Suppose
. Suppose 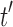 is a tree of size n such that
is a tree of size n such that 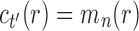 . The number of root configurations of
. The number of root configurations of 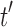 is given by Proposition 1 as the product
is given by Proposition 1 as the product 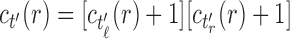 , where
, where 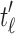 and
and 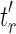 are the root subtrees of
are the root subtrees of 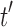 . Because
. Because 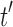 has the minimal number of root configurations,
has the minimal number of root configurations, 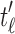 and
and 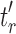 must separately possess the minimal number of root configurations among trees of their size. We can then write
must separately possess the minimal number of root configurations among trees of their size. We can then write  and
and 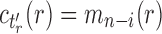 , where, without loss of generality, i is a certain value with
, where, without loss of generality, i is a certain value with 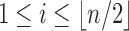 . Therefore,
. Therefore, 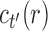 has the form
has the form 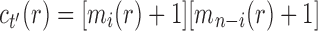 . It is determined from the minimum
. It is determined from the minimum
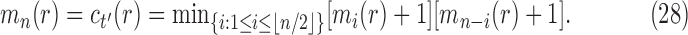 |
Applying the inductive hypothesis [Eq. (27)], we obtain 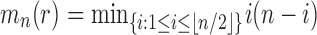 . In the permissible range for i, the product
. In the permissible range for i, the product 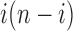 reaches its minimum value at
reaches its minimum value at 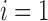 , equaling
, equaling 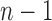 as desired.
as desired.
By induction, we have shown that Equation (27) holds for each 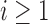 . Furthermore, the fact that the product
. Furthermore, the fact that the product 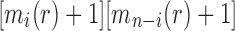 in Equation (28) is minimal only at
in Equation (28) is minimal only at 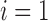 also demonstrates that those tree shapes of size n with the smallest number of root configurations can be recursively obtained by appending the 1-taxon tree and the tree shape of size
also demonstrates that those tree shapes of size n with the smallest number of root configurations can be recursively obtained by appending the 1-taxon tree and the tree shape of size 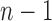 with the smallest number of root configurations to a shared root node. Trees resulting from this recursive construction are exactly those having a caterpillar shape.
with the smallest number of root configurations to a shared root node. Trees resulting from this recursive construction are exactly those having a caterpillar shape.
4.2. Largest number of root configurations
For the largest number of root configurations, we denote 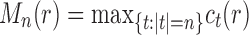 . Similarly to Equation (28), we seek to identify the trees t that produce the maximum in the following equation and to evaluate that maximum:
. Similarly to Equation (28), we seek to identify the trees t that produce the maximum in the following equation and to evaluate that maximum:
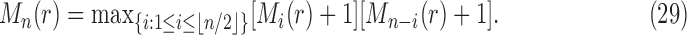 |
Note that  . Taking
. Taking 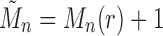 , we have the recursion
, we have the recursion
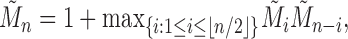 |
starting with  . The sequence
. The sequence 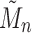 was studied by de Mier and Noy (2012, Theorems 1 and 2), where it was shown (i) taking
was studied by de Mier and Noy (2012, Theorems 1 and 2), where it was shown (i) taking 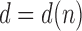 as the power of 2 nearest to
as the power of 2 nearest to 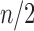 , we have
, we have 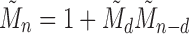 , so that
, so that
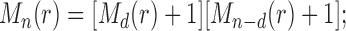 |
(ii) for all 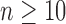 ,
,  , that is,
, that is,
 |
where the constant k0 has been already computed in Equation (26).
For small n, the labeled topologies with the largest numbers of root configurations appear in Figure 3. Collecting the results for the smallest and largest number of root configurations, we can state the following facts.
Proposition 4 (i) For each
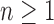 , the smallest number of root configurations in a tree of size n is
, the smallest number of root configurations in a tree of size n is
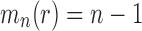 . The caterpillar tree shape of size n has exactly
. The caterpillar tree shape of size n has exactly
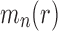 root configurations. (ii) For each
root configurations. (ii) For each
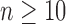 , the largest number of root configurations in a tree of size n,
, the largest number of root configurations in a tree of size n,
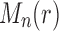 , can be bounded as in Equation (30). For
, can be bounded as in Equation (30). For
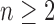 , if
, if
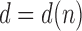 denotes the power of 2 nearest to
denotes the power of 2 nearest to
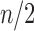 , then
, then
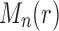 is the number of root configurations in the tree shape tn recursively defined as
is the number of root configurations in the tree shape tn recursively defined as
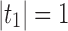 ,
,
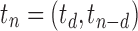 . When
. When
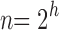 for integers h, tn is the completely balanced tree of depth h and
for integers h, tn is the completely balanced tree of depth h and
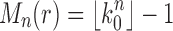 [Eq. (21)].
[Eq. (21)].
As a corollary, we obtain the following result, the proof of which appears in Appendix 3.
Corollary 1  The exponential growth of the sequences
The exponential growth of the sequences
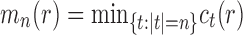 and
and
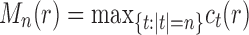 follows
follows
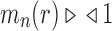 and
and
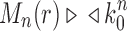 .
.
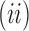 The sequences
The sequences
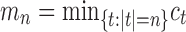 and
and
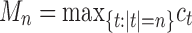 , giving, respectively, the smallest and the largest total number of configurations ct in a tree t of size n, have exponential growth
, giving, respectively, the smallest and the largest total number of configurations ct in a tree t of size n, have exponential growth
 and
and
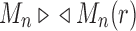 .
.
The family of tree shapes 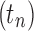 defined in Proposition 4 by the recursive decomposition
defined in Proposition 4 by the recursive decomposition 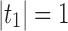 and
and 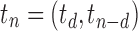 , where d is the power of 2 nearest to
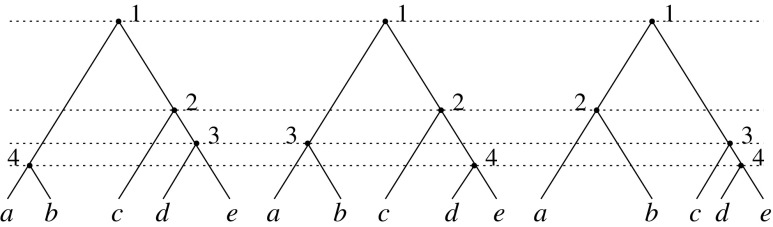
, where d is the power of 2 nearest to 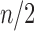 , already has a place in the study of gene trees and species trees, as it provides the maximally probable tree shapes of Degnan and Rosenberg (2006). Given a labeled topology t of size n, a labeled history of t is a linear ordering of the
, already has a place in the study of gene trees and species trees, as it provides the maximally probable tree shapes of Degnan and Rosenberg (2006). Given a labeled topology t of size n, a labeled history of t is a linear ordering of the  internal nodes of t such that the order of the nodes in each path going from the root of t to a leaf of t is increasing (Fig. 5). As reported by Harding (1974) and proved by Hammersley and Grimmett (1974), each labeled topology with tn as its underlying unlabeled topology possesses the maximal number of labeled histories among labeled topologies of size n. Consider the Yule model for the probability distribution of tree shapes, in which pairs of lineages in a labeled set of n lineages are joined together, at each step choosing uniformly among pairs (Yule, 1925; Harding, 1971; Brown, 1994; McKenzie and Steel, 2000; Steel and McKenzie, 2001; Rosenberg, 2006; Disanto et al., 2013; Disanto and Wiehe, 2013). Among all labeled topologies with size n, those with the largest number of labeled histories—and hence with shape tn—have the highest probability under the model.
internal nodes of t such that the order of the nodes in each path going from the root of t to a leaf of t is increasing (Fig. 5). As reported by Harding (1974) and proved by Hammersley and Grimmett (1974), each labeled topology with tn as its underlying unlabeled topology possesses the maximal number of labeled histories among labeled topologies of size n. Consider the Yule model for the probability distribution of tree shapes, in which pairs of lineages in a labeled set of n lineages are joined together, at each step choosing uniformly among pairs (Yule, 1925; Harding, 1971; Brown, 1994; McKenzie and Steel, 2000; Steel and McKenzie, 2001; Rosenberg, 2006; Disanto et al., 2013; Disanto and Wiehe, 2013). Among all labeled topologies with size n, those with the largest number of labeled histories—and hence with shape tn—have the highest probability under the model.
FIG. 5.
The three labeled histories of the labeled topology 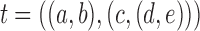 of size
of size 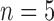 . Each labeled history can be represented by bijectively labeling the
. Each labeled history can be represented by bijectively labeling the 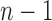 internal nodes of t with the integers in
internal nodes of t with the integers in 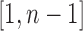 in such a way that each path from the root of t to a leaf of t is labeled by an increasing sequence.
in such a way that each path from the root of t to a leaf of t is labeled by an increasing sequence.
For  , the maximally probable labeled topologies of size n—those with the most labeled histories—can be recursively characterized as those labeled topologies whose two root subtrees are maximally probable labeled topologies of sizes
, the maximally probable labeled topologies of size n—those with the most labeled histories—can be recursively characterized as those labeled topologies whose two root subtrees are maximally probable labeled topologies of sizes 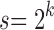 and
and 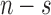 , where
, where 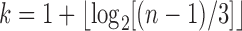 (Hammersley and Grimmett, 1974; Harding, 1974). This characterization matches our characterization that the unlabeled shapes with the largest number of root configurations are those for which the subtrees have the most root configurations and sizes d and
(Hammersley and Grimmett, 1974; Harding, 1974). This characterization matches our characterization that the unlabeled shapes with the largest number of root configurations are those for which the subtrees have the most root configurations and sizes d and  , where
, where 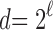 is the nearest power of 2 to
is the nearest power of 2 to 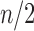 .
.
To see that the characterizations are identical so that  , note that a specific
, note that a specific 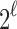 is the nearest power of 2 to
is the nearest power of 2 to 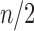 precisely for integers
precisely for integers 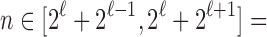
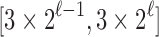 . On the endpoints of the interval, there are two choices for d, but in both cases, one choice is
. On the endpoints of the interval, there are two choices for d, but in both cases, one choice is 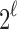 . At the same time, the integers n for which
. At the same time, the integers n for which 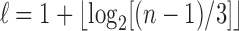 are precisely those in
are precisely those in  . Thus,
. Thus,  for all integers n in
for all integers n in 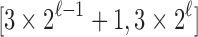 . On the lower boundary, for
. On the lower boundary, for 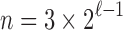 ,
, 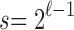 and
and 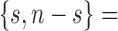
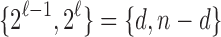 . Dividing the integers in
. Dividing the integers in 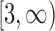 into a union of intervals
into a union of intervals 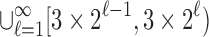 , we see that
, we see that  on each interval and hence
on each interval and hence  for all
for all 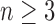 .
.
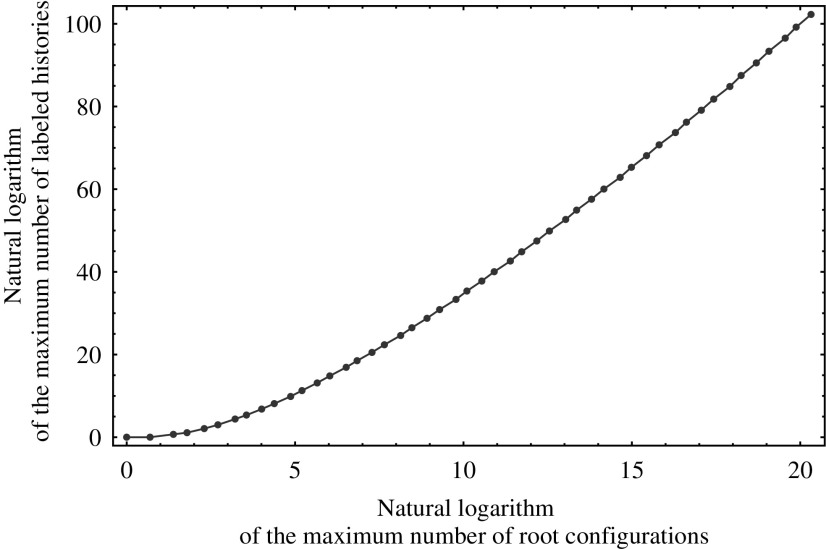
This result shows that for a given tree size, those labeled topologies whose shapes belong to the family 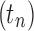 maximize both the number of root configurations and the number of labeled histories. For these labeled topologies, in Figure 6, we plot the logarithm of the maximum number of labeled histories possible for a labeled topology of size n as a function of the logarithm of the maximum number of root configurations. Although the shapes are the same, the number of labeled histories is considerably larger than the number of root configurations. The growth is approximately linear, suggesting that the maximal number of labeled histories increases approximately exponentially in the maximal number of root configurations.
maximize both the number of root configurations and the number of labeled histories. For these labeled topologies, in Figure 6, we plot the logarithm of the maximum number of labeled histories possible for a labeled topology of size n as a function of the logarithm of the maximum number of root configurations. Although the shapes are the same, the number of labeled histories is considerably larger than the number of root configurations. The growth is approximately linear, suggesting that the maximal number of labeled histories increases approximately exponentially in the maximal number of root configurations.
FIG. 6.
Natural logarithm of the maximum number of histories possible for a labeled topology of size n as a function of the natural logarithm of the maximum number of root configurations possessed by a labeled topology of the same size (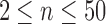 ). The maxima occur at the same set of labeled topologies.
). The maxima occur at the same set of labeled topologies.
5. The Number of Root Configurations in a Random Labeled Topology
We now study through generating functions the number of root configurations when trees of a given size are randomly selected under a uniform distribution on the set of labeled topologies. In Section 5.1, we show that the expectation 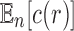 of the number of root configurations in a random labeled topology of size n has exponential growth
of the number of root configurations in a random labeled topology of size n has exponential growth 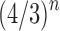 . In Section 5.2, we show that the variance
. In Section 5.2, we show that the variance  of the number of root configurations has exponential growth
of the number of root configurations has exponential growth 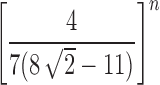 . The same results hold for the random total number of configurations.
. The same results hold for the random total number of configurations.
5.1. Mean number of root configurations
Define the exponential generating function
 |
where 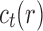 is the number of root configurations in tree t. As shown in Appendix 4, the function F satisfies
is the number of root configurations in tree t. As shown in Appendix 4, the function F satisfies
 |
where 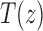 is the exponential generating function in Equation (3). Solving Equation (32), we obtain a closed form for
is the exponential generating function in Equation (3). Solving Equation (32), we obtain a closed form for 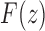 ,
,
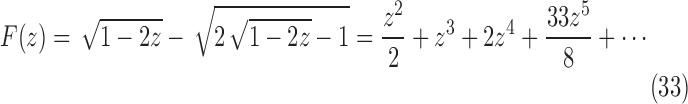 |
We have taken the negative root of the quadratic equation, as it is the root that produces the correct value of 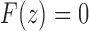 at
at 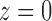 . It can be seen that
. It can be seen that 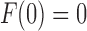 is required by noting that the first term in Equation (31) is the z1 term, as the set T contains only trees of size at least 1, so that Equation (31) has no constant term.
is required by noting that the first term in Equation (31) is the z1 term, as the set T contains only trees of size at least 1, so that Equation (31) has no constant term.
The value of z that cancels the second square root in Equation (33) is 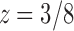 , which is smaller than the value
, which is smaller than the value 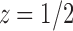 that cancels the first square root,
that cancels the first square root,  . In the complex plane, both
. In the complex plane, both 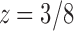 and
and 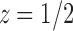 are singularities of
are singularities of 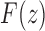 . The dominant singularity is
. The dominant singularity is 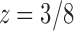 as it is nearer to the origin. To highlight the type of singularity that
as it is nearer to the origin. To highlight the type of singularity that 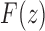 has at the point
has at the point 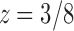 , it is convenient to factor the second square root in Equation (33), writing
, it is convenient to factor the second square root in Equation (33), writing 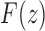 as
as
 |
where
 |
is an analytic function in the circle 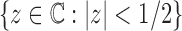 , except at a removable singularity
, except at a removable singularity 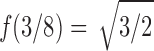 . Thus, we see that at
. Thus, we see that at 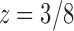 , the generating function
, the generating function 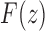 has a singularity of the square root type.
has a singularity of the square root type.
We can then apply Theorems VI.1 and VI.4 of Flajolet and Sedgewick (2009) to recover the asymptotic behavior of the nth coefficient of 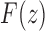 ,
,
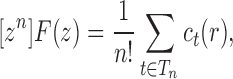 |
as the nth coefficient of the expansion of 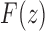 at the singularity
at the singularity 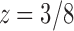 . This expansion is given by
. This expansion is given by
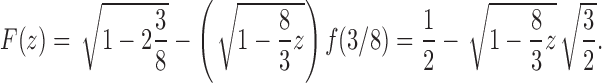 |
We thus have
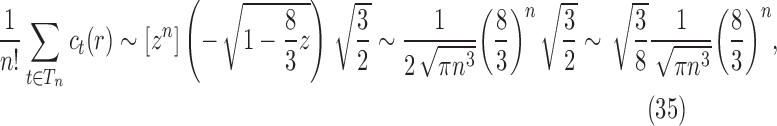 |
where we have used the asymptotic relationship 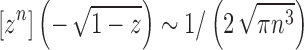 (Flajolet and Sedgewick, 2009). Dividing by the number of trees of size n,
(Flajolet and Sedgewick, 2009). Dividing by the number of trees of size n,  , as given in Equation (1), using Stirling's formula
, as given in Equation (1), using Stirling's formula 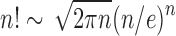 , and noting the definition of
, and noting the definition of 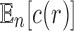 as a mean over all labeled topologies, we obtain the asymptotic expected number of root configurations in a random labeled topology of size n:
as a mean over all labeled topologies, we obtain the asymptotic expected number of root configurations in a random labeled topology of size n:
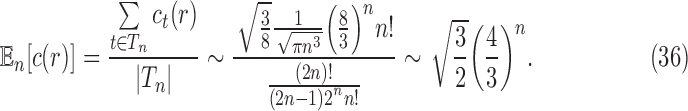 |
We summarize these results in a proposition.
Proposition 5 The mean number of root configurations in a random labeled topology of size n among the
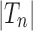 labeled tree topologies is asymptotically
labeled tree topologies is asymptotically
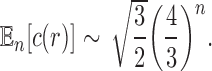 |
The mean total number of configurations has exponential growth
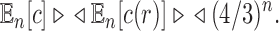 |
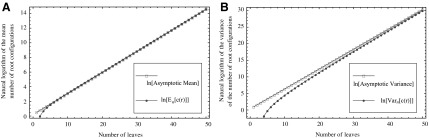
In Figure 7A, we can see that the approach of the natural logarithm of the exact mean number of root configurations—computed by evaluating the expansion of the generating function 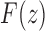 —to the asymptotic value
—to the asymptotic value 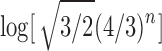 proceeds quickly, so that even with small values of n, the exact mean and the asymptote are quite close on a logarithmic scale.
proceeds quickly, so that even with small values of n, the exact mean and the asymptote are quite close on a logarithmic scale.
FIG. 7.
Mean and variance of the number of root configurations in random labeled topologies of fixed size. (A) Exact natural logarithm of the mean, computed from the power series expansion of  [Eq. (33)], and its asymptotic approximation from Proposition 5. (B) Exact natural logarithm of the variance, computed from the power series expansion of
[Eq. (33)], and its asymptotic approximation from Proposition 5. (B) Exact natural logarithm of the variance, computed from the power series expansion of 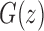 [Eq. (39)], and its asymptotic approximation from Proposition 6.
[Eq. (39)], and its asymptotic approximation from Proposition 6.
5.2. Variance of the number of root configurations
By applying the same approach used to determine the mean value of the number of root configurations across labeled topologies, in this section, we study the expectation 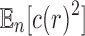 and then derive the asymptotic variance
and then derive the asymptotic variance 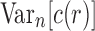 of the number of root configurations.
of the number of root configurations.
Define the generating function
 |
As shown in Appendix 5, the function 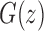 satisfies
satisfies
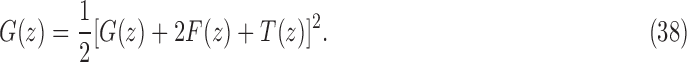 |
This equation relates 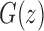 to the generating functions
to the generating functions 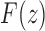 and
and 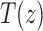 appearing in Equations (33) and (3). Solving for
appearing in Equations (33) and (3). Solving for 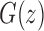 , we obtain the function
, we obtain the function
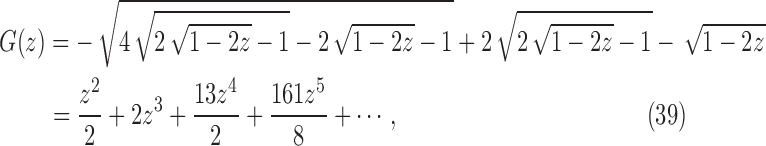 |
which has its dominant singularity at 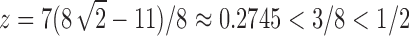 . In the same way as in the derivation of
. In the same way as in the derivation of 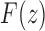 , we have taken the negative root of the quadratic Equation (38) as it is this root that produces the correct value of
, we have taken the negative root of the quadratic Equation (38) as it is this root that produces the correct value of  at
at  . At the dominant singularity for z, the first square root in Equation (39) cancels. Factoring this square root, the function
. At the dominant singularity for z, the first square root in Equation (39) cancels. Factoring this square root, the function 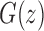 can be written as
can be written as
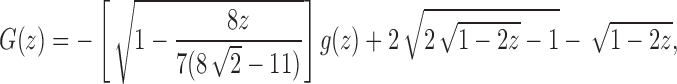 |
where
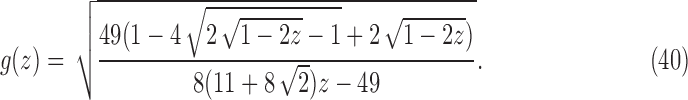 |
The function 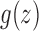 is analytic in the circle
is analytic in the circle 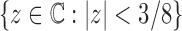 , except at the removable singularity
, except at the removable singularity 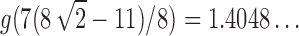 . By Theorems VI.1 and VI.4 of Flajolet and Sedgewick (2009), we can recover the asymptotic behavior of the nth coefficient
. By Theorems VI.1 and VI.4 of Flajolet and Sedgewick (2009), we can recover the asymptotic behavior of the nth coefficient 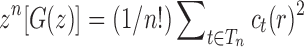 as
as
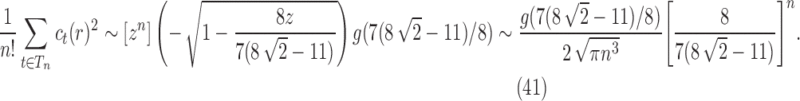 |
Dividing by 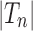 and using Stirling's approximation, we get
and using Stirling's approximation, we get
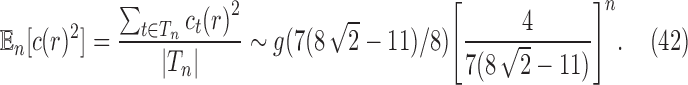 |
To obtain an asymptotic estimate for the variance, we use Equation (36) to note that the exponential growth of 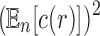 is
is 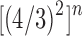 . Because
. Because 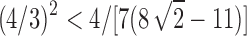 , we have that as
, we have that as 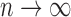 ,
,
 |
and thus, the variance asymptotically satisfies 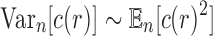 .
.
Furthermore, because 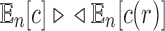 and
and 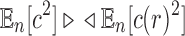 as shown in Equations (12) and (13), Equation (43) also holds when we replace
as shown in Equations (12) and (13), Equation (43) also holds when we replace 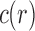 by c. Thus, the variance
by c. Thus, the variance 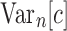 of the total number of configurations in a random labeled topology of size n satisfies
of the total number of configurations in a random labeled topology of size n satisfies
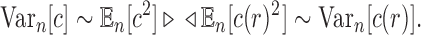 |
We summarize these results in a proposition.
Proposition 6 The variance of the number of root configurations in a random labeled topology of size n among the
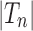 labeled tree topologies is asymptotically
labeled tree topologies is asymptotically
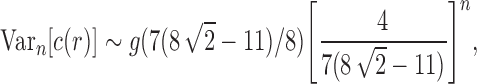 |
where
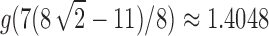 . The variance of the total number of configurations has exponential growth
. The variance of the total number of configurations has exponential growth
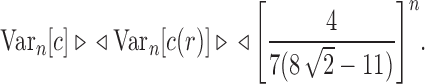 |
Figure 7B demonstrates that on a logarithmic scale, the approach of the exact variance of the number of root configurations—computed from 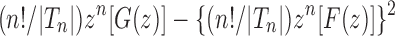 —to the asymptotic value
—to the asymptotic value 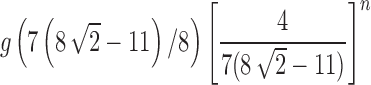 occurs rapidly in n, although slower than was seen for the mean in Figure 7A.
occurs rapidly in n, although slower than was seen for the mean in Figure 7A.
6. Conclusions
Under the assumption that the labeled gene tree topology matches the species tree topology, 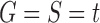 , we have studied the number of ancestral configurations in a given phylogenetic tree t. In particular, we have focused on the exponential growth of the number of root configurations in t, a quantity that also describes the exponential growth of the total number of configurations in t.
, we have studied the number of ancestral configurations in a given phylogenetic tree t. In particular, we have focused on the exponential growth of the number of root configurations in t, a quantity that also describes the exponential growth of the total number of configurations in t.
In Section 3, extending results of Wu (2012), in which the enumeration of ancestral configurations for caterpillar trees and a lower bound for their number in completely balanced trees were determined, we considered special families of trees generated by arbitrary seed trees s, namely the unbalanced family 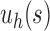 and the balanced family
and the balanced family 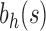 (Fig. 4). The main results describing the influence of tree balance and the seed tree topology on the number of ancestral configurations are collected in Proposition 2 and Proposition 3 for the unbalanced and balanced cases. We have shown that for each fixed seed tree s, the number of ancestral configurations in the balanced family
(Fig. 4). The main results describing the influence of tree balance and the seed tree topology on the number of ancestral configurations are collected in Proposition 2 and Proposition 3 for the unbalanced and balanced cases. We have shown that for each fixed seed tree s, the number of ancestral configurations in the balanced family 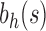 grows exponentially faster than in the unbalanced family
grows exponentially faster than in the unbalanced family 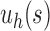 . When the size of the seed tree s is large, however, the difference between the exponential orders of the two integer sequences can become small. We have also observed that the choice of the seed tree can have an important influence on the number of root configurations. In fact, the number of root configurations in the family
. When the size of the seed tree s is large, however, the difference between the exponential orders of the two integer sequences can become small. We have also observed that the choice of the seed tree can have an important influence on the number of root configurations. In fact, the number of root configurations in the family 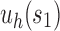 can grow exponentially faster than in the family
can grow exponentially faster than in the family 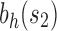 when the number of root configurations in s1 exceeds that of s2.
when the number of root configurations in s1 exceeds that of s2.
When 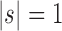 , the unbalanced family
, the unbalanced family 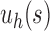 reduces to the caterpillar family, and the balanced family
reduces to the caterpillar family, and the balanced family 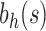 gives the family of completely balanced trees. As shown in Proposition 4, among trees of size n, the caterpillar tree with n taxa possesses the smallest number of root configurations. When n is a power of 2, the completely balanced tree of size n has the largest number; more generally, the largest number of root configurations occurs at precisely those labeled topologies that for a fixed n generate the largest number of labeled histories. As the caterpillar labeled topologies give rise to the smallest number of labeled histories at fixed n—only one—both the largest and smallest numbers of root configurations occur at trees producing the extrema in the number of labeled histories. The growth of the number of root configurations in the caterpillar family is polynomial, whereas for the completely balanced trees, it is exponential with order
gives the family of completely balanced trees. As shown in Proposition 4, among trees of size n, the caterpillar tree with n taxa possesses the smallest number of root configurations. When n is a power of 2, the completely balanced tree of size n has the largest number; more generally, the largest number of root configurations occurs at precisely those labeled topologies that for a fixed n generate the largest number of labeled histories. As the caterpillar labeled topologies give rise to the smallest number of labeled histories at fixed n—only one—both the largest and smallest numbers of root configurations occur at trees producing the extrema in the number of labeled histories. The growth of the number of root configurations in the caterpillar family is polynomial, whereas for the completely balanced trees, it is exponential with order 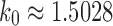 .
.
Assuming a uniform distribution over the labeled topologies with a given size n, in Section 5 we studied the mean and the variance of the number of ancestral configurations in a random labeled topology of size n. By using a generating function approach, in Propositions 5 and 6, we have shown that the mean number of ancestral configurations has exponential growth 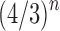 , whereas for the variance, we have
, whereas for the variance, we have
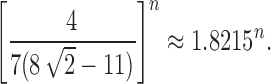 |
Our results can assist in relating the complexity of algorithms for computing gene tree probabilities based on ancestral configurations—STELLS (Wu, 2012)—to those that use an evaluation based on a different class of combinatorial objects, the coalescent histories (Degnan and Salter, 2005; Rosenberg, 2007; Than et al., 2007; Rosenberg and Degnan, 2010; Rosenberg, 2013; Disanto and Rosenberg, 2015, 2016). In such comparisons, we expect that the ancestral configurations will often grow slower, as is seen in comparing the polynomial growth of the number of ancestral configurations in the caterpillar case with the corresponding exponential growth of the number of coalescent histories. However, the trees with the largest numbers of coalescent histories and the largest number of ancestral configurations are not the same, so that potential exists for each type of algorithm to be favorable in different cases. It remains to be seen whether the complexity of gene tree probability calculations can be reduced by choosing the computational approach based on tree sizes and shapes under consideration.
Many enumerative problems on ancestral configurations remain open. First, we assumed that the gene tree and species tree have the same labeled topology, and we did not study nonmatching gene trees and species trees. As has been seen for coalescent histories (Rosenberg and Degnan, 2010), however, the nonmatching case merits further analysis, as a nonmatching gene tree labeled topology can have more root configurations and more total configurations than the topology that matches the species tree. Consider a caterpillar species tree topology 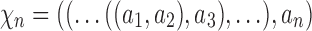 , labeling the unique internal node with k descendants bk for
, labeling the unique internal node with k descendants bk for 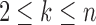 . For a matching caterpillar gene tree, by Proposition 1, the number of configurations at node bk is
. For a matching caterpillar gene tree, by Proposition 1, the number of configurations at node bk is 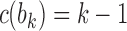 , so that the number of root configurations is
, so that the number of root configurations is 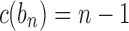 and the total number of configurations is
and the total number of configurations is 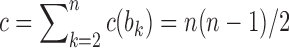 .
.
Now consider a pseudocaterpillar gene tree topology 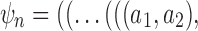
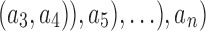 with
with 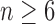 , continuing with
, continuing with 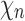 as the species tree topology. Topology
as the species tree topology. Topology 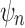 differs from
differs from 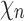 only in the placement of a4. We label the node of
only in the placement of a4. We label the node of 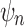 ancestral to a1 and a2 by d2, the node ancestral to a3 and a4 by
ancestral to a1 and a2 by d2, the node ancestral to a3 and a4 by 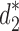 , and the unique node ancestral to k taxa,
, and the unique node ancestral to k taxa, 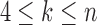 , by dk. At nodes b2, b3, b4, and b5 of
, by dk. At nodes b2, b3, b4, and b5 of 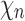 , the configurations are
, the configurations are 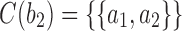 ,
, 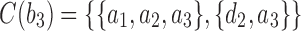 ,
, 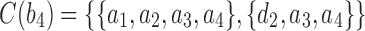 , and
, and 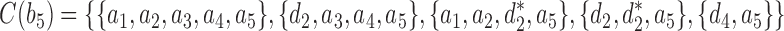 , with
, with  ,
,  ,
, 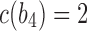 , and
, and 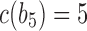 . For
. For 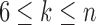 ,
,  is obtained by adding taxon ak to each configuration in
is obtained by adding taxon ak to each configuration in 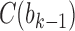 and noting the existence of one additional configuration,
and noting the existence of one additional configuration, 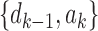 , so that
, so that 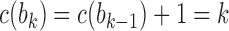 . The number of root configurations of
. The number of root configurations of 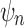 for
for  is
is  , and the number of total configurations is
, and the number of total configurations is 
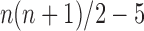 . Because
. Because 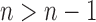 and
and 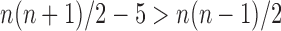 for
for 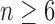 , root configurations and total configurations are more numerous for the nonmatching pseudocaterpillar topology than for the matching caterpillar.
, root configurations and total configurations are more numerous for the nonmatching pseudocaterpillar topology than for the matching caterpillar.
Second, when ancestral configurations are grouped according to an equivalence relationship defined in the appendix of Wu (2012) that accounts for symmetries in gene trees, the number of the resulting equivalence classes—the number of nonequivalent ancestral configurations—remains to be investigated. For gene trees and species trees with a matching labeled topology, our enumerations can be used as upper bounds for the number of nonequivalent ancestral configurations, and they can help in measuring the decrease in the number of ancestral configurations when the equivalence relationship is taken into account. We defer this analysis for future work.
7. Appendix 1. Proof of Equation (9)
Given a tree t, fix without loss of generality one of the possible planar representations of the tree t: one of the possible drawings of t in which edges do not cross and intersect only at their endpoints (Fig. 1A).
A root configuration of t uniquely determines a partition of the set of leaves of t in the following way. If 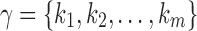 is a root configuration of t, where each ki is a node of t, then the associated partition is
is a root configuration of t, where each ki is a node of t, then the associated partition is 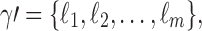 where
where 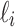 is the set of leaves of t descended from node ki (including ki itself when ki is a leaf). For instance, the partition of the leaf label set
is the set of leaves of t descended from node ki (including ki itself when ki is a leaf). For instance, the partition of the leaf label set 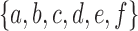 associated with the root configuration
associated with the root configuration 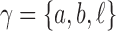 depicted in Figure 1B is
depicted in Figure 1B is 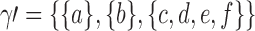 . Note that for each pair of indices
. Note that for each pair of indices  with
with  , the leaves in
, the leaves in  are either all on the left or all on the right of the leaves in
are either all on the left or all on the right of the leaves in 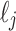 in the planar representation of t.
in the planar representation of t.
Without loss of generality, we can assume that the set  is indexed such that if
is indexed such that if 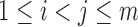 , then the leaves in
, then the leaves in 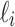 are all depicted in the planar representation to the left of the leaves in
are all depicted in the planar representation to the left of the leaves in 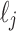 . Taking the cardinality of each element
. Taking the cardinality of each element  of
of 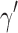 determines the vector
determines the vector 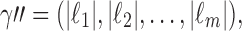 which represents a composition, or ordered partition, of the integer
which represents a composition, or ordered partition, of the integer  . For instance, for the root configurations of the tree of size
. For instance, for the root configurations of the tree of size 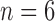 depicted in Figure 1A, we obtain the following compositions of 6:
depicted in Figure 1A, we obtain the following compositions of 6:
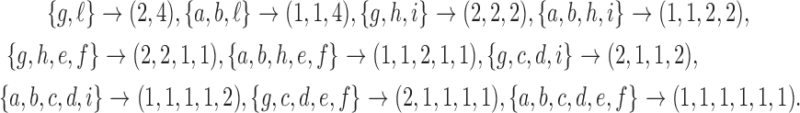 |
As can be seen in this example, for a given planar representation of t, the mapping 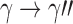 is injective (i.e.,
is injective (i.e., 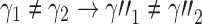 ). For
). For 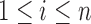 , there are
, there are 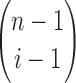 compositions of n into i parts, as
compositions of n into i parts, as 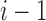 demarcations must be placed among
demarcations must be placed among 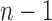 possible positions between entries of the length-n vector
possible positions between entries of the length-n vector 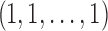 to separate groups of 1s that will be aggregated together. Using the binomial theorem to sum over all possible values of i, the number of distinct compositions of n is
to separate groups of 1s that will be aggregated together. Using the binomial theorem to sum over all possible values of i, the number of distinct compositions of n is 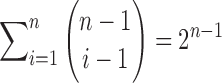 . Because each root configuration is associated with a distinct composition of n, we obtain
. Because each root configuration is associated with a distinct composition of n, we obtain 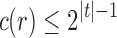 , and the proof of Equation (9) is complete.
, and the proof of Equation (9) is complete.
8. Appendix 2. Proof of Equation (17)
We obtain Equation (17) from Equation (16) by noting that for z close to 0, the following expansion holds:
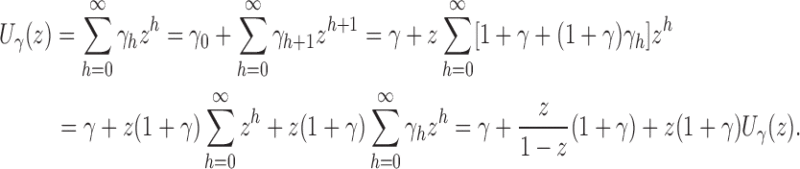 |
9. Appendix 3. Proof of Corollary 1
The proof follows from the properties of  and
and 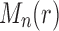 stated in Proposition 4. Part (i) is immediate from Proposition 4 and the definition of the exponential order.
stated in Proposition 4. Part (i) is immediate from Proposition 4 and the definition of the exponential order.
For (ii), we start with mn. Let 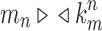 be the exponential growth of the sequence mn, so that km is its exponential order. Denote by
be the exponential growth of the sequence mn, so that km is its exponential order. Denote by 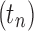 the caterpillar family of trees, where tn is the caterpillar with
the caterpillar family of trees, where tn is the caterpillar with 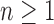 taxa. Thus,
taxa. Thus, 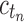 is the total number of configurations in tn and
is the total number of configurations in tn and 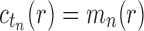 is its number of root configurations. By Equation (11), we have
is its number of root configurations. By Equation (11), we have 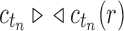 , and
, and 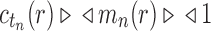 from part (i) of the corollary. Thus,
from part (i) of the corollary. Thus, 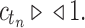 Because total configurations are at least as numerous as root configurations,
Because total configurations are at least as numerous as root configurations, 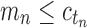 . Then the growth of mn has exponential order at most that of
. Then the growth of mn has exponential order at most that of 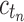 , so that
, so that  . Clearly, however, we cannot have
. Clearly, however, we cannot have  , because
, because 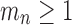 for
for 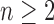 and
and  would imply that the sequence mn decreases below 1 with increasing n. Thus,
would imply that the sequence mn decreases below 1 with increasing n. Thus, 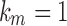 .
.
For the sequence Mn, let 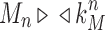 be the exponential growth of the sequence
be the exponential growth of the sequence 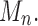 This sequence has exponential order kM. Suppose
This sequence has exponential order kM. Suppose 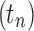 is any sequence of trees with
is any sequence of trees with 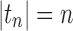 such that
such that 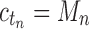 ; that is, tn has the largest total number of configurations among trees of size n. From Equation (11),
; that is, tn has the largest total number of configurations among trees of size n. From Equation (11), 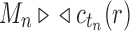 , where the latter sequence has order smaller than or equal to k0 because by definition
, where the latter sequence has order smaller than or equal to k0 because by definition 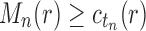 for all n, and
for all n, and 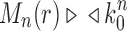 from part (i) of the corollary. Thus,
from part (i) of the corollary. Thus, 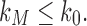 At the same time, for all n, we have
At the same time, for all n, we have 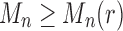 , as the largest total number of configurations is larger than the largest number of root configurations. Thus,
, as the largest total number of configurations is larger than the largest number of root configurations. Thus, 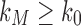 . It follows that
. It follows that 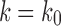 .
.
10. Appendix 4. Proof of Equation (32)
The proof follows from the tree decomposition procedure that is illustrated in Figure 8. According to this procedure, each tree t of size n is either the 1-taxon tree 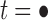 or it can be created in a unique way by relabeling and appending to a shared root node two smaller trees t1 and t2 that become the root subtrees of t. From Proposition 1, the number
or it can be created in a unique way by relabeling and appending to a shared root node two smaller trees t1 and t2 that become the root subtrees of t. From Proposition 1, the number 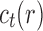 of root configurations of t can be computed in this case as the product
of root configurations of t can be computed in this case as the product  . Summing over all possible trees t, the tree decomposition described in Figure 8 translates into the following decomposition for the generating function
. Summing over all possible trees t, the tree decomposition described in Figure 8 translates into the following decomposition for the generating function 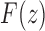 :
:
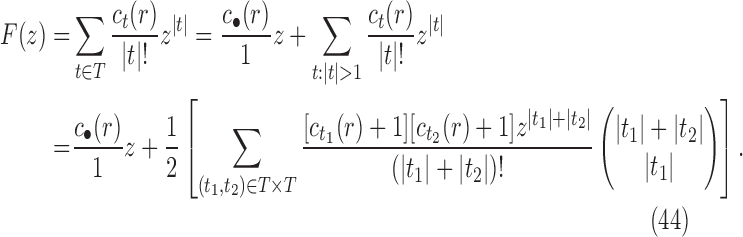 |
FIG. 8.
Composition of two trees t1 and t2 of sizes 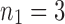 and
and 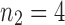 to obtain a tree t of size
to obtain a tree t of size 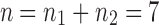 . (A) Trees t1 and t2, with leaves labeled by
. (A) Trees t1 and t2, with leaves labeled by 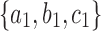 and
and 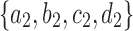 . As in Section 2.1, we impose without loss of generality a linear order
. As in Section 2.1, we impose without loss of generality a linear order  for the leaves of a tree; here, we have
for the leaves of a tree; here, we have  and
and  . (B) Relabeling of trees t1 and t2. After relabeling, t1 and t2 have leaves labeled in the set
. (B) Relabeling of trees t1 and t2. After relabeling, t1 and t2 have leaves labeled in the set  of size
of size 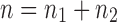 . For the relabeling procedure, we choose (dotted circles) n1 elements among the n possible new labels
. For the relabeling procedure, we choose (dotted circles) n1 elements among the n possible new labels 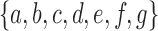 . There are exactly
. There are exactly 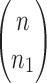 different choices. The chosen elements relabel t1, whereas the elements not selected (dotted squares) relabel t2. With respect to the order
different choices. The chosen elements relabel t1, whereas the elements not selected (dotted squares) relabel t2. With respect to the order  , the ith label of t1 is assigned the label determined by the ith circle. Similarly, the ith label of t2 is assigned the label determined by the ith square. (C) After relabeling t1 and t2, the new tree t is obtained by appending t1 and t2 to a shared root node. Starting with trees t1 and t2 in (A), the same procedure can generate
, the ith label of t1 is assigned the label determined by the ith circle. Similarly, the ith label of t2 is assigned the label determined by the ith square. (C) After relabeling t1 and t2, the new tree t is obtained by appending t1 and t2 to a shared root node. Starting with trees t1 and t2 in (A), the same procedure can generate 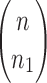 different trees t, one for each possible choice of the n1 elements (dotted circles) among the n new labels. The only exception is when
different trees t, one for each possible choice of the n1 elements (dotted circles) among the n new labels. The only exception is when 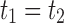 , for which the
, for which the 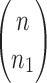 relabelings generate each tree exactly twice.
relabelings generate each tree exactly twice.
The first equality is the definition of  . In the second equality, the set of trees over which the sum is evaluated is partitioned into two parts, the 1-taxon tree
. In the second equality, the set of trees over which the sum is evaluated is partitioned into two parts, the 1-taxon tree 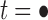 and the trees of size larger than 1. In the third equality, the set of trees t with
and the trees of size larger than 1. In the third equality, the set of trees t with  is realized taking all possible pairs of trees
is realized taking all possible pairs of trees 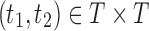 and applying to each pair the procedure in Figure 8, considering all
and applying to each pair the procedure in Figure 8, considering all 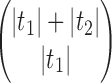 possible relabelings of t1 and t2. The quantity
possible relabelings of t1 and t2. The quantity 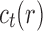 in the sum
in the sum 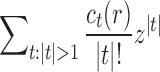 is replaced by the product
is replaced by the product  and the term
and the term 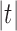 is replaced by
is replaced by 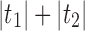 . Note the factor
. Note the factor 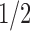 that appears in Equation (44) before the summation. This factor takes into account the fact that for each pair
that appears in Equation (44) before the summation. This factor takes into account the fact that for each pair 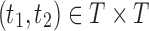 with
with  , there exists a symmetric pair
, there exists a symmetric pair  . Symmetric pairs generate exactly the same trees according to the procedure in Figure 8, and multiplying by
. Symmetric pairs generate exactly the same trees according to the procedure in Figure 8, and multiplying by  is required to avoid double counting. When
is required to avoid double counting. When 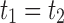 , the factor
, the factor 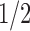 is still required because only half of the
is still required because only half of the 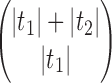 relabelings of t1 and t2 (Fig. 8B) create nonisomorphic trees when t1 and t2 are appended to a shared root node. Finally, observe that the number
relabelings of t1 and t2 (Fig. 8B) create nonisomorphic trees when t1 and t2 are appended to a shared root node. Finally, observe that the number 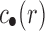 of root configurations in the 1-taxon tree is 0.
of root configurations in the 1-taxon tree is 0.
From Equation (44) and the definitions of 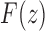 and
and 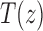 in Equations (2) and (31), algebraic manipulations yield
in Equations (2) and (31), algebraic manipulations yield
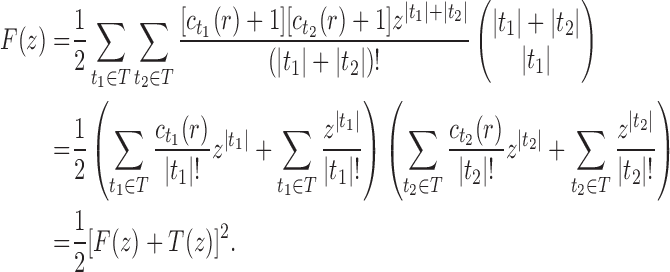 |
11. Appendix 5. Proof of Equation (38)
The proof follows the case of Equation (32). For  , the number
, the number 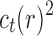 can be obtained as the product
can be obtained as the product 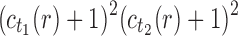 , where t1 and t2 are the root subtrees of t. The tree decomposition described in Figure 8 yields
, where t1 and t2 are the root subtrees of t. The tree decomposition described in Figure 8 yields
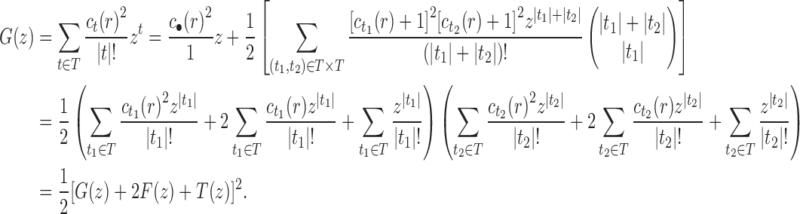 |
Acknowledgments
The authors thank Elizabeth Allman, James Degnan, and John Rhodes for discussions and NIH grant R01 GM117590 for financial support.
Author Disclosure Statement
No competing financial interests exist.
References
- Aho A.V., and Sloane N.J.A. 1973. Some doubly exponential sequences. Fibonacci Q. 11, 429–437 [Google Scholar]
- Brown J.K.M. 1994. Probabilities of evolutionary trees. Syst. Biol. 43, 78–91 [Google Scholar]
- Degnan J.H., and Rosenberg N.A. 2006. Discordance of species trees with their most likely gene trees. PLoS Genet. 2, 762–768 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Degnan J.H., Rosenberg N.A., and Stadler T. 2012. The probability distribution of ranked gene trees on a species tree. Math. Biosci. 235, 45–55 [DOI] [PubMed] [Google Scholar]
- Degnan J.H., and Salter L.A. 2005. Gene tree distributions under the coalescent process. Evolution 59, 24–37 [PubMed] [Google Scholar]
- de Mier A., and Noy M. 2012. On the maximum number of cycles in outerplanar and series-parallel graphs. Graphs Combinator. 28, 265–275 [Google Scholar]
- Disanto F., and Rosenberg N.A. 2015. Coalescent histories for lodgepole species trees. J. Comput. Biol. 22, 918–929 [DOI] [PubMed] [Google Scholar]
- Disanto F., and Rosenberg N.A. 2016. Asymptotic properties of the number of matching coalescent histories for caterpillar-like families of species trees. IEEE/ACM Trans. Comput. Biol. Bioinf. 13, 913–925 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Disanto F., Schlizio A., and Wiehe T. 2013. Yule-generated trees constrained by node imbalance. Math. Biosci. 246, 139–147 [DOI] [PubMed] [Google Scholar]
- Disanto F., and Wiehe T. 2013. Exact enumeration of cherries and pitchforks in ranked trees under the coalescent model. Math. Biosci. 242, 195–200 [DOI] [PubMed] [Google Scholar]
- Felsenstein J. 1978. The number of evolutionary trees. Syst. Zool. 27, 27–33 [Google Scholar]
- Flajolet P., and Sedgewick R. 2009. Analytic Combinatorics. Cambridge University Press, Cambridge [Google Scholar]
- Hammersley J.M., and Grimmett G.R. 1974. Maximal solutions of the generalized subadditive inequality. Pages 270–285 in Harding E.F., and Kendall D.G. eds. Stochastic Geometry. Wiley, London [Google Scholar]
- Harding E.F. 1971. The probabilities of rooted tree-shapes generated by random bifurcation. Adv. Appl. Probab. 3, 44–77 [Google Scholar]
- Harding E.F. 1974. The probabilities of the shapes of randomly bifurcating trees. Pages 259–269 in Harding E.F., and Kendall D.G., eds. Stochastic Geometry. Wiley, London [Google Scholar]
- Maddison W.P. 1997. Gene trees in species trees. Syst. Biol. 46, 523–536 [Google Scholar]
- McKenzie A., and Steel M. 2000. Distributions of cherries for two models of trees. Math. Biosci. 164, 81–92 [DOI] [PubMed] [Google Scholar]
- Rosenberg N.A. 2006. The mean and variance of the numbers of r-pronged nodes and r-caterpillars in Yule-generated genealogical trees. Ann. Comb. 10, 129–146 [Google Scholar]
- Rosenberg N.A. 2007. Counting coalescent histories. J. Comput. Biol. 14, 360–377 [DOI] [PubMed] [Google Scholar]
- Rosenberg N.A. 2013. Coalescent histories for caterpillar-like families. IEEE/ACM Trans. Comp. Biol. Bioinf. 10, 1253–1262 [DOI] [PubMed] [Google Scholar]
- Rosenberg N.A., and Degnan J.H. 2010. Coalescent histories for discordant gene trees and species trees. Theor. Popul. Biol. 77, 145–151 [DOI] [PubMed] [Google Scholar]
- Steel M., and McKenzie A. 2001. Properties of phylogenetic trees generated by Yule-type speciation models. Math. Biosci. 170, 91–112 [DOI] [PubMed] [Google Scholar]
- Than C., and Nakhleh L. 2009. Species tree inference by minimizing deep coalescences. PLoS Comp. Biol. 5, e1000501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Than C., Ruths D., Innan H., and Nakhleh L. 2007. Confounding factors in HGT detection: Statistical error, coalescent effects, and multiple solutions. J. Comput. Biol. 14, 517–535 [DOI] [PubMed] [Google Scholar]
- Wu Y. 2012. Coalescent-based species tree inference from gene tree topologies under incomplete lineage sorting by maximum likelihood. Evolution 66, 763–775 [DOI] [PubMed] [Google Scholar]
- Yule G.U. 1925. A mathematical theory of evolution based on the conclusions of Dr. J.C. Willis, F.R.S. Phil. Trans. R. Soc. Lond. B 213, 21–87 [Google Scholar]