ABSTRACT
A mathematical model of the passive permeation of a novel solute into bacteria that explicitly accounts for intracellular dilution through growth was developed. A bacterial cell envelope permeability coefficient of approximately >10−8 cm2 · s−1 is predicted to ensure passive permeation into rapidly replicating bacterial cells. The relative importance of the permeability coefficients of the cytoplasmic and outer membranes of Gram-negative bacteria in determining the overall envelope permeability coefficient was analyzed quantitatively. A mathematical description of the balance between passive influx and active efflux was also developed and shows that bacterial expansion through growth can usually be neglected for compounds likely to be prepared in antibacterial drug discovery programs and the balance between passive inward permeation and active outwardly directed efflux predominates. A new parameter, efflux efficiency (η, where η is equal to k/P, in which k is the rate coefficient for the efflux pump and P is the permeability coefficient for the membrane across which the pump acts), is introduced, and the consequences for the efficiency of efflux pumping by a single pump, two pumps in parallel across either the cytoplasmic or the outer membrane, and two pumps in series, one across the cytoplasmic membrane and one across the outer membrane of Gram-negative bacteria, are explored. The results, showing additive efficiency for two pumps acting across a single membrane and multiplicative efficiency for two pumps acting in series across the cytoplasmic and outer membranes, can be quantitatively related to the ratios between MICs measured against pump-sufficient and pump deletion strains and agree with those of previous experimental and theoretical studies.
KEYWORDS: antibacterial drug discovery, bacterial permeability, efflux
INTRODUCTION
In the early stages of the discovery of new antibacterial agents, an assumption is often made that if a potent inhibitor of a particular cellular target lacks direct antibacterial activity, then it does not enter the compartment of the bacterial cell containing the target (1). It is now understood that the key barriers to the passive permeation of compounds into bacteria are the cytoplasmic membrane, which is a barrier to hydrophilic solutes in both Gram-positive and Gram-negative bacteria, and the outer membrane, which is a barrier in Gram-negative bacteria to lipophilic solutes and also a barrier to hydrophilic solutes above a certain size, where the size exclusion limit differs between species (it is about 500 g · mol−1 in Escherichia coli, for example) (2, 3). This raises the following interesting question: what is the baseline permeability coefficient (P) for a compound to cross the bacterial cell envelope at a rate fast enough for it to be considered permeant or, conversely, at a rate slow enough for it to be considered impermeant? This is an important practical question because permeability coefficients for a compound to cross lipid bilayers can be measured or even calculated from physical properties directly or by extrapolation from the permeability coefficients of known compounds (4–6), whereas measurements of the passive permeability of compounds into intact bacterial cells are generally exceedingly difficult, except for special cases (7). In nature, intact bacteria also pump compounds outwardly from the cytoplasm across the cytoplasmic membrane and, in the case of Gram-negative bacteria, outwardly from the periplasm across the outer membrane (8, 9). This is superimposed upon the inwardly directed, passive permeation of nontransported solutes, such as novel potential antibacterial agents (2). As will be shown below, growing bacteria self-dilute intracellular solutes, so a critical permeability to a novel antibacterial compound is predicted to be necessary to ensure the achievement of a timely and adequate internal growth-inhibitory concentration. Despite many molecular biological and microbiological studies of efflux over recent years, a quantitative model for the passive influx process that can yield an estimate of a limiting permeability coefficient remains absent. The present work presents and analyzes a simple mathematical model that allows that question to be answered in terms of a solute's permeability coefficient, enabling comparison with the measured permeability coefficients of known solutes, including known antibacterial agents. The model was also able to be adapted to analyze quantitatively the interplay between passive inwardly directed permeation and active efflux.
Mathematical model building to assist understanding is common in engineering and physics (10, 11). There is precedent for it, albeit less frequently, in microbiology (e.g., see references 12 to 15). It is proposed that the kinetic model described here will advance understanding of the penetration of novel antibacterial agents into Gram-negative bacteria, which in turn should help efforts to discover new antibacterial agents active against Gram-negative bacteria, a notoriously difficult enterprise (16–18).
Some generalizations established from the model, but not the modeling derivations per se, have been reviewed elsewhere (2).
RESULTS
Background: quantitative treatment of permeability. (i) Passive membrane permeability.
Classically, a membrane's passive permeability to a specific compound is described by its permeability coefficient for that compound (19). The permeability coefficient (P) relates flux across the membrane per unit area, i.e., the rate of flow per unit area, to the difference in the concentration of the compound in the two aqueous phases at either side of the membrane.
Thus, in its nondifferential form
| (1) |
in which J (in units of mass · time−1 · surface area−1) is the magnitude of the flux from a high to a low concentration through a unit area of the membrane, and c1 and c2 (in units of mass · volume−1) are the concentrations of the compound at either side of the membrane. P thus has dimensions distance · time−1, e.g., centimeter · second−1. Note that by this well-established model, diffusion across the membrane can occur in either direction, so that J effectively represents the net outcome of two fluxes, Pc1 in one direction and Pc2 in the other direction. Equation 1 is very useful when directionality is understood from the context of the modeling. The algebraically accurate form of equation 1 has the directionality of flux. However, in the model presented below, the directionality is understood from the initial conditions, whereby a suspension of bacterial cells is exposed to a static concentration of solute at time zero. With that understanding, only the magnitude of flux appears in the derivations of equations, and positive flux is considered to be from outside the cell at a higher concentration to inside the cell at a lower concentration. Thus, flux can be expressed as the rate of transfer of the mass of solute and in differential form:
| (2) |
in which dm/dt (in units of mass · time−1) is the rate of passage of the substance through a given area, A, of the membrane, and the other symbols are as defined above. Note that it follows that m is the amount (in nanomoles) of solute that has moved into (if the external concentration exceeds the internal concentration) the internal compartment through the specified surface area over any given time period from time point 1 (t1) to t2. In the model presented below, it is represented by m3, defined as the amount of solute dissolved in the cytoplasmic water (Table 1), starting with 0 nmol at time zero, and the applicable area is that which surrounds that cytoplasmic water.
TABLE 1.
Symbols and units used in modeling the kinetics of passive permeation
| Symbola | Description | Units |
|---|---|---|
| J | Flux of solute per unit of cell surface area | nmol · cm−2 · s−1 |
| F (t) | Flux of solute into the population of cells in the volume element of suspension at time t; this flux increases with growth owing to the increasing total surface area of the population of cells in a unit volume of suspension | nmol · s−1 |
| P | Permeability coefficient | cm · s−1 |
| t | Time | s |
| m3 (t) | Total amount of solute in the cytoplasm of the population of cells at time t in the volume element of the suspension considered | nmol |
| c1 | Concentration of compound outside the cells (assumed to be constant) | nmol · cm−3 |
| c3 (t) | Concentration of compound in the cytoplasm at time t | nmol · cm−3 |
| A | Specific area of the cell envelope; the specific area does not vary with time | cm2 · (mg dry mass−1) |
| V3 | Specific volume of the cytoplasm; the specific volume does not vary with time | cm3 · (mg dry mass−1) |
| M (t) | Mass of cells at time t in the volume element considered | mg dry mass |
| M0 | Mass of cells at time zero in the volume element of the suspension considered, which determines the initial surface area and volume of cytoplasm of the population in that volume | mg dry mass |
| μ | Specific growth rate constant | s−1 |
Dependency is shown in parentheses.
Another way of expressing permeability as applied to a physiological unit of biomass (e.g., milligrams dry mass) is the permeability parameter (20). The permeability parameter, often given the symbol C, is the permeability coefficient multiplied by the area of the physiological unit of biomass, C = P × A. The permeability parameter typically has the dimensions of distance3 · time−1 · biomass−1 [e.g., centimeters3 · minute−1 · (milligrams dry mass)−1]. Occasionally, authors use a different basic physiological unit. For example, Snyder and McIntosh (21) used the area of lipid as the base unit denominator. For the sake of consistency and avoidance of nonfundamental units, the permeability parameter is not used in the analyses that follow.
(ii) Passive permeability of multiple layers.
Although the classical treatment of permeability generally refers to the permeability of single-unit membranes, such as the bacterial or eukaryotic cell cytoplasmic membrane, or the membranes of unilamellar liposomes or planar films, the quantitative treatment has also been applied to more complex layers, such as a bacterial envelope (7) or a mammalian tissue (22). That is reasonable, as long as no active processes are occurring or as long as they are accounted for in the model, shown as follows.
From the basic transmembrane diffusion equation (equation 1), it can be shown that under conditions of a constant rate of flow of solute across multiple membranes, the composite permeability coefficient for a series of layers (n = 3 in this example) is given by the following relationship (23):
| (3) |
In this expression, P is the overall permeability coefficient and P1, P2, P3, etc., are the individual permeability coefficients of each layer in the series. Equation 3 can be derived as follows. Say that there are two layers (as in Gram-negative bacteria, for example) with permeability coefficients P1 (left-hand layer) and P2 (right-hand layer) and that a constant flux governed by an overall permeability coefficient, P, is occurring across both layers. There are three compartments, each containing a different, constant concentration of solute (assuming rapid mixing and/or a negligible thickness of the central compartment). These concentrations can be assigned symbols, c1 (e.g., on the left), c2 (between the layers), and c3 (e.g., on the right), where c1 > c2 > c3. From equation 1 and because flux is constant across both layers
| (3a) |
From equation 3a, one can write the following three relationships.
| (3b) |
from which
| (3c) |
Substituting for c2 in the expression for J/P2 from equation 3b and rearranging yields
| (3d) |
Also from equation 3a, c1 – c3 = J/P, which when substituted in equation 3d gives
| (3e) |
Dividing both sides of equation 3e by J results in a relationship for two layers of the form of equation 3. It is then straightforward to model a third layer, permeability P3, by considering the first two layers to act as a single layer, permeability P1 + 2. The same derivation is followed, leading to the relationship:
| (3f) |
Then, 1/P1 + 2 is replaced by (1/P1) + (1/P2) to yield the general equation 3.
The relationship of equation 3, which is not immediately intuitive without the formal analysis presented above, is useful to understand because it allows one to analyze what happens when the permeability coefficient of one layer is much lower than the permeability coefficients of the other layers. The overall permeability coefficient is then slightly lower than the lowest permeability coefficient, which is therefore rate limiting. For example, for a small hydrophilic compound (i.e., a compound able to pass through the nonspecific, protein-mediated, outer membrane aqueous channels of a Gram-negative bacterium) penetrating to the cytoplasm of a bacterial cell, the lowest permeability coefficient is that of the cytoplasmic membrane, the nonspecific permeability properties of which are largely determined by the properties of the lipid bilayer (2). Thus, for such a compound, the permeability coefficient for the passive penetration into an intact Gram-negative bacterial cell is expected to be very similar to the permeability coefficient for the penetration into liposomes. In good agreement with this, Sigler et al. (7) found that the passive permeation of tetracycline into intact cells of Escherichia coli was governed by a permeability coefficient (5.6 × 10−9 cm · s−1) similar to the permeability coefficient found for the diffusion into phospholiposomes (2.4 × 10−9 cm · s−1). It should be noted, however, that these measurements were internally consistent, but an approximately 1,000-fold higher permeability coefficient of about 6 × 10−6 cm · s−1 has been calculated by others on the basis of measurements of the percentage of undissociated tetracycline in solution at pH 7.4 (6).
Quantitative analysis of impermeant or impermeable.
The terms “permeant” and “impermeant” are used to describe diffusing compounds, whereas the terms “permeable” and “impermeable” refer to the membrane or other element across which diffusion occurs. The approach to defining impermeant or impermeable quantitatively was to model the kinetics of passive permeation (i.e., in the absence of any active efflux) balanced against the kinetics of the growth of new cell mass and volume. The derivations presented below show analytically how continuous cell growth dilutes the compound, even though the total surface area of a growing suspension of cells is continuously expanding. The following thought experiments describe two extreme cases to help gain an intuitive picture of the dynamic model. First, in the case of a nongrowing suspension of cells after a time period determined by the permeability coefficient and the cell area and volume, the internal concentration of a passively diffusing solute approaches the same value as the external concentration. Now imagine that the cells start to grow and thus increase the internal volume: this dilutes the internal solute, creating a concentration difference across the cell envelope. This concentration difference in turn results in further passive inward diffusion of solute. The steady position is then one in which the rate of inward flow of solute driven by the concentration difference just balances the increase in the internal volume resulting from growth. The model describes the kinetics of the approach to that steady balanced position for cells that are continuously growing. In the second hypothetical example, imagine a suspension of growing cells in which the permeability coefficient for the solute drops to zero, resulting in no further influx. As the cells continue to grow, each doubling of the volume of the population of cells results in a halving of the average internal concentration of the preexisting internal solute. In the dynamic model, however, the permeability coefficient is not zero, and the bacterial internal volume and surface area expand while the internal concentration of solute increases until the steady value is reached when influx just balances dilution through growth. The derivation presented below finds the analytic solution for how the internal concentration in growing cells responds to this set of relationships as a continuous process, starting from an initial value of zero.
(i) Model description and assumptions.
Figure 1 shows the conceptual two-compartment, single-barrier model used. The model assumes a low-number-density population of exponentially growing bacterial cells in a fixed volume of medium, e.g., the suspension of bacteria shortly after inoculation and mixing in a conventional susceptibility test, ∼5 × 105 cells/ml (24). This low-number-density assumption enables the simplifying assumption that the external concentration remains constant over the time taken for the internal concentration to approach the external concentration. The population of cells in a unit volume of suspension is treated as though each cell possessed a uniform shape and an average surface area and cytoplasmic volume. As growth continues and the number of individual cells per unit volume of suspension increases, the total area and cytoplasmic volume of the population increase exponentially. However, the ratio between the two remains constant. A dividing cell population is described, but the absolute number of cells does not enter the equations presented below. Rather, all cell parameters are based on dry bacterial mass consisting of cells of average size. It will be noted that the concentration-dependent determinant of the flux through a given surface area of the cells (P × A below) divided by the volume of the cells (V3 below) is effectively a kinetic coefficient for the increase in the internal concentration of solute (for example, as used by Demchick and Koch [25]).
FIG 1.
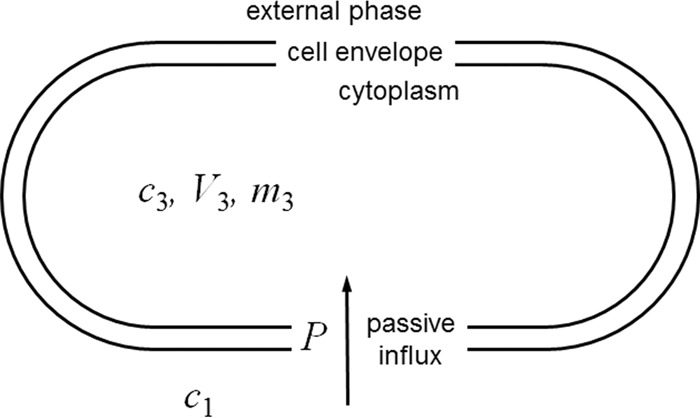
Conceptual model used for the kinetic analysis of the passive penetration of a solute into bacterial cells in the absence of efflux. Each bacterial cell is represented by a single compartment with a single surface, across which passive diffusion governed by a single permeability coefficient occurs. This permeability coefficient incorporates the diffusion gradient between the bulk aqueous solution and the cell surface, i.e., the unstirred layer, and it incorporates the diffusion across the peptidoglycan layer within the cell envelope. Exponential expansion (i.e., growth) is modeled by assuming that the total volume and the surface area of the population of cells (in a unit volume of suspension) increase exponentially with time at a constant specific growth rate. That is, the changes in shape that occur between each cell division are ignored so that each cell is modeled as having an average volume and surface area. Symbols referring to cytoplasmic parameters are assigned the subscript 3 in order to be consistent with other kinetic models, in which the subscript 2 refers to the periplasm. For explanations of the symbols, see Table 1 and the text.
The ratio between surface area and volume remains constant for a given modeled average cell, but the following question arises: by how much does the ratio of the surface area to volume (A/V) vary as a rod-shaped cell elongates and shortens during the division cycle? Imagining the rod-shaped cell as a cylinder capped by two hemispherical poles, one can derive a formula for A/V using geometric formulae for the surface area and volume of the cylinder portion of the cell and of the surface area and volume of the two polar hemispheres. For a sphere (i.e., when the cylinder part of the rod is of negligible length) A/V is equal to 3/r, where r is the radius. As the cylinder part of the rod lengthens, the value A/V approaches a limiting value of 2/r. Thus, throughout the cell division cycle, the value of A/V for a rod-shaped bacterium is likely to oscillate somewhere between 2/r and 3/r. For a species such as E. coli, in which the diameter is about 0.75 μm, A/V remains between the values of 5.3 × 104 and 8 × 104 cm−1, which is a range narrow enough to allow it to be represented by an average A/V value. To put this into context, experimentally determined representative values of A and V for a Gram-negative rod and a Gram-positive coccus are provided in Table 2. The values of A/V calculated from these were 9.4 × 104 and 15.1 × 104 cm−1, respectively, implying diameters slightly smaller than 0.75 μm.
TABLE 2.
Parameters used to calculate the cytoplasmic/external concentration ratio as a function of permeability when inward diffusion just balances dilution caused by exponential bacterial growth
| Parametera | Value | Source |
|---|---|---|
| μ | ln(2)/1,800 = 3.851 × 10−4 s−1 | Specific growth rate constant equivalent to a mean generation (doubling) time of 30 min |
| AGm+ve | 35.5 cm2 · (mg dry mass)−1 | Staphylococcus epidermidis surface; based on a spherical radius of 389 nm estimated from Fig. 5 of reference 66b |
| V3Gm+ve | 2.35 × 10−4 cm3 · (mg dry mass)−1 | S. epidermidis cytoplasm water volume, based on the cytoplasm spherical radius of 350 nm estimated from Fig. 5 of reference 66 and assuming 70% of the volume to be water (67)b |
| AGm−ve | 132 cm2 · (mg dry mass)−1 | Surface area of Salmonella enterica serovar Typhimurium (68) |
| V3Gm−ve | 1.4 × 10−3 cm3 · (mg dry mass)−1 | Cytoplasm water volume of E. coli (53, 69) |
Gm+ve and Gm−ve, measurements and estimates based on experimental data from, respectively, Gram-positive and Gram-negative bacteria.
The relationship between cell number and dry mass for a Gram-positive coccus was estimated to be 1.867 × 109 cells · (mg dry mass)−1 from data for Staphylococcus aureus (70).
The concentration of solute inside the cell, c3, refers to that in the cytoplasm. The cell envelope is treated as a single permeability barrier with a permeability coefficient that describes the passive permeation of a given solute across that whole barrier. This is most easily envisaged for a Gram-positive bacterial cell in which the cytoplasmic membrane is the principal permeability barrier. However, it can be used for Gram-negative bacteria, with the understanding that the permeability coefficient represents a composite of the processes of permeation across the outer and cytoplasmic membranes (7) (cf. equation 3). In order to be able to characterize the idea of a nonpermeant solute, as might unintentionally be prepared in a medicinal chemistry program based on a novel scaffold, for example, the cells are assumed to exhibit no efflux, and solute in the cytoplasm is assumed not to alter the cell growth rate. Also, the solute itself is assumed not to alter its own permeation (discussed below under limitations of the model). The external concentration of solute can be assumed to be constant because the model is being applied to low cell number densities, for which the volume of cytoplasm is several orders of magnitude lower than the volume of external medium (and it is assumed that the solute is chemically stable and not subject to inactivation by bacterial enzymes, as might occur for a β-lactam susceptible to β-lactamase-catalyzed hydrolysis in the periplasm, for instance). Under those conditions, a negligible amount of solute disappears from the external phase for the concentration in the cytoplasm to rise to the same as that in the external phase.
(ii) Derivation of model equations.
The symbols and units used in the equations are shown in Table 1. As a clarification, the mass of solute is measured in units of nanomoles, whereas the mass of cells, M, is measured in units of milligrams. The mass of cells is a physiological denominator equivalent to the number of cells and serves to distinguish quantitatively between the external compartment and the internal (growing) compartment in a unit volume of suspension. In the various derivations below, the mass of solute is not conflated with the mass of cells.
For culture biomass, M, the equation governing exponential growth can be written (12)
| (4) |
where M0 is the mass of cells at time zero in the volume element of the suspension considered, μ is the specific growth rate constant, and t is time. The equation that describes the variation in the concentration of the solute in the cytoplasm, c3, with time is derived from the total amount of solute in the cytoplasm of the population of cells, m3, at time t divided by the coincident cytoplasmic volume (V3 × M):
| (5) |
For the single-permeability-barrier, 2-compartment system shown in Fig. 1, the net flux across a specified area of the barrier in response to the concentrations of solute in the two compartments can be written as (26) (equation 1)
| (6) |
In this equation, the area term, A, refers to the specific area [centimeters2 · (milligrams dry mass)−1 in the present work; Table 1] and JA applies to the net flux across the area of the permeability barrier in units of milligrams dry mass, i.e., the specific flux. In order to obtain the flux (F) for the whole population at a given time point, the specific flux (JA) is multiplied by the size of the population at that time point, that is,
| (7) |
That net inward flux for the population (in units of nanomoles · second−1) is the same as the rate of increase in the amount of solute in the cytoplasm of the population of cells in the volume element considered, that is,
| (8) |
Substituting for F from equation 8 and JA from equation 6 in equation 7 yields
| (9) |
Substituting for c3 from equation 5 yields
| (10) |
Substituting for M from equation 4 and rearranging gives
| (11) |
This is a nonhomogeneous linear differential equation of the first order for which the solution is (27)
| (12) |
Using this expression to substitute for m3 in equation 5 and expressing M as M0eμt yields
| (13) |
This is a relationship of a form similar to that in the equations described by Demchick and Koch (25) for the diffusion of fluorescent solutes of various sizes into (nongrowing) isolated peptidoglycan sacculi [C = CO × (1 − e–kt), where C is the concentration of solute inside the sacculus at time t, CO is the concentration outside in the bulk phase, and k is a first-order kinetic constant that applies to both the entry and the exit processes] and Sigler et al. (7) for the diffusion of tetracyclines into (nongrowing) liposomes and into nongrowing E. coli {cin(t) = cin(∞) × [1 − e−(AP/V)t], where cin(t) is the internal concentration at time t, cin(∞) is the asymptotically approached internal concentration as t approaches ∞, and A, P, V, and t are as used in the present work}. If one considers the nongrowing special case of equation 13 by setting μ equal to 0, then it reduces to the same relationship, {c3 = c1 × [1 − e−(PA/V3)t]}, with the ratio PA/V3 now being equal to empirical kinetic constant, k, of Demchick and Koch (25).
Equation 13 can be rewritten to show the time course of the rise of the cytoplasmic concentration as a proportion of the external concentration:
| (14) |
Note that the population of bacterial cells in the foregoing analysis applies to a fixed volume element; that is, the growing bacteria continue to be retained in the same volume (e.g., 200 μl in a broth microdilution MIC measurement), such that the population biomass, M, refers to that constant total volume element. As assumed above, equation 14 holds when the suspension of cells is at a low number density, such that the cytoplasmic water volume is negligible compared with the volume of the external medium. Under those conditions, the external concentration of solute, c1, does not change during the period of application of the equation.
Equation 14 was used as follows to estimate what permeability coefficient can be said to be the threshold value associated with impermeability. If the solute does not impede growth (although an effective inhibitor of any growth-limiting reaction, such as a step in protein synthesis, would impede growth, as discussed below), then as t approaches ∞, the expansion becomes more and more closely matched by a steady inflow of compound that maintains a constant concentration gradient across the envelope and constant internal concentration, c3. This is because as t approaches ∞, the term e−[(PA/V3) + μ]t approaches 0 and the ratio c3/c1 asymptotically approaches a constant value, given by equation 15 below. When the permeability coefficient is relatively high, e.g., approximately >1 × 10–6 cm · s−1 (see below), that asymptotic ratio will be close to unity and the internal concentration will be close to the external concentration. In contrast, a relatively low permeability coefficient will result in the asymptotically approached balance position reflecting a correspondingly much lower internal concentration relative to the external concentration. Likely threshold values were estimated by examining the limit of equation 14 as the exponential term approaches 0 at long times:
| (15) |
Equation 15 shows the relationship between internal concentration, permeability, and growth rate that is approached asymptotically, when influx is just balanced by growth (bearing in mind the assumptions of the absence of efflux, the absence of a chemical reaction, and the absence of substantial binding of solute, made to enable modeling of just the permeation and expansion kinetics).
(iii) Modeling using experimentally determined values.
Table 2 shows the experimentally derived cell size and surface area data for Gram-positive and Gram-negative bacteria used for calculations of the limiting asymptotic ratios between internal and external concentrations. Table 3 shows the predicted limiting concentration ratios [(c3/c1)t → ∞] obtained from equation 15 for a range of permeability coefficients. The permeability coefficients analyzed include examples measured for the passive diffusion of known compounds across natural or artificial phospholipid bilayers.
TABLE 3.
Theoretical limiting ratios of cytoplasmic/external concentrations of solutes with different cell envelope permeability coefficients when growth balances inward diffusion, based on average geometries of Gram-positive and Gram-negative bacterial cells
| Solutea | P (cm · s−1) | (c3/c1)t
→ ∞b |
|
|---|---|---|---|
| Gm+ve | Gm−ve | ||
| Water | 1.90 × 10−3 | 1.00 | 1.00 |
| p-Aminobenzoate | 1.16 × 10−5 | 1.00 | 1.00 |
| —c | 1.00 × 10−6 | 0.997 | 0.996 |
| 2′-Deoxyadenosine | 9.40 × 10−7 | 0.997 | 0.996 |
| — | 1.00 × 10−7 | 0.975 | 0.961 |
| Erythromycin | 2.12 × 10−8 | 0.893 | 0.838 |
| — | 1.00 × 10−8 | 0.797 | 0.710 |
| Tetracycline (E. coli) | 5.60 × 10−9 | 0.687 | 0.578 |
| Tetracycline (liposomes) | 2.40 × 10−9 | 0.485 | 0.370 |
| — | 1.00 × 10−9 | 0.282 | 0.197 |
| Tryptophan, pH 6.0 | 4.10 × 10−10 | 0.139 | 0.0912 |
| — | 1.00 × 10−10 | 0.0378 | 0.0239 |
| Glycine, pH 7.0 | 5.30 × 10−12 | 0.00208 | 0.00130 |
| Phosphate, pH 4.0 | 5.00 × 10−12 | 0.00196 | 0.00122 |
| Lysine, pH 7.0 | 3.70 × 10−12 | 0.00145 | 0.000905 |
| Na+ | 1.20 × 10−14 | 4.71 × 10−6 | 2.94 × 10−6 |
The sources of the phospholipid bilayer permeability coefficients (or cell envelope permeability coefficient in the one tetracycline example) were as follows: for water and 2′-deoxyadenosine, reference 71; for p-aminobenzoate, reference 72; for erythromycin, reference 2; for tetracycline, reference 7; for tryptophan, glycine, phosphate, and lysine, reference 73; for Na+, references 74 and 75.
Gm+ve and Gm−ve, measurements and estimates of cell surface area and cytoplasm volume based on experimental data from, respectively, Gram-positive and Gram-negative bacteria (Table 2).
—, illustrative intermediate permeability coefficients not specific to any particular solute.
Note that for tetracycline the lipid bilayer permeability coefficient (likely to be equivalent to the cytoplasmic membrane permeability coefficient) was similar to the whole-envelope permeability coefficient measured during its diffusion into the cytoplasm of E. coli (i.e., the composite value representing diffusion across both the outer membrane and the cytoplasmic membrane in series). Based on equation 3, this is also likely to be the case for other small water-soluble molecules that cross the Gram-negative bacterial outer membrane through porin-mediated aqueous pores (e.g., for molecules with a molecular mass of approximately <500 g · mol−1 in E. coli [2, 3]). That is, the overall permeability coefficient is predicted to be slightly lower than the limiting cytoplasmic membrane permeability coefficient. In Gram-positive bacteria, the principal passive barrier of the envelope to hydrophilic compounds is the phospholipid bilayer of the cytoplasmic membrane (2). From the predictions in Table 3, one can infer that if the permeability coefficient is less than about 1 × 10−10 cm · s−1, a growing bacterial cell is effectively impermeable to that compound, because the highest concentration attainable in growing cells is predicted to be about 2 to 4% of the external concentration. For compounds whose bacterial cell envelope permeability coefficient is ≥1 × 10−8 cm · s−1, the internal concentration is predicted to attain 70 to 80% or greater of the external concentration as diffusion proceeds (as stated in the derivation, this assumed an absence of efflux, the absence of a chemical reaction, and the absence of substantial binding). Clearly, at both ends of the scale of permeability coefficients, a compound that inhibited the expansion of a bacterial cell, for example, an inhibitor of protein synthesis active in the cytoplasmic environment, would reach an internal concentration higher than that predicted by the data in Table 3, depending on the reduction in the growth rate, but this analysis does show the principle for medicinal chemistry that simply to ensure that a novel antibacterial compound can reasonably readily enter bacterial cells by passive permeation, the lipid bilayer permeability coefficient needs to be higher than about 10−8 cm · s−1. Interestingly, this can include some hydrophilic solutes, with 2′-deoxyadenosine being one example (Table 3).
Compounds that are in the impermeant region include glycine, phosphate monoanion, lysine, and Na+ (Table 3), hydrated ions that indeed would not be expected to cross the bacterial cytoplasmic membrane passively to any great extent. Clinically used antibacterial agents are generally less lipophilic than other drug classes (18, 28, 29), with the consequence that lipid membrane permeability coefficients are likely to be on the low side, so the permeability coefficient cutoff range of about 10−8 cm · s−1 referred to above is proposed to be a useful medicinal chemistry benchmark for assessment of the passive permeability of bacteria to novel compounds.
(iv) Estimating how long it takes for passive permeation to be balanced by growth.
A further estimate that can be derived from equation 14 is how long it takes for the balance position described above to be established. A final asymptote is reached only as t approaches ∞, but a practical answer can be obtained by calculating the time taken for the cytoplasmic concentration to reach 99% of the asymptotic value, t99. This is when the {1 − e−[(PA/V3) + μ]t} term in equation 14 rises to 0.99 or the exponential term falls to 0.01, i.e.,
| (16) |
This can be rearranged as follows:
| (17) |
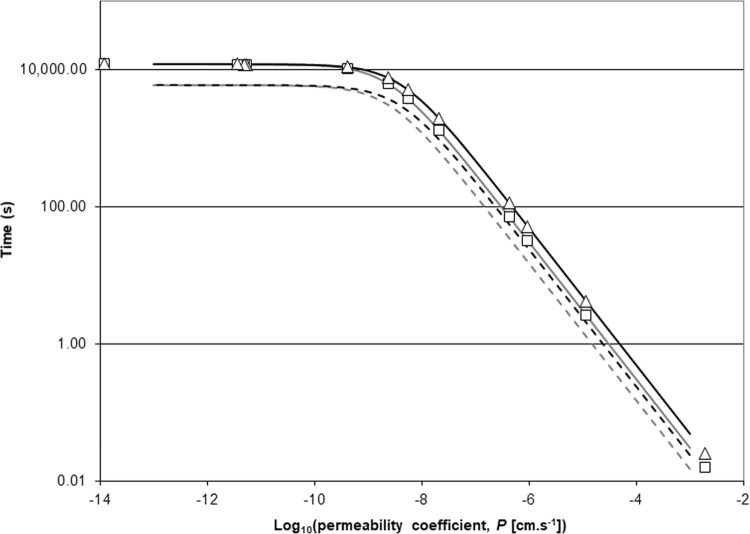
Equation 17 demonstrates that the time to rise to 99% of the limiting position as t approaches ∞ depends on the absolute rates of permeation and growth, as would be expected. Thus, the faster that the growth is, or the higher that the permeability coefficient is, the quicker that the approach to the asymptotic concentration ratio is, although, clearly, one of those processes might dominate. Figure 2 displays curves for typical values of surface area and cytoplasmic volume for a Gram-positive coccus and a Gram-negative rod growing with a mean generation time of 30 min. The theoretical time to reach 99% of the value at the limit varies from less than 1/10 s for a compound with a high permeability coefficient in the region of 10−3 cm · s−1 to about 50 s for a moderately permeant compound like 2′-deoxyadenosine (P ≈ 10−6 cm · s−1) and to slightly greater than 3 h for a low-permeant compound like tryptophan (P ≈ 4 × 10−10 cm · s−1). Note further that the longer times are also associated with the lower eventual internal/external concentration ratios (Table 3). For comparison, times to reach 90% of the asymptotic value of c3/c1 (t90) are also plotted in Fig. 2 {from the relationship t90 = 2.30/[(PA/V3) + μ]}. These values of t90 were half as long as the values of t99. For the Gram-negative rod, t90 for 2′-deoxyadenosine was about 26 s rather than 50 s and t90 for tryptophan was about 1.5 h rather than >3 h. It was proposed above that novel compounds made in antibacterial drug discovery programs aimed at inhibiting cytoplasmic targets usually display permeability coefficients of >1 × 10−8 cm · s−1. The time to rise to the asymptotic cytoplasmic concentration for this permeability coefficient was calculated from equation 17 to be about 60 min, or two generations (this can also be roughly estimated visually from Fig. 2). This was calculated from the parameters for Gram-negative bacteria, but the value for Gram-positive bacteria would be similar (Fig. 2).
FIG 2.
Theoretical time for the ratio between the external and cytoplasmic concentrations of a solute to reach 90 or 99% of its steady position, where influx just balances dilution caused by growth in exponentially growing cells of a typical Gram-negative bacterium and a typical Gram-positive bacterium as a function of the permeability coefficient. The solid lines are the t99 plots of equation 17 for Gram-positive bacterial (gray) and Gram-negative bacterial (black) cell surface area and cytoplasmic volume (Table 2). In both cases, the bacteria were assumed to be growing rapidly with a doubling time of 30 min. The symbols (□, Gram-positive bacteria; Δ, Gram-negative bacteria) show the t99 values calculated using equation 17 for the permeability coefficients given in Table 3, with the addition of one further example: 4.3 × 10−7 cm · s−1, calculated for the cell envelope of Staphylococcus epidermidis and the unprotonated form of erythromycin at 37°C and pH 7.8 from uptake data from Goldman and Capobianco (65). The dashed lines show equivalent plots of 90% equilibration times from the analogous equation, t90 = [−ln 0.1]/[(PA/V3) + μ] = 2.30/[(PA/V3) + μ], for Gram-positive bacterial cells (gray) and Gram-negative bacterial cells (black).
Relative importance of permeability and efflux. (i) Aim.
The aim of the following analysis is to show how the internal concentration of a compound penetrating into the cell by passive diffusion is affected by the coefficients that govern that passive inward permeation on the one hand and active efflux on the other. This is partly to help understand the medicinal chemistry impact of changing the permeability coefficient of a compound. It was shown above that if the only factor restricting the internal concentration is dilution by cell growth, most compounds made by medicinal chemists (i.e., those with a wide range of log P and log D values [see below for the definitions of log P and log D]) will rapidly permeate to a concentration inside the cell equal to a substantial fraction of the external concentration (for example, values of log D calculated for a series of LigA inhibitors varied from 0 to 3.5 [1], and values calculated for 147 antibacterial compounds of various classes either clinically licensed or under clinical investigation ranged from approximately −10 and 4.5 [30]). However, in bacteria, outwardly directed pumping occurs (9, 31), and this counters the passive inflow. In this case, as judged from the analysis presented below, the absolute value of the permeability coefficient per se for a compound crossing the cell envelope becomes very important.
[The following definitions of log D and log P are taken from reference 18: log D is the log10 of the distribution coefficient, measured as the relative partitioning of all ionizable forms of a small molecule between a hydrophobic (octanol) and aqueous phase buffered to a particular pH, usually pH 7.4. This term describes the relative hydrophobicity of a chemical compound and is different from the related partition coefficient, log P, which describes the partitioning of only the neutral (nonionized) form of the compound between phases.]
(ii) Conceptual model.
The simple model for understanding efflux is shown in Fig. 3. This is identical to Fig. 1 but with the introduction of efflux governed by a single, first-order kinetic constant. This is a simplification that allows relationships to be examined analytically but clearly can be built upon to yield less artificial simulations, which would be more accurately addressed using kinetics governed by Hill equations (32, 33) or by the often-used Michaelis-Menten equation, which is mathematically a special case of the general Hill equation (34).
FIG 3.
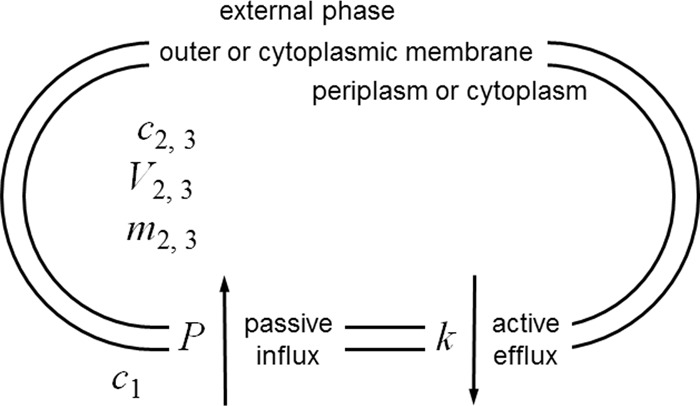
Conceptual model used for kinetic analysis of the interplay between inward diffusion and outwardly directed active efflux. A single permeability barrier, the cell envelope, is modeled for simplicity. This could apply to permeation into the cytoplasm of a Gram-positive bacterium, as drawn (symbols with the subscript 3), or permeation into the periplasm or cytoplasm of a Gram-negative bacterium, where the barrier shown would be the outer or cytoplasmic membrane and the inner compartment would be the periplasm or cytoplasm (the same symbols with the subscripts 2 and 3, respectively). It is important to note, however, that a solute's permeability coefficient, determined by a particular set of physical properties, will differ depending on whether permeation occurs across a fluid lipid bilayer like the cytoplasmic membrane or across the outer membrane via its less fluid lipid bilayer or via aqueous pores (2). The analysis considers a single compartment with a single surface, across which passive diffusion governed by a single conventional permeability coefficient occurs. As described in the legend to Fig. 1, this permeability coefficient incorporates the diffusion gradient between the bulk aqueous solution and the cell surface, the unstirred layer. See Table 1 and the text for explanations of symbols and their units.
(iii) Assumptions: permeability and cell growth.
The key assumptions are the same as those that were used above. First, with respect to cell growth, a population of cells is being dealt with as if they were all identical with an average surface area and volume of the cytoplasm. Thus, as growth continues, the total area and cytoplasmic volume of the population increase exponentially but the ratio between the two stays constant. Second, the external concentration of compound remains nearly constant because the cellular volume is negligible in comparison with the external volume, as would occur with an inoculum typical of an MIC measurement. Third, the expression for m3 (the amount of compound inside cells) throughout refers to the whole population in the volume element considered. Thus, if m3 needs to be expressed as a specific amount, it is modified by dividing by M (which is equal to M0eμt), where M is the number or mass of cells in the volume element at time t, and M0 is the number or mass of cells at time zero, when the (antibacterial) compound and the inoculum are mixed.
New symbols are introduced as follows: E is the efflux per unit membrane area (in nanomoles · centimeters−2 · second−1). This is analogous (but oppositely directed) to and possesses the same dimensions as the influx parameter, J (Table 1). k is the specific efflux constant (in centimeters · second−1). The dimensions of length · time−1 occur because the constant relates flux (in units of mass · length−2 · time−1) to concentration (in units of mass · length−3); see equation 18 below. Note that the dimensions are identical to those of the permeability coefficient, which also relates flux to concentration (Table 1; equation 1).
(iv) Further assumptions adopted in order to model efflux.
For simplicity, it is assumed that only one molecular species of pump (e.g., AcrAB-TolC, QacA, or CmlA) is acting. Within the concentration range of interest, the pump is not saturated by the substrate. This assumption allows the derivation of an analytic expression that clearly shows the relationship between the efflux pump kinetic coefficient and the permeability coefficient. The less simple, but more realistic, approach would be to model the efflux as a saturable process, which occurs in reality (32, 33). Although a saturable process can be modeled mathematically to produce simulated curves, that approach would somewhat obscure the underlying relationship between efflux and permeation. The model provided below is applicable only at low internal concentrations of antibiotic, when the efflux pump can be considered to be far enough from saturation that its rate is proportional to the concentration of solute.
The efflux rate is governed by the concentration of compound in the internal compartment, exemplified here as that in the cytoplasm, c3. Note that the binding site of the transporter might be within the lipidoidal, cytoplasm-facing, interior phase of the membrane, but the modeling assumption is reasonable, in that the concentration of solute in the cytoplasmic half of the lipid phase is often modeled linearly as c3 × KP, where KP is the lipid-water partition coefficient.
These assumptions lead to the following relationship between E, k, and the internal concentration:
| (18) |
(v) The quantitative model.
As described above, the approach to modeling passive influx in the presence of efflux was to consider the internal amount of compound, m3, rather than the internal concentration as the primary function of time.
The net rate of change of m3, the amount of compound in the population of cells, is governed by the difference between the rate of compound inflow per milligram dry mass, JA, and the efflux per milligram dry mass, EA, i.e., (JA − EA). JA and EA are the specific fluxes; the net flux, F, for the population of cells in the volume element considered is therefore (cf. equation 7)
| (19) |
Substituting for F from equation 8, for JA from equation 6, and for E from equation 18 and rearranging yields the relationship
| (20) |
Substituting for c3 from equation 5, replacing M by the exponential growth term shown in equation 4, and rearranging yields
| (21) |
The method of Kreysig (27), as used in the earlier analysis (see above), yielded the following solution to equation 21:
| (22) |
Note the similarity of form between equation 22 and equation 14, derived for the identical model but without efflux. Equation 22 is identical to equation 14 if k, the efflux coefficient, is set equal to 0.
It is interesting to examine some consequences of equation 22. For example, what relationship is approached after long time periods, i.e., when passive influx is balanced by active efflux? As t approaches ∞, the expression in braces in equation 22 approaches unity, such that
| (23) |
This makes intuitive sense. The asymptotically approached internal concentration at long time periods is lower than the external concentration by a pump versus passive influx term (k/P) in the denominator and an exponential expansion versus passive influx term [μ/(PA/V3)] identical to the one presented above (equation 15), also in the denominator. If k and P are about equal, the final internal concentration that is approached after long time intervals is about half of the external concentration reduced by the dilution caused by expansion.
To show that efflux and cell volume expansion act together against influx, another way of writing equation 23 is
| (24) |
Using the values from Table 2 for the generalized Gram-negative rod, μ(V3/A) amounts to about 4.1 × 10−9 cm · s−1, and for the Gram-positive coccus, it is about 2.5 × 10−9 cm · s−1. Considering only the outer membrane barrier of Gram-negative bacterial cells, if one takes V3 to be the water volume of the periplasm of a Gram-negative rod, using E. coli as an example [1 × 10−3 cm3 · (mg dry mass)−1], then the corresponding expansion term is about 3 × 10−9 cm · s−1. Nagano and Nikaido (32) measured the efflux kinetics of the AcrAB-TolC pump of E. coli. Efflux kinetic constants measured from the linear portion of the concentration-rate curves of that publication are displayed in Table 4. The values of these experimentally estimated efflux coefficients are of the order of 104-fold higher than the values of the cell expansion term. Therefore, for such compounds that are pumped out efficiently, the expansion term is negligible and the following approximation holds:
| (25) |
where cint and cext are internal and external concentrations, respectively, and could be applied to the outer or cytoplasmic membrane barrier or the whole-cell envelope barrier, as long as k and P apply to the same barrier. This simple relationship can be summarized intuitively as follows. If permeability were substantially higher than the values of k shown in Table 4, the internal and external concentrations would eventually equilibrate. In the presence of dominating efflux, when k is much higher than the permeability coefficient, the eventual concentration ratio tends to P/k, the ratio between the permeability and efflux coefficients. When the permeability and efflux coefficients are the same, the internal concentration would eventually poise at half the external concentration, as would be predicted intuitively. Curves of c3/c1 versus the permeability coefficient for different efflux coefficients using equation 25 have been presented elsewhere (2).
TABLE 4.
Kinetic coefficients for outer membrane efflux of cephalosporins from the periplasm of Escherichia coli
| Compound | k (cm · s−1) | Concn range (μM)a | Sourceb |
|---|---|---|---|
| Nitrocefin | 3.2 × 10−5 | 0–3 | 3 |
| Cefamandole | 12.3 × 10−5 | 7–13 | 4 |
| Cephalothin | 4.9 × 10−5 | 20–100 | 5 |
| Cephaloridine | 2.7 × 10−5 | 50–250 | 6 |
Range of periplasmic concentrations over which the rate of efflux was proportional to the concentration.
The numbers refer to the figure numbers in the article presented by Nagano and Nikaido (32), from which the efflux coefficients, k, were calculated.
Efficiencies of two efflux systems acting in series or in parallel. (i) Aim.
The kinetic model developed above was extended to analyze the effects of two efflux systems acting in series or in parallel. However, full derivations are not provided because they yielded equations analogous to those presented by Palmer (8), who analyzed cytoplasmic versus periplasmic substrate capture by multicomponent efflux pumps spanning two membranes. The reason for re-presenting those equations here is to show that in all the different pump combinations, the efflux coefficients are found in ratio with the permeability coefficient for the membrane across which the efflux pump acts. This allows all the pump configurations to be analyzed in terms of a novel parameter, efflux pump efficiency (see below).
(ii) Model and explanation of symbols.
The conceptual model and symbols used are shown in Fig. 4. Briefly, as in the efflux analysis described above, the rate of efflux by each system is proportional to the concentration of solute in the compartment from which the pumping occurs. The assumption was also made that the dynamic balance position when influx and efflux are equal is approached rapidly compared with the generation time of the cells. Thus, unlike the model described above, bacterial growth is neglected. This is consistent with the conclusion from the comparison of kinetics presented above that when a solute is subject to efflux, the rate is high enough that the cell expansion term can be neglected. Otherwise, assumptions are as described above. Expressions were derived for the ratio between the concentrations in the external and cytoplasmic compartments when the fluxes are kinetically balanced (i.e., permeation balancing efflux) for each of the models (models A to E) described in the legend to Fig. 4. The basis of all the derivations was to set passive influx to be equal to active efflux. One example is shown here for model A (one efflux pump traversing the outer membrane).
| (26) |
FIG 4.
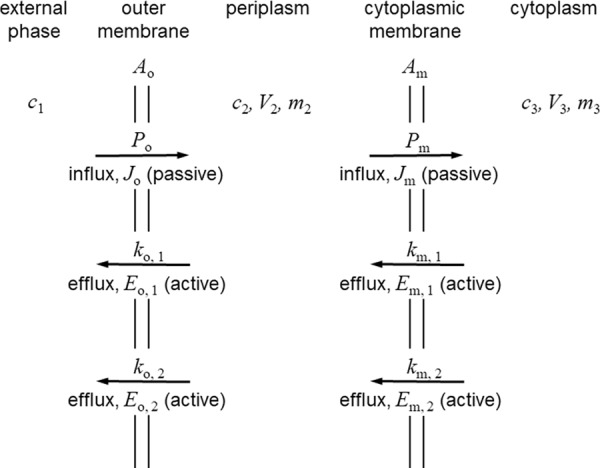
Conceptual model used for the kinetic analysis of the interplay between inward diffusion and two efflux systems in parallel or in series in Gram-negative bacteria. This is a composite diagram that displays the various different systems that might be present when a single efflux pump operates or when two pumps that are arranged in parallel or in series operate. The external compartment is represented by the subscript 1, the periplasm is represented by the subscript 2, and the inner, cytoplasmic compartment is represented by the subscript 3. Parameters related to the outer membrane are represented by the subscript o, and parameters related to the cytoplasmic membrane are represented by the subscript m. Passive diffusion governed by the permeability coefficient, P, and flux, J, are present in all the models. See Table 1 and the text for the quantities represented by the symbols and for their units. Five arrangements are analyzed. Model A represents a single active efflux system that crosses the outer membrane, represented by Eo,1 with kinetic constant ko,1. The other efflux systems shown are not present in this model. Model B represents one active efflux system only that this time crosses the cytoplasmic membrane, represented by Em,1 with kinetic constant km,1. Other efflux systems are not operating. Model C represents two active efflux systems, both of which are across the outer membrane, represented by Eo,1 and Eo,2 with kinetic constants ko,1 and ko,2, respectively. Cytoplasmic membrane efflux pumps are absent. Model D represents two active efflux systems acting in parallel across the cytoplasmic membrane, represented by Em,1 and Em,2 with kinetic constants km,1 and km,2, respectively. Outer membrane efflux pumps are absent. Model E represents two active efflux systems in series, one across the outer membrane, represented by Eo,1 with kinetic constant ko,1, and one across the cytoplasmic membrane, represented by Em,1 with kinetic constant km,1. No other pumps are operating.
The other key assumption was that the absence of any efflux pump in a particular membrane resulted in equilibration of concentrations across that membrane. Thus, in model A (one efflux pump in the outer membrane), c3 is equal to c2, and in model B (one efflux pump in the cytoplasmic membrane) c2 is equal to c1. The equations obtained (equations 27 to 31) are shown in Table 5.
TABLE 5.
Ratio between cytoplasmic and external concentrations of solute under conditions of dynamic balance when the rates of inward permeation and efflux become equal
The models correspond to those described in the legend to Fig. 4.
Abbreviations: OM, outer membrane; CM, cytoplasmic membrane.
(iii) Analysis of efflux model equations.
Equation 27 from model A, which describes the effect of a single efflux pump across the outer membrane, is identical to the t approaches ∞ limit of equation 25 derived from the model that included the bacterial growth rate. Equation 28 from model B, the effect of a single pump across the cytoplasmic membrane, is identical in form to that of model A. Equations 27 and 28 lead to the interesting conclusion that a single-stage efflux pump is mathematically identically effective whether it pumps across the cytoplasmic membrane from the cytoplasm to the periplasm or across the outer membrane from the periplasm to the external medium. That is, the concentration ratio between the cytoplasm and the external medium depends on the ratio between the permeability and the efflux coefficients for the membrane that is protected by the efflux system. Thus, as a teleological generalization, for a given antibiotic that acts within the cytoplasm, the most effective location for an efflux pump, if there should be only one pump, is across the membrane with the lower permeability coefficient for that compound. One can speculate that evolutionary selection by toxic xenobiotics over long time periods might result in the optimized substrate specificity of pumps operative at either the cytoplasmic membrane or the outer membrane, depending on the compound class of the xenobiotic concerned. For example, the outer membrane of E. coli is of lower permeability to lipophilic antibacterial agents, such as novobiocin, than the cytoplasmic membrane (2, 35), and the predominant efflux pump for lipophilic agents, including novobiocin, is AcrAB-TolC, which pumps solutes from the periplasm across the outer membrane to the external medium (36).
Equation 29, derived from model C, two pumps operating in parallel across the outer membrane, demonstrates that two pumps acting in parallel are additive. The two kinetic constants combine additively to oppose the inward permeation governed by the permeability coefficient for that membrane. Model D for the cytoplasmic membrane yielded the same form of equation (equation 30), except that the relevant permeability coefficient is that of the cytoplasmic membrane toward the solute in question. In summary, models C and D are the theoretical description of pumps in parallel, and they were indeed additive when single and parallel paired pumps were analyzed experimentally (37).
In the case of model E, two efflux systems operating in series, one each across the outer and cytoplasmic membranes, there were two kinetic balance relationships. One was the relationship for the outer membrane, and the other was the relationship for the cytoplasmic membrane. The periplasmic concentration, c2, was eliminated to yield equation 31 (Table 5). The form of equation 31 is similar to the form already analyzed for a single pump (equations 27 and 25). There is an additive term, as was found for two pumps in parallel in the same membrane, but a multiplicative term, (ko,1/Po) × (km,1/Pm) (where ko,1 and km,1 represent the kinetic constants for the outer membrane and the cytoplasmic membrane in the external compartment, respectively, and Po and Pm represent the permeability coefficients for the outer membrane and the cytoplasmic membrane, respectively), also appears. Once again, this agrees well with the conclusion drawn on the basis of experimental evidence: that efflux pumps in series provide a multiplicative reduction in the antibiotic concentration in the cytoplasm compared with that in the external medium (37).
(iv) Relationship between efflux and permeability coefficients: efflux efficiency.
In all of the models described above, the one common feature is that whenever an efflux pump coefficient appears in the equation for the ratio between internal and external concentrations, it is always linked with the permeability coefficient for the same membrane. This was the case both for the additive relationships and for the multiplicative relationship. To simplify the comparisons below, a new parameter, the efficiency of an efflux pump acting against a particular solute, is defined. The efficiency of a pump in a particular membrane is symbolized by η, where
| (32) |
and k and P refer to either the outer membrane or the cytoplasmic membrane but the same membrane for a particular efficiency, η. For example, to distinguish between the efficiencies of different pumps and on the basis of the subscript designations in Fig. 4 and Table 5, one can specify ηo,1 = ko,1/Po, ηo,2 = ko,2/Po, etc.
This allows an illustrative comparison of the overall efficiency of different composite pump systems based on equations 25 and 27 to 31 by considering the case of a particular solute for which all the pumps are equally efficient in their ratio between permeability and efflux coefficients. Table 6 illustrates the quantitative differences between the additive and multiplicative pump arrangements described above. The greater effect of pumps in series is clear, and equations 27 to 31 provide a theoretical basis for the conclusion previously drawn from experimental data (37). For example, for an efficiency of 1, where the efflux and permeability coefficients are equal, a single pump yields a cytoplasmic concentration that is half the external concentration and two pumps in parallel reduce the cytoplasmic concentration to one-third of the external concentration, but a pair of pumps in series yields a cytoplasmic concentration reduced to one-quarter of the external concentration. The greater effect of the pair of pumps in series is seen even more strongly if the efficiency is 10, i.e., if the pump coefficient is 10-fold higher than the permeability coefficient. Then, the single pump yields a cytoplasmic concentration that is 9% of the external concentration and two pumps in parallel reduce the cytoplasmic concentration to 5% of the external concentration, but a pair of pumps with an efficiency of 10 in series yields a cytoplasmic concentration reduced to 1% of the external concentration.
TABLE 6.
Abilities of a single efflux pump, two efflux pumps in parallel, and two efflux pumps in series to decrease the cytoplasmic concentration of a solute below its external concentration under conditions of dynamic balance when the rates of inward permeation and efflux become equal
| Pump efficiency (η) |
c3/c1 for: |
||
|---|---|---|---|
| A single pumpa | Two pumps in parallelb | Two pumps in seriesc | |
| 1 | 0.500 | 0.333 | 0.250 |
| 2 | 0.333 | 0.200 | 0.111 |
| 3 | 0.250 | 0.143 | 0.062 |
| 5 | 0.167 | 0.091 | 0.028 |
| 10 | 0.091 | 0.048 | 0.008 |
Where c3/c1 = 1/(1 + η), which is equivalent to equations 25 and 27.
Where c3/c1 = 1/(1 + 2η), which is equivalent to equations 29 and 30.
Where c3/c1 = 1/(1 + 2η + η2), which is equivalent to equation 31.
(v) Efflux efficiency and the MIC ratio between pump-sufficient and -deficient strains.
A method commonly used to understand whether a potentially antibacterial compound is subject to efflux pumping is to compare its antibacterial activity against a bacterial construct in which an efflux pump is expressed to its activity against an isogenic strain that does not express the pump (37, 38). Frequently, this is summarized as an MIC ratio or efflux ratio, which is equal to (MIC for the pump-sufficient strain)/(MIC for the pump knockout strain) (39). A natural question to ask is how the efflux pump efficiencies described in the present work relate to this pragmatic MIC ratio measurement. The answer to this question requires the assumption, used previously (33, 40, 41), that an MIC measured in vitro represents the attainment of some critical concentration of the antibacterial compound in the intracellular compartment containing the target to be inhibited. That principle has been applied here to analyze ratios derived from the MICs of chloramphenicol measured against an E. coli strain in which the acrAB gene had been deleted and against isogenic variants that expressed AcrAB at one of two levels and in all three cases with or without the simultaneous expression of a cytoplasmic membrane efflux pump, CmlA or MdfA. Table 7 presents the source data (37), the values of efflux pump efficiency (η) for the outer and cytoplasmic membranes calculated from the source MIC values (ηo and ηm, respectively), and predicted and measured MIC ratios for the strains expressing multiple pumps. The MIC of 1 mg/liter obtained against the ΔacrAB construct expressing neither of the cytoplasmic membrane pumps was assumed to be equal to the critical growth-inhibitory concentration of chloramphenicol achieved in the cytoplasm during the MIC measurement (i.e., rapid permeation to the cytoplasm was assumed, such that cint approached 1 mg/liter quickly compared to the time of cell doubling). As described previously (33, 40, 41), it was assumed that the same 1-mg/liter critical internal concentration of chloramphenicol had been achieved during measurements of MICs against the various pump-expressing constructs. Those values were combined to calculate cint/cext and, hence, single-membrane pump efficiencies, as shown in Table 7. The pump efficiencies calculated from the MICs determined against the strains expressing a single pump were then substituted into equation 31, as modified by equation 32, to predict the MIC ratios for the strains in which pumps were simultaneously expressed in both the cytoplasmic and outer membranes. Two of the four predicted MIC ratios were within 1 doubling dilution of the measured values (MIC ratios, 128 versus 64 and 32 versus 16), one was in the same range (MIC ratios, 512 versus >128), and one was the same as the measured value (MIC ratio, 128). Given that the measurements from which the efficiencies were calculated and that the experimental ratios used for comparison to predicted ratios were based on doubling dilution MIC values, the agreement between the results obtained with the model and the experimental measurements was reasonable. In summary, the model predicts that the MIC ratio will be 1 plus an efflux pump efficiency term that depends on the number and arrangements of the efflux pumps. That is, in the case of pumps in both membranes, the MIC ratio is approximately equal to 1 + ηo + ηm + ηo × ηm. Thus, according to the model, for MIC ratios of >10, say, the 1 term becomes negligible and the MIC ratio does indeed approximate the combined efflux pumping efficiencies against the test compound, as had been assumed previously (39).
TABLE 7.
Chloramphenicol MIC ratios measured against efflux pump-expressing and -nonexpressing strains compared with values predicted from efflux pump efficienciese
| Efflux pump |
MIC (mg/liter) | Calculated efficiency |
MIC ratioa |
|||
|---|---|---|---|---|---|---|
| CM | OM | ηob | ηmc | Predictedd | Measured | |
| None | ΔacrAB | 1 | — | — | — | — |
| None | WT AcrAB | 4 | 3 | — | — | — |
| None | Hi AcrAB | 16 | 15 | — | — | — |
| CmlA | ΔacrAB | 32 | — | 31 | — | — |
| CmlA | WT AcrAB | 64 | 3 | 31 | 128 | 64 |
| CmlA | Hi AcrAB | >128 | 15 | 31 | 512 | >128 |
| MdfA | ΔacrAB | 8 | — | 7 | — | — |
| MdfA | WT AcrAB | 16 | 3 | 7 | 32 | 16 |
| MdfA | Hi AcrAB | 128 | 15 | 7 | 128 | 128 |
MIC ratio = (MIC of chloramphenicol against the specified strain)/(MIC against the ΔacrAB strain expressing neither the CmlA nor the MdfA cytoplasmic membrane pump).
Efflux pump efficiencies for the outer membrane (ηo) were calculated from cint/cext = 1/(1 + ηo) according to equations 27 and 32, using the approximation that cint is approximately equal to the MIC of chloramphenicol against the ΔacrAB strain expressing neither the CmlA nor the MdfA cytoplasmic membrane pump and cext is approximately equal to the MIC of chloramphenicol against each of the AcrAB-expressing strains also not expressing CmlA or MdfA.
Efflux pump efficiencies for the cytoplasmic membrane (ηm) were calculated from cint/cext = 1/(1 + ηm) according to equations 28 and 32, using the approximation that cint is approximately equal to the MIC of chloramphenicol against the ΔacrAB strain expressing neither the CmlA nor the MdfA cytoplasmic membrane pump and cext is approximately equal to the MIC of chloramphenicol against the strain expressing either CmlA or MdfA in the ΔacrAB background.
MIC ratio values were predicted from equations 31 and 32 using the values of ηo and ηm estimated from the single-pump-expressing strains and shown in the table, and the approximation that the MIC against the specified strain is approximately equal to cext and that the MIC against the ΔacrAB strain expressing neither of the cytoplasmic membrane pumps is approximately equal to cint. The predicted MIC ratio is equal to 1 + ηo + ηm + ηo × ηm.
DISCUSSION
Relationship with previous work.
The derivation of the equations that describe the balance between the kinetics of passive inward permeation of a solute and the kinetics of bacterial growth (equations 14 to 17) is new. Also new is the similar derivation that shows the balance between passive inward permeation, active efflux, and bacterial growth (equations 22 to 24), which has allowed for the first time an explicit demonstration that the dilution of inwardly diffusing compound resulting from cell growth is negligible if a typical efflux pump is operating (leading to equation 25). The equations that describe the dependence of the cytoplasmic concentration of an inwardly diffusing solute on efflux pumping by pumps in parallel and/or series (Table 5) agree with analogous equations presented earlier (8). It was useful to re-present those equations here with a further analysis of their implications. Namely, because an efflux pump protects the membrane in which it is embedded, its effectiveness can be described by the novel parameter efflux efficiency, η, which is equal to k/P, where P applies only to the membrane across which the pump operates. Moreover, in the case of pumps in series or the equivalent case, in which pumps possess two binding sites, one in the cytoplasm and one in the periplasm (8), the efficiency of pumping across each membrane can be considered separately (i.e., by use of a different value of η per membrane) and then combined mathematically. The quantitative comparison between predictions of the model based on efflux pump efficiencies and measured MIC ratios between isogenic pump-expressing and nonexpressing strains (Table 7) is new.
Limitations of the model presented.
In mathematical modeling, it is helpful to understand the boundaries of the models, i.e., where the simplifying assumptions do not apply.
(i) Inhibition of growth.
First, in the analysis of growth versus inward diffusion of a novel compound in the absence of efflux described above, if that compound were to inhibit growth, then μ would decrease and a permeability coefficient lower than ∼1 × 10−8 cm · s−1 could still yield effective permeation (i.e., a cytoplasmic concentration approaching the external concentration within a reasonably short time); see equation 15.
(ii) Saturable efflux.
Second, efflux pumps show saturable kinetics (32, 33). Thus, at periplasmic and cytoplasmic concentrations of novel compounds that are higher than the concentration of solute that yields the half-maximal rate of efflux (K0.5), the efficiency of pumping is predicted to decrease. It is unlikely that novel compounds would be pumped out with low K0.5 values because there has been no evolutionary selection for specificity, although that could change, once a new compound has been introduced into clinical use. It is noted that even with β-lactam compounds, which are based on a naturally occurring pharmacophore, the range of concentrations over which the efflux rate was a linear function of concentration was up to 100 μM for cephalothin and 250 μM for cephaloridine (approximately 40 and 100 mg/liter, respectively; Table 4) (32). However, lower linear concentration ranges were noted for cefamandole and nitrocefin (up to 13 and 3 μM, respectively, or approximately 6 and 1.5 mg/liter, respectively; Table 4) (32). Interestingly, penicillins and 3 of the cephalosporins mentioned above displayed sigmoidal concentration-rate relationships for efflux (32, 33). That would mean that at low periplasmic concentrations of effluxed solute, the efficiency of efflux, η, would be lower than the efficiency of efflux at higher concentrations. As a final point on the assumption of the linearity of concentration-rate relationships, it is noted that nonspecific diffusion through the outer membrane of E. coli was not saturable for two probe compounds, ampicillin and benzylpenicillin (42), indicating that equation 1, which implicitly assumes that the rate of passive permeation is linearly related to the concentration difference between compartments, is likely to be valid at concentrations within the range of MICs typical of useful antibacterial agents (e.g., up to 16 mg/liter), while recognizing that maximum concentrations in vivo can be higher than that (for instance, in a study of subjects with different degrees of renal function, the mean maximum concentration of piperacillin in serum was up to 329 mg/liter following a bolus dose of 4 g [43]) and that MICs against resistant strains will also be higher. Likewise, it is already well established that nonspecific diffusion through phospholipid bilayers similar to those of bacterial cytoplasmic membranes behaves according to equation 1 (2, 19, 44). Nonetheless, it will be important to measure efflux kinetics and permeability coefficients for key compounds in synthetic antibacterial discovery programs, in order to determine whether the efflux pump K0.5 is in the range of antibacterially effective periplasmic and/or cytoplasmic concentrations and how strongly sigmoidal the relationship between the periplasmic or cytoplasmic concentration and the efflux rate is. This will be particularly important when the models outlined here are applied to medically important species, such as Pseudomonas aeruginosa or Acinetobacter baumannii, that have not been studied in as much detail as the experimentally more tractable species E. coli.
(iii) Saturable permeability.
At one time, it was thought that diffusion across the outer membrane through porin-mediated aqueous pores might be a saturable process, which would limit the range of concentrations of solute under which the fundamental equation (equation 1) would be applicable (45, 46). However, later studies reinterpreted the data to conclude that the transmembrane diffusion of test β-lactam compounds was indeed nonspecific (42, 47). Specificity of passive permeation across the outer membrane has been described, however. For example, the diffusion of solutes via pores formed by the LamB protein in E. coli requires a specific binding step (48). In drug discovery, designing antibacterial agents that cross the outer membrane via a specific diffusion channel is unlikely to be productive, first, because maintaining diffusion specificity while optimizing target site binding and all other drug-like properties (17) is likely to be too constraining and, second, because specific channels are likely to mutate specificity or expression, leading to resistance with little fitness cost (except in defined minimal medium). That is, the model presented here, whereby the permeability coefficient, P (equation 1), is not a function of the external or periplasmic solute concentration, is reasonable for new compounds likely to be synthesized and tested in antibacterial drug discovery programs.
(iv) Chemical reaction and binding or adsorption trapping.
The model presented here assumes the absence of a chemical reaction or significant binding or adsorption that removes compound from free solution on the diffusion pathway or in the cytoplasm. The presence of either of these processes could change the kinetics of diffusion considerably (13). For example, the kinetics of the establishment of a steady periplasmic concentration of a novel β-lactam might be modified by periplasmic β-lactamase activity (32).
(v) Other special cases.
As in most analyses of the mechanism of action of antibacterial compounds, the assumption has been made that the single bacterial cell is bathed in a homogeneous solution of the compound of interest. In infections, there are many other modes of existence for a bacterial cell. It might be living intracellularly (49), it might be in a biofilm or other multicell aggregate (50), or it might be growing relatively slowly owing to nutrient deprivation, including oxygen depletion, or to other mechanisms that cause infections to persist (51). In the first two of these situations, the permeation of compound to the bacterial cell surface might be compromised; the case of slow growth has already been analyzed, and other mechanisms of persistence involve switching to a nonsusceptible phenotype, interpreted to be unrelated to compound permeation, although that assumption appears not to have been tested experimentally (51). Furthermore, the analysis does not take into account differences in electric potential (Δψ) that exist across both the cytoplasmic membrane (52) and the outer membrane of Gram-negative bacteria (53). The effect of a transmembrane Δψ on the kinetics of passive permeation of an electrically charged solute across the outer membrane of Gram-negative bacteria has been analyzed only theoretically (54), although it has been demonstrated that a variation in the magnitude of the Donnan potential across the outer membrane of E. coli does not affect the permeability of porin-mediated channels to compounds generally (55). It is proposed that other physical properties of compounds, such as surface polarity, dipole moment, zwitterionic status, or lipophilicity, are taken into account in the model by the magnitude of the permeability coefficient, P. Similarly, the overall membrane permeability coefficient for a compound in a particular bacterial species incorporates whether the compound diffuses across the lipid bilayer, through one or more aqueous channels, or by a mixture of the two processes. As long as the permeation is driven by diffusion and not active transport, the end product of different mechanisms can be incorporated into the net passive flux coefficient, P.
The model presented here is not applicable to the special cases of self-promoted uptake of polycations (56, 57). It is difficult to envisage self-promoted routes of permeation being applicable to a novel series of putatively antibacterial compounds because multiple cationic substituents on a compound are likely to weaken specific binding to most physiological targets; except, perhaps, for binding to the sites on the ribosome where aminoglycosides bind (58). For antibacterial agents that cause misfolding of proteins, there is the theoretical possibility that they could increase or decrease their own permeability coefficient or decrease their own efflux (59), and this mechanism has been suggested for the observed self-increased energy-dependent uptake of aminoglycosides (60, 61). Similarly, inhibitors of lipopolysaccharide biosynthesis might increase the permeability of the outer membrane to lipophilic solutes (62, 63). The model does not explicitly account for such potential secondary modifications of permeability and efflux coefficients but does enable permeation time course predictions that would allow significantly deviating behavior to be recognized.
(vi) Applicability.
With careful thought about the details, the model presented here is expected to be adaptable to all the medically important Gram-negative and Gram-positive bacteria and a wide range of series of novel compounds with the foregoing provisos.
Conclusion.
For a novel compound to be likely to permeate into a Gram-negative or a Gram-positive bacterium, the cell envelope permeability coefficient should be approximately >10−8 cm2 · s−1. For a Gram-positive bacterium, the envelope permeability coefficient is similar to the phospholipid bilayer permeability coefficient, which can be measured in model systems. For Gram-negative bacteria, the lipid bilayer permeability coefficient is likely to dominate only for compounds of low enough molecular mass and high enough hydrophilicity to cross the outer membrane via water-filled pores (e.g., as a guide, ca. <500 g · mol−1 in E. coli, <1,400 g · mol−1 in P. aeruginosa, and <1,400 g · mol−1 in Haemophilus influenzae [reviewed in reference 2]), but the value is not exhaustively known for all Gram-negative bacterial pathogens, and it should be recognized that mutations selected by antibiotic exposure can change the permeability of the outer membrane to specific compounds in clinically isolated strains; e.g., the loss of production of OprD confers resistance to imipenem in P. aeruginosa (64). For compounds of higher molecular mass or for compounds that selectively pass only via a restricted number of channels, the permeability coefficient of the outer membrane for that compound might predominate (see equation 3).
If the overall permeation of a compound into the bacterial cytoplasm is only by passive diffusion, its internal concentration is predicted eventually to reach a steady value in which influx is balanced by intracellular dilution resulting from growth. However, if an efflux pump accepts the solute in question as a substrate, the absolute values of both the permeability coefficient and the pump's kinetic coefficient become important. In that new balance, it is the permeability coefficient for the membrane that the pump traverses that is relevant. A potentially helpful parameter, the efficiency of a given pump, η, can be summarized as η = k/P, which applies to the membrane and solute in question. If the pump is efficient and k is ≫P, the ratio between the internal and external concentrations of solute is predicted to approach 1/η = P/k (from equation 25), as long as the absolute internal concentration is not so high as to saturate the pump.
There is a clear need in antibacterial drug discovery for the measurement of the permeability and efflux coefficients of novel compounds across both the outer membrane and the cytoplasmic membrane in the case of Gram-negative bacteria. Measurement of only one of these two kinetic parameters, especially if for only one of the membranes, is predicted not to lead to an adequate understanding of the physical properties and structure-activity relationships that govern overall penetration to the target site, whether that be in the cytoplasm or in the periplasm. The MIC ratio or efflux ratio, as analyzed in Table 7, might serve as a surrogate for the estimation of efflux efficiencies using a panel of carefully constructed single- and multiple-pump-expressing bacterial strains (37, 39).
ACKNOWLEDGMENTS
Thanks are expressed to T. J. Dougherty, M. Pucci, and L. Silver for discussions.
REFERENCES
- 1.Buurman ET, Laganas VA, Liu CF, Manchester JL. 2012. Antimicrobial activity of adenine-based inhibitors of NAD+-dependent DNA ligase. Med Chem Lett 3:663–667. doi: 10.1021/ml300169x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nichols WW. 2012. Permeability of bacteria to antibacterial agents, p 849–879. In Dougherty TJ, Pucci MJ (ed), Antibiotic discovery and development, vol II Springer Publishing Company, New York, NY. [Google Scholar]
- 3.Nikaido H. 2003. Molecular basis of bacterial outer membrane permeability revisited. Microbiol Mol Biol Rev 67:593–656. doi: 10.1128/MMBR.67.4.593-656.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Collander R. 1954. The permeability of Nitella cells to non-electrolytes. Physiol Plant 7:420–445. doi: 10.1111/j.1399-3054.1954.tb07589.x. [DOI] [Google Scholar]
- 5.Camenisch G, Alsenz J, van de Waterbeemd H, Folkers G. 1998. Estimation of permeability by passive diffusion through Caco-2 cell monolayers using the drugs' lipophilicity and molecular weight. Eur J Pharm Sci 6:313–319. [PubMed] [Google Scholar]
- 6.Nikaido H, Thanassi DG. 1993. Penetration of lipophilic agents with multiple protonation sites into bacterial cells: tetracyclines and fluoroquinolones as examples. Antimicrob Agents Chemother 37:1393–1399. doi: 10.1128/AAC.37.7.1393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sigler A, Schubert P, Hillen W, Niederweis M. 2000. Permeation of tetracyclines through membranes of liposomes and Escherichia coli. Eur J Biochem 277:527–534. [DOI] [PubMed] [Google Scholar]
- 8.Palmer M. 2003. Efflux of cytoplasmically acting antibiotics from Gram-negative bacteria: periplasmic substrate capture by multicomponent efflux pumps inferred from their cooperative action with single-component transporters. J Bacteriol 185:5287–5289. doi: 10.1128/JB.185.17.5287-5289.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nikaido H, Pagès JM. 2012. Broad specificity efflux pumps and their role in multidrug resistance of Gram-negative bacteria. FEMS Microbiol Rev 36:340–363. doi: 10.1111/j.1574-6976.2011.00290.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Redish EF. 2016. Analysing the competency of mathematical modelling in physics. Cornell University Library, Ithaca, NY: https://arxiv.org/abs/1604.02966. Accessed 18 February 2017. [Google Scholar]
- 11.Cha PD, Rosenberg JJ, Dym CL. 2000. Fundamentals of modeling and analysing engineering systems, p 1–11. In Fundamental concepts in mathematical modeling. Cambridge University Press, Cambridge, United Kingdom. [Google Scholar]
- 12.Tempest DW. 1978. Dynamics of bacterial growth. In Norris JR, Richmond MH (ed), Essays in microbiology. John Wiley & Sons, Chichester, United Kingdom. [Google Scholar]
- 13.Nichols WW, Evans MJ, Slack MPE, Walmsley HL. 1989. Diffusion of antibiotics into aggregates of mucoid and non-mucoid Pseudomonas aeruginosa. J Gen Microbiol 135:1291–1303. [DOI] [PubMed] [Google Scholar]
- 14.Stewart PS. 2003. Diffusion in biofilms. J Bacteriol 185:1485–1491. doi: 10.1128/JB.185.5.1485-1491.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vesselinova N, Alexandrov BS, Wall ME. 2016. Dynamical model of drug accumulation in bacteria: sensitivity analysis and experimentally testable predictions. PLoS One 11:e0165899. doi: 10.1371/journal.pone.0165899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.The Pew Charitable Trusts. 2016. A scientific roadmap for antibiotic discovery. The Pew Charitable Trusts, Philadelphia, PA: http://www.pewtrusts.org/antibiotic-discovery Accessed 26 February 2017. [Google Scholar]
- 17.Basarab GS, Eakin AE, Nichols WW. 2014. Design of antibacterial agents, p 611–626. In Tang Y-W, Sussman M, Liu D, Poxton I, Schwartzman J (ed), Molecular medical microbiology, 2nd ed Academic Press, New York, NY. [Google Scholar]
- 18.Tommasi R, Brown DG, Walkup GK, Manchester JI, Miller AA. 2015. ESKAPEing the labyrinth of antibacterial discovery. Nat Rev Drug Discov 14:529–542. doi: 10.1038/nrd4572. [DOI] [PubMed] [Google Scholar]
- 19.Lieb WR, Stein WD. 1986. Simple diffusion across the membrane bilayer, p 69–112. In Stein WD. (ed), Transport and diffusion across cell membranes. Academic Press, New York, NY. [Google Scholar]
- 20.Zimmermann W, Rosselet A. 1977. Function of the outer membrane of Escherichia coli as a permeability barrier to β-lactam antibiotics. Antimicrob Agents Chemother 12:368–372. doi: 10.1128/AAC.12.3.368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Snyder DS, McIntosh TJ. 2000. The lipopolysaccharide barrier: correlation of antibiotic susceptibility with antibiotic permeability and fluorescent probe kinetics. Biochemistry 39:11777–11787. doi: 10.1021/bi000810n. [DOI] [PubMed] [Google Scholar]
- 22.Hill AV. 1928. The diffusion of oxygen and lactic acid through tissues. Proc R Soc B 104:39–96. doi: 10.1098/rspb.1928.0064. [DOI] [Google Scholar]
- 23.Brodin B, Steffansen B, Nielsen CU. 2010. Passive diffusion of drug substances: the concepts of flux and permeability, p 135–152. In Steffansen B, Brodin B, Nielsen CU (ed), Molecular biopharmaceutics. Pharmaceutical Press, London, United Kingdom. [Google Scholar]
- 24.International Organization for Standardization. 2006. Clinical laboratory testing and in vitro diagnostic test systems—susceptibility testing of infectious agents and evaluation of performance of antimicrobial susceptibility test devices. Part 1 Reference method for testing the in vitro activity of antimicrobial agents against rapidly growing aerobic bacteria involved in infectious diseases. ISO 20776-1:2006 International Organization for Standardization, Geneva, Switzerland. [Google Scholar]
- 25.Demchick P, Koch AL. 1996. The permeability of the wall fabric of Escherichia coli and Bacillus subtilis. J Bacteriol 178:768–773. doi: 10.1128/jb.178.3.768-773.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Stein WD. 1986. Thermodynamics and kinetics of the diffusion process, p 35–46. In Stein WD. (ed), Transport and diffusion across cell membranes. Academic Press, New York, NY. [Google Scholar]
- 27.Kreysig E. 1983. Advanced engineering mathematics, p 28–29. John Wiley & Sons, Inc, New York, NY. [Google Scholar]
- 28.Gualtieri M, Banéres-Roquet F, Villain-Guillot P, Pugnière M, Leonetti J-P. 2009. The antibiotics in the chemical space. Curr Med Chem 16:390–393. doi: 10.2174/092986709787002628. [DOI] [PubMed] [Google Scholar]
- 29.Macielag MJ. 2012. Chemical properties of antimicrobials and their uniqueness, p 793–820. In Dougherty TJ, Pucci MJ (ed), Antibiotic drug discovery and development, vol II Springer Publishing Company, New York, NY. [Google Scholar]
- 30.O'Shea R, Moser HE. 2008. Physichochemical properties of antibacterial compounds: implications for drug discovery. J Med Chem 51:2871–2878. doi: 10.1021/jm700967e. [DOI] [PubMed] [Google Scholar]
- 31.Lomovskaya O, Watkins W. 2001. Efflux pumps: their role in antibacterial drug discovery. Curr Med Chem 8:1699–1711. doi: 10.2174/0929867013371743. [DOI] [PubMed] [Google Scholar]
- 32.Nagano K, Nikaido H. 2009. Kinetic behavior of the major multidrug efflux pump AcrB of Escherichia coli. Proc Natl Acad Sci U S A 106:5854–5858. doi: 10.1073/pnas.0901695106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lim SP, Nikaido H. 2010. Kinetic parameters of efflux of penicillins by the multidrug efflux transporter AcrAB-TolC of Escherichia coli. Antimicrob Agents Chemother 54:1800–1806. doi: 10.1128/AAC.01714-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Goutelle S, Maurin M, Rougier F, Barbaut X, Bourguignon L, Ducher M, Maire P. 2008. The Hill equation: a review of its capabilities in pharmacological modelling. Fundam Clin Pharmacol 22:633–648. doi: 10.1111/j.1472-8206.2008.00633.x. [DOI] [PubMed] [Google Scholar]
- 35.Nikaido H. 2005. Restoring permeability barrier function to outer membrane. Chem Biol 12:507–509. [DOI] [PubMed] [Google Scholar]
- 36.Li X-Z, Plésiat P, Nikaido H. 2015. The challenge of efflux-mediated antibiotic resistance in Gram-negative bacteria. Clin Microbiol Rev 28:337–418. doi: 10.1128/CMR.00117-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lee A, Mao W, Warren MS, Mistry A, Hoshino K, Okumura R, Ishida H, Lomovskaya O. 2000. Interplay between efflux pumps may provide either additive or multiplicative effects on drug resistance. J Bacteriol 182:3142–3150. doi: 10.1128/JB.182.11.3142-3150.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Masuda N, Sakagawa E, Ohya S, Gotoh N, Tsujimoto H, Nishino T. 2000. Substrate specificities of MexAB-OprM, MexCD-OprJ, and MexXY-OprM efflux pumps in Pseudomonas aeruginosa. Antimicrob Agents Chemother 44:3322–3327. doi: 10.1128/AAC.44.12.3322-3327.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Manchester JI, Buurman ET, Bisacchi GS, McLaughlin RE. 2012. Molecular determinants of AcrB-mediated bacterial efflux implications for drug discovery. J Med Chem 55:2532–2537. doi: 10.1021/jm201275d. [DOI] [PubMed] [Google Scholar]
- 40.Nichols WW. 1988. Towards a fundamental understanding of the MIC of β-lactam antibiotics. J Antimicrob Chemother 22:275–283. doi: 10.1093/jac/22.3.275. [DOI] [PubMed] [Google Scholar]
- 41.Lakaye B, Dubus A, Lepage S, Groslambert S, Frère JM. 1999. When drug inactivation renders the target irrelevant to antibiotic resistance: a case story with β-lactams. Mol Microbiol 31:89–101. doi: 10.1046/j.1365-2958.1999.01150.x. [DOI] [PubMed] [Google Scholar]
- 42.Kojima S, Nikaido H. 2013. Permeation rates of penicillins indicate that Escherichia coli porins function principally as nonspecific channels. Proc Natl Acad Sci U S A 110:E2629–E2634. doi: 10.1073/pnas.1310333110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Welling PG, Craig WA, Bundtzen RW, Kwok FW, Gerber AU, Madsen PO. 1983. Pharmacokinetics of piperacillin in subjects with various degrees of renal function. Antimicrob Agents Chemother 23:881–887. doi: 10.1128/AAC.23.6.881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Stein WD. 1997. Kinetics of the multidrug transporter (P-glycoprotein) and its reversal. Physiol Rev 77:545–590. [DOI] [PubMed] [Google Scholar]
- 45.Hewinson RG, Lane DC, Slack MPE, Nichols WW. 1986. The permeability parameter of the outer membrane of Pseudomonas aeruginosa varies with the concentration of a test substrate, cephalosporin C. J Gen Microbiol 132:27–33. [DOI] [PubMed] [Google Scholar]
- 46.James CE, Mahendran KR, Molitor A, Bolla JM, Bessonov AN, Winterhalter M, Pagès JM. 2009. How β-lactam antibiotics enter bacteria: a dialogue with the porins. PLoS One 4:e5453. doi: 10.1371/journal.pone.0005453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Nichols WW. 1987. The time course of hydrolysis of a β-lactam antibiotic by intact Gram-negative bacteria possessing a periplasmic β-lactamase. Biochem J 244:509–513. doi: 10.1042/bj2440509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Benz R, Schmid A, Vos-Scheperkeuter GH. 1987. Mechanism of sugar transport through the sugar-specific LamB channel of Escherichia coli outer membrane. J Membr Biol 100:21–29. doi: 10.1007/BF02209137. [DOI] [PubMed] [Google Scholar]
- 49.Buyck J, Luyckx C, Muccioli G, Krause K, Nichols WW, Tulkens P, Van Bambeke F. 2017. Pharmacodynamics of ceftazidime-avibactam against extracellular and intracellular forms of Pseudomonas aeruginosa. J Antimicrob Chemother 72:1400–1409. doi: 10.1093/jac/dkw587. [DOI] [PubMed] [Google Scholar]
- 50.Lebeaux D, Ghigo JM, Beloin C. 2014. Biofilm-related infections: bridging the gap between clinical management and fundamental aspects of recalcitrance toward antibiotics. Microbiol Mol Biol Rev 78:510–543. doi: 10.1128/MMBR.00013-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Grant SS, Hung DT. 2013. Persistent bacterial infections, antibiotic tolerance, and the oxidative stress response. Virulence 4:273–283. doi: 10.4161/viru.23987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Krulwich TA, Sachs G, Padan E. 2011. Molecular aspects of bacterial pH sensing and homeostasis. Nat Rev Microbiol 9:330–343. doi: 10.1038/nrmicro2549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Stock JB, Rauch B, Roseman S. 1977. Periplasmic space in Salmonella typhimurium and Escherichia coli. J Biol Chem 252:7850–7861. [PubMed] [Google Scholar]
- 54.Nichols WW, Hewinson RG, Slack MPE, Walmsley HL. 1985. Estimation of the permeability parameter (C) for the flux of a charged molecule across the Gram-negative outer membrane. Biochem Soc Trans 13:697–698. doi: 10.1042/bst0130697. [DOI] [Google Scholar]
- 55.Sen K, Hellman J, Nikaido H. 1988. Porin channels in intact cells of Escherichia coli are not affected by Donnan potentials across the outer membrane. J Biol Chem 263:1182–1187. [PubMed] [Google Scholar]
- 56.Epand RM, Epand RF. 2009. Lipid domains in bacterial membranes and the action of antimicrobial agents. Biochim Biophys Acta 1788:289–294. doi: 10.1016/j.bbamem.2008.08.023. [DOI] [PubMed] [Google Scholar]
- 57.Delcour AH. 2009. Outer membrane permeability and antibiotic resistance. Biochim Biophys Acta 1794:808–816. doi: 10.1016/j.bbapap.2008.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Borovinskaya MA, Pai RD, Zhang W, Schuwirth BS, Holton JM, Hirokawa G, Kaji H, Kaji A, Cate JH. 2007. Structural basis for aminoglycoside inhibition of bacterial ribosome recycling. Nat Struct Mol Biol 14:727–732. doi: 10.1038/nsmb1271. [DOI] [PubMed] [Google Scholar]
- 59.Bednarska NG, Schymkowitz J, Rousseau F, Van Eldere J. 2013. Protein aggregation in bacteria: the thin boundary between functionality and toxicity. Microbiology 159:1795–1806. doi: 10.1099/mic.0.069575-0. [DOI] [PubMed] [Google Scholar]
- 60.Taber HW, Mueller JP, Miller PF, Arrow AS. 1987. Bacterial uptake of aminoglycoside antibiotics. Microbiol Rev 51:439–457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Scholar EM, Pratt WB. 2000. Bactericidal inhibitors of protein synthesis. The aminoglycosides, p 127–158. In Scholar EM, Pratt WB (ed), The antimicrobial drugs, 2nd ed Oxford University Press, Oxford, United Kingdom. [Google Scholar]
- 62.Zhang G, Meredith TC, Kahne D. 2013. On the essentiality of lipopolysaccharide to Gram-negative bacteria. Curr Opin Microbiol 16:779–785. doi: 10.1016/j.mib.2013.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.May JM, Sherman DJ, Simpson BW, Ruiz N, Kahne D. 2015. Lipopolysaccharide transport to the cell surface: periplasmic transport and assembly into the outer membrane. Philos Trans R Soc Lond B Biol Sci 370:20150027. doi: 10.1098/rstb.2015.0027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Livermore DM. 2002. Multiple mechanisms of antimicrobial resistance in Pseudomonas aeruginosa: our worst nightmare? Clin Infect Dis 34:634–640. doi: 10.1086/338782. [DOI] [PubMed] [Google Scholar]
- 65.Goldman RC, Capobianco JO. 1990. Role of an energy-dependent efflux pump in plasmid pNE24-mediated resistance to 14- and 15-membered macrolides in Staphylococcus epidermidis. Antimicrob Agents Chemother 34:1973–1980. doi: 10.1128/AAC.34.10.1973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Beveridge TJ. 2000. Ultrastructure of Gram-positive cell walls, p 3–11. In Fischetti VA, Novick RP, Ferretti JJ, Portnoy DA, Rood JI (ed), Gram-positive pathogens. ASM Press, Washington DC. [Google Scholar]
- 67.Sundararaj S, Guo A, Habibi-Nazhad B, Rouani M, Stothard P, Ellison M, Wishart DS. 2004. The CyberCell Database (CCDB): a comprehensive, self-updating, relational database to coordinate and facilitate in silico modeling of Escherichia coli. Nucleic Acids Res 32(Database issue):D293–D295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Smit J, Kamio Y, Nikaido H. 1975. Outer membrane of Salmonella typhimurium: chemical analysis and freeze-fracture studies with lipopolysaccharide mutants. J Bacteriol 124:942–958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Kashket ER. 1981. Effects of aerobiosis and nitrogen source on the proton motive force in growing Escherichia coli and Klebsiella pneumoniae cells. J Bacteriol 146:377–384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Duncan JL, Cho GJ. 1971. Production of staphylococcal alpha toxin. I. Relationship between cell growth and toxin formation. Infect Immun 4:456–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Xiang T-X, Anderson BD. 1994. The relationship between permeant size and permeability in lipid bilayer membranes. J Membr Biol 140:111–122. [DOI] [PubMed] [Google Scholar]
- 72.Bean RC, Shepherd WC, Chan H. 1968. Permeability of lipid bilayer membranes to organic solutes. J Gen Physiol 52:495–508. doi: 10.1085/jgp.52.3.495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Chakrabarti AC, Deamer DW. 1992. Permeability of lipid bilayers to amino acids and phosphate. Biochim Biophys Acta 1111:171–177. doi: 10.1016/0005-2736(92)90308-9. [DOI] [PubMed] [Google Scholar]
- 74.Deamer DW, Bramhall J. 1986. Permeability of lipid bilayers to water and ionic solutes. Chem Phys Lipids 40:167–188. doi: 10.1016/0009-3084(86)90069-1. [DOI] [PubMed] [Google Scholar]
- 75.Hauser H, Oldani D, Phillips MC. 1973. Mechanism of ion escape from phosphatidylcholine and phosphatidylserine single bilayer vesicles. Biochemistry 12:4507–4517. [DOI] [PubMed] [Google Scholar]