Using Multi-Order Time Correlation Functions (TCFs) to Elucidate Biomolecular Reaction Pathways from Microsecond Single-Molecule Fluorescence Experiments

Abstract

Recent advances in single-molecule fluorescence imaging have made it possible to perform measurements on microsecond time scales. Such experiments have the potential to reveal detailed information about conformational changes in biological macromolecules, including the reaction pathways and dynamics of the rearrangements involved in processes such as sequence-specific DNA ‘breathing’ and the assembly of protein-nucleic acid complexes. Because microsecond resolved single-molecule trajectories often involve ‘sparse’ data – i.e., they contain relatively few data points per unit time – they cannot be easily analyzed using the standard protocols that were developed for single-molecule experiments carried out with tens-of-millisecond time resolution and high ‘data density.’ We here describe a generalized approach, based on time correlation functions (TCFs), to obtain kinetic information from microsecond-resolved single-molecule fluorescence measurements. This approach can be used to identify short-lived intermediates that lie on reaction pathways connecting relatively long-lived reactant and product states. As a concrete illustration of the potential of this methodology for analyzing specific macromolecular systems, we accompany the theoretical presentation with a description of a specific biologically-relevant example drawn from studies of the reaction mechanisms of the assembly of the single-stranded DNA binding protein of the T4 bacteriophage replication complex onto a model DNA replication fork.

I. Introduction

During the past several years, significant advances have been made in the use of single-molecule fluorescence methods to monitor conformational changes in the structure and dynamics of fluorescently labeled macromolecular systems. Such studies can provide detailed information about the assembly and function of protein-DNA complexes.^1–9 The recent development of sub-millisecond (tens-of-microseconds) single-molecule Förster resonance energy transfer (smFRET) experiments has opened the possibility to study relatively fast macromolecular processes, such as DNA ‘breathing’ and its role in the regulation of biochemical reactions,^{2, 10–11} which cannot be resolved on the time scales of most current single-molecule methods (~100 milliseconds). DNA breathing involves the thermal activation of segments of duplex DNA to form short-lived local ‘bubble-like’ states. Such locally disordered regions of DNA are thought to function as transient, secondary-structural motifs that can be bound by regulatory proteins as intermediate steps in the assembly and function of DNA-protein complexes. Microsecond-resolved smFRET experiments have the potential to reveal the mechanisms by which DNA-associated proteins can ‘harvest’ such specific thermally populated states in the course of carrying out reactions involved in the processes of genome expression.

Fast detection techniques, such as phase-synchronous single-photon-counting methods, can provide time-resolved data with tens-of-microsecond resolution.² Such experiments rapidly detect individual fluorescence photons from a single molecule, and store information about the intervening time intervals and optical phase conditions associated with each detection event. Even under optimal conditions, microsecond-resolved single-molecule fluorescence experiments produce ‘sparse’ data sets, because the average interval between successively detected signal photons can greatly exceed the experimental time resolution. In order to extract sub-millisecond kinetic information from sparse data sets, certain experimental challenges must be overcome. For example, transient intermediates may be difficult to detect due to the limited signal integration period. Under such low-signal conditions, the signal-to-noise (S/N) ratio is often too small to construct single-molecule trajectories in which transitions between distinct ‘states’ can be unambiguously identified and state-to-state transition ‘pathways’ can be visualized. Thus, the analysis of sparse trajectories must be carried out in non-standard ways.

In this paper, we show how mechanistic information can be obtained from microsecond single-molecule fluorescence experiments by applying generalized concepts of time correlation functions (TCFs).^12–21 TCFs provide a statistically meaningful way to characterize the time scales of stochastically fluctuating biochemical systems. Moreover, the time resolution of single molecule experiments can be maximized using TCFs, as demonstrated by Scherer and co-workers.²² By correlating the fluctuations of individual molecules as a function of time, one can learn about the pathways connecting the conformational states that are accessible to the system at equilibrium. A commonly used approach to analyze single-molecule trajectories is to directly visualize the transition steps within a finite data set by fitting to a so-called hidden Markov model (HMM).²³ When utilized to their full advantage, TCFs constructed as a function of multiple time intervals can, in principle, provide more accurate and detailed information than HMM analyses.

In optimal situations, one can obtain several pieces of information from the analysis of single-molecule trajectories: (i) the number of conformational states reported by an experimental observation (such as a FRET measurement); (ii) the values of the observables associated with each state; and (iii) kinetic parameters associated with the inter-conversion between the states. When the experimental signal is especially noisy, as is the case for microsecond-resolved smFRET experiments, the application of HMM methods is inadequate to determine the above information. In contrast, TCFs provide an excellent approach to analyze the microsecond kinetics of macromolecular conformational transitions.

The situation can be described using the theory of Markov chains.²⁴ We assume that the instantaneous state of the system is mapped onto an experimentally accessible stochastic variable A(t) that can be measured at discrete times. The distribution of A is characterized by its moments, and the time-dependent moments are the TCFs. In general, the n^th-order TCF, C⁽ⁿ⁾(τ₁, τ₂, …, τ_n−1), can be written as the average product of n successive observations 〈A(t₁)A(t₂) … A(t_n)〉, which depends on the n − 1 time intervals τ₁ = t₂ − t₁, τ₂ = t₃ − t₂, …, τ_n−1 = t_n − t_n−1. The complexity of information that is potentially available from a TCF depends on its order. For example, the 2^nd-order (two-point) TCF, C⁽²⁾(τ) = 〈A(t₁)A(t₂)〉, is the average product of two successive observations written as a function of the time interval τ = t₂ − t₁. The 2^nd-order TCF thus describes the average loss (or gain) in correlation of A over time, which can be used to obtain the average time scales of the fluctuations of the system. Nevertheless, 2^nd-order TCFs do not provide information about ‘transition pathways’ – that is, whether a particular state-to-state transition must follow or precede another, or whether two such transitions occur independently. Such information is available through a higher-order TCF analysis. In the analysis that follows, we skip over 3^rd-order TCFs and focus on the 4^th-order (four-point) TCFs C⁽⁴⁾(τ₁, τ₂, τ₃), because the latter contain more information and can handle reaction pathways that include a larger number of elementary steps. In principle, even higher-order TCFs (e.g., 5^th-, 6^th-order, etc.) could be employed, although this would require increasingly complex analyses that become more difficult due to the S/N limitations of finite data sets. We show, by performing a global analysis that includes 4^th-order TCFs, that it is possible to characterize fundamental time scales of the system, including intervening (exchange) times that might be associated with short-lived chemical intermediates.

In addition, 4^th-order TCFs are widely applied in molecular spectroscopy, such as two-dimensional (2D) NMR, 2D infra-red and 2D electronic spectroscopy.^25–26 For example, the nonlinear optical response of a molecule can be formulated in terms of the 4^th-order TCFs of the appropriately defined transition dipole moment operator.²⁵ 4^th-order TCFs have also been applied to study the stochastic microscopic fluctuations of complex chemical systems,^20–21 including protein reaction dynamics,¹⁴ protein diffusion in solution,^15–16 liquid polymer diffusion,^{17, 27} and protein conformation fluctuations in Molecular Dynamics (MD) simulations.¹⁸

In spite of their advantages, higher-order TCFs have not been previously used to study conformational transition pathways of biological macromolecules. This may be because the underlying concepts of TCFs are relatively abstract, and there are few sources on this topic that are accessible to a general scientific audience. Here we seek to demonstrate the utility of TCFs to extract mechanistic information from single-molecule fluorescence experiments. We show that by using TCFs of sufficiently high order, it is possible to distinguish between macromolecular binding pathways of varying levels of complexity.

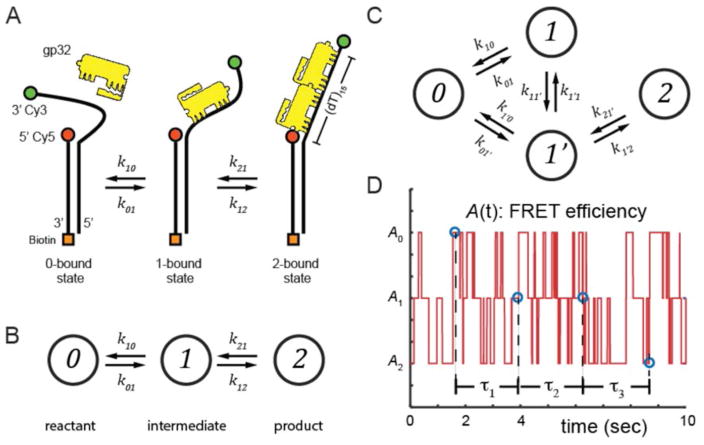
In a recent study from our laboratory,⁸ smFRET experiments were employed to analyze the cooperative binding of the single-stranded (ss) DNA binding protein of the T4 bacteriophage DNA replication complex (gp32) to single-stranded segments of primer-template (p/t) DNA constructs of varying lengths and polarities. These constructs can serve as models of DNA replication forks. Throughout this paper, we use a particular model experiment based on this study as an explicit molecular illustration of the principles and approaches developed in our analysis. As background, we note that gp32 protein molecules bind cooperatively and preferentially to ssDNA, with a binding site size of 7 nucleotide residues (nts, or DNA lattice positions) per gp32 molecule.²⁸ We have shown⁸ that p/t DNA substrates with a ssDNA ‘tail’ region of 15 nts in length, which can cooperatively bind up to two gp32 proteins, can undergo stochastic fluctuations between 0-, 1- and 2-bound states (see Fig. 1A). In these experiments the ssDNA tail region was labeled on opposite ends with a FRET donor-acceptor chromophore pair that moves to longer inter-dye distances as gp32 molecules bind between them and thus increase the rigidity of the intervening ssDNA sequence. As a consequence, the sequential binding of gp32 molecules to the ssDNA tail can be monitored by tracking the changes in the FRET signal, as discussed further below.

Figure 1.

(A) A hypothetical 3-state reaction scheme for the ssDNA binding protein gp32, which can bind up to two proteins to the p(dT)₁₅ ‘tail’ region of a p/t DNA construct. FRET donor and acceptor chromophores (depicted as green and red circles) label the 3′ end of the ssDNA region and the p/t junction, respectively. The gp32 protein is shown in yellow. (B) The 0-, 1- and 2-bound states of the N = 3 system shown in Panel (A) are depicted as a linear reaction scheme, in which the reactant (state-0) and product (state-2) are coupled by a single intermediate (state-1). (C) The reaction is depicted as an N = 4 system, in which the conformational end-states are inter-connected by a ‘non-productive’ intermediate (state-1) and a ‘productive’ intermediate (state-1′). Stochastic transitions from state-i to state-j occur with probabilities determined by the rate constants k_ij, where i, j ∈ {0,1, …, N − 1}. (D) A simulated trajectory of the stochastic variable A(t) is shown for the N = 3 system. Here we have assigned the three states to the resolvable values A₀ = 0.8, A₁ = 0.5, and A₂ = 0.2, and we have used the transition rates k₀₁ = k₂₁ = 5 s⁻¹, and k₀₁ = k₁₂ = 10 s⁻¹. An example of a four-point sequence of data points are shown corresponding to the time intervals τ₁, τ₂, and τ₃. Figure partially adapted from reference 28.

While such experiments could detect the presence of distinct conformational sub-states of the ssDNA involved in association / dissociation events, the time-resolution of the experiments described in Lee et al.⁸ (~100 ms) was not sufficient to determine either the lifetimes of the short-lived singly-bound intermediates, or to directly observe their conversions to longer-lived end-states. Nevertheless, this model system can serve as a concrete illustration of the potential uses of the theoretical approaches developed here. We are currently applying these TCF methods to analyze new microsecond-resolved single-molecule experiments on this gp32 binding system.

II. Conformational Transition Pathways and the Role of Intermediates

We consider an equilibrium system composed of N discrete microscopic states. At any instant, the system can undergo a transition from state-i to state-j where i,j ∈ {0,1,…, N −1}. We assume that there exists an experimentally accessible stochastic variable A(t) that is coupled to the conformation of the system. For example, A might be a fluorescence signal from a single fluorophore or a collective signal from a FRET donor-acceptor pair that site-specifically labels a biological macromolecular complex and is sensitive to its local conformation or to a similar reaction coordinate. When the system occupies state-i, the variable A assumes a corresponding value A_i.

As indicated above, we illustrate our approach using the macromolecular system studied by Lee et al.,⁸ in which a ssDNA template interacts with the T4 bacteriophage gp32 binding protein (see Fig. 1A). The N = 3 reaction scheme (shown in Fig. 1B) is the simplest possible to describe the p(dT)₁₅-(gp32)_n system (with n = 0, 1, or 2), which involves 0-, 1- and 2-bound gp32 molecule states. Since the gp32 protein occludes 7 nts on the ssDNA template, there are nine possible binding conformations available to the 1-bound state (e.g., at positions 1 – 7, 2 – 8, …, and 9 – 15). This simplest model treats all 1-bound states as experimentally indistinguishable species that may lie on the accessible pathway connecting the reactant 0-bound state to the product 2-bound state. In this reaction scheme, we do not indicate direct transitions between 0- and 2-bound states, since it is known that gp32 does not directly bind to ssDNA as a dimer.²⁹

Despite the appealing simplicity of the N = 3 scheme (Fig. 1B) for the p(dT)₁₅-(gp32)_n system, further consideration suggests that this mechanism cannot provide an adequate description of this gp32-binding model system because all of the 1-bound states on the 15 nts ssDNA ‘tail’ lattice cannot be treated as identical. Rather there are a number of ways in which a gp32 monomer might initially bind to the ssDNA template that would partially occlude the second binding site of 7 contiguous unoccupied nts, which is required to allow a second gp32 monomer to bind to the ssDNA tail of the p/t construct.³⁰ Such 1-bound states that ‘overlap’ the potential second binding site represent ‘unproductive’ intermediates, and thus inhibit transitions between the 0-bound and 2-bound states. Clearly, the first gp32 protein can bind productively only at the four possible positions (1 – 7, 2 – 8, 8 – 14 or 9 – 15) to allow the ssDNA ‘tail’ sequence to retain a contiguous (7 nts) binding site that can accommodate a second gp32 monomer.³¹ These latter 1-bound states would function as ‘productive’ intermediates through which the 0-bound state can undergo transitions to the 2-bound states. The kinetics of a model of this type can be diagramed using the N = 4 scheme shown in Fig. 1C, in which we have labeled the ‘unproductive’ and ‘productive’ intermediates as state-1 and state-1′, respectively.

As pointed out above, the binding states of the ssDNA-(gp32)_n system and their inter-conversion pathways can be studied using smFRET techniques.⁸ In the experiments by Lee et al.,⁸ which were performed using 100-ms time resolution, only two states – a 0-bound state and a 2-bound state – could be unambiguously observed, although indirect evidence for the existence of short-lived 1-bound states was also obtained. These results suggested that 1-bound states are present, but are too short-lived to be resolved in experiments conducted at 100-ms resolution. Because gp32 binding to ssDNA is known to be highly cooperative, 1-bound states are expected to be unstable in comparison to 2-bound states. A reasonable model for the assembly mechanism of the system might involve an initial singly bound gp32 molecule that either rapidly recruits a second gp32 protein to the ssDNA lattice to form a high affinity (cooperatively bound) dimer of gp32 molecules, or that rapidly dissociates from the ssDNA lattice. The relative probabilities of these competing scenarios should depend in part on the location of the initially bound gp32 protein, as described by the four state scheme of Fig. 1C. Indeed, a common situation for many single-molecule experiments is that intermediates can be very short-lived, and their observed signals might be degenerate. An idealized stochastic smFRET trajectory for the N = 3 scheme is shown in Fig. 1D, in which case A₀, A₁ and A₂ are the values of the observable A(t) when the system is in states 0, 1 or 2, respectively.

To fully appreciate the kinetics of the ssDNA-(gp32)_n system, one must properly account for the short-lived 1-bound intermediates, which may well give rise to indistinguishable signals. Experimentally, this requires making measurements at a higher time resolution than that used in the Lee et al. study.⁸ As the time resolution of a single-molecule fluorescence measurement approaches a few milliseconds, the signal will necessarily become too noisy to extract the state of the system through direct visualization of single-molecule trajectory data (e.g., by HMM analysis). Rather, we show below how equivalent information may be obtained through the application of the generalized concepts of TCFs.

III. Definitions of 2^nd- and 4^th-Order Time Correlation Functions

The 2^nd-order TCF of A is the average product of two successive measurements, made at times t₁ and t₂, which are separated by the interval τ = t₂ − t₁

$$C^{(2)}(\tau )=\langle A(0)A(\tau )\rangle .$$ (1)

In Eq. (1), the angle brackets denote that the average has been performed over all possible starting times, according to $C^{(2)}(\tau )={\int }_{-\infty }^{\infty }A(t)A(t+\tau )dt$. If the longest relaxation time of the system exceeds the duration of an individual data set, then the average two-point product is additionally integrated over a large number of single-molecule data sets. For a stochastic chemical system, C⁽²⁾(τ) decays from its maximum value 〈A²〉 at τ = 0 to its asymptotic minimum 〈A〉² in the limit τ → ∞. For this reason, we define the fluctuation δA(t) = A(t) − 〈A〉, and its TCF:

$${\overline{C}}^{(2)}(\tau )=\langle \delta A(0)\delta A(\tau )\rangle =\langle A(0)A(\tau )\rangle -{\langle A\rangle }^2$$ (2)

The TCF C̄⁽²⁾(τ) defined by Eq. (2) decays from its maximum 〈δA²〉 to zero over the characteristic time scales of the system.

One can predict the form of C̄⁽²⁾(τ) for a given model using the theory of Markov chains, which assumes that the time interval between successive observations is long in comparison to ‘internal relaxation times,’ and that the probability that the system undergoes a transition from state-i to state-j depends only on its occupancy of state-i.²⁴ This assumption ignores the possibility of memory effects, which become important if internal barriers associated with state-i influence the transition probability. The Markov chain expression for the 2^nd-order TCF is:

$${\overline{C}}^{(2)}(\tau )=\sum _{i,j=0}^{N-1}\delta A_j{p}_{ji}(\tau )\delta A_i{p}_i^{eq}$$ (3)

In Eq. (3), $p_i^{eq}$ is the equilibrium (time-independent) probability to observe the system in state-i, δA_i is the value of the fluctuation observable associated with that state, and p_ji(τ) is the conditional probability that the system will be in state-j at a time τ after it was initially observed to be in state-i. Equation (3) shows that the 2^nd-order TCF is the second moment of the time-dependent stochastic variable δA(t), which is the weighted average of all possible two-point products δA_jδA_i occurring within the time interval τ. It is instructive to note that when τ is short in comparison to the shortest transition time of the system, the two-point product is dominated by terms δA_iδA_i, such that ${\overline{C}}^{(2)}(\tau \to 0)={\sum }_{i=0}^{N-1}\delta A_i^2{p}_i^{eq}=\langle \delta A^2\rangle$. In contrast, for τ longer than the longest transition time, the two-point product is dominated by uncorrelated successive observations, such that ${\overline{C}}^{(2)}(\tau \to \infty )=\left[{\sum }_{j=0}^{N-1}\delta A_j{p}_j^{eq}\right]\times \left[{\sum }_{i=0}^{N-1}\delta A_i{p}_i^{eq}\right]=0$. When the time interval τ is comparable to the time scale of a particular transition from state-i to state-j, the two-point product is dominated by terms δA_jδA_i, which reflect the weighted contributions of these particular transitions.

The information provided by the 2^nd-order TCF alone cannot be used to determine whether the states visited during a single-molecule trajectory occur independently, or are connected through a ‘pathway’ of correlated sequential events. One can imagine that a particular fluctuation must occur first in order for a subsequent fluctuation to follow. For example, the N = 3 and N = 4 schemes depicted in Fig. 1B and Fig. 1C, respectively, illustrates the ssDNA-(gp32)_n assembly pathways as a system of coupled elementary chemical steps in which the 0-bound and 2-bound states are inter-connected through ‘productive’ (and sometimes ‘unproductive’) intermediates. The 2^nd-order TCF does not contain information, for example, about how a transition between any particular 1-bound and 2-bound state might be correlated to a preceding transition between the 0-bound and a 1-bound state. As we shall see, information about the preferred sequences of transitions that occur at equilibrium is contained in ‘higher-order’ TCFs.

To distinguish between different mechanisms of coupled chemical transformations, we consider the information contained within 4^th-order TCFs. The 4^th-order TCF of δA is the average product of four sequential observations, separated by the three time intervals τ₁ = t₂ − t₁, τ₂ = t₃ − t₁, and τ₃ = t₄ − t₃ (see Fig. 1D)

$$C^{(4)}({\tau }_1,{\tau }_2,{\tau }_3)=\langle \delta A(0)\delta A({\tau }_1)\delta A({\tau }_2)\delta A({\tau }_3)\rangle$$ (4)

In Eq. (4), the angle brackets have the same meaning as those in Eqs. (1) and (2). The 4^th-order TCF C⁽⁴⁾(τ₁, τ₂, τ₃) depends on the probability of sampling each possible time-ordered sequence of δA. For the N = 4 scheme of Fig. 1C, for example, we might observe the sequence δA₀δA₀δA₁, δA₂ at the four times sampled. If, for a particular set of time intervals, we were to observe this sequence with greater frequency than sequences that contain sequential occurrences of δA₀ followed by δA₂, then we might conclude that direct transitions between state-0 and state-2 are unlikely, and must proceed through an intermediate state-1′. Because the timescales of transitions between the various states have definite values, certain sequences will be more prevalent for short time intervals, while others will occur with greater frequency for long time intervals. Thus, the information encoded in C⁽⁴⁾(τ₁, τ₂, τ₃) provides direct insight into the kinetic scheme that defines the time-ordered fluctuations of a single-molecule trajectory.

It is helpful to visualize C⁽⁴⁾(τ₁, τ₂, τ₃) as a series of two-dimensional (2D) contour plots, with horizontal and vertical axes given by the intervals τ₁ and τ₃. We present model calculations of C⁽⁴⁾(τ₁, τ₂, τ₃) in the next section. Such plots are presented as a parametric function of the interval τ₂, which is referred to as the waiting time. As mentioned above, the 4^th-order TCF contains information about the presence of ‘higher-order temporal correlations’ between successive transitions, with the first transition occurring during τ₁ and the second during τ₃. By examining a series of 4^th-order TCFs as a function of τ₂, we can determine the average timescales over which successive transitions are correlated. In the absence of higher-order correlations, upstream and downstream transitions occur independently. In the limit that the waiting time τ₂ becomes very long, or that higher-order correlations are short-lived, we see from Eq. (4) that lim_τ2→∞ C⁽⁴⁾(τ₁, τ₂, τ₃) = 〈δA(0)δA(τ₁)〉〈δA(0)δA(τ₃)〉 = C̄⁽²⁾(τ₁)C̄⁽²⁾(τ₃). In this limit, the 4^th-order TCF is equal to the square product of the 2^nd-order TCF defined in Eq. (2). To isolate the effects of higher order correlations from those due to 2^nd-order ‘background’ correlations, it is useful to define the 4^th-order difference TCF

$${\overline{C}}^{(4)}({\tau }_1,{\tau }_2,{\tau }_3)=\langle \delta A(0)\delta A({\tau }_1)\delta A({\tau }_2)\delta A({\tau }_3)\rangle -{\overline{C}}^{(2)}({\tau }_1){\overline{C}}^{(2)}({\tau }_3)$$ (5)

The 4^th-order difference TCF C̄⁽⁴⁾(τ₁, τ₂, τ₃) defined by Eq. (5) decays as a function of τ₂ from its maximum value 〈δA(0)[δA(τ₁)]²δA(τ₃)〉 to zero over the characteristic time scales for which higher-order correlations exist.

The Markov chain expression for the 4^th-order TCF can be written

$$\langle \delta A(0)\delta A({\tau }_1)\delta A({\tau }_2)\delta A({\tau }_3)\rangle =\sum _{i,j,k,l=0}^{N-1}\delta A_l{p}_{lk}({\tau }_3)\delta A_k{p}_{kj}({\tau }_2)\delta A_j{p}_{ji}({\tau }_1)\delta A_i{p}_i^{eq}$$ (6)

where the conditional probability p_ji(τ) is defined similarly as in Eq. (3). Since the system may only occupy discrete states, the 4^th-order TCF is the weighted sum of a finite number of four-point products δA_lδA_kδA_jδA_i. For the N = 3 example of Fig. 1B, each observation can take only one of three possible values: δA_0, δA_1, or δA_2,. Thus for N = 3, the four-point product can acquire (3)(3)(3)(3) = 81 possible outcomes (or pathways). In general, the number of possible outcomes for an N-state system is N⁴, and the 4^th-order TCF is composed of the weighted average of these outcomes as described by Eq. (6). In order to apply Eqs. (3) and (6) to a specific N-state system, one must solve for the conditional probabilities p_ji(τ). In the following sections, we show how the conditional probabilities may be obtained as the formal solution to a master equation for a system of N coupled differential equations that characterize the reaction pathway.

IV. Calculation of TCFs using Markov Chains

We apply the theory of Markov chains to relate the 2^nd- and 4^th-order TCFs defined in the previous sections to specific N-state models.^24,32 Such analyses are generally useful for the interpretation of single-molecule trajectories in which stochastic transitions occur between a few discrete states. We write the memory-less master equation for an N-state system

$$\stackrel{.}{\mathit{p}}(t)=\mathit{Kp}(t)\equiv \left[\begin{array}{c}{\stackrel{.}{p}}_0\\ {\stackrel{.}{p}}_1\\ ⋮\\ {\stackrel{.}{p}}_{N-1}\end{array}\right]=\left[\begin{array}{cccc}-\sum _{i=0}^{N-1}{k}_{0,i}& k_{1,0}& \dots & k_{N-1,0}\\ k_{0,1}& -\sum _{i=0}^{N-1}{k}_{1,i}& \ddots & ⋮\\ ⋮& \ddots & \ddots & k_{N-1,N-2}\\ k_{0,N-1}& \dots & k_{N-2,N-1}& -\sum _{i=0}^{N-1}{k}_{N-1,i}\end{array}\right]\left[\begin{array}{c}{p}_0\\ p_1\\ ⋮\\ p_{N-1}\end{array}\right]$$ (7)

In Eq. (7), p(t) is an N-dimensional vector containing the probabilities to find the system in each of its N states at time t, and K is the N×N rate matrix, with elements k_ij associated with the transitions from state-i to state-j. We constrain the diagonal elements of the rate matrix $k_{ii}=-{\sum }_{j\ne i}^{N-1}{k}_{ij}$ to enforce the mass action law, and we set the sum of the instantaneous state probabilities ${\sum }_{i=0}^{N-1}{p}_i(t)=1$.

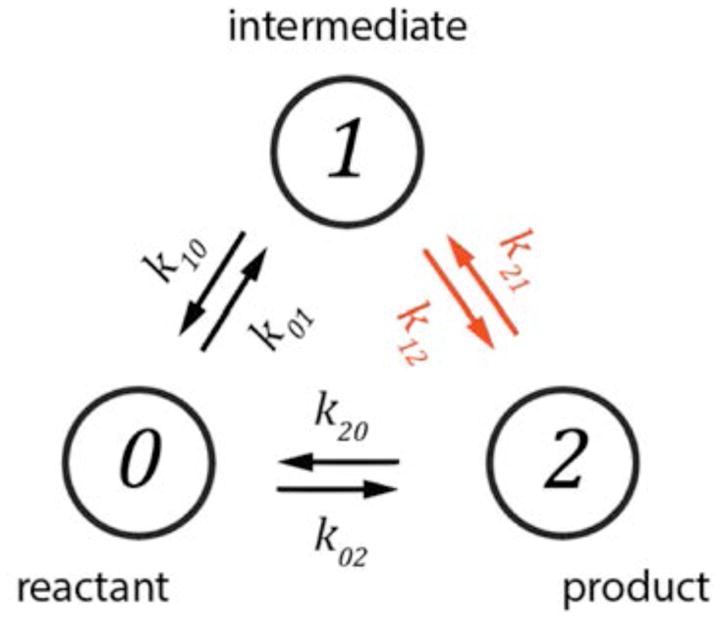
When constructing the rate matrix K, the elements k_ij must be chosen to satisfy the detailed balance condition, $p_i^{eq}{k}_{ij}=p_j^{eq}{k}_{ji}$ where $p_i^{eq}={\mathit{lim}}_{t\to \infty }{p}_i(t)$ is the stationary (equilibrium) occupancy of state-i. The detailed balance condition requires that in the long-time limit, the flow of probability from state-i to state-j is equal to the flow of probability from state-j to state-i. For coupled reactions that involve cyclical pathways, the requirements of the detailed balance condition lead to additional inter-dependencies of the rate constant matrix elements. In Fig. 2, we depict three reaction schemes as examples to illustrate this point. For a system that contains a single cyclical pathway (Fig. 2A), the product of rate constants moving along the clockwise path must equal the product of rate constants moving along the clockwise path must equal the product of rate constants moving along the counter-clockwise path; i.e. k₃₀k₃₂k₂₁k₁₀ = k₃₀k₀₁k₁₂k_23. Thus, a system that contains a single cyclical pathway leads to the constraint that one rate constant must depend on all others. This relationship ensures that the flow of probability in the clockwise direction is precisely balanced by the flow of occupancies in the counter-clockwise direction, as must be the case for an equilibrium system. In the absence of a cyclical pathway, the detailed balance condition can be satisfied locally for each successive step of the coupled chemical reaction (see Fig. 2B), so that the rate constants may be chosen independently of each other. When the system contains multiple cyclical pathways, such as the situation depicted in Fig. 2C, more complicated interrelationships between rate constants exist. The relationship between cyclical pathways in this instance leads to the requirement that two rate constants must be dependent on all others. An excellent description of enforcing detailed balance can be found in reference 33.

Figure 2.

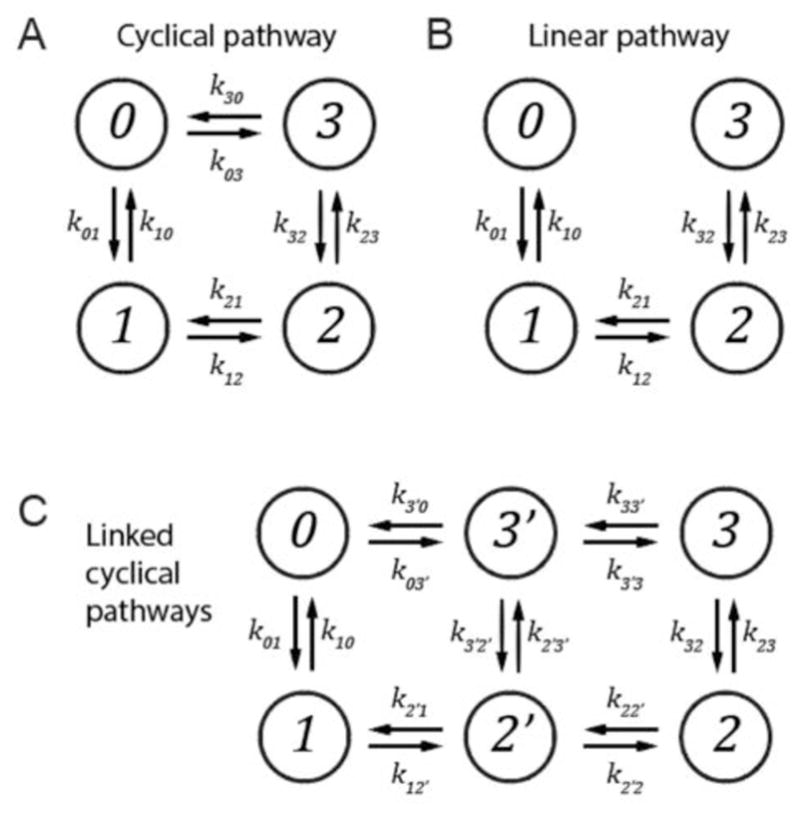
Example kinetic schemes for which the detailed balance condition requires different constraints to be applied to the rate constant relationships due to the presence or absence of cyclical pathways. (A) Single cyclical pathway. (B) Linear pathway. (C) Linked cyclical pathways.

Provided that a rate matrix K can be found to satisfy the detailed balance condition, a general solution of Eq. (7) can be obtained using the spectral decomposition method²⁴

$$\mathit{p}(t)\equiv \sum _{i=0}^{N-1}{c}_i{\mathit{v}}_i{e}^{-{\lambda }_{i}t}=c_0{\mathit{v}}_0{e}^{-{\lambda }_{0}t}+c_1{\mathit{v}}_1{e}^{-{\lambda }_{1}t}+\cdots +c_{N-1}{\mathit{v}}_{N-1}{e}^{-{\lambda }_{N-1}t}$$ (8)

In Eq. (8), λ_i and v_i are, respectively, the eigenvalues and the corresponding eigenvectors of the rate matrix of Eq. (7). We set the first eigenvalue λ₀ = 0 to allow the time-dependent populations to decay to the constant equilibrium distribution c₀v₀ = p^eq. We may thus rewrite Eq. (8) explicitly in terms of the equilibrium distribution

$$\mathit{p}(t)={\mathit{p}}^{eq}+c_1{\mathit{v}}_1{e}^{-{\lambda }_{1}t}+\cdots +c_{N-1}{\mathit{v}}_{N-1}{e}^{-{\lambda }_{N-1}t}$$ (9)

The conditional probabilities p_ji(τ) needed for the evaluation of 2^nd-order and 4^th-order TCFs described by Eqs. (3) and (6) respectively, can be obtained using Eq. (9), with proper enforcement of the boundary conditions. For example, p₂₁(τ) is the conditional probability that the system resides in state-2 at time τ, given that it was in state-1 at time zero. In this case, the initial condition is p₁(0) = 1 and p_i≠1(0) = 0. We may thus solve Eq. (9) for the set of expansion coefficients {c₁, c₂, …, c_N−1}, and for the conditional probability p₂₁(τ). We carry out a similar procedure for each conditional probability p_ji(τ) with i, j ∈ {0,1, …, N − 1}.

Analytical expressions for the 2^nd- and 4^th-order TCFs for N = 2 and N = 3

We next consider analytical expressions for the 2^nd and 4^th-order TCFs that follow from Eq. (9) for common situations with N = 2 and N = 3. Although the expressions for N = 2 systems are trivial, we include them for completeness before examining the more complex situations with N = 3.

Two-state system

For an N = 2 scheme, the 2^nd-order TCF described by Eq. (2) is a weighted average of 4 possible two-point product pathways, as shown schematically in Fig. 3A.

Figure 3. Transition pathway contributions to 2^nd- and 4^th-order TCFs for two-state (N = 2) system.

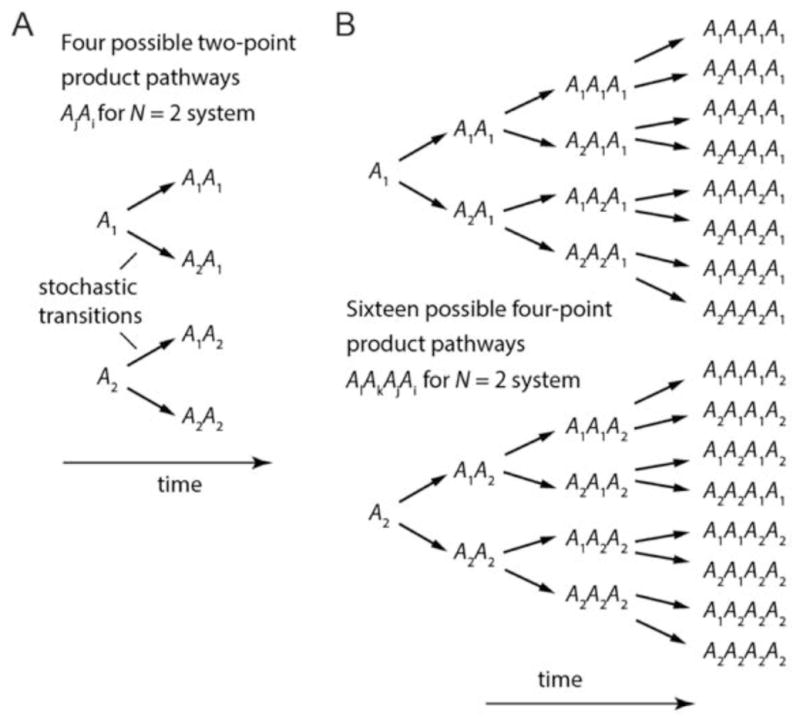
(A) There are N² = 2² = 4 possible outcomes of a time-ordered two-point product of the observable A(t), which are used to construct the 2^nd-order TCF C̄⁽²⁾(τ). (B) There are N⁴ = 2⁴ = 16 such sequences for the four-point product that is used to construct the 4^th-order TCF C̄⁽⁴⁾(τ₁, τ₂, τ₃). The conditional probability p_ji(τ) that a stochastic transition will occur from state-i to state-j within the time interval τ is given by Eq. (10).

The master equation solution [Eq. (9)] specified for N = 2 yields the time-dependent conditional probabilities

$$p_{ji}(\tau )=p_j^{eq}+[p_j(0)-p_j^{eq}]e^{-{\lambda }_1\tau },N=2$$ (10)

where λ₁ = k₁₂ + k₂₁ is the only non-zero eigenvalue. An analytical expression for the 2^nd-order TCF follows from substitution of Eq. (10) into Eq. (3).

$${\overline{C}}^{(2)}(\tau )=\langle \delta A^2\rangle e^{-{\lambda }_1\tau },N=2$$ (11)

Equation (11) shows that the 2^nd-order TCF for a two-state system decays exponentially with rate constant λ₁ = k₁₂ + k₂₁.

For the N = 2 scheme, the 4^th-order TCF described by Eq. (4) is a weighted average of 16 possible four-point product pathways, as shown schematically in Fig. 3B. Upon substitution of Eq. (10) into Eq. (6), it is straightforward to show that the 4^th-order TCF for a two-state system has the form

$$\langle \delta A(0)\delta A({\tau }_1)\delta A({\tau }_2)\delta A({\tau }_3)\rangle ={\mathcal{A}}_{11}{e}^{-{\lambda }_1({\tau }_1+{\tau }_3)},N=2$$ (12)

where the constant 𝒜₁₁ = 〈A²〉². Equation (12) shows that the 4^th-order TCF for an N = 2 system is simply the product of the 2^nd-order TCFs C̄⁽²⁾(τ₁) C̄⁽²⁾(τ₃) for all values of τ₂. This follows since there are no intermediates in an N = 2 scheme, and therefore no ‘higher-order’ transition pathways can exist. In this case, the 4^th-order difference TCF C̄⁽⁴⁾(τ₁, τ₂, τ₃), defined by Eq. (5), is equal to zero for all values of τ₂.

Three-state system

We next consider the three-state scheme (N = 3) introduced in Fig. 1B, and redrawn for the following discussion in Fig. 4. In the redrawn scheme, we have allowed for the hypothetical transition between the 0-bound (reactant) state and the 2-bound (product) state, so that these might (or might not) be bridged by a 1-bound (intermediate) state. The 0 ⇄ 2 reaction pathway would require the binding of an appropriately pre-formed gp32 dimer directly from solution. This does not happen in the real system, but we include the possibility here to provide generality. Such schemes are the simplest that may exhibit higher-order temporal correlations, as reflected by the behavior of the 4^th-order TCF. The derivations of the corresponding analytical expressions are straightforward, yet somewhat involved. We present the derivation here to illustrate how higher-order correlations emerge.

Figure 4.

The N = 3 reaction redrawn from Fig. 1 as a cyclical scheme. This allows for the product state-2 to form either directly from the reactant state-0, or through the intermediate state-1. The ‘coupling step’ is indicated in red.

The master equation for an N = 3 system is specified, using Eq. (7), according to:

$$\left[\begin{array}{c}{\stackrel{.}{p}}_0\\ {\stackrel{.}{p}}_1\\ {\stackrel{.}{p}}_2\end{array}\right]=\left[\begin{array}{ccc}-k_{01}-k_{02}& k_{10}& k_{20}\\ k_{01}& -k_{10}-k_{12}& k_{21}\\ k_{02}& k_{12}& -k_{20}-k_{21}\end{array}\right]\left[\begin{array}{c}{p}_0\\ p_1\\ p_2\end{array}\right]$$ (13)

The general solution to Eq. (13) is

$$\mathit{p}(t)={\mathit{p}}^{eq}+c_1{\mathit{v}}_1{e}^{-{\lambda }_{1}t}+c_2{\mathit{v}}_2{e}^{-{\lambda }_{2}t},N=3$$ (14)

where the eigenvalues λ₁ and λ₂ and the eigenvectors ${\mathit{v}}_1=[v_1^0,v_1^1,v_1^2]$ and ${\mathit{v}}_2=[v_2^0,v_2^1,v_2^2]$ are functions of the rate constants (derivation given in Appendix 1). To satisfy detailed balance, one rate constant must depend on the others, such that k₂₀ = k₀₂k₂₁k₁₀/k₁₂k₀₁. The equilibrium populations ${\mathit{p}}^{eq}=[p_0^{eq},p_1^{eq},p_2^{eq}]$ are found by solving Eq. (13) with the boundary condition ṗ(t) = 0. These solutions must also satisfy completeness: ${\sum }_{i=0}^2{p}_i(t)=1$. The above conditions lead to explicit forms for the component equilibrium populations $p_0^{eq},p_1^{eq}$ and $p_2^{eq}$, which are explicit functions of the rate constants (see Appendix 1).

To determine the nine conditional probabilities p_ji(τ) with i, j ∈ {0,1,2}, we solve Eq. (14) for the expansion coefficients c₁ and c₂, while assuming the appropriate boundary conditions. We label each expansion coefficient with a superscript to indicate the boundary condition. For example, the expansion coefficient $c_1^0$ corresponds to the case when all population resides in state-0 at time zero, i.e. p₀(0) = 1 and p₁(0) = p₂(0) = 0. This leads to closed form expressions for the six expansion coefficients: $c_2^0,c_2^1,c_2^2,c_1^0,c_1^1$ and $c_1^2$ (see Appendix 1). Upon substitution of these into Eq. (14), obtain the conditional probabilities

$$p_{ji}(\tau )=p_j^{eq}+c_1^i{v}_1^j{e}^{-{\lambda }_1\tau }+c_2^i{v}_2^j{e}^{-{\lambda }_2\tau },N=3$$ (15)

Substitution of Eq. (15) into Eqs. (3) and (6) provides analytical expressions for the 2^nd- and 4^th-order TCFs, respectively. Although these expressions are unwieldy to write in extended form, their solutions are readily obtained using a desktop computer. The 2^nd-order TCF can be written succinctly

$${\overline{C}}^{(2)}(\tau )={\mathcal{A}}_1{e}^{-{\lambda }_1\tau }+{\mathcal{A}}_2{e}^{-{\lambda }_2\tau },N=3$$ (16)

Equation (16) is composed of two exponentially decaying terms, with decay rates λ₁ and λ₂ and amplitudes 𝒜₁ and 𝒜₂, respectively. The constants λ₁, λ₂, 𝒜₁ and 𝒜₂ are polynomial functions of the six rate constants k_ij, with i,j ∈ {0,1,2} and i≠j.

It is straightforward to show that the difference 4^th-order TCF, which is given by Eq. (5), has the succinct form

$${\overline{C}}^{(4)}{({\tau }_1,{\tau }_3)\rceil }_{{\tau }_{2\mathit{fixed}}}={\mathcal{A}}_{11}({\tau }_2)e^{-{\lambda }_1({\tau }_1+{\tau }_3)}+{\mathcal{A}}_{12}({\tau }_2)e^{-{\lambda }_1{\tau }_1-{\lambda }_2{\tau }_3}+{\mathcal{A}}_{21}({\tau }_2)e^{-{\lambda }_2{\tau }_1-{\lambda }_1{\tau }_3}+{\mathcal{A}}_{22}({\tau }_2)e^{-{\lambda }_2({\tau }_1+{\tau }_3)},N=3$$ (17)

Equation (17) is composed of four terms, each with an amplitude 𝒜_mn [n,m ∈ {1,2}] that depends on the waiting time τ₂. Similar to the 2^nd-order TCF, the 4^th-order TCF decays exponentially. For a fixed waiting time τ₂, the decay of the 4^th-order TCF occurs in two dimensions, corresponding to the time intervals τ₁ and τ₃. The characteristic decay rates of the 4^th-order TCF are the same as those of the 2^nd-order TCF. In Eq. (17), the two terms with amplitudes 𝒜₁₁ and 𝒜₂₂ designate global relaxation self-terms (i.e. terms that each depend on a single eigenvalue, λ₁ or λ₂, respectively), while the terms with amplitudes 𝒜₁₂ and 𝒜₂₁ designate inter-dependent cross-terms, which each depend on both decay constants, λ₁ and λ₂. For an equilibrium system, the detailed balance condition requires that 𝒜₁₂ = 𝒜₂₁.¹⁹ As we discuss further below, the self-term amplitudes, 𝒜₁₁ and 𝒜₂₂, indicate the relative weights of the global relaxation processes, while the sign and magnitude of the cross-term amplitudes, 𝒜₁₂ and 𝒜₂₁, indicate positive or negative 4^th-order correlations that effectively couple these processes.

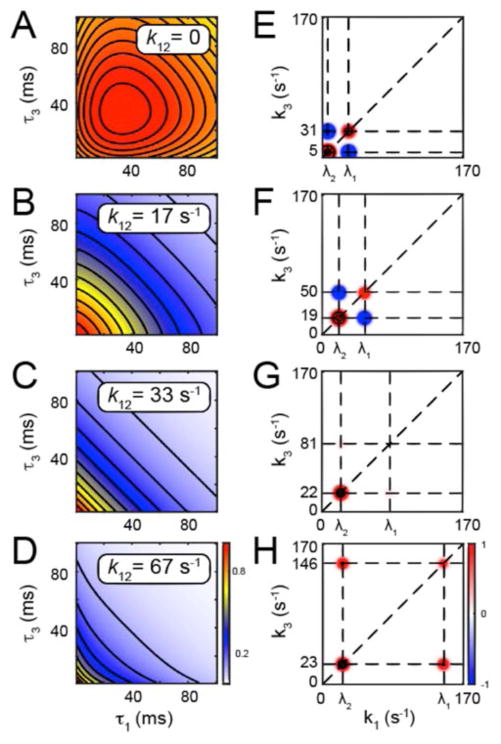
We now return to the example of the ssDNA-(gp32)₂ assembly reaction, as depicted in Fig. 4. To illustrate how the local connectivity between states can affect the collective dynamics characterized by the 4^th-order TCF, we present in Fig. 5A – 5D calculations for a specific case in which the rate constants k₁₂ and k₂₁ are varied while the remaining parameters are held fixed. For the purpose of this discussion, we have set the waiting time interval τ₂ = 1 ms, and we have chosen plausible values for the rate constants k₀₁ = 10 s⁻¹, k₁₀ = 20 s⁻¹, k₀₂ = 2 s⁻¹, and k₂₀ = 4 s⁻¹ with signal observables A₀ = 0.9, A₁ = 0.3, and A₂ = 0.1. This particular choice of parameters assumes that the time scales of exchange between reactant state-0 and intermediate state-1 are much faster than those between reactant and product state-2. It is worth noting that for time intervals in which four-point pathways are dominated by recurring observations of the end state-0 or state-2 (e.g., δA₀δA₀δA₀δA₀), the 4^th-order TCF will tend to be high-valued. Alternatively, for intervals in which the majority of four-point pathways include observations of the intermediate state-1 (e.g., δA₀δA₀δA₀δA₀), the 4^th-order TCF will tend to be low-valued. For this particular example with the given rates under the detailed balance condition, the symmetry of the system dictates that for all values of the rate constants k₁₂ = k₂₁, the equilibrium distribution of populations are given by $p_0^{eq}=0.5,p_1^{eq}=0.25$, and $p_2^{eq}=0.25$.

Figure 5.

Calculated 4^th-order TCFs (panels A – D) and associated two-dimensional (2D) rate spectra (panels E – H) for the cyclical N = 3 system shown in Fig. 4. Here we have taken the waiting time interval τ₂ = 1 ms, and the rate constants k₀₁ = 10 s⁻¹, k₁₀ = 20 s⁻¹, k₀₂ = 2 s⁻¹, and k₂₀ = 4 s⁻¹. The TCFs are described by Eq. (17) and the 2D rate spectra by Eq. (18). The rate constants of the ‘coupling step,’ k₁₂ = k₂₁ are adjusted over the range (A and E) 0, (B and F) 16.7 s⁻¹, (C and G) 33.3 s⁻¹, and (D and H) 66.7 s⁻¹. For each of these conditions, values of the self- and cross-term amplitudes 𝒜₁₁, 𝒜₂₂, 𝒜₁₂ = 𝒜₂₁, respectively, are given in the text.

We initially consider the case in which transitions between state-1 and state-2 are prohibitively slow (i.e., k₁₂ = 0). The time scales of the local elementary chemical reaction steps 0 ⇄ 1 and 0 ⇄ 2 can be estimated by assuming that these transitions occur independently of one another. We thus estimate the time scale of ‘fast’ transitions between state-0 and state-1 as (k₀₁ + k₁₀)⁻¹ = 33 ms, and that of ‘slow’ transitions between state-0 and state-2 as (k₀₂ + k₂₀)⁻¹ = 167 ms. By solving the master equation for the coupled system [Eq. (13)], we determine the time scales of the global relaxations (eigenvalues) λ₁ = 31 s⁻¹ and λ₂ = 5.2 s⁻¹, which correspond to the times ${\mathrm{\lambda }}_1^{-1}=32\text{ms}$ and ${\mathrm{\lambda }}_2^{-1}=193\text{ms}$, respectively. Because in this example there is a clear separation between fast and slow elementary chemical steps (i.e. 0 ⇄ 1 and 0 ⇄ 2), these time scales closely approximate those of the eigenvalues of the coupled system (1 ⇄ 0 ⇄ 2). In Fig. 5A, we plot the 4^th-order TCF corresponding to these conditions. We note that this function slowly rises to a peak value close to the point τ₁ = τ₃ ~ 33 ms and then gradually decays to zero with increasing values of τ₁ and τ₃. This behavior reflects the fact that multi-step transitions occur only rarely on time scales shorter than the fastest exchange process of the system. For values of τ₁ and τ₃ that match the time scale of the fast 0 ⇄ 1 exchange process, the 4^th-order TCF is heavily weighted by terms that involve successive observations of the reactant and intermediate states (e.g., δA₀δA₁δA₁δA₀). For values of τ₁ and τ₃ in which one or the other of these intervals approaches time scales comparable to the slow 0 ⇄ 2 exchange process, the 4^th-order TCF is composed mostly of terms that include successive observations of all three states involved in both fast and slow local reactions (e.g., δA₁δA₀δA₀δA₂), which in turn cause the function to decay. The self- and cross-term amplitudes corresponding to these conditions are 𝒜₁₁ = 1.08, 𝒜₂₂ = 6.73, and 𝒜₁₂ = 𝒜₂₁ = −2.68, which indicates that the slow eigen-mode is dominant. We note that the negative sign of the cross-term amplitudes are responsible for the concave downward shape of the three-dimensional surface, and for its convex contours for values of τ₁, τ₃ > 32 ms. From the above analysis, we conclude that for this model, the 32 ms time scale serves as an experimental demarcation point. For short time intervals (τ₁, τ₃ ≈ 32 ms), the system primarily undergoes ‘fast’ exchange of population between state-0 and state-1, and for longer time intervals (τ₁, τ₃ > 32 ms), the system undergoes a combination of ‘fast’ and ‘slow’ processes that exchanges population between all three states.

We next examine the possibility that state-1 shown in Fig. 4 can function as an intermediate, so that the exchange reactions 1 ⇄ 2 (shown in red) can bridge the 0 ⇄ 1 and the 0 ⇄ 2 reactions (shown in black). We first outline our expectations based on qualitative arguments before examining the theoretical results of the model. Suppose, for example, that when a gp32 monomer binds to the ssDNA template to form state-1, that it might rapidly slide to a ‘productive’ site allowing for a second gp32 monomer to bind cooperatively, and thus to form a stable dimer. Were this the prevalent mechanism, it would be reflected by the occurrence of four-point pathways at short time intervals that lead to the assembly of the ssDNA-(gp32)₂ product (e.g., δA₀δA₁δA₁δA₂). The resulting 4^th-order TCF would then decay rapidly with increasing values of τ₁, τ₃, and exhibit a pattern of positive correlation between successive elementary steps 0 ⇄ 1 and 1 ⇄ 2, which collectively lead to the formation of product. In contrast, if the gp32 monomer state-1 were unstable (due to its presumably slow exchange with state-2), its rapid dissociation would block its ability to act as a ‘gateway’ intermediate along the assembly pathway. In this latter situation, the intermediate state-1 behaves as a competitive inhibitor to the direct formation of state-2, so that the 4^th-order TCF would decay slowly and exhibit a pattern of negative correlation between the successive elementary steps 0 ⇄ 1 and 1 ⇄ 2 (or 0 ⇄ 2). Therefore, depending on whether the 1 ⇄ 2 exchange time scale is fast, slow or intermediate in comparison to the fastest local relaxation time of the system (in the current example, ~ 32 ms), the global rate of population exchange can either be sped up, slowed down, or left unaffected by the presence of the intermediate state-1. These three scenarios correspond to positive, negative, and zero 4^th-order correlation, respectively, between successive elementary chemical steps. The signs and magnitudes of the cross-term amplitudes, 𝒜₁₂ and 𝒜₂₁ serve to characterize whether 4^th-order correlation is positive, negative or zero.

We now consider the case in which the exchange rate constants between state-1 and state-2 are assigned to an intermediate value $k_{12}=17{\mathrm{s}}^{-1}(k_{12}^{-1}=60\text{ms})$ in comparison to the ‘fast’ and ‘slow’ local exchange processes (30 s⁻¹ and 6 s⁻¹, respectively) described for the case of k₁₂ = 0. These conditions are expected to mimic the scenario of competitive inhibition described above. In Fig. 5B, we plot the 4^th-order TCF using these parameters, which decays for all non-zero values of τ₁ and τ₃ with collective relaxation rates λ₁ = 50 s⁻¹ and ${\mathrm{\lambda }}_2=19{\mathrm{s}}^{-1}({\lambda }_1^{-1}=20\text{ms}\text{and}{\lambda }_2^{-1}=53\text{ms})$. The introduction of the 1 ⇄ 2 step permits a new pathway for population exchange to occur between all three states, which leads to a dramatic speedup of the slow collective relaxation (i.e. the second eigenvalue λ₂: 5.2 → 19 s⁻¹). Under these conditions, the self-term amplitudes are determined to be 𝒜₁₁ = 0.472, 𝒜₂₂ = 4.94, and the cross-term amplitudes 𝒜₁₂ = 𝒜₂₁ = −1.52. As in the previous case, the convex contour lines exhibited by the 4^th-order TCF are due to the negative cross-term amplitudes, which indicate the presence of kinetic ‘bottleneck’ states within the four-point pathways that lead to the exchange of population between all three states. Under these conditions, the reactant state-0 is much more likely to form the intermediate state-1 than to directly form the product state-2. However, once formed, the intermediate is much more likely to undergo the reverse dissociation reaction than to proceed to form product. Thus, for short intervals τ₁ and τ₃ (< 32 ms), the 4^th-order TCF is most heavily weighted by the ‘fast’ exchange between state-0 and state-1. Only at longer time intervals does the 4^th-order TCF decay due to the contributions of slower processes such as the coupling step from state-1 to state-2.

In Fig. 5C, we plot the 4^th-order TCF for the case $k_{12}=33{\mathrm{s}}^{-1}(k_{12}^{-1}=30\text{ms})$. Under these conditions the rate constants for the 1 ⇄ 2 exchange reactions closely match those of the 0 ⇄ 1 process discussed above for the k₁₂ = 0 ms⁻¹ case. The 4^th-order TCF decays for all values of τ₁ and τ₃ with collective relaxation rates λ₁ = 81 s⁻¹ and ${\mathrm{\lambda }}_2=22{\mathrm{s}}^{-1}({\lambda }_1^{-1}=12\text{ms}\text{and}{\lambda }_2^{-1}=45\text{ms})$, and with self- and cross-term amplitudes 𝒜₁₁ = 0.0001, 𝒜₂₂ = 2.26, and 𝒜₁₂ = 𝒜₂₁ = 0.017, respectively. Under these conditions, only the slower of the two collective relaxation processes carries significant amplitude, and the curvature of the 4^th-order TCF is neither convex nor concave. From Eq. (17), we see that in the absence of cross-term amplitude (i.e., for 𝒜₁₂ = 𝒜₂₁ ≈0), a cross-section of the 4^th-order TCF along a vertical slice (with respect to τ₃ and, for example, setting τ₁ = 0) decays at precisely half the rate as does the decay along the diagonal line (with respect to τ₁+τ₃, and setting τ₁ = τ₃), so that the contours of the 2D surfaces are straight anti-diagonal lines. The absence of 4^th-order correlation can be understood as a consequence of the close matching of time scales between the 1 ⇄ 2 and 0 ⇄ 1 exchange processes. Because population can readily exchange between all three states via the intermediate state-1, successive elementary reaction steps may occur in an uncorrelated manner.

By further increasing the 1 ⇄ 2 exchange rate constants to the value $k_{12}=67{\mathrm{s}}^{-1}(k_{12}^{-1}=15\text{ms})$, we model the situation of enhanced kinetic exchange between the intermediate and product states, as described above. In Fig. 5D, we plot the 4^th-order TCF for these conditions, which decays for all non-zero values of τ₁ and τ₃ with characteristic relaxation rates λ₁ = 146 s⁻¹ and ${\mathrm{\lambda }}_2=23{\mathrm{s}}^{-1}({\lambda }_1^{-1}=6.8\text{ms}\text{and}{\lambda }_2^{-1}=43\text{ms})$, and with self- and cross-term amplitudes 𝒜₁₁ = 0.155, 𝒜₂₂ = 1.16, and 𝒜₁₂ = 𝒜₂₁ = 0.419, respectively. In this case, the 1 ⇄ 2 exchange rate constants are much faster than those of the 32 ms 0 ⇄ 1 process. This leads the 4^th-order TCF to decay much more rapidly than in any of the previous situations, and to exhibit concave surface contours as a consequence of the positive-valued cross-term amplitudes. The concave surface curvature indicates that under these conditions, the intermediate state-1 functions as a ‘gateway’ species whose presence enhances the formation of the product state.

It is often useful to represent Eq. (17) as a two-dimensional (2D) rate domain spectrum through the inverse Laplace transform (ILT) – i.e., ${\overline{C}}^{(4)}{({\tau }_1,{\tau }_3)\rceil }_{{\tau }_2\mathit{fixed}}\stackrel{\text{ILT},{\tau }_1,{\tau }_3}{\to }$

$${\widehat{C}}^{(4)}{(k_1,k_3)\rceil }_{{\tau }_{2\mathit{fixed}}}={\mathcal{A}}_{11}({\tau }_2)\delta (k_1-{\lambda }_1)\delta (k_3-{\lambda }_1)+{\mathcal{A}}_{12}({\tau }_2)\delta (k_1-{\lambda }_1)\delta (k_3-{\lambda }_2)+{\mathcal{A}}_{21}({\tau }_2)\delta (k_1-{\lambda }_1)\delta (k_3-{\lambda }_2)+{\mathcal{A}}_{22}({\tau }_2)\delta (k_1-{\lambda }_2)\delta (k_3-{\lambda }_2).$$ (18)

The 2D rate spectrum is a sum of four delta functions, which are defined in the k₁,k₃-plane. Comparison between Eq. (17) and Eq. (18) shows that exponentially decaying terms in the 4^th-order TCF are represented as delta functions centered at values corresponding to the collective relaxation rates, λ₁ and λ₂ (see Figs. 5E – 5H). The two terms positioned along the ‘diagonal’ line (k₁ = k₃), which occur at the positions (k₁,k₃) = (λ₁,λ₁) and (λ₂,λ₂), respectively, correspond to the self-terms with amplitudes 𝒜₁₁ and 𝒜₂₂. The cross-terms with amplitudes 𝒜₁₂ and 𝒜₂₁ occur above and below the diagonal, at the positions (k₁,k₃) = (λ₁,λ₂) and (λ₂,λ₁), respectively. These self- and cross-term features of the 2D rate spectrum represent the same amplitudes discussed above for the 4^th-order TCF, and thus serve as an equivalent representation of the collective dynamics of the coupled cyclical N = 3 system.

Such 2D rate spectra are made in analogy to the often-used frequency domain spectra of 2D Fourier transform spectroscopy.^{17, 25–27} The diagonal and off-diagonal terms generally decay as a function of the waiting time τ₂. Cross-term amplitudes indicate the ‘exchange’ of populations between states involved in collective relaxation processes, and these terms decay on time scales that match the exchange dynamics. For situations in which the cross-term amplitudes are zero, the collective relaxation processes (defined by the eigenvectors v₁and v₂) are independent as depicted in Fig. 5G. Negative or positive cross-term amplitudes (as depicted in Figs. 5F and 5H, respectively) indicate that such processes are negatively or positively correlated, which is possible for pathways with N ≥ 3. As discussed in the context of our model calculations, the N = 3 scheme shown in Fig. 4, in which the intermediate state-1 functions as a rate-limiting ‘bottleneck’ (i.e., with k₀₁,k₁₀ ≫ k₁₂ ≈ k₂₁ ≫ k₀₂,k₂₀), exhibits negative 4^th-order correlation. In contrast, the same scheme in which the intermediate functions as a ‘gateway’ species (i.e., with k₀₁,k₁₀ ≪ k₁₂ ≈ k₂₁ ≫ k₀₂,k₂₀) exhibits positive 4^th-order correlation. For display purposes, we have artificially broadened the diagonal and off-diagonal features in our 2D rate spectra in Figs. 5E – 5H using a Gaussian convolution.

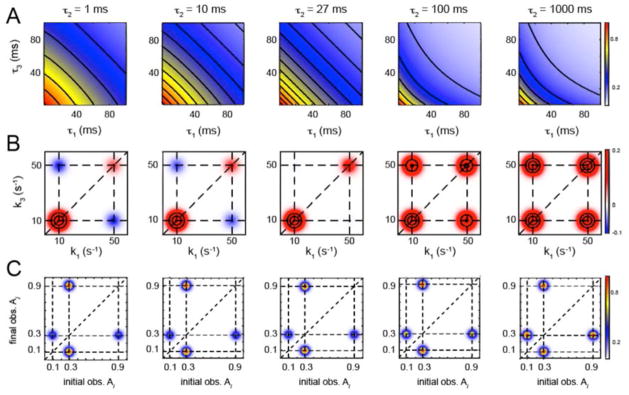
As previously mentioned, both TCF and HMM analyses can, in principle, provide similar information about the states and kinetics of a stochastically fluctuating chemical system. To illustrate this point, we plot in Fig. 6 the so-called ‘transition density plot’ (TDP) alongside the corresponding 4^th-order TCFs and 2D rate spectra. A TDP is a useful way to present the information about transition pathways that is potentially available from an HMM analysis.²³ The TDP describes the time-integrated joint distribution p_ji(A_j,τ;A_i,0) of molecules that are initially in state-i with observable value A_i, and which at a later time τ undergo a transition directly to state-j with observable value A_j. The weights of the TDP are given by the expression

Figure 6.

Model calculations for (A) the 4^th-order TCFs, (B) the 2D rate spectra, and (C) the transition density plots (TDPs) as a function of time. For these calculations, we have used the linear N = 3 kinetic scheme diagrammed in Fig. 1B, with values A₀ = 0.9, A₁ = 0.3, and A₂ = 0.1, and the rate constants k₀₁ = k₂₁ = 10 s⁻¹, and k₁₀ = k₁₂ = 20 s⁻¹.

$$p_{ij}(A_j,\tau ;A_i,0)=k_{ij}{p}_i^{eq}(1-e^{-k_{ji}\tau })$$ (19)

(see Appendix 2 for derivation). Thus, a time-dependent TDP contains information about the direct state-to-state transitions that occur within the time interval τ, and such information could be useful, in principle, to infer assignments to the various states involved within a transition pathway. We note that in the long-time limit, the joint distribution must be a symmetric function, i.e., $p_{ji}^{eq}(A_j,A_i)=k_{ij}{p}_j^{eq}·k_{ji}{p}_i^{eq}$ with $p_j^{eq}=p_i^{eq}$, which is necessary to satisfy detailed balance. Nevertheless, this symmetry need not be valid at short or intermediate times, since the various state-to-state transitions may occur on entirely different time scales. Only in the limit of very long time intervals (i.e., longer than the slowest relaxation of the system) are the forward and backward flow of state occupancies along all inter-connected transition paths expected to be equal.

In Fig. 6, we present model calculations for the linear N = 3 scheme (shown in Fig. 1B) of the 4^th-order TCFs, the 2D rate spectra, and the TDPs as a function of the waiting period τ₂. For these calculations, we have chosen the rate constants k₀₁ = k₂₁ = 10 s⁻¹ and k₁₀ = k₁₂ = 20 s⁻¹, with signal observables A₀ = 0.9, A₁ = 0.3, and A₂ = 0.1 (see Fig. 1B). The collective relaxation rates of the system are λ₁ = 50 s⁻¹ and ${\mathrm{\lambda }}_2=10{\mathrm{s}}^{-1}({\lambda }_1^{-1}=20\text{ms}\text{and}{\lambda }_2^{-1}=100\text{ms})$, and the equilibrium distribution of populations is given by $p_0^{eq}=0.4,p_1^{eq}=0.2$, and $p_2^{eq}=0.4$. This system has the interesting property that it crosses over from a regime of negative 4^th-order correlation at short waiting intervals (τ₂ < 27 ms) to one of positive 4^th-order correlation at long waiting intervals (τ₂ > 27 ms). The time-dependent crossover is evident from the shapes of the contour lines of the 4^th-order TCFs (Fig. 6A) and the signs of the cross-term amplitudes of the 2D rate spectra (Fig. 6B). This is due to the fact that for waiting periods less than 27 ms, the four-point pathways are heavily weighted by transitions leading away from the intermediate state-1, either in the backward direction toward the reactant state-0, or in the forward direction toward the product state-2. An initial step in either direction will tend to inhibit the successive step in the opposite direction, thereby inhibiting the global exchange of population between all three states. An example four-point pathway for a short waiting time is δA₁δA₀· τ_2,short · δA₀δA₁. In contrast, for waiting time intervals greater than 27 ms, the four-point pathways will tend to be dominated by sequences in which an initial fast step in the direction away from the intermediate state-1 (towards state-0 or state-2) will, after an intervening waiting time that exceeds the fast process, be positively correlated to a subsequent fast step in the opposite direction. An example four-point pathway such a waiting time is δA₁δA₀···τ _2,long ···δA₁δA₂. This example illustrates that the time-dependences of the 4^th-order TCFs, 2D rate spectra, and the TDPs can provide information about the connectivity of a chemical network, its rate constants, and the observable values A₀, A₁and A₂.

V. Optimization of N-State Kinetic Models to Sub-Millisecond Single-Molecule Fluorescence Data

In the preceding discussion, we have shown that analytical expressions for the TCFs of discrete stochastic systems with N = 2 or 3 can be readily obtained. For systems of higher complexity (N ≥ 4), it is often practical to solve Eq. (8) numerically. These solutions can be used to rapidly generate: (i) the 2^nd-order TCF C̄⁽²⁾ (τ); (ii) the 4^th-order TCF C̄⁽⁴⁾ (τ₁,τ₂,τ₃) and its corresponding 2D rate spectrum; (iii) the equilibrium distribution of states $p_i^{eq}(A_i)$; and (iv) the time-dependent joint distribution of states (i.e. the time-dependent transition density plot, TDP) p_ji(A_j,τ;A_i,0). By applying the algorithms discussed in Section IV to calculate quantities (i) – (iv), we may implement a multi-parameter optimization strategy to obtain the simplest kinetic scheme that can accurately represent the experimental behavior of single-molecule fluorescence data.

As indicated above, conventional single-molecule fluorescence experiments performed on discrete-state systems often employ 100-ms time resolution. Such measurements can provide useful kinetic information on this time scale through direct visual inspection, or by using hidden Markov model (HMM) analyses to obtain idealized single-molecule trajectories.²³ Single-molecule experiments with sub-millisecond time resolution provide only sparse trajectory data² that are not strictly amenable to direct visual inspection or HMM analyses. This is mostly due to the influence of stochastic noise – i.e., when a fixed number (n) of data points is measured over a short period of time, the signal-to-noise ratio (S/N) during this interval has a lower bound of $\sqrt{n}$. We therefore turn to the analysis described in this work, which is based on the use of TCFs and state distribution functions to extract detailed and useful kinetic information about multi-step transition pathways.

Here we prescribe a step-by-step protocol to analyze sparse single-molecule trajectory data. This approach is based on multi-parameter optimization algorithms that have been widely applied in numerous experimental contexts.^34–36 We must first consider the 2^nd-order TCF, which is constructed from individual single-molecule trajectories as described by Eq. (2). Each TCF may vary from trajectory-to-trajectory, depending on system heterogeneity, the experimental S/N, and on the number of data-points included in the calculation. The characteristic relaxation times are reflected by the decay of the 2^nd-order TCF. These are limited in range by the time-resolution of the measurement and by the maximum duration of a single-molecule trajectory. To reduce the effects of stochastic noise, the TCFs constructed from many individual trajectories should be averaged together.¹⁷ By fitting this decay to a model multi-exponential function, one determines the minimum number (N − 1) of relaxation components necessary to represent the system. The value of N so determined represents the minimum number of states, since the presence of additional relaxation components might be difficult to detect due to relatively small contributing amplitudes, or to the presence of eigen-mode degeneracy – i.e. the possibility that multiple relaxation components share the same (or nearly the same) relaxation time (eigenvalue).

Information about forward and backward rate constants associated with individual steps along the reaction pathway is contained within the 4^th-order TCF. The 4^th-order TCF is constructed from experimental trajectories using Eq. (5). The time intervals τ₁ and τ₃ must be varied over a range that spans the individual decay components present in the 2^nd-order TCF, while the waiting time interval τ₂ must be varied over a range that spans slow exchange time dynamics of the system.

Simulated expressions for the 2^nd- and 4^th-order TCFs, and the equilibrium distribution of states, are calculated using the N-state master equation that is described by Eq. (7). An optimized solution can be determined by minimizing the difference between the experimentally derived functions, and the simulated functions while varying the input parameters specified by the rate constants k_ij and the observable values A_i. We thus achieve a globally optimized solution to the kinetic problem of the N-state system.

VI. Conclusions

We have shown how the analysis of 2^nd- and 4^th-order TCFs of single-molecule trajectories can be used to learn about the roles of short-lived intermediates in biochemical reactions. In principle, 6^th-order and higher TCFs could be used to study the details of even more complex biochemical reactions than the relatively simple N = 3 and N = 4 schemes examined here. The implementation of higher dimensionality TCFs is, of course, limited by S/N and data availability. Nevertheless, with the steady improvements that are currently underway to single-molecule methodology and detector technologies, such applications of generalized TCFs to elucidate complex biochemical pathways are now feasible.

The implementation of a generalized TCF analysis to microsecond-resolved single-molecule fluorescence measurements can be a powerful way to extract detailed information when the signal is too noisy to warrant analysis by direct visualization methods (e.g., HMM). However, unlike HMM, generalized TCFs are rarely utilized for such experiments. This is likely because the theory surrounding this analysis is relatively abstract and not easily approached by a general biophysical audience. In this manuscript, we have outlined the theoretical foundations to apply a generalized TCF approach to analyze single-molecule data, and we illustrated these ideas in the context of the ssDNA- (gp32)_n binding system shown in Fig. 1A.

While the generalized concepts of TCF have not yet been widely applied to the analysis of single-molecule fluorescence measurements, they hold great promise for future microsecond kinetic studies, and for experiments carried out under low signal conditions. Since many important bio-molecular interactions occur on sub-millisecond timescales, we anticipate that the application of TCF methodology can help to provide new insights to understand these dynamics, which have thus far proven difficult to access experimentally.

Appendix 1 Analytical Expression for N = 3 System

The general solution to Eq. (13) is

$$\mathit{p}(t)={\mathit{p}}^{eq}+c_1{\mathit{v}}_1{e}^{-{\lambda }_{1}t}+c_2{\mathit{v}}_2{e}^{-{\lambda }_{2}t},N=3$$ (A1)

where the eigenvalues are given by λ₁ = a + b and λ₂ = a − b with $a=\frac{1}{2}(k_{01}+k_{10}+k_{12}+k_{21}+k_{02}+k_{20})$ and $b=\frac{1}{2}[{(k_{01}-k_{12})}^2+{(k_{02}-k_{21})}^2+{(k_{10}-k_{20})}^2+2k_{01}(k_{02}+k_{10}-k_{20}-k_{21})+2k_{02}(k_{20}-k_{10}-k_{12})+2k_{12}(k_{10}-k_{20}+k_{21})-2k_{10}{k}_{21}+2k_{20}{k_{21}]}^{\frac{1}{2}}$, and the eigenvectors are given by ${\mathit{v}}_1=[v_1^0,v_1^1,v_1^2]$ and ${\mathit{v}}_2=[v_2^0,v_2^1,v_2^2]$ with $v_1^0=(k_{12}+k_{20}+k_{21}-a-b)/(k_{02}-k_{12}),v_1^1=(a+b-k_{02}-k_{20}-k_{21})/(k_{02}-k_{12}),v_2^0=(k_{12}+k_{20}+k_{21}-a+b)/(k_{02}-k_{12}),v_2^1=(a-b-k_{02}-k_{20}-k_{21})/(k_{02}-k_{12})$, and $v_1^2=v_2^2=1$.

To satisfy detailed balance, one rate constant must depend on the others, such that k₂₀ = k₀₂k₂₁k₁₀/k₁₂k₀₁. The equilibrium populations ${\mathit{p}}^{eq}=[p_0^{eq},p_1^{eq},p_2^{eq}]$ are found by solving Eq. (13) with the boundary condition ṗ(t) = 0. These solutions must also satisfy completeness: ${\sum }_{i=0}^2{p}_i(t)=1$. This gives $p_0^{eq}=\{1+[(k_{01}+k_{02})/k_{10}]+[(1-k_{20})/k_{10}]·(k_{10}+k_{12})(k_{01}+k_{02})-k_{01}{k}_{10}/[(k_{10}+k_{12})k_{20}+k_{21}{k_{10}]\}}^{-1},p_2^{eq}=p_0^{eq}·[(k_{10}+k_{12})(k_{01}+k_{02})-k_{01}{k}_{10}]·{[(k_{10}+k_{12})k_{20}+k_{21}{k}_{10}]}^{-1}$, and $p_1^{eq}=k_{10}^{-1}·[p_0^{eq}(k_{01}+k_{02})-p_2^{eq}{k}_{20}]$.

To determine the nine conditional probabilities p_ji(τ) with i,j ∈ {0,1,2}, we solve Eq. (A1) for the expansion coefficients c₁ and c₂, while assuming the appropriate boundary conditions. We label each expansion coefficient with a superscript to indicate the boundary condition. For example, the expansion coefficient $c_1^0$ corresponds to the case when all population resides in state-0 at time zero, i.e. p₀(0) = 1 and p₁(0) = p₂(0) = 0. This leads to the following expressions for the expansion coefficients: $c_2^0={(v_1^0{v}_2^1-v_1^1{v}_2^0)}^{-1}[v_1^1{p}_0^{eq}-v_1^0{p}_1^{eq}-v_1^1],c_2^1={(v_1^0{v}_2^1-v_1^1{v}_2^0)}^{-1}[v_1^0-v_1^0{p}_1^{eq}+v_1^1{p}_0^{eq}],c_2^2={[v_1^0{v}_2^1-v_1^1{v}_2^0]}^{-1}[v_1^1{p}_0^{eq}-v_1^0{p}_1^{eq}],c_1^0={(v_1^0)}^{-1}[1-p_0^{eq}-c_2^0{v}_2^0],c_1^1={(v_1^0)}^{-1}[-p_0^{eq}-c_2^1{v}_2^0]$, and $c_1^2={(v_1^0)}^{-1}[-p_0^{eq}-c_2^2{v}_2^0]$. Upon substitution of these into Eq (A1), we obtain the conditional probabilities described by Eq. (15) of the text.

Appendix 2. Analytical Description of Time-Dependent Transition Density Plots (TDPs)

Consider an N-state Markov system at equilibrium for which stochastic transitions may occur from state-i to state-j. At any instant in time, the probability to observe the system in state-i is given by the rate expression

$${\stackrel{.}{p}}_i=-k_{ij}{p}_i,$$ (A2)

which decays according to the general solution

$$p_i(t)=A{e}^{-k_{ij}t},$$ (A3)

where A is an integration constant. The elements of the time-dependent TDP are described by the probabilities that a transition occurs from state-i to state-j within a time interval τ. By integrating Eq. (A3) over this time interval, we obtain:

$$p_{ij}(\tau )=A{\int }_0^{\tau }{e}^{-k_{ij}t}dt=\frac{A}{k_{ij}}(1-e^{-k_{ij}\tau }).$$ (A4)

In the limit of very long times (τ → ∞), we expect the transition probability pij(τ → ∞) to depend on the equilibrium probability that the system resides in state-i, according to $p_{ij}(\tau \to \infty )=k_{ij}{p}_i^{eq}$. Taking the long-time limit of Eq. (A4), we obtain p_ij (τ → ∞) = A/k_ij. Solving for A, and substitution into Eq. (A4) gives the expression for the elements of the time-dependent TDP:

$$p_{ij}(\tau )=k_{ij}{p}_i^{eq}(1-e^{-k_{ij}\tau }).$$ (A5)