H4 Tails Potentially Produce the Diversity in the Orientation of Two Nucleosomes

Abstract

Histone tails play an important role in internucleosomal interaction and chromatin compaction. To understand how the H4 tails are involved in the internucleosomal interaction, an adaptively biased molecular dynamics simulation of 63 models of two stacked nucleosomes, each with the H4 tails in different locations, was carried out. This simulation generated a variety of orientations of the separated nucleosomes depending on the formation of the H4 tail bridge between the H4 tails and the DNA of the neighboring nucleosomes. For the models that showed distinctive orientations of the two nucleosomes, the free energies of the separation of the nucleosomes were further investigated using umbrella sampling simulations. The attractive force between the nucleosomes was estimated from the free energies; the force when two H4 tail bridges formed varied from 36 to 63 pN, depending on the formation of the H4 tail-bridge and the interfacial interaction, whereas the force reduced to 15–18 pN after either one of the H4 tail bridges had broken, regardless of the conformation of the H4 tail. Additional simulations of the nucleosomes show that when the H4 tail was truncated, the force between the nucleosomes became repulsive (from−3 to −7 pN). We concluded that the H4 tails potentially produce the diversity in the orientation of the two nucleosomes, which would contribute to the polymorphism of the chromatin structure.

Introduction

Human genes are encoded by a genome DNA that consists of ∼3,000,000,000 basepairs, and the length of which is ∼2 m long. The genome DNA of eukaryotes, including that of humans, is stored compactly and folded into a higher-order structure called “chromatin”. The DNA in chromatin is safely stored in the cell nucleus, which is approximately several micrometers long. At the same time, decompaction of the chromatin structure is also required for the DNA to directly interplay with DNA binding factors such as regulatory proteins and RNA polymerases for transcription, replication, repair, and recombination (1).

The basic structural unit of chromatin is called the “nucleosome”, in which ∼150 basepairs of DNA are wrapped around a protein core called a “histone octamer”. The histone octamer consists of two H2A-H2B dimers and an (H3-H4)₂ tetramer. Crystal structures show the nucleosome core particle (NCP) has a disk-like shape (2, 3). One NCP with 147-bp DNA has a charge of −150 e with −294 e from the DNA molecule and +144 e from the positively charged histone octamer. The electrostatic interaction between negatively charged NCPs can be switched from repulsive to attractive in the presence of ions by their screening the charge of the NCP (4, 5).

The N-terminal regions of H2A, H2B, H3, and H4 and the C-terminal region of H2A protrude from the nucleosome structure and are called “histone tails”. These histone tails contain many basic Arg and Lys residues and have a large positive charge. These basic residues can be subjected to posttranslational modifications such as acetylation and methylation, which regulate the activity of the genome (1). The positively charged histone tails contribute to the attractive interaction between nucleosomes, which is called “histone tail bridging” (6). Without histone tails, nucleosomes cannot fold into compact conformations due to the DNA-DNA electrostatic repulsion (7, 8).

Studies of the arrays of reconstituted NCPs that were linked to each other by linker DNA have revealed detailed interaction between the histone tails and the NCP (6, 7, 8, 9, 10). They showed that the positively charged histone tails interact differently with the negatively charged patches of the histone and DNA within the NCP compared with the spatially adjacent NCPs according to the ionic environment, which is mainly categorized into three cases: 1) the intranucleosome interaction, 2) the internucleosome interaction within the same NCP array (intraarray), and 3) the internucleosome interaction between different NCP arrays (interarrays). Case 1 is observed in low salt conditions (<0.5 mM Mg²⁺), and the NCP arrays adopt a fully extended beads-on-a-string 10-nm conformation, where histone tails interact with their own nucleosome. The NCP arrays exhibit a dynamic conformational equilibrium between case 2 and case 3 under physiological ionic conditions (100 mM Na⁺, >0.5 mM Mg²⁺) (6). At intermediate ionic concentrations (0.5–2 mM Mg²⁺, 1 mM Mg²⁺), the former (the internucleosomal interaction in an intraarray) contributes to folding the NCP array into a secondary chromatin structure (the so-called “30-nm-thick chromatin fibers”) (7). At higher (divalent cation) ionic concentrations (>2 mM Mg²⁺), the internucleosomal interactions in the interarrays aggregate by self-association into large globular oligomers, which stabilize the higher-order tertiary chromatin structure (8). As for the H4 tails, cross-linking experiments showed that the H4 tails of one NCP and the negatively charged region on the surface of the H2A/H2B dimer (called the “acidic patch” (2)) of the neighboring NCP in the intraarray (in case 2) interacted with each other (7, 9, 10, 11). Moreover, the H4 tails interact with the DNA through either intranucleosomal interaction (in case 1) (10) or internucleosomal interaction between interarrays (in case 3) (10). This indicates that the H4 tails alternatively change interactions with the acidic patch of the histone core and the DNA according to the ionic strength (9, 10).

The H4 tails extend in the direction normal to the flat faces of the NCP in the crystal structure, which are located at optimal positions on the surface of the NCP to bridge stacked NCPs (2). The involvement of the H4 tails in the stability of the stacked NCPs has been observed by x-ray and electron microscopy (EM). X-ray (2, 3, 12), EM (13), and liquid crystalline structures (14, 15) have shown that isolated NCP and NCP arrays in vitro form face-to-face stacks with the relatively flat surface of the histone octamer. In crystal structures of the NCP (2, 3), two H4 tails from one NCP contact the DNA and the acidic patch of a neighboring NCP, respectively, as crystal packings. The two NCPs are stacked and have the head-to-tail NCP-NCP orientation with their dyad axes reversed. (The head of the NCP is defined as the position of the dyad axis.) In contrast to the head-to-tail orientation of the NCPs, a head-to-head orientation of the NCPs in the stacked structures has been observed by x-ray (12) and EM (13). In the crystal structure of the tetranucleosome, an interaction among α1-helix in H2B (Ser³⁸−Val⁴⁸), C-terminal αC-helix in H2B (Gly¹⁰⁴−Thr¹²²), and α2-helix in H2A (Gly⁴⁶−Arg⁷¹) of neighboring octamers in each dinucleosomal stack was observed (12). The visible N-terminal residues of the H4 tails from residue Val²¹ interact with their own DNA and the DNA on the neighboring NCP within the tetranucleosome unit. In the cryo-EM structure of the histone octamer helical tubes, an interaction between α3-helix in H2B (Ser⁹¹−Leu¹⁰¹) and αC-helix in H2B helices of neighboring octamers was observed (13). The visible N-terminal residues of the H4 tails from residue Asn²⁵ do not interact with the neighboring histone octamer. Moreover, cryo-EM studies of liquid crystalline structures of isolated NCPs showed that at concentrations from a few millimolar to 150 mM Na⁺ and under pressures of ∼2−3 atm, the NCPs stacked on top of each other in a columnar isotropic phase and the NCPs were free to rotate along the axis of the column (14, 15). This implies that the H4 tails or the histone octamer in the NCP are not involved in a specific interaction with the neighboring NCPs, so as to fix their rotational movement. However, these static structures cannot explain the large-scale conformational change of the histone tails and nucleosomes.

Computer simulations of the NCPs using coarse-grained (CG) models have been intensively carried out to understand the dynamics of the NCPs (16). A CG model of the NCPs developed by the Takada group uses one particle to represent the amino acids of the histone cores (17) and three particles to represent the nucleotides of the DNA (18). The residue-resolved molecular simulations of trinucleosomes with this CG model showed that the tail acetylation in each histone played an important role in the folding of the trinucleosomes (19). Another CG model of the NCP developed by the Nordenskiöld group (20) uses one particle to represent the amino acids of the histone cores and five particles to represent two basepairs of the DNA. The molecular dynamics (MD) simulations of these models of isolated NCPs with explicit ions showed that the NCPs aggregated in the presence of multivalent ions, where the attractive interactions among the NCPs through histone tails were critical for the aggregation (21). A further CG model for a mesoscale model of chromatin developed by Wedemann and Langowski (22) uses oblate ellipsoids and beads to represent the NCP and the linker DNA, whereas another CG model developed by the Schlick group (23) uses a discrete surface charge optimization model of the NCP with histone tails. The Monte Carlo simulations of the NCP arrays using these CG models showed distinctive characteristics of the NCP array folding depending on the ionic environment and the linker DNA length between nucleosomes (24, 25). However, it would be difficult for the CG model to understand the dynamics of the nucleosome in detail at the atomic level. In addition, the CG models still have less reliability for describing the dynamics at a high spatial resolution because it is difficult for their force-field functions to elucidate a significant change in molecular interactions in response to a subtle change in atomic movements.

Several all-atom simulations of stacked nucleosomes were carried out to understand the role of histone tails in the internucleosomal interaction between two NCPs (26, 27, 28). Collepardo-Guevara et al. (26) examined the wild-type and acetylated stacked NCP-NCP structural models that were constructed based on the stacked head-to-head structure of NCP-NCP in the tetranucleosome crystal (12), with one H4 tail placed near the acidic patch of its neighboring nucleosome and the other H4 tail oriented toward the nucleosomal DNA. Zhang et al. (27) investigated the role of the acetylation of Lys¹⁶ in the H4 tail based on the stacked head-to-tail structure of NCP-NCP in a crystal, where one H4 tail contacts the neighboring acidic patch as crystal packings (3). The all-atom simulations of these structures showed that the acetylated H4 tails weaken the interaction with the acidic patch (26, 27). Saurabh et al. (28) considered the stacked NCPs that were constructed so that the NCPs were separated by ∼2 nm and aligned in parallel head-to-head orientation. These conventional and steered MD simulations of the modeled structures (with and without tails, at different ionic strengths of 0 and 150 mM salt) showed the separation of the NCP depended on the presence of the tails and the strength of the ionic environment. However, although a steered MD simulation is useful to observe crucial interactions between the NCPs for the stability of the stacked NCPs, the force between the NCPs reached >500 pN when the H4 tail was involved, which is far in excess of the ∼5 pN obtained by a single-molecule mechanic measurement (29).

Our motivation is to obtain the free energies of a variety of the internucleosomal interactions between the NCPs, and to understand the role of the histone tails in the internucleosomal interaction from the free energies. As far as we know, systematic analysis of the diversity of the internucleosomal interactions has not been reported at the atomic level. Previously, we investigated the intranucleosomal interaction: the dynamics of DNA breathing and unwrapping from the histone octamer surface in the mononucleosome (30, 31, 32). This work about internucleosomal interaction will give further insight into the understanding of the polymorphic nature of the chromatin structure. To obtain a variety of conformations of the separated NCPs, we carried out an adaptively biased MD (ABMD) simulation of the stacked NCPs. We further carried out umbrella sampling simulations to obtain the free energies of the models that had distinctive orientations in the ABMD simulation. We found that the H4 tails played an important role in the diversity of the orientation of the separated NCPs. In this article, we report 1) the diversity of the NCP-NCP conformations that were determined by how the H4 tail-bridge formed, and 2) the free energies of the separated NCPs.

Materials and Methods

Modeling of two nucleosomes

To prepare the initial atomic structure of the two nucleosomes, the positions and orientations of two stacked nucleosomes in the x-ray structure of the Escherichia coli tetra-nucleosome with a 167-bp NRL (PDB: 1ZBB, resolution 2.20 Å) (12) were used. The missing parts of the histone tails in the structure were modeled by using the corresponding parts in the Thermus aquaticus mononucleosome (from PDB: 1KX5, resolution: 1.9 Å) (3) as templates.

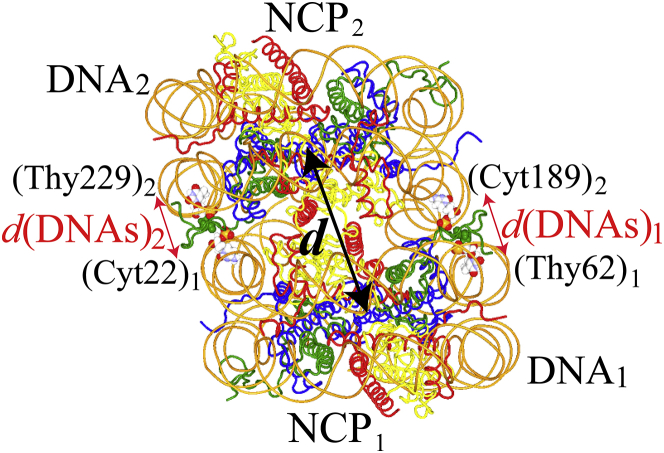
We refer to the DNA, H4 tail, and histone (excluding the H4 tail) of one NCP as DNA₁, H4 tail₁, and histone₁, and those of the other NCP as DNA₂, H4 tail₂, and histone₂ (see Fig. 1). DNA_1/2 have 167 basepairs. (The sequence of the nucleotides in the DNA_1/2 is listed in Table S1.) Note that even though a nucleosome with ∼147-bp DNA is usually referred to as the “NCP”, in this study, so long as there is no confusion, we also refer to the nucleosome with 167-bp DNA_1/2 as the “NCP”. To reduce the size of the system, the N-terminal residues of H3 (residues Ala¹ to Pro³⁰) and H2B (residues Pro² to Lys²¹) that protruded from the DNA gyres were truncated. In the initial structure, His¹⁸ of the H4 tail_1/2 is located between DNA_1/2 gyres. The distance between the phosphorus atom of Cyt²²/Cyt¹⁸⁹ in DNA_2/1 (which is closest to His¹⁸ of the H4 tail_1/2) and the phosphorus atom of Thy²²⁹/Thy⁶² in DNA_1/2 (which is closest to Cyt²²/Cyt¹⁸⁹ in DNA_2/1) was used as the indicator for the orientation of the NCPs, and is referred to as “d(DNAs)_1/2”. d(DNAs)_1/2 were monitored to observe how the NCP-NCP conformation changed during the separation of the NCPs. In this study, d (the distance between the centers of mass of rigid parts of each NCP, Gly³³−Ala¹³⁵ of H3, Asn²⁵−Gly¹⁰² of H4, Lys¹⁵−Thr¹²⁰ of H2A, and Pro⁵⁰−Lys¹²⁵ of H2B histones) was set as the reaction coordinate for our simulations (see “ABMD Simulation”). The values of d and d(DNAs)_1/2 in the initial structure were 57.2 and 9.4/9.3 Å, respectively. In this study, we call the orientation of the separated NCPs in which d(DNAs)₁ > d(DNAs)₂, d(DNAs)₁ < d(DNAs)₂, and d(DNAs)₁ ∼ d(DNAs)₂ “RIGHT”, “LEFT”, and “PARALLEL”, respectively. Moreover, to understand how each of the H4 tails (residues Ser¹−Ile²⁶) interacts with the DNA of the neighboring NCP, their atomic interactions within a distance of 3.5 Å were monitored. The H4 tail_1/2-bridge was defined as being formed at d when atomic interactions between any residue from Ser¹ to Ile²⁶ of the H4 tail_1/2 and the DNA_2/1 were observed in >10% of all the trajectories at d.

Figure 1.

The initial structure of the two nucleosomes. Two NCPs are shown in the tube model. Cyt²² and Thy⁶² in DNA₁ and Cyt¹⁸⁹ and Thy²²⁹ in DNA₂ are shown in the CPK model. His¹⁸ of the H4 tail in the NCP_1/2 is shown in the CPK model in green. H3, H4, H2A, and H2B are shown in blue, green, yellow, and red, respectively. The N-terminal residues of H3 (Ala¹ to Pro³⁰) and H2B (Pro² to Lys²¹) that protruded from DNA gyres were truncated. The reaction coordinate, d, and between the phosphorus atom of Cyt²²/Cyt¹⁸⁹ in DNA_1/2 and the phosphorus atom of Thy²²⁹/Thy⁶² in DNA_2/1, d(DNAs)_1/2, at the initial structure were 57.2 Å and 9.4/9.3 Å, respectively. To see this figure in color, go online.

Simulated annealing in vacuum

All the MD simulations were carried out using an MD simulation program called SCUBA (33, 34, 35, 36, 37) with the AMBER ff99SB (38), ff99bsc0 (39), and ff99ions08 (40) force fields for histones, DNAs, and ions, respectively. To optimize the conformation of the modeled tails, simulated annealing (SA) was performed in vacuum by assuming a distance-dependent dielectric constant of 4.0r with the value of r in Ångstroms. After the SA was repeated 150 times, the 63 lowest-energy structures were selected as representatives of the two NCPs with H4 tails located in different positions. Details are given in the Supporting Material.

MD simulations of the systems in water

After the SA, the 63 structures were each placed in an aqueous medium. Each system of the two NCPs was placed in a rectangular box ∼140 × 165 × 215 Å with the axis of the stacking of the two NCPs in the z direction. In each box, all atoms of the two NCPs were separated >15 Å from the lateral edge of the box and 40 Å from the top edge of the box. To neutralize the charges of each system, sodium ions were placed at positions with large negative electrostatic potential. Moreover, sodium and chloride ions were added to each box at random positions at a concentration of 150 mM NaCl. Then ∼135,000 TIP3P water molecules (41) were added to surround each system. In total, each system comprised ∼460,000 atoms.

All the systems were equilibrated at a constant pressure of one bar and a temperature of 300 K for 5 ns. The dielectric constant used was 1.0 and the van der Waals interactions were evaluated with a cutoff radius of 9 Å. The particle-particle particle-mesh method (42, 43) was used for the electrostatic interactions for the direct space cutoff of 9 Å. The Langevin dynamics algorithm was utilized to control the temperature and pressure of the system. The coupling times for the temperature and pressure control were both set at 2 ps⁻¹. The SHAKE algorithm (44, 45) was used to constrain all the bond lengths involving hydrogen atoms. The leap-frog algorithm with a time step of 2 fs was used throughout the simulation to integrate the equations of motion. Details are given in the Supporting Material.

ABMD simulation

To observe the separation of the NCPs in the two NCPs, the ABMD method (46) combined with the multiple walker method (47) was employed in SCUBA. The equations of motion used in the ABMD method are expressed as (46)

$$\begin{array}{c}{m}_a\frac{d^2{\mathbf{r}}_a}{d{t}^2}={\mathbf{F}}_a-\frac{\partial }{\partial {\mathbf{r}}_a}U\left[t|\sigma \left(\mathbf{R}\right)\right],\\ \frac{\partial U\left(t|d\right)}{\partial t}=\frac{k_{\text{B}}T}{{\tau }_F}K\left[d-\sigma \left(\mathbf{R}\right)\right],\end{array}$$ (1)

where R ≡ (r₁, …, r_N) are the coordinates of the NCP, and N is the number of atoms in the two NCPs. d is the reaction coordinate, and σ(R) is a function to give the value of the reaction coordinate. k_B is the Boltzmann constant, T is the constant temperature, τ_F is the flooding timescale, and K is the kernel that has distribution around the reaction coordinate. The first equation is for atom a, with an additional force coming from the biasing potential U(t|d) with an ordinary atomic force of F_a. The second equation is the time-evolving equation of the biasing potential. Details of the ABMD algorithm used in SCUBA are given in (36).

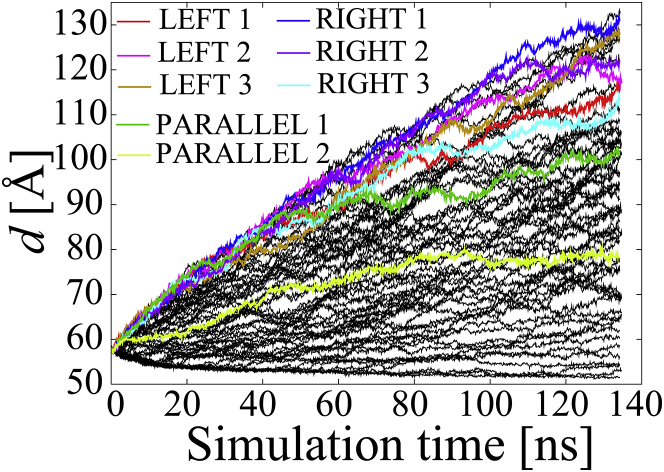
The ABMD simulations were carried out at a constant volume and a temperature of 300 K for 134 ns per system (a total of 8.4 μs for all 63 systems). The value of the reaction coordinate in the initial structure was 57.2 Å, and the range of the reaction coordinate for the ABMD simulations was set at d ≥ 50.0 Å. The resolution of the reaction coordinate, Δd, was set at 1.0 Å. The relaxation time for the free-energy profile in Eq. 1, τ, was set at 5000 ps. The two NCPs separated from each other in many systems, as shown in Fig. 2. The conformation of the NCPs was stored every 1 ps for analysis.

Figure 2.

The evolution of the reaction coordinate, d, of all 63 models during the ABMD simulation. The eight models that were selected to evaluate the free energies using umbrella sampling simulations are colored (red, magenta, and brown in LEFTs 1–3; blue, cyan, and purple in RIGHTs 1–3; and dark green and light green in PARALLEL 1–2, respectively). To see this figure in color, go online.

Umbrella sampling simulations

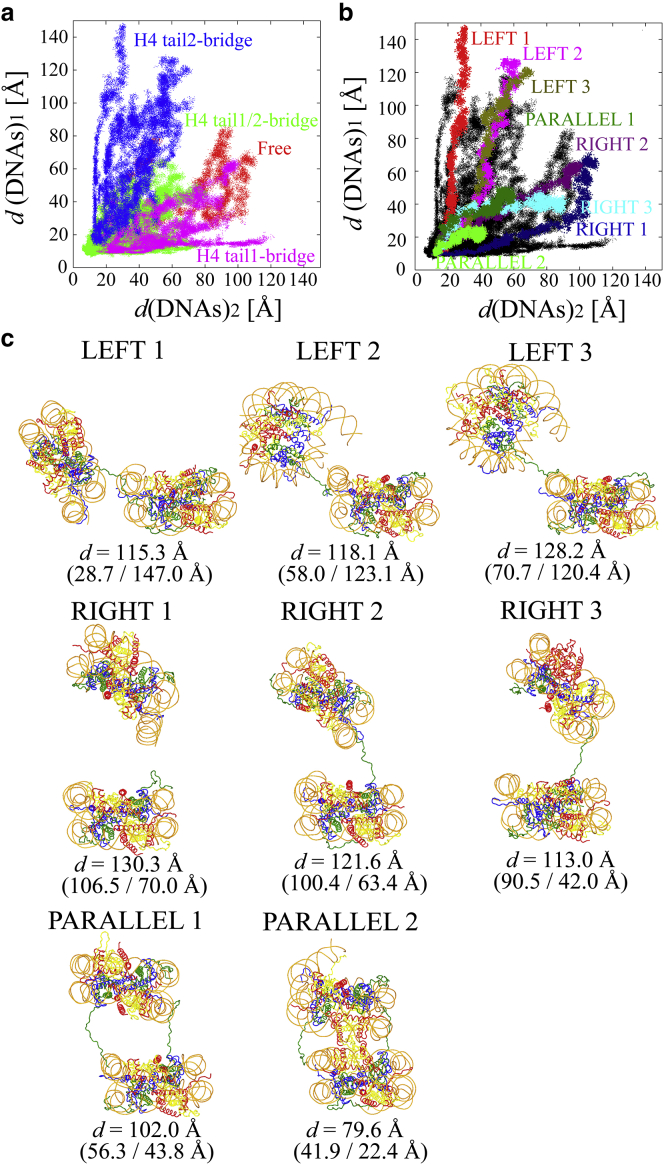
Theoretically, for large enough τ_F and small enough width of the kernel, U(t|d) converges toward the free-energy F(d) times −1 as the simulation time elapses from t = 0 to ∞ (46). Using τ_F with a certain finite amount of time, the biasing potential (free-energy landscape times −1) fluctuates around the free energy during the ABMD simulation (36, 46). However, the biased potential did not show any fluctuation as shown in Fig. S1 a, indicating that the convergence of the free energy is not accomplished. Moreover, as 63 systems moved to different conformations from each other as shown in Fig. 3, the identical biasing potential in our ABMD simulation would not be appropriate to represent possible different free energies for each system. In this study, we paid attention to some models that we observed had distinctive orientations of the NCPs in the ABMD simulation (LEFTs 1–3, RIGHTs 1–3, and PARALLELs 1–2 as shown in Fig. 3). Instead of continuing the ABMD simulation, we carried out umbrella sampling simulations of these models to obtain their free energies.

Figure 3.

(a) The trajectories of d(DNAs)_1/2 of all 63 models during the ABMD simulation. The points are colored in red, blue, and purple when only one H4 tail₁-bridge formed, when only one H4 tail₂-bridge formed, and when both H4 tail_1/2-bridges formed, respectively. (b) The trajectories of d(DNAs)_2/1 in LEFTs 1–3, RIGHTs 1–3, and PARALLELs 1–2. The colors are the same as in Fig. 2. (c) The final structures in LEFTs 1–3, RIGHTs 1–3, and PARALLELs 1–2 with d and d(DNAs)_2/1. To see this figure in color, go online.

The weighted histogram analysis method (48) was used to evaluate the free energy from the sampled trajectories in the umbrella sampling simulations. In the weighted histogram analysis approach, the unbiased probability distribution P(R) is calculated from the biased probability distribution of the sampled coordinates as

$$P\left(\mathbf{R}\right)=\sum _{i=1}^{N_{\text{win}}}{n}_i\left(\mathbf{R}\right)P_i^{\left(b\right)}\left(\mathbf{R}\right)\times {\left(\sum _{j=1}^{N_{\text{win}}}{n}_j\left(\mathbf{R}\right)\text{exp}\left\{\left[F_j-V_j\left(\mathbf{R}\right)\right]/k_{\text{B}}T\right\}\right)}^{-1},$$ (2)

where R is the atomic coordinates, N_win is the number of windows, n_i(R) is the number of data points in the ith window, P_i^(b)(R) is a biased probability from the raw data obtained in the umbrella sampling simulation, and V_j(R) is the biasing potential in the jth window. In this study, V_j(R) was selected to be the sum of a harmonic potential and the ABMD biasing potential in the final stage of the ABMD simulation, which has the form

$$V_i\left(\mathbf{R}\right)=k_i{\left[d\left(\mathbf{R}\right)-d_i^{\text{fix}}\right]}^2+c\cdot \left\{U_{\text{abmd}}\left[d\left(\mathbf{R}\right)\right]-U_{\text{abmd}}\left(d_0\right)\right\},$$ (3)

where d(R) is the umbrella sampling coordinate, which was set to be σ(R). d_i^fix is a fixed distance to sample umbrella coordinates of d(R) around the desired position of d_i^fix. The initial coordinates of R for the ith window were selected from the trajectories that had similar d_i^fix in the ABMD simulation. The values of d_i^fix were set from 58 Å to 110, 115, and 110 Å for LEFTs 1–3; 122, 118, and 105 Å for RIGHTs 1–3; and 100 and 80 Å for PARALLELs 1–2, respectively, with intervals of 1 Å (i = 1,…, N_win). k_i is an arbitrary harmonic force constant, which was set at 0.2 kcal/mol/Ų. U_abmd is the biasing potential at the final stage of the ABMD simulation (Fig. S1 a). Here, d₀ is a constant such that U_abmd[d(R)] −U_abmd(d₀) is zero at d = d₀. c is the arbitrary constant to scale U_abmd. In this study, c = 0.25 and 0.0 were used for d > d₀ and d ≤ d₀ with d₀ = 60.0 Å, respectively (see Fig. S1 b). The umbrella sampling simulation was carried out for 30 ns. The conformations of the NCPs were stored every 1 ps for analysis. The trajectory for the last 20 ns was used for the calculation of the free-energy landscape.

The relative free-energy F(R) at a given R is obtained as

$$F\left(\mathbf{R}\right)=-k_{\text{B}}T\text{ln}P\left(\mathbf{R}\right).$$ (4)

Details are given in the Supporting Material.

Umbrella sampling simulations of the two NCPs without the H4 tails

To understand the role of the H4 tails, umbrella sampling simulations of the two NCPs without the H4 tails were also carried out for LEFT 1, RIGHT 1, and PARALLEL 1, which had distinctive orientations of the NCPs. Details are given in the Supporting Material.

The conformational entropies of the H4 and H2A tails

The conformational entropies of the H4 and H2A tails were calculated using the quasiharmonic approximation (49) as follows:

$$S_{\mathrm{conf}}=0.5k_{\text{B}}\text{ln}\det \left[\mathbf{1}+\left(k_{\text{B}}T{e}^2/{\hslash }^2\right)\mathit{\sigma }\right],$$ (5)

where e is Euler’s number, and ħ is Planck’s constant divided by 2π. σ = 〈x x^T〉 represents the mass-weighted covariance matrix, where x is the coordinates of the H4 tail_1/2 (residues 1–26) and the H2A tail_1/2 (residues 1–17). Details are given in the Supporting Material.

Computational time

All the simulations, requiring a total time of 27 μs (8.4 μs for the ABMD simulation and 18.6 μs for the umbrella sampling simulations), were mainly performed on the Fujitsu BX900 and SGI ICE X supercomputers at Japan Atomic Energy Agency. The total computational time was >30,000,000 CPU core hours.

Results

The diversity in the orientation of the two separated NCPs

The time evolution of d and the trajectory of d(DNAs)_2/1 for all 63 models during the ABMD simulation show that a variety of types of separation of the NCPs occurred in LEFTs, RIGHTs, and PARALLELs (Figs. 2, 3, and S2). As only the H4 tail conformation was different in the initial 63 configurations, the origin of the diversity in the separation must have come from the H4 tails. To understand what kind of interactions between the H4 tails and NCPs correlated with the diversity of separation, the formation of the H4 tail-bridge between H4 tail_1/2 and DNA_2/1 was analyzed. Fig. 3 a shows that the orientations of the NCPs in LEFTs, RIGHTs, and PARALLELs were different from each other, where one H4 tail-bridge between H4 tail₁ and DNA₂, one H4 tail-bridge between H4 tail₂ and DNA₁, and two H4 tail-bridges between H4 tail_1/2 and DNA_2/1 formed, respectively. These results clearly show that the diversity of separation of the NCPs is correlated with the formation of the H4 tail-bridge interaction.

The free energies of the two separated NCPs

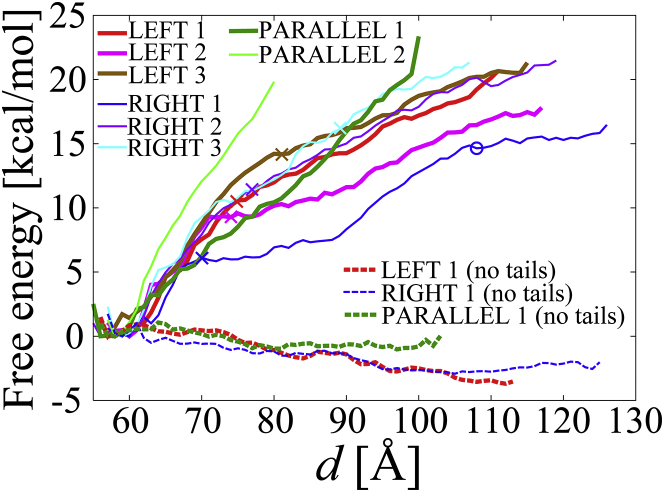
We selected eight out of 63 models that had distinguishing internucleosomal interactions (LEFTs 1–3, RIGHTs 1–3, and PARALLELs 1–2 (Fig. 3)), and calculated their free energies using umbrella sampling simulations. Fig. 4 shows all the free energies of the NCPs against d. (The root mean square errors in the free energies were estimated to be ∼0.3 kcal/mol against d (Fig. S3).) The free energies increased from 0 at d = 58 Å up to ∼20 kcal/mol at each final position of d = ∼80−120 Å. This indicates that the internucleosomal interaction between the NCPs was attractive. It should be noted that in the LEFTs 1–3 the distance between one NCP and the image of the periodically neighboring NCP in the direction of z was <15 Å at d ≥ 106, 107, and 107 Å, respectively (see Fig. S4), indicating that the free energy in LEFTs 1–3 at d > 105 Å may include an artifact from the periodic boundary condition.

Figure 4.

The free energies of the two separated NCPs against d in LEFTs 1–3, RIGHTs 1–3, and PARALLELs 1–2. The unit is Å. The colors are the same as in Fig. 2. To see this figure in color, go online.

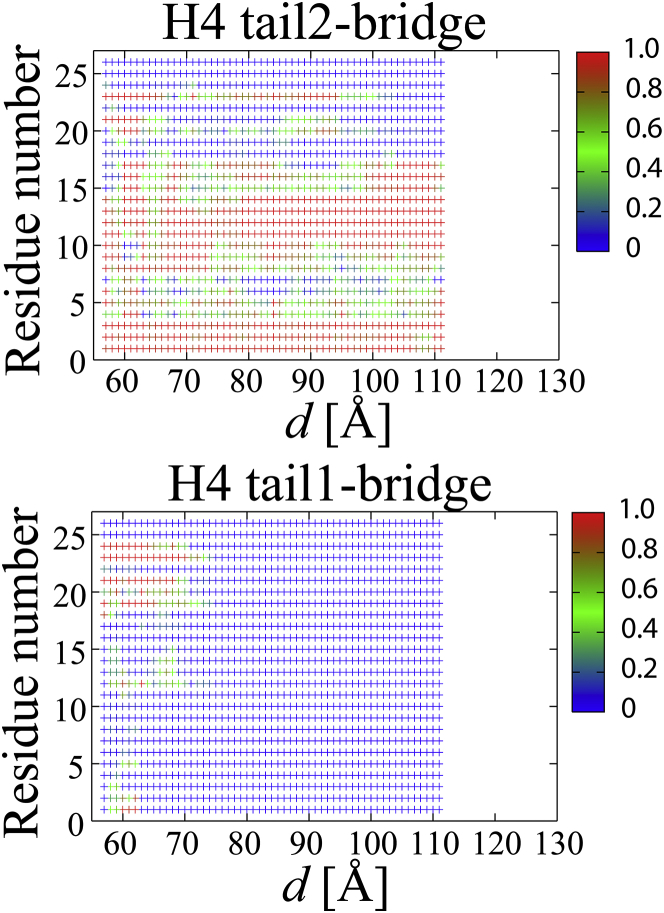
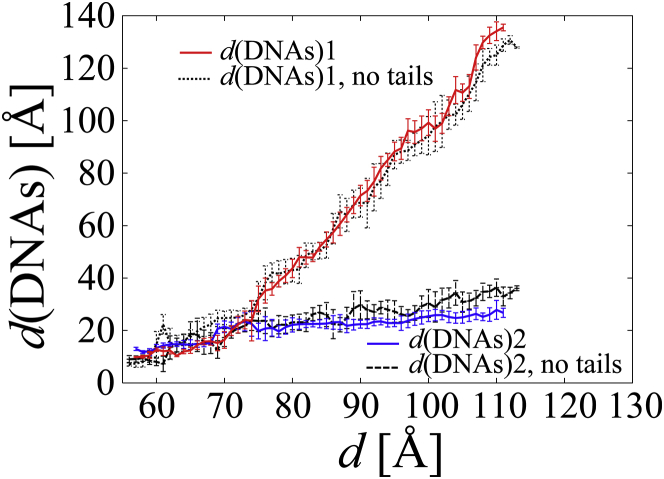
To understand how the H4 tail-bridge interaction correlated with the orientation of the NCPs, the population of the interaction between each residue in the H4 tail and the DNA was counted as shown in Figs. 5 and S5. (As a reference, the number of atomic contacts between the NCPs is shown in Fig. S6.) Figs. 5 and S5 show that a high population around Arg¹⁹−Arg²³ was observed in all the cases in the range of d = ∼58 to 70 Å. On the contrary, the population around Ser¹−Lys¹⁶ varied among the cases. In LEFTs 1–3, H4 tail₁ maintained the bridge interaction, during which d(DNAs)₂ gradually increased but did not reach >30, 60, and 60 Å, respectively (see Figs. 6 and S7). This indicates that the strong interaction between H4 tail₁ and DNA₂ prevented d(DNAs)₂ from increasing during the separation of the NCPs. On the other hand, after H4 tail₂ detached from DNA₁ at d = 75, 74, and 81 Å in LEFTs 1–3, respectively, d(DNAs)₁ rapidly increased. Consequently, the maintenance of the H4 tail₁-bridge and the breakage of the H4 tail₂-bridge facilitated the opening of the NCPs on the left side.

Figure 5.

The average population of residues that participated in the formation of H4 tail_1/2-bridge in LEFT 1. The average was calculated according to Eq. S8. The average population in LEFTs 2–3, RIGHTs 1–3, and PARALLELs 1–2 are shown with LEFT 1 in Fig. S5. To see this figure in color, go online.

Figure 6.

d(DNAs)_2/1 against d in LEFT 1 with and without the H4 tails. The average and RMSD were calculated according to Eqs. S8 and S9, respectively. d(DNAs)_2/1 in LEFTs 2–3, RIGHTs 1–3, and PARALLELs 1–2 are shown with LEFT 1 in Fig. S7. To see this figure in color, go online.

In RIGHT 1, after H4 tail₂ detached from DNA₁ at d = 70 Å (see a cross on the blue curve in Fig. 4), the H4 tail₁-bridge gradually stretched until H4 tail₁ detached from DNA₂ at d = 108 Å (see open circle). The increase in the free energy substantially stopped after d = ∼108 Å because the attraction between the NCPs by H4 tail_1/2-bridges disappeared. Fig. S7 b1 shows that from d = 108 to 123 Å, d(DNAs)₁ changed from 36.8 to 54.8 Å whereas d(DNAs)₂ changed from 99.2 to 108.6 Å, showing that the change of d(DNAs)₁, 18.0 Å, was larger than that of d(DNAs)₂, 9.4 Å. This indicates that the electrostatic repulsion between DNAs at d(DNAs)₁ was stronger than the repulsion at d(DNAs)₂, resulting in the partial recovery of a parallel conformation from the tilted conformation (see also Fig. S8 b1). The recovery from the tilted conformation toward a parallel conformation after the two H4 tail_1/2-bridges were broken was also observed in two models in the ABMD simulation, as shown in Fig. S2 d. In RIGHTs 2 and 3, the H4 tail₁ maintained the bridge interaction in a similar way to RIGHT 1, whereas H4 tail₂ detached from DNA₁ at d = 77 and 89 Å. When d(DNAs)₂ increased to reach ∼100 Å in RIGHTs 2 and 3, the separation of the NCPs reached d = 120 and 110 Å, respectively, as shown in Fig. S7, b2 and b3 (see also Fig. S8, b3 and b4).

In PARALLELs 1 and 2, both H4 tail_1/2-bridges were retained. The sharp rise of the free energies up to ∼20 kcal/mol at d = 80−100 Å was thought to be because the two H4 tail_1/2-bridges strongly prevented the NCPs from separating from each other. In PARALLEL 1, although the H4 tail₂-bridge around Arg¹⁹−Arg²³ disappeared at d = 74 Å, Ser¹−Lys⁵ of the H4 tail₂ newly participated in the H4 tail₂-bridge formation after d = 74 Å (Fig. S5 c1), which maintained the parallel conformation. In PARALLEL 2, in addition to the two H4 tail_1/2-bridges, internucleosomal interactions among the N-terminal of histone H2A_1/2, the C-terminal of histone H2B_1/2, and DNA_2/1 were intermittently retained (data not shown). Moreover, Lys¹¹⁷ in the C-terminal αC-helix of histone H2B₁ had a new interaction with Pro⁴⁷ in a loop between α1-helix and β1-sheet of H2B₂ at d = ∼80 Å, which did not exist in the initial structure (Fig. S8 c3). These internucleosomal interactions among H2A_1/2, H2B_1/2, and DNA_2/1 are thought to be electrostatically stabilized and have contributed to the rapid rise in the free energy to 20 kcal/mol, whereas the two NCPs were still relatively close to each other (d = 80 Å).

Figs. 5 and S5, a and b, show that H4 tail₁ in LEFTs 1–3 and H4 tail₂ in RIGHTs 1–3 detached from DNA₂ and DNA₁ at d = 75, 74, 81 Å and d = 70, 77, 89 Å, respectively (see also Fig. S8, a and b). These values of d (the crosses in Fig. 4) roughly correspond to the values of d when the increase in their free energies slowed down. This indicates that the maintenance of the two H4 tail_1/2-bridges greatly contributed to the free energy until one H4 tail-bridge broke. After that, the free energy gradually increased until the remaining bridge was broken.

The H4 tail-bridge interaction is the main contributor to the free energy

To confirm whether the H4 tails were the main contributor to the free energies, the free energies of the NCPs without the H4 tails for LEFT 1, RIGHT 1, and PARALLEL 1 were calculated as shown in Fig. 4. The free energies of the NCPs without the H4 tails had broad peaks of ∼1−2 kcal/mol at d = ∼58−75, ∼58−63, and ∼58−70 Å in LEFT 1, RIGHT 1, and PARALLEL 1, respectively. Fig. S6 d shows that the composition of the interfacial interaction (between histone₁ and histone₂; histone_1/2 and DNA_2/1; and DNA₁ and DNA₂) varies among the three cases. These peaks of ∼1−2 kcal/mol seem to come from interfacial interaction between the stacked NCPs. After the interfacial interaction disappeared, the free energies became negative, indicating that the interaction between NCPs without the H4 tails became repulsive. This is consistent with experimental data, which shows that the removal of the H4 tails prevents the NCP array from folding (7) and oligomerizing (8). The comparison of the NCP–NCP conformations with and without the H4 tails at the same d indicates that without the H4 tails, d(DNAs)₂ increased by 4.2 Å on average in the range of d = ∼75 to 111 Å for LEFT 1, and d(DNAs)₁ increased by 4.0 Å on average in the range of d = ∼63 to 107 Å for RIGHT 1 (Figs. 6 and S7, a and b). This indicates that the DNA–DNA repulsion was strong between the NCPs because they lost the attractive interaction that is produced by H4 tails. Consequently, we confirmed that the H4 tail-bridge was the main contributor to the attractive interaction between the NCPs in the simulations.

The H4 tail-bridge enthalpically stabilizes the stacked NCPs

The screening of the electrostatic repulsive interaction between negatively charged NCPs has been suggested to be due not only to the presence of a cation such as a sodium ion and a magnesium ion (4, 28) but also the flexible cationic tails that form bridges and reduce the repulsion between NCPs (28, 50). We analyzed the screening of the negatively charged NCPs by the positively charged Lys and Arg in the H4 and H2A tails. Fig. S9 shows that the H4 tails mainly interacted with the atoms of the phosphate groups in the DNA (in PARALLEL1). This indicates that the H4 tail-bridge screens the DNA-DNA repulsion between the NCPs to stabilize the stacked NCPs. Fig. S9 also shows that the H4 tail-bridge was dynamic as the sites of their interactions continuously changed during the simulation. The major interaction between the H4 tails and the phosphate groups, and the dynamic behavior of the H4 tails, were also observed in the other cases, LEFTs 1–3, RIGHTs 1–3 (figure not shown), and PARALLEL 2 (Figs. S9 d–f). As for the H2A tails, they interacted with the DNA of the neighboring NCP at d = 58 Å in PARALLEL 1 (Fig. S9 a) but not at d > 62 Å, which was similar to other cases except in PARALLEL2, where the H2A tail-bridge was observed at d = 80 Å (Fig. S9 f). This may indicate that the H2A tail stabilizes the stacking of the NCPs when they are close together.

The secondary structure of the H4 and H2A tails was also analyzed as shown in Fig. S10. The structures observed at all d were mainly turn or coil. The regular secondary structures such as α-helix, 3₁₀-helix, and β-strand were not substantially observed at any d. This trend was true for other cases (LEFTs 1–3, RIGHTs 1–3, and PARALLEL 2) (see Table S2). These results indicate that the H4 tails were disordered at any d, thus the stretching of the H4 tail itself (the internal energy within the H4 tail) as d increased would not significantly contribute to the free energy.

Moreover, the conformational entropies of the H4 and H2A tails were analyzed using the quasiharmonic approximation (49). Overall, the conformational entropies of the H4 tails increased as d decreased whereas those of the H2A tails were constant (Fig. S11). These observations indicate that the enthalpically unfavorable breakage of the H4 tail-bridge counteracted the entropically favorable increase in the flexibility of the tails during the separation of the NCPs. Consequently, strong electrostatic interaction for screening is thought to be an important enthalpic component for the stabilization of the nucleosome stacking, and the increase in the free energy is thought to be mainly from the breakage of the electrostatic interaction.

Forces for the two separated NCPs

The magnitude of the attractive force between the NCPs was calculated from the slope of the free energies before and after one H4 tail-bridge broke. The force between NCP₁ and NCP₂, which was derived from the interfacial interaction and the two H4-tail bridges, was estimated from the regression line for the free energy in the range of d = 58 Å to d just before the first H4 tail-bridge had broken (shown by crosses in Fig. 4). This resulted in 48.0, 49.3, 47.4, 41.2, 47.4, and 36.6 pN in LEFTs 1–3 and RIGHTs 1–3, respectively (6.97 pN = 1 kcal/mol/nm). The force between NCP₁ and NCP₂, which is derived from the remaining bridge, was estimated from the regression line for the free energy in the range of d at the first bridge breakage to the final d to be 18.2, 15.6, 14.9, 18.4, 16.8, and 18.4 pN in LEFTs 1–3 and RIGHTs 1–3, respectively. Note that in LEFTs 1 and 3, the free energy at d = 111 and 115 Å, respectively, was not used in the analysis because the free energy was not reliable. In fact, the number of data points at d = 111 and 115 Å (n_i(d) in Eq. 2) to calculate the free energy was <1% of the number of data points (20,000) for each window. In RIGHT 1, d = 107 Å, just before all the H4 tail_1/2-bridges broke, was used as the final d. The attractive force between NCP₁ and NCP₂ due to the two H4 tail_1/2-bridges in PARALLEL 1 was estimated to be 35.6 pN using the values of the free energy in the range of d = 58 to 99 Å (as the free energy at d =100 Å was not reliable for the aforementioned reason), which is roughly double of ∼15−18 pN from one tail bridging. Similarly, using the values of the free energy in the range of d = 58 to 80 Å, the force in PARALLEL 2 was estimated to be 62.6 pN, indicating that the strong internucleosomal interactions among the N-terminal of the H2A_1/2, C-terminal H2B_1/2, and DNA_2/1 (Figs. S6 c2 and S8 c3) contributed to the large force. The force between NCP₁ and NCP₂ without the H4 tails was estimated using the regression line for the free energy in the range of d = 70, 62, and 65 to 100 Å in LEFT 1, RIGHT1, and PARALLEL1, respectively. The free energy at d > 100 Å was not used, as the increase in the free energy may include an artifact from the periodic boundary condition (see Fig. S4). This resulted in −7.2, −4.3, and −2.7 pN for LEFT 1, RIGHT 1, and PARALLEL 1, respectively.

Discussion

Comparison of the computational results from the NCPs with the experimental data

The free energies of the two separated NCPs can give an insight into the understanding of the internucleosomal interaction between NCPs observed in experiments. The free energies in LEFTs 1–3, RIGHTs 1–3, and PARALLELs 1–2 were stable at d = ∼58 Å. The results of the all-atom simulation of the stacked NCPs with all the tails and 147 × 2 bp DNAs at 150 mM NaCl by Saurabh et al. (28) showed that the inter-NCP distance fluctuated between ∼56 and 58 Å, which is consistent with our result. It should be noted that the NCP-NCP orientation was different from that in our study; the NCPs in their system were in a head-to-head orientation with their dyad axes aligned parallel to each other (the dyad-dyad angle of the NCPs was 0°). In contrast, the dyad-dyad angle of the NCPs at d = ∼58 Å in our system was >20° (12). These results indicate that the stability of the NCPs may not depend on the rotation of the NCP. This independence is consistent with the experimental data that the stacked NCPs in the columnar isotropic phase of liquid crystalline structures were free to rotate along the axis of the column (14, 15).

We found that the free-energy curves against d were different among LEFTs 1–3, RIGHTs 1–3, and PARALLELs 1–2. This is thought to come from the difference in the direct interfacial interaction between the histones (excluding the H4 tails) (Fig. S6) and the difference in the H4 tail-bridge interaction (Figs. 5 and S5). The former is estimated to be 1−2 kcal/mol from the results of the free energies of the NCPs without the H4 tails (Fig. 4). The latter is evaluated by how far H4 tail-bridges were retained. Arg¹⁹−Arg²³ at the root of the H4 tails_1/2 were located at the interface between NCP₁ and NCP₂, and interacted with DNA_2/1 at d = ∼58−70 Å. Arg¹⁹−Arg²³ appear to contribute to the large increase in the free energy at d = ∼58−70 Å, before the stabilized interfacial interaction is broken. At d > ∼70 Å, some of Ser¹−Lys¹⁶ were involved in forming the H4 tail_1/2-bridges. In LEFTs 1–3 and RIGHTs 1–3, the d values when the first H4 tail-bridge broke are shown by crosses in Fig. 4. The farther the H4 tail_1/2-bridges were retained, the more the free energy increased. The wide range of d values (75, 74, 81, 70, 77, and 89 Å) at which the bridge was broken may explain the large variation in the force-extension curve of the NCP arrays in a single-molecule experiment (51). In this experiment (51), a single-molecule force spectroscopy on folded NCP arrays (10 chromatin fibers reconstituted on 15 repeats of a 197-bp nucleosome) at the physiological salt concentration of 100 mM K⁺ and 2mM Mg²⁺ showed that the transitions from a folded NCP array to a string of nucleosomes in an extended conformation occurred at different extensions for 10 different fibers (51). The large variation in extension was attributed to the variation in the composition of the NCP array (such as an incomplete NCP-array reconstitution and/or partial dissociation of nucleosomes) (51). The variation in the H4 tail_1/2-bridges observed in our study may also contribute to the variation in extension.

The internucleosomal stretching force was estimated to be 4.5 pN by a single-molecule mechanic measurement of the 197-bp NRL nucleosomal array of 25 nucleosomes with 50-bp linker DNA at the physiological salt concentration of 100 mM K⁺ and 2 mM Mg²⁺ (29). The force was considered to come from an extension of a single stack of perpendicular nucleosomes (29). The height of the nucleosomal array of 25 stacked NCPs was measured to be ∼200 nm, meaning that the length of stacking per one NCP was ∼80 Å. This indicates that these NCPs can have irregular stacking conformations as observed in our study at d = ∼80 Å where the neighboring NCPs usually interacted with each other by one H4 tail-bridge. As cross-linking experiments have suggested that the internucleosomal interaction in the intraarray was between the H4 tails and the acidic patch of the neighboring NCP (7, 9, 10), the internucleosomal stretching in the single molecule experiment may be derived from the H4 tail–acidic patch interaction.

The results of the all-atom steered MD simulation of two NCPs by Saurabh et al. (28) indicate that the H4 tail-acidic patch interaction significantly reduced at d = ∼80 Å because the Arg²³-acidic patch interaction that was observed at d = ∼58−60 Å was not maintained up to d = ∼80 Å. Interestingly, in the simulation, Arg¹⁷ maintained its interaction with the DNA of the neighboring NCP at d = ∼80 Å even after the H4 tail-acidic patch interaction was lost (28). This indicates that the H4 tail can maintain the interaction with the DNA even when the H4 tail-acidic patch interaction is lost at d = ∼80 Å. Consequently, we assume that the H4 tail-acidic patch interaction could be replaced by the H4 tail-DNA interaction in the single-molecule experiment at d = ∼80 Å, and thus the force in the experiment would be similar to the calculated force of 15−18 pN. However, this value is ∼4 times larger than the experimental value of 4.5 pN.

One reason for the difference may be because the linker DNA was not included in this study. The linker DNA that connects the neighboring NCPs adopts a stressed form, i.e., a bent and twisted conformation in the NCP array. This energetically unfavorable conformation of the linker DNA would be relaxed by the stretching of the NCP array. The repulsion between the negatively charged linker DNAs would also be relaxed. Therefore, the repulsive internucleosomal interaction that is derived from the linker DNA will counteract the attractive interaction between the NCPs by the H4 tail-bridge, which would result in the reduced value of 4.5 pN that was observed in the experiment.

Another reason for the difference may be because the H4 tail does not always interact with the acidic patch in the intraarray. A CG simulation of an NCP array of 24 nucleosomes showed that the H4 tails interacted with not only the acidic patch but also the DNA (23) (in the presence of 150 mM monovalent salt, 1 mM divalent salt, and linker histone). This indicates that the H4 tails exchange interaction with the acidic path and the DNA, during which the H4 tails would not strongly interact with the neighboring NCP and the force between the NCPs could be reduced to the calculated force of ∼−3 to −7 pN. The CG simulation also showed that the time the H4 tails spent engaged in internucleosomal interactions with neighboring nucleosomes was ∼30%, and with nonparental linker DNA, ∼0%; whereas the time spent in intranucleosomal interactions with the parent nucleosome was ∼40%, and with parental linker DNA, ∼0%. The time spent in free interaction was ∼30%. Assuming that the rate of the nucleosomal interactions is the same as that of the single stack of perpendicular nucleosomes in the experiment, the stretching force would be reduced to ∼15−18 pN × 30% + ∼−3 to −7 pN × 30%, which equals ∼3–5 pN, within which the single-molecule mechanic measurement of 4.5 pN falls.

Consequently, the experimental data of the internucleosomal stretching would be the averaged value derived from many different conformations of the NCPs in the specific NCP array, where some NCPs have specific H4 tail-bridge interactions and others have nonspecific interactions without the H4 tails being involved.

Mechanism of structural polymorphism and dynamics of chromatin

In this study, the main contributor to the free energies for the separation of the NCPs was found to be the H4 tail-bridge. Arg¹⁹−Arg²³ were involved in the interfacial interaction between the NCPs at d = ∼58−70 Å. Arg¹⁹−Arg²³ are likely to be involved in the internucleosomal interaction when the NCPs are close together. There are four Lys residues in the H4 tail that are known as sites of acetylation in vivo—Lys⁵, Lys⁸, Lys¹², and Lys¹⁶. At least one residue of Lys⁵, Lys⁸, and Lys¹² was almost always involved in the H4 tail-bridge interaction in all the cases (Figs. 5 and S5). As residues Ser¹−Lys¹² can extend far enough to reach the neighboring NCP from their own NCP, it is likely that they are involved in the internucleosomal interaction when the NCPs are far apart. In this study, Lys¹⁶ between Ser¹−Lys¹² and Arg¹⁹−Arg²³ acted as a pivot in opening the NCPs. Lys¹⁶ is known to be unique as the acetylation of Lys¹⁶ leads to the disruption of the intra-NCP-array interaction (52) or weakens the inter-NCP-array interaction (53), which cannot be simply explained by the charge neutralization. In the crystal structure that has a head-to-tail orientation (PDB: 1AOI (2)), Lys¹⁶−Arg²³ interacted with the acidic patch of the neighboring NCP at d = ∼65−68 Å. However, in the head-to-head orientation in our study, the interaction between Lys¹⁶−Arg²³ and the acidic patch was not observed at any d. This indicates that H4 tail-acidic patch interaction may not be essential for the stability of the nucleosome stacking. The all-atom simulation of the two NCPs by Saurabh et al. (28) also showed that Lys¹⁶, which interacted with the DNA not the acidic patch, was critical for the stability of the NCPs. Therefore, Lys¹⁶ would stabilize the NCP by interacting with either the DNA or the acidic patch according to the conformational change of the NCPs in the chromatin.

Chromatin is generally considered to have an irregular structure in vivo (54), although a regular structure can be present in specific cells (55) (for a review, see (54)). Our simulations suggest that Ser¹−Lys¹² may contribute to the formation of the irregular structure as the H4 tail-bridge is able to extend far enough to form a variety of internucleosomal interactions, as observed at d > ∼80 Å. The irregular conformation would be facilitated when Ser¹−Lys¹² are dominant in the internucleosomal interaction that forms the long H4 tail-bridge, whereas the regular structure would be facilitated when Arg¹⁹−Arg²³ are dominant in the internucleosomal interaction that forms the short H4 tail-bridge. Consequently, the variety of internucleosomal H4 tail-bridges would drive the NCPs to form the regular and irregular structures of chromatin according to different formations of the H4 tail-bridge.

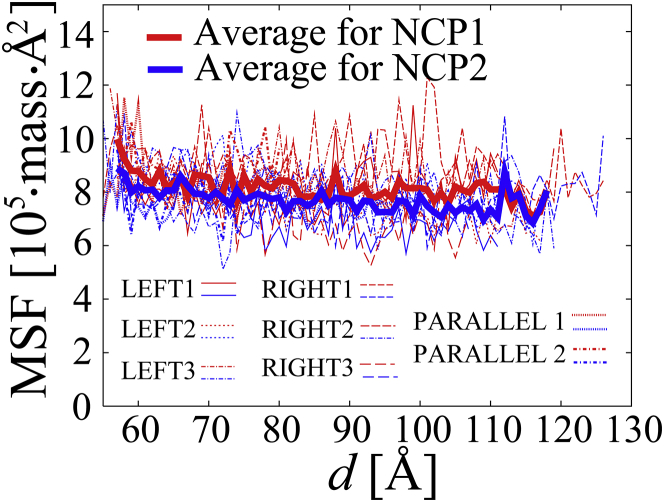
Finally, we examined the change in the dynamics of the NCPs from the regular stacked conformation to the separated irregular conformation. The total mass-weighted mean square fluctuation (MSF) of ${\sum }_{\alpha \in \text{atoms}}{m}_{\alpha }\Delta {\mathbf{r}}_{\alpha }^2$ for each NCP was measured against d. Fig. 7 shows that the MSF of each of the regular stacked NCPs was no lower than that of each of the irregularly separated NCPs. Contrary to our expectation, the dynamics of the NCP in the stacked state was maintained to a similar extent to that in the separated state. Probably, some of the entropy loss of the translational and rotational movements of each NCP in the stacked form was compensated for by the fluctuation of the NCP itself (56). This observation that the stacked NCPs maintained the large dynamics would be consistent with experimental data, which shows that the nucleosome arrays were intrinsically dynamic even when they were condensed (57), and that inactive compact chromatin (heterochromatin) remains dynamic (58).

Figure 7.

The total mass-weighted MSF for each NCP against d in LEFTs 1–3, RIGHTs 1–3, and PARALLELs 1–2. The averages of the total mass-weighted MSF for NCP₁ and NCP₂ for all the cases in the range of d = 57 to 119 Å are shown in thick red and blue lines, respectively. The coordinates of each NCP were best-fit in the rigid parts of the initial coordinate of each NCP (as defined for the calculation of the center of mass for each NCP). The unit is 10⁵ atomic mass Ų. To see this figure in color, go online.

Computational limitation

First, we simplified the model by truncating the H3 and H2B tails and by ignoring the connections between the 20-bp linker DNA. Thus, the NCPs are isolated in our system. Experimental data showed that the isolated NCPs were separated in solute at 150 mM NaCl (53) (at a pressure of one bar (14, 15)), which is different from our observation that the stacked NCPs were stable at 150 mM NaCl. This may be interpreted that the state of the stabilized NCPs with strong H4 tail-bridge interaction in our system is a semistable one. Indeed, the free energy in RIGHT1 did not increase after two H4-tail bridges were lost, indicating that the free energy of 15−20 kcal/mol for separation would be much smaller if such strong H4 tail-bridges were not formed at d = 58 Å. Therefore, our system may represent a specific state of the stacked NCPs with the extremely strong H4 tail-bridge in the solution at 150 mM NaCl. In contrast, in the moderately folded NCP arrays at ∼150 mM NaCl (6), there would exist a significant number of NCPs with the H4 tail-bridge. Our simulation evaluated the free energy of the NCPs from the stacked to separated state. Considering that our system did not include the positively charged H3 and H2B tails (and included the negatively charged 20-bp linker DNA), inclusion of these tails (and truncation of the 20-bp linker DNA) would further screen the DNA-DNA repulsion and stabilize the stacked NCPs. The possible involvement of the H3 tail-bridge and H2B tail-bridge remains to be elucidated. Despite the limitation of this simplified model of the NCP array, the free energies for the different orientations of the NCPs obtained in our study can give insight into the understanding of the chromatin structure.

Second, to check whether the sampling of the H4 and H2A tails was sufficient, the convergence of the conformational entropies of the tails was calculated (Fig. S12; Table S3). In addition, the spatial distributions of the tails are shown in Fig. S13. Fig. S12 and Table S3 show that the conformational entropies did not converge in 20 ns in the umbrella sampling simulation but the increase every 5 ns became small after 20 ns. This indicates at least 25 ns of sampling is necessary to evaluate the entropy, because the location of the interaction between the H4 tail and the surface of the DNA frequently changed (Fig. S9). Although the entropies did not fully converge within 30 ns sampling, we do not think this would critically affect the accuracy of the free energy because the increase in the entropy appears uniform for the entire range of d considered and would become smaller during a longer simulation time.

Conclusions

The internucleosomal interactions between NCPs can be classified into three categories: 1) direct interfacial interaction between NCPs (d = from 58 to ∼70 Å), which was estimated to be ∼1−2 kcal/mol; 2) two bridge interactions between two H4 tails and the DNAs of the neighboring NCP (d = from 58 to ∼70−89 Å) that prompt a variety of bridge interactions and promote diversity in the orientation of the NCPs; and 3) one left bridge interaction (d > ∼70−89 Å) in which the attractive force (from the bridge interaction and the electrostatic interaction between NCPs) was estimated to be ∼15−18 pN per one H4 tail regardless of the different orientations of the NCPs and the different conformations of the H4 tails. The simulations of the NCPs without the H4 tails showed that the force between the NCPs was repulsive due to the electrostatic interaction between the DNAs, which confirmed the crucial role of the H4 tails in the attraction between the NCPs. The NCPs would open when the H4 tails are not involved in the formation of the H4 tail-bridge. Consequently, we concluded that the H4 tail plays a crucial role in a variety of internucleosomal interactions with the DNA of the spatially adjacent nucleosome, which would contribute to the polymorphism of the chromatin structure. In this study, H2B and H3 tails were not included, and the connection between the linker DNAs was ignored. Linker DNA would dominate the stability of the chromatin structure when the NCPs are spatially separated from each other because conformational stress in compact forms is relaxed. Nonetheless, this study suggests that the diversity of internucleosomal H4 tail-bridge interactions is essential in the polymorphic nature of the chromatin structure.

Author Contributions

H.I. and H.K. designed the research. H.I. carried out all simulations, analyzed the data, and wrote the article. H.K. assisted in analyzing the data and writing the article.

Editor: Tamar Schlick.

Supporting Citations

References (59, 60) appear in the Supporting Material.