Spatially Different Tissue-Scale Diffusivity Shapes ANGUSTIFOLIA3 Gradient in Growing Leaves

Abstract

The spatial gradient of signaling molecules is pivotal for establishing developmental patterns of multicellular organisms. It has long been proposed that these gradients could arise from the pure diffusion process of signaling molecules between cells, but whether this simplest mechanism establishes the formation of the tissue-scale gradient remains unclear. Plasmodesmata are unique channel structures in plants that connect neighboring cells for molecular transport. In this study, we measured cellular- and tissue-scale kinetics of molecular transport through plasmodesmata in Arabidopsis thaliana developing leaf primordia by fluorescence recovery assays. These trans-scale measurements revealed biophysical properties of diffusive molecular transport through plasmodesmata and revealed that the tissue-scale diffusivity, but not the cellular-scale diffusivity, is spatially different along the leaf proximal-to-distal axis. We found that the gradient in cell size along the developmental axis underlies this spatially different tissue-scale diffusivity. We then asked how this diffusion-based framework functions in establishing a signaling gradient of endogenous molecules. ANGUSTIFOLIA3 (AN3) is a transcriptional co-activator, and as we have shown here, it forms a long-range signaling gradient along the leaf proximal-to-distal axis to determine a cell-proliferation domain. By genetically engineering AN3 mobility, we assessed each contribution of cell-to-cell movement and tissue growth to the distribution of the AN3 gradient. We constructed a diffusion-based theoretical model using these quantitative data to analyze the AN3 gradient formation and demonstrated that it could be achieved solely by the diffusive molecular transport in a growing tissue. Our results indicate that the spatially different tissue-scale diffusivity is a core mechanism for AN3 gradient formation. This provides evidence that the pure diffusion process establishes the formation of the long-range signaling gradient in leaf development.

Introduction

Many developmental patterns are critically dependent on spatial gradients of signaling molecules in multicellular organisms. A seminal work theoretically postulated that pure diffusion of signaling molecules from a restricted source is sufficient to establish such tissue-scale gradients (1). Despite the prominence of this diffusion-based framework in development (2, 3), quantitative studies, mainly conducted in animal developmental systems, have not yet demonstrated this hypothetical model in multicellular tissues. This is due to complex processes involved in morphogen transport in animals, such as interactions with proteoglycans, that influence the tissue-scale mobility of signaling molecules, in addition to rapid extracellular diffusion (4, 5, 6). This complex interplay makes it difficult to link cellular-scale molecular transport with tissue-scale mobility to understand signaling-gradient formation. Given this situation, the diffusion-based model is still restricted in a Drosophila Bicoid (Bcd) gradient within a syncytium, a single multinucleated cell without growth (7, 8, 9, 10, 11, 12).

In plants, some signaling molecules form such long-range gradients by intercellular mobility to determine the cell-proliferation domain (13, 14). Tissue growth is also proposed to be involved in the spread of signaling molecules through cell-lineage transport (14, 15, 16, 17, 18, 19). It is thus important to quantitatively evaluate these two modes of molecular transport to address how tissue-scale signaling gradients are formed in a growing tissue. However, integrative approaches using quantitative imaging and theoretical analyses to precisely explain the mechanism of the gradient formation in plants are largely limited (14, 20, 21).

Leaves of Arabidopsis thaliana (Arabidopsis) is one model system used to experimentally and theoretically examine tissue patterning in plants (22, 23, 24, 25). The flat leaf tissue is composed of essentially immobile cells surrounded by rigid cell walls. Quantitative imaging would be possible in this tissue because of its moderate size (∼200 μm in length, corresponding to 30–50 cells). Interestingly, plasmodesmata, cellular channel structures unique to plants, directly connect neighboring cells to facilitate non-selective molecular trafficking (26, 27, 28). The aperture size of plasmodesmata and molecular size are well established as critical elements to determine molecular mobility through plasmodesmata (26, 27, 28). This simple mode of molecular transport suggests that developing leaf tissue could be a potential morphogenetic field, in which the diffusion-based framework is working. Thus, it is of great interest to test this hypothesis by linking tissue-scale molecular mobility with its cellular-scale kinetics by quantitative imaging in leaves. This would uncover whether the general framework of the diffusion-based model is viable in developmental patterning of multicellular organisms.

Cell-proliferation activity is uniform in an entire part of the Arabidopsis leaf primordia at a very young stage and is then arrested from the distal part, followed by post-mitotic cell differentiation. The cell-proliferation domain is maintained at a constant distance from the junction between leaf blade and petiole during early leaf development (29, 30, 31, 32, 33, 34). ANGUSTIFOLIA3 (AN3, also called GRF-INTERACTING FACTOR1) is a transcriptional co-activator that activates cell proliferation in the leaf primordia (35, 36). The an3 mutant shows defective cell proliferation, in which cell number is decreased by >70% compared with the wild-type (WT) (35). On the other hand, overexpression of AN3 activates cell proliferation, resulting in larger leaves (35). It has been revealed that AN3 is incorporated into chromatin remodeling complexes to modulate a broad spectrum of gene expression involved in the transition from cell proliferation to cell differentiation (37, 38). At the molecular level, AN3 plays a pivotal role in regulating cell-proliferation activity in leaf primordia and hence in leaf tissue patterning. However, it remains unclear how AN3 regulates the spatiotemporal dynamics of cell proliferation in leaves, because cell proliferation occurs more broadly than a tissue where the AN3 gene is expressed (26, 35).

Here, we measured tissue- and cellular-scale molecular mobilities in the leaf primordia by fluorescence recovery assays using green fluorescent protein (GFP) to characterize biophysical properties of non-selective macromolecular trafficking through plasmodesmata. Based on these quantitative data, we constructed a diffusion-based theoretical model that connects cellular-scale molecular trafficking to tissue-scale distribution. This model was then applied to the endogenous signaling molecule AN3, which was shown, in this study, to form a long-range gradient along the leaf proximal-to-distal axis to determine the cell-proliferation domain. In combination with this theoretical analysis, we experimentally evaluated each contribution of intercellular mobility and cell-lineage transport of AN3 by genetically engineering AN3 mobility. Our experimental and theoretical approaches demonstrated that pure diffusion in a growing tissue is sufficient to explain AN3 gradient formation, and they therefore suggested a core mechanism for determination of the cell-proliferation domain in growing leaf tissue.

Materials and Methods

Plant materials and growth conditions

The Arabidopsis WT line used in this study was Colombia-0. The 35S::GFP line was established using a previously reported vector (39) by the floral dip method (40). The an3-4/pAN3::AN3-GFP and an3-4/pAN3::AN3-3xGFPs lines have been described elsewhere (41). Plants were grown on rockwool at 22°C under a 16-h light (fluorescent illumination at ∼50 μmol m⁻² s⁻¹)/8-h dark cycle and watered daily with 0.5 g L⁻¹ Hyponex solution (Hyponex, Osaka, Japan).

Square fluorescence recovery after photobleaching assay

First, leaf primordia dissected from 6- or 10-day-old 35S::GFP seedlings were soaked in phosphate-buffered saline (PBS) on a glass slide. Microscopic observation was performed from the adaxial side of the leaf primordia using a coverslip (24 × 36 mm, thickness no. 1, 0.12–0.17 mm; Matsunami, Osaka, Japan).

Microscopy was performed using a confocal laser-scanning microscope with an objective lens Plan-Apochromat 20×/0.75 NA and a 488-nm Argon laser on standby (LSM510 equipped with a META device; Carl Zeiss, Oberkochen, Germany). The pinhole was set to 120 μm in diameter, which yields a 10-μm optical slice in this condition. Fifteen z-stack images of size 512 × 512 pixels were acquired at 2-μm steps and 5-min intervals before and after photobleaching over a 95-min period. The laser intensities were 100% and 7% for photobleaching and time-lapse imaging, respectively. A subepidermal cell plane was selected from z-stack collections for image analysis. We confirmed that leaky fluorescence from adjacent cell layers was undetectable. A region of interest (ROI) that was 54 × 54 μm was photobleached for the square fluorescence recovery after photobleaching (FRAP) assay. A one-dimensional profile of GFP fluorescence intensity along the leaf proximal-to-distal and medial-to-lateral axes was defined as an average intensity over a width of 18.4 μm. Because this analysis region was 18 μm away from the ROI edge along the leaf proximal-to-distal axis, GFP movement perpendicular to the axis was negligible in our observation time span. The averaged intensity was normalized by GFP fluorescence intensity outside of the ROI. The boundary between the GFP-positive and GFP-negative regions was defined by a threshold fluorescence intensity of 5.0 a.u. to quantify the GFP recovery as velocity. This value corresponded to 5–10% of GFP fluorescence intensity in the non-photobleached region.

All image analyses and numerical simulations, unless otherwise described, were conducted using customized scripts written in MATLAB software, R2012b, with Statistics and Machine Learning Toolbox, Image Processing Toolbox, Optimization Toolbox, and Curve Fitting Toolbox (The MathWorks, Natick, MA).

Single-cell FRAP assay

Leaf samples were prepared and imaged as described in Square FRAP Assay. An ROI within a cell was used for photobleaching. The GFP intensity in the photobleached cell was measured manually for each time point. Experimental data from the single-cell FRAP assay (from 0 to 45 min after photobleaching) was fitted by an exponential function as

$$I\left(t\right)=\left(I_0-I_{\max }\right)e^{\left(-t/\tau \right)}+I_{\max },$$ (1)

where I(t) and I₀ are GFP fluorescence intensities at time t and just after photobleaching, respectively; I_max is a maximal GFP fluorescence intensity, determined directly from the time-course data; and τ is a time constant of GFP diffusivity. I₀ and τ are free parameters and are determined by minimizing the residual sum of squares. We confirmed that the time constant of GFP diffusivity in the leaf lower half was not larger than that in the upper half when we analyzed the data from the single-cell FRAP assay from 0 to 95 min after photobleaching using the exponential function

$$I\left(t\right)=\left(I_0-I_{\text{conv}}\right)e^{\left(-t/\tau \right)}+I_{\text{conv}},$$ (2)

where I_conv is a free parameter for the convergence value of GFP fluorescence recovery during observation (Fig. S2 A). I_conv, in addition to I₀ and τ, was determined by minimizing the residual sum of squares.

Given that GFP fluorescence was stably recovered in a single-exponential manner throughout observation in our single-cell FRAP assay, we judged that GFP trafficking through plasmodesmata was not perturbed by, e.g., plasmodesmata gating due to damages by tissue excision and/or photobleaching treatment. Indeed, a similar timescale of protein diffusivity through plasmodesmata was observed in other published works, in which protein diffusivities were non-invasively measured using the photoconvertible fluorescence protein Dendra2 (26 kDa) and its fusion protein (42, 43).

Measurement of the projected cell area

Subepidermal palisade cells in the images of the square FRAP assay at the leaf upper and lower halves were outlined as shown (Fig. 3 A) to measure the projected area. Each cell position in the image was determined by a centroid, represented as pixel coordinates. This image analysis was performed using custom MATLAB script (described below). Spatial distribution of cell size along the leaf proximal-to-distal axis was estimated from these independent photographs. Cell length was measured by ImageJ software at an arbitrary part of a cell in the leaf upper and lower halves using the same image sets as for the square FRAP assay (http://imagej.nih.gov/ij/).

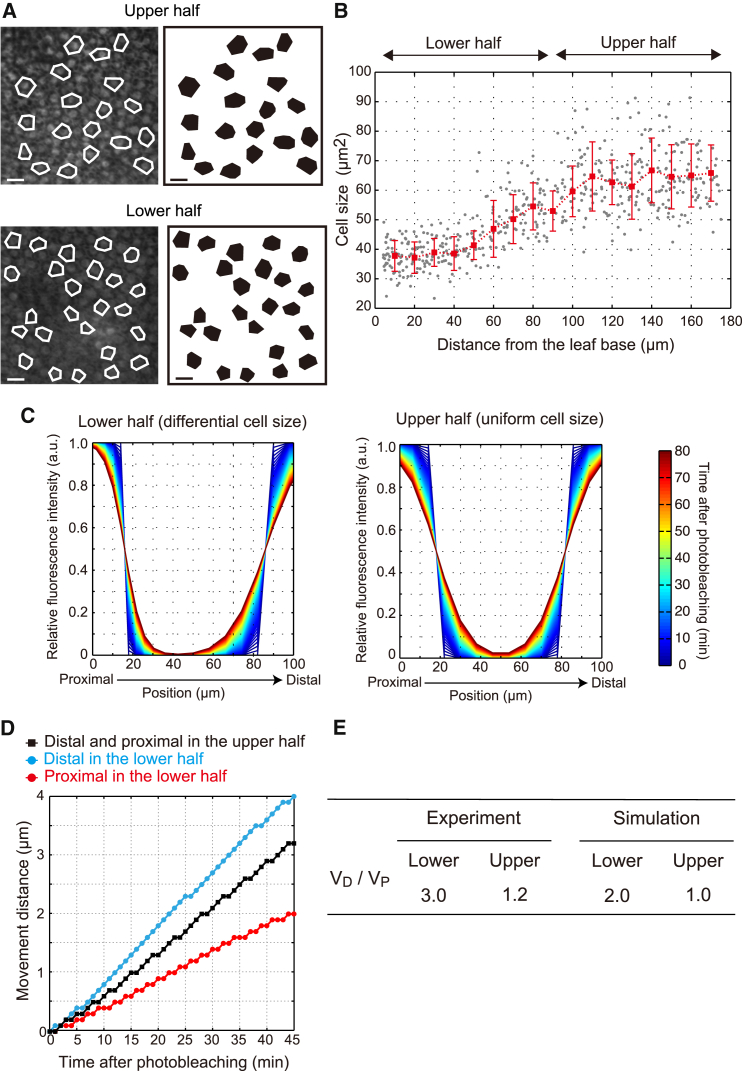
Figure 3.

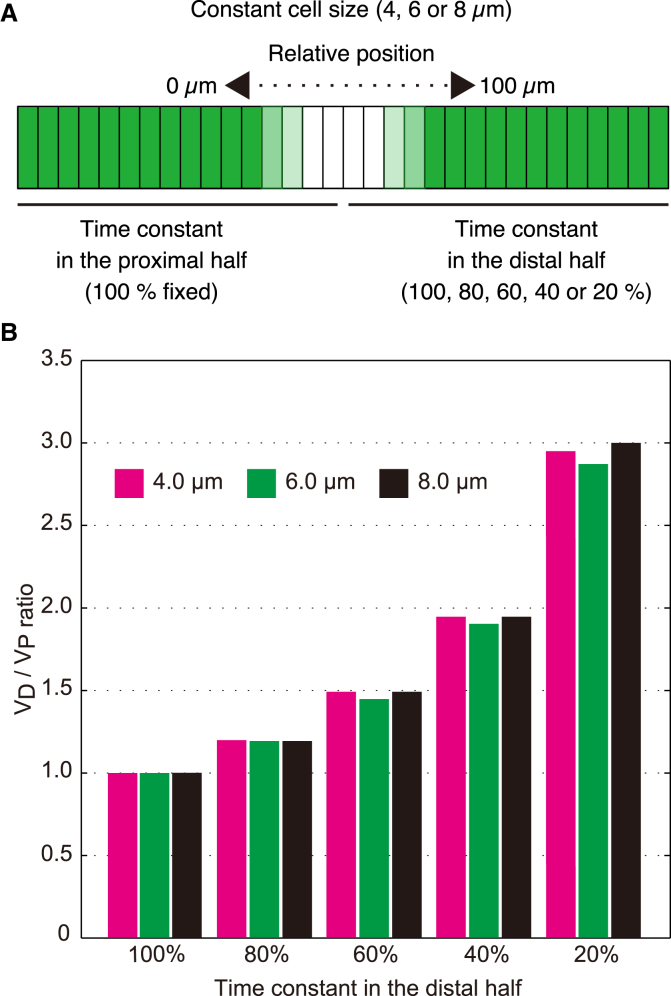
Cell-size gradient underlies the spatially different tissue-scale GFP diffusivity. (A) GFP fluorescence images of subepidermal palisade cells in the leaf upper and lower halves. Representative cells are outlined in white (left), and their diagrams are shown (right). Scale bars, 10 μm. (B) Distribution of average cell size binned by distance at 10-μm intervals from the leaf base. The mean ± SD from more than eight independent leaf primordia (n = 16–37 cells in each position) are shown in red. Gray dots indicate each cell size. (C) Computed relative fluorescence intensity from our diffusion-based numerical simulation for the square FRAP assay was plotted against the relative position (see Figs. 1B and S3 for summary diagrams of the simulation). a.u., arbitrary unit. (D) Simulated movement distance of distal- and proximal-side boundaries of the leaf upper half (black squares) and lower half (blue and red circles), plotted as a function of time after photobleaching. (E) The ratio between V_D and V_P was determined from experiment and simulation in the upper and lower halves. See also Fig. 1E. All parameters used are summarized in Table S1. To see this figure in color, go online.

Quantification of AN3-GFP and AN3-3xGFPs distributions

The first leaf primordia were dissected from the 6-day-old an3-4/pAN3::AN3-GFP and an3-4/pAN3::AN3-3xGFPs lines and subjected to confocal microscopy (LSM510 equipped with a META device; Carl Zeiss). Subepidermal tissue in the adaxial side was selected for observation of AN3-GFP and AN3-3xGFPs signals. We observed three independent lines for AN3-GFP and AN3-3xGFPs distributions and obtained reproducible results.

We developed a MATLAB package that allowed us to interactively measure the GFP fluorescence intensity and cellular parameters from the confocal images. The outlines of cells or nuclei were determined manually based on the fluorescence signal. The results were displayed in another window, which enabled us to check and correct the segmentation. The fluorescence intensity, projected area, and centroid of the cells or nuclei, represented as pixel coordinates, were determined automatically. More than 1450 nuclei from 12 independent leaves were analyzed for AN3-GFP and AN3-3xGFPs intensity.

Detection of nuclei in S-phase cells by EdU absorption experiment

Six-day-old seedlings were cut at the hypocotyls, and above-ground parts were floated on 10-μM 5-ethynyl-2′-deoxyuridine (EdU) solution for 3 h under normal growth conditions. Detection of EdU was performed as described elsewhere (44). The subepidermal palisade cells were examined by confocal microscopy as described above. Since cells showed a polygonal shape in the leaf primordia, the observed fluorescence was derived just from the dividing cells, not from the endoreduplicating cells.

Mathematical models and simulations

We here summarized our mathematical models and simulation methods. More details are described in the Supporting Material.

Model setup: We considered a simplified one-dimensional geometry to simulate the tissue-scale GFP mobility (Fig. S3) and the AN3 gradient formation along the proximal-to-distal axis of a growing leaf tissue (Fig. S4). Our models consist of discrete cells in which synthesis and degradation of a signaling molecule and its diffusive transport between neighboring cells occur. We directly measured cell-size distribution based on the experimental observations (Figs. 3 B and S2 D) and incorporated it into the models to analyze the tissue-scale molecular dynamics in a realistic spatial field. All parameters for the simulations are summarized in Tables S1–S3.

Molecular synthesis and degradation: We assumed that GFP synthesis and degradation are negligible in the timescale of our model for tissue-scale GFP mobility based on the experimental observations in the square and single-cell FRAP assays (Figs. S1, A and B, and S2 B).

In contrast, to model the AN3 gradient formation, we considered that AN3 is produced and maintained at a constant level in time within the source cells at the proximal boundary. The number of the source cells was determined by analyzing the AN3-3xGFPs gradient (Fig. 5 C). We investigated the degradation process with our model using a wide range of the degradation constant and found that the AN3 gradient could not be achieved if we included active degradation (Fig. S7). This is intuitively consistent with the longer timescale of the AN3 gradient formation. Based on these data, we considered that protein degradation is negligibly small in the AN3 gradient formation.

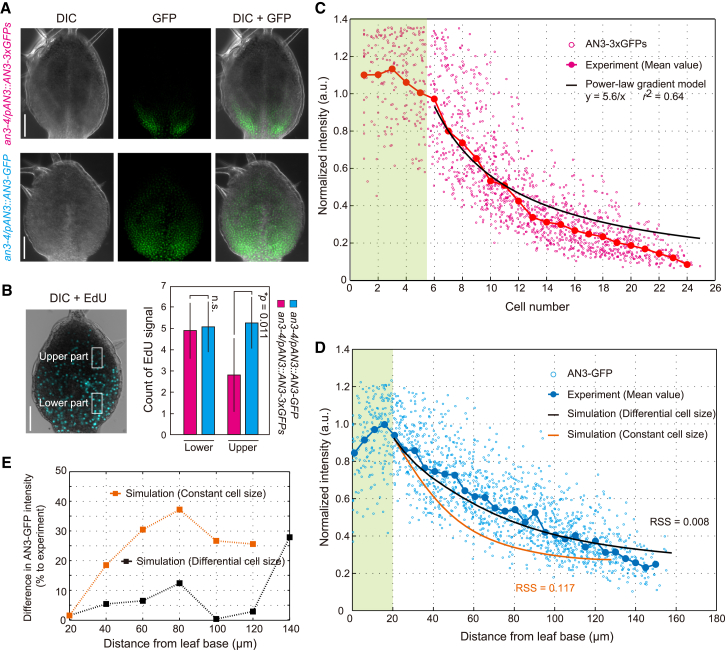
Figure 5.

AN3 gradient formation by pure diffusion process in a growing leaf tissue. (A) Leaf primordia from an3-4/pAN3::AN3-3xGFPs (upper) and an3-4/pAN3::AN3-GFP (lower). DIC (left), GFP fluorescence (middle), and their merged images (right) are shown. Scale bars, 50 μm. (B) Distribution of proliferating cells in leaf primordia. A DIC image merged with EdU-positive signal (blue) is shown (left). Numbers of EdU-positive nuclei per 20 × 40 μm area (white rectangles) at leaf lower and upper parts were counted. The mean ± SD with the p value from the Student’s t-test are shown (n > 12). n.s., non-significant (p > 0.05). Scale bars, 50 μm. (C and D) Distribution profiles for AN3-3xGFPs and AN3-GFP fluorescence intensities along the leaf proximal-to-distal axis. Normalized intensities of AN3-3xGFPs (C) and AN3-GFP (D) in nuclei are plotted as a function of cell number and distance from the leaf base, respectively. The mean of AN3-3xGFPs and AN3-GFP intensities binned by cell position (red dots in C) and distance from the leaf base at 5-μm intervals (blue dots in D) are indicated. A fitting curve with a power-law gradient to the AN3-3xGFPs profile in the targeted tissue is shown in black in (C). Simulated curves through the 4-μm constant-cell-size field (orange) and the differential (from 4 to 8 μm) cell-size field (black) are shown in (D). a.u., arbitrary unit. The green shaded area indicates the region of source tissue. RSS, residual sum of squares. (E) Difference in AN3-GFP intensity between simulated and experimentally determined profiles. The differences of the simulated curve with 4-μm constant cell size (orange) and with differential cell size (black) against experimentally measured values are plotted as a function of the distance from the leaf base. Mean deviations were calculated based on the data for 20–120 μm from the leaf base. All parameters used are summarized in Table S2. To see this figure in color, go online.

Diffusive molecular transport: We focused on molecular movement across the cell-cell boundary through plasmodesmata, because movement in the cytoplasm was much faster, so that the intracellular molecular profile was kept uniform (Fig. 2 A). Molecular transport was modeled as Fick’s law of diffusion, where the molecular flux across the cell-cell boundary is proportional to a difference in molecular concentration between these cells. Because the kinetic constant was experimentally measured by the single-cell FRAP assay (Fig. 2 C), a change in plasmodesmata pattern, if there was any, was intrinsically implemented in our simulations.

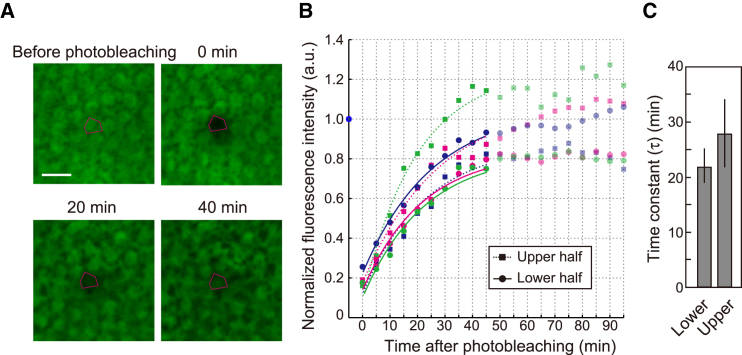
Figure 2.

Uniform cellular-scale GFP diffusivity along the leaf proximal-to-distal axis. (A) Constitutively expressed GFP was photobleached in a single cell (magenta-outlined area). Scale bar, 10 μm. (B) Recovery kinetics of GFP fluorescence plotted as a function of time after photobleaching. Data for three representative leaves, with exponential fits (to the data from 0 to 45 min after photobleaching) in each leaf upper and lower half, are shown. See also Fig. S2A. (C) Time constant of GFP diffusivity between cells in the leaf upper and lower halves. The mean ± SD are shown by the vertical lines (n = 7). To see this figure in color, go online.

Tissue growth mediated by cell division: Although the timescale for the tissue-scale GFP mobility was ∼45 (or ∼90) min, that for the AN3 gradient formation was ∼48 h. Because the cell cycle of leaf cells at the stage we considered is ∼16 h (31, 45), tissue growth mediated by cell division occurs in the AN3 gradient formation but not in the tissue-scale GFP movement.

Results

Tissue-scale molecular mobility is spatially different along the leaf proximal-to-distal axis

We first characterized tissue-scale molecular mobility using Arabidopsis leaf primordia constitutively expressing a gene encoding a GFP (molecular mass, 27 kDa) as a model system for molecular transport through the plasmodesmata. In our square FRAP assay, GFP fluorescence was irreversibly photobleached in a rectangular ROI corresponding to ∼50 cells (Fig. 1 A). After photobleaching, the intensity of GFP fluorescence was scanned from the proximal to the distal parts of the observed region (Fig. 1 A; Movie S1). Recovery of GFP fluorescence at the center of the ROI was undetectable, at least until 45 min after photobleaching (Fig. S1, A and B), suggesting that de novo GFP synthesis and GFP influx into the ROI plane across cell layers was negligible in this timescale and that the recovery of GFP fluorescence depended on the movement of GFP between cells within the same layer. We found that recovery of GFP fluorescence around the distal part of the ROI was greater than in the proximal part at the lower half of the leaf primordia (Fig. 1 B). This preferential recovery in a distal-to-proximal direction was less obvious at the upper half of the leaf primordia (Fig. 1 B). We did not detect any preferential recovery along the leaf medial-to-lateral axis in either the upper or lower half in the same samples (Fig. S1, C and D). These data showed that tissue-scale GFP mobility varied along the leaf proximal-to-distal axis.

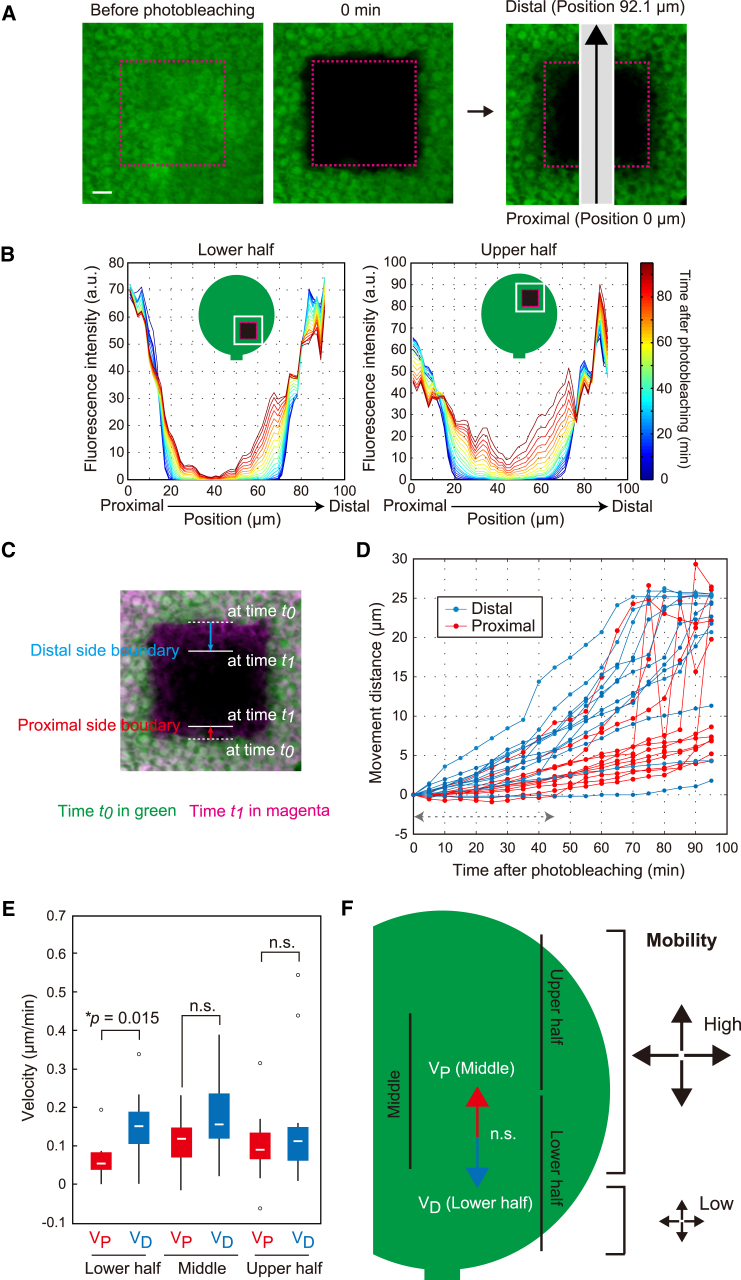
Figure 1.

Spatial difference of tissue-scale macromolecular trafficking in leaf primordia. (A and B) Constitutively expressed GFP was photobleached in the leaf primordia (magenta dashed box). After photobleaching, recovery of GFP fluorescence was scanned along the leaf proximal-to-distal axis, as indicated by the gray stripe (A), and plotted against the position of the analysis region from the proximal to the distal end (B). Scale bar, 10 μm. Representative data are shown. a.u,. arbitrary unit. (C) Boundaries of GFP fluorescence moved inward over time (e.g., from t₀ to t₁). A representative picture at time t₀ (green) merged with that at time t₁ (magenta) is shown. Blue and red arrows indicate movement distances of the distal- and proximal-side boundaries from t₀ to t₁ as defined by threshold fluorescence intensity at 5.0 a.u. (D) Movement distances of the distal-side boundary (blue) and proximal-side boundary (red) in the lower half were plotted against time after photobleaching (n = 12). The data from 0 to 45 min after photobleaching (dashed arrow) were used for further analysis to avoid the effect of de novo GFP synthesis. See also Fig. S1, A and B. (E) V_D and V_P in the upper half, middle region, and lower half. Each box includes the data from 25 to 75%, with the horizontal line as the median. Outlying values >50% are indicated as circles. The p value was calculated according to the Mann-Whitney test (n = 12). n.s., non significant (p > 0.05). (F) V_D in the lower half and V_P in the middle region are shown as blue and red arrows, respectively. There were no significant differences between these velocities. In sum, GFP mobility occurred in a non-directional manner, but it was lower in the most proximal part of the leaf lower half. To see this figure in color, go online.

In the square FRAP assay, a sharp boundary of GFP fluorescence between the ROI and the surrounding region became smooth and moved inward over time. We defined the distal- and proximal-side boundaries by threshold fluorescence intensity at 5.0 a.u. and quantified their velocities (V_D and V_P, respectively) (Fig. 1, C and D). The V_D was significantly three times greater than the V_P at the lower half (Fig. 1 E). There were no significant differences between V_D and V_P in the middle region or the upper half (Fig. 1 E). To know whether this spatial difference of tissue-scale GFP mobility is induced by preferential protein flow in the distal-to-proximal direction, we measured V_D in the lower half and V_P in the middle region within an overlapping part and found no significant differences (Fig. 1, E and F). This indicated that there was no convection dynamics of GFP mobility, nor was there preferential flow mediated by polar distribution of plasmodesmata in the distal-to-proximal direction. The GFP fluorescence recovered in a non-preferential manner at the lower half when we examined older leaf primordia in which cell proliferation was entirely arrested (Fig. S1, E and F). We thus concluded that tissue-scale GFP mobility in the most proximal part of the leaf primordia was significantly slower than that in the other parts (Fig. 1 F).

A gradient in cell size induces the spatial difference of tissue-scale diffusivity

We next examined kinetics of GFP mobility between neighboring cells using a single-cell FRAP assay, in which GFP fluorescence in a single targeted cell was irreversibly photobleached and then monitored over time (Fig. 2 A). Because recovery of GFP fluorescence within the targeted cell occurred uniformly (Fig. 2 A), intracellular movement of GFP was considered to be much more rapid than intercellular movement through the plasmodesmata. These data indicated that the kinetics of GFP fluorescence recovery was largely determined by GFP mobility through plasmodesmata. Recovery of GFP fluorescence reached the level present before photobleaching, and the kinetics were well fitted with a single exponential function (Figs. 2 B and S2 A). GFP fluorescence intensity in cells adjacent to the targeted cell was constant during the observation period (Fig. S2 B). These results strongly suggest that GFP mobility through plasmodesmata is a pure diffusion process. We obtained the characteristic time (τ) of the exponential GFP recovery from the fitting curves (τ = 22 ± 3 and 28 ± 6 min in the lower and upper halves, respectively) (Figs. 2 C and S2 C). Although a longer characteristic time indicates lower diffusivity, the time in the lower half was largely similar to (or was not larger than) that in the upper half (Figs. 2 C and S2 C). This result indicates that the spatial difference of tissue-scale mobility could not be explained by a difference in the cellular-scale diffusivity along the leaf proximal-to-distal axis. These data thus suggested that an additional element contributes to tissue-scale GFP mobility in leaf primordia.

Cell-proliferation activity is higher at the leaf proximal part and decreases toward the leaf distal part (30, 31, 32, 33, 34). This causes cell-size gradient along the leaf proximal-to-distal axis (38 ± 5 and 66 ± 10 μm² at the lower and upper halves, respectively) (Figs. 3, A and B, and S2 D). We hypothesized that tissue-scale GFP mobility is slowed down in the leaf proximal part because the cells are smaller, as GFP must pass through more plasmodesmata to travel a given distance. In other words, because the effective diffusion coefficient (D) of tissue-scale GFP mobility is described as D ∼ cell size/τ (μm²/min), cell-size gradient may contribute to the spatially different tissue-scale GFP mobility. To test this hypothesis, we simulated tissue-scale GFP mobility using the measured value for GFP diffusivity between neighboring cells in uniform or differential cell-size fields along the leaf proximal-to-distal axis (see Fig. S3 for details of the simulation). We here considered simplified one-dimensional geometry, because tissue-scale GFP mobility along the leaf medial-to-lateral axis was uniform in both the upper and lower halves (Fig. S1, C and D). When we implemented the differential cell size to simulate tissue-scale GFP mobility in the lower half, V_D became two times greater than V_P, in contrast to the uniform cell-size field in the upper half (Fig. 3, C–E). This result was in good agreement with data from the square FRAP assay (Fig. 3 E). A difference of >2.5 in the time-constant value is required to reproduce the spatial difference of tissue-scale GFP mobility in a uniform cell-size field in the upper half (Fig. 4). Such a difference in values lies outside the 95% confidence interval of our measured data (Figs. 2 C and S2 C), further excluding the possibility that the local GFP diffusivity through plasmodesmata is modulated along the leaf proximal-to-distal axis to produce the spatial difference of tissue-scale mobility. Based on these results, we concluded that tissue-scale mobility is determined by a simple sum of diffusive transport through the plasmodesmata and that a gradient in cell size underlies the spatial difference of tissue-scale diffusivity.

Figure 4.

In silico perturbation experiment on local GFP diffusivity. (A) The time constant of GFP diffusivity in the distal half was set to 100, 80, 60, 40, or 20%, compared with that in the proximal half (100% fixed), and fluorescence recovery was computed through the constant cell-size field (4, 6, or 8 μm) over time by diffusion-based numerical simulation. See also Fig. S3. (B) Ratios of V_D to V_P (V_D/V_P) from the in silico experiment. Magenta, green, and black bars indicate data on 4-, 6-, and 8-μm constant-cell-size fields, respectively. The time constant in the proximal half was 2.5 times larger than that in the distal half when we used 40% as the time constant in the distal half. To see this figure in color, go online.

A pure diffusion process is a core mechanism in establishing the AN3 signaling gradient

To examine how a spatial difference of tissue-scale diffusivity works for gradient formation of endogenous signaling molecules and its developmental relevance, we examined the transcriptional co-activator AN3 (molecular mass, 22 kDa) (35, 36, 37, 38). The AN3 promoter is active within the most proximal part of the leaf primordia, whereas the cell-proliferation domain is formed more broadly in the distal part (26, 35). One potential explanation for this spatial inconsistency is that AN3 moves along the leaf proximal-to-distal axis from the localized source, in addition to the inner-to-outer axis (41). To investigate AN3 mobility, we observed spatial distribution of AN3 in leaf primordia using an3-4 transgenic lines expressing AN3 fused with GFP (AN3-GFP) or fused tandemly with three GFPs (AN3-3xGFPs) under the control of the functional AN3 promoter (an3-4/pAN3::AN3-GFP and an3-4/pAN3::AN3-3xGFPs, respectively) (41). In contrast to the AN3-GFP, the AN3-3xGFPs is not capable of moving between cells due to its larger molecular size (41, 46), suggesting that AN3 protein transport is mediated through plasmodesmata. The AN3-GFP expressed by the AN3 promoter rescues the cell-proliferation defect in the an3-4 genetic background, resulting in normal leaf size comparable to the WT, in the an3-4/pAN3::AN3-GFP (41). Although constitutively expressed AN3-3xGFPs by cauliflower mosaic virus 35S promoter also could complement the defective proliferation and smaller leaf size in the an3-4 genetic background, the an3-4/pAN3::AN3-3xGFPs shows defective proliferation and smaller leaves compared to the WT (41, 46). When we compared the distribution patterns of these AN3-GFP and AN3-3xGFPs, the AN3-GFP signal was broader than that of AN3-3xGFPs (Fig. 5 A), indicating that AN3-GFP moved between cells along the leaf proximal-to-distal axis. To investigate whether the AN3 movement contributed to establishing the cell-proliferation domain, we examined the distribution of proliferating cells in both lines. Premature arrest of cell proliferation was detected specifically in the leaf distal part of an3-4/pAN3::AN3-3xGFPs, when compared to an3-4/pAN3::AN3-GFP (Fig. 5 B). This result indicated that AN3 forms a graded distribution along the leaf proximal-to-distal axis through mobility to regulate the proliferation domain.

Lastly, based on the spatial difference of tissue-scale diffusivity, we quantitatively analyzed the AN3-GFP and AN3-3xGFPs distributions along the leaf proximal-to-distal axis to examine AN3 gradient formation. The AN3-3xGFPs was produced in a restricted source tissue and transported by dilution, through cell proliferation, away from the source (cell-lineage transport). In this scheme, the AN3-3xGFPs level becomes half after cell division in the target tissue, but due to subsequent cell growth, its distribution length is doubled along the developmental axis when the one-dimensional geometry is considered. An expression gradient established solely by cell-lineage transport in the targeted tissue is thus inversely proportional to the number of cells from the source tissue. This is theoretically proposed to follow a power-law form as

$$C\left(x\right)=a/x,$$ (3)

where a is a constant value, x is the cell number away from the leaf base, and C(x) is the intensity of AN3-3xGFPs at position x (14, 15, 16, 17, 18, 19, 47) (see Fig. S4 A for details). To compare this theoretical prediction with the in vivo AN3-3xGFPs distribution, we quantified the expression profile of AN3-3xGFPs along the leaf proximal-to-distal axis. Fluorescence intensity was maintained at a high level from the first to fifth cells (corresponding to 0–20 μm) along the axis, and dropped steeply as the distance from the leaf base increased (Fig. 5 C). The AN3-3xGFPs profile more than six cells away from the leaf base was well-fitted by the power-law form (a = 5.6, with fitting accuracy r² = 0.65; Fig. 5 C). These data indicated that AN3-3xGFPs was produced in the source tissue located at the most proximal part of the leaf primordia (first to fifth cells), and spread into the targeted tissue by cell-lineage transport (away from the sixth cell).

The AN3-GFP profile showed a longer-range distribution than the AN3-3xGFPs profile in the targeted tissue (Fig. 5 D). We performed a one-dimensional simulation for formation of an AN3-GFP gradient, in which AN3-GFP spread from a restricted source tissue by diffusive transport through plasmodesmata in combination with cell-lineage transport (see Fig. S4 for details). Using the values determined experimentally by a single-cell FRAP assay and quantitative analysis of the AN3-3xGFPs profile, our simulation summarized the AN3-GFP gradient in the targeted tissue well (Fig. 5 D). Strikingly, the mean deviation between measured and simulated AN3-GFP profiles, except at the furthermost distal part, was <5% (Fig. 5 E). This higher reproducibility was also maintained when we used the theoretically predicted diffusivity of two tandemly fused GFPs, which is experimentally shown to be capable of moving through plasmodesmata in a non-selective fashion (28) (54 kDa, τ = 40 min; mean deviation of 14%; Figs. S5 A and S6). These values were much better than those found assuming constant cell size from the leaf base (mean deviations of 23% (τ = 25 min; Fig. 5, D and E) and 31% (τ = 40 min; Fig. S6 A)). Therefore, we concluded that the spatial difference of tissue-scale diffusivity could be a critical mechanism for formation of the long-range AN3 gradient along the leaf proximal-to-distal axis, which further guides spatial distribution of cell-proliferation activity (Fig. 6).

Figure 6.

Proposed model for AN3 gradient formation. Although molecular diffusivity through plasmodesmata is uniform in the early leaf primordia, tissue-scale diffusivity is spatially varied due to smaller cell size in the most proximal part. In addition, cell-lineage molecular transport mediated by cell proliferation intrinsically occurs in a growing tissue. This spatial difference of tissue-scale diffusivity in a growing tissue is sufficient to explain how the long-range AN3 gradient from a restricted source tissue is established in leaves. To see this figure in color, go online.

Discussion

We have addressed the key question of how a dynamic signaling gradient is established in a growing tissue. First, using trans-scale florescence recovery assays, we characterized the distribution of molecular diffusivity in leaf primordia and found that tissue-scale diffusivity, but not cellular-scale diffusivity, is spatially varied along the proximal-to-distal axis. Our work uncovered that the gradient in cell size underlies this phenomenon, strongly suggesting that tissue-scale molecular mobility can be described as a diffusion process if position-dependent cell size is appropriately considered. Second, by genetically engineering AN3 mobility, we quantitatively dissected the contributions of diffusive transport through the plasmodesmata and of tissue growth in establishing the AN3 gradient. Based on these data, we concluded that the simplest mechanism of diffusion could be a core determinant for the AN3 gradient formation. This is, to our knowledge, the first report linking cellular-scale diffusion to tissue-scale diffusivity, thereby showing how the long-range signaling gradient is formed along the developmental axis of compartmentalized tissue. In addition, we proposed that this signaling gradient contributes to determination of the cell-proliferation domain. We thus suggest that the diffusion equation fulfills the dynamic formation of a signaling gradient, and hence a tissue growth mechanism, as conceptualized in the seminal work of Crick (1).

Diffusion-based framework for signaling-gradient formation in a growing tissue

Most studies of signaling-gradient formation hypothesized that mobility of the signaling molecule is uniform within organ primordia. However, inhomogeneous distribution of the cell-proliferation rate occurs widely in a growing tissue in animals and plants (30, 48, 49, 50). We pointed out that such a spatial difference could induce differential cell-size distribution; thereafter, it plays an important role in determination of spatially different tissue-scale diffusivity and establishment of a signaling gradient. In contrast to tissue-scale diffusivity, our data showed that cellular-scale diffusivity is uniform along the leaf proximal-to-distal axis. The characteristic time for GFP diffusivity on a cellular scale measured by the single-cell FRAP assay (τ = ∼25 min) is similar to the mobility of the animal morphogen Decapentaplegic restricted by non-diffusive hindrance factors (τ = 10–30 min at the 10 μm scale), although its extracellular diffusion is much faster (τ on the order of several seconds at the 10 μm scale) (2, 6). These data indicate that, in plants, diffusive molecular transport between neighboring cells through plasmodesmata is a major determinant of tissue-scale mobility, in contrast to the case for animals, in which non-diffusive processes are rate-limiting steps (2, 6, 51). This difference highlights that the diffusion-based framework is a critical system for signaling gradient formation in particular in plants.

Plasmodesmata shape and density might be changed depending on cellular developmental stage, as observed during the physiological transition from sink to source leaves (52, 53). Plasmodesmata conductivity is also affected by callose deposition around its neck region, which is involved in the modulation of mobility of signaling molecules (27, 54, 55). However, we demonstrated that local molecular transport through plasmodesmata is comparable between the upper and lower halves of leaf primordia by single-cell FRAP assay. This result indicates that changes in local molecular mobility by plasmodesmata modifications are not obvious or, if there were any, they might have canceled each other out, resulting in uniform cellular-scale diffusivity throughout the leaf primordia at this developmental stage.

Dynamics of AN3 signaling and proliferation control in leaves

Our study showed that the AN3 signaling gradient became steeper when we perturbed the AN3 mobility, resulting in premature arrest of cell proliferation in the leaf distal part. Manipulation of the AN3 expression level by overexpression or antisense/RNA interference experiments revealed that cell-proliferation activity was well correlated with expression level in leaf primordia (35, 56, 57). These facts strongly suggest that the concentration gradient of AN3 plays an important role in regulating cell-proliferation dynamics along the leaf proximal-to-distal axis. We speculate that spatial difference of tissue-scale diffusivity along the leaf proximal-to-distal axis might help to maintain the higher AN3 concentration in the leaf proximal part for vigorous proliferation, and also to form long-range distribution toward the leaf distal part for lower, but detectable, proliferation activity. Despite differences in molecular components and tissue contexts, a developmental mechanism using the spatial gradient of a signaling molecule to regulate determinate tissue growth might be a preferable strategy across kingdoms.

Emerging evidence suggests that mechanical stress due to tissue growth induces feedback regulation on cell-proliferation activity in Arabidopsis petals and Drosophila wing discs (48, 58, 59). Given a relationship between the AN3 gradient and the proliferation activity, the shape of the AN3 gradient would be affected by mechanical feedback in response to tissue growth. Such a regulatory architecture operating in time and space has been suggested as a proprioception system for tight regulation of tissue growth (48, 60, 61, 62). Our proposed framework would be a basis to consider a dynamic regulatory principle that integrates genetic and non-genetic cues for robust patterning in multicellular organisms. Because AN3 is capable of moving across cell layers (41), the inter-cell-layer mobility would affect the AN3 distribution when we consider a longer timescale. It would be interesting to test this cross talk in future work using a more complex model than our one-dimensional one that incorporates this inter-cell-layer movement and also mechanical feedback in three-dimensional geometry. Implementing the kinetics of AN3 mobility in this future model will also be helpful for further investigation of AN3 gradient formation.

Author Contributions

K.K. and H. Tanimoto conceived and designed the project. G.H. and H. Tsukaya helped design the project. K.K. carried out all experiments. H. Tanimoto developed the scripts for image analysis and mathematical modeling. K.K. and H. Tanimoto analyzed the data and performed the computational simulations. G.H. provided material. K.K., H. Tanimoto, G.H., and H. Tsukaya discussed the data and wrote the manuscript.

Editor: Anatoly Kolomeisky.

Supporting Citations

References (63, 64) appear in the Supporting Material.