Exposure assessment models for elemental components of particulate matter in an urban environment: A comparison of regression and random forest approaches

Abstract

Exposure assessment for elemental components of particulate matter (PM) using land use modeling is a complex problem due to the high spatial and temporal variations in pollutant concentrations at the local scale. Land use regression (LUR) models may fail to capture complex interactions and non-linear relationships between pollutant concentrations and land use variables. The increasing availability of big spatial data and machine learning methods present an opportunity for improvement in PM exposure assessment models. In this manuscript, our objective was to develop a novel land use random forest (LURF) model and compare its accuracy and precision to a LUR model for elemental components of PM in the urban city of Cincinnati, Ohio. PM smaller than 2.5 μm (PM2.5) and eleven elemental components were measured at 24 sampling stations from the Cincinnati Childhood Allergy and Air Pollution Study (CCAAPS). Over 50 different predictors associated with transportation, physical features, community socioeconomic characteristics, greenspace, land cover, and emission point sources were used to construct LUR and LURF models. Cross validation was used to quantify and compare model performance. LURF and LUR models were created for aluminum (Al), copper (Cu), iron (Fe), potassium (K), manganese (Mn), nickel (Ni), lead (Pb), sulfur (S), silicon (Si), vanadium (V), zinc (Zn), and total PM2.5 in the CCAAPS study area. LURF utilized a more diverse and greater number of predictors than LUR and LURF models for Al, K, Mn, Pb, Si, Zn, TRAP, and PM2.5 all showed a decrease in fractional predictive error of at least 5% compared to their LUR models. LURF models for Al, Cu, Fe, K, Mn, Pb, Si, Zn, TRAP, and PM2.5 all had a cross validated fractional predictive error less than 30%. Furthermore, LUR models showed a differential exposure assessment bias and had a higher prediction error variance. Random forest and other machine learning methods may provide more accurate exposure assessment.

1. Introduction

1.1. Land use regression models

Many air pollution exposure assessment methods assume that the spatial distribution of air pollutant concentrations are directly related to the use of the surrounding land. Physical features like elevation as well as the location and intensity of known pollutant sources including industrial emitters and traffic have been found to correlate well with pollutant concentrations (Briggs, 2005; Kolovos et al., 2010). Specifically, land use regression (LUR) uses predictors within a regression framework and has been the main focus of many land use models, becoming a popular tool for exposure assessment in air pollution research (Ryan et al., 2007; Henderson et al., 2007; Kashima et al., 2009; Ross et al., 2006). However, land use modeling is a complex problem due to the high spatial and temporal variations in pollutant concentrations on the local scale (Briggs et al., 1997; Beelen et al., 2010). LUR models have provided valuable insights and while more complex approaches have been applied to variable selection, the methodology has not included current predictive machine learning techniques. Therefore, there is an opportunity to improve the accuracy and precision of land use models, resulting in better exposure assessment for air pollution related epidemiological studies.

1.2. Using random forest in land use models

Land use models inherently use a high number of features that are highly correlated, for example, the length of highways within 100, 200, 300, and 400 m. Selection of which features to use in the final model is the outstanding challenge in land use model building and several approaches have been implemented (see Ryan and LeMasters 2007 for a review), most of which revolve around stepwise variable selection in a regression framework. Inclusion of correlated predictors generate problems for regression, often leading to unstable model estimates and variance inflation (Hastie et al., 2005). Although methods like variance inflation tests and influence statistics exist to combat this problem, they work by removing variables from the model that might otherwise be useful for prediction. Another challenge rising from regression-based land use models is the difficulty in capturing non-linear relationships and complex interactions. Because of the usually small sample size (n = 20 to 40) and very large number of possible predictors (p = 50 to over 500), it is often not feasible to evaluate all possible regression models.

Random forests are resistant to these problems. A key advantage of random forest is its ability to capture complex and non-linear relationships between predictors and the outcome with small sizes of training data. Random forests may be more accurate predictors of pollutant concentrations if they can indeed capture more patterns based on land use data. A random forest has been empirically shown to estimate concentrations of nitrogen dioxide based on land use data in the urban area of Geneva with a lower error when compared to regression (Champendal et al., 2014), although the authors did not compare the model’s cross validated performance with a traditional land use regression model. We hypothesize that land use random forest (LURF) models, as compared to LUR models, will result in more accurate and precise estimates of PM2.5 elemental component concentrations.

1.3. Random forests

Random forests (James et al., 2013; Liaw and Wiener, 2002) are often implemented in prediction analyses because of their increased accuracy and resistance to multi-collinearity and complex interaction problems as compared to linear regression (Hastie et al., 2005). The technique itself is an ensemble learning method that builds on bagging – specifically the bootstrapped aggregation of several regression trees – to predict an outcome. Bagging is most often used to reduce the variance of an estimated prediction function and is most useful for models which are unbiased but have a high variance, like regression trees (Hastie et al., 2005). Random forests, first proposed by Breiman (Breiman et al., 1984), modify the bagging technique by ensuring that the individual trees are de-correlated by using a bootstrap sample for each tree and also randomly selecting a subset of predictors for testing at each split point in each tree. The random forest comes with the advantages of tree-based methods, namely the ability to capture complex interactions and maintain low bias, while at the same time alleviating the problem of high variance of predictions usually associated with tree-based methods by growing the individual trees to a very deep level (usually one observation per terminal node) and averaging their predictions.

1.4. Land use models for elemental PM2.5 components

Particulate matter (PM) is a complex mixture of chemical and elemental constituents and epidemiological studies have shown that these components and their sources are associated with adverse cardiovascular and respiratory health outcomes in adults (Zanobetti et al., 2009; Simkhovich et al., 2008; Dockery, 2009). Further studies suggest that certain components of PM2.5 are responsible for adverse health effects and characterizing these health effects of PM components has been identified as a research priority by the National Research Council for the National Academies (N. R. C. U. C, 2004). Recently, successful LUR models have been developed for PM components in twenty areas in Europe as a part of the ESCAPE study (de Hoogh et al., 2013) and for an urban area in Canada (Zhang et al., 2015). These land use models have allowed for assessment of exposure to individual components of PM and the study of their association with health outcomes (Beelen, 2015; Eeftens et al., 2014; Hampel et al., 2015). Although some models have been developed, limited information on PM components has impeded progress in identifying their health effects (Bell et al., 2007).

2. Methods

2.1. Elemental PM2.5 measurements

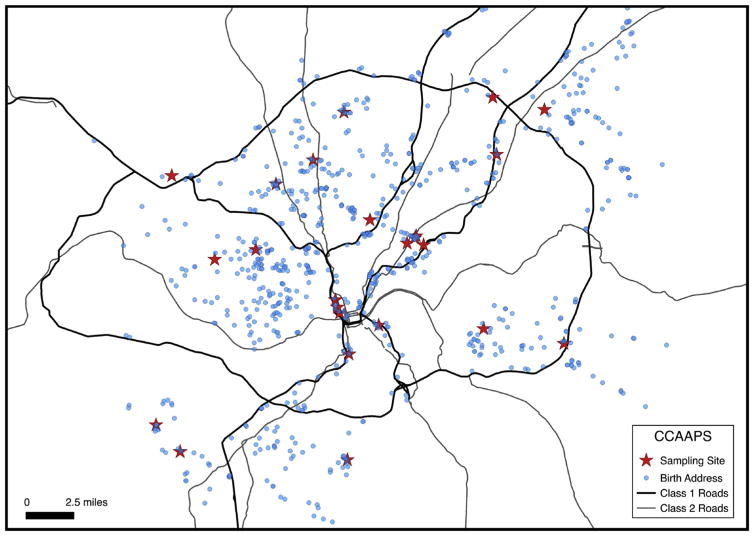
Measurements were collected at 24 sites across Cincinnati, Ohio as a part of CCAAPS, with full details available elsewhere (Ryan et al., 2007). Briefly, sites were selected based on the location of the CCAAPS cohort as well as wind direction, and proximity to pollution sources. Nine of the total sites were located within 400 m of a major roadway, while the rest of the sites were all located at least 1500 m away from a major roadway. Fig. 1 shows the location of the CCAAPS sampling sites and the birth addresses for the CCAAPS cohort. Between 2001 and 2005, PM2.5 samples were collected on 37-mm Teflon membrane filters and 37-mm quartz filters with Harvard-type Impactors. The increase in weight of the Teflon filters after sampling was used to determine the total PM2.5 mass (Hu et al., 2006) and X-ray fluorescence was used with the quartz filters to determine elemental concentrations for a total of 38 elements. Traffic related air pollution (TRAP) was calculated as the fraction of elemental carbon that was attributable to traffic by using a multivariate receptor model (Henry, 2000, 2003), UNMIX, to identify source signatures. One of the signatures was identified as TRAP because it was similar to comparison measurements conducted for cluster sources of trucks and buses (Hu et al., 2006) in Cincinnati, Ohio. Mean elemental concentrations for each site were calculated as averages and were considered missing if at least 75% of their measurements were classified as below the threshold of measurement certainty. For implementation of the land use models, in addition to total PM2.5 and TRAP, we restricted our building of models to the following eleven elements, which were selected for their previous association with health effects and a high percentage (≥ 75%) of detected samples: Al, Cu, Fe, K, Mn, Ni, Pb, S, Si, V, and Zn. All elements had complete information for all sites (n = 24) except for V, which had one site with missing concentration information. All concentrations were log transformed prior to building models and back transformed to their natural scale after predictions.

Fig. 1.

The location of the CCAAPS sampling sites in red and the birth addresses of the CCAAPS cohort in black. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2.2. Land use predictors

The predictors made available for inclusion in the final models for each element were based on previously validated LUR models for elements in PM2.5 (de Hoogh et al., 2013; Zhang et al., 2015) and on a previously validated LUR model for TRAP built using the same ambient sampling data in Cincinnati, Ohio (Ryan et al., 2007). Where applicable, geographic predictors were extracted based on the area within circles centered on the sampling site locations with varying buffer radii. In brief, land use predictors included measurements related to road location, traffic intensity, elevation, population density, greenspace, land cover, and emission point sources. See Table 1 for a full list of predictors, their units of measurement, and buffer radii. The Supplementary Information contains methodological details on all land use predictors.

Table 1.

Land use predictors considered for inclusion in final models.

Predictor	Units	Buffer radius in meters (intervals)
Transportation
Distance to nearest Class 1 road	meters	n/a
Distance to nearest Class 2 road	meters	n/a
Distance to nearest Class 3 road	meters	n/a
Distance to nearest Class 4 road	meters	n/a
Distance to nearest Class 5 road	meters	n/a
Length of roads: Class 1	meters	100–1000 (50)
Length of roads: Class 2	meters	100–1000 (50)
Length of roads: Class 3	meters	100–1000 (50)
Length of roads: Class 4	meters	100–1000 (50)
Length of roads: Class 5	meters	100–1000 (50)
Average daily truck count on interstates	count	100–1000 (50)
Average daily truck count on highways	count	100–1000 (50)
Number of major intersections	count	50–1000 (50)
Distance to nearest railroad line	meters	n/a
Length of railroads	meters	100–1000 (50)
Length of bus routes	meters	100–1000 (50)
Physical Features
Elevation	meters above sea level	n/a
Average elevation	meters above sea level	100–1000 (50)
Standard deviation of elevation	meters	100–1000 (50)
Fraction of elevation points > 20 m uphill	count	100–1000 (50)
Fraction of elevation points < 20 m downhill	count	100–1000 (50)
Community Characteristics
Population count	count	n/a
Population density	count/meters2	500–2500 (250)
Greenspace
Average NDVI value	n/a	100–1000 (100)
Land Cover
Open water	%	100–1500 (100)
Developed open	%	100–1500 (100)
Developed low	%	100–1500 (100)
Developed medium	%	100–1500 (100)
Developed high	%	100–1500 (100)
Barren	%	100–1500 (100)
Deciduous forest	%	100–1500 (100)
Evergreen forest	%	100–1500 (100)
Mixed forest	%	100–1500 (100)
Shrub	%	100–1500 (100)
Grassland	%	100–1500 (100)
Pasture	%	100–1500 (100)
Crops	%	100–1500 (100)
Woody wetlands	%	100–1500 (100)
Herbaceous wetlands	%	100–1500 (100)
NEI Point Sourcesa
Distance to nearest point source	meters	n/a
Point source count	meters	1000–10000 (1000)
Point source total emissions	tons	1000–10000 (1000)
Point source average emissions	tons	1000–10000 (1000)
Point source emissions weighted by distance	tons/meters	1000–10000 (1000)

^aPM2.5, PM10 (all models) and Ni, Pb, Mn (element specific models).

2.3. Land Use Regression (LUR) models

The approach for building the LUR models was based as closely as possible on a supervised stepwise selection procedure previously used to develop LUR models for elemental components of PM2.5 in urban areas of Europe (de Hoogh et al., 2013; otherset al, 2012). Each predictor in Table 1 was initially ranked based on the model R² value from a univariate regression with the elemental concentrations at all 24 sites. Because of the inherent correlation between variables of the same category (i.e. length of class 1 roads within 100 m and length of class 1 roads within 200 m), only one variable from each category was considered for inclusion in the model. The initial regression model was fit using only the highest associated predictor with the expected direction of effect and the remaining predictors were tried for addition to the model in order of decreasing association with the elemental concentration. At each step, the predictor was retained only if it increased the adjusted model R² by at least 0.01 and its coefficient was of the expected direction and it also did not change the direction of any of the previously included variables. After trying each variable, the final models were refit after removing variables with a p-value greater than 0.1. Next, variance inflation factors (VIF) were calculated for all variables and if any of the VIFs were greater than three, the variable with the highest VIF was removed and the model refit. The VIF process was repeated until all variables had VIFs of less than or equal to three. Furthermore, if the removal of a site with a Cook’s D statistic greater than one from the final LUR model caused large changes in a predictor’s coefficient, that predictor was removed from the model.

2.4. Land Use Random Forest (LURF) models

The approach for building the LURF models were based on implementations taken previously in the literature for microarray data (Díaz-Uriarte and De Andres, 2006; Alvarez et al., 2005; Izmirlian, 2004; Wu et al., 2003; Gunther et al., 2003; Man et al., 2004; Schwender et al., 2004). Like land use modeling of spatial pollutants, these type of studies utilize predictors that far outnumber the sample size, are littered with noise, and are often highly correlated with one another. As in the LUR models, the best buffer radii for each variable category was determined based on the model R² value from a univariate regression with the elemental concentrations. An initial random forest was trained using all of the best predictors from each category in order to rank these according to the random forest variable importance measure. Several random forests were built, each one by removing the least important predictor one at a time. The variable importance was used from the initial random forest and not recalculated at each step to avoid severe overfitting (Svetnik et al., 2004). The final random forest model was chosen based on pseudo $R^2=1-\frac{\mathit{MSE}}{\mathit{var}(Y)}$ where Y is a vector of the outcomes and MSE is the mean of the out of bag squared errors for all prediction points. Finally, the random forest was optimized for the best value of m_try based on pseudo R².

2.5. Cross validated model accuracy

Cross validation of the accuracy of land use models is an important step because it quantifies the accuracy of the model when it is used to make predictions based on new observations. In the specific case of land use models, this will estimate the accuracy for when the model is used to predict elemental concentrations at new locations not included in the original sampling sites. Leave one out cross validation (LOOCV) was used with the predictor selection step included as a part of the cross validation, so each fold of the LOOCV resulted in a different final model. The mean absolute prediction error (MAPE) was calculated for each cross validation fold as $\frac{1}{n}{\sum }_{i=1}^n\left|\frac{y_i-\widehat{y_i}}{y_i}\right|$. MAPE is equivalent to the absolute difference between the actual and predicted concentration as a fraction of the actual concentration.

2.6. Study cohort

The Cincinnati Childhood Allergy and Air Pollution Study (CCAAPS) is an ongoing prospective birth cohort of high-risk atopic children (LeMasters et al., 2006; Ryan et al., 2005). Children born between October 2001 and July 2003 in the Greater Cincinnati and Northern Kentucky region were screened by birth record and enrolled if they lived less than 400 m or more than 1500 m from the nearest major road (Ryan et al., 2005). Each child needed one parent with symptoms of rhinitis, asthma, or eczema and allergic sensitization by a positive skin prick test result to one of 15 aero-allergens. Informed consent was obtained and the study was approved by the University of Cincinnati Institutional Review Board.

2.7. Computing

All statistical and geospatial computing was done in R, version 3.1.2 (Core Team, 2014), using the rgdal (Bivand et al., 2014), rgeos (Bivand and Rundel, 2014), and sp (Bivand et al., 2005) packages.

3. Results

3.1. PM2.5 elemental measurements

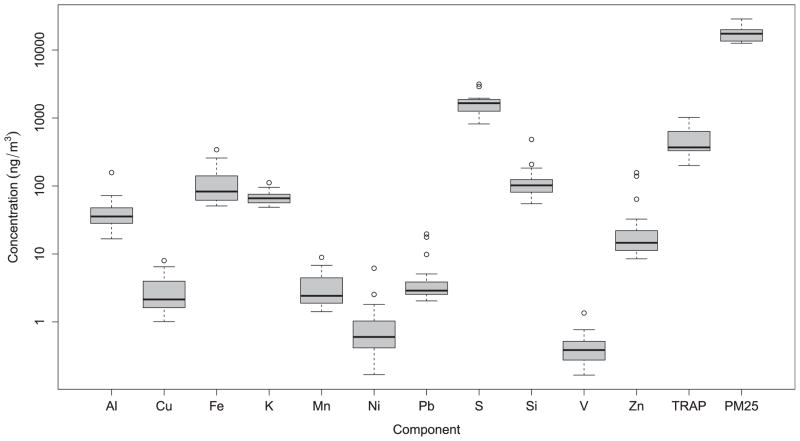
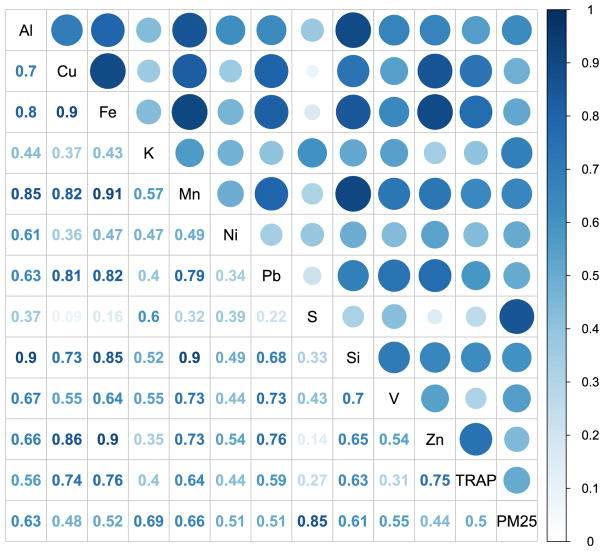
Measurements from the 24 sites were collected and described as averages in ng/m³. Fig. 2 shows the average concentrations as a boxplot on the log scale. In general, measurements had similar ranges to elemental PM2.5 components from previous studies (de Hoogh et al., 2013; Zhang et al., 2015; Beelen, 2015; Eeftens et al., 2014; Hampel et al., 2015). More specific descriptive numbers along with the variance are listed in Table 2. Fig. 3 illustrates the Spearman correlation matrix of all of the average measured concentrations. All elements, including TRAP and PM2.5, were highly correlated with one another. However, K, Ni and S were less correlated compared to the rest of the elements.

Fig. 2.

Box plot of average elemental concentrations, TRAP, and total PM2.5 used to train the land use models.

Table 2.

Summary of average elemental concentrations, TRAP, and total PM2.5 used to train the land use models. All elements contained complete measurements for all 24 sites, except for V, which had one site with a missing measurement. Concentration units are ng/m³.

Element	Minimum	25th Percentile	Median	Mean	75th Percentile	Maximum	SD
Al	16.7	28.3	35.6	42.1	46.9	157.6	28.2
Cu	1.0	1.6	2.1	3.0	3.9	8.0	1.9
Fe	50.9	62.5	83.0	112.0	139.7	342.3	73.7
K	48.6	56.8	65.9	67.1	75.4	111.8	14.8
Mn	1.4	1.9	2.4	3.3	4.4	8.9	2.1
Ni	0.2	0.4	0.6	1.0	1.0	6.2	1.3
Pb	2.0	2.6	2.9	4.7	3.9	19.7	4.6
S	819	1267	1653	1648	1861	3151	557
Si	55	83	102	122	124	484	86
V	0.2	0.3	0.4	0.4	0.5	1.4	0.3
Zn	8.5	11.4	14.6	28.7	21.5	156.9	38.6
TRAP	200	335	370	485	608	1020	248
PM2.5	12,595	13,558	17,396	17,582	19,665	28,623	4110

Fig. 3.

Spearman correlation matrix of average elemental concentrations, TRAP, and total PM2.5. A darker blue and larger circle in the upper triangle of the grid corresponds to a larger Spearman’s rho statistic shown in the lower triangle of the grid. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.2. Land use models

Both LUR and LURF models were built for total PM2.5 mass, TRAP, and eleven elemental components of PM2.5 including Al, Cu, Fe, K, Mn, Ni, Pb, S, Si, V, and Zn. Land use variables as well as the varying buffer radii made available for selection by each model are listed in full in Table 1.

3.3. Land Use Regression (LUR)

The final LUR models for most pollutants (Table 3) resulted in a high fraction of explained variance, with Cu, Fe, Mn, Pb, Si, Zn, and TRAP all having a model R² of at least 0.85. Models for Al, V, and PM2.5 all had a model R² of at least 0.6. The models with the least amount of explained variance were K (model R² = 0.49), Ni (0.40), and S (0.32).

Table 3.

Summaries of final LUR models for each element. Each model R² is from the final regression model and the model predictors are from the final models and Table 1 with a buffer radius in meters, if applicable.

Element	Model R2	Model Predictors
Al	0.77	Developed high (1200), Length of bus routes (100)
Cu	0.92	Developed high (1000), Shrub (1500), Average daily truck count on interstates (800)
Fe	0.94	Developed high (1000), Average daily truck count on interstates (800)
K	0.49	Distance to class 2 roads, Population density (1750), Length of bus routes (150)
Mn	0.86	Developed high (1000), Length of railroads (1000)
Ni	0.40	Barren (1100)
Pb	0.91	Length of bus routes (900), Population density (500)
S	0.32	Average daily truck count on highways (350)
Si	0.87	Developed high (1100), Length of bus routes (100)
V	0.60	Developed high (1500), Mixed forest (1100)
Zn	0.85	Length of bus routes (850), Distance to class 3 roads
TRAP	0.88	Developed high (1000), Average daily truck count on interstates (800), Length of class 1 roads (1000), Fraction of elevation points more than 20 m uphill (1000), Shrub (1500)
PM25	0.64	Length of bus routes (350), Length of railroads (150), Woody Wetlands (1300), Distance to class 2 roads

The most commonly selected land use predictor was the fraction of highly developed land from the National Landcover Database, utilized in the models for all pollutants except for K, Ni, Pb, S, and PM2.5. Transportation related variables also dominated the models, with truck traffic volume and length of roads or bus routes being the most common. Other than the use of population density in the models for K and Pb as well as the use of an uphill measurement in the model for TRAP, only transportation and land use variables were selected. Of note, intersections, greenspace variables, and known emission point sources were not selected for any of the LUR pollutant models. Model coefficient tables, including estimates, standard errors, and p-values for each LUR model is available in the Supplemental Information.

3.4. Land Use Random Forest (LURF)

The final LURF models (Table 4) also showed a generally high fraction of explained variance with Cu, Fe, Mn, Pb, and Zn having a model pseudo R² of at least 0.8. All other models had a model pseudo R² of at least 0.5 except for K, Ni, and V. Although the model R² from the LUR model is not directly comparable to the model pseudo R² from the LURF model, it is interesting to note that Ni and K were two of the three worst performing pollutant models in both model types. In general, the LURF models utilized a higher number and more diverse selection of land use predictors for each pollutant than the LUR models. This is likely due to the ability of the model to detect more relationships between land use variables and pollutant concentrations, rather than over-parameterization because variable selection was included as a part of the cross validation process. The fraction of highly developed land was still important, appearing in all models except for K.

Table 4.

Summaries of final LURF models for each element. Each model pseudo R² is from the final random forest model and the model predictors are from the final models and denoted as in Table 1 with a buffer radius in meters, if applicable.

Element	Model Pseudo R2	mtry	Model Predictors
Al	0.56	2	Deciduous forest (1000), Developed high (1200), Distance to class 4 roads
Cu	0.82	3	NDVI (1000), Distance to Nearest PM2.5 point source, Distance to Nearest PM10 point source, Developed high (1000), Distance to railroads, Total PM2.5 point sources (3000), Elevation 650, Fraction of elevation points more than 20 m downhill (1000), Distance to class 1 roads, Total PM10 point source emissions weighted by distance (3000), Total PM10 point sources (4000), Total PM10 point source emissions (3000), Length of railroads (1000), Total PM2.5 emissions weighted by distance (3000), Population density (1500), Developed medium (400), Developed open (1100), Elevation, Shrub (1500), Mean PM2.5 point source emissions (3000), Developed low (800), Fraction of elevation points more than 20 m uphill (1000), Length of bus routes (350), Average daily truck count on interstate (800), Total PM2.5 point sources (4000), Standard deviation of elevation (1000), Mean PM10 point source emissions (3000), Deciduous forest (1500), Length of class 1 roads (1000)
Fe	0.88	2	Developed high (1000), NDVI (1000), Distance to nearest PM2.5 point source
K	0.36	3	Mean PM2.5 emissions (7000), Length of class 3 roads (350), Mean PM10 point source emissions (7000), Average daily truck count on interstate (300), Distance to nearest class 3 road, Pasture 500, Average daily truck count on highways (350), Population density (1750), Evergreen Forest (600), Total PM10 point sources (7000), Mixed forest (1200)
Mn	0.87	2	Total PM2.5 point sources (2000), Total PM10 point sources (2000), Distance to closest PM2.5 point source, Distance to closes PM10 point source, Developed high (1000), Population
Ni	0.23	1	Deciduous forest (1000), NDVI (700), Mean PM10 point source emissions (2000), Total PM10 point sources (2000), Developed high (1000), Mean PM2.5 point source emissions (2000), Average Elevation (600), Length of class 4 roads (200), Developed medium (1400), Total PM10 point sources (2000), Grassland (1200), Average daily truck count on highways (1000)
Pb	0.89	2	NDVI (1000), Pasture (800), Developed Open (1100), Developed medium (400), Length of bus routes (900), Population density (500), Developed low (900), Developed high (1500)
S	0.50	2	Average daily truck count on highways (350), Distance to nearest class 5 roads, Developed high (1500), Average daily truck count on interstate (300), Length of class 3 roads (350), Distance to nearest railroad
Si	0.60	2	NDVI (1000), Developed high (1100), Deciduous forest (900), Developed open (1100), Developed low (800), Average elevation (400), population, Length of bus routes (100), Developed medium (400), Elevation
V	0.46	1	Grassland (1200), Deciduous forest (1400), Developed open (700), Total PM2.5 emissions (8000), Distance to nearest PM10 emissions source (8000), Mixed forest (1100), Population density (1750), Total PM2.5 point sources (6000), Total PM10 point sources (6000), Mean PM2.5 point source emissions (3000), Developed medium (400), Distance to nearest PM10 point source, NDVI (1000), Distance to class 2 roads, Length of class 2 roads (1000), Total intersections (1000), Length of bus routes (850), Mean PM2.5 point source emissions weighted by distance (8000), Distance to nearest railroad, Average daily truck count on highways (650), Developed high (1500)
Zn	0.80	2	Developed medium (400), Developed high (1500), Total intersections (1000), Developed low (900), Deciduous forest (1500), Length of bus routes (850), NDVI (1000), Length of class 4 roads (1000), Developed open (1500), Population density (500), Length of class 1 roads (1000), Average daily truck count on interstates (300)
TRAP	0.78	1	Mean elevation (100), Elevation, Average daily truck count on interstates (800), Developed high (1000), Developed low (900), Length of class 1 roads (1000)
PM25	0.51	1	Length of bus routes (350), Herbaceuous wetlands (1500), Barren (1500), Average daily truck count on interstates (300), Standard deviation of elevation (1000), Developed high (1500)

However, other variables not included in the LUR models were frequently utilized in the LURF models. Examples include green-space (used models for Cu, Fe, Ni, Pb, Si, V, and Zn), intersections (used in models for V and Zn), and point sources from the National Emissions Inventory Database (used in models for Cu, K, Ni, and V). The optimization of m_try resulted in low values relative to the total number of variables in each final model, suggesting that this use of auxiliary noise in the random forest was useful in increasing the model accuracies.

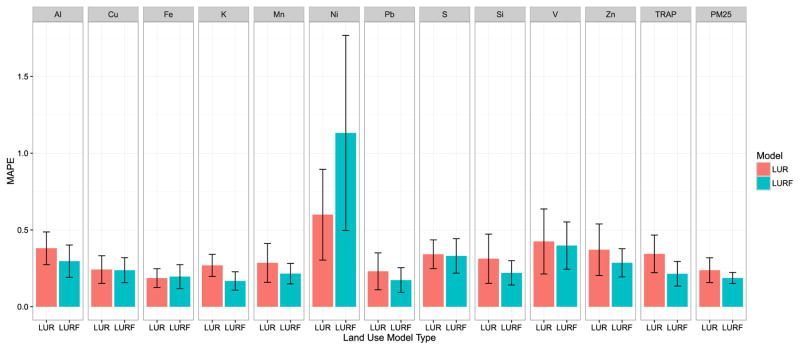
3.5. Cross validated model accuracy

LOOCV was used to quantitatively compare the accuracy between the LUR and LURF models. Each site was left out once and the remaining 23 sites were used to create both a LUR and LURF model to predict the elemental PM2.5 concentrations. This process was repeated for all 24 sites. The cross validated MAPE for each element and model type are presented in Table 5. The MAPE along with its 95% confidence interval is also plotted in Fig. 4 for each model. The LURF models for all elements except Fe and Ni had a lower MAPE than the LUR models. The difference in the MAPE for the Fe models was less than 0.01 and the Ni model increased from 0.60 to 1.13 when using a LURF model instead of a LUR model. The largest reduction in MAPE was seen for TRAP (0.24–0.19 for LUR and LURF, respectively) and the models for Al, K, Mn, Pb, Si, Zn, and PM2.5 also all showed a decrease in MAPE of at least 5%. The MAPE for these elements also had much more variation using the LUR models as compared to the LURF models, seen in the confidence intervals in Fig. 4.

Table 5.

Cross validated mean absolute predictive error (MAPE) of LUR and LURF elemental PM models.

Element	MAPE (LUR)	MAPE (LURF)
Al	0.38	0.30
Cu	0.24	0.24
Fe	0.19	0.20
K	0.27	0.17
Mn	0.29	0.22
Ni	0.60	1.13
Pb	0.23	0.17
S	0.34	0.33
Si	0.31	0.22
V	0.43	0.40
Zn	0.37	0.29
TRAP	0.34	0.21
PM25	0.24	0.19

Fig. 4.

Cross validated absolute predictive error and 95% confidence interval for each elemental model, each built both using a LUR model and a LURF model.

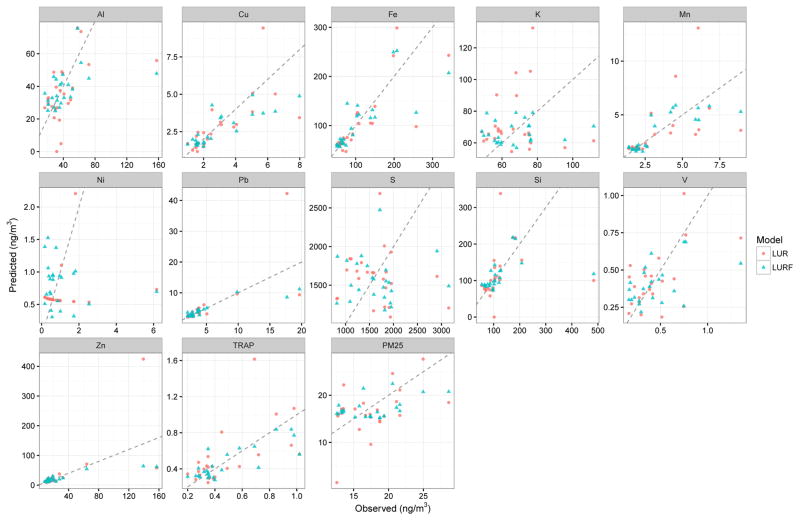
Fig. 5 shows the individual predictions plotted against the observed concentrations for each fold of the cross validation according to model type and shows that the LUR models often make predictions that are very high compared to the actual value and the LURF predictions. It is these extreme errors that are likely driving the large variation in the MAPE. Although these high predictions could be due to extreme values for some of the land use predictors at the held out sampling station used for prediction testing, this result highlights the advantage of LURF in that it is able to accurately predict exposures at locations that might not be similar to the locations used to train the models.

Fig. 5.

LOOCV predictions from the LURF and LUR land use models according to the true observed values. The dotted line represents the perfect agreement between observed and predicted concentrations.

4. Discussion

Here, we have successfully created LUR and LURF models for elemental components of PM. We have also shown that our novel land use models based on random forests are more accurate than LUR models for most of the elements. As assessed by LOOCV, the best performing models (MAPE <0.2) were for Fe, K, Pb, and PM2.5. Models for Al, Cu, Mn, Si, Zn, TRAP (MAPE < 0.3), as well as S and V (MAPE <0.4) also performed well. The model for Ni performed the worst by far (MAPE = 1.13). Furthermore, we identified a differential bias in exposure assessment using the LUR models which was not present using the LURF models. The identification of relatively lower accuracy when predicting relatively high concentrations in the LUR models implies that this misclassification is differential and could result in biased associations with health outcomes. This problem was not found in the LURF models and highlights the advantage in our novel model, which is not only an increased accuracy, but a decreased variance of the amount of prediction error.

An epidemiology study that used the ESCAPE elemental exposure assessment model truncated extreme values of GIS predictors to the range observed at the sampling sites (Eeftens et al., 2014). Although removing these types of outliers may improve the performance of the land use regression models, it does not guarantee that new predictions will be improved. In fact, it is likely that the differential truncation of predictor variables will lead to a differential misclassification bias and errors in future epidemiological studies. An exposure assessment model must be externally valid in that it should be able to predict accurate exposures that are slightly outside of the range of the measured concentrations and land use variables. Here we show using cross validation that LURF improves on LUR with respect to accurately predicting PM2.5 concentrations at new locations.

Other LUR models have been developed for elemental components of PM (de Hoogh et al., 2013; Zhang et al., 2015) which all used regression based approaches. Specifically, the model created for Calgary, Alberta (Zhang et al., 2015) used models specific to summer and winter seasons to predict elemental components of PM10. Their measured elemental concentrations were similar to ours and followed the same correlation patterns, with all elements except for S being highly correlated with one another. They found that industrial point sources explained the most variance in their models, followed by developed land use. Although our elemental LUR models did not incorporate any pollutant point source information, highly developed land use did explain the largest amount of variation in almost all of the models. These models did include other potential predictors, like traffic volume, road density, housing, and population density, but, unlike our LUR models, these did not explain much variance in their final models. The authors found that only 11 of their 30 elemental models had a model R² of at least 0.7 for both seasons, whereas eight of our eleven elemental models had a model R² of at least 0.7. The ESCAPE study (de Hoogh et al., 2013) developed LUR models for elemental components of both PM10 and PM2.5 for twenty different areas of Europe. Again, the correlation patterns and concentrations of measured elements were similar to our results. The model R² for each element varied greatly across the locations, but on average, they found a model R² greater than 0.7 for two of eight total modeled elements. Similar to our results, they found the elements with the highest model R² to be Cu and Fe, and the element with the lowest model R² to be Ni.

One potential drawback of our study is the location of the sampling sites. These sites were originally selected to capture both near-roadway and residential exposures and the initial LUR model developed using these sites was the first for elemental carbon (Ryan et al., 2007). We did not consider buffer radii less than 100 m for several of the transportation land use predictors because none of the sites from the ambient air monitoring campaign designed for CCAAPS were within 100 m of a major roadway. However, the final selected set of land use predictors for both the LUR and LURF models were very similar to the predictors used in our original LUR model for traffic related air pollution (Ryan et al., 2007).

Variable selection techniques other than the method employed here and in the ESCAPE study have been used for land use regression models and a potential drawback of our study is that the LURF model is not compared to these approaches. These include manual forward selection (Ross et al., 2006; Moore et al., 2007; Jerrett et al., 2007), automated stepwise methods (Zhang et al., 2015; Aguilera et al., 2007; Crouse et al., 2009), the distance decay strategy (Su et al., 2009), and the deletion/substitution/addition algorithm (Beckerman et al., 2013). Although they differ in the variable selection procedure all of these approaches are based on a parametric regression framework, whereas our LURF models are a non-parametric machine learning approach.

Although the LURF model provides more accurate exposure assessment, another potential drawback of our method is the lack of a model statistic comparable to regression coefficients that allow for elucidation of the direction and magnitude of air pollution sources with predicted airborne concentrations. In order to detect complicated interactions and non linear relationships, the random forest uses hundreds or thousands of individual regression trees that make it difficult to interpret the overall effect of a single land use variable. Researchers utilizing machine learning methods in general must trade off some interpretability for increased accuracy and this trade-off may be more appropriate for some areas of research than others. However, recent work has been done to establish causal inference methods for random forests (Wager et al., 2014; Wager and Athey, 2015) and implementing these methods into LURF will be a promising avenue for future research.

LURF will be a useful exposure assessment tool for epidemiological studies associating elemental components of PM with health effects. More generally, random forest and other machine learning methods may be incorporated into future land use models for more accurate exposure assessment.

5. Software

The code used to calculate the land use predictors and generate exposure estimates for each location along with the necessary land use data and examples has been made into an R package and is available online at https://github.com/cole-brokamp/aiRpollution (Brokamp, 2016). The code used to build and cross validate the LUR and LURF models is available on request from the corresponding author.

HIGHLIGHTS.

• Land use models based on regression (LUR) and random forest (LURF) were created for elemental PM2.5

• LURF models were more accurate and precise than LUR models for most elements.

• Random forest may be used in future land use models for more accurate exposure assessment.

Appendix A. Supplementary data

Supplementary data related to this article can be found at http://dx.doi.org/10.1016/j.atmosenv.2016.11.066.