All-optical photoacoustic projection imaging

Abstract

We introduce all-optical photoacoustic projection imaging. An array of fiber-optic interferometers is used to measure photoacoustic signals. The obtained images represent the projection of the three-dimensional spatial light absorbance within a sample onto a two-dimensional plane. We assess the performance of the system by phantom measurements and show that the fiber-optic detectors achieve a noise-equivalent pressure of 24 Pascal at a 10 MHz bandwidth. Furthermore, we demonstrate the ability to acquire high-resolution projection images of large volumes within a short period of time.

1. Introduction

Photoacoustic tomography (PAT) is an emerging technology for noninvasive imaging of biological structures and functions [1]. Images are formed from ultrasonic waves generated by optical absorption of short laser pulses within a sample. In contrast to imaging modalities relying on reflected or transmitted light, the image resolution in PAT is not affected by the scattering of light in biological tissue and, therefore, offers high spatial resolution in relatively large imaging depths. The achievable resolution is limited by acoustic attenuation [2–4] and depends on the imaging depth. By a rule of thumb, the minimal spatial resolution is in the order of 1/200 of the imaging depth [5]. Various photoacoustic techniques were demonstrated, offering imaging depths ranging from millimeters in acoustic-resolution photoacoustic microscopy (AR-PAM) [6] up to several centimeters in photoacoustic scanning macroscopy (PASMac) [7,8] and photoacoustic computed tomography (PACT) [9]. AR-PAM and PASMac use focused element ultrasound transducers and the images are formed by a scanning technique. In PACT, transducer arrays pick up the photoacoustic signals in order to increase acquisition speed and, to some extent, resolution. The transducers can be arranged in various geometries. E.g., linear [10], arc-shaped [11,12], (hemi-)spherical [13–16], planar [17,18], or circular arrangements [19,20] have been demonstrated. In general, a large number of detector elements is required in order to image a volume at high resolution. Since this is technically challenging and expensive, usually multiple measurements at different positions of the detector array all around the sample have to be conducted. A three-dimensional image of the investigated volume can then be rendered by using adequate image reconstruction methods [21–23].

In this paper, we introduce all-optical photoacoustic projection imaging (O-PAPI). Ultrasound detection is performed with an array of integrating line detectors [23,24]. The individual line detectors are arranged in parallel on a cylindrical surface. Thereby, the resulting images represent the projection of the three-dimensional spatial absorbance within a sample onto the two-dimensional plane perpendicularly to the line detectors [23,24]. This can be interpreted as the photoacoustic analogue to X-Ray radiography, where the spatial structure of the object is projected onto the plane perpendicularly to the X-Ray beam. In contrast to the photoacoustic methods mentioned above, the proposed technique allows to observe the complete volume via highly resolved projection images, acquired with a single measurement. Thus, fast processes within a volume, e.g. perfusion, could be imaged at high frame rates. Also, analogously to X-Ray computed tomography, O-PAPI can be used to acquire full three-dimensional images. In this case, several images of the sample, obtained from different projection angles, can be composed to form a 3D image by inverse Radon transformation [25,26].

The integrating line detectors of our O-PAPI prototype consist of fiber-optic interferometers [8,24]. An overview of different types of optical fiber based interferometers and other optical detection techniques used for photoacoustic imaging can be found in [27]. Additionally, integrating line detectors based on probe beam deflection have been demonstrated [28,29]. Receiving the photoacoustic signals with optical fibers instead of commonly used piezoelectric detectors offers various advantages [8,27]. Optical sensors exhibit low cross-talk and do not need electrical shielding. Due to the cylindrical symmetry of the fibers, the ultrasonic sensitivity is independent on the azimuth angle of the incident ultrasonic wave. As a consequence, an impinging wave front will lead to the same detected signal, independent on the location of the origin, as long as the minimum distance between source and fiber is constant. In addition, the photodetector of the interferometer is the only bandwidth-limiting element for the used detection scheme. Thereby, the detection bandwidth of the detector array can be adjusted by the used photodetectors without changing the actual detector elements. Moreover, fiber-optic ultrasound detectors offer higher sensitivity [8,27].

In this paper, we present the first prototype of an O-PAPI device which is intended to be used for imaging small animals. By scaling of the array geometry, the device could also be used, e.g., for imaging of the human breast.

Subsequent to this introduction, the composition and functionality of the fiber-optic detector array is explained. The next section presents the methods used for demonstrating the capabilities and features of our O-PAPI prototype. This includes subsections on phantom manufacturing on the performed experiments and on the conducted simulations. After showing the results of the experiments in section 4, the findings are discussed in section 5.

2. Fiber-optic detector array

The photoacoustic signals are measured with fiber-optic Mach-Zehnder interferometers (FOMZIs). In short, elastic strains within the measurement arm of the interferometer, induced by ultrasonic waves, change the refractive index in the fiber core. The resulting phase shift is then detected by interferometric means. A detailed explanation of the functionality of the used FOMZI can be found in Bauer-Marschallinger et al. [8,30]. Graded-index polymer optical fibers (GIPOF) act as ultrasound sensitive elements in the measurement arms within these interferometers. By using GIPOFs instead of common glass fibers, a higher sensitivity and a more uniform frequency response is achieved [31]. The schematic of the array is shown in Fig. 1. The O-PAPI prototype features a FOMZI array with 64 GIPOFs and 16 evaluation channels. Each evaluation channel consists of a reference arm, a fiber-optic coupler, a balanced photodetector, a controller, and an analog-digital converter. Optical switches are used to multiplex the 16 evaluation channels to the 64 GIPOFs. This multiplexing is done in order to reduce costs. As only 16 evaluation channels are used, four subsequent measurements are required for readout of the whole detector array. To achieve best sensitivity, the Mach-Zehnder interferometer has to operate at a working-point phase-difference of π/2 between measuring and reference arm. This operational-point is maintained by an analog controller in conjunction with a phase shifter (φ, Phoenix Photonics) in the reference arm. Light of the reference and measurement arm is superposed within the 50/50 fiber coupler. The superposed light is transformed into electric signals by a self-made balanced photodetector [8] with a high-frequency (HF) and low-frequency (LF) output. The HF outputs with a bandwidth of 43 MHz provide the photoacoustic signals, which are sampled by two 8-channel A/D converters (NI PXI 5105, sample rate 60 MS/s). The LF outputs of the photodetectors, representing low-frequency deviations from the working-points, are fed to the analog controller board. A 200 mW cw fiber laser (Koheras AdjustiK) powers the FOMZIs. A software on a PC controls the signal acquisition.

Fig. 1.

Schematic of the detector array for photoacoustic projection imaging with 64 detector positions. Photoacoustic detection is based on 16 fiber-optic Mach-Zehnder interferometers (FOMZIs). Each FOMZI consists of a pressure-receiving measuring arm, a working-point stabilizing reference arm, a 50/50 fiber coupler, and a balanced photo detector. In the measuring arm, a 4x1 optical switch connects 4 graded-index polymer optical fibers (GIPOFs), e.g. the pressure-sensitive parts, to the 50/50 coupler. Hence, the 64 GIPOFs are multiplexed to 16 fiber couplers. In the reference arm, an electronic phase shifter (φ) establishes a working-point phase difference between both arms for best sensitivity. A photodetector transforms the outputs of the 50/50 coupler into high-frequency (HF) and low-frequency (LF) electric signals. The HF signals, i.e. the actual photoacoustic signals, are sampled by a 16 channel A/D converter. The LF signals are fed to 16 analog controllers which power the phase shifters (φ). A 1550 nm fiber laser supplies the FOMZIs via fiber couplers.

The GIPOFs are aligned in parallel and are uniformly distributed along a circular arc [32]. The arc covers an angle of 289 degree and has a radius of 4 cm (see also Fig. 2). The lengths of the GIPOFs are 20 cm. During the installation of the array four fibers were damaged. Since the replacement of fibers is rather complex, we decided to use the array with 60 fiber only.

Fig. 2.

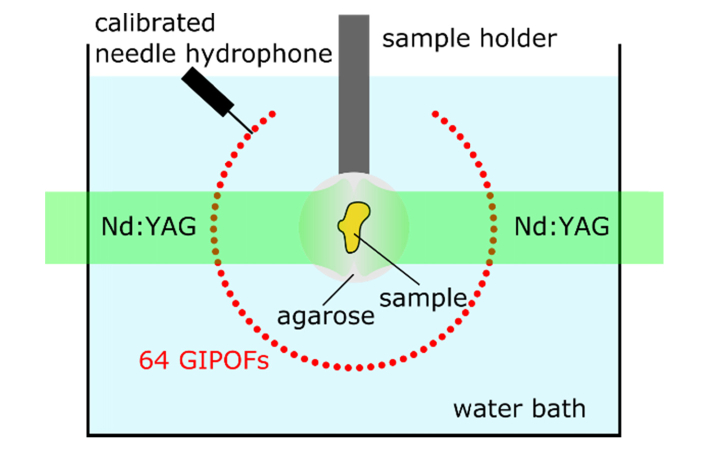
Schematic of the performed experiments. In relation to Fig. 1, the schematic shows the cross-section of the GIPOFs. This view is identical to the imaging plane whereupon the photoacoustic signals are projected. The circular GIPOF array covers an angle of 289 degree. The samples are embedded in agarose and held by a sample holder. A pulsed laser beam coming from a frequency doubled Nd:YAG laser is split to illuminate the samples from two sides. To determine the sensitivity of the fiber, a calibrated needle hydrophone is used to quantitatively measure the pressure.

3. Methods

3.1 Phantoms

In order to investigate the performance of our O-PAPI prototype, we prepared four different phantoms. They are denoted as phantom A, B, C, and D. The phantoms consist of different objects embedded in agarose gel. The gel was prepared with 2% agarose in distilled water. To increase optical scattering, Intralip was added to the gel in phantoms A-C with a concentration of 0.5%. The objects in phantoms A-C where embedded in three steps. First, a cylindrical base of the agarose gel with a diameter of 36 mm and a height of approximately 20 mm was prepared. Then, the object was placed in the middle of the cylinder and fixated with a few drops of the agarose/Intralipid mixture. Finally, another layer of agarose gel with a thickness of 20 mm was formed on top of the sample object.

In phantom A, a single black polyethylene microsphere (Cospheric, Santa Barbara, CA) with a diameter of approximately 200 µm was embedded. An approximately triangular shaped piece of an ink-stained leaf skeleton was used in phantom B. In phantom C, a cross-shaped structure was formed by two black porcine bristles with diameters in the range of 120–145 µm and lengths of 5.6 mm and 8 mm. For phantom D, an ink-filled flexible polymer tube with an inner diameter of 300 µm was inserted in a piece of chicken breast. For hygienic reasons and for mounting purposes, the chicken breast was embedded in an agarose cylinder.

3.2 Experiments

We performed 5 different experiments which are explained in the following subsections. Table 1 provides a compilation of the main characteristics of the individual experiments and Fig. 2 shows the experimental setup. The fiber-optic detector array is immersed in a water bath and the phantoms are positioned within the detector array by a sample holder. Photoacoustic excitation of the phantoms is achieved by two-sided illumination with pulses from a frequency-doubled Nd:YAG laser (Continuum Surelite, 20 Hz repetition rate, 6 ns pulse duration, 532 nm center wavelength). This laser also triggers the signal acquisition. At each laser pulse, 16 of the 64 optical line detectors are read out. After data acquisition, another subset of the 64 fibers are addressed with the optical switches. In total, four different measurements are needed for acquiring the photoacoustic signals on all 64 channels. If required, averaging can be applied. The diameter of the two excitation laser beams is approximately 15 mm. A calibrated needle hydrophone was only used in the first experiment.

Table 1. Characteristics of performed experiments.

			Maximal exposure [mJ/cm2]			Number of Averages
Experiment	Phantom		Mean	STDa			Duration [s]
Sensitivity	A / microsphere		-	-		128	-
Image quality	B / leaf skeleton		21	1.08		32	23
Image resolution	C / bristles		21	1.1		32	20
Image area	A / microsphere		25	1.1		32	22
Blood vessel	D / ink-filled tube		24	1.05		16	10

^aSTD, standard deviation.

3.2.1 Determination of the sensitivity

Phantom A was used to determine the sensitivity of the GIPOF ultrasound detectors. The acoustic pressure next to a fiber was quantitatively measured by a calibrated needle hydrophone (Onda HNC1000).

3.2.2 Image quality

The quality of the reconstructed images was assessed by imaging the ink-stained leaf skeleton (phantom B). The mean radiant exposure was below 21 mJ/cm². The standard deviation of the pulses was 1.08 mJ/cm². The signals were 32-times averaged and the measurements took 23 seconds.

3.2.3 Estimation of the imaging resolution

The attainable imaging resolution was estimated by imaging of phantom C. The average radiant exposure was below 21 mJ/cm². The standard deviation of the pulses was 1.1 mJ/cm². The signals were 32-times averaged and the measurements took 20 seconds.

3.2.4 Testing the imaging area

Our O-PAPI system aims for small animal imaging. Such a system should be capable of imaging within an area with a diameter of a few centimeters. The dependence of the image quality on the sample location within the detector array was investigated with phantom A. Several images at different locations of the phantom were acquired. The mean radiant exposure was below 25 mJ/cm². The standard deviation of the pulses was 1.1 mJ/cm². The signals were 32-times averaged and one measurements took 22 seconds on average.

3.2.5 Imaging of a blood vessel phantom

Phantom D was used to verify if the O-PAPI prototype can resolve structures in tissue. The mean radiant exposure was below 24 mJ/cm². The standard deviation of the pulses was 1.05 mJ/cm². The signals were 16-times averaged and one measurements took 10 seconds.

3.3 Signal processing and image formation

The ultrasound sensitivity is different for each sensing fiber. This is caused by several effects, which are addressed in the discussion section of the paper. The relative sensitivities were used to normalize the recorded photoacoustic signals. Signals were set to zero outside a time window, given by the minimal and maximal arrival times of photoacoustic signals originating from a defined region of interest (ROI). The arrival times were calculated using the speed of sound in the water bath and the distance of the fiber to the RIO. Low- and high-pass filtering was performed optionally. After signal processing, the image was reconstructed within the RIO using a two-dimensional back projection algorithm [23].

3.4 Simulations

Numerical simulations were performed in order to evaluate the experimentally obtained image quality in experiment 3.2.2. To this end, a photograph of the ink-stained leaf skeleton was taken before embedding in agarose and converted into a gray scale image. This image was used as ultrasonic source in the forward simulation using the MATLAB k-Wave toolbox [22]. The simulation grid had 4056x4056 points. One grid point covered an area of 20.7x20.7 µm. The time step was 16.7 ns. The detection signals were simulated at 253 positions equally distributed at the circular arc defined by the fibers of the O-PAPI prototype. Hence, every fourth simulated point is located at an actual fiber of the detector array. With the additional detector positions, the influence of the number of detectors on the resulting image quality was assessed. Optionally, simulated noise was added to the data. The influence of the variable sensitivity of the fiber sensors on the image reconstruction was also taken into account by scaling the added noise relative to the inverse sensitivity of the fibers. I.e., a lower relative sensitivity resulted in a higher noise level.

4. Results

4.1 Determination of the sensitivity

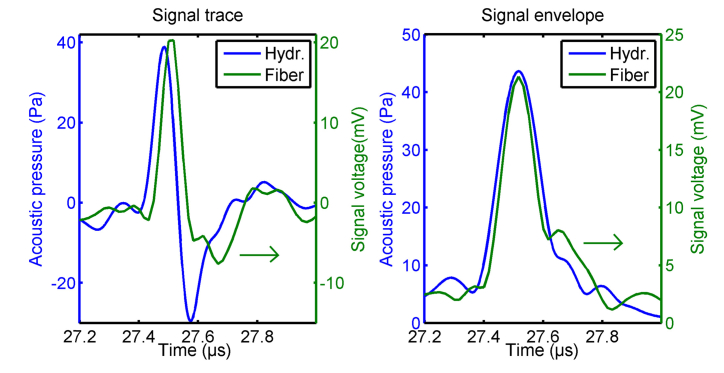
In addition to the measurement with the fiber-optic detector, the photoacoustic signals originating from phantom A (microsphere) were measured by a calibrated needle hydrophone. Both signals were bandpass filtered with cutoff-frequencies of 1 MHz and 10 MHz. The resulting signal traces and envelops are shown in Fig. 3. The signals appear similar, except for the wider negative peak in the fiber signal trace, which is predicted by theory [31]: When the circular wave front, stemming from the microsphere, reaches the line detector, the intersection length is small and the line detector behaves similar to a point-like detector. After this initial interaction, the wave front crosses the line detector in two points. The spatial integration of the propagating bipolar pressure wave leads to a prolonged tail in the temporal signal. By comparing the maxima of the signal envelopes, the conversion factor from pressure to voltage of the fiber detector was determined to be 490 µV/Pa. The root-mean-square of the detector noise was measured to be 11.8 mV. Thus, the fiber-optic detector achieves a noise equivalent pressure of 24 Pascal at an ultrasonic bandwidth of 10 MHz.

Fig. 3.

Signal traces and envelopes of a photoacoustic wave stemming from a black polyethylene microsphere with a diameter of 200 µm embedded in agarose/Intralipid. The acoustic pressure of the wave is shown by the blue curves (left axis) and was measured with a calibrated needle hydrophone. The green curves (right axis) present the signal voltage acquired by the fiber-optic line detector. The curves were averaged 128-times.

4.2 Image quality

Imaging quality was tested with a piece of an ink-stain leaf skeleton (see Fig. 4(a)). The strongest branches had a diameter of approximately 160-190 µm and the smallest measured about 50 µm. Figures 4(b)-4(c) show image reconstructions from measurements with the O-PAPI prototype. For the image in Fig. 4(b), the data was bandpass filtered with a bandwidth between 300 kHz to 10 MHz. For Fig. 4(c), 4 MHz low-pass filtering was applied. The strong and medium branches are visible more distinctly in the low-pass filtered image. However, the fine structures disappear. Artifacts next to the leaf skeleton appear in both images. To identify the origin of the artifacts, numerical simulations were carried out. Figures 4(d)-4(f) present reconstructions on basis of forward simulated signals (see section 3.4). The first image (Fig. 4(d)) was computed from simulated signals at 253 detection positions. In this case, no simulated noise was added. All the features of the leaf are reproduced well. Only the smallest structures appear slightly widened. The image quality hardly suffers from artifacts. The data for reconstructing the image in Fig. 4(e) was adjusted in order to match the situation in Fig. 4(b) as closely as possible. Thus, only the positions of operating fibers were considered, the same bandpass filtering was applied, the relative sensitivity was taking into account, and simulated noise was added. The same data processing was applied for Fig. 4(f), however in this case, 127 positions were used. The opening angle of the simulated detector array was maintained constant in all cases. The measured image in Fig. 4(b) appears very similar to the simulated image in Fig. 4(e). The artifact patterns surrounding the phantom in both images show only very little differences. In Fig. 4(f), the intensity of the artifacts is clearly reduced. We therefore conclude that the artifacts in Fig. 4(b)-4(c) are caused by the low number of detector positions. Further analysis reveals that the medium and small branches are slightly better visible in the simulated image (Fig. 4(e)) compared to the measurement in Fig. 4(b). However, these differences remain relatively low, considering that several effects were not taken into account in the simulation. E.g. the effects of non-uniform illumination of the sample, variations in the speed of sound, and inhomogeneous intake of the light absorbing ink by the leaf skeleton were not considered in the simulation.

Fig. 4.

(a) Photograph of an ink-stained leaf skeleton before embedding in agarose. The strong branches at the lower boarder of the skeleton measure approximately 160–190 µm in diameter. (b) Photoacoustic projection image of leaf skeleton based on signals with a bandwidth of 300 kHz to 10 MHz. Imaging artifacts around the leaf are clearly visible. Within the leaf, the occurrence of artifacts seems to be lower. The resulting image with a signal-bandwidth of 4 MHz is shown in (c). The leaf stands out more clearly from the artifact background. However, finer details are lost. In (d)-(f) different reconstructions based on forward simulated data using the k-Wave toolbox [21] are shown. For reconstruction (d) 253 sensor positions were used. In (e) only sensor positions available in the measurement were considered and the forward simulated data was frequency filtered to achieve a bandwidth of 300 kHz-10MHz. Also, noise comparable to the actual measurement noise was added. The same forward data, however at 127 positions, were used to calculate image (f). From (d)-(f) it can be concluded that the artifact background in the measurement (b) around the leaf originates from the limited number of sensor positions.

4.3 Estimation of the imaging resolution

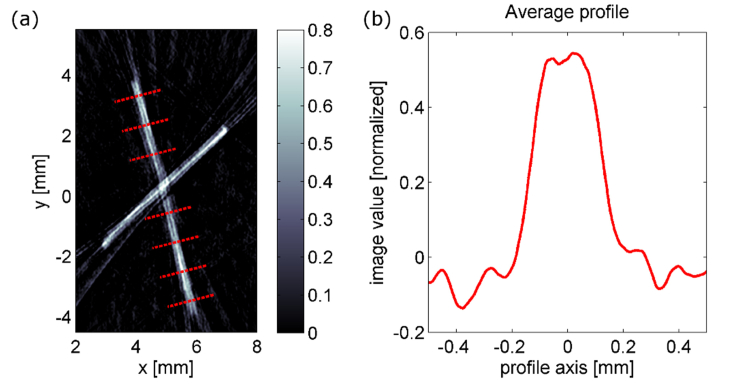
The imaging resolution was estimated by imaging porcine bristles (phantom C). Figure 5(a) shows the reconstructed image. The dotted red lines indicate where the profiles of the bristle were evaluated. The average of these profiles is plotted in Fig. 5(b). The 10% to 90% edge responses show a width of 85 µm and 102 µm, respectively. Due to inhomogeneities of the bristle and imaging artifacts, the evaluation of the edge response was not possible for single profiles. The full width at half maximum (FWHM) of the profile is 257 µm. We state a lower limit of the imaging resolution of 100 µm based on the edge response and a higher limit of 260 µm based on the FWHM.

Fig. 5.

(a) Photoacoustic projection image of two crossed porcine bristles. The bristles have a diameter in the range of 120-145 µm and are embedded in agarose/Intralipid. The red lines indicate where the profiles for the averaged profile in (b) are taken from. The 10% to 90% edge responses of the average profile are 85 µm and 102 µm respectively. The full-width-at-half-maximum is 257 µm.

4.4Testing the imaging area

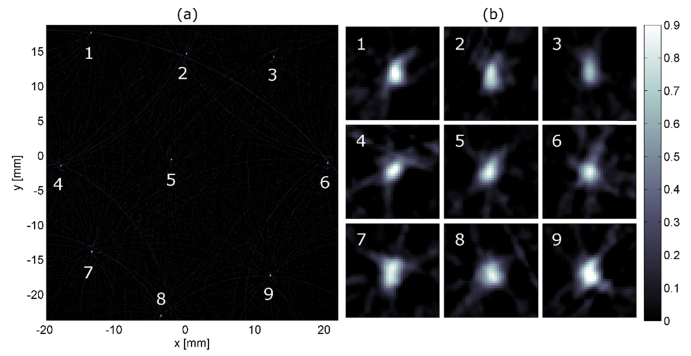
Photoacoustic responses of the microsphere in phantom A were acquired at different locations within the imaging volume. The acquired signals were super-imposed and used to reconstruct the image shown by Fig. 6(a). The microspheres appear as small bright spots with very few artifacts. Figure 6(b) shows zoom-ins at each position. Artifacts and small distortions in the enlarged images are evident. At each position, the intensity of artifacts and image distortions seem to be similar and the imaging resolution appears to be the same. Therefore, the image quality should show only little variation within this area of 40x40 mm. This is expected from theory, as line detectors correspond to ideal point detectors for the two-dimensional wave equation [33] for which exact inversion formulas exist [23] as long as the detection curve, i.e. the positions of the point-receivers, completely surrounds the object [34].

Fig. 6.

(a) shows a single polyethylene microsphere with a diameter of 200 µm embedded in agarose/Intralipid, measured at different locations within an area of 40x40 mm. The image values are normalized to 1. At each position, a measurement of the sphere was performed. The image is a result of a single reconstruction based on summation of the acquired signals. (b) presents zoom-ins at each positon of the sphere. Except for position 6, the images of the sphere deviate slightly from a round shape. However, the point-like shape of the sphere is maintained at every position. In addition, there is no apparent trend indicating an area where the image-quality is significantly reduced.

4.5 Imaging of a blood vessel phantom

An overview image resulting from the experiments with phantom D is shown in Fig. 7(a). The vertical bright bands with a thickness of approximately 1 mm mark the surface of the chicken breast. The ink-filled polymer tube is clearly visible in a distance of about 3 mm from the left and 4 mm from the right surface of the chicken tissue. A zoom-in of the central area is presented in Fig. 7(b). The diameter of the tube in the image matches well with the specified diameter of 300 µm. Although imaging artifacts are present, they remain low.

Fig. 7.

Blood vessel phantom consisting of an ink-filled polymer tube in chicken breast. An overview is presented in (a) and an enlargement of the central region is shown in (b).

5. Discussion

5.1 Noise-equivalent pressure

The achieved noise-equivalent pressure (NEP) of the fibers-optic detectors of 24 Pa at a bandwidth of 10 MHz undercuts the NEP reported for broadband piezoelectric transducers [35] and most optical detection schemes [27]. NEP values of 200 Pa and 70 Pa at a detection bandwidth of 20 MHz were, e.g., reported for planar Fabry-Perot film sensors, using soft [36] and hard [37] dielectric mirrors, respectively. Recently, we have reported on photoacoustic scanning macroscopy using a large array of annular optical detectors were an NEP of 3 Pa at a detection bandwidth of 16 MHz was achieved [8]. However, not every fiber-detector of the presented prototype performs that well. In average, the array shows a NEP of 37 Pa at 10 MHz bandwidth. There are several reasons for the variation of sensitivity. The most dominant effect originates from the connection of the pressure-sensing graded-index polymer optical fiber with a core-diameter of 57 µm with the single-mode fiber (SMF) input of the optical switch (see Fig. 1). The loss of light at this interface depends on how well the effective beam diameter at the end of the GIPOF matches the mode-field diameter of the glass fiber (~10.4 µm). The beam diameter within the GIPOF periodically changes along the propagation path [38]. Thus, in order to optimize the light transmission through the GIPOF/SMF interface, the end face of the GIPOF should be located exactly at a location where the beam waist diameter is minimal. In our setup, this is accomplished by a stretching mechanism, which is used to adjust the length of the GIPOFs until the light throughput is maximal. Due to inevitable errors in the concentricity and alignment of the fiber-cores, this optimization does not work equally well for all fibers and, thereby, contributes to the variation of the NEP. The necessary stretch mechanism and the accuracy-requirements for the fiber positions lead to complex manufacturing and assembly of the fiber-optic detector array. In the process, some fibers undergo small damages. These damages also contribute to the variation of optical transmission and, hence, influence the NEP. Ideally, the used GIPOFs could be replaced by single-mode polymer fibers (SM-POF). However, SM-POF s are not commercially available for the used wavelength of 1550 nm. Fiber tapering of the GIPOF [39] is another promising approach to reduce transmission losses.

A mismatch of light polarization in the reference and measuring arm of the interferometer represents another cause for the different NEPs. This mismatch can be minimized by carefully laying out all fiber-optic components or by using fiber-optic polarization controller. The first method does not perform equally well for all individual interferometers and the latter approach was discarded because of additional costs. Moreover, variation of the splitting ratios of the 1x64 and 1x16 coupler effects the respective NEP of a fiber-detector.

In future work, we will investigate if tapering of the GIPOFs will result in a stable light throughput at the interface between the GIPOFs and the SMFs and if the losses remain acceptable. We also plan to improve the setup by controlling the polarization. Thereby, the NEP of the line detectors will be decreased. We also note that the photodiodes were operated at approximately half of their saturation threshold. Hence, the NEP could be further reduced significantly by using a detection laser with higher optical power.

5.2 Image quality

The photoacoustic images presented in this paper were reconstructed using a back-projection algorithm. In the obtained reconstructions, artifacts are apparent. These artifacts are caused by the low number of sensor positions, being only 60 in the current implementation of the setup. A significant reduction of artifacts can be expected by increasing the number of fibers to 128. Before building a 128-channel system, the loss of light at the GIPOF/SMF interfaces, as discussed in section 5.1, should be minimized without requiring fiber stretching mechanism. If fiber tapering works, or if SM-POF become available, the next generation prototype should feature at least 128 ultrasound detecting fibers. As an intermediate step, we will examine the possibility to increase the number of detector channels artificially. To this end, the sample will be mounted on a programmable x-y-translation stage and measurements will be repeated on 2-8 different positions. This will increase the number of detection positions to be between 128 and 512, respectively.

A comparison between measurement and simulation in Fig. 4(b) and 4(e) showed an excellent agreement. Artifacts appearing in the measurement are also found in the reconstruction using the simulated data set. Model based iterative reconstruction methods are well known to be able to reduce imaging artifacts [40], especially in the case of limited data [41]. In these methods, an image is formed by minimizing the difference between the measured signals and the theoretical signals predicted by a forward model [42,43]. Although model-based reconstruction is computationally expensive, it was demonstrated that efficient implementation allows real-time imaging in two-dimensional optoacoustic tomography [44]. We are convinced that a model-based reconstruction algorithm could largely reduce these artifacts and we will implement such a method in the future.

Due to the presence of imaging artifacts, an accurate determination of the imaging resolution seemed inappropriate. Instead, we report a reasonable estimation in section 4.3. One targeted application of our approach is the monitoring of perfusion in small animals. We expect the imaging resolution of our approach to be sufficient for directly imaging perfusion on the artery level. In order to resolve smaller vessels and capillaries, the resolution will be too low. For a dense network of capillaries, perfusion could still be monitored, however, the individual capillaries will not be resolved.

Acoustic heterogeneities might introduce further imaging artifacts. By using reconstruction methods accounting for the varying speed of sound (SOS), these artifacts can be largely reduced. For this, the distribution of the SOS within the measurement area needs to be determined. This can be achieved either by iterative methods or by direct measurements. E.g. Wurzinger et al. [45] acquired a map of the SOS by using a free-beam integrating line detector and laser-ultrasonically generated pressure waves. A dual-speed-of-sound reconstruction algorithm, which requires no additional computational costs and no additional hardware, was recently proposed by Li et al. [20]. Such methods could be implemented in the presented O-PAPI system for reducing artifacts caused by acoustic heterogeneities. Note that our system images whole volumes, projected onto a two-dimensional reconstruction plane. Therefore, also a projection of the SOS onto this plane has to be used for reconstruction. Depending on the geometry of the measured specimen, the resulting reduction of artifacts might thus be lower compared to, e.g., cross-sectional imaging.

The strong signals at the chicken surface in Fig. 7(a) indicate that a considerable portion of the excitation pulses were absorbed at the surface. In order to increase the light transmission into the tissue, we plan to use excitation pulses with variable wavelengths generated by an optical parametric oscillator. Thereby, the image quality within tissue should be further enhanced.

5.3 Image acquisition time

The necessary time to acquire one projection image without averaging is about 0.5 seconds in the present setup and 32-times averaging requires 20 seconds. In order to reduce the acquisition times, we are planning to avoid multiplexing by installing the same number of evaluation channels as measurement arms. We expect that projection images of mouse-sized objects could then be acquired at video rate. If the complete three-dimensional structure of the sample is required, projections from different angles need to be acquired. A 3D reconstruction can then be obtained by using the inverse Radon transform [23]. The imaging duration is estimated to be below 15 seconds if 72 projection angles with 4-times averaging are acquired at a rate of 20 single-shot frames per second. We would like to point out that the ability to monitor large volumes by acquiring projection images at a high frame rate would be outstanding compared to other approaches for small animal imaging using piezoelectric transducer arrays. To acquire sufficiently dense photoacoustic data for high-resolution volumetric imaging of small animals or the human breast with hemispherical [14,16] or arc-shaped [11,12] piezoelectric transducer arrays, multiple measurements at different rotational angels are necessary. The required time for such measurements is in the range of several tens of seconds to minutes. Using a circular array, single-impulse cross sectional imaging was recently demonstrated at a frame rate of 50 Hz [20]. Acquisition of a whole volume significantly increases the measuring duration since various cross-sectional images at different axial positions have to be acquired. Imaging of a three-dimensional volume consisting of 600 individual slides required 12 seconds [20]. In [15] a system featuring a spherical array with 256 detectors achieving 3D imaging at video rate was presented. However, high spatial resolution was only offered in a volume of less than 1 cm³.

6. Conclusion

In summary, we introduced all-optical photoacoustic projection imaging (O-PAPI). An array of integrating line detectors on basis of fiber-optic interferometers were used to measure the photoacoustic signals. The feasibility of the method was demonstrated by presenting measurements and images acquired with the developed O-PAPI prototype. The performance of the system was assessed regarding sensitivity, image quality, imaging resolution, acquisition time, and imaging area. The fiber-optic integrating line detectors achieve a noise equivalent pressure of 24 Pascal at an ultrasonic bandwidth of 10 MHz. The imaging resolution was estimated to be between 100µm and 260 µm for an imaging depth of 20 mm. Image acquisition typically required 20 seconds for 32-times averaging. We plan to develop a revised version of the presented prototype with improvements of usability, sensitivity, image quality, and acquisition time. We are convinced that such a device will allow high-resolution photoacoustic examination of large volumes at high frame rates and that such a system will be well suited for, e.g., small animal imaging and monitoring dynamic processes like perfusion.

Disclosures

The authors declare that there are no conflicts of interest related to this article.

Funding

This work has been supported by the Austrian Research Funding Association (FFG), project number 846559, the European Regional Development Fund (EFRE) in the framework of the EU-program IWB 2014-2020, and the federal government of Upper Austria within the strategic economic-research program “Innovative Upper Austria 2020”.