Abstract
Worldwide, polypoidal choroidal vasculopathy (PCV) is a common vision-threatening exudative maculopathy, and pigment epithelium detachment (PED) is an important clinical characteristic. Thus, precise and efficient PED segmentation is necessary for PCV clinical diagnosis and treatment. We propose a dual-stage learning framework via deep neural networks (DNN) for automated PED segmentation in PCV patients to avoid issues associated with manual PED segmentation (subjectivity, manual segmentation errors, and high time consumption).The optical coherence tomography scans of fifty patients were quantitatively evaluated with different algorithms and clinicians. Dual-stage DNN outperformed existing PED segmentation methods for all segmentation accuracy parameters, including true positive volume fraction (85.74 ± 8.69%), dice similarity coefficient (85.69 ± 8.08%), positive predictive value (86.02 ± 8.99%) and false positive volume fraction (0.38 ± 0.18%). Dual-stage DNN achieves accurate PED quantitative information, works with multiple types of PEDs and agrees well with manual delineation, suggesting that it is a potential automated assistant for PCV management.
OCIS codes: (110.4500) Optical coherence tomography; (170.3880) Medical and biological imaging; (100.0100) Image processing; (100.4996) Pattern recognition, neural networks
1. Introduction
Worldwide, polypoidal choroidal vasculopathy (PCV) is a common, vision-threatening exudative maculopathy. Pigment epithelium detachment (PED), which occurs secondary to leakage and bleeding beneath the retinal pigment epithelium (RPE), is an important clinical characteristic of this chorioretinal disease. As PED volume can predict the treatment outcome of PCV disease [1–4], precise and reliable PED segmentation is required for quantification in clinical practice. Generally, PEDs can be divided into the three following types: serous, vascularized and drusenoid PEDs [3]. This work focuses on PEDs among PCV patients, i.e., serous and vascularized PEDs. Serous PED is caused by a collection of fluid in the sub-RPE space [5, 6]. Vascularized PED, which is the result of angiogenesis and sub-RPE neovascularization, is more sight threatening than other types of PED but is more responsive to treatment [7, 8]. Drusenoid PED seldom appears in PCV patients because it is caused by drusen, which is uncommon in PCV patients [9].
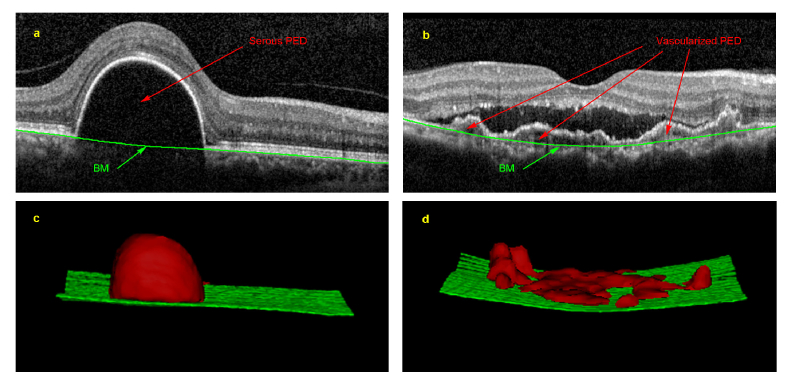
Compared with other imaging modalities, optical coherence tomography (OCT) provides noninvasive, in vivo, high-resolution cross-sectional view [10]. OCT is now the preferred imaging modality for PCV disease management and has been widely utilized for PED segmentation [1, 11, 12]. As manual interpretation of PED images is time consuming and prone to human errors [13–15], recent research studies are developing computer-aided diagnosis systems to provide efficient, reproducible and reliable information [16]. However, three main challenges significantly impede precise PED segmentation: (1) distorted morphology that limits the use of prior knowledge [17]; (2) blurred boundaries by unexpected speckles and undesirable abnormalities impeding precise delineation; and (3) intensity inhomogeneity between serous and vascularized PED that hinders accurate segmentation. As illustrated in Fig. 1, serous PED appears as an arch-shaped region with homogenously hypo-reflective regions below the RPE layer, whereas vascularized PED has heterogeneous signals with hyperreflective vascular lesions and hypo-reflective lumens beneath the RPE layer [3]. Thus, the homogeneity among the neighboring tissues together with the heterogeneity within PED pose difficult challenges for automated segmentation of vascularized PED in PCV patients.
Fig. 1.
An example of serous and vascularized pigment epithelium detachments (PED). (a) is a cross-sectional OCT image of serous PED, and (b) is a cross-sectional OCT image of vascularized PED. (c) and (d) are the 3D visualizations of the segmentation results with the red region representing the PED regions and the green surface representing Bruch’s membrane (BM).
Several computer software algorithms have been proposed for the purpose of PED segmentation from OCT images, including the conventional threshold-based and more recent graph theory-based methods (state-of-art methods) [13, 18–21]. All aforementioned methods were reliant on carefully hand-crafted, low-level image features, which are sensitive to image quality and intensity variance, and therefore sometimes result in non-reproducibility under different scenarios (serous and vascularized PEDs). In recent years, with the emergence of deep neural networks (DNN), there has been tremendous improvement in the ability to automate feature extraction in which the learned features are highly convolved to encode the intrinsic structures of the image for classification, recognition and segmentation [22, 23]. DNN methods have been successfully applied to bio-image segmentation of tissues, such as prostate, skin, liver and bone tumors [24–29]. Among the existing DNN methods, FCN and U-Net are the representative structures for bio-image segmentation [30, 31]. FCN embeds fully convolution layers on DNN and then employs a deconvolution layer to gain a segmentation probability map. Compared to FCN which directly upsamples feature maps, U-Net uses a sequence of upsampling and convolution layers to progressively enlarge feature maps. In terms of OCT image, DNN had also been applied successfully for layer boundary segmentation in OCT. A DNN segmentation model associated with graph search was proposed on OCT images [32]. Roy et al. proposed purely DNN model (ReLayNet) to achieve retinal layer and fluid segmentation [33]. Among the aforementioned DNN model, we adopt FCN to construct our progressive learning scheme as FCN is a classic and general model for image segmentation [30].
In this study, we propose a novel DNN-based framework to automatically segment PEDs in PCV patients. We validated this framework against two specialists as well as other state-of-art algorithms on PED segmentation performance. To the best of our knowledge, we presented the first dual-stage DNN learning framework for automated PED segmentation on PCV patients. The novelty of this paper is the dual-stage DNN learning. We first learn the BM layers on images via DNN; then we employ the obtained BM layers as constraints to assist another DNN to segment PED regions. While the single-stage network cannot solve different types of OCT imaging issues, our framework focuses on different issues in different stages so that our framework performs better than single-stage network.
2. Methods
2.1. Dual-stage PED segmentation framework
Given a denoised image, we will use convolutional neural networks (CNN), a proven powerful DNN-feature extractor, to capture image features and utilize these features to differentiate PED regions from. We propose to segment PED in a dual-stage manner. We built two DNN networks (named S1-Net and S2-Net) to form the main structure of our framework (shown in Fig. 2). Fully convolutional networks (FCN), which is an off-the-shelf powerful CNN model to extract PED-oriented whole image features to learn end-to-end PED segmentation [30], was adopted as the structures of both S1-Net and S2-Net (listed in Table 1). Following FCN, as the five pooling layers of FCN makes the feature map 32 × subsampled resolution, we set filter size to 64 and set stride to 32 to make sure that the resolution of obtained segmentation map is same with input image. In our dual-stage learning scheme, after normalization and denoising process, we first capture the BM layer from the image via the S1-Net model and then use the recognized BM layer as a constraint for the later PED recognition and delineation via the S2-Net model. We explain the framework architecture in detail as follows.
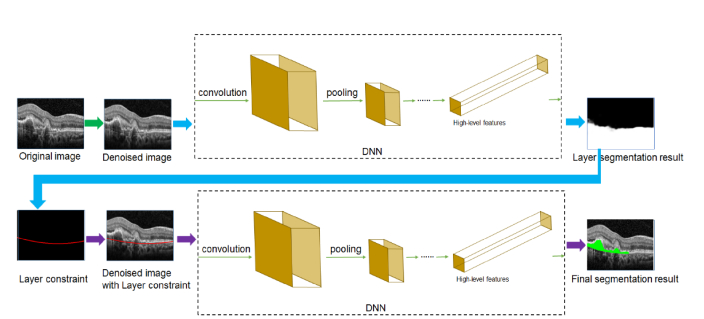
Fig. 2.
The flowchart of the proposed framework (dual-stage DNN). The segmentation framework mainly consists of two major processing steps in the workflow. First, the location of Bruch’s membrane (BM) is determined based on the first deep neural network (DNN) (named S1-Net). Then, the pigment epithelium detachment (PED) regions are segmented based on the second DNN (named S2-Net) using the BM layer constraint.
Table 1. Structures of Fully Convolutional Networks a.
| Type | Channel | Filter/Pooling size | Output size |
|---|---|---|---|
| c1 + bn1 + r1 | 64 | 3 × 3 | 384 × 384 |
| c2 + bn2 + r2 | 64 | 3 × 3 | 384 × 384 |
| p1 | 64 | 2 × 2 | 192 × 192 |
| c3 + bn3 + r3 | 128 | 3 × 3 | 192 × 192 |
| c4 + bn4 + r4 | 128 | 3 × 3 | 192 × 192 |
| p2 | 128 | 2 × 2 | 96 × 96 |
| c5 + bn5 + r5 | 256 | 3 × 3 | 96 × 96 |
| c6 + bn6 + r6 | 256 | 3 × 3 | 96 × 96 |
| c7 + bn7 + r7 | 256 | 3 × 3 | 96 × 96 |
| p3 | 256 | 2 × 2 | 48 × 48 |
| c8 + bn8 + r8 | 512 | 3 × 3 | 48 × 48 |
| c9 + bn9 + r9 | 512 | 3 × 3 | 48 × 48 |
| c10 + bn10 + r10 | 512 | 3 × 3 | 48 × 48 |
| p4 | 512 | 2 × 2 | 24 × 24 |
| c11 + bn11 + r11 | 512 | 3 × 3 | 24 × 24 |
| c12 + bn12 + r12 | 512 | 3 × 3 | 24 × 24 |
| c13 + bn13 + r13 | 512 | 3 × 3 | 24 × 24 |
| p5 | 512 | 2 × 2 | 12 × 12 |
| 512 | 4096 | 7 × 7 | 12 × 12 |
| fc2 + r15 | 4096 | 1 × 1 | 12 × 12 |
| fc3 | 2 | 1 × 1 | 12 × 12 |
| dc | 2 | 32 × 32 | 384 × 384 |
| softmax | 2 | - | 384 × 384 |
Abbreviations: c, convolution layer; bn, batch normalization; r, rectified linear unit; p, pooling layer; fc, fully convolution layer; dc, deconvolution layer; c + r: convolution layer followed by rectified linear unit. softmax, decision layer to get segmentation probability map.
Fully convolutional network (FCN) is a type of deep neural network (DNN), which forms the basis of our framework. The whole settings in the network, from the input to the output of the network, are shown from top to bottom.
2.1.1 Pre-processing
As the original images of our data were 512 × 496 pixels, the images were subjected to an imresize process to 384 × 384 pixels when fitted in the network, and when final results were output from the framework, we use bilinear interpolation to restore the images to the original resolution and obtain the final results. Although our used DNN structure (FCN) could adopt images with any resolution, we did the normalization for input size to improve efficiency of our framework. Normalization for input size is widely used in many DNN based segmentation methods [34, 35]. According to the experimental results of these segmentation methods, normalization for input size does not affect much in performance. As shown in Fig. 3(a), due to the signal transmission in OCT machines or other sources of noise, OCT images in real clinical practices usually contain unexpected speckles and patterns. To reduce the influence of this imaging noise, the probability-based non-local means filter [36, 37], which was competitive with other state-of-the-art speckle removal techniques and able to accurately preserve edges and structural details with small computational cost on denoising process of OCT images, was used to denoise the original images.
Fig. 3.
Illustration of experimental results by different methods. (a) to (f) represent our dual-stage DNN framework at different steps. (a) original image; (b) result of the denoising process; (c) result using the line-based ground truth in the layer recognition learning step; (d) result using padded ground truth; (e) input of the pigment epithelium detachment (PED) delineation learning step; (f) final result of the automatic PED segmentation; (g) result of the ground truth; and (h) result using single-stage DNN. (i) Layer segmentation result of GS + ML. From top to bottom, the internal limiting membrane (ILM), the roof of the ellipsoid zone, retinal pigment epithelium (RPE) floor and Bruch’s membrane are displayed. (j) PED segmentation result of GS + ML.
2.1.2 BM layer recognition learning
To recognize the BM layer from the OCT image, we input the denoised image(shown in Fig. 3(b)) into S1-Net in whichis passed into a sequence of convolution and pooling layers (as listed in Table 1). The output of the sequence of convolution and pooling layers is highly convolved data, which could represent the intrinsic and semantic information of . Afterwards, the obtained highly convolved data are passed into a deconvolution layer (the last layer of S1-Net in Table 1), which is the transpose of the convolution to upsample the convolved data. The ground truth of the BM layer corresponding to each training image is required for this learning. We pad the regions below the BM layer with foreground pixels on the ground truth such that the positive and negative samples are relatively balanced. We utilize the padded ground truth to train S1-Net. As shown in Fig. 3(c) and 3(d), we can obtain a more compact and precise BM layer with this training compared with training with the line-based ground truth. Therefore, we could gain a probability map (shown in Fig. 3(d)), which has the same resolution with . We useas the BM layer recognition result.
2.1.3 PED delineation learning
In the PED learning stage, we employobtained in the previous stage as prior knowledge to assist S2-Net training for PED delineation. Specifically, the intensity imageis transformed into a RGB image (shown in Fig. 3(e)) such that the recognized BM layer appears red on. We inputinto S2-Net and train it with the ground truth of PED regions. Thus, the size of input data and the first filter bank are different with S1-Net. As the BM layer is imposed on the input data of S2-Net, this constraint is successively and inherently attached to the PED-region-oriented feature maps. We use the output of the S2-Net as the segmentation map and then adopt a threshold of 0.5 to delineate the PED contour (shown in Fig. 3(f)).
2.2. Framework settings
We implemented our framework using MatConvNet [38]; the implementation was accelerated via GPU computation. The number of training epochs was set to 50, batch size was set to 20 and learning rate was set to 0.0001; these parameters were derived empirically to produce optimal results. Consistent with the original MatConvNet [38], other parameters, including batch size, momentum and weight decay, followed the default settings as these were shown to be robust in previous works [24, 34]. Our experiments followed a ten-fold cross validation protocol where each validation process contains 45 patient scans as a training set and 5 scans as a validation set.
2.3. DNN and optimization in the framework
The main structure of our framework is FCN that is widely used for image segmentation [30]. In this kind of CNN model, convolution and pooling are the two essential layers. When the data pass into the convolution layer, a filter bank will convolve to produce a -dimensional feature map. During the training phase, these filters and biases will update so that the produced feature maps are more discriminative to differentiate PED. Pooling layers usually follow convolution layers in which the resolution of feature maps is reduced. These procedures result in obtained features that are less sensitive to input shift and distortions [39]. In practice, the input data normally pass into a set of convolution layers and pooling layers such that the extracted feature maps are more intrinsic and semantic than the low-level hand-crafted features [40].
After extracting feature maps, deconvolution layer is embedded to obtain segmentation probability map with the same resolution of input image. Deconvolution is the transpose of convolution defined as [38]:
| (1) |
where is the weight of deconvolution, and are the input and output of deconvolution respectively. is the size of padding in deconvolution, and is the stride of the filter..
To train the CNN, we minimize softmax log-loss to make CNN evolve to optimal segmentation. The loss function is defined as [38]:
| (2) |
whereis the set of pixels of all training images, is the output of deconvolution layer of -th channel at the position of,is the label ofandis the weight decay for regularization of learnable weights .is set to 0.0005 empirically.
2.4. Data set
Spectral domain OCT volume scans of patients diagnosed with PCV were obtained with a Heidelberg Spectralis device (Heidelberg Engineering, Heidelberg, Germany) between March 2015 and December 2015. The dimension of each OCT volume image is 512 × 97 × 496 voxels (97 B-scans of 512 × 496 pixels); the resolution is 11.13 µm × 59 µm × 3.83 µm(Distance between B-scans is 59 µm).1800 OCT B-scans from the 50 patients were used. All the B-scans were taken continuously from the PED regions. The tenets of the Declaration of Helsinki were followed, and the Institutional Review Board of Shanghai General Hospital, Shanghai Jiao Tong University approved the study. Informed consent was obtained from all subjects. The diagnosis of PCV was based on the EVEREST study using angiographic criteria [41]. To evaluate the layer segmentation results, two retinal specialists manually labeled PED regions, the BM layer and inner limiting membrane (ILM) on each scan (which contains 97 slices). The results generated by one of the specialists (Expert I) defined the ground truth. For subgroup analysis, Expert I classified the PED cases as either simple or complicated, following the rule that vascularized PEDs in less than 50% of the slices were defined as simple cases, whereas the vascularized PEDs in more than 50% of the slices and with hyperreflective exudates around the PED regions were defined as the complicated cases. The unsigned border positioning error was calculated by measuring the vertical absolute Euclidean distances between the positioned BM layers from the different methods and the ground truth [15].
2.5. Problem statement and approach to the major challenges
Given a denoised OCT image, the task is to differentiate PED regions fromin our PCV data set. To assign each pixel location to a particular label l in the label space ℒ = { l } = { 1,…, K} for K classes. We treat the current segmentation task as a K = 2 class classification problem. The approach of our dual-stage framework to deal with the major challenges as listed below.
We recognized three major challenges in the previous section: (1) We used DNN to address the issue of distorted morphology. Specifically, in DNN, convolution layer is to extract and mix image information. With deep convolution layers, the extracted image information is more intrinsic to interpret the image. The pooling layers of DNN makes our framework less sensitive to the input rotation and shift. Therefore, although there is some distorted morphology on OCT images, our DNN based framework could still recognize most of PED regions. (2) Our dual-stage learning could solve the challenges of speckles, abnormalities and inhomogeneous regions. While a single DNN cannot handle so many issues, our proposed model addresses different learning aim in different stage, so it expectably decreases the impacts by various issues, so it expectably decreases the impacts by various issues. For example, S1-Net is responsible for the recognition of BM layer. As the speckles and abnormalities around BM layer is the biggest major issue, S1-Net expectably learns to solve the issue by deep learning, regardless of solving intensity homogeneity. On the contrary, S2-Net is responsible for PED region detection. In this stage, intensity homogeneity inside of PED region becomes the major challenge, so S2-Net expectably learns to solve it regardless of other issues.
2.6. Comparison methods
The graph theory-based algorithm proposed by Sun, et al [40]. However, the source codes are not available and thus we implemented their algorithm as the benchmark in our evaluation. The first step of their segmentation algorithm was a multi-scale graph search (GS) algorithm, which is mainly based on the work of Shi et al [15]. This theory defines layers in order from top to bottom by calculating the dark-to-bright and bright-to-dark boundaries, and the RPE layer is defined as one of these boundaries. Then, the BM layer is created by the convexity of RPE. PED boundary delineation was conducted via a machine learning (ML) (AdaBoost) combined algorithm for marking the regions between these two layers in Sun’s work [40]. The parameters we used are shown in Table 2, which are the same from their papers [15, 40]. We denote their approach as GS + ML (shown in Fig. 3(i) and 3(j) for the two following steps mentioned in their algorithm: layer segmentation and PED segmentation). To verify our implemented methods of Sun’s work [40], we validated it on the arbitrary 100 serous PED slices from our private data set. We gained 91.77 ± 4.41% DSC, which is consistent with the published result (91.20 ± 3.77% DSC) from Sun’s private data set, demonstrating the accuracy and robustness of our implemented methods of the data sets from Sun’s work [40].
Table 2. Detailed Constraints and Parameter Selection in Layer Detection of a Method Based on Graph Theory.
| Order in detectiona | Layer | Layer above | Layer below | Initial detection levelb | Δy in initial levelc |
|---|---|---|---|---|---|
| 1 | ILM | N/A | N/A | 1 | 6 |
| 2 | EZ roof | ILM | N/A | 1 | 6 |
| 3 | RPE floor | EZ roof | N/A | 1 | 6 |
Abbreviations: EZ = ellipsoid zone; ILM = inner limiting membrane; RPE = retinal pigment epithelium.
Bruch’s membrane was detected after the RPE floor using the convhull algorithm. PED region segmentation was conducted by first locating the area between the RPE and BM, and then a graph cut and morphology combined algorithm was used to obtain the final results using AdaBoost. The details were given in the work of Sun et al [40].
Initial detection level: According to Shi et al., the 3D OCT scan is downsampled by a factor of 2 twice in the z-direction to form three resolution levels [15]. Level 1 represents the lowest resolution, and level 3 represents the highest resolution, i.e., the original data. In this manner, their algorithm is multi-resolution.
The following two facts are considered when determining the smoothness constraints Δx and Δy for each surface: the image resolution and the shape of surfaces. Δx = 1 for all layers and all levels. These two factors form the basis of graph search theory. Please find the details in the work of Shi et al [15].
In addition, a single-stage DNN framework (FCN), directly adopting OCT images without the notation of BM layer (shown in Fig. 3(b)), is also comparatively evaluated. The basic settings of single-stage DNN framework are the same with our proposed framework as shown in Table 1. The example segmentation result of the single-stage DNN framework is shown in Fig. 3(g).
2.7. Evaluation metrics
The true positive volume fraction (TPVF), dice similarity coefficient (DSC), positive predictive value (PPV) and false positive volume fraction (FPVF) are used in our evaluation [40] and defined as follows:
| (3) |
| (4) |
| (5) |
| (6) |
where, and are the segmentation results, ground truth and retina volume, respectively, between BM and ILM.
2.8. Statistical analyses
The results are presented as the mean ± standard deviation (SD) for continuous variables. Intergroup differences were tested by t-test. Correlation analysis was used to display the correlation of PED volumes measured between different methods and different specialists. Bland-Altman analysis was used to analyze agreement [42]. We used 95% limits of agreement (LoA) to evaluate agreement between the different methods and experts. Statistical significance was set at p<0.05 (two tailed).
3. Results
Fifty SD-OCT scans of PCV patients from Shanghai General Hospital were collected to evaluate our proposed framework. The average age of the patients was 66.5 years (95% confidence interval [CI], 64.8 – 68.1 years); 64% (32/50) of the patients were male with an average best corrected visual acuity (logMAR) of 0.68 (95% CI, 0.58-0.78). Twenty-four patients were classified as simple cases, and 26 patients were complicated cases. The final segmentation results on SD-OCT images are illustrated in Fig. 4. For serous PED, segmentation error mainly occur when there are some discontinuity in the RPE layer (shown in the last row of column a). For vascularized PED, segmentation error mainly occurred when the PED regions are difficult to distinguish from the surrounding tissues (shown in last three rows of column c).
Fig. 4.
Final automatic pigment epithelium detachment segmentation result of our framework compared with the result of the ground truth on different types of PED. The green line represents the result of our dual-stage DNN, and the red line represents the ground truth. Column (a) and (b) show the serous PEDs and their results. From top to bottom, a small serous PED, a large serous PED, two separate serous PEDs and one merged serous PED are displayed. Columns (c) and (d) show the vascularized PEDs and their results. Vascularized PED regions are more challenging as they may have different intensities and hyperreflective exudates above them. The segmentation performance on vascularized PED shows more segmentation error than that on serous PED.
Our framework was implemented in MATLAB R2016a and run on a desktop PC with a GPU NVIDIA GeForce GTX 980 equipped on an Intel Core i7 2.60 GHz machine. The average running time of our framework per B-Scan is 0.92 seconds.
3.1. Segmentation accuracy of the different methods and experts
Quantitative assessments of the segmentation performance achieved by the different methods are summarized in Table 3. Results from Expert II is comparable with ground truth (Expert I), proving the robustness of ground truth. In terms of accuracy, the mean and standard deviation of TPVF, DSC, PPV and FPVF for the proposed framework are 85.74 ± 8.69%, 85.69 ± 8.08%, 86.02 ± 8.99% and 0.38 ± 0.18%, respectively. Higher values of TPVF and DSC indicate the PED region is segmented more accurately. Over 85% PPV and less than 0.5% FPVF indicates less incorrectly segmented PED regions. Compared with the results from state-of-the-art methods based on the graph theory (GS + ML) and single-stage DNN, our results exhibited better performance by over 5%.
Table 3. Pigment Epithelium Detachment Segmentation Accuracy Results by Different Methods and Experts a.
| Group |
Method/Expert
Vs Ground Truth |
True positive
volume fraction (%) |
False positive
volume fraction (%) |
Dice
similarity coefficient (%) |
Positive
predictive value (%) |
|
|---|---|---|---|---|---|---|
| All | GS + ML | 80.30 ± 13.70 (p = 0.0197) b |
0.54 ± 0.31 (p = 0.0021) b |
80.52 ± 11.25 (p = 0.0097) b |
81.83 ± 10.67 (p = 0.0362) b |
|
| Single-stage DNN | 80.39 ± 13.92 (p = 0.0 3) b |
0.56 ± 0.38 (p = 0.0032) b |
80.30 ± 10.89 (p = 0.0060) b |
81.92 ± 10.07 (p = 0.0342) b |
||
| Dual-stage DNN | 85.74 ± 8.69 | 0.38 ± 0.18 | 85.69 ± 8.08 | 86.02 ± 8.99 | ||
| Expert II | 96.85 ± 2.42 (p<0.0001)b |
0.18 ± 0.10 (p<0.0001)b |
94.87 ± 3.19 (p<0.0001)b |
93.08 ± 4.85 (p<0.0001)b |
||
|
| ||||||
| Simple | GS + ML | 88.80 ± 7.82 (p = 0.0249) b |
0.63 ± 0.36 (p = 0.0216) b |
88.96 ± 5.84 (p = 0.0080) b |
89.47 ± 5.88 (p = 0.0433) b |
|
| Single-stage DNN | 88.35 ± 7.95 (p = 0.0146) b |
0.67 ± 0.42 (p = 0.0150) b |
87.99 ± 4.99 (p = 0.0002) b |
88.27 ± 5.96 (p = 0.0058) b |
||
| Dual-stage DNN | 92.93 ± 3.87 | 0.43 ± 0.20 | 92.59 ± 2.64 | 92.42 ± 3.71 | ||
| Expert II | 97.33 ± 1.08 (p<0.0001)b |
0.18 ± 0.09 (p<0.0001)b |
96.94 ± 1.61 (p<0.0001)b |
96.59 ± 2.59 (p<0.0001)b |
||
|
| ||||||
| Complicated | GS + ML | 71.40 ± 12.93 (p = 0.0085) b |
0.46 ± 0.21 (p = 0.0132) b |
71.70 ± 8.36 (p = 0.0004) b |
73.84 ± 8.46 (p = 0.0098) b |
|
| Single-stage DNN | 72.43 ± 14.16 (p = 0.0323) b |
0.45 ± 0.30 (p = 0.0741) |
72.61 ± 9.70 (p = 0.0039) b |
75.57 ± 9.36 (p = 0.0712) |
||
| Dual-stage DNN | 79.11 ± 6.23 | 0.33 ± 0.15 | 79.32 ± 5.79 | 80.11 ± 8.37 | ||
| Expert II | 96.39 ± 2.95 (p<0.0001)b |
0.19 ± 0.10 (p<0.0001)b |
93.06 ± 2.97 (p<0.0001)b |
90.03 ± 4.13 (p<0.0001)b |
||
Abbreviations: DNN = deep neural network; GS + ML = a method based on graph theory proposed in Sun. et al [40]. p = statistical significance test between dual-stage DNN and other methods.
All the results are listed as the mean ± standard deviation in percentage. Statistical tests: To test for differences of segmentation accuracy results between dual-stage DNN and other methods/expert, t-test was applied.
p<0.05
3.2. Correlation between the different methods and experts
A strong correlation is obtained between Expert I and Expert II (r = 0.9997, p < 0.001) in all cases, proving the robustness of the ground truth. There is a significant positive correlation between our dual-stage DNN framework and different experts (Expert I correlation coefficient 0.9986, Expert II 0.9981,p < 0.001 for each).The correlation coefficient of single-stage DNN (Expert I 0.9666, Expert II 0.9691, p < 0.001 for each) and GS + ML (Expert I 0.9775, Expert II 0.9781, p < 0.001 for each) are not as high as that of our framework.
3.3. Agreement of the different methods and experts
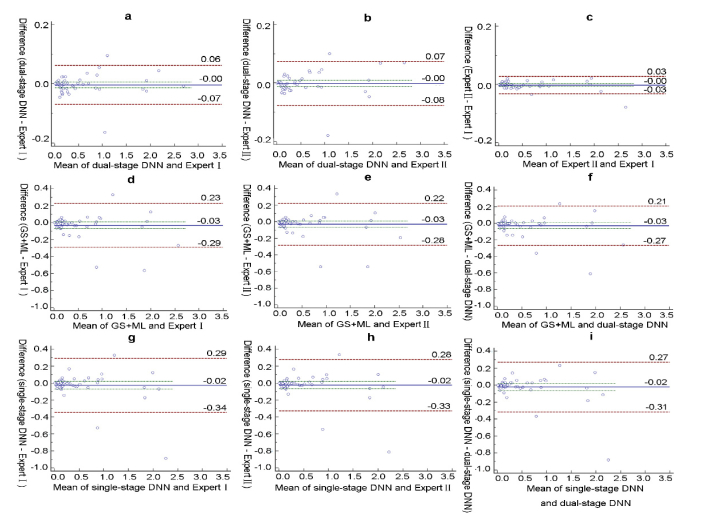
A comparison of PED volumes measured by the three methods is summarized in Table 4. Mean PED volume measurements were not significantly different between different methods and experts. However, dual-stage DNN showed the least difference with Expert I (0.0032 mm3) and Expert I (0.0016 mm3), which is comparable to the difference between experts (0.0017 mm3). The difference of the other two methods with different experts is almost ten times larger than that of dual-stage methods. In Bland-Altman analysis, dual-stage DNN has the lowest 95% LoA with Expert I (−0.0691 to 0.0627 mm3) and Expert II (−0.0765 to 0.0734 mm3), which is nearly a quarter of the LoA from the other two methods (shown in Fig. 5). These differences are acceptable for clinical purposes, as noted in a previous work [40]. Less than 5% of points are outside the agreement limits, and the bias is not significant as the line of equality is within the confidence interval of the mean difference.
Table 4. Agreement between the Different Methods and Experts for Pigment Epithelium Detachment Segmentation a.
| Agreement | Mean difference (mm3) | P value | 95% LoA (mm3) |
|---|---|---|---|
| Expert II vs Expert I | 0.0017 | 0.4362 | −0.0313 to 0.0279 |
| Progressive DNN vs Expert I | 0.0032 | 0.5003 | −0.0691 to 0.0627 |
| Progressive DNN vs Expert II | 0.0016 | 0.7753 | −0.0765 to 0.0734 |
| Universal DNN vs Expert I | 0.0248 | 0.2865 | −0.3441 to 0.2944 |
| Universal DNN vs Expert II | 0.0231 | 0.2960 | −0.3268 to 0.2805 |
| GS + ML vs Expert I | 0.0313 | 0.1017 | −0.2912 to 0.2286 |
| GS + ML vs Expert II | 0.0296 | 0.1110 | −0.2825 to 0.2232 |
Abbreviations: DNN = deep neural network; GS + ML = a method based on graph theory proposed in Sun. et al [40]; LoA = limits of agreement.
Statistical tests: To test for agreement between the different methods and different experts, t-test and Bland-Altman analyses were applied.
Fig. 5.
Evaluation of the volume agreement of pigment epithelium detachment (PED) between different methods and different experts represented by separate Bland-Altman plots in the whole database. The red dotted line represent the 95% limits of agreement (LoA) (mm3).The blue line represent the mean difference (mm3). The agreements of our dual-stage DNN framework with Expert I (ground truth) and Expert IIare illustrated in the top row as (a) and (b). The agreement between the different experts is illustrated in (c). The two bottom rows show the agreements of the comparison methods with Expert I, Expert II and the dual-stage DNN: the GS + ML method (illustrated in (d), (e) and (f)) and single-stage DNN (illustrated in (g), (h) and (i)). The lowest volume deviation between methods and experts occurred for dual-stage DNN.
3.4. Segmentation performance of the different methods within the subgroups
The segmentation performance by dual-stage DNN is different within subgroups. In simple cases, the mean TPVF, DSC and PPV of our segmentation results are over 92%, and the standard deviation is less than 4% (3.87%, 2.64% and 3.71%, respectively). This performance is the highest on simple cases among all comparison methods. In complicated cases, the proposed method also outperforms all the comparison methods. The results from our framework are TPVF and DSC of nearly 80% (79.11% and 79.32%, respectively) and PPV over 80% (80.11%).
3.5. BM layer recognition performance between the different methods
BM layer recognition is compared between dual-stage DNN and GS + ML because this constraint is important for improving segmentation performance. The unsigned border positioning error of our layer segmentation methods is 5.71 ± 3.53 μm. The number of errors of our dual-stage DNN framework is almost half the number of errors of GS + ML (10.53 ± 4.69μm, p<0.0001). In addition to the performance difference between algorithms, we also notice that the layer recognition result of dual-stage DNN on simple cases is better than that on complicated cases by 0.91 μm (p<0.0001).
4. Discussion
PCV is characterized by abnormal choroidal vascular networks with aneurismal or polypoidal terminations. These choroidal vascular changes lead to morphology changes in RPE, characterized as various forms of PED. Multiple PEDs, sharp PED peaks, PED notches, and rounded polyp lumens inside the PED regions were helpful in diagnosing PCV based on SD-OCT [43]. Decreased PED volumes have been observed during resolution with anti-VEGF therapy in clinical studies [21, 44]. Treatment based on changes in PED morphology rather than on exudatives or hemorrhagic recurrences may improve the long-term visual outcomes of this disease. Nevertheless, large samples and long-term clinical studies are needed to obtain enough data to support this treatment paradigm. However, data analyses by manual segmentation are time consuming and thus limit the design of clinical studies [14]. Automatic PED segmentation is the first step for PED morphology analysis of large clinical samples. DNN has been successfully applied to tumor segmentation from the normal tissue, such as skin, liver and bone tumors [27–29]. Thus, DNN has the potential to be the solution.
Our dual-stage DNN framework achieved a mean DSC and TPVF of over 85%, outperforming the comparative methods. A strong correlation was found between dual-stage DNN and different experts. In terms of agreement with human experts, dual-stage DNN has the least difference. The mean volume difference with Expert II (0.0016 mm3) is comparable to that between different experts (0.0017 mm3). Compared with other methods, dual-stage DNN had the closest 95% LoA between different experts. These results demonstrate the ability to apply dual-stage DNN for PED segmentation and volume monitoring in PCV treatment.
These improvements can be attributed to the following reasons: (1) using the advantages of high-level features from DNN; and (2) utilizing the prior knowledge from BM recognition in a dual-stage manner to later assist DNN for PED delineation. The highly reflective exudatives above the PED region, which disturb the bright-to-dark boundary delineation, lower segmentation performance of GS + ML. However, our learned, highly convolved features can effectively represent the intrinsic data structures of different image scenarios to self-adapt to various PED cases (serous and vascularized). The BM layer is blurred in some cases and thus impedes the feature extraction by a single-stage DNN; in dual-stage DNN, the millions of learnable parameters in the DNN model are trained simultaneously to fit the BM layer recognition task. Compared to conventional classifier such as AdaBoost with countable parameters, DNN adjusts millions of parameters to address the issues of poor quality images. Millions of parameters should work better than countable parameters to complicated scenarios.
Due to the different ratios of serous PEDs to vascularized PEDs between different subgroups, the segmentation performance of dual-stage DNN on simple cases is better than that on complicated cases. Compared with the image quality in simple cases, poor image quality in complicated cases, typically caused by speckles and abnormalities around the PED region, lowers the precision of layer recognition and PED region segmentation. As shown in Fig. 4, compared with the ground truth, the predicted results of vascularized PEDs by our framework could have over/under-segmented, as the PED regions are difficult to distinguish from the surrounding tissues. However, the proposed framework still had the highest performance.
In a recent study [21], PED segmentation was conducted in PCV patients using built-in commercial software, which was originally developed for drusenoid PED segmentation [20] based on threshold-based methods, and manual correction was performed when the automated results were incorrect. However, there are some limitations in the software [18, 20]. First, as noted in an earlier study, for the PED surrounded by abnormal and highly reflective exudatives, the built-in commercial software could not precisely recognize the RPE layer, which eventually causes incorrect PED segmentation [18]. We utilized information from the whole image fully convolved into the framework to obtain PED segmentation and theoretically overcome this challenge. Second, the software was designed to ignore PED with a height below a given threshold set to 20 μm [20]. However, branching vascular networks and small PEDs in PCV occurred within the 20-μm limitation beneath the RPE layer in some cases, which is shown in the first row of column (c) in Fig. 4. Our algorithm set no limitations to avoid this problem. With our framework, automated segmentation has the least segmentation error; thus this method requires fewer manual corrections, which will save time that would otherwise be devoted to manual correction and will therefore permit a larger scale population analysis.
In this study, the algorithm was developed and evaluated with data acquired from a Spectralis device. As our framework adopted OCT images with fixed resolution, we used the imresize process to ensure that the size of input images was 384 × 384. After the final results were obtained from the framework, another imresize process was conducted to restore the images to their original size. Furthermore, prior to the segmentation procedure, all images were pre-processed for speckle noise reduction by the probability-based non-local means filter [36]. Although there are many denoising methods that had good performance, such as sparsity based denoising [45, 46], we choose this method as it is competitive with other state-of-the-art speckle removal techniques and able to accurately preserve edges and structural details with small computational cost. Denoising methods such as sparsity based denoising could be an option in our framework and will be studied in the future. Besides, FCN was used as the basis of our framework, while other single-stage network such as U-net and RelayNet could also be employed in our framework [31, 33]. We would like to investigate their performance in our framework in the future. Because our segmentation algorithm focuses on diseased images, we will build a classifier to separate normal and diseased images prior to segmentation in our future work. In addition, our database limited our algorithm testing on drusenoid PED, which seldom appears in PCV [47]. Since this type of PED did not show up in our PCV database, we will test the performance of our algorithm on it and other diseases in the future.
5. Conclusion
Our dual-stage DNN framework can be applied to multiple types of PED segmentation (serous and vascularized) in PCV patients, which is in contrast to the existing algorithm studies that only focused on a particular type of PED. Moreover, our framework can be further extended to PED segmentations in central serous chorioretinopathy [48], choroidal neovascularization secondary to age-related macular degeneration [7] and myopic choroidal neovascularization [49] in which serous and vascularized PEDs commonly occur. Dual-stage DNN, suitable for large database segmentation, can provide needed information for better disease management.
Disclosures
The authors declare that there are no conflicts of interest related to this article.
Funding
National Natural Science Foundation of China (NSFC) (81570851, 81273424) and Project of the National Key Research Program on Precision Medicine (2016YFC0904800)
References and links
- 1.Kim J. H., Kang S. W., Kim T. H., Kim S. J., Ahn J., “Structure of polypoidal choroidal vasculopathy studied by colocalization between tomographic and angiographic lesions,” Am. J. Ophthalmol. 156(5), 974–980 (2013). [DOI] [PubMed] [Google Scholar]
- 2.Liu R., Li J., Li Z., Yu S., Yang Y., Yan H., Zeng J., Tang S., Ding X., “Distinguishing polypoidal choroidal vasculopathy from typical neovascular age-related macular degeneration based on spectral domain optical coherence tomography,” Retina 36(4), 778–786 (2016). 10.1097/IAE.0000000000000794 [DOI] [PubMed] [Google Scholar]
- 3.Mrejen S., Sarraf D., Mukkamala S. K., Freund K. B., “Multimodal imaging of pigment epithelial detachment: a guide to evaluation,” Retina 33(9), 1735–1762 (2013). 10.1097/IAE.0b013e3182993f66 [DOI] [PubMed] [Google Scholar]
- 4.Wong C. W., Yanagi Y., Lee W. K., Ogura Y., Yeo I., Wong T. Y., Cheung C. M., “Age-related macular degeneration and polypoidal choroidal vasculopathy in Asians,” Prog. Retin. Eye Res. 53, 107–139 (2016). 10.1016/j.preteyeres.2016.04.002 [DOI] [PubMed] [Google Scholar]
- 5.Cohen S. M., Kokame G. T., Gass J. D., “Paraproteinemias associated with serous detachments of the retinal pigment epithelium and neurosensory retina,” Retina 16(6), 467–473 (1996). 10.1097/00006982-199616060-00001 [DOI] [PubMed] [Google Scholar]
- 6.Gass J. D., Bressler S. B., Akduman L., Olk J., Caskey P. J., Zimmerman L. E., “Bilateral idiopathic multifocal retinal pigment epithelium detachments in otherwise healthy middle-aged adults: a clinicopathologic study,” Retina 25(3), 304–310 (2005). 10.1097/00006982-200504000-00009 [DOI] [PubMed] [Google Scholar]
- 7.Schmidt-Erfurth U., Waldstein S. M., Deak G. G., Kundi M., Simader C., “Pigment epithelial detachment followed by retinal cystoid degeneration leads to vision loss in treatment of neovascular age-related macular degeneration,” Ophthalmology 122(4), 822–832 (2015). 10.1016/j.ophtha.2014.11.017 [DOI] [PubMed] [Google Scholar]
- 8.Nagai N., Suzuki M., Uchida A., Kurihara T., Kamoshita M., Minami S., Shinoda H., Tsubota K., Ozawa Y., “Non-responsiveness to intravitreal aflibercept treatment in neovascular age-related macular degeneration: implications of serous pigment epithelial detachment,” Sci. Rep. 6(1), 29619 (2016). 10.1038/srep29619 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tan A. C., Simhaee D., Balaratnasingam C., Dansingani K. K., Yannuzzi L. A., “A perspective on the nature and frequency of pigment epithelial detachments,” Am. J. Ophthalmol. 172, 13–27 (2016). 10.1016/j.ajo.2016.09.004 [DOI] [PubMed] [Google Scholar]
- 10.Castillo M. M., Mowatt G., Elders A., Lois N., Fraser C., Hernández R., Amoaku W., Burr J. M., Lotery A., Ramsay C. R., Azuara-Blanco A., “Optical coherence tomography for the monitoring of neovascular age-related macular degeneration: a systematic review,” Ophthalmology 122(2), 399–406 (2015). 10.1016/j.ophtha.2014.07.055 [DOI] [PubMed] [Google Scholar]
- 11.Sato T., Kishi S., Watanabe G., Matsumoto H., Mukai R., “Tomographic features of branching vascular networks in polypoidal choroidal vasculopathy,” Retina 27(5), 589–594 (2007). 10.1097/01.iae.0000249386.63482.05 [DOI] [PubMed] [Google Scholar]
- 12.Khan S., Engelbert M., Imamura Y., Freund K. B., “Polypoidal choroidal vasculopathy: simultaneous indocyanine green angiography and eye-tracked spectral domain optical coherence tomography findings,” Retina 32(6), 1057–1068 (2012). 10.1097/IAE.0b013e31823beb14 [DOI] [PubMed] [Google Scholar]
- 13.Chen Q., Leng T., Zheng L., Kutzscher L., Ma J., de Sisternes L., Rubin D. L., “Automated drusen segmentation and quantification in SD-OCT images,” Med. Image Anal. 17(8), 1058–1072 (2013). 10.1016/j.media.2013.06.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Golbaz I., Ahlers C., Stock G., Schütze C., Schriefl S., Schlanitz F., Simader C., Prünte C., Schmidt-Erfurth U. M., “Quantification of the therapeutic response of intraretinal, subretinal, and subpigment epithelial compartments in exudative AMD during anti-VEGF therapy,” Invest. Ophthalmol. Vis. Sci. 52(3), 1599–1605 (2011). 10.1167/iovs.09-5018 [DOI] [PubMed] [Google Scholar]
- 15.Shi F., Chen X., Zhao H., Zhu W., Xiang D., Gao E., Sonka M., Chen H., “Automated 3-D retinal layer segmentation of macular optical coherence tomography images with serous pigment epithelial detachments,” IEEE Trans. Med. Imaging 34(2), 441–452 (2015). 10.1109/TMI.2014.2359980 [DOI] [PubMed] [Google Scholar]
- 16.Doi K., “Computer-aided diagnosis in medical imaging: historical review, current status and future potential,” Comput. Med. Imaging Graph. 31(4-5), 198–211 (2007). 10.1016/j.compmedimag.2007.02.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Garvin M. K., Abràmoff M. D., Wu X., Russell S. R., Burns T. L., Sonka M., “Automated 3-D intraretinal layer segmentation of macular spectral-domain optical coherence tomography images,” IEEE Trans. Med. Imaging 28(9), 1436–1447 (2009). 10.1109/TMI.2009.2016958 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Penha F. M., Rosenfeld P. J., Gregori G., Falcão M., Yehoshua Z., Wang F., Feuer W. J., “Quantitative imaging of retinal pigment epithelial detachments using spectral-domain optical coherence tomography,” Am. J. Ophthalmol. 153(3), 515–523 (2012). 10.1016/j.ajo.2011.08.031 [DOI] [PubMed] [Google Scholar]
- 19.Ahlers C., Simader C., Geitzenauer W., Stock G., Stetson P., Dastmalchi S., Schmidt-Erfurth U., “Automatic segmentation in three-dimensional analysis of fibrovascular pigmentepithelial detachment using high-definition optical coherence tomography,” Br. J. Ophthalmol. 92(2), 197–203 (2008). 10.1136/bjo.2007.120956 [DOI] [PubMed] [Google Scholar]
- 20.Gregori G., Wang F., Rosenfeld P. J., Yehoshua Z., Gregori N. Z., Lujan B. J., Puliafito C. A., Feuer W. J., “Spectral domain optical coherence tomography imaging of drusen in nonexudative age-related macular degeneration,” Ophthalmology 118(7), 1373–1379 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chan E. W., Eldeeb M., Lingam G., Thomas D., Bhargava M., Chee C. K., “Quantitative changes in pigment epithelial detachment area and volume predict retreatment in polypoidal choroidal vasculopathy,” Am. J. Ophthalmol. 177, 195–205 (2017). 10.1016/j.ajo.2016.12.008 [DOI] [PubMed] [Google Scholar]
- 22.Zhang F., Du B., Zhang L., “Saliency-guided unsupervised feature learning for scene classification,” IEEE Trans. Geosci. Remote Sens. 53(4), 2175–2184 (2015). 10.1109/TGRS.2014.2357078 [DOI] [Google Scholar]
- 23.LeCun Y., Bengio Y., Hinton G., “Deep learning,” Nature 521(7553), 436–444 (2015). 10.1038/nature14539 [DOI] [PubMed] [Google Scholar]
- 24.K. Yan, C. Li, X. Wang, A. Li, Y. Yuan, D. Feng, M. Khadra, and J. Kim, “Automatic prostate segmentation on MR images with deep network and graph model,” in 2016 IEEE 38th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), (IEEE, 2016),pp. 635–638. 10.1109/EMBC.2016.7590782 [DOI] [PubMed] [Google Scholar]
- 25.Guo Y., Gao Y., Shen D., “Deformable MR prostate segmentation via deep feature learning and sparse patch matching,” IEEE Trans. Med. Imaging 35(4), 1077–1089 (2016). 10.1109/TMI.2015.2508280 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hu P., Wu F., Peng J., Liang P., Kong D., “Automatic 3D liver segmentation based on deep learning and globally optimized surface evolution,” Phys. Med. Biol. 61(24), 8676–8698 (2016). 10.1088/1361-6560/61/24/8676 [DOI] [PubMed] [Google Scholar]
- 27.Yuan Y., Chao M., Lo Y. C., “Automatic skin lesion segmentation using deep fully convolutional networks with Jaccard distance,” IEEE Trans. Med. Imaging 99, 2695 (2017). [DOI] [PubMed] [Google Scholar]
- 28.Sun C., Guo S., Zhang H., Li J., Chen M., Ma S., Jin L., Liu X., Li X., Qian X., “Automatic segmentation of liver tumors from multiphase contrast-enhanced CT images based on FCNs,” Artif. Intell. Med. in press (2017). [DOI] [PubMed]
- 29.Huang L., Xia W., Zhang B., Qiu B., Gao X., “MSFCN-multiple supervised fully convolutional networks for the osteosarcoma segmentation of CT images,” Comput. Methods Programs Biomed. 143, 67–74 (2017). 10.1016/j.cmpb.2017.02.013 [DOI] [PubMed] [Google Scholar]
- 30.Shelhamer E., Long J., Darrell T., “Fully Convolutional Networks for Semantic Segmentation,” IEEE Trans. Pattern Anal. Mach. Intell. 39(4), 640–651 (2017). 10.1109/TPAMI.2016.2572683 [DOI] [PubMed] [Google Scholar]
- 31.O. Ronneberger, P. Fischer, and T. Brox, “U-Net: Convolutional Networks for Biomedical Image Segmentation,” in Medical Image Computing and Computer-Assisted Intervention (MICCAI) (Springer International Publishing, Cham, 2015), pp. 234–241. [Google Scholar]
- 32.Fang L., Cunefare D., Wang C., Guymer R. H., Li S., Farsiu S., “Automatic segmentation of nine retinal layer boundaries in OCT images of non-exudative AMD patients using deep learning and graph search,” Biomed. Opt. Express 8(5), 2732–2744 (2017). 10.1364/BOE.8.002732 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Roy A. G., Conjeti S., Karri S. P. K., Sheet D., Katouzian A., Wachinger C., Navab N., “ReLayNet: retinal layer and fluid segmentation of macular optical coherence tomography using fully convolutional networks,” Biomed. Opt. Express 8(8), 3627–3642 (2017). 10.1364/BOE.8.003627 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.F. Milletari, N. Navab, and S.-A. Ahmadi, “V-net: Fully convolutional neural networks for volumetric medical image segmentation,” in 3D Vision (3DV), 2016 Fourth International Conference (IEEE, 2016), pp. 565–571. 10.1109/3DV.2016.79 [DOI] [Google Scholar]
- 35.Li G., Yu Y., “Deep contrast learning for salient object detection,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (IEEE, 2016), pp. 478–487. 10.1109/CVPR.2016.58 [DOI] [Google Scholar]
- 36.Yu H., Gao J., Li A., “Probability-based non-local means filter for speckle noise suppression in optical coherence tomography images,” Opt. Lett. 41(5), 994–997 (2016). 10.1364/OL.41.000994 [DOI] [PubMed] [Google Scholar]
- 37.Buades A., Coll B., Morel J.-M., “A non-local algorithm for image denoising,” in 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (IEEE, 2005), 60–65. 10.1109/CVPR.2005.38 [DOI] [Google Scholar]
- 38.Vedaldi A., Lenc K., “Matconvnet: Convolutional neural networks for matlab,” in Proceedings of the 23rd ACM international conference on Multimedia, (ACM, 2015),pp. 689–692. 10.1145/2733373.2807412 [DOI] [Google Scholar]
- 39.H. Li, R. Zhao, and X. Wang, “Highly efficient forward and backward propagation of convolutional neural networks for pixelwise classification,” arXiv preprint arXiv:1412.4526 (2014).
- 40.Sun Z., Chen H., Shi F., Wang L., Zhu W., Xiang D., Yan C., Li L., Chen X., “An automated framework for 3D serous pigment epithelium detachment segmentation in SD-OCT images,” Sci. Rep. 6(1), 21739 (2016). 10.1038/srep21739 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Koh A., Lee W. K., Chen L. J., Chen S. J., Hashad Y., Kim H., Lai T. Y., Pilz S., Ruamviboonsuk P., Tokaji E., Weisberger A., Lim T. H., “EVEREST study: efficacy and safety of verteporfin photodynamic therapy in combination with ranibizumab or alone versus ranibizumab monotherapy in patients with symptomatic macular polypoidal choroidal vasculopathy,” Retina 32(8), 1453–1464 (2012). 10.1097/IAE.0b013e31824f91e8 [DOI] [PubMed] [Google Scholar]
- 42.Giavarina D., “Understanding Bland Altman analysis,” Biochem Med (Zagreb) 25(2), 141–151 (2015). 10.11613/BM.2015.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.De Salvo G., Vaz-Pereira S., Keane P. A., Tufail A., Liew G., “Sensitivity and specificity of spectral-domain optical coherence tomography in detecting idiopathic polypoidal choroidal vasculopathy,” Am. J. Ophthalmol. 158(6), 1228–1238 (2014). 10.1016/j.ajo.2014.08.025 [DOI] [PubMed] [Google Scholar]
- 44.Yamashita M., Nishi T., Hasegawa T., Ogata N., “Response of serous retinal pigment epithelial detachments to intravitreal aflibercept in polypoidal choroidal vasculopathy refractory to ranibizumab,” Clin. Ophthalmol. 8, 343–346 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Fang L., Li S., Cunefare D., Farsiu S., “Segmentation based sparse reconstruction of optical coherence tomography images,” IEEE Trans. Med. Imaging 36(2), 407–421 (2017). 10.1109/TMI.2016.2611503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Fang L., Li S., McNabb R. P., Nie Q., Kuo A. N., Toth C. A., Izatt J. A., Farsiu S., “Fast acquisition and reconstruction of optical coherence tomography images via sparse representation,” IEEE Trans. Med. Imaging 32(11), 2034–2049 (2013). 10.1109/TMI.2013.2271904 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wong C. W., Wong T. Y., Cheung C. M., “Polypoidal Choroidal Vasculopathy in Asians,” J. Clin. Med. 4(5), 782–821 (2015). 10.3390/jcm4050782 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Roberts P., Baumann B., Lammer J., Gerendas B., Kroisamer J., Bühl W., Pircher M., Hitzenberger C. K., Schmidt-Erfurth U., Sacu S., “Retinal pigment epithelial features in central serous chorioretinopathy identified by polarization-sensitive optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 57(4), 1595–1603 (2016). 10.1167/iovs.15-18494 [DOI] [PubMed] [Google Scholar]
- 49.Wong T. Y., Ohno-Matsui K., Leveziel N., Holz F. G., Lai T. Y., Yu H. G., Lanzetta P., Chen Y., Tufail A., “Myopic choroidal neovascularisation: current concepts and update on clinical management,” Br. J. Ophthalmol. 99(3), 289–296 (2015). 10.1136/bjophthalmol-2014-305131 [DOI] [PMC free article] [PubMed] [Google Scholar]