Kinetic analyses of single-stranded break repair by human DNA ligase III isoforms reveal biochemical differences from DNA ligase I

Abstract

Humans have three genes encoding DNA ligases with conserved structural features and activities, but they also have notable differences. The LIG3 gene encodes a ubiquitous isoform in all tissues (LIG3α) and a germ line–specific splicing isoform (LIG3β) that differs in the C-terminal domain. Both isoforms are found in the nucleus and the mitochondria. Here, we determined the kinetics and thermodynamics of single-stranded break ligation by LIG3α and LIG3β and compared this framework to that of LIG1, the nuclear replicative ligase. The kinetic parameters of the LIG3 isoforms are nearly identical under all tested conditions, indicating that the BRCA1 C terminal (BRCT) domain specific to LIG3α does not alter ligation kinetics. Although LIG3 is only 22% identical to LIG1 across their conserved domains, the two enzymes had very similar maximal ligation rates. Comparison of the rate and equilibrium constants for LIG3 and LIG1 nevertheless revealed important differences. The LIG3 isoforms were seven times more efficient than LIG1 at ligating nicked DNA under optimal conditions, mainly because of their lower K_m value for the DNA substrate. This could explain why LIG3 is less prone to abortive ligation than LIG1. Surprisingly, the affinity of LIG3 for Mg²⁺ was ten times weaker than that of LIG1, suggesting that Mg²⁺ availability regulates DNA ligation in vivo, because Mg²⁺ levels are higher in the mitochondria than in the nucleus. The biochemical differences between the LIG3 isoforms and LIG1 identified here will guide the understanding of both unique and overlapping biological roles of these critical enzymes.

Introduction

Human DNA ligases I (LIG1), III (LIG3), and IV (LIG4) catalyze the ultimate steps in DNA replication and repair pathways. All three of the LIG genes are required for mouse embryonic development (1–5), and clinical mutations have been identified in both LIG1 and LIG4 genes that cause immunodeficiencies (6–8). LIG1 is believed to be the primary nuclear replicative DNA ligase; however, recent studies indicate that LIG1 and nuclear LIG3 have overlapping functions (9–12). The LIG3 proteins are translated from two start sites to generate mitochondrial and nuclear isoforms, the latter of which is suggested to be dispensable (10, 11, 13–16). Two alternative splice isoforms of LIG3 are known that differ in their C-terminal regions. The major LIG3 isoform (LIG3α) contains a C-terminal BRCA1 C terminal (BRCT)² domain that has been shown to interact with XRCC1 (17–21). Alternative splicing in male germ cells (22, 23) gives rise to a shorter isoform (LIG3β) that lacks the BRCT domain (Fig. 1A). Although the beneficial roles of nuclear LIG3 isoforms are not clear, LIG3 has been implicated in error-prone alternative end joining, which can lead to chromosomal translocations (11, 24) and telomere fusions (25, 26). Furthermore, elevated levels of LIG3 have been detected in cancer, making LIG3 a candidate for anticancer therapeutics (27–30).

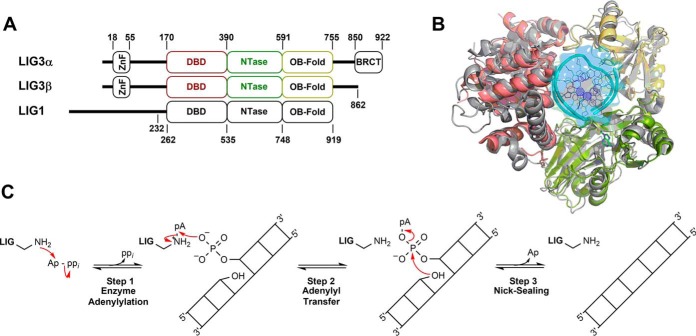
Figure 1.

Conserved structure and mechanism of human DNA ligases. A, schematic representation of human DNA LIG3α, LIG3β and LIG1. The numbers indicate domain boundaries of the enzymes. LIG3α contains a C-terminal BRCT domain. The LIG1 Δ232 truncation mutant used throughout this study is catalytically identical to full-length LIG1 (34). LIG3 isoforms and LIG1 possess conserved DBDs, NTase domains, and OB-fold domains. B, PyMOL (48) rendered superimposition of LIG1 (gray) and LIG3 (color-coded; DBD, red; NTase, green; OB-fold, yellow) structures with Protein Data Bank codes 1X9N and 3L2P, respectively (31, 32). C, mechanism of ATP-dependent DNA ligases.

Crystal structures of the human DNA ligases (31, 32) show a conserved catalytic core made up of three distinct domains that encircle the substrate (Fig. 1B). However, the N- and C-terminal extensions differ significantly, and these regions of the protein are likely to contribute to physiological differences between the ligases (Fig. 1A). LIG1 has an unstructured N-terminal region that facilitates protein-protein interactions (31, 33), but this region is dispensable for ligase activity in vitro (31, 34). LIG3 also has an N-terminal extension containing a unique zinc-finger (ZnF) domain that has been implicated in DNA binding (32, 35–40). Furthermore, this ZnF domain has been hypothesized to be a “nick sensor” responsible for increasing LIG3 specificity and affinity toward DNA substrates containing a single-stranded DNA break (19, 32, 35, 38). The C-terminal extension of LIG3α contains a BRCT domain that is constitutively bound to XRCC1 in the nucleus. Because XRCC1 is not found in the mitochondria, it is of interest to characterize the biochemical properties of LIG3α in the absence of XRCC1 (41).

The human DNA ligases employ a conserved three-step chemical mechanism (Fig. 1C) to harness the energy of ATP to catalyze the formation of a phosphodiester bond between adjacent 3′-hydroxyl and 5′-phosphate groups in DNA (42). During the first chemical step of ligation (step 1), ligase catalyzes the transfer of AMP from ATP to the active-site lysine forming an adenylylated enzyme intermediate and releasing inorganic pyrophosphate. The adenylylated enzyme binds to a DNA substrate containing a single-stranded break and, during the second chemical step, catalyzes the transfer of the AMP group to the 5′-phosphate at the break (nick), thereby generating an adenylylated DNA intermediate. During step 3, the 3′-hydroxyl at the nick attacks the adenylylated 5′-phosphate to generate a new phosphodiester bond and release AMP (Fig. 1C). All three of these chemical steps are dependent on divalent metal ions (presumably Mg²⁺), and previous work has supported a two–metal ion mechanism for step 1 (enzyme adenylylation) catalyzed by human LIG1 (34).

As a starting point for understanding the biochemical differences between LIG1 and LIG3, we describe the kinetic and thermodynamic framework for LIG3-catalyzed ligation of a single-stranded break. LIG3α and LIG3β exhibit similar kinetic parameters under all tested conditions, indicating that the C-terminal BRCT domain of LIG3α does not directly contribute to ligation of nicked DNA substrates. Comparison of the biochemical properties of LIG3 and LIG1 reveals similar rates of the three chemical steps under conditions of saturating Mg²⁺, but LIG3 has a higher k_cat/K_m value for nicked DNA and does not release adenylylated DNA intermediates as readily as LIG1. Unexpectedly, we found that LIG3 does not bind Mg²⁺ as tightly as LIG1, and this weaker binding by LIG3 is most pronounced in the nick-sealing step of catalysis. The apparent Mg²⁺ affinity of ∼6 mm required for the stimulation of steady-state ligation catalyzed by LIG3 suggests that LIG3 activity can be regulated by the availability of free Mg²⁺, which is typically between 0.2 and 1 mm in the nucleus and cytosol (43). Intriguingly, mitochondrial Mg²⁺ concentration has been reported to be 10-fold greater than cytosolic Mg⁺² levels (44), which could contribute to higher LIG3 activity in the mitochondria where it is the sole DNA ligase. This kinetic and thermodynamic framework for LIG3 identifies the different biochemical properties that distinguish it from LIG1, and it will enable future studies investigating the roles of isoform-specific accessory proteins and their contributions to ligase activity.

Results

Purity, stability, and adenylylation state of the LIG3 isoforms

Recombinant human DNA LIG3α and LIG3β were purified to homogeneity over four chromatographic steps: phosphocellulose, Ni²⁺–nitrilotriacetic acid, Cibacron Blue, and gel filtration (Fig. 2A). LIG3α and LIG3β eluted at the same salt concentration from the Cibacron Blue (HiTrap Blue) column but eluted at different volumes with gel filtration, consistent with the greater molecular weight of LIG3α. Prior to detailed kinetic studies, the stabilities of LIG3α and LIG3β were investigated at 4 and 37 °C using a gel-based DNA ligation assay (supplemental Fig. S1). Both LIG3α and LIG3β maintain activity when stored at 4 °C for more than 1 month (supplemental Fig. S2A). LIG3β is quite stable at 37 °C (t_½ ≫ 4 h); however, LIG3α is significantly less stable at this temperature (t_½ = 2 h; supplemental Fig. S2B). These findings are consistent with previous reports suggesting LIG3α is less stable than LIG3β (45). Nevertheless, the stability studies established that both LIG3 isoforms are sufficiently stable for rigorous biochemical analysis.

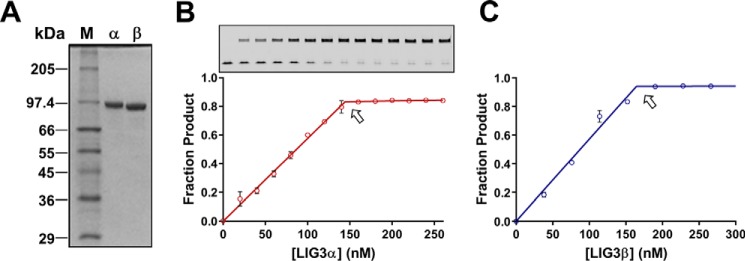
Figure 2.

Purity and active site titrations of LIG3 isoforms. A, 12% SDS-PAGE gel containing 0.5 μg of purified LIG3α and LIG3β with molecular masses of 102.7 and 95.9 kDa. M, protein sizing standards; α, Lig3α; β, Lig3β. B and C, representative active site titrations of LIG3α and LIG3β isoform, inset gel shows product (upper bands) and substrate (lower bands). In the absence of ATP, the adenylylated enzyme is limited to a single turnover ligation. Reactions contained 150 nm 28-mer nicked DNA substrate and 20 mm Mg²⁺ (see “Experimental procedures” for details). The equivalence point of the titration (denoted by arrow) indicates the concentration of adenylylated enzyme (data points are the means ± S.D.; n = 2).

Consistent with a previous report from the Ellenberger lab, we obtained a mixture of adenylylated and deadenylylated recombinant LIG3 from our initial four-step purification scheme (36). Adenylylated enzyme can be quantified by performing ligation reactions in the absence of ATP, because the number of ligated DNA molecules corresponds to the number of active adenylylated enzyme molecules (Fig. 2, B and C). To assess the adenylylation status of our initial LIG3 preparations, enzyme samples were preincubated with ATP and MgCl₂ to fully adenylylate any deadenylylated enzyme species prior to the addition of the DNA substrate (Fig. 3A). Under these conditions a pre–steady-state burst was observed followed by a slower steady-state phase (Fig. 3, B–E). Comparison of the burst amplitude with the amplitude of ligation in the absence of ATP allowed us to determine that the preparations of LIG3α and LIG3β were 73 and 81% adenylylated, respectively (Fig. 3, B and C). The heterogeneity in adenylylation status of the purified ligases was remedied in future purification protocols by treating LIG3 fractions with excess ATP and MgCl₂ prior to the final gel filtration step of purification (Fig. 3, D and E). The LIG3 proteins used in all subsequent experiments were purified using the improved protocol that yields homogeneous adenylylated enzyme.

Figure 3.

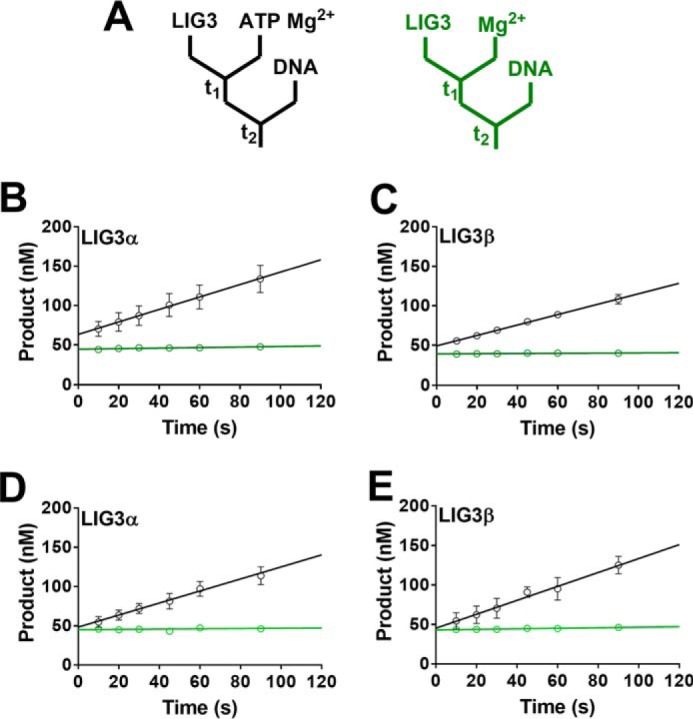
Adenylylation state of purified LIG3 isoforms. A, schematics for burst experiments. The left (black) scheme indicates that LIG3 was incubated in the presence of ATP and Mg²⁺ to ensure complete enzyme adenylylation prior to the addition of DNA. The scheme to the right (green) displays reaction conditions in which no ATP was added to the reaction solution. The colors of the diagrams correspond to the colors of the linear fits in B–E. B and C, burst kinetics indicate LIG3α and LIG3β are 73 and 81% adenylylated, respectively. D and E, burst kinetics of LIG3α and LIG3β, respectively, after the addition of an adenylylation step during protein purification generates 100% adenylylated protein. Burst experiments after preincubation of LIG3 with ATP and Mg²⁺ did not increase burst amplitude. All experiments contained an estimated 50 nm enzyme, 200 nm DNA, and 20 mm Mg²⁺ in the presence and absence of 0.5 μm ATP. Each experiment was completed in triplicate (means ± S.D.).

Substrate dependence of the LIG3 isoforms

Steady-state conditions were used to investigate the substrate dependence of both LIG3 isoforms. The ATP concentration dependences for multiple-turnover ligation were determined in the presence of saturating Mg²⁺ (20 mm) and saturating nicked DNA substrate (1 μm). The reaction progress curves generated at each ATP concentration were linear in all cases (Fig. 4A), and the initial rates were plotted as a function of ATP concentration (Fig. 4B). Fitting the Michaelis–Menten equation (Equation 1) to the ATP dependence data yielded almost identical k_cat and K_{m, ATP} values for LIG3α and LIG3β (Table 1). These K_m values are roughly 3-fold higher than the previously reported value for LIG1 that was obtained under similar reaction conditions (34).

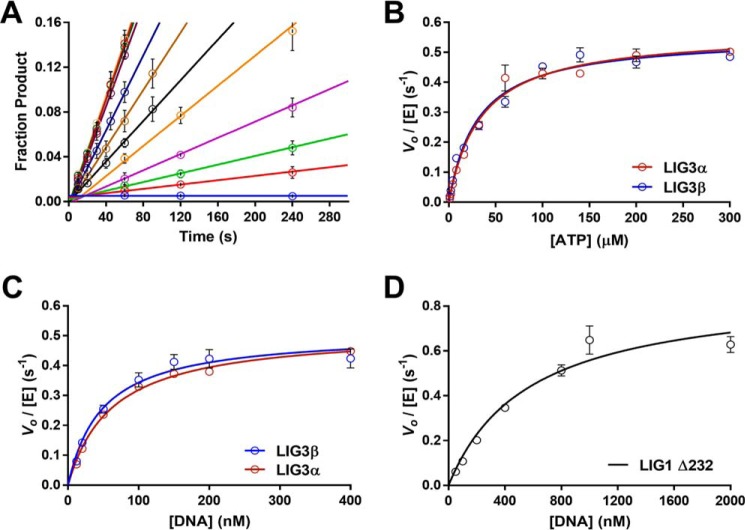
Figure 4.

Substrate dependence of LIG3α, LIG3β, and LIG1. A, representative ATP concentration dependence of LIG3β used to determine initial velocities under multiple-turnover conditions. Reactions performed at each ATP concentration (0–300 μm) were fit using linear regression to determine initial rates. B, ATP dependence was measured under multiple-turnover conditions in the presence of saturating DNA (1 μm) and Mg²⁺ (20 mm). Initial velocities are plotted as a function of ATP concentration and fit using the Michaelis–Menten equation yielding k_{cat, ATP} values of 0.57 ± 0.02 and 0.55 ± 0.02 s⁻¹ for LIG3α and LIG3β, respectively. The respective K_{m, ATP} values are 34 ± 4 and 31 ± 3 μm. C, DNA dependence was measured at 300 mm ionic strength with 1 mm ATP and 20 mm Mg²⁺. LIG3α and LIG3β have k_{cat, DNA} values of 0.52 ± 0.02 and 0.51 ± 0.03 s⁻¹ and K_{m, DNA} values of 62 ± 6 and 49 ± 8 nm, respectively. D, LIG1 DNA concentration dependence was measured under the same condition as for LIG3 in C. The k_cat, _DNA value for LIG1 is 0.87 ± 0.10 s⁻¹ and the K_{m, DNA} value is 570 ± 170 nm. Each experiment was completed in triplicate (means ± S.D.).

Table 1.

Comparison of kinetic parameters for multiple-turnover ligation by human DNA ligases

Multiple-turnover parameters were obtained at 150 and 300 mm ionic strength. The ATP dependence was determined with 20 mm fixed concentration of Mg²⁺, and the Mg²⁺ dependence was determined with 1 mm fixed concentration of ATP.

	LIG3α	LIG3β	LIG1a	Relative LIG3α/LIG3β	Relative LIG1/LIG3β
150 mm I
kcat, ATP (s−1)	0.57 ± 0.02	0.55 ± 0.02	0.74 ± 0.09	1.0	1.3
kcat, Mg (s−1)	0.69 ± 0.04	0.69 ± 0.03	0.81 ± 0.10	1.0	1.2
Km, ATP (μm)	34 ± 4	31 ± 3	11 ± 3	1.1	0.35
KMg (mm)	5.6 ± 0.9	7.4 ± 0.7	0.71 ± 0.2	0.76	0.10
kcat/Km, ATP (m−1 s−1)	1.7 ± 0.2 × 104	1.8 ± 0.2 × 104	6.7 × 104	0.94	3.7
kcat/KMg (m−1 s−1)	120 ± 20	93 ± 10	1.1 ± 0.4 × 103	1.3	12
300 mm I
kcat, DNA (s−1)	0.52 ± 0.02	0.51 ± 0.03	0.87 ± 0.10	1.0	1.7
Km, DNA (nm)	62 ± 6	49 ± 8	570 ± 170	1.3	12
kcat/Km, DNA (m−1 s−1)	8.4 ± 0.9 × 106	1.0 ± 0.2 × 107	1.5 ± 0.5 × 106	0.84	0.15

^a The LIG1 values at 150 mm NaCl were previously published (34). The error is represented as S.D. from the mean (n ≥ 3).

We next examined the concentration dependence of the nicked DNA substrate, keeping fixed saturating concentrations of ATP (1 mm) and Mg²⁺ (20 mm). Under the standard conditions of 150 mm ionic strength, LIG3β saturated at a very low concentration of DNA (K_m ≤ 5 nm; supplemental Fig. S3). It was not possible to test lower concentrations of DNA using the gel-based fluorescence assay, and therefore the salt concentration was increased to 300 mm to weaken the protein-DNA interaction. At this higher salt condition, complete Michaelis–Menten curves were obtained for both of the LIG3 isoforms (Fig. 4C). LIG3α and LIG3β have K_mvalues for DNA of ∼60 and ∼50 nm and catalytic efficiency (k_cat/K_m) values of 8.4 × 10⁶ and 1.0 × 10⁷ m⁻¹ s⁻¹, respectively (Table 1). The very similar rate constants observed for the two LIG3 isoforms indicate that the C-terminal BRCT domain of LIG3α does not directly affect the ligation reaction. To compare the catalytic efficiency of LIG3 isoforms to that of LIG1, it was necessary to determine the DNA concentration dependence of LIG1 at the same higher ionic strength conditions (Fig. 4D). LIG1 is approximately an order of magnitude less efficient than LIG3 under these conditions, with a K_{m, DNA} value of 570 nm and a k_cat/K_{m, DNA} value of 1.5 × 10⁶ m⁻¹ s⁻¹ (Table 1). The higher catalytic efficiencies of the LIG3 isoforms are primarily due to the decreased K_{m, DNA} values.

Mg²⁺ concentration dependence for multiple-turnover ligation

The preceding experiments were performed in the presence of a high concentration of Mg²⁺ (20 mm). This ensures that Mg²⁺, which is an essential cofactor for DNA ligases, is saturating. Free Mg²⁺ levels in the cell are typically much lower, and therefore it is important to investigate the Mg²⁺ dependence on ligation (43). The free Mg²⁺ concentration dependence for multiple-turnover ligation was determined in the presence of saturating ATP and nicked DNA substrate (1 mm ATP, 1 μm DNA). A hyperbolic one site-specific binding equation (Equation 2) fit well to the data, providing the half-maximal concentration of free Mg²⁺ (K_Mg) required for ligase activity. Free Mg²⁺ concentrations were calculated using the K_d values for ATP·Mg²⁺ and ATP·2Mg²⁺. It is likely that K_Mg is equal to the K_d for Mg²⁺ binding to the enzyme, because dissociation equilibrium constants in the millimolar range are typically indicative of fast dissociation rate constants. The observation that LIG3 is rapidly and efficiently quenched using EDTA on the millisecond time scale is consistent with fast dissociation of Mg²⁺. The Mg²⁺ dependences of LIG3α and LIG3β are essentially superimposable, and the fits yield similar k_{cat, Mg} and K_Mg values (Fig. 5A and Table 1). It is striking that the affinity for Mg²⁺ (K_Mg = ∼6 mm) is ∼10-fold weaker than was previously observed for LIG1 under similar conditions (Table 1).

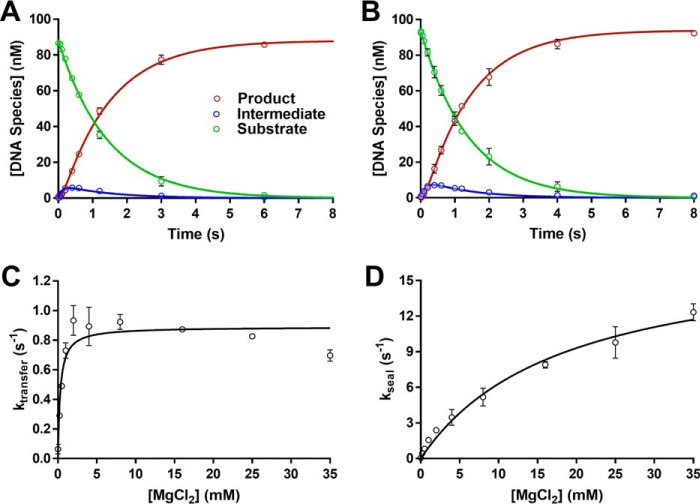
Figure 5.

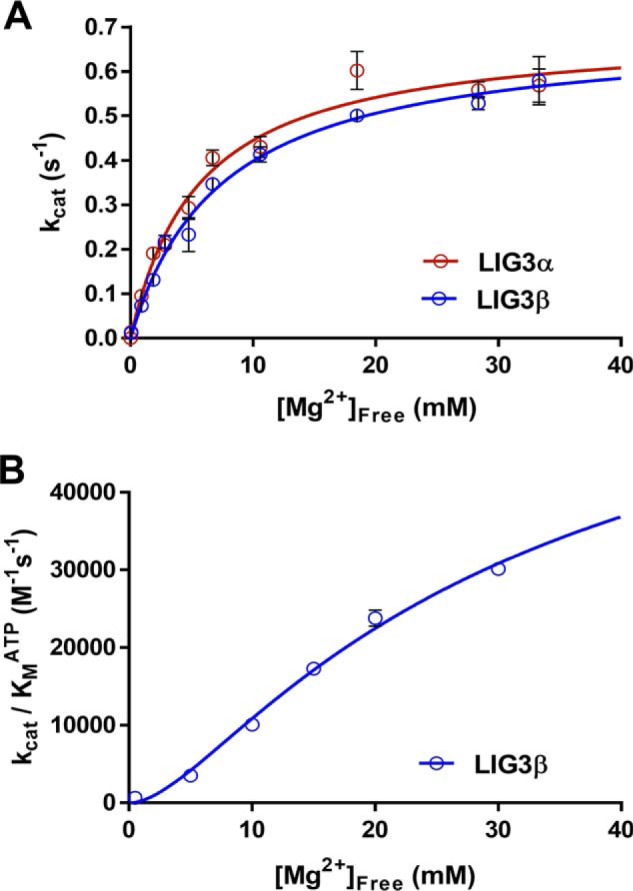
Magnesium dependence for multiple-turnover ligation. A, reactions contained 1 μm DNA, 1 mm ATP, and the concentration of free Mg²⁺ was varied between 0 and 35 mm. The data were fit using a hyperbolic one site-specific binding equation (Equation 2) yielding maximal k_{cat, Mg} values of 0.69 ± 0.04 and 0.69 ± 0.03 s⁻¹ and K_Mg values of 5.6 ± 0.9 and 7.4 ± 0.7 mm for LIG3α and LIG3β, respectively. B, investigation of the Mg²⁺ concentration dependence of enzyme adenylylation. The Mg²⁺ concentration dependence was performed using subsaturating ATP concentrations (supplemental Fig. S4). The magnesium concentration dependence of (k_cat/K_m)^ATP for LIG3β was fit using a two metal random binding model (Equation 3). Each experiment was completed in at least triplicate (means ± S.D.).

We next determined the catalytic efficiency (k_cat/K_m)^ATP for LIG3β as a function of Mg²⁺ concentration, which monitors the steps up to and including enzyme adenylylation. This can be most conveniently accomplished by measuring the linear dependence of the reaction rate as a function of ATP concentration when ATP is subsaturating (supplemental Fig. S4). The Mg²⁺ dependence of (k_cat/K_m)^ATP (Fig. 5B) could not be fit well by a hyperbolic dependence on a single essential Mg²⁺ but could be better fit by a two-metal ion, random binding model (Equation 3). These data support a two-metal mechanism for the reaction of LIG3 with ATP, analogous to the two–metal ion mechanism proposed for LIG1 (34).

Single-turnover ligation kinetics

Although the LIG3 isoforms exhibited very similar steady-state kinetic parameters, it is possible that larger differences could exist for steps that are not rate-limiting. Therefore, we also performed single-turnover ligation experiments using excess amounts of saturating LIG3α and LIG3β. As previously observed for other DNA ligases, LIG3-catalyzed single-turnover ligation followed a two-step irreversible mechanism. Simultaneous fitting of the substrate, intermediate, and product yielded the microscopic rate constants for adenylyl transfer (k_{obs, transfer}) and nick-sealing (k_{obs, seal}). At a high concentration of Mg²⁺ (20 mm), LIG3α and LIG3β exhibit almost identical microscopic rate constants for both steps (Fig. 6, A and B). Given the identical kinetic parameters for the two LIG3 isoforms, and the greater stability of LIG3 β, we chose to perform a comprehensive single-turnover kinetic analysis of LIG3β.

Figure 6.

Single-turnover ligation kinetics. A and B, representative single turnover kinetics of DNA LIG3α (A) and LIG3β (B) indicate the two enzymes behave similarly under single-turnover conditions at 20 mm Mg²⁺. The data were fit using a two-step irreversible mechanism using the program Berkeley Madonna. The rate constants for adenylyl transfer are 0.7 and 0.8 s⁻¹ and for nick sealing are 8.7 and 8.9 s⁻¹ for LIG3α and LIG3β, respectively. Experiments contained 100 nm fluorescein-labeled DNA, 600 nm enzyme, and 20 mm MgCl₂ with no added ATP. C, Mg²⁺ concentration dependence for the adenylyl transfer step using LIG3β. D, Mg²⁺ concentration dependence of the nick-sealing step for LIG3β. The data were fit using a hyperbolic one site-specific binding equation (Equation 2) yielding k_transfer and k_seal values of 0.89 ± 0.03 and 19 ± 6 s⁻¹, respectively. The K_Mg values for adenylyl transfer and nick-sealing steps are 0.30 ± 0.06 and 18 ± 3 mm, respectively. Each experiment was completed in at least triplicate (means ± S.D.).

To evaluate the metal cofactor requirements for each chemical step of ligation, the Mg²⁺ binding affinities and microscopic rate constants were systematically determined under single-turnover conditions. The observed rate constants for adenylyl transfer (Fig. 6C) and nick sealing by LIG3β (Fig. 6D) are plotted as a function of Mg²⁺ concentration. These data were fit by a hyperbolic dependence to yield the maximal k_transfer and k_seal rate constants of 0.90 and 18 s⁻¹, respectively (Table 2). Using the net rate constants method (Equation 5), the rate constant for enzyme adenylylation (k_{adenylylation}) was calculated to be 1.6 s⁻¹ (Table 2). The rate constants at saturating Mg²⁺ for all three of the chemical steps catalyzed by LIG3β are strikingly similar to the kinetic parameters for LIG1 that were previously obtained under similar reaction conditions. The apparent affinity for Mg²⁺ in the adenylyl transfer step is only 2-fold weaker for LIG3 compared with LIG1 with K_Mg values of 0.3 and 0.15 mm, respectively. In contrast, the Mg²⁺ affinity for nick-sealing is 7-fold weaker for LIG3 as compared with LIG1 with values of 18 and 2.6 mm, respectively (Table 2).

Table 2.

Comparison of single-turnover parameters of LIG3β and LIG1

Single-turnover parameters were obtained at 150 mm ionic strength. All reactions contained 600 nm adenylylated enzyme and 100 nm nicked DNA substrate in the presence of 20 mm Mg²⁺ and the absence of ATP.

Kinetic parameter	LIG3β	LIG1a	Relative LIG1/LIG3β
kadenylylation (s−1)b	1.6 ± 0.2	1.3 ± 0.3	0.81
ktransfer (s−1)	0.89 ± 0.03	2.6 ± 0.6	2.9
kseal (s−1)	19 ± 6	12 ± 2	0.63
KMg, transfer (mm)	0.30 ± 0.07	0.15 ± 0.06	0.50
KMg, seal (mm)	18 ± 3	2.6 ± 0.9	0.14

^a LIG1 values were previously reported for Δ232 LIG1 under similar experimental conditions (34).

^b The microscopic rate constant for enzyme adenylylation was calculated using a k_cat value of 0.55 s⁻¹ with the net rate constants equation (Equation 4). The error is represented as S.D. from the mean (n ≥ 3).

Accumulation of adenylylated DNA intermediates

Previous study of LIG1 revealed that this ligase releases adenylylated DNA intermediates under conditions of low free Mg²⁺ concentration (34). LIG1 is quickly adenylylated and cannot rebind the intermediate, resulting in abortive ligation (Fig. 7A). The propensity for abortive ligation under Mg²⁺-starved conditions was attributed to differential affinity for Mg²⁺ in the adenylyl transfer and nick-sealing steps (34). Because LIG3 shows a similar reduction in Mg²⁺ affinity for nick sealing as compared with adenylyl transfer steps, we investigated whether LIG3 is also susceptible to abortive ligation on a nicked DNA substrate. Guided by the previous investigation of LIG1, multiple-turnover assays were conducted in the presence of low concentration of free Mg²⁺ (70-fold below K_Mg). Analogous ligation reactions using LIG1 were performed for direct comparison between the enzymes. The fraction abortive ligation was calculated for both LIG1 and LIG3β (Equation 4 and Fig. 7B). Whereas 8% of attempted ligation events were aborted by LIG1, only 1% of ligation events were aborted by LIG3β. Thus, LIG3 appears to be less susceptible than LIG1 to abortive ligation of nicked DNA substrates.

Figure 7.

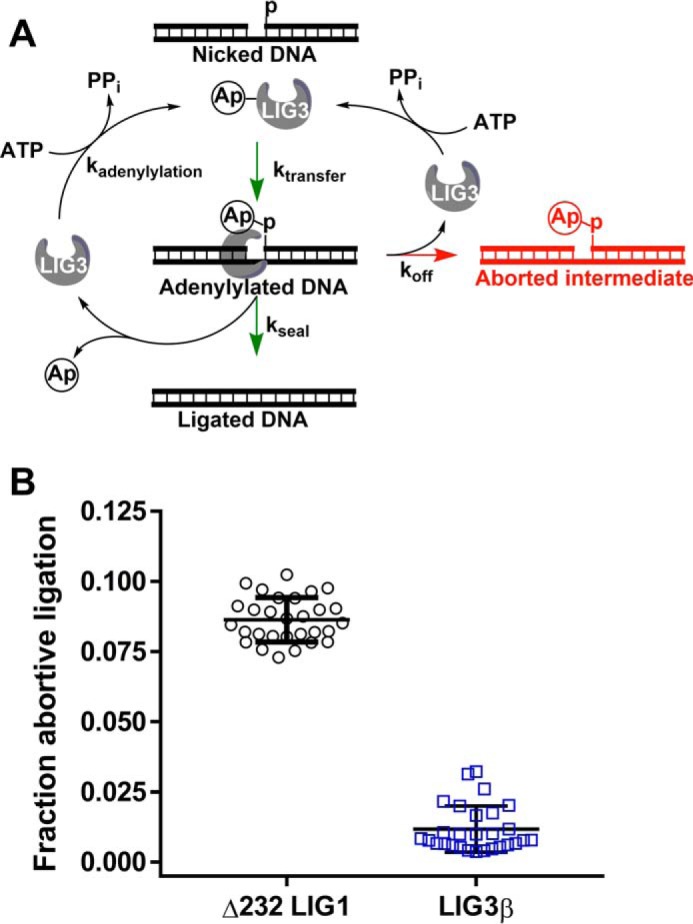
Accumulation of adenylylated DNA intermediate. A, abortive ligation mechanism observed under Mg²⁺-starved conditions. Adenylylated ligase interacts with nicked DNA substrates, generating adenylylated DNA intermediate. The partitioning between the nick-sealing steps and abortive ligation is represented with k_seal and k_off, respectively. Following successful or abortive ligation, ligase becomes adenylylated, preventing the enzyme from rebinding the adenylylated DNA intermediate and completing the nick-sealing step. B, propensity of DNA ligases for abortive ligation. Free Mg²⁺ concentrations were 70-fold below K_Mg for LIG1 and LIG3β in all experiments. The abortive ligation data represent multiple time points obtained from multiple-turnover time courses conducted in quadruplicate (see “Experimental procedures” for details). Error bars indicate S.D. from the mean.

Discussion

DNA ligases I and III contain three structurally conserved domains (DBD, NTase, and OB-fold domains; Fig. 1) that each contribute to substrate binding and ligation (32). Despite this high degree of structural homology, LIG1 and LIG3 share only 22% primary sequence identity across these three domains (Fig. 1B). On the one hand, the high degree of structural homology might indicate similar biochemical activities, but on the other hand, there are numerous substitutions throughout the proteins, including the DNA-binding interfaces of the DBD and OB-fold domains that could lead to distinct biochemical properties. Outside of the core three-domain architecture of the ligases, the human ligases also have unique N- and C-terminal domains that likely influence their localization, protein-protein interactions, and substrate specificity. As a first step toward understanding the biochemical differences between the human DNA ligases, we have characterized recombinant human LIG3α and LIG3β under single- and multiple-turnover conditions and compared the kinetic framework to that of the previously studied human DNA LIG1. This analysis reveals similarities and differences that are relevant to understanding their unique biological functions. Furthermore, this information provides an essential starting point for future studies that explore the functional consequences of mutations in LIG3, as well as the regulatory effects of LIG3 interacting proteins, such as XRCC1.

Recombinant LIG3α was found to be less stable than LIG3β, with a half-life of roughly 2 h, as compared with at least 4 h for LIG3β in our assay conditions (supplemental Fig. S2). This is consistent with the previous findings by the Caldecott group (45) that LIG3α exhibits limited stability in vivo and that interaction with XRCC1 is important for stability. It remains unclear whether mitochondrial LIG3α requires a mitochondrial-specific protein binding partner or whether it functions as a homodimer (41). Nevertheless, the stability of recombinant Lig3α was sufficient for a complete in vitro kinetic characterization. We found that the two LIG3 isoforms are indistinguishable under all experimental conditions tested using a nicked DNA substrate (Table 1). This has implications for mitochondrial DNA ligation and establishes that the different C termini of the LIG3 isoforms do not change the kinetics of single-stranded break ligation.

We can also directly compare the kinetic parameters for the LIG3 isoforms to those of the previously studied LIG1. Comparison of the substrate dependences of the enzymes under conditions of saturating Mg²⁺ demonstrates that these enzymes have very similar efficiencies for utilization of ATP. However, the LIG3 isoforms have higher catalytic efficiency than LIG1 toward nicked DNA substrates because of the reduced K_{m, DNA} of the LIG3 isoforms. These findings are consistent with previous studies suggesting that the ZnF domain of LIG3 contributes to DNA binding during ligation of both single- and double-strand breaks (19, 32, 35, 38). A “jackknife” model for nick recognition has been previously proposed for explaining how LIG3 uses two independent DNA-binding domains to bind to a nick (32). Our studies do not directly test this model but require that the proposed conformational changes upon nick recognition would have to be fast to obtain such similar kinetics for the LIG3 isoforms and LIG1, for LIG1 lacks a ZnF domain (Fig. 1A). These overall similarities in the rates of the chemical steps at saturating Mg²⁺ concentration are consistent with the strong conservation of the active site architecture (Fig. 1B).

Surprisingly, LIG3 requires a much higher concentration of Mg²⁺ cofactor to achieve maximal activity as compared with LIG1. The structural basis for this biochemical difference is unknown, but the observation of an approximate 10-fold reduction in K_Mg for steady-state ligation raises the possibility that this difference in Mg²⁺ affinity is biologically relevant. The free Mg²⁺ concentration in nuclei has been estimated to be between 0.2 and 2 mm, which would be subsaturating for LIG3 and lead to suppressed catalytic activity (46). In contrast, recent studies have suggested that mitochondria have up to 10-fold higher concentration of free Mg²⁺ compared with the cytosol (44). We speculate that this difference in Mg²⁺ affinity could reflect an adaption to limit LIG3 activity in the nucleus where multiple ligases are present and yet allow for high catalytic activity in the mitochondria where it is the sole DNA ligase.

The weaker affinity of LIG3 for Mg²⁺ is most apparent in the adenylylation step and in the nick-sealing step of the reaction, whereas the adenylyl transfer step is more similar for LIG3 and LIG1 (Table 2). These differences in Mg²⁺ affinity in the different steps of the reaction leads to a greater buildup of adenylylated intermediate for LIG3 (supplemental Fig. S5) as compared with LIG1 at a physiological free Mg²⁺ concentration of 1 mm. Nevertheless, LIG3 is more efficient at ligation than LIG1 under conditions of low free Mg²⁺, and LIG3 is not susceptible to abortive ligation on a normal nick (Fig. 7). Because abortive ligation involves the release of adenylylated DNA intermediate, we can infer that LIG3 must have greater DNA binding affinity as compared with LIG1.

Conclusions

This study provides the foundational kinetic and thermodynamic framework for ligation of single-stranded breaks catalyzed by the LIG3 isoforms. We suggest that the BRCT domain of LIG3α does not contribute to ligation of single-stranded breaks, revealing nearly identical kinetic parameters for the LIG3 isoforms. The LIG3 isoforms differ from LIG1 in their substrate and Mg²⁺ dependence, despite a high degree of structural similarity in the catalytic domain. The kinetic and thermodynamic framework presented here for LIG3 will facilitate future investigations of the functional differences between human DNA ligases and their variants.

Experimental procedures

Expression and purification of LIG3 isoforms

Full-length human DNA LIG3α and LIG3β cDNAs were cloned into a modified pET28 plasmid containing an N-terminal His₆-SUMO tag, and the open reading frames were confirmed by Sanger sequencing of both strands. The enzymes were expressed in Escherichia coli C41 pRare 2 cells. Bacterial cultures were grown in LB and induced at an A₆₀₀ of 0.6 using 300 μm isopropyl β-d-thiogalactopyranoside followed by an incubation at 16 °C for 24 h at 230 RPM. Cells were harvested via centrifugation at 6,000 × g for 20 min at 4 °C. Pellets were suspended in lysis buffer (50 mm Tris, pH 7.5, 300 mm NaCl, 3 mm EDTA, 10 mm BME, 10% glycerol, 1 mm benzamidine-HCl, and 1 mm PMSF) and stored at −80 °C. Prior to purification, the cells were thawed and lysed by three passages through a cell homogenizer. Lysates were clarified by centrifugation for 1 h at 39,000 × g at 4 °C and further clarified using a 0.45 μm filter. All purification steps were performed at 4 °C. The clarified lysate was loaded onto a cellulose phosphate column (Sigma) equilibrated with purification buffer (50 mm Tris, pH 7.5, 10% glycerol, 2 mm BME) containing 250 mm NaCl and 3 mm EDTA. The enzyme was eluted with purification buffer containing 2 m NaCl and then loaded onto a HisTrap HP column (GE Healthcare) equilibrated with purification buffer containing 1 m NaCl and 20 mm imidazole. Loaded protein was washed using 200 mm NaCl and 20 mm imidazole and then eluted using a linear imidazole gradient of 20–600 mm. Ligase containing fractions were pooled, and the His₆-SUMO tag was digested using ubiquitin-like protease (ULP1) prior to loading onto a HiTrap Blue column (GE Healthcare) equilibrated with purification buffer containing 200 mm NaCl. The bound protein was eluted using a linear gradient of 200 mm to 2 m NaCl. Protein containing fractions were collected and concentrated using 30,000 molecular weight cutoff Amicon Ultra concentrators. To ensure that the purified protein was 100% adenylylated, 20 mm MgCl₂ and 1 mm ATP were added to the concentrated HiTrap Blue fractions and incubated for 30 min on ice. Purification buffer was exchanged with LIG3 storage buffer (50 mm NaMOPS, pH 7.5, 300 mm NaCl, 10% glycerol, 1 mm TCEP) over a Superdex S200 26/60 gel filtration column. Protein containing fractions were collected and concentrated to 40 mg/ml, snap frozen using liquid nitrogen, and stored at −80 °C. The purity of the ligase isoforms was greater than 95% as judged by SDS-PAGE (Fig. 2A). Human DNA ligase I (LIG1) was prepared as previously described (34).

DNA substrates

Oligonucleotides were obtained from Integrated DNA Technologies and purified using 15% polyacrylamide, 8 m urea DNA sequencing gels as previously described (34). The double-stranded nicked DNA substrate used throughout this study was generated by annealing the following oligonucleotides: 5′-CCGAATCAGTCCGACGACGCATCAGCAC, 5′-GTGCTGATGCGTC, and 5′P-GTCGGACTGATTCGG-FAM, where P indicates the presence of a 5′-phosphate, and FAM indicates the presence of 3′-fluorescein. The oligonucleotides were annealed at equimolar equivalents in annealing buffer (10 mm NaMES, pH 6.5, 50 mm NaCl) by heating the solution to 95 °C and cooling to 4 °C at a rate of 12 °C/min.

Gel-based ligation assay

All single- and multiple-turnover reactions were performed at 37 °C, in standard reaction buffer (50 mm NaMOPS, pH 7.5, 10% glycerol, 1 mm TCEP, 100 μg/ml BSA (MP Biomedicals)) at an ionic strength of 150 mm unless otherwise stated. Multiple-turnover ligation reactions were quenched at designated times into quench solution (90% formamide, 50 mm EDTA, 0.006% bromphenol blue, 0.006% xylene cyanol). Single-turnover experiments were quenched using 0.2 m NaOH, followed by 2-fold dilution into the quench solution described above. Quenched samples were incubated at 95 °C for 3 min, snap-cooled using ice water, and then loaded onto a 15% (w/v) polyacrylamide, 8 m urea, 1× TBE DNA denaturing gel. The gels were scanned using a Typhoon Trio⁺ imager (GE Healthcare) set to monitor excitation at 488 nm and emission through a 520-nm band-pass filter. DNA substrate, intermediate, and product bands were quantified using ImageQuant TL (GE Healthcare). The data were plotted and analyzed using GraphPad Prism.

Multiple-turnover kinetics

Steady-state reactions were performed in standard reaction buffer at 150 mm ionic strength unless otherwise stated. Multiple-turnover reaction volumes were 30 μl, from which 3 μl was quenched into 30 μl of quench solution at designated times. The initial rates were determined by the linear rate of product formation within the first 10% of product formation. The results represent the average of least three independent experiments. Burst experiments contained an estimated 50 nm ligase and 200 nm DNA. LIG3 isoforms were preincubated in the absence and presence of 20-fold greater molar concentration of ATP in the presence of 20 mm Mg²⁺ for 1 h on ice followed by 10 min at 37 °C. Following the enzyme adenylylation incubations, the samples were diluted 500-fold to achieve reaction concentrations prior to mixing with DNA. The adenylylation state was determined by comparison between ATP-treated and ATP-omitted samples. Burst amplitudes are proportional to adenylylated enzyme concentration. The ATP concentration dependences of the LIG3 isoforms were investigated using 5 nm enzyme in the presence of saturating Mg²⁺ (20 mm) and saturating 28-mer DNA (1 μm) while adjusting ATP concentrations between 0 and 300 μm. The initial rates (V₀/[E]) were plotted as a function of ATP concentration and fit using the Michaelis–Menten equation (Equation 1). The free Mg²⁺ concentration dependence (0–35 mm) was investigated under both saturating and subsaturating ATP concentrations. Free Mg²⁺ concentrations were calculated using K_d values for ATP·Mg²⁺ and ATP·2Mg²⁺ of 12 μm and 17 mm as previously described (34, 47). In the presence of saturating ATP (1 mm), the initial rates were fit by a hyperbolic curve (Equation 2). In the presence of subsaturating ATP (0.5, 1, and 2 μm), (k_cat/K_m)^ATP values were generated and plotted as a function of Mg²⁺ concentrations revealing cooperative enzymatic behavior that best fit to a two-site random binding model (Equation 3). The DNA concentration dependence for multiple-turnover ligation was obtained using standard reaction buffer at ionic strengths of 150 and 300 mm. DNA concentration dependence values of LIG1 and LIG3 were compared under the 300 mm ionic strength reaction conditions. The reactions contained 5 nm enzyme, 1 mm ATP, 20 mm Mg²⁺, and 0.02–1 μm nicked DNA substrate. Initial rates versus DNA concentration data were fit to the Michaelis–Menten equation (Equation 1).

$$\frac{V_{\text{init}}}{\left[E\right]}=\frac{k_{\text{cat}}\times \left[S\right]}{\left(K_m+\left[S\right]\right)}$$ (Eq. 1)

$$\frac{V_{\text{init}}}{\left[E\right]}=\frac{k_{\text{cat}}\times \left[{\text{Mg}}^{2+}\right]}{\left(K_m+\left[{\text{Mg}}^{2+}\right]\right)}$$ (Eq. 2)

$${\left(\frac{k_{\text{cat}}}{K_m}\right)}^{\text{ATP}}=\frac{{\left(\frac{k_{\text{cat}}}{K_m}\right)}_{\text{Max}}^{\text{ATP}}}{\frac{K_1\times K_2}{{\left[{\text{Mg}}^{2+}\right]}^2}+\frac{K_1+K_2}{\left[{\text{Mg}}^{2+}\right]}+1}$$ (Eq. 3)

Quantifying adenylylated DNA intermediate

Ligation experiments were performed under multiple-turnover conditions (5 nm LIG1 or LIG3β, 200 nm nicked DNA) in standard reaction buffer. Using LIG1 as previously described (34), the accumulation of abortive ligation intermediates was observed when free Mg²⁺ concentration was 70-fold below its respective K_Mg value. Free Mg²⁺ concentrations were calculated as described above. Accumulation of abortive ligation intermediates was investigated using 1 mm Mg²⁺, and the ATP concentration was adjusted to achieve a free Mg²⁺ concentration that was 70-fold below the individually measured K_Mg values for LIG1 and LIG3. 2 mm ATP was required to achieve 10.5 μm free Mg²⁺ in the case of LIG1, whereas 1 mm ATP was needed to achieve 98 μm free Mg²⁺ in the LIG3β containing reactions. The fraction of aborted ligation events was calculated from the concentration of intermediate (I) and product (P) formed under the free Mg²⁺-starved conditions at various points during the initial rates portion of the ligation reaction (Equation 4).

$$\text{Fraction}\hspace{0.17em}\text{abortive}\hspace{0.17em}\text{ligation}=\frac{\left[I\right]}{\left(\left[I\right]+\left[P\right]\right)}$$ (Eq. 4)

Single-turnover ligation kinetics

Single-turnover ligation kinetics were investigated using a KinTek RFQ-3 rapid mixing apparatus. Reaction times varied from 5 ms to 10 min. Experiments were performed by rapidly mixing equal volumes of 1.2 μm LIG3, and 200 nm nicked DNA substrate to generate 600 nm enzyme and 100 nm substrate. Enzyme and substrate concentrations were varied to ensure single-turnover conditions were saturating (data not shown). For experiments investigating the magnesium dependence for adenylyl-transfer and nick-sealing steps of catalysis, ionic strength was calculated using the Debye-Hückel theory of electrolytes and held constant at 150 mm using NaCl. The samples were allowed to equilibrate at 37 °C for at least 1 min prior to each reaction. Reactions were allowed to age for predetermined times and the reactions stopped using 200 mm NaOH, because the aforementioned quench solution used for multiple-turnover ligation kinetics was not sufficient to stop catalysis at 5 ms after mixing (supplemental Fig. S6). NaOH-quenched samples were diluted 2-fold in formamide quench solution and processed as previously described (34). The observed rates of adenylyl transfer and nick-sealing were plotted as a function of Mg²⁺ concentration and fit using a hyperbolic single-site binding equation (Equation 2). The concentrations of total and free Mg²⁺ were assumed equal because of the absence of ATP in the single-turnover reactions. The value of k_{adenylylation} was calculated using the net rate constant method (k_cat = 0.55 s⁻¹).

$$\frac{1}{k_{\text{cat}}}=\frac{1}{k_{\text{adenylylation}}}+\frac{1}{k_{\text{transfer}}}+\frac{1}{k_{\text{seal}}}$$ (Eq. 5)

Author contributions

J. R. M. performed the experiments, J. R. M. and P. J. O. designed the study, analyzed the data, and wrote the manuscript.