Simulation of Vacuum UV Absorption and Electronic Circular Dichroism Spectra of Methyl Oxirane: the Role of Vibrational Effects

Abstract

Vibrationally resolved one-photon absorption and electronic circular dichroism spectra of (R)-methyl oxirane were calculated with different electronic and vibronic models selecting, through an analysis of the convergence of the results, the best compromise between reliability and computational cost. Linear-response TD-DFT/CAM-B3LYP/SNST electronic computations in conjunction with the simple vertical gradient vibronic model were chosen and employed for systematic comparison with the available experimental data. Remarkable agreement between simulated and experimental spectra was achieved for both one photon absorption and circular dichroism concerning peak positions, relative intensities, and general spectral shapes considering the computational efficiency of the chosen theoretical approach. The significant improvement of the results with respect to smearing of vertical electronic transitions by phenomenological Gaussian functions and the possible inclusion of solvent effects by polarizable continuum models at a negligible additional cost paves the route toward the simulation and analysis of spectral shapes of complex molecular systems in their natural environment.

1. Introduction

Oxirane derivatives have been extensively studied over the years^1–36 and have become a reference for theoretical and experimental methodologies developed for chiroptical spectroscopies.^37–44 However, they also show several spectral features which could not be described by too simplified theoretical models, and still represent challenging test cases for computational spectroscopy studies. In particular, for methyl oxirane and trans-2,3-dimethyl oxirane the electronic and vibrational absorption and circular dichroism spectra recorded in the gas phase^8,13,14,45 or low-temperature matrices^1,31 allow for direct comparison with theoretical results emphasising anharmonic and/or vibronic effects, without broadening or other perturbations by an environment. For vibrational spectroscopies, an excellent agreement has been demonstrated for both band positions and infrared (IR) intensities, combining the harmonic Coupled Cluster (CC) contributions with anharmonic effects computed by methods based on density functional theory (DFT).³² Theoretical studies of vibrational circular dichroism (VCD) are more challenging, as in addition to the electric moments involved in the IR intensities also the magnetic moments are required.^37,46 However, recent simulations of fully anharmonic VCD spectra, based on the CC/DFT force field in conjunction with DFT property surfaces has led to remarkable agreement with experimental data,⁴³ highlighting also improvements in relative band ratios due to variational inclusion of resonant terms. Similarly, for electronic spectra, accurate computations of rotatory strengths needed for electronic circular dichroism (ECD) are more challenging than vertical electronic energies or electric transition dipole moments, in terms of both quantum mechanical (QM) model and basis set convergence.^38,47,48 Moreover, inclusion of vibrational effects is often mandatory for reliable simulation of ECD spectra as demonstrated by the spectrum of dimethyl oxirane, the overall line shapes of which are due to cancellation of positive and negative vibronic transitions from close-lying electronic states.²¹ Hence, inclusion of anharmonic and/or vibronic effects is often as important as improvement of the level of applied electronic structure theory beyond DFT level. Thus, oxirane derivatives still represent non-trivial cases, and due to their small size allow for comparison of more demanding computational models with cost-effective ones, to critically analyze the latter and provide practical recipes toward feasible computational protocols applicable also to larger systems.

In this work we will focus on vacuum UV (VUV) absorption and electronic circular dichroism spectra of (R)–methyl oxirane (RMO, Figure 1), analyzing in detail the computational aspects relevant for vibronic spectra simulations. In this context, issues of accurate modelling of excited state potential energy surfaces and corresponding transition moments, by DFT and its time-dependent extension (TD-DFT),^49,50 will be addressed focusing on the choice of the exchange-correlation (xc) functional and basis set convergence, taking as reference available experimental data^8,14 and accurate post-Hartree-Fock computations. Moreover, we will consider models of different sophistication aimed at the simulation of absorption and ECD spectral line-shapes, as implemented in the virtual multi-frequency spectrometer (VMS)^42,51,52 developed by some of us and allowing userfriendly access to the latest developments of computational spectroscopy.^{30,48,53–58} The advantages of a dedicated graphical interface (VMS-draw),⁵⁹ facilitating direct comparison with experiment and analysis of computational outcomes will also be highlighted.

Figure 1.

The sceletal sctructure of (R)–methyl oxirane (left) and a three-dimensional ball-and-stick model (right).

This paper is organized as follows: first the details of the computational strategy are described in Section 2. Then the vertical electronic excitations computed at different levels of theory are benchmarked (section 3.1), afterwards the dependence of the spectral line shape on the basis set used for the computation of excited state properties are investigated (section 3.2). In section 3.3 the absorption and ECD spectra of the first excited electronic state simulated using different levels of approximations for the vibronic transitions, including temperature and anharmonic effects, are discussed. The total absorption spectrum is analyzed and compared to experiment in section 3.4 for one-photon absorption and afterwards also for electronic circular dichroism (section 3.5). Finally Section 4 gives some general conclusions and perspectives.

2. Computational Strategy

The small size of (R)-methyl oxirane (RMO) permits to compare state-of-the-art computationally demanding methods with cost-effective ones, in order to check the reliability of the latter for the study of larger systems.

Concerning electronic structure calculations, our aim is to further validate a DFT/TD-DFT methodology in conjunction with medium-sized basis sets. In this respect we have resorted to the CAM-B3LYP^60,61 xc-functional, well known for providing a balanced description of properties for both ground and excited electronic states.^62–65 The remarkable accuracy of ground state equilibrium structures, harmonic frequencies and anharmonic corrections delivered by the CAM-B3LYP functional in conjunction with double and triple-ζ basis sets (SNSD^66,67 and aug-cc-pVTZ⁶⁸) has been confirmed for methyl oxirane by comparison with the best-theoretical estimates and experimental data.³² Moreover, TD-DFT/CAM-B3LYP computations have shown to provide correct description of Rydberg and charge transfer states,^69,70 representing significant improvements over the standard B3LYP⁷¹ global hybrid functional concerning oscillator and rotatory strengths,^48,72 for several systems including also RMO, once coupled with basis sets of at least double-ζ plus polarisation quality with diffuse functions on heavy atoms.⁴⁸ All these issues are of particular relevance for the simulation of vibrationally resolved VUV and ECD spectra.

In the present work, CAM-B3LYP and TD-DFT/CAM-B3LYP computations are performed in conjunction with effective double- and triple-ζ basis sets (SNSD and SNST, respectively), which have been built in the framework of the SNS^66,67 and the N07^67,73–75 families, aiming at cost-effective computations of spectroscopic properties of medium-to-large molecular systems. These basis sets have been extensively tested for the reliable prediction of excited-state properties,^48,76 including rotatory strengths and transition dipole moments.⁴⁸ The performance of SNS basis sets is compared with the standard 6-31+G* and 6-31++G** Pople⁷⁷ basis sets along with a series of augmented correlation consistent basis sets by Dunning,⁶⁸ up to the quintuple-ζ quality, denoted aug-cc-pVXZ (X = D, T, Q, 5). The TD-DFT/CAM-B3LYP results, are also compared with the benchmark post-Hartree-Fock computations at the “Equation-of-Motion Coupled-Cluster Singles and Doubles” (EOM-CCSD)^78–82 level, employing basis sets up to quadruple-ζ quality.

First, the ground state equilibrium geometry of (R)–methyl oxirane optimized at the CAM-B3LYP/SNST level, enforcing tight convergence criteria, shows a very good agreement with the semi-experimental structure from Ref.32 The CAM-B3LYP/SNST equilibrium structure has then been used for the computation of vertical excited state properties, at the TD-DFT/CAM-B3LYP and EOM-CCSD levels of theory, with all basis sets described above. Moreover, for selected QM approaches, excited state data required for the simulation of vibronic spectra (energy gradients, equilibrium geometries, vibrational frequencies) have also been computed at the TD-DFT/CAM-B3LYP level in conjunction with selected basis sets.

All vibronic computations have been performed making use of an integrated time-independent/time-dependent framework, which is described in detail in Refs.^30,48,57 This approach can be applied to one-photon absorption and emission (OPA/OPE), electronic circular dichroism (ECD), circularly polarized luminescence (CPL)⁴² and Resonance-Raman spectra,^58,83 making use of models of different sophistication.⁸⁴ Vertical models (vertical gradient (VG) or Vertical Hessian (VH)) employ the same reference geometry for both initial and final state (the equilibrium geometry of the initial state for absorption spectra), i.e. focus on the region corresponding to the most intense transitions, while the equilibrium geometry of the final state is extrapolated. Within adiabatic models (Adiabatic Shift (AS) or Adiabatic Hessian (AH)), the focus is on the equilibrium structure of the final state, and the spectral features close to the 0-0 transition involving the vibrational ground states of two electronic states. For semi-rigid systems both types of approaches provide similar results, while in non-rigid systems anharmonic effects enhance the differences between them.^84–87 It is noteworthy, that computation times of the vibronic part are comparable for all models, so the overall computational costs are determined by the level of electronic structure theory required to describe the PES of the final (excited) state. The ground state PES is computed at the same level of theory in all cases, i.e. DFT/CAM-B3LYP. In fact, AH (and VH) approaches require Hessians of excited states, which are computationally very intensive. Moreover, for both AH and AS models additional problems related to the excited state optimisation might arise. Furthermore, the VG model is identical for different sets of coordinates (Cartesian and curvilinear).⁸⁶ This strict equivalence explains the better performance of the VG model with respect to its AH counterpart (in Cartesian coordinates) for systems where initial and final states are significantly different^85,86 and AH computations require internal coordinate approaches for a reliable comparison with experimental data (see for instance Ref.86,88,89 and references therein). Finally, the VG approach represents a feasible route to simulation of absorption spectra in large energy ranges encompassing several excited electronic states. Concerning transition dipole moments, the so-called Franck-Condon approximation^90,91 assumes that they retain their equilibrium values during the transition. While this model is sufficiently accurate in most cases (in particular for fully-allowed transitions) for weakly-allowed or dipole-forbidden transitions it can be corrected by inclusion of a linear variation of transition dipole moments with respect to normal coordinates, as done by Herzberg and Teller (HT).⁹² The HT effects might become very important for ECD spectra due to the relationship between the transition intensity and the dot product of two different transition dipole moments (electric and magnetic), whose relative orientation thus becomes an additional factor to be taken into account. For instance, even when both electric and magnetic moments are large, the overall intensity might be almost negligible whenever their relative orientations are nearly orthogonal.⁴⁸

Finally, the general harmonic procedure described above can be corrected for anharmonicity, in both the ground and excited electronic states. Starting from anharmonic computations for the ground state, performed for example within second order vibrational perturbation theory (VPT2)^56,93,94 (see Ref.66 for detailed discussion) and making use of the Duschinsky⁹⁵ transformation, it is possible to derive mode-specific anharmonic corrections to be applied for excited state wavenumbers.⁹⁶

In order to obtain spectral line-shapes the theoretical VUV and ECD stick spectra, including all relevant vibronic transitions, have been convoluted by means of Gaussian distribution functions with Full-Width at Half-Maximum (FWHM) ranging from 0.01 eV to 0.1 eV. The former FWHM has been applied to highlight vibronic features masked in experimental data, while the latter value has been used for purposes of a direct vis-à-vis comparison with broad features of the reference experimental spectra. The simulated VUV and ECD spectra have been obtained in the 7-9 eV range by summing up the contributions from all electronic transitions. All computations were performed using the GAUSSIAN09 package.⁹⁷ A new graphical user interface (VMS-Draw)⁵⁹ was employed to analyze the outcome of vibronic computations in detail by investigating shift vectors (K), closely-related to Huang-Rhys (HR) factors⁹⁸ (the squares of the components of the excited state gradient normalized with respect to the corresponding initial-state vibrational frequency), Duschinsky matrices (J) and plots of vibrationally resolved electronic spectra.

3. Results and Discussion

3.1. Vertical Excitations

Let us start with a comparison of vertical purely electronic excitation energies (VE), oscillator strengths (f) and rotatory strengths (R), computed with different electronic structure methods and basis sets. Although the VE up to the eighth excited electronic state are given, in the discussion of rotatory strengths we will focus on the first four states, which agree well with available experimental results for ECD spectra in the gas phase.^8,14 All these excitations correspond to excitations from n(O), a lone pair orbital on oxygen, to R(3s), R(3p) or R(3d) Rydberg type orbitals.

The results of post-Hartre-Fock computations with the EOM-CCSD model^78–82 and basis sets of double- to quadruple-ζ quality are reported in Table 1. At this level of theory, the excitation energies are essentially converged with the aug-cc-pVTZ basis set (322 basis functions), with differences below 0.07 eV with respect to aug-cc-pVQZ computations (596 basis functions). All other basis sets (except the smallest 6-31+G* one) underestimate excitation energies by 0.05-0.3 eV. The VE computed with the SNST basis set (194 basis functions) show improved agreement, with discrepancies reduced below 0.2 eV, at only slightly larger computational cost than the SNSD basis set (158 basis functions). The oscillator strengths obtained with all basis sets agree quite well with each other, except for the smallest 6-31+G* one. Much larger differences between basis sets are observed for the rotatory strength, which in the length-gauge formulation, reported in Table 1, exhibits in general faster basis set convergence than its velocity-gauge counterpart.⁴⁷ Since methyl oxirane is chiral, the reliable predictions of the sign and magnitude of rotatory strengths are crucial for simulations of ECD spectra. In this respect the basis sets convergence is essentially achieved at the aug-cc-pVTZ level, the differences with respect to aug-cc-pVQZ results being always lower than 0.25 cgs. The results obtained with the SNST basis set never deviate by more than 1.0 cgs from the aug-cc-pVQZ reference, while larger discrepancies are observed for SNSD. We can conclude that the SNST basis set can be recommended as the best compromise between cost and reliability for EOM-CCSD computations delivering results essentially on pair with aug-cc-pVTZ ones at significantly reduced cost (40% less basis functions), potentially allowing for accurate post-Hartee-Fock excited state computations for larger molecular systems.

Table 1.

Vertical electronic excitations (VE in eV), oscillator strengths (f) and Rotatory strengths (R in cgs computed within the length gauge) for (R)–methyl oxirane computed with EOM-CCSD and basis sets ranging from 6-31+G* to aug-cc-pVQZ.

	6-31+G*			6-31++G**			aug-cc-pVDZ			aug-cc-pVTZ			aug-cc-pVQZ			SNSD			SNST
	VE	f	R	VE	f	R	VE	f	R	VE	f	R	VE	f	R	VE	f	R	VE	f	R
S1	7.47	0.023	-18.74	7.15	0.015	-18.65	7.18	0.013	-18.11	7.36	0.012	-17.50	7.43	0.012	-17.35	7.19	0.014	-19.39	7.24	0.013	-18.10
S2	7.55	0.017	-4.05	7.53	0.011	-2.34	7.50	0.015	-4.81	7.63	0.015	-4.85	7.68	0.015	-4.81	7.52	0.015	-4.19	7.48	0.018	-5.85
S3	7.93	0.012	4.71	7.63	0.021	9.50	7.64	0.019	10.15	7.81	0.016	9.37	7.88	0.016	9.12	7.67	0.021	11.31	7.71	0.017	9.82
S4	8.22	0.032	9.52	7.84	0.025	7.77	7.85	0.022	7.53	8.02	0.022	7.02	8.09	0.021	6.86	7.89	0.023	7.95	7.93	0.025	6.85
S5	8.38	0.006	12.77	8.09	0.005	11.19	8.07	0.005	10.82	8.20	0.005	10.57	8.25	0.005	10.46	8.14	0.005	11.06	8.15	0.005	11.43
S6	8.72	0.035	-14.00	8.60	0.010	-2.19	8.53	0.015	-4.90	8.62	0.021	-11.03	8.65	0.022	-12.97	8.61	0.009	-5.61	8.54	0.023	-14.65
S7	8.85	0.016	21.93	8.65	0.010	0.64	8.59	0.024	-10.66	8.69	0.013	0.02	8.73	0.010	14.34	8.66	0.010	11.62	8.62	0.021	20.37
S8	8.94	0.037	-10.04	8.69	0.061	-9.70	8.61	0.034	9.22	8.70	0.032	6.84	8.75	0.031	-5.89	8.69	0.058	-12.55	8.67	0.026	-7.20

Going from EOM-CCSD to density functional theory, the TD-DFT/CAM-B3LYP results are reported in Table 2. All basis sets (except 6-31+G*) agree for excitation energies within 0.1 eV, with the aug-cc-pVXZ series fully converged at the triple-ζ level. Concerning oscillator strengths the same conclusions as for the EOM-CCSD apply. Interestingly, for the rotatory strengths, the Dunning basis sets show slower convergence at the TD-DFT than at the EOM-CCSD level. While the SNST results show very good agreement with their aug-cc-pV5Z counterparts, with average differences lower than 0.8 cgs, thus outperforming all double-ζ basis sets, which show discrepancies larger than 1.5 cgs in several cases.

Table 2.

Vertical electronic excitations (VE in eV), oscillator strengths (f) and Rotatory strengths (R in cgs computed within the length gauge) for (R)–methyl oxirane computed with TD-CAM-B3LYP and basis sets ranging from 6-31+G* to aug-cc-pV5Z.

	6-31+G*			6-31++G**			aug-cc-pVDZ			aug-cc-pVTZ			aug-cc-pVQZ			aug-cc-pV5Z			SNSD			SNST
	VE	f	R	VE	f	R	VE	f	R	VE	f	R	VE	f	R	VE	f	R	VE	f	R	VE	f	R
S1	7.48	0.014	-16.49	7.15	0.014	-19.38	7.14	0.011	-17.49	7.16	0.010	-16.32	7.16	0.009	-15.89	7.15	0.009	-15.50	7.18	0.011	-18.83	7.20	0.010	-16.96
S2	7.57	0.022	-8.59	7.51	0.011	-3.16	7.49	0.014	-5.95	7.49	0.015	-6.85	7.48	0.016	-7.15	7.46	0.016	-7.37	7.51	0.015	-5.48	7.47	0.018	-7.87
S3	7.92	0.010	3.13	7.60	0.019	9.23	7.57	0.017	9.18	7.58	0.015	8.88	7.58	0.015	8.79	7.57	0.014	8.71	7.62	0.019	10.53	7.65	0.014	9.23
S4	8.13	0.032	12.47	7.76	0.024	8.93	7.74	0.021	8.44	7.74	0.019	7.63	7.74	0.019	7.32	7.73	0.018	7.01	7.80	0.021	8.77	7.82	0.024	7.71
S5	8.19	0.005	11.44	7.89	0.007	11.60	7.88	0.007	10.89	7.88	0.007	10.70	7.87	0.006	10.54	7.87	0.006	10.35	7.92	0.007	11.05	7.95	0.007	10.79
S6	8.52	0.034	-11.85	8.37	0.009	0.80	8.34	0.008	1.01	8.32	0.009	0.77	8.31	0.010	-0.40	8.30	0.012	-1.98	8.39	0.009	0.11	8.37	0.021	-10.91
S7	8.66	0.011	20.42	8.45	0.041	-22.14	8.40	0.036	-19.57	8.38	0.037	-19.55	8.36	0.034	-18.02	8.34	0.030	-15.99	8.45	0.033	-18.37	8.44	0.016	1.29
S8	8.73	0.038	-10.69	8.51	0.018	5.38	8.45	0.022	8.03	8.43	0.016	9.56	8.42	0.016	10.31	8.39	0.016	10.39	8.51	0.028	8.59	8.47	0.028	5.98

Comparing the EOM-CCSD and TD-DFT/CAM-B3LYP results, both methods give very similar excitation energies for the Pople and SNS basis sets. That is not the case for the Dunning basis sets, for which all TD-DFT/CAM-B3LYP results yield excitation energies very similar to the EOM-CCSD/aug-cc-pVDZ ones, so by about 0.1-0.25 eV lower than EOM-CCSD/aug-cc-pVQZ. Concerning rotatory strengths, the absolute values of the corresponding basis sets usually differ between 1.0 and 3.0 cgs, but the general trends are the same. Finally, the prediction of reliable rotatory strengths becomes very challenging for higher excited states, in particular S₇ and S₈. In the absence of unequivocal experimental data in this energy range, it is difficult to asses the accuracy of the different computational models. It is, however, noteworthy that, also in this case, the SNST basis set yields qualitatively similar results (positive band) at EOM-CCSD and TD-DFT/CAM-B3LYP levels, while the aug-cc-pVTZ and aug-cc-pVQZ basis set predicts bands of positive and negative sign, respectively. Thus the SNST basis set represents a good compromise between computational effort and accuracy not only for TD-DFT but also for EOM-CCSD computations.

In summary, linear-response TD-DFT in combination with the CAM-B3LYP xc-functional yields reliable results compared to EOM-CCSD, at least for the lower excited states, which are the focus of the present study. Comparison with the experiment is postponed to the next sections, in which experimental and computed spectral line shapes are analyzed.

3.2. Basis Set Dependence of Spectral Line Shapes

Before discussing in detail the individual spectra computed with different vibronic models, let us investigate the dependence of the spectral line shape on the size of the basis set, in view of increasing cost of underlying excited state computations. To this end, we resort to a vertical framework, starting from the simplest vertical gradient model, for which only TD-DFT gradients at the ground state equilibrium structure are required, along with the frequency computations for the latter. All spectra reported in Figure 2 have been computed using the same data for the ground state (CAM-B3LYP/SNST), while the excited state properties (i.e. the analytical excited state gradients) were calculated at the TD-CAM-B3LYP level in conjunction with aug-cc-pVXZ (X=D-5) and SNST basis sets. For the sake of comparison, the vertical excitation energy has been kept the same, namely at the TD-CAM-B3LYP/SNST value.

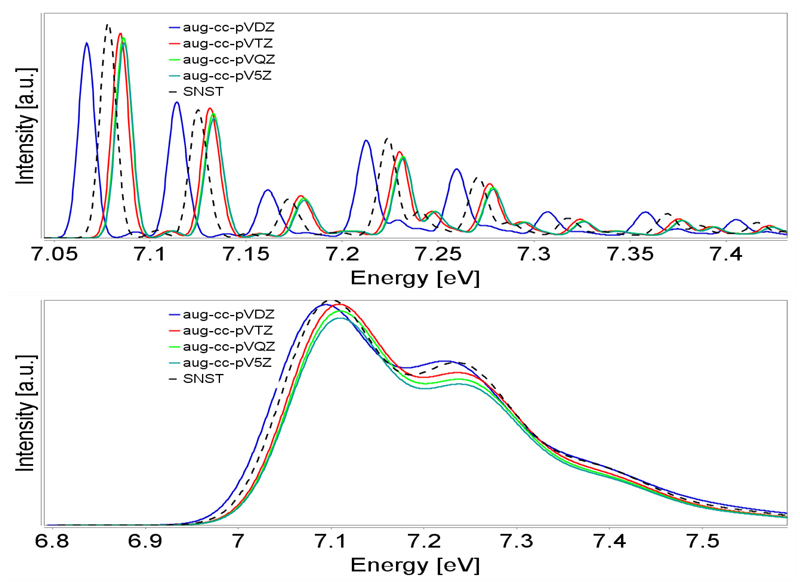
Figure 2.

The S₁ ← S₀ absorption spectra of RMO, computed at VG|FC/TD-CAM-B3LYP level and basis sets up to aug-cc-pV5Z quality. Spectra convoluted by Gaussian distribution functions with a FWHM of 0.01 eV (upper panel) and 0.1 eV (lower panel).

We start with a comparison of the medium-resolution spectra, shown in the upper panel of Figure 2, in which single vibronic transitions have been convoluted with Gaussian functions with FWHM of 0.01 eV. All computed spectra show rather similar line shapes, having, essentially, just shifted absolute energy ranges. Considering that the vertical electronic excitation energies have been set equal and that the VG model does not account for zero-point vibrational energy (ZPVE) differences between initial and final state, this shift can only originate from non negligible changes of vectors (estimated differences between the ground and excited state equilibrium structures) computed with different basis sets. The largest difference is observed between the aug-cc-pVDZ and aug-cc-pVTZ basis set, with all the bands produced by the former computations shifted by about 0.02 eV towards lower energies. On the other hand, the difference between triple- and quadruple-ζ, and especially between quadruple- and quintuple-ζ basis sets is negligible, showing that basis set convergence is essentially reached at the aug-cc-pVTZ level. As already observed for VEs, the SNST basis set yields results closer to aug-cc-pVTZ than to the aug-cc-pVDZ basis set, with an energy shift of only 0.01 eV. A more detailed analysis shows that the shape of the smaller peaks (or shoulders) on the high-energy wing of the major peaks, present in spectra obtained using the aug-cc-pVTZ to aug-cc-pV5Z basis sets, is much better reproduced with the SNST than with the aug-cc-pVDZ basis set. On top of that, in the higher energy region above 7.4 eV, SNST approaches even more closely the peak shapes obtained with the aug-cc-pV5Z basis set.

The small discrepancies highlighted above for medium-resolution spectra are essentially removed, if we compare low-resolution spectra as the ones obtained with a convolution ten times broader (FWHM = 0.1 eV), shown in the lower panel of Figure 2. In fact, all low-resolution spectra show only two peaks at about 7.1 and 7.25 eV as well as a shoulder (at about 7.4 eV) that are very similar both in position and (relative) intensities. This indicates that for comparison with experimental spectra which show broad, not-well resolved bands (corresponding to a broad convolution), the basis set dependence of the simulated spectra is essentially negligible. The same holds true for the VG|FC ECD spectrum, which is very close to its OPA counterpart, except for sign inversion of the intensities, due to the negative value of the rotatory strength.

Going from the VG to the vertical Hessian model, allows to investigate basis set effects on the excited state frequencies computed at TD-CAM-B3LYP level (in all cases at the CAM-B3LYP/SNST equilibrium geometry of the ground state). In the cases of S₁ ← S₀ transition of RMO the VH|FC OPA and ECD spectra show again the same line-shapes (just mirrored) and as Herzberg–Teller terms have a negligible impact on the results, only the Vertical Hessian Franck-Condon Herzberg-Teller (VH|FCHT) ECD spectrum is shown and discussed.

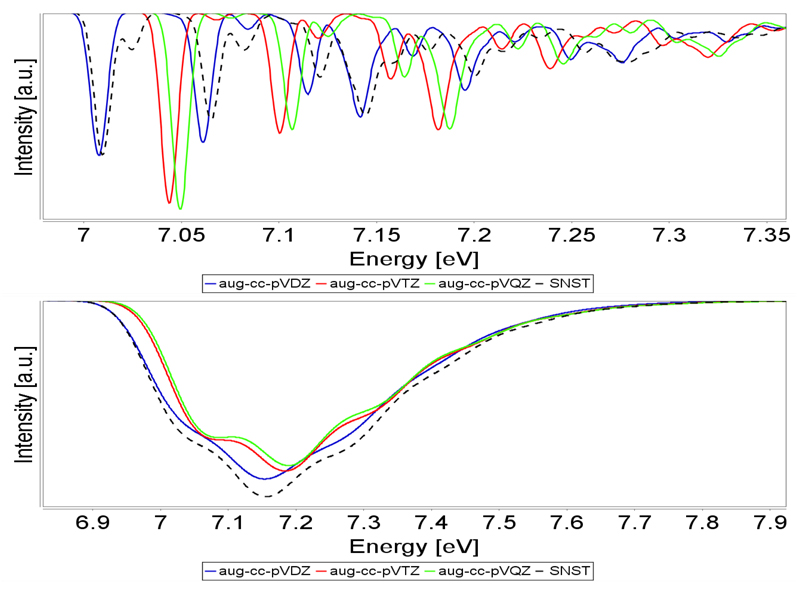
Le us start again by discussing the medium-resolution spectra shown in the upper panel of Figure 3, where the aug-cc-pVDZ and SNST basis sets give nearly the same results concerning peak positions on an absolute energy range, shifted by only about 0.05 eV with respect to the aug-cc-pVTZ and aug-cc-pVQZ basis sets, which yield essentially the same spectrum (with an energy shift lower than 0.01 eV). However, comparing SNST and aug-cc-pVQZ results, one can see that the shape of the spectra is very similar, i.e. all important features are well reproduced with just an energy shift of about 0.05 eV. This shift, which is larger than those observed using the VG model, can be mainly attributed to the variation of the ZPVE computed with different basis sets. Thus it can be concluded that smaller basis sets reproduce number and intensities of bands with respect to larger ones, but may show some discrepancies in their relative positions. For the low-resolution spectra, obtained with a broader convolution (FWHM of 0.1 eV) and reported in the lower panel of Figure 3, once again the aug-cc-pVDZ and SNST basis sets on the one hand, and the aug-cc-pVTZ and aug-cc-pVQZ basis sets on the other, provide similar results. Yet, an important point to underline concerning ECD spectroscopy is that all basis sets lead to similar results also with inclusion of HT terms, which are particularly sensitive to the magnitude and sign of the rotatory strength derivatives (and orientation of electric and magnetic moments).48

Figure 3.

The S₁ ← S₀ ECD spectra of RMO, computed at VH|FCHT/TD-CAM-B3LYP level and basis sets up to aug-cc-pVQZ quality. Spectra convoluted by Gaussian distribution functions with a FWHM of 0.01 eV (upper panel) and 0.1 eV (lower panel).

3.3. Simulation of spectral line shapes: S₁ ← S₀ Electronic Transition

3.3.1. Vertical and Adiabatic Models

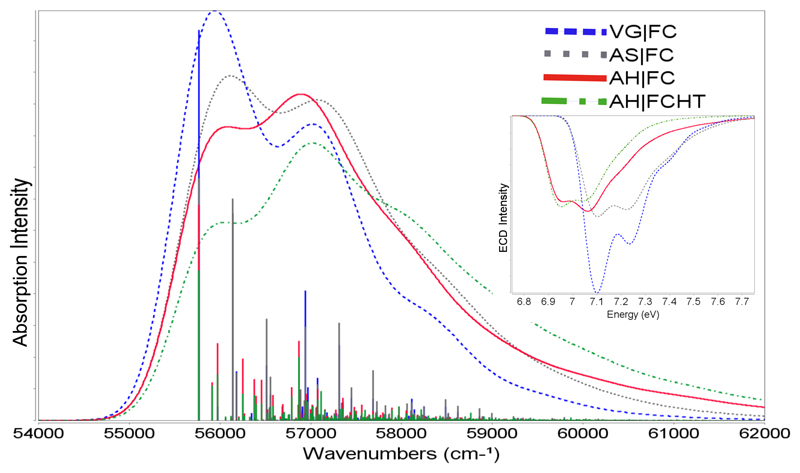
Let us now analyze vibrationally resolved one-photon absorption and ECD spectra of RMO computed with different models with specific reference to the lowest excited electronic state as selected test case. At first, we will analyze spectra at 0K, without considering explicit temperature effects, which corresponds to including only transitions originating from the ground vibrational level of the initial electronic state. We will employ only the simplest vertical model, Vertical Gradient, in which harmonic frequencies and normal modes of both electronic states are considered equal to those of the initial state at its equilibrium geometry. The more refined Vertical Hessian model (which takes into account frequency and normal mode variations between the two states) cannot be systematically employed due to the presence (especially for high-energy excited electronic states) of several imaginary harmonic frequencies. The VG approach is then compared to adiabatic models, namely Adiabatic Shift and Adiabatic Hessian, in which changes in the excited state structure, as depicted in Figure 4 (AS, AH) and possibly also in normal modes and frequencies (AH only) are taken into account. For the AH model we have also examined different approximations for the calculation of the electronic transition dipole moment, starting from the zero-order Franck-Condon approximation and proceeding to include first-order corrections via the Herzberg–Teller terms (FCHT).

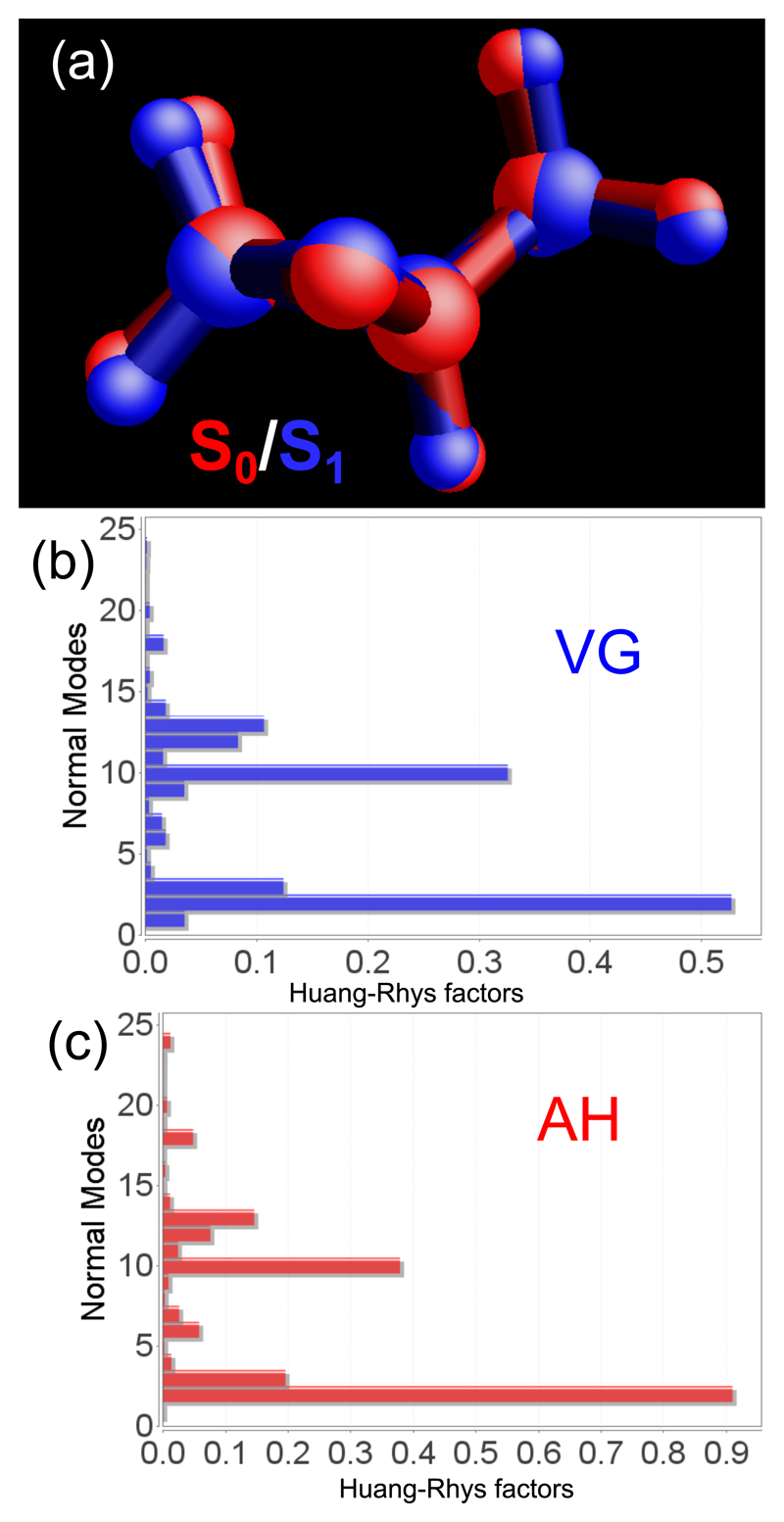
Figure 4.

Structures of methyl oxirane (a) in the electronic ground state (red) and first excited state (blue), along with the Huang-Rhys factors simulated within Vertical-Gradient (b) and Adiabatic-Hessian (c) models.

The VG|FC, AS|FC, AH|FC and AH|FCHT spectra are depicted in Figure 5, for both OPA and ECD. In order to facilitate the comparison of the spectral line-shapes in the main panel the VG|FC and AS|FC spectra have been shifted by -1264 cm⁻¹ and -1110 cm⁻¹, respectively, to match the transition origin of AH|FC at 55760 cm⁻¹. At variance, the ECD spectra (inset of Figure 5) are presented considering the 0-0 transition as resulting from the respective computations, i.e. 57024 cm⁻¹ for VG|FC and 56870 cm⁻¹ for AS|FC. These energy differences for the 0-0 transition are due to the fact that in the VG and AS models the vibrational frequencies (hence the ZPVE) in the final state are considered equal to those of the initial state, whereas in the AH model the harmonic frequencies (hence the ZPVE) of the final state are calculated explicitly. Moreover, for VG the excited state structure is extrapolated by assuming a parabolic form of the PES. Here, both VG and AS yield 0-0 shifted to the higher energies, but in more general terms it is not possible to assess a priori the sign of the shifts due to neglect of ZPVE changes and the PES extrapolation, which are system-dependent.

Figure 5.

The S₁ ← S₀ absorption (main panel) and ECD (inset) spectra of R-methyl oxirane computed using VG|FC, AS|FC, AH|FC, and AH|FCHT approaches. Spectra convoluted by Gaussian distribution function with a FWHM of 0.1 eV. OPA VG and AS spectra have been shifted by -1264 cm^–1 and -1100 cm^–1, respectively, in order to match the 0-0 transition of AH models.

It can be noted that all low-resolution spectra show rather similar patterns with two main bands and a shoulder in the high-energy wing. These spectral features agree in the energetic position of maxima but the relative intensities vary slightly among different models. For the VG|FC approximation the most intense band is the 0-0 transition, while the next band at + 373 cm⁻¹ is dominated by a <0|2¹ > transition, in which the normal mode υ₂ corresponds to a methyl bending, followed by its <0|2² > overtone at +747 cm⁻¹. The third most intense band at + 1172 cm⁻¹ corresponds to the <0|10¹ > transition (υ₁₀ is the CH₂ wagging), followed by a band at + 1546 cm⁻¹, during which modes υ₂ and υ₁₀ are excited simultaneously. Most of the remaining intense transitions are due to overtones and combination bands involving these two modes.

The band positions obtained from the AS|FC model are very close to those of their VG|FC counterparts, but the relative intensities show some minor variations. For instance the 0-0 transition is marginally more intense than the next band (<0|2¹ >), which falls at + 373 cm⁻¹. The intensities of the next three bands, corresponding to the first overtone of mode υ₂, the <0|10¹ > transition and the simultaneous excitation of modes υ₂ and υ₁₀ become significantly closer when going from VG|FC to AS|FC computations. The following bands are again dominated mainly by overtones of modes 2 and 10 or their simultaneous excitations, occasionally along with other modes and their intensity decreases exponentially.

Going from the AS to the AH model, the band positions approach more closely their correct energies. The 0-0 transition is still the most intense single vibronic transition, but the first broad band is slightly less intense with respect to the band at about + 1200 cm⁻¹. This effect cannot be attributed to a single vibronic transition, but rather to the cumulative increase of intensity in this spectral region. Duschinsky effects lead to the presence of two rather intense bands at + 147 cm⁻¹ and + 207 cm⁻¹, which correspond to the excited state vibrations υ₁’ and υ₂’ derived from mixing of the corresponding ground state modes (CH₃ torsion and bending, respectively). The other single most intense transition is still <0|10¹ > , at + 1102 cm⁻¹. In addition, there are also increased contributions from (<0|4¹ >) and (<0|5¹ >) at + 484 cm⁻¹ and + 610 cm⁻¹, respectively, with modes υ₄’ and υ₅’ originatig from CO asymmetric stretching and ring CC stretching with small contributions form other modes, in particular υ₂. The most significant vibronic contributions to the next, very broad, band are due to the simultaneous excitation of modes 2, 4, 5, and 10. Inclusion of Herzberg–Teller terms has a negligible effect on the main vibronic transitions, but the variation of relative intensities leads to a modified spectral shape, with the first band less intense with respect to its AH|FC counterpart.

In summary, the 0-0 transition gives rise, according to all models, to the most intense peak with methyl bending as well as CH₂ wagging progressions playing the most important role in determining the shapes of all the spectra. Indeed, the υ₂ and υ₁₀ modes show significantly larger Huang-Rhys (HR) factors⁹⁸ which are related to the probability of specific electronic-vibrational transitions in the Franck-Condon regime. Figure 4 highlights also the similarities of vibronic contributions between VG|FC and AH|FC models. Therefore, despite some modifications in relative intensities, it is evident that all approaches lead to rather similar band shapes with the second pronounced band at about + 1200 cm⁻¹, a shoulder in the high frequency wing at about + 2600 cm⁻¹, and essentially the same spectral envelope. These findings are of particular importance in connection with the simulation of overall spectra encompassing several electronic states, where the sum of single electronic transitions lead to the final spectral line-shape. As a matter of fact, in order to obtain AH or AS spectra, the excited state equilibrium geometry needs to be determined, which may cause severe problems especially for high-energy excited electronic states. In the present case, after extensive investigation of the excited state potential energy surfaces of RMO, only three distinct minima were found (as confirmed by all positive vibrational frequencies) and identified as the first three excited electronic states in the Franck–Condon region. These problems are related to the complex pattern of excited state potential energy surfaces, with many close-lying and intersecting states. In such cases, non-adiabatic effects, which are not included in the present model built within the Born-Oppenheimer approximation, may play a role. Possible extensions would require non-adiabatic vibronic models, which are presently feasible only for limited-dimensionality approaches, like, e.g., the 3×3 linear vibronic model applied for the case of trans-2,3-dimethyl oxirane.²² Moreover, HT effects, which turned out to be negligible for the S₁ ← S₀ transition, might be enhanced for the higher excited states. Having these limitations in mind, the simulation of OPA and ECD spectra encompassing broader energy ranges turns out to be feasible only within the VG|FC model.

3.3.2. Temperature Effects

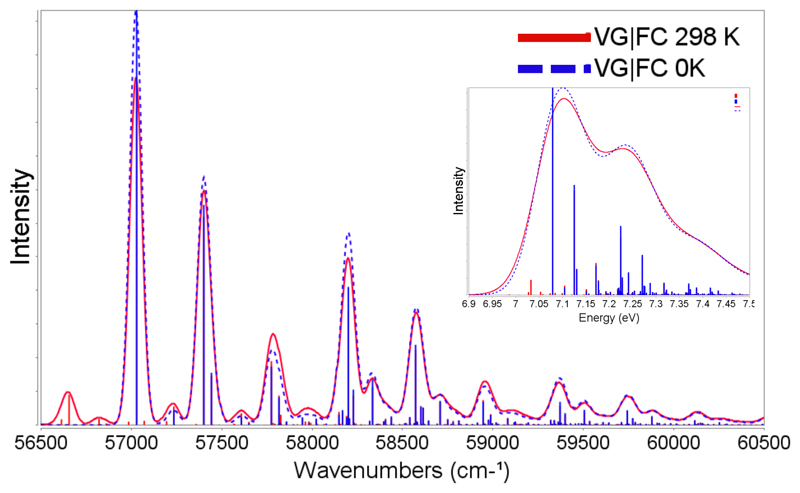
As mentioned above, all spectra so far have been simulated at 0 K, whereas experimental spectra were recorded at room temperature. At absolute zero, all molecules are in their vibrational ground states, i.e. all transitions originate from this initial state. At higher temperatures a certain amount of molecules is in excited vibrational states, populated according to Boltzmann statistics, and thus some transitions which originate from these states become possible (the so-called hot bands). Although temperature effects are most naturally included by Time-Dependent FC approaches,³⁰ the low-size of RMO allows to obtain well converged results also by a time-independent route, including all the vibrational initial states showing Boltzmann populations at 298.15 K of at least 1% of the fundamental state. Comparison between VG|FC spectra at room temperature and at 0 K (Figure 6) shows that temperature effects are only marginal in the high-energy range with just very small intensity decreases for most bands. The largest difference is the presence of an additional small peak at energies lower than the 0-0 transition (about - 374 cm⁻¹) in the room temperature spectrum. This band is mainly due to transitions from the first excited level of υ₂ of the ground electronic state to the vibrational ground state of the final electronic state (< 2¹|0 >). Similar effects have been observed for the spectra simulated with adiabatic models.

Figure 6.

The S₁ ← S₀ absorption spectrum of methyl oxirane computed using VG|FC approach at 0 K and 298.15 K. Spectra convoluted by Gaussian distribution function with a FWHM of 0.01 eV (main panel) and 0.1 eV (inset).

3.3.3. Anharmonicity Effects

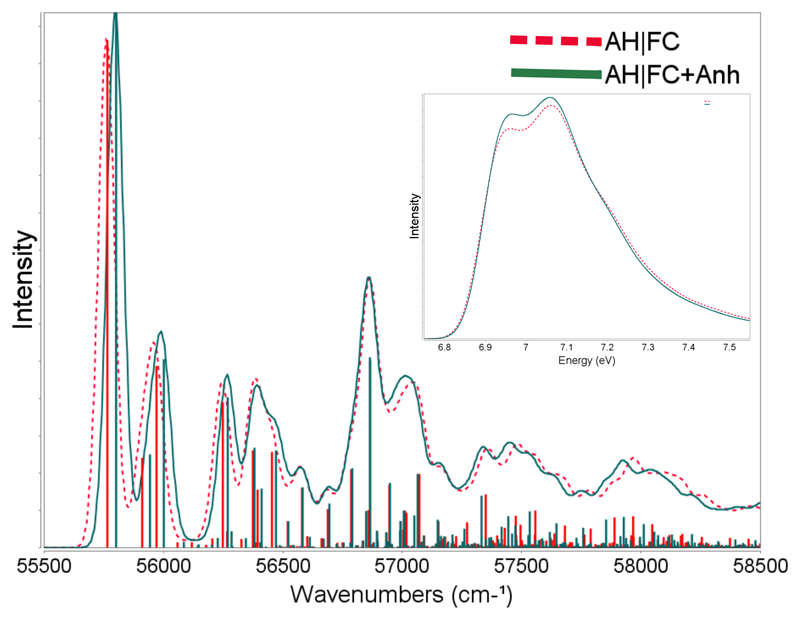
The computations of Franck-Condon factors and resulting vibrationally resolved electronic spectra are performed within the harmonic approximation; however, in order to achieve better agreement with experimental results (in particular for higher resolution spectra^99,100) it is often mandatory to apply some corrections for anharmonicity. In this work this task is performed by applying anharmonic corrections only to the initial and final state energies. The ground state anharmonic frequencies were obtained in the framework of the second-order vibrational perturbation approach,^101,102 by the generalized approach developed by Barone and Bloino.^54–56,94 In the present work the best-estimated (CC/B2PLYP) theoretical values from Ref.,³² have been used to derive mode-specific scaling factors for the ground electronic state (the ratios between anharmonic and harmonic frequencies, i.e. $a_k=\frac{v_k}{w_k}).$ In a next step, these factors were used to obtain excited state scaling factors,⁹⁶ $a{\prime }_k={\displaystyle {\sum }_i{\left(J_{ik}\right)}^2·a_i}$ where J_ik are elements of the Duschinsky matrix J. AH|FC harmonic and ’anharmonic’ spectra (see Figure 7) are very similar both at high (FWHM of 0.01 eV) and low (FWHM = 0.1 eV) resolution, showing only small energy shifts. In particular, the 0-0 transition is 0.005 eV higher in energy in the anharmonic spectrum, while the band positions (with respect to the 0-0) of the main transitions are shifted to lower energies (for instance: <0|2¹ > at + 201 cm⁻¹ and <0|10¹ > at + 1064 cm⁻¹). These small anharmonic effects observed for RMO can be traced back to the fact that the ’vibronically active’ normal modes do not show large intrinsic anharmonicties. The situation could be, of course, different for systems for which the most intense vibronic transitions are related to strongly anharmonic vibrations, for instance X-H stretches. Nevertheless, at least for RMO, the harmonic approximation leads to nearly the same results – especially when a broad convolution is used – and is thus sufficient for a reliable prediction of OPA and ECD vibronic spectra.

Figure 7.

The S₁ ← S₀ absorption spectrum of methyl oxirane computed using AH|FC harmonic and anharmonic models (at 0K). Spectra convoluted by Gaussian distribution function with a FWHM of 0.01 eV (main panel) and 0.1 eV (inset).

3.4. Absorption Spectrum: comparison with experiment

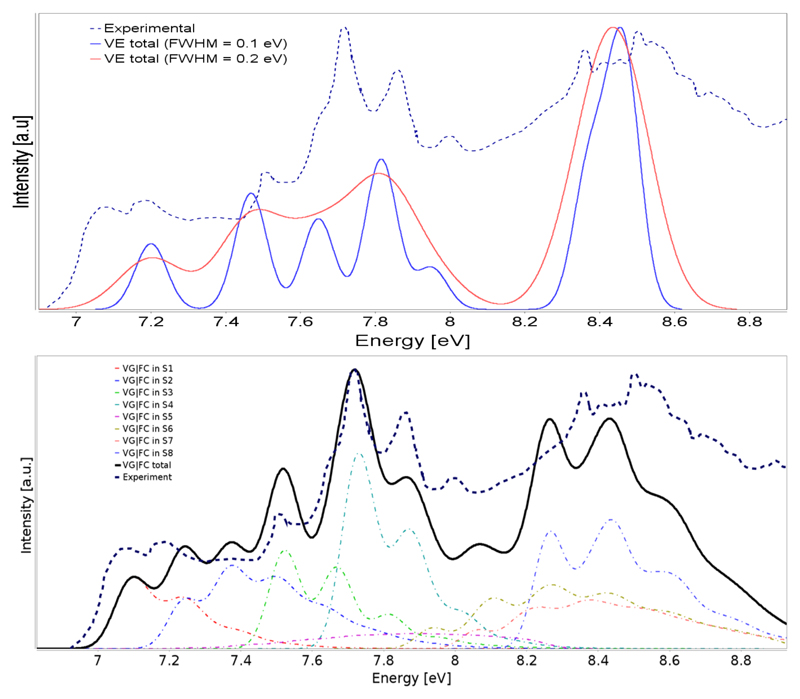
For absorption spectra we will refer to the experimental data in the 7-9 eV energy range, as reported in Refs.^8,14 Thus, we will consider all eight excited electronic states encompassing this energy range, with their sum referred to as the “total absorption spectrum”. Since the different electronic states are not very far apart in energy it is expected that the vibrational progressions of the different peaks “overlap”, defining the final shape of the spectrum. First of all, the pure vertical electronic spectrum is compared to experiment in the upper panel of Figure 8. The calculated electronic spectrum, where the first eight vertical excitations were considered (as calculated with TD-DFT in combination with the CAM-B3LYP functional and the SNST basis set), was convoluted with a FWHM of 0.1 eV and 0.2 eV. Experimental and theoretical spectra have been normalized with reference to their respective spectral maxima. It is clear that none of the theoretical band-maxima obtained in this way matches the experimental spectrum well. The position of S₁ at about 7.2 eV is clearly overestimated and no further fine structure is visible. The next four excited states S₂ – S₅ somehow match the next bands at 7.4-8 eV, but the correct intensity of its features is not reproduced nor is any shoulder visible. The last broad band present in the simulated spectrum around 8.5 eV is actually composed of three electronic transitions, but, at variance with experiment, it does not show any fine structure. Moreover, further band-width increase does not improve the agreement with experiment: for instance already with FWHM of 0.2 eV the double-maxima feature of band at 7.7-7.8 eV is removed.

Figure 8.

The theoretical and experimental⁸ VUV spectra of RMO. For theoretical spectra eight electronic states (S₁ – S₈) have been considered, upper panel vertical electronic spectrum, lower panel the VG|FC spectrum convoluted with FWHM of 0.1 eV.

The situation is very different for the spectra computed at the VG|FC//TD-DFT/CAM-B3LYP/SNST level (at 298 K) reported in the lower panel of Figure 8. It becomes now evident that the first band at about 7.1 eV is mainly due to vibronic transitions into the first excited electronic state, while both S₁ and S₂ contribute to the next band at about 7.2 eV. Moreover the S₂ band is very broad, encompassing an energy ranging between 7.2 and 7.8 eV, and adding its intensity to the transitions into S₁, S₃ and S₄, but does not show characteristic features. In turn the bands at 7.52, 7.67 and 7.81 eV, derive from the vibrational progressions of transitions to the third and fourth excited electronic states, with the most intense peak at about 7.8 eV, corresponding primarily to the excitation to S₄. VG|FC spectra reproduce well also the high-energy region, concerning both the rough band-shape and the relative intensities of the spectrum, while the excitation energies are slightly underestimated. This can be traced back to the TD-DFT/CAM-B3LYP/SNST vertical energies, which are about 0.3 eV lower than best estimated values at EOM-CCSD/aug-cc-pVQZ level, for S₆-S₈. Thus a better agreement is obtained by hybrid models with the vertical excitation energies computed at higher levels of theory, like e.g EOM-CCSD (employed here), ADC(3)^103,104 or MRCI.¹⁰⁰ Moreover, the underestimation of the intensity of the VG|FC spectra in the 7.9-8.2 eV region, where several excited electronic states overlap, can be attributed to non-adiabatic effects. However, it should be noted that the simplest VE model shows vanishing intensity in this spectrum range. Overall, the failure of the VE model is clearly related to diverse vibrational progression for different electronic transitions (very broad or narrow bands), which can not be accounted for by a single broadening factor. These results highlight that the overall agreement with experiment of the simple VG|FC//TD-DFT/CAM-B3LYP/SNST model is fairly good, and actually much better than the pure electronic spectrum at only slightly increased computational cost. More specifically, for the TD-DFT approach a single excited state computation of analytical energy derivatives (forces) is essentially twice as expensive as the corresponding VE one, and this factor is independent on the system size. So, the increased cost of electronic structure computations required for the simulation of VG|FC spectra can be estimated as 2×n, with n corresponding to the number of bright excited states in the studied spectral range.

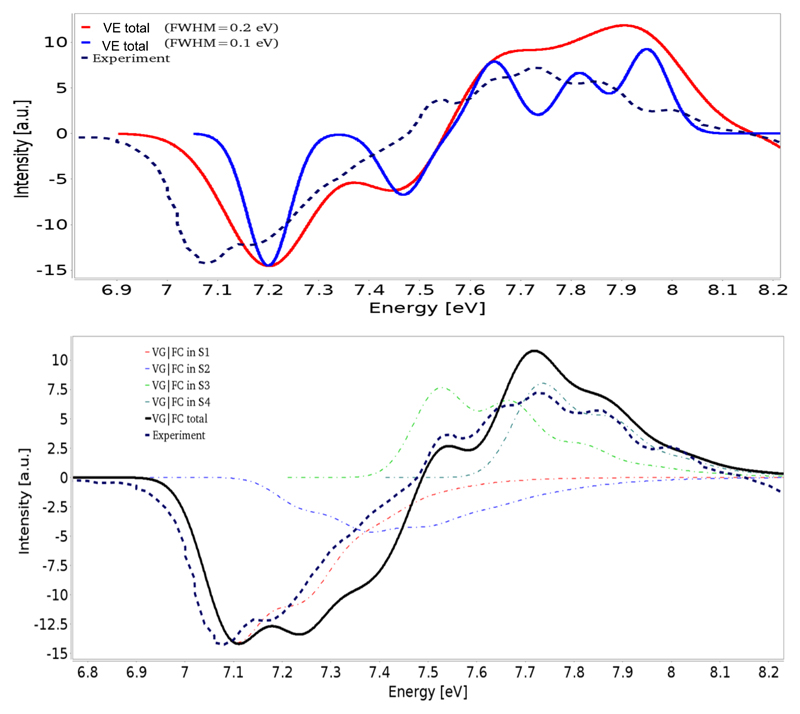
3.5. Electronic Circular Dichroism: comparison with experiment

For the evaluation of the simulated ECD spectrum of RMO, we will refer to the experimental data in the 7-8.2 eV energy range, so covering the first four excited electronic states. The analysis of ECD spectra of RMO at energies higher than 8.5 eV faces against some difficulties for both experiment and computational approaches. In fact both ECD spectra reported in Refs.^8,14 show only weak features, but their relative intensities do not match well, the ECD signal from 8.4 to 9 eV oscillates from negative to positive⁸ or it is exclusively negative.¹⁴ Thus these experimental data are not adequate for validation of theoretical approaches, which in turn show large deviations of rotatory strengths, for the higher lying excited electronic states, as discussed previously, and new measurements would be welcome to solve this issue.

Let us start again with the spectrum obtained by the conventional VE approach, i.e. with the computed vertical rotatory strengths convoluted with Gaussian broadening functions with FWHMs of 0.1 and 0.2 eV. The VE model shows significant shortcomings for ECD, yielding a negative band at about 7.5 eV, so in the spectral range where experiment shows inequivocally a positive signal. This artifact is due to the second excited state, which shows a rather large negative value of R (about -7 cgs). A similar situation has previously been reported for dimethyl oxirane (DMO),¹³ which for long time puzzled the comparison between experiment and theory, casting severe doubts on the accuracy of electronic structure computations. The discrepancies have been explained once vibrational effects had been taken into account by Neugebauer and co-workers²¹ by an approach similar to the VG|FC model.

Indeed, also for RMO the VG|FC model leads to a qualitative agreement with the experimental spectrum. The excitation energy of S₁ at about 7.1 eV is only slightly overestimated, but the line shape is reproduced rather well, with two negative bands spaced by about 0.1 eV. After these two peaks the (absolute value of the) intensity is overestimated, yet the simulated spectra change sign at about 7.5 eV, in line with experimental findings, and the following positive band matches well its experimental counterpart concerning both position and intensity. The next broad band from 7.7 eV onward matches well the experimental features, although the overall intensity is somewhat overestimated. In summary, it is clear that negative features are related essentially to S₁, and positive ones to S₃ and S₄. The transition to the second excited electronic state is characterized by a very broad band, as already observed for the OPA spectrum, but for ECD this effect is even more important as the large negative value of its rotatory strength is ’smeared out’ over large energy range and essentially cancelled out at higher energies. As a result there is no negative band at 7.5 eV, and the VG|FC spectrum matches very well its experimental counterpart. This situation is very similar to that found for trans-2,3-dimethyl oxirane^21,22 where large negative rotatory strength (about -17 cgs) is associated to the very broad vibronic band (2B state) encompassing 7-8 eV energy region. Also in this case the negative band cancels out with several other electronic transitions showing positive values of R, so the VG|FC simulations correctly predict the spectral shape, at variance with the simplest VE model. However, for DMO the agreement between the VG|FC model and experiment significantly worsens at higher energies, with improved results provided by non-adiabatic vibronic model with non-linear HT effects.²² For both RMO and DMO experimental ECD spectra at higher energies show rather low intensity, at variance with large positive and negative R for several excited states. These results further confirm the challenges in the simulations of oxiranes ECD spectra where the overall line-shapes result from cancellation of vibronic transitions of opposite signs. However, the good agreement between the VG|FC model and experiment observed at lower energies for RMO (and DMO^21,42) and the qualitative improvement with respect to the VE model highlights the reliability of the underlying theoretical approach and the importance of vibronic effects for meaningful comparison with experimental measurements.

4. Conclusions & Outlook

In this work vibrationally resolved one-photon absorption and electronic circular dichroism spectra of (R)–methyl oxirane were calculated with different electronic and vibronic models, critically analyzed and compared to their experimental counterparts. To this end, TD-DFT computations employing the CAM-B3LYP functional and the SNST basis set were validated with reference to EOM-CCSD vertical excitation energies and Rotatory strengths employing several basis sets up to aug-cc-pVQZ. The good agreement between both computational models (especially for energetically low-lying excited states) shows that the TD-CAM-B3LYP/SNST approach represents a very good compromise between reliability and computational cost. Different vibronic models (VG, VH, AS and AH) were analyzed and compared for the lowest electronic transition, discussing their limitations and possible extensions, finally validating the use of the simplest VG model for the simulation of overall VUV absorption and ECD spectra.

The VG|FC OPA and ECD spectra, with all underlying electronic structure computations performed at the TD-CAM-B3LYP/SNST level showed a very good agreement with experiment, regarding both band positions and fine structure. It is noteworthy that it was crucial to take into account realistic band envelopes, which vary strongly between transitions (broad vs narrow peaks), and can only be reproduced by considering explicitly vibrational structure of single electronic transitions. Most importantly, the S₂ ← S₀ transition encompasses an energy range of over 0.6 eV, so that its contributions add to the intensity of OPA peaks for the S₁, S₃ and S₄ transitions. On the other hand, the overall ECD spectral shapes result from a delicate cancellation of positive and negative vibronic bands.

In our opinion these results underline the importance of vibronic effects for a direct comparison of computed and experimental electronic absorption and circular dichroism spectra, providing also a cost-effective solution applicable to rather large molecular systems (at least tens of heavy atoms) at a computational cost increasing with respect to the simplest vertical computations by a factor of 2 times the number of electronic states to be considered. Moreover, improved results can be obtained by coupling DFT/TD-DFT vibrational analyses with calculations of vertical transition energies and dipoles by post-Hartree-Fock approaches. More advanced vibronic approaches, taking into account Duschinsky rotation, Herzberg-Teller and anharmonic effects, can be, of course, advocated when the focus is on single electronic transitions, in particular the lowest ones, with reference to high- or medium-resolution spectra.

Figure 9.

The theoretical and experimental⁸ ECD spectra of RMO. For theoretical spectra four electronic states (S₁ – S₄) have been considered, upper panel vertical electronic spectrum, lower panel the VG|FC spectrum convoluted with FWHM of 0.1 eV.