Design and Test of Magnetic Wall Decoupling for Dipole Transmit/Receive Array for MR Imaging at the Ultrahigh Field of 7T

Abstract

Radio-frequency coil arrays using dipole antenna technique have been recently applied for ultrahigh field magnetic resonance (MR) imaging to obtain the better signal–noise-ratio (SNR) gain at the deep area of human tissues. However, the unique structure of dipole antennas makes it challenging to achieve sufficient electromagnetic decoupling among the dipole antenna elements. Currently, there is no decoupling methods proposed for dipole antenna arrays in MR imaging. The recently developed magnetic wall (MW) or induced current elimination decoupling technique has demonstrated its feasibility and robustness in designing microstrip transmission line arrays, L/C loop arrays and monopole arrays. In this study, we aim to investigate the possibility and performance of MW decoupling technique in dipole arrays for MR imaging at the ultrahigh field of 7T. To achieve this goal, a two-channel MW decoupled dipole array was designed, constructed and analyzed experimentally through bench test and MR imaging. Electromagnetic isolation between the two dipole elements was improved from about −3.6 dB (without any decoupling treatments) to −16.5 dB by using the MW decoupling method. MR images acquired from a water phantom using the MW decoupled dipole array and the geometry factor maps were measured, calculated and compared with those acquired using the dipole array without decoupling treatments. The MW decoupled dipole array demonstrated well-defined image profiles from each element and had better geometry factor over the array without decoupling treatments. The experimental results indicate that the MW decoupling technique might be a promising solution to reducing the electromagnetic coupling of dipole arrays in ultrahigh field MRI, consequently improving their performance in SNR and parallel imaging.

1 Introduction

Ultrahigh magnetic resonance imaging (MRI) could provide a high signal–noise-ratio (SNR) and a high contrast in human imaging [1–10]. Dipole arrays, which have a simple structure, have been proposed to increase the B₁ field penetration and SNR gain in the deep area of human head or body and have demonstrated promising capability in human imaging at ultrahigh magnetic fields [11, 12]. It is known that the electromagnetic (EM) coupling among coil elements is critical to SNR and parallel imaging performance [13–19] of coil arrays. Due to the unique structure of the dipole antennas, the traditional decoupling methods, such as element overlapping [20] and L/C decoupling network [21–28], face challenges and are not readily feasible for dipole transmit/receive (transceiver) arrays. Insufficient decoupling among dipole array elements in current dipole array designs has negatively impacted the imaging performance. The recently developed magnetic wall (MW) or induced current elimination (ICE) decoupling technique has demonstrated its superior capability of decoupling resonant elements in various coil arrays, including microstrip transmission line (MTL) arrays [29–32], traditional L/C loop arrays [33–35], and monopole arrays [36]. For the MW decoupling method, an independent resonator/antenna was used to eliminate the current induced in the resonant elements by EM coupling. This method does not need physical connection between coil elements and should be promising for dipole transceiver arrays.

In this study, we aim to test the feasibility and investigate the performance of the MW decoupling method in the dipole array. A two-channel MW decoupled dipole array was designed and constructed for 7T MR imaging. As a comparison, we also constructed a 7T dipole array without any decoupling treatments. Bench test, MR imaging and geometry factor results obtained from the two dipole arrays demonstrate that MW decoupling method is capable of obtaining a high degree of EM decoupling between dipole elements and provides enhanced imaging performance at the ultrahigh field of 7T.

2 Materials and Methods

2.1 Design and Construction of the Two-Channel Dipole Array Without and With Magnetic Wall Decoupling Method

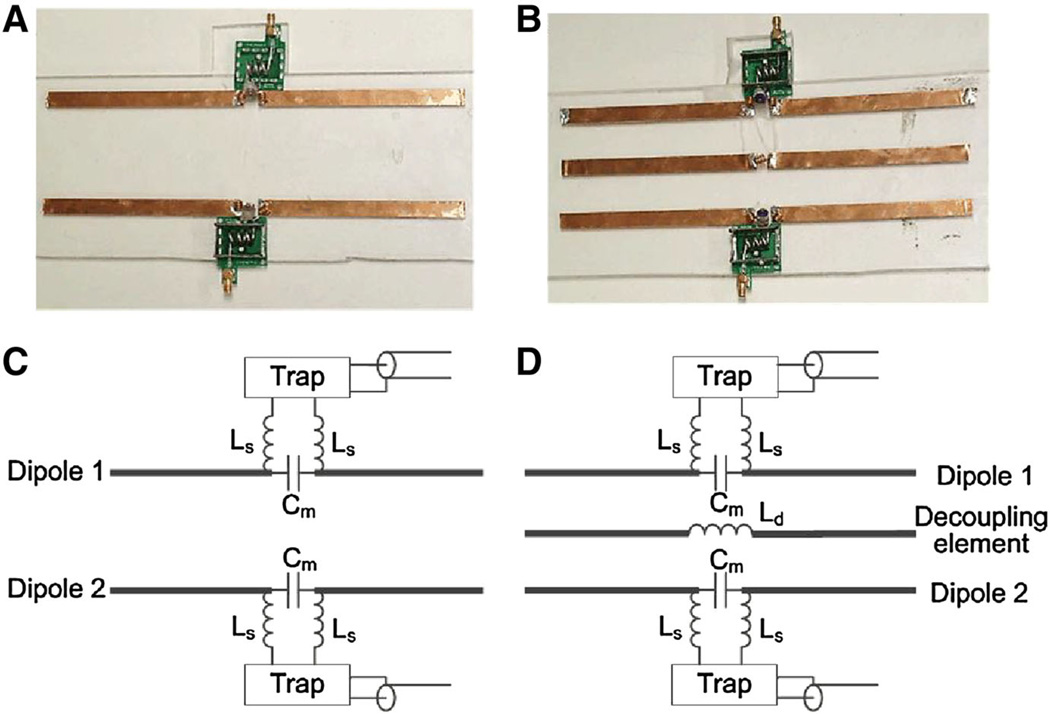
Figure 1 shows the photographs and sketches of the constructed two-channel dipole arrays without decoupling treatments and with the MW decoupling method. A simple dipole antenna is equal to 1/2 wavelength of the electromagnetic wave in the free space [37]. At 297.2 MHz, the Larmor frequency of our 7T MRI scanner, the corresponding length of a simple dipole antenna is about 50 cm, which is a little longer and not suitable for most MRI applications. In this study, the length of each dipole was shortened by two series inductors (Ls, as shown in Fig. 1c, d) to 26 cm, which is suitable for human head MR imaging. Each series inductor was wound with a copper wire of four turns and 4.0 mm in diameter. The distance between two dipole elements of each array is 7 cm. Each dipole element was matched to 50 Ω with a trimmer capacitor Cm [12], and was tuned to 297.2 MHz by slightly changing the gap between the turns of Ls. Traditional L/C trap circuits were applied to remove the possible “cable resonance” of each dipole element at the high frequency of 297.2 MHz.

Fig. 1.

Photographs and sketches of the two-channel dipole arrays without decoupling treatments (a and c) and with magnetic wall decoupling (b and d)

For the magnetic wall decoupled two-channel dipole array, an independent dipole antenna, referred to as the decoupling element, was symmetrically placed between the two dipole elements to reduce the EM coupling. The decoupling element had the same length as the dipole element and was shorted by a series inductor Ld, referred to as the decoupling inductor (Fig. 1d). The decoupling inductor was wound with a copper wire of three turns and 4.0 mm in diameter. The resonance frequency of the decoupling element is about 400 MHz. All conductor strips described above were made of the 10 mm-wide copper tape (3 M, St, Paul, MN).

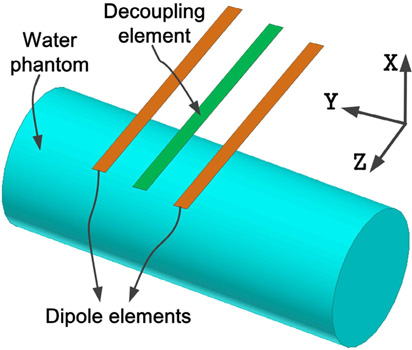
Figure 2 shows the position of the water phantom vs. dipole arrays. A cylindrical water phantom with an outer diameter of 16 cm and a length of 37 cm was placed 2.5 cm below the dipole arrays. The EM parameters of the water phantom were measured by a dielectric probe (DAK-12, Speag, Switzerland): conductivity σ = 0.59 S/m; relative permittivity ε_r = 78.

Fig. 2.

Position of the dipole arrays vs. the water phantom

2.2 Bench Tests and MR Imaging Experiments

Scattering (S−) parameters, including reflection coefficient (S₁₁) and transmission coefficient (S₂₁), of the dipole elements with and without the MW decoupling method were measured with an Agilent E5071C network analyzer. The reflection coefficient measurements were also used to calculate the coil’s Q value.

To demonstrate the decoupling performance of the MW decoupling method for dipole arrays, gradient recalled echo (GRE) images and geometry factor maps on the water phantom using the two dipole elements with and without the decoupling element were measured, calculated and compared. The slice chosen for MR imaging was in the central transverse plane of the dipole elements. The imaging acquisition parameters were: flip angle (FA) = 25°, TR = 100 ms, TE = 10 ms, field of view (FOV) = 250 × 171 mm², matrix = 256 × 176, slice thickness = 5 mm, bandwidth = 320 Hz/pixel, number of excitation (NEX) = 1. The MRI experiments were performed on a whole-body MRI scanner (7T MAGNETOM, Siemens Healthcare, Erlangen, Germany). During the experiments, one dipole element was used for both transmission and reception with the other one terminated with 50-Ω load. The geometry factor maps were calculated using an radio-frequency coil array design and analysis software Musaik (Speag, Switzerland).

3 Results

3.1 Bench Test Results

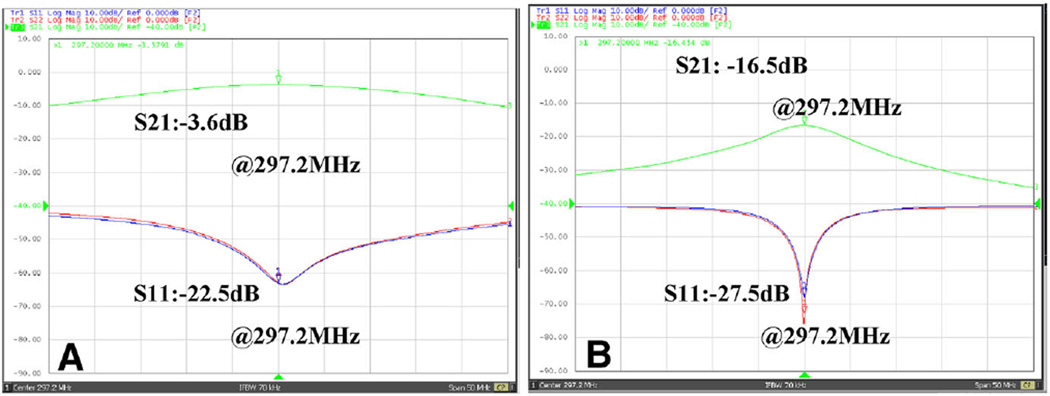
The reflection coefficient (S₁₁) of each dipole element is better than −20 dB, as shown in Fig. 3. For the dipole array without decoupling treatments, the transmission coefficient S₂₁ between two dipole elements was only about −3.6 dB (Fig. 3a). It is worth noting that no obvious peak split was observed even when the coupling achieved −3.6 dB, which is unlike near-field coil such as loop or MTL coil. The average unloaded Q value (Q_UL) and Q value loaded with water phantom (Q_L) of a single element were about 13.3 and 9.5, respectively.

Fig. 3.

Measured S₁₁ and S₂₁ plots vs. frequency of two dipole elements loaded with the water phantom. a Without decoupling treatments. b With the MW decoupling method. The isolation between the two dipole elements could be reduced from about −3.6 dB to about −16.5 dB, indicating the strong decoupling capability of the MW decoupling method for the dipole array

For the MW decoupled two-channel dipole array, the length of the decoupling element was chosen the same as the dipole elements (26 cm). The transmission coefficient S₂₁ between the dipole elements could be reduced from −3.6 to −16.5 dB, as shown in Fig. 3b. The average Q_UL and Q_L of a single element were 48.1 and 29.2, respectively. Like the results of our previous work [36], the MW decoupled array exhibits higher Q value which might be due to the better decoupling performance and shielding effect of the decoupling element.

3.2 MR Images and Geometry Factor Maps

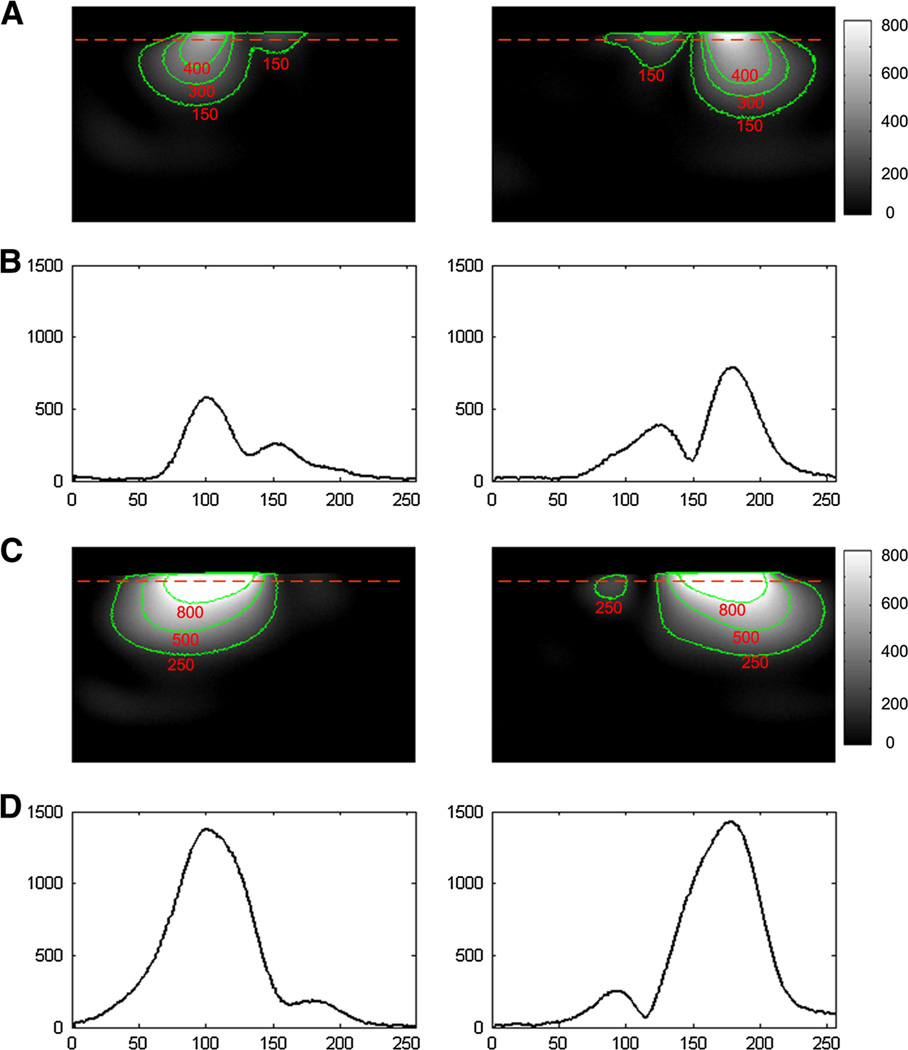
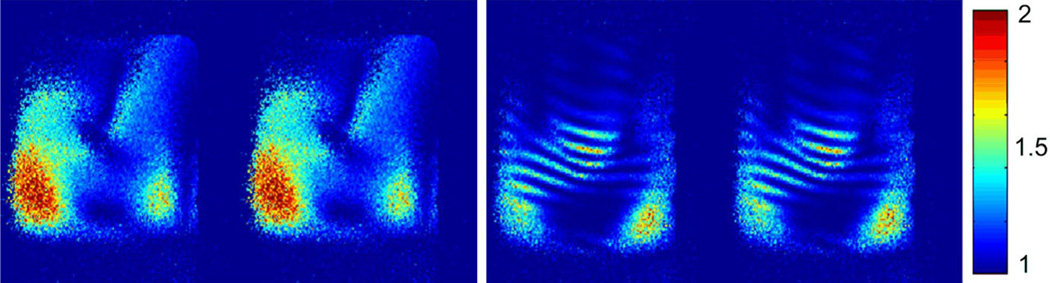
GRE images from each dipole element of the two-channel arrays were shown in Fig. 4. Figure 4a, b show the images from two coupled dipoles and the 1D profiles of the images. Figure 4c, d show the images from two MW decoupled dipoles and the 1D profile of the images. This significant decoupling effect, as obtained from the S₂₁ plots, could also be clearly observed in MR images. Well-defined image profiles of MW decoupled dipole array were obtained, indicating sufficient electromagnetic decoupling between the two elements.

Fig. 4.

GRE images from each dipole element of the two-channel array without and with the magnetic wall decoupling. a Images from two coupled dipole elements. b Profile of the red dotted line of the images in a. The S₂₁ between the two dipole antennas was about −3.6 dB, which indicates that about half of the signal power was coupled to the other element. The strong coupling between the two dipoles could also be observed from figures a and b. c Images from two MW decoupled dipole elements. d Profiles of the red dotted line of the images in c. Figures c and d show the strong decoupling performance between the two dipoles

Geometry factor maps with reduced factor (R) of two were shown in Fig. 5. The average and maximum geometry factors of the coupled dipole array are 1.14 and 3.2, respectively; whereas the average and maximum geometry factor of the MW decoupled dipole array are 1.08 and 2.4, respectively. Both average and maximum geometry factor results reveal that the MW decoupled array exhibits better parallel imaging ability, which can also be verified by the comparison of S-parameter results as described above. In parallel imaging, the SNR of accelerated images is inversely proportional to the geometry factor [14]. Therefore, the results of the geometry factor measurements suggest that better quality-accelerated images can be achieved using MW decoupled transceiver dipole array over the array without decoupling treatments.

Fig. 5.

Geometry factors of the two-channel dipole arrays without (left) and with the MW decoupling method (right) at reduction factor R = 2. The MW decoupled dipole array has better geometry factor results, indicating the image reconstruction related noise amplifications can be reduced

4 Discussions and Conclusions

The feasibility of magnetic wall decoupling technique for dipole coil arrays has been validated through bench tests and MR imaging experiments at the ultrahigh field of 7T in this study. The experimental results demonstrate that the transmission coefficient S₂₁ of the strongly coupled dipole elements is reduced from −3.6 to −16.5 dB using the MW decoupling technique. The EM isolation between the dipole elements might be further improved by optimizing the length of the MW decoupling element. Due to improved decoupling performance, the MW decoupled dipole elements demonstrate well-defined image profiles and improved geometry factors, indicating that better parallel imaging capability over the dipole array without decoupling treatments can be expected. This study has paved the way for designing MW decoupled multi-channel volume-typed dipole array for human MR imaging at ultrahigh fields.