Semiparametric Single-Index Model for Estimating Optimal Individualized Treatment Strategy

Abstract

Different from the standard treatment discovery framework which is used for finding single treatments for a homogenous group of patients, personalized medicine involves finding therapies that are tailored to each individual in a heterogeneous group. In this paper, we propose a new semiparametric additive single-index model for estimating individualized treatment strategy. The model assumes a flexible and nonparametric link function for the interaction between treatment and predictive covariates. We estimate the rule via monotone B-splines and establish the asymptotic properties of the estimators. Both simulations and an real data application demonstrate that the proposed method has a competitive performance.

1. Introduction

In modern clinical researches, the goal to achieve better outcomes as well as lower cost and burden for individual patients has generated tremendous interest in personalized medicine. Individualized treatment rules (ITRs) operationalize personalized medicine as a decision function from patient’s individual biomarkers to a recommended treatment and the optimal ITRs should be the one which maximizes clinical benefit if implemented. Specifically, if we use A to denote treatment assignment taking values of −1 and 1, X to denote all biomarker and prognostic information associated with each patient and let Y be the clinical outcome of interest (assuming large values are desirable), then an individualized treatment rule (ITR), denoted by d(x), takes a given value x of X and provides a treatment choice from {−1, 1}. Furthermore, let P^d denote the distribution of (X, A, Y ) and expectation with respect to this distribution by E^d, where the individualized treatment rule d(x) is used to assign treatments. Define the value function as V (d) = E^d(Y ). Then an optimal ITR, d₀, is a rule that has the maximal value, i.e., d₀ is the maximizer of V (d) over decision rules d.

There has been growing interest in developing valid inference methods for estimating the optimal ITRs, d₀, using clinical trial data. With trial data, it holds V (d) = E[Y I(A = d(X))/π(A|X)] [15], where π(a|X) is the known randomization probability of A = a given X, so it is easy to see d₀(x) = sign{E[Y|A = 1,X = x] – E[Y|A = −1,X = x]}, where sign(·) function is defined as sign(x) = 1 when x > 0, sign(x) = −1 when x < 0. Therefore, most of the existing methods tend to model E[Y |A = a,X = x] including the interactions between the treatment and the covariates either parametrically or nonparametrically. Such literature include likelihood-based approach [19, 18, 20], parametric Q-learning in [1], and machine learning based methods [25]. Alternatively, one can parametrically model E[Y|A = a,X = x] – E[Y|A = d₀(X),X = x] which is called A-learning as discussed in [14] and [16]. Recently, directly maximizing V (d) has been proposed using support vector machine in [26] or via robust parametric models in Zhang et al. [24]. However, all parametric methods potentially suffer from model misspecification especially when X is not low-dimensional and the optimal ITRs depends on high-order interactions among X’s. On the other hand, although the nonparametric methods such as machine-learning methods are flexible, the resulting rules are complicated so may not be interpretable in practice. The latter often comes with no rigorous inference procedures as in the parametric methods.

In this paper, we propose a semiparametric single-index model to estimate the optimal ITRs. Our model retains a flexible and nonparametric formulation of the treatment-covariate interactions but also yields a simple decision rule which only depends on a linear combination of X. Specifically, our proposal assumes the following model between Y and (X,A):

$$E[Y\mid X,A]=\mu (X)+\psi ({\beta }^{T}X)A,$$ (1)

where X is a p-dimensional covariate vector and may contain 1 as the intercept, β^TX is a single index and both μ and ψ are unknown functions. Moreover, ψ is a monotone increasing function with ψ(0) = 0. The proposed model has the following advantages in developing individualized treatment strategy. First, it provides a more flexible interaction between the covariates and the treatment as compared to the traditional parametric models, in which we allow a fully nonparametric baseline function of the covariates X, μ(X), and a close-to nonparametric interaction between the treatment A and the covariates X. Second, we can easily derive the best treatment strategy as d₀ : X – → sign(ψ(β^TX)). Since ψ is increasing, the resulting rule is practically interpretable. Moreover, if ψ(0) = 0, the above treatment strategy d₀ can be simplified as a simple rule:

$$d_0:X\to \text{sign}({\beta }^{T}X).$$

That is, only the sign of a risk score β^TX needs to be evaluated for each patient. As a separate note, single index models have been studied extensively in literature with a number of inference methods developed, including the average derivative method [5], the sliced inverse regression [12, 3, 11], the iterative average derivative method [6] and other related methods [23]. Estimating both the single index and the link function at the same time has also been studied in [9, 8, 4]. However, none of these works have considered the single index model for estimating the optimal ITRs, especially that our model (1) assumes the main effect of X, μ(X), to be fully nonparametric.

The rest of the paper is organized as follows. In Section 2, we provide a full inference procedure for the proposed semiparametric single index model. Extensive simulation studies are presented in Section 3 and a real data analysis is presented in Section 4, followed by a discussion section.

2. Inference Procedure

Note that model (1) remains the same if we replace ψ(x) by ψ(rx) for any r > 0. Therefore, for identifiability, we further require ||β|| = 1 where || · ||is the Euclidean ℓ₂-norm in R^p. Assume that data are obtained from a randomized trial with i.i.d observations (Y_i,X_i,A_i), i = 1, ..., n. The randomization probability P(A = a|X) = π(a|X) is known by the trial design.

To avoid estimating the nonparametric function μ(X) when making inference for β, we first observe that,

$$\begin{array}{l}E\left[\frac{AY}{2\pi (A\mid X)}\mid X\right]=E\left[\frac{A}{2\pi (A\mid X)}E[Y\mid A,X]\mid X\right]\\ =E[Y\mid A=1,X]/2-E[Y\mid A=-1,X]/2=\psi ({\beta }^{T}X).\end{array}$$

Therefore, a natural estimate of β is obtained by minimizing the least square, given as

$$\sum _{i=1}^n{\left\{\frac{A_i{Y}_i}{2\pi (A_i\mid X_i)}-\psi ({\beta }^T{X}_i)\right\}}^2,$$

subject to ||β|| = 1. Since ψ is an increasing function, we approximate ψ(x) using monotone B-spline basis [2, 10],

$$\psi (x)\approx \sum _{j=1}^{K_n+M}{\xi }_j{N}_j(x),{\xi }_i\le \cdots \le {\xi }_{K_n+M},$$

where N₁(x), ...,N_{K_n+M}(x) are B-spline basis, K_n is the number of interior knots with equal partition in an interval containing β^TX and M is B-spline order, i.e., for cubic B-spline, M = 4. The condition ξ₁ ≤ ⋯ ≤ ξ_{K_n+M} assures monoticity of the ψ(·) function [10]. Additionally, we impose an upper bound M_n for the summation of absolute values of all the B-spline coefficients of ψ(·) for theoretical consideration. M_n is a constant depending on n and the rate of M_n is given in Section 3. Thus, the minimization becomes

$$\begin{array}{ll}\hfill \underset{\xi ,\beta }{min}& \sum _{i=1}^n{\left\{\frac{A_i{Y}_i}{2\pi (A_i\mid X_i)}-\sum _{j=1}^{K_n+M}{\xi }_j{N}_j({\beta }^T{X}_i)\right\}}^2,\hfill \\ \hfill \text{subject}\text{to}& \Vert \beta \Vert =1,{\xi }_1\le \cdots \le {\xi }_{K_n+M},\sum _{j=1}^{K_n+M}\mid {\xi }_j\mid \le M_n.\hfill \end{array}$$ (1)

Set d = K_n + M. The objective function in (1) is quadratic in ξ and quite nonlinear in β. The constraint ||β|| = 1 is nonlinear in the elements of β. The inequality constraint in (1) is linear in ξ since it can be expressed as Bξ ≤ 0, where ξ = (ξ₁, ⋯ , ξ_d)^T and B is a (d–1) ×d matrix with B(i, i) = 1,B(i, i+1) = −1 and the rest of its entries being zero. To facilitate the implementation, we now propose an iterative estimation algorithm to solve (1). In particular, we iteratively solve β with ξ fixed at their current values, and then solve ξ with β fixed at their current values, and repeat them until the convergence criterion is met. The computation procedure can be summarized as the following.

• Step 1: Get an initial estimator β̂⁽⁰⁾. For example, we can set N_j(β^TX) = β ^TX as a linear function in (1) and compute the ordinary least squares (OLS) estimator for β. Normalize β⁽⁰⁾ such that ||β⁽⁰⁾|| = 1. Set ℓ = 0.

• Step 2: Given the initial estimates of the index values {Z_i = β̂^(ℓ)TX_i, i = 1, ⋯ , n}, minimize over ξ by solving the followng quadratic programming (QP) problem:

  $$\begin{array}{ll}\hfill \underset{\xi }{min}& Q(\xi )=\sum _{i=1}^n{\left\{\frac{A_i{Y}_i}{2\pi (A_i\mid X_i)}-\sum _{j=1}^d{\xi }_j{N}_j(Z_i)\right\}}^2,\hfill \\ \hfill \text{subject}\text{to}& B\xi \le 0\text{and}\sum _{j=1}^{K_n+M}\mid {\xi }_j\mid \le M_n.\hfill \end{array}$$ (2)

  Denote the solution as ξ̂^(ℓ).

• Step 3: Fix ξ at the current values, minimize

  $$\sum _{i=1}^n{\left\{\frac{A_i{Y}_i}{2\pi (A_i\mid X_i)}-\sum _{j=1}^d{\widehat{\xi }}_j^{(\ell )}{N}_j({\beta }^T{X}_i)\right\}}^2,\text{s.t.}\Vert \beta \Vert =1.$$

  Denote the solution as β̂^(ℓ+1). This problem can be solved using the nonlinear least squares (NLS) algorithm.

• Step 4: Set ℓ = ℓ + 1. Go to Step 2 and iterate until convergence, i.e. ||β̂^(ℓ) − β̂^(ℓ−1)|| ≤ ε (1 + ||β̂^(ℓ−1)||) and ||ξ̂^(ℓ) − ξ̂^(ℓ−1)|| ≤ ε (1 + ||ξ̂^(ℓ−1)||) for a small ε > 0, which takes value 1e-3 in our numerical studies.

In our numerical examples, we use the MATLAB’s optimization toolbox: the function quadprog() for QP in Step 2 and lsqnonlin() for NLS in Step 3. In this paper, we choose cubic B-spline for all numerical studies and real data application. Our algorithm usually converges in less than 10 iterations.

Given K_n, we choose to place the interior knots at equally-spaced sample quantile of the predictor variable, which is β^TX in this context. For example, if there are 4 interior knots, then they would be respectively at the 20th, 40th, 60th, 80th percentile. The boundary knots are naturally chosen as the minimum and maximum values of the predictor variable. During the iteration, the estimated single index β could change at each step, therefore the knots also change in the iteration. The number of knots K_n can be tuned with cross-validation. In general, 5 to 10 knots will be sufficient to have very good results.

3. Asymptotic Results

We establish the asymptotic properties of the estimators (β̂_n, ψ̂_n), including their consistency under certain metric, the convergence rates, and the asymptotic distribution of $\sqrt{n}({\widehat{\beta }}_n-{\beta }_0)$. We need the following conditions.

• (C.1)β₀ is assumed to be in the unit ball ℬ of R^p and X has a compact support. In addition, $E(X{X}^T\mid {\beta }_0^{T}X)$ is positive definite. and $E[X\mid {\beta }_0^{T}X=x]$ is kth continuously differentiable with bounded derivatives for some k > 3.
• (C.2)ψ₀ has bounded kth derivative in an open interval containing the support of ${\beta }_0^{T}X$ for some k > 3; moreover, ${\psi }_0^{\prime }(0)>0$.
• (C.3)
  $E[{\psi }_0({\beta }_0^{T}X)\mid {\beta }^{T}X]$ is continuously differentiable in β and moreover,

  $$E\left[{\nabla E[{\psi }_0({\beta }_0^{T}X)\mid {\beta }^{T}X]|}_{\beta ={\beta }_0}^{\otimes 2}\right]>0.$$

Under these conditions, we first obtain the consistency and convergence rate of (β̂_n, ψ̂_n).

Theorem 1

Under (C.1)–(C.3), we further assume K_n = C₁n_γ and M_n = C₂n^τ for some positive constants C₁, C₂ with γ > 0, τ ≥ 0, and 11γ + 9τ ≤ 1, 2τ ≤ (2k − 5)γ. Let 0 < ν < 1/2, then

$${\Vert {\widehat{\beta }}_n-{\beta }_0\Vert }^2+{\Vert {\widehat{\psi }}_n-{\psi }_0\Vert }_{L_2[a,b]}^2=o_p(n^{-1+\nu })+O_p(n^{-2k\gamma }).$$

Furthermore,

$${\Vert {\widehat{\psi }}_n-{\psi }_0\Vert }_{W^{1,\infty }[a,b]}=o_p(1),$$

where W^s,∞ is the Sobolev space consisting of functions with bounded lth derivatives for any l ≤ s. Furthermore, the Sobolev norm is defined as ||ψ|| _W^1,∞[a,b] = max_α≤1 ||ψ^(α)||_L^∞[a,b].

The asymptotic distribution of β̂_n is stated in the following theorem.

Theorem 2

In addition to (C.1)–(C.3), we assume K_n = C₁n^γ and M_n = C₂n^τ for some positive constants C₁, C₂ with γ > 1/(4k − 4), τ ≥ 0 and 11γ +9τ ≤ 1, 2τ ≤ (2k − 5)γ. Then $\sqrt{n}({\widehat{\beta }}_n-{\beta }_0)$ converges in distribution to a mean-zero normal distribution with covariance ${\mathrm{\sum }}_1^{-1}{\mathrm{\sum }}_2{\mathrm{\sum }}_1^{-1}$, where

$${\mathrm{\sum }}_1=E\left[{\psi }_0^{\prime }{({\beta }_0^{T}X)}^{2}X{X}^T\right]$$

and

$${\mathrm{\sum }}_2=E\left\{\text{Var}\left[\frac{AY}{2\pi (A\mid X)}\mid X\right]{\psi }_0^{\prime }{({\beta }_0^{T}X)}^{2}X{X}^T\right\}.$$

Based on Theorem 2, a consistent estimator for the asymptotic covariance is given by ${\widehat{\mathrm{\sum }}}_1^{-1}{\widehat{\mathrm{\sum }}}_2{\widehat{\mathrm{\sum }}}_1^{-1}$ in which Σ̂₁ and Σ̂₂ are given as follows. Then an estimator for Σ₁ is given as

$${\widehat{\mathrm{\sum }}}_1=n^{-1}\sum _{i=1}^n{\widehat{\psi }}_n^{\prime }{({\widehat{\beta }}_n^T{X}_i)}^2{X}_i{X}_i^T.$$

Since

$${\mathrm{\sum }}_2=E\left\{{\left[\frac{AY}{2\pi (A\mid X)}-{\psi }_0({\beta }_0^{T}X)\right]}^2{\psi }_0^{\prime }{({\beta }_0^{T}X)}^{2}X{X}^T\right\},$$

an estimator for Σ₂ is given by

$${\widehat{\mathrm{\sum }}}_2=n^{-1}\sum _{i=1}^n{\left[\frac{A_i{Y}_i}{2\pi (A_i\mid X_i)}-{\widehat{\psi }}_n({\widehat{\beta }}_n^T{X}_i)\right]}^2{\widehat{\psi }}_n^{\prime }{({\widehat{\beta }}_n^T{X}_i)}^2{X}_i{X}_i^T.$$

Under Theorem 1, it is clear that both Σ̂₁ and Σ̂₂ are consistent estimators for Σ₁ and Σ₂ respectively when the sample size converges to infinity. Finally, we estimate the optimal decision rule as $\text{sign}({\widehat{\beta }}_n^{T}X)$. Under such a rule, for any subject, the reward gain of using the optimal rule vs the non-optimal rule is estimated to be $2{\mathbb{P}}_n\left[\mid {\widehat{\psi }}_n({\widehat{\beta }}_n^{T}X)\mid \right]$.

4. Numerical Studies

In this section, we conduct extensive simulations to investigate the empirical performance of our proposed method. We first use three examples (Examples I–III) to compare our method with the inverse probability weighted estimator( IPWE), augmented inverse probability weighted estimator(AIPWE) in [24] and ordinary least square based on minimizing

$$\sum _{i=1}^n{\left\{\frac{A_i{Y}_i}{2\pi (A_i\mid X_i)}-{\beta }^T{X}_i\right\}}^2.$$

Finally, in Example IV, we investigate the performance of our method under model misspecification (i.e. when ψ(·) is not monotone).

We consider the model Y = μ(X) + ψ(β^TX)A + ε where X is generated uniformly from [−1, 1]^p, A is generated as −1 and 1 with equal probability 0.5 and the noise ε follows a normal distribution with mean 0 and standard deviation σ = 0.5. The four examples are:

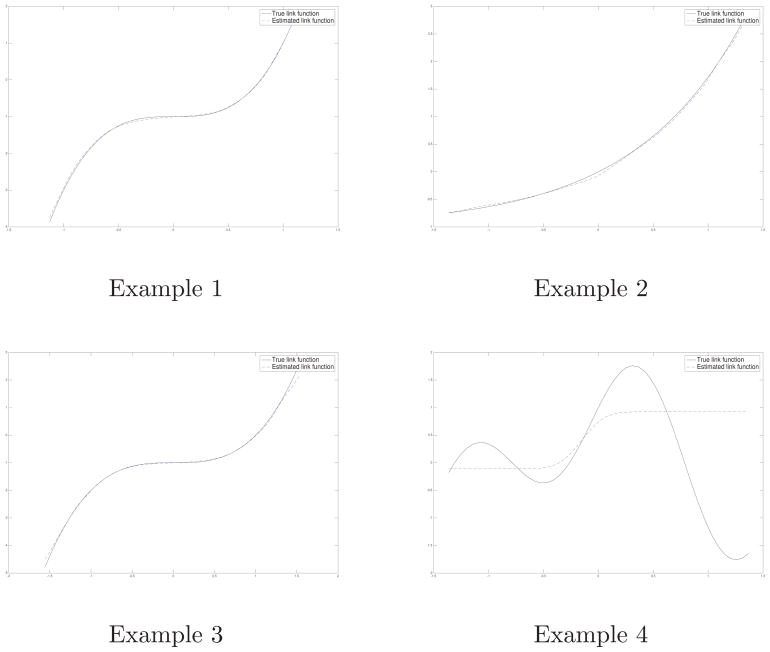
• Example I : p = 2, $\mu (X)=X_1{X}_2+X_2^2$, ψ(u) = 2u³ − 1, ${\beta }_0=\frac{1}{\sqrt{2}}{(1,-1)}^T$.

• Example II : p = 3, $\mu (X)=X_1^2+2X_1{X}_2$, ψ(u) = exp(u) − 1, ${\beta }_0=\frac{1}{\sqrt{3}}{(1,-1,1)}^T$.

• Example III : p = 4, $\mu (X)=X_1{X}_2+X_3^2$, ψ(u) = u³ − 1, ${\beta }_0=\frac{1}{\sqrt{2}}{(1,-1,1,-1)}^T$.

• Example IV : p = 3, $\mu (X)=X_1{X}_2+X_3^2$, ψ(u) = cos(2u) + sin(4u), ${\beta }_0=\frac{1}{\sqrt{3}}{(1,-1,1)}^T$.

To evaluate the estimation performance of the single index coefficient, we report its bias and the mean squared error MSE(β) = average over replications of ||β̂− β₀||²/p. To evaluate the estimation performance of the link function, we report its mean squared error MSE(ψ) = average over replications of $\frac{1}{n}{\sum }_{i=1}^n{\Vert \widehat{\psi }({\widehat{\beta }}^T{X}_i)-\psi ({\beta }_0^T{X}_i)\Vert }^2$. To evaluate the accuracy of a treatment assignment rule sign(β^TX), we calculate the percentage of making correct decisions (PCD), i.e. $1-\frac{1}{2n}{\sum }_{i=1}^n\mid \text{sign}(\widehat{\psi }({\widehat{\beta }}^T{X}_i))-\text{sign}(\psi ({\beta }_0^T{X}_i))\mid$. We also study the behavior of the value function estimates. Based on the estimated rule, the value function can be estimated as $\frac{1}{n}{\sum }_{i=1}^n\frac{Y_{i}1(A_i=g_i)}{P(A_i=g_i\mid X_i)}$, where g_i is the estimated rule. We compare the proposed method with [24] in terms of parameter estimates, percentage of making correct decisions (PCD) and value function estimates.

From Tables 1–3, we observe that our method shows better results compared with the inverse probability weighted estimator (IPWE) and the augmented inverse probability weighted estimator (AIPWE) [24] in terms of smaller bias of estimated single index coefficient, smaller mean square error of estimated link function. In most cases, the bias of estimated single index coefficient of our proposed approach is about ten times smaller than the other two approaches. As a result, our method also makes more correct decisions and gives estimated value function much closer to its theoretical value. We also note that as sample size increases, the mean squared error of the single index coefficient and estimated link function for three methods decreases, the PCD increases and the estimated value function gets closer to the true value function. However, Table 2 indicates that the ordinary least square method performs comparably with our method but gives larger PCD than all the other methods when ψ(0) = 0. This is simply because that, ψ′ > 0,

Table 1.

Estimation and classification results for Example I. PCD denotes percentage of correct decisions, Val denotes value function estimates based on large sample. We report mean of estimated single index coefficient biases, mean squared errors of estimated single index coefficients, mean squared errors of estimated link functions, PCD and Val over 1000 replications with their empirical standard deviations one line below.

Method	Bias of (β1, β2)		MSE(β)	MSE(ψ)	PCD	Val(1.553)
	n = 500
SIM	0.000 (0.026)	0.001 (0.026)	0.001 (0.001)	0.007 (0.003)	0.994 (0.005)	1.552 (0.003)
LSQ	−0.001 (0.046)	0.002 (0.046)	0.002 (0.003)	1.405 (0.085)	0.598 (0.022)	0.905 (0.002)
IPWE	−0.018 (0.089)	−0.007 (0.084)	0.015 (0.022)		0.985 (0.009)	1.561 (0.070)
AIPWE	−0.011 (0.085)	−0.001 (0.084)	0.015 (0.021)		0.986 (0.008)	1.559 (0.069)
	n = 1000
SIM	0.001 (0.018)	0.001 (0.018)	0.000 (0.000)	0.004 (0.002)	0.996 (0.003)	1.552 (0.002)
LSQ	−0.001 (0.033)	0.001 (0.033)	0.001 (0.002)	1.410 (0.060)	0.597 (0.015)	0.903 (0.005)
IPWE	−0.010 (0.069)	−0.003 (0.066)	0.009 (0.013)		0.989 (0.006)	1.558 (0.049)
AIPWE	−0.006 (0.067)	0.001 (0.065)	0.009 (0.013)		0.989 (0.007)	1.557 (0.049)
	n = 1500
SIM	0.000 (0.015)	0.000 (0.015)	0.000 (0.000)	0.003 (0.001)	0.996 (0.003)	1.551 (0.001)
LSQ	0.000 (0.027)	0.001 (0.027)	0.001 (0.001)	1.409 (0.050)	0.597 (0.012)	0.902 (0.007)
IPWE	−0.010 (0.059)	−0.005 (0.056)	0.007 (0.010)		0.990 (0.005)	1.555 (0.041)
AIPWE	−0.005 (0.057)	−0.000 (0.056)	0.007 (0.009)		0.990 (0.006)	1.554 (0.041)

Table 3.

Estimation and classification results for Example III. Other captions are the same as Table 1.

Method	Bias of (β1, β2, β3, β4)				MSE(β)	MSE(ψ)	PCD	Val(1.403)
	n = 500
SIM	−0.004 (0.049)	0.003 (0.047)	−0.001 (0.049)	0.001 (0.044)	0.002 (0.002)	0.010 (0.005)	0.968 (0.005)	1.407 (0.003)
LSQ	−0.010 (0.097)	0.012 (0.092)	−0.010 (0.093)	0.004 (0.094)	0.009 (0.007)	1.135 (0.043)	0.547 (0.021)	0.648 (0.006)
IPWE	−0.044 (0.132)	0.031 (0.135)	0.016 (0.126)	0.009 (0.117)	0.022 (0.030)		0.983 (0.008)	1.420 (0.057)
AIPWE	−0.025 (0.126)	0.019 (0.126)	−0.002 (0.129)	0.019 (0.121)	0.022 (0.028)		0.983 (0.008)	1.418 (0.056)
	n = 1000
SIM	0.000 (0.033)	0.000 (0.033)	−0.002 (0.034)	0.002 (0.029)	0.001 (0.001)	0.005 (0.002)	0.995 (0.003)	1.402 (0.001)
LSQ	−0.005 (0.067)	0.005 (0.069)	−0.003 (0.065)	0.005 (0.067)	0.005 (0.004)	1.136 (0.031)	0.544 (0.016)	0.635 (0.004)
IPWE	−0.024 (0.107)	0.022 (0.102)	0.016 (0.095)	0.012 (0.096)	0.014 (0.020)		0.987 (0.006)	1.411 (0.040)
AIPWE	−0.014 (0.100)	0.013 (0.099)	0.001 (0.098)	0.013 (0.096)	0.014 (0.018)		0.987 (0.006)	1.410 (0.040)
	n = 1500
SIM	0.000 (0.028)	0.001 (0.026)	−0.001 (0.029)	0.001 (0.024)	0.001 (0.001)	0.004 (0.002)	0.996 (0.002)	1.402 (0.002)
LSQ	−0.002 (0.053)	0.005 (0.054)	−0.003 (0.055)	0.001 (0.053)	0.003 (0.002)	1.137 (0.025)	0.543 (0.013)	0.633 (0.005)
IPWE	−0.018 (0.093)	0.012 (0.091)	0.009 (0.086)	0.010 (0.078)	0.010 (0.014)		0.989 (0.005)	1.410 (0.033)
AIPWE	−0.009 (0.086)	0.008 (0.086)	−0.003 (0.088)	0.009 (0.080)	0.010 (0.013)		0.989 (0.005)	1.409 (0.033)

Table 2.

Estimation and classification results for Example II. Other captions are the same as Table 1.

Method	Bias of (β1, β2, β3)			MSE(β)	MSE(ψ)	PCD	Val(0.855)
	n = 500
SIM	−0.003 (0.062)	0.004 (0.063)	−0.002 (0.050)	0.003 (0.004)	0.017 (0.008)	0.947 (0.026)	0.861 (0.016)
LSQ	−0.002 (0.064)	0.005 (0.064)	−0.002 (0.049)	0.004 (0.004)	0.105 (0.016)	0.968 (0.019)	0.856 (0.018)
IPWE	−0.007 (0.141)	−0.007 (0.130)	−0.047 (0.127)	0.026 (0.038)		0.911 (0.038)	0.907 (0.067)
AIPWE	−0.004 (0.129)	0.016 (0.128)	−0.020 (0.115)	0.026 (0.032)		0.917 (0.036)	0.903 (0.067)
	n = 1000
SIM	−0.003 (0.043)	0.002 (0.045)	−0.003 (0.035)	0.002 (0.002)	0.010 (0.004)	0.956 (0.024)	0.857 (0.013)
LSQ	−0.004 (0.046)	−0.001 (0.045)	−0.002 (0.035)	0.002 (0.002)	0.103 (0.011)	0.977 (0.014)	0.853 (0.016)
IPWE	−0.013 (0.112)	−0.010 (0.106)	−0.026 (0.093)	0.017 (0.025)		0.928 (0.032)	0.887 (0.046)
AIPWE	−0.013 (0.104)	−0.001 (0.104)	−0.014 (0.087)	0.017 (0.023)		0.933 (0.030)	0.885 (0.046)
	n = 1500
SIM	−0.001 (0.035)	0.000 (0.036)	−0.002 (0.028)	0.001 (0.001)	0.007 (0.003)	0.965 (0.020)	0.860 (0.009)
LSQ	−0.002 (0.037)	−0.001 (0.038)	−0.003 (0.028)	0.001 (0.001)	0.102 (0.009)	0.981 (0.011)	0.857 (0.010)
IPWE	−0.007 (0.101)	−0.010 (0.095)	−0.026 (0.081)	0.013 (0.018)		0.937 (0.027)	0.882 (0.038)
AIPWE	−0.005 (0.090)	−0.001 (0.088)	−0.015 (0.076)	0.013 (0.015)		0.943 (0.024)	0.880 (0.038)

$$\begin{array}{l}\text{sign}(\mathit{X}{\widehat{\beta }}_{\text{ols}})=\text{sign}(\mathit{X}{({\mathit{X}}^T\mathit{X})}^{-1}{\mathit{X}}^T(\psi (\mathit{X}{\beta }_0)+\mathit{\epsilon }))\\ =\text{sign}(\mathit{X}{({\mathit{X}}^T\mathit{X})}^{-1}{\mathit{X}}^T({\psi }^{\prime }(\mathbf{u})\odot (\mathit{X}{\beta }_0)+\mathit{\epsilon }))\\ =\text{sign}({\psi }^{\prime }(\mathbf{u})\odot (\mathit{X}{\beta }_0)+\mathit{X}{({\mathit{X}}^T\mathit{X})}^{-1}{\mathit{X}}^T\mathit{\epsilon })\\ =\text{sign}(\mathit{X}{\beta }_0+{({\psi }^{\prime }(\mathbf{u}))}^{-1}\odot [\mathit{X}{({\mathit{X}}^T\mathit{X})}^{-1}{\mathit{X}}^T\mathit{\epsilon }]).\end{array}$$

Table 4 indicates that all the methods are much worse under model misspecification. However, our method is still better compared to IPWE, AIPWE and the ordinary least square method. We also investigate our proposed inferential procedure for the single index coefficient β. It shows in Table 5 that, as sample size increases, the empirical standard error and the mean estimated standard error are getting closer to each other. For almost all cases, the empirical coverage rates are very close to the nominal level, as expected.

Table 4.

Estimation and classification results for Example IV. Other captions are the same as Table 1.

Method	Bias of (β1, β2, β3)			MSE(β)	MSE(ψ)	PCD	Val(1.143)
	n = 500
SIM	−0.051 (0.243)	0.048 (0.231)	−0.034 (0.188)	0.051 (0.158)	0.564 (0.085)	0.777 (0.051)	0.905 (0.143)
LSQ	−0.090 (0.329)	0.118 (0.330)	−0.085 (0.303)	0.113 (0.128)	1.192 (0.068)	0.616 (0.053)	0.606 (0.051)
IPWE	−1.109 (0.208)	1.106 (0.213)	−1.127 (0.217)	0.446 (0.129)		0.738 (0.023)	1.029 (0.069)
AIPWE	−1.120 (0.186)	1.117 (0.187)	−1.133 (0.189)	0.446 (0.119)		0.738 (0.023)	1.027 (0.069)
	n = 1000
SIM	−0.005 (0.080)	0.003 (0.055)	−0.007 (0.089)	0.006 (0.055)	0.554 (0.046)	0.775 (0.024)	0.906 (0.050)
LSQ	−0.051 (0.239)	0.058 (0.240)	−0.046 (0.239)	0.006 (0.066)	1.200 (0.049)	0.635 (0.038)	0.649 (0.038)
IPWE	−1.141 (0.107)	1.138 (0.109)	−1.154 (0.109)	0.454 (0.088)		0.740 (0.016)	1.024 (0.049)
AIPWE	−1.146 (0.100)	1.142 (0.101)	−1.150 (0.102)	0.454 (0.081)		0.740 (0.015)	1.023 (0.049)
	n = 1500
SIM	−0.002 (0.011)	0.000 (0.012)	0.000 (0.012)	0.001 (0.000)	0.546 (0.011)	0.802 (0.007)	0.908 (0.004)
LSQ	−0.043 (0.193)	0.022 (0.194)	−0.036 (0.195)	0.039 (0.041)	1.199 (0.042)	0.645 (0.027)	0.674 (0.025)
IPWE	−1.148 (0.057)	1.153 (0.059)	−1.155 (0.055)	0.444 (0.070)		0.740 (0.012)	1.022 (0.042)
AIPWE	−1.149 (0.066)	1.150 (0.067)	−1.153 (0.067)	0.444 (0.065)		0.741 (0.013)	1.021 (0.042)

Table 5.

Inference for the single index parameters of Example 1–3. std1: empirical standard deviation, std2: mean estimated standard deviation, cover: empirical coverage rate of 95% confidence intervals.

Example I
	n = 500				n = 1000				n = 1500
	bias	std1	std2	cover	bias	std1	std2	cover	bias	std1	std2	cover
β1	0.000	0.026	0.026	0.958	0.001	0.018	0.019	0.959	0.000	0.015	0.015	0.956
β2	0.001	0.026	0.028	0.971	0.001	0.018	0.020	0.968	0.000	0.015	0.016	0.966
Example II
	n = 500				n = 1000				n = 1500
	bias	std1	std2	cover	bias	std1	std2	cover	bias	std1	std2	cover
β1	−0.003	0.062	0.066	0.961	−0.003	0.043	0.047	0.960	−0.001	0.035	0.039	0.968
β2	0.004	0.063	0.062	0.938	−0.002	0.045	0.045	0.957	0.000	0.036	0.037	0.958
β3	−0.002	0.050	0.049	0.928	−0.003	0.035	0.035	0.949	−0.002	0.028	0.028	0.945
Example III
	n = 500				n = 1000				n = 1500
	bias	std1	std2	cover	bias	std1	std2	cover	bias	std1	std2	cover
β1	−0.004	0.049	0.050	0.949	0.000	0.033	0.037	0.962	0.000	0.028	0.030	0.965
β2	0.003	0.047	0.050	0.951	0.000	0.033	0.036	0.959	0.001	0.026	0.030	0.974
β3	−0.001	0.049	0.046	0.937	−0.002	0.034	0.033	0.943	−0.001	0.029	0.027	0.932
β4	0.001	0.044	0.041	0.928	0.002	0.029	0.029	0.950	0.001	0.024	0.024	0.952

5. Data application

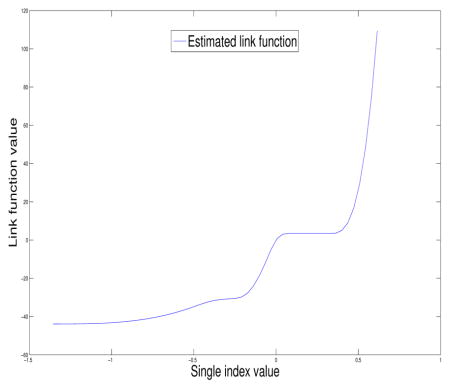
To further illustrate the performance of our method, we consider its application to data from AIDS Clinical Trials Group Protocol 175 (ACTG175). The complete data contain 2139 HIV-infected subjects with study subjects randomized to four different treatment groups: zidovudine (ZDV) monotherapy, ZDV + didanosine (ddI), ZDV + zalcitabine and ddI monotherapy. The CD4 count (cells/mm³ ) at 20±5 weeks post-baseline is chosen as the continuous response Y, where large values are desired. Among all subjects, 524 subjects received the treatments ZDV + didanosine (ddI) and 522 subjects received the treatment ZDV + zalcitabine. For illustration purpose, we consider these two group of patients with the goal to find their individualized optimal treatment rules. We use A = 1 to denote treatment ZDV + zalcitabine and A = −1 to denote treatment ZDV + didanosine (ddI). Besides the treatment indicator, we also include two covariates: age and homosexual activity (in short as homo), which are selected as important covariates in [13].

We apply the proposed method to estimate the optimal treatment and perform statistical inference for the corresponding parameters. The estimates for the single index coefficients are 0.902, −0.036, and 0.430 respectively and the estimated variance of the single index coefficients are 0.2232, 0.0004 and 0.0984, respectively. The optimal treatment rule is sign(0.902-0.036×age+0.430×homo). That is, if 0.902-0.036×age+0.430×homo ≥ 0, the optimal treatment for this patient is ZDV + zalcitabine, otherwise, the optimal treatment is ZDV + didanosine( ddI). In other words, for a patient with homo = 0, the optimal treatment A = −1 if age > 25.2 and the optimal treatment A = 1 otherwise; while for a patient with homo = 1, the optimal treatment A = −1 if age > 37.2 and the optimal treatment A = 1 otherwise. We note that the age of study subjects ranges from 12 to 70. According to the estimated optimal rule, 565 out of 1046 patients (54.02%) in this subset should be assigned to treatment ZDV+didanosine (ddI).

6. Discussion

In this paper, we proposed a novel semiparametric single-index model for individualized treatment selection. Our model plays an important role as a compromise between parametric models and nonparametric models [24]. The decision rule based on our method is a simple linear combination of covariates. We provide statistical inference for this rule. The asymptotic properties for the proposed method are established. The proposed method demonstrates superior numerical behavior in terms of smaller bias and means square error. Based on the estimated rule, our method also provides more precise decisions than existing methods and gives more precise value function estimates.

In many clinical studies, the state space is often of very high dimension. To develop optimal individualized treatment rules in this case, it will be important to develop simultaneous variable selection and treatment rule estimation. Variable selection techniques such as penalized regression and variable screening can be nested into our semiparametric single index modeling framework as powerful tools to develop optimal individualized treatment rules.

In our current procedure, we assume the propensity score π(A|X) is known. In observational studies, the propensity scores are often unknown. For such observational data, we can estimate π(A|X) via logistic regression and plug-in the estimated propensity score funtion π(A|X) into the optimization equation (1). It is beyond the scope of the current work and is an interesting topic for future study.

Fig 1.

Estimation performance for link function based on mean of 10 replications of Example 1–4 when n = 500.