High-Speed Whole-Brain Oximetry Via Golden-Angle Radial MRI

Abstract

Purpose

To determine whole-brain cerebral metabolic rate of oxygen (CMRO₂), an improved imaging approach, based on radial encoding, termed ‘radial OxFlow’ (rOxFlow), was developed to simultaneously quantify draining vein venous oxygen saturation (SvO₂) and total cerebral blood flow (tCBF).

Methods

To evaluate the efficiency and precision of the rOxFlow sequence, 10 subjects were studied during a paradigm of repeated breath-holds with both rOxFlow and Cartesian Ox-Flow (cOxFlow) sequences. CMRO₂ was calculated at baseline from OxFlow-measured data assuming an arterial O₂ saturation of 97%, and the SvO₂ and tCBF breath-hold responses were quantified.

Results

Average neurometabolic-vascular parameters across the ten subjects for cOxFlow and rOxFlow were, respectively: SvO₂ (%) baseline: 64.6 ± 8.0 vs. 64.2 ± 6.6; SvO₂ peak: 70.5 ± 8.5 vs. 72.6 ± 5.4; tCBF (mL/min/100g) baseline: 39.2 ± 3.8 vs. 40.6 ± 8.0; tCBF peak: 53.2 ± 5.1 vs. 56.1 ±11.7; CMRO₂ (μmol O₂/min/100g) baseline: 111.5 ± 26.8 vs. 120.1 ± 19.6. The above measures were not significantly different between sequences (p>0.05).

Conclusion

There was good agreement between the two methods in terms of the physiologic responses measured. Comparing the two, rOxFlow provided higher temporal resolution and greater flexibility for reconstruction while maintaining high SNR.

Introduction

Oxygen consumption of the brain (defined as the cerebral metabolic rate of oxygen CMRO₂) is an important physiologic parameter. Unlike most organs, the brain is highly metabolically active at all times, and even in the absence of mental tasks (1). However, CMRO₂ is reduced globally during sleep (2) and anesthesia (3), and in a number of disorders including obstructive sleep apnea (4), Alzheimer’s disease (5) and multiple sclerosis (6).

Fick’s Law relates CMRO₂ to cerebral blood flow and the difference in arterio-venous oxygen saturation:

$${\mathit{CMRO}}_2=Ca{O}_2·\mathit{CBF}·({\mathit{SaO}}_2-{\mathit{SvO}}_2)$$ [1]

where, CaO₂ is the oxygen carrying capacity of blood expressed in ml O₂/100 g blood, and can be written as CaO₂ = C_a · [Hgb]. Here, [Hgb] is the concentration of hemoglobin (Hgb), and C_a = 1.34 mL O₂/g hemoglobin is the amount of oxygen that 1g of Hgb can bind. CBF is cerebral blood flow (mL/min/100g), and SaO₂ and SvO₂ are the oxygen saturation levels of arterial and venous blood, respectively (% HbO₂).

MRI is the only imaging modality able to quantify whole-brain CMRO₂ noninvasively from a joint measurement of CBF – typically via phase-contrast MRI (PC-MRI) methods (7) – and SvO₂ (8–10). A whole-brain (i.e. global) MRI measurement of CMRO₂, while forgoing regional information, allows for potentially higher temporal resolution, which is essential for quantifying dynamic processes such as the response to a breath-hold stimulus (11).

One of the two common MRI oximetry techniques, referred to as susceptometry-based oximetry, relies on the measurement of the intra- to extravascular phase difference resulting from deoxygenated blood in a target vein (8). From the measured phase difference the blood’s relative magnetic susceptibility is obtained, which scales linearly with oxygen saturation. Prior implementations of the technique (referred to as ‘OxFlow’ as it quantifies both oxygen saturation and blood flow within a single imaging sequence (10,12)) are based on Cartesian k-space coverage. By quantifying both CBF and SvO₂ in the same vessel and incorporating a BRISK view-sharing scheme (13) an effective temporal resolution on the order of 2 seconds was achieved (14). However, the temporal footprint (here defined as the period of time over which a complete dataset for one reconstructed image is acquired) of BRISK and other such Cartesian view sharing techniques is, considerably longer than the temporal resolution. Furthermore, BRISK view-sharing may not be ideal as it provides limited flexibility since the sampling pattern and hence temporal resolution has to be chosen a priori. In contrast, a golden-angle radial sampling strategy (15) is amenable to a variety of reconstruction options tailored to the specific application’s needs, and may permit superior effective temporal resolution and a smaller temporal footprint than the BRISK-based Cartesian sampling strategy. Golden-angle radial scanning is optimal for sampling k-space in two dimensions since it provides nearly evenly spaced projections and potentially higher SNR (15).

In this work a velocity-encoded, multi-echo, golden-angle radial imaging sequence, termed radial OxFlow (rOxFlow) is presented for rapid quantification of SvO₂ and CBF in the superior sagittal sinus (SSS). The performance of the sequence was evaluated in 10 subjects both at baseline and during a series of breath-hold challenges, and the results were compared to those obtained with Cartesian OxFlow (cOxFlow).

Methods

Principle of OxFlow

Blood’s magnetic susceptibility relative to tissue (Δχ ) scales with deoxyhemoglobin concentration and thus (1−SvO₂):

$$\mathrm{\Delta }\chi =\mathit{Hct}·(\mathrm{\Delta }{\chi }_{do}·(1-{\mathit{SvO}}_2)+\mathrm{\Delta }{\chi }_{\mathit{oxy}})$$ [2]

where Δχ_do and Δχ_oxy are the susceptibility differences between fully deoxygenated blood and water, and between fully oxygenated blood and water, respectively. Values used in the present work were 4π × 0.273 ppm and −4π × 0.008 ppm (SI) (16). The hematocrit (Hct) represents the volume fraction of red blood cells compared to the total blood volume (red blood cells and plasma), which is related to [Hgb] by multiplication with an empirical factor of 3.

Assuming that the vein can be modelled as a long cylinder (length≫diameter), the incremental magnetic field ΔB due to the susceptibility difference Δχ between the intra- and extravascular compartment obeys the following relationship:

$$\mathrm{\Delta }B\approx \frac{\mathrm{\Delta }\chi }{6}(3co{s}^2\theta -1)B_0$$ [3]

where θ is the vessel tilt angle relative to B₀ (which is measured based on a projection venogram). ΔB is obtained by computing the inter-echo phase difference, Δϕ, over a period of time, ΔTE:

$$\mathrm{\Delta }\varphi =\gamma ·\mathrm{\Delta }B·\mathrm{\Delta }TE$$ [4]

where γ is the gyromagnetic ratio. SvO₂ therefore can be calculated as:

$${\mathit{SvO}}_2=\left[1-\frac{6\mid \mathrm{\Delta }\varphi \mid }{\gamma \mathrm{\Delta }{\chi }_{do}{B}_0\mathit{\Delta }TE(3{\mathit{cos}}^2\mathrm{\theta }-1)\mathit{Hct}}+\frac{\mathrm{\Delta }{\chi }_{\mathit{oxy}}}{\mathrm{\Delta }{\chi }_{do}}\right]\times 100\%$$ [5]

|Δϕ| is the difference of average phase between intra and extravascular compartments. For quantification of CMRO₂, SvO₂ is combined with the measurement of blood flow velocity, obtained by means of PC-MRI as described in (10), and blood flow is obtained as the product of average velocity across the vessel and vessel’s cross-sectional area.

MRI Acquisition and Processing

Cartesian and radial OxFlow data were acquired continuously for 10 minutes during a series of repeated breath-hold challenges, each lasting 30 s, separated by 90 s of normal breathing. All imaging experiments were performed at 1.5 T with a 12-channel head coil. The Institutional Review Board of the University of Pennsylvania approved all aspects of this study. A total of 10 healthy volunteers (6 males and 4 females, 23–33 years old) were recruited to participate after providing written, informed consent.

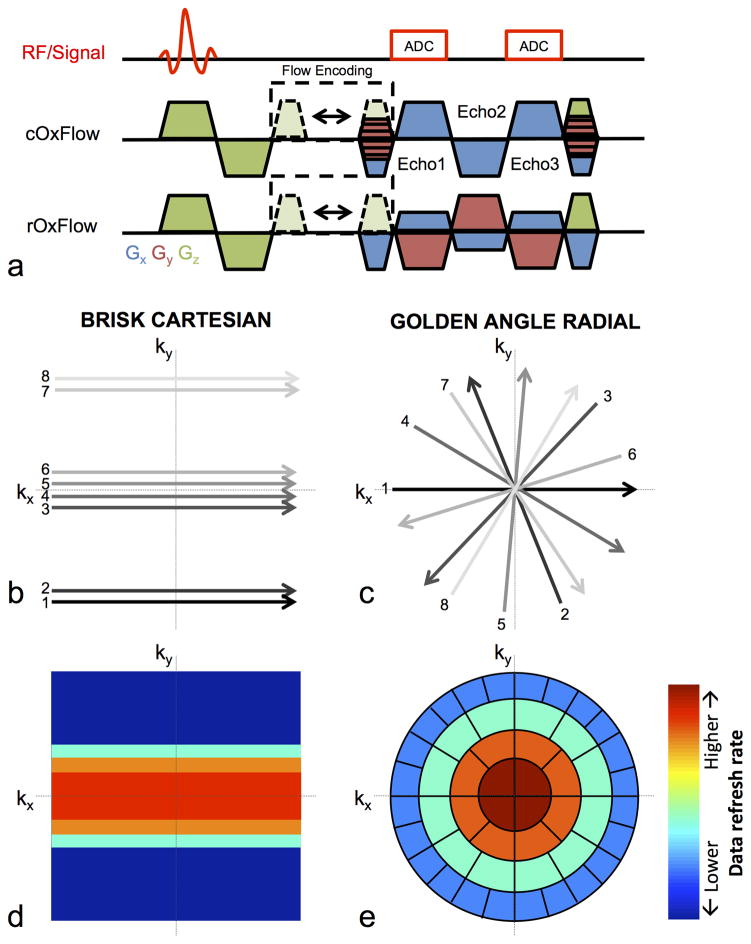
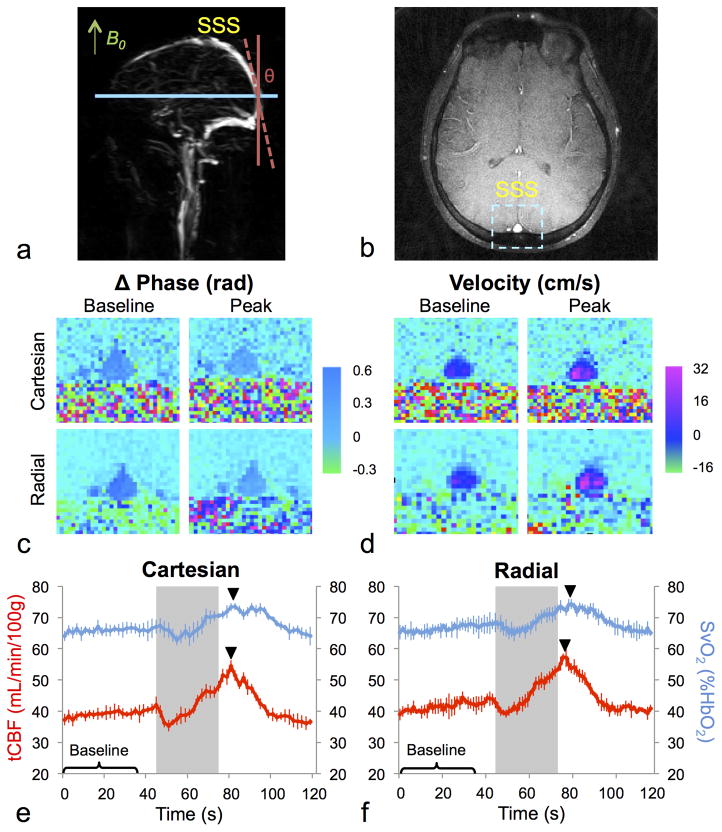
Before acquisition of the OxFlow images, an axial time-of-flight (TOF) 2D sequence was run (slice thickness = 5 mm; total number of slices = 40; 20% overlap between slices; TR (the repetition time between excitations)/TE = 17/5.58 ms; flip angle = 60°; acquisition matrix = 256×256; FOV = 220×220 mm²) for the purpose of determining the imaging plane in which the SSS had a minimal tilt angle relative to B₀. Both cOxFlow and rOxFlow are RF-spoiled velocity-encoded multi-echo GRE sequences (Figure 1). Figures 2a–b show a sagittal scout angiogram and axial magnitude image indicating measurement locations. Cartesian and radial OxFlow sequences were designed in SequenceTree (17) and were executed with the following sequence parameters: cOxFlow: FOV = 176×176 mm²; slice thickness = 5 mm; flip angle = 15°; TR/TE1/ΔTE = 19.0/5.73/7.04 ms; bandwidth = 321 Hz/pixel; velocity encoding (VENC) = 76 cm/s; 208 points per readout; reconstructed matrix size = 208×208; voxel size = 0.846×0.846×5 mm³. rOxFlow: FOV = 240×240 mm²; slice thickness = 5 mm; flip angle = 15°; TR/TE1/ΔTE = 19.2/6.75/8 ms; bandwidth = 278 Hz/pixel; VENC = 76.42 cm/s; 240 points per view; reconstructed matrix size = 240×240; voxel size = 1×1×5 mm³.

Figure 1.

(a) RF-spoiled, velocity-encoded, multi-echo GRE OxFlow pulse sequence diagram showing gradient structure for Cartesian and radial trajectories. Velocity encoding is achieved by shifting the flow-compensating gradient. Example k-space trajectory to encode 8 lines of k-space using BRISK-based Cartesian (b) and golden angle radial (c) encoding strategies (for detail see text). Heat maps show schematically the rate that different portions of k-space are updated (increasing from blue to red) for Cartesian (d) and radial (e) image reconstruction. In radial OxFlow reconstruction, KWIC filtering is applied, in which 34 views are used to encode the central k-space region and the number of views increases gradually toward higher k-values.

Figure 2.

Representative sagittal maximum intensity projection venogram (a) for prescribing an axial slice of interest (b) for OxFlow data acquisition as the straightest segment of the SSS, approximately parallel to the main magnetic field. Sample phase difference images from the radial and Cartesian OxFlow sequences used to compute SvO₂ (c) and corresponding velocity images computed from pairs of images acquired with different velocity-encoding (d). tCBF and SvO₂ time courses during the breath-hold paradigm in a representative subject for cOxFlow (e) and rOxFlow (f). Time courses show the mean over the five breath-hold periods, and error bars represent standard deviation. Baseline corresponds to the first 38 s, the breath-hold period is denoted by the grey box (45–75 s), and peak is indicated by the black triangle.

Raw data from cOxFlow and rOxFlow k-space data were reconstructed with custom-designed MATLAB scripts. Cartesian OxFlow used a BRISK encoding and reconstruction scheme (13) described previously (11), yielding an effective temporal resolution of 2.0 s and a total temporal footprint of 40.0 s for each time frame. The radially acquired data were first phase-corrected for direction-dependent gradient delays (18). KWIC filtering (19) was applied, in which 34 views were used to encode the central k-space region and the number of views in-creased gradually toward higher k-values. Since the angular spacings between adjacent views in golden angle acquisition are unevenly distributed, 610 views were used in the outer-most region to fulfill the Nyquist criterion for a 240×240 image matrix (15). A sliding-window step of 34 views was used for the dynamic series, resulting in 447 frames during the 600-second duration of the sequence. This reconstruction scheme yielded an effective temporal resolution of 1.29 s (i.e. the time between consecutive images of the reconstructed series, of the radial sequence, and is the time required to acquire the central 34 views for each image (multiplied by two for flow encoding)) and temporal footprint of 23.2 s (defined as the time required to acquire all 610 views used to reconstruct each image (times two for flow encoding)).

Data Analysis

After reconstruction, image analysis was performed identically for rOxFlow and cOxFlow data using in-house written MATLAB scripts and ImageJ in a region of interest in the SSS. Velocity was computed from the phase difference of images reconstructed from the first echo acquired with different gradient first moments (Figure 1). SSS blood flow was calculated by averaging velocity over the ROI chosen that fully contains the SSS. Since SSS is known to drain approximately half of total CBF (tCBF), the latter was estimated by dividing measured SSS flow by a factor of 0.51 (11).

For computation of SvO₂, the inter-echo phase difference between first and third echoes (Fig. 1a), averaged over the two velocity encoding acquisitions, was measured. The contribution of the static field inhomogeneity on tissue phase was corrected by fitting the background brain tissue surrounding the SSS to a second-order polynomial (20). The difference between the inter-echo phase accumulation of blood and background tissue, |Δϕ|, was used to compute SvO₂ via Eq. 5. The SSS ROI used for analysis of velocity was eroded by one voxel in order to exclude voxels impacted by blood-tissue partial volume mixing. Background tissue phase was calculated in an ROI one vessel radius away from the SSS ROI boundary and one vessel radius wide and was used to correct the background phase offset. The SSS tilt angle θ was calculated from TOF images by measuring the centroid of the SSS two slices below and above the OxFlow imaging plane. Hgb value was obtained via finger prick using the HemoCue (HemoCue America) analyzer.

The performance of the two sequences was compared both at baseline and during the breath-hold challenge to assess agreement across a range of flow and SvO₂ values. To smooth effects of small inconsistencies in the coached timing and imperfect protocol adherence, flow and SvO₂ time courses were averaged over the five breath-holds to yield the mean response to the stimulus as well as its standard deviation. Data points from the first 38 s were chosen to represent baseline, and the peak value was calculated as the maximum following cessation of breath-hold (see Figure 2e–f).

Baseline CMRO₂ was calculated from Eq. 1 assuming SaO₂ = 97%. To normalize CMRO₂ to 100 gram of brain mass, T₁-weighted MP-RAGE images with whole-brain coverage and 1 mm isotropic spatial resolution were acquired to estimate brain volume. FAST (FSL, version 5.0.5) was used to segment the MP-RAGE images into grey matter, white matter, and CSF. Volumes of grey matter and white matter were summed to yield total brain volume, which was converted to brain mass assuming an average tissue density of 1.05 g/mL.

Statistical analysis

Bland-Altman tests (21) were conducted to investigate possible inter-sequence bias. Means of baseline and peak SvO₂ and velocity over five breath-hold and rest periods were compared between cOxFlow and rOxFlow data, via paired Student’s t-tests.

Signal-to-noise ratio (SNR) was measured on magnitude, velocity, and phase images. SNR was calculated as the average magnitude signal in the SSS divided by the average magnitude of the background (obtained from a circular ROI outside the brain). For velocity images, SNR was calculated as the average phase in the ROI defined in the SSS divided by standard deviation of the background tissue. For phase images, SNR was calculated as the average phase in the ROI defined in the SSS divided by standard deviation of the SSS ROI. To compare performance of the two sequences, the somewhat larger voxel size used for rOxFlow was accounted for by dividing measured rOxFlow SNR values by 1.4 (voxel size ratio).

Temporal signal-to-noise ratio (tSNR) was measured on flow and SvO₂ time courses. tSNR was computed as the peak response divided by the standard deviation of baseline values.

Paired Student’s t-tests were conducted on each variable including baseline CMRO₂, baseline and peak SvO₂, baseline and peak flow, volume-normalized SNR, and tSNR, to determine possible differences between the Cartesian and radially acquired data. In all cases, P<0.05 was considered to be significant.

Results

Sample velocity and phase cOxflow and rOxFlow images and response time courses are displayed in Figure 2 highlighting the similarity of data acquired by the two sequences in both the parametric images and over the time-course of the breath-hold response. The time courses of both SvO₂ and tCBF display an initial rise and fall followed by a peak about 5 s after the end of the breath-hold period.

The initial rise and fall of flow has previously been attributed to the breath-hold-induced intra-thoracic pressure change causing modulation in cerebral venous return (22). During breath-hold, apnea-induced hypercapnia and hypoxia causes cerebral vasodilation and a sub-sequent rise in CBF, exceeding that needed to maintain adequate oxygen delivery. This flow-metabolism mismatch results in an increase in SvO₂. Upon cessation of breath-hold, a transient sharp increase in flow is observed, possibly due to the large initial inhalation at the end of breath-hold.

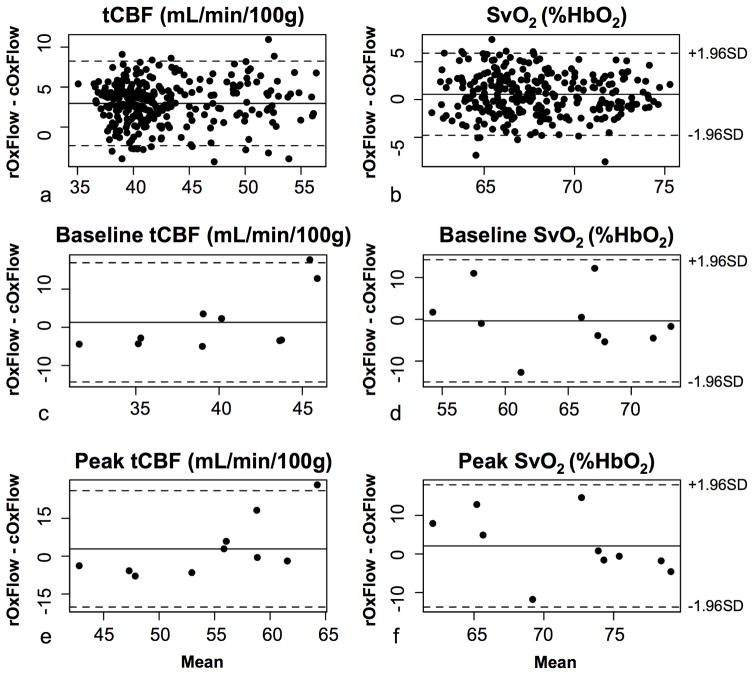
Bland-Altman plots comparing cOxFlow to rOxFlow in one subject during the time-course of the experiment are displayed in (Figure 3a–b). The data suggest negligible bias given that zero is within the limits of agreement (here defined as ±1.96 SD). Comparing metabolic parameters in the ten subjects again shows no measurable bias between the two sequences (Figure 3c–f).

Figure 3.

Bland-Altman plots comparing all rOxFlow and cOxFlow measurements during back-to-back 10-minute scans in one representative subject for tCBF (a) and SvO₂ (b). Plots suggest absence of significant bias between cOxFlow and rOxFlow sequences over the entire range of tCBF or SvO₂ values encountered during the breath-hold stimulus. Bland-Altman plots for baseline (c, e) and peak (d, f) measurements in all ten subjects, again suggesting no significant bias between data obtained with the two sequences. For all Bland-Altman plots, dotted lines indicate 1.96 standard deviations, representing the limits of agreement.

Table 1 lists SvO₂ and tCBF data in all ten subjects as well as means and standard deviations. No significant differences were observed between cOxFlow and rOxFlow data for any of the parameters measured (P>0.05 in all cases). Fractional changes in peak response relative to baseline in CBF were 35.2 ± 4.9% (cOxFlow) vs. 38.0 ± 5.4% (rOxFlow). For SvO₂ the corresponding temporal changes were 9.2 ± 2.1% (cOxFlow) vs.13.4 ± 3.4% (rOxFlow). A significant difference was not observed based on the paired t-test of baseline CMRO₂ computed from data obtained with the two sequences: 111.5 ± 26.8 μmol/100g/min (cOxflow) and 120.1 ± 19.6 μmol/100g/min (rOxFlow) with P = 0.25.

Table 1.

Baseline and peak tCBF and SvO₂ in physiologic units for all 10 subjects obtained by cOxFlow and rOxFlow. Note close mutual agreement between global means. No significant differences were observed between Cartesian and radial OxFlow data.

	Cartesian OxFlow					Radial OxFlow
	tCBF (mL/min/100g)		SvO2 (%HbO2)		CMRO2 (μmol/100g/min)	tCBF (mL/min/100g)		SvO2 (%HbO2)		CMRO2 (μmol/100g/min)
Subject	Baseline	Peak	Baseline	Peak	Baseline	Baseline	Peak	Baseline	Peak	Baseline
1	37.3	51.8	74.0	81.4	77.8	33.0	43.9	69.5	76.8	82.4
2	37.3	53.1	53.4	58.1	147.1	40.8	59.0	55.1	66.0	154.6
3	36.7	50.2	67.6	75.1	83.7	33.9	44.4	54.9	63.3	111.5
4	41.5	56.2	52.0	58.8	145.8	36.5	49.7	63.0	71.6	115.7
5	39.5	49.7	74.0	79.3	73.0	52.3	67.9	72.3	77.5	117.0
6	45.4	59.1	69.3	75.7	129.1	42.1	58.6	65.4	75.1	136.6
7	36.6	50.1	61.0	65.4	100.9	54.3	78.4	73.2	80.0	120.4
8	45.4	62.5	70.6	75.1	123.3	41.9	60.6	65.2	73.5	136.8
9	33.8	44.7	58.6	63.2	120.2	29.4	40.9	57.6	68.1	106.6
10	39.0	54.4	65.8	73.5	114.4	41.3	57.3	66.3	74.3	119.5
Mean	39.2	53.2	64.6	70.5	111.5	40.6	56.1	64.2	72.6	120.1
STD	3.8	5.1	8.0	8.5	26.8	8.0	11.7	6.6	5.4	19.6

Significantly higher SNR was observed in the magnitude and phase images from the rOxFlow sequence even after adjustment for voxel size at P<0.05 (Table 2). However, the difference in SNR of the velocity images between cOxFlow and volume-corrected rOxFlow was not significant, nor were there significant differences in tSNR for either CBF or SvO₂ between the two methods.

Table 2.

Summary of SNR comparison between cOxFlow and rOxFlow from datasets in 10 subjects.

	cOxFlow SNR	rOxFlow SNR	P-value		cOxFlow tSNR	rOxFlow tSNR	P-value
Magnitude	6.6 ± 1.6	9.1 ± 2.0	0.007	-	-	-	-
Velocity	5.0 ± 1.6	5.5 ± 1.0	0.178	tCBF	13.3 ± 7.2	12.4 ± 4.3	0.953
Phase	5.3 ± 1.9	7.4 ± 3.6	0.049	SvO2	5.9 ± 2.1	7.6 ± 2.6	0.060

Discussion and Conclusion

We have introduced an improved MRI method to quantify CMRO₂ in the human brain. Compared to previous methods (11), the radial acquisition strategy provides superior effective temporal resolution, here 1.29 s, without compromising SNR. The temporal footprint of rOxFlow is also lower by 41.5% relative to that of cOxFlow (23.2 s versus 40.0 s), providing better temporal fidelity. Therefore, rOxFlow may have greater sensitivity to detect sudden changes in these functional parameters, which are progressively smoothed with decreasing temporal resolution. The difference in temporal resolution (1.29 vs. 2.0 seconds) becomes significant when attempting to parameterize the CMRO₂ response to dynamic stimuli such as a breath-hold, which the authors have previously demonstrated to be perturbed in patients with obstructive sleep apnea (11). Furthermore, the smaller footprint of the radial acquisition strategy make rOxFlow less susceptible to artifacts from involuntary subject movement as, for instance in studies involving pediatric populations (23) or patients with movement disorders.

Somewhat higher SNR of the radial strategy, even after correcting for differences in voxel volume, is likely the result of greater number of data points used for image reconstruction as required by the Nyquist criterion. Given rOxFlow’s superior temporal resolution and SNR, it may allow for fewer breath-hold stimuli to evaluate stimulus response, which is of particular importance in patients unable to comply with multiple successive breath-holds.

In this work, reconstruction using the KWIC filter was employed for rOxFlow data, with 610 total views per image (yielding fully-sampled k-space at all k-space radii) and 34 views shifted per time point. Undersampled outer k-space could lead to even smaller temporal foot-print, albeit at the expense of somewhat reduced SNR. Other radial reconstruction schemes exist which may also offer improved temporal resolution, including one which combines golden-angle radial sampling with compressed sensing and parallel imaging (24). Similar to the KWIC strategy, the latter method also permits the determination of the temporal resolution retrospectively during reconstruction. In contrast, the reconstruction used for BRISK-based Cartesian sampling is pre-defined, and therefore much less flexible.

The neurometabolic parameters obtained herein are in agreement with those from previous studies. For example, mean baseline SvO₂ was obtained as 64.2 ± 6.6% in the present study, similar to results obtained with a projection-based T₂ method (65.6 ± 3.5%) (25), and the T₂-relaxation under spin tagging (TRUST) method (64.3 ± 6.8%) (9). Further, baseline tCBF found was 40.6 ± 8.0 ml/100 g/min, whereas CBF measured by PET was 44.2 ± 9 ml/100 g/min (26), and by arterial spin labeling was 41.5 ± 9 ml/100 g/min (26), all measured in similar cohorts. Taken together, the whole-brain averaged CMRO₂ values measured in young, healthy subjects was 132.1 ± 20.0 μmol/100g/min by TRUST (27), and 139 μmol/100g/min from PET (28), versus 120 ± 19.6 μmol/100g/min obtained in the present study by rOxFlow.

The study has limitations. SaO₂ was not monitored during scans. Based on previous studies, we might expect SaO₂ to drop as much as 7% during breath-hold (11). Without time-resolved measurement of SaO₂, CMRO₂ could not be computed during the breath-hold period. Another limitation is that sequence parameters were not identically matched between cOxFlow and rOxFlow methods. Instead in this study, the optimized rOxFlow sequence was compared to a previously published version of cOxFlow (14). Although this may somewhat impact the image SNR comparison, the overall goal of this study was to directly compare the quantified physiological parameters obtained with the two sequences. Finally, since the size of the raw data acquired with rOxFlow was larger, more reconstruction time was needed, which could be improved in future development.

In summary, the results from radial and Cartesian OxFlow sequences were found to be in good agreement. With improved temporal resolution and more flexible image reconstruction, rOxFlow is suggested to be a superior method to acquire SvO₂ and flow time courses and ultimately to measure CMRO₂.