Predictions of Speech Chimaera Intelligibility Using Auditory Nerve Mean-Rate and Spike-Timing Neural Cues

Abstract

Perceptual studies of speech intelligibility have shown that slow variations of acoustic envelope (ENV) in a small set of frequency bands provides adequate information for good perceptual performance in quiet, whereas acoustic temporal fine-structure (TFS) cues play a supporting role in background noise. However, the implications for neural coding are prone to misinterpretation because the mean-rate neural representation can contain recovered ENV cues from cochlear filtering of TFS. We investigated ENV recovery and spike-time TFS coding using objective measures of simulated mean-rate and spike-timing neural representations of chimaeric speech, in which either the ENV or the TFS is replaced by another signal. We (a) evaluated the levels of mean-rate and spike-timing neural information for two categories of chimaeric speech, one retaining ENV cues and the other TFS; (b) examined the level of recovered ENV from cochlear filtering of TFS speech; (c) examined and quantified the contribution to recovered ENV from spike-timing cues using a lateral inhibition network (LIN); and (d) constructed linear regression models with objective measures of mean-rate and spike-timing neural cues and subjective phoneme perception scores from normal-hearing listeners. The mean-rate neural cues from the original ENV and recovered ENV partially accounted for perceptual score variability, with additional variability explained by the recovered ENV from the LIN-processed TFS speech. The best model predictions of chimaeric speech intelligibility were found when both the mean-rate and spike-timing neural cues were included, providing further evidence that spike-time coding of TFS cues is important for intelligibility when the speech envelope is degraded.

INTRODUCTION

The time-frequency analysis performed by the mammalian cochlea leads to both a rate-place representation and a spike-timing representation of acoustic frequency components. In the rate-place representation, higher firing rates are produced in auditory nerve (AN) fibers tuned to more intense frequency components in an acoustic signal (Kiang et al. 1965). In the spike-timing representation, AN fibers synchronize to the phase of acoustic tones at least up to frequencies of 4–5 kHz (Rose et al. 1967). Which of these neural cues are used to support perceptual performance in both basic psychophysical tasks and in speech perception has thus been long debated. For example, the formant frequencies of a vowel are represented both by rate-place (Sachs and Young 1979) and spike-timing cues (Young and Sachs 1979). However, the spike-timing cues are more robust as a function of sound pressure level (Sachs and Young 1979; Young and Sachs 1979) and in background noise (Sachs et al. 1983). Furthermore, there appear to be spike-timing cues at the onset of speech transients in addition to mean-rate cues (Delgutte 1997). However, the necessity for spike-timing cues to support speech perception cannot be determined without quantitative predictions of speech intelligibility data.

Speech intelligibility predictors found in the literature vary greatly in the degree to which they incorporate aspects of peripheral auditory processing. However, several have been developed that do incorporate detailed physiological models including spike generation. The Neural Articulation Index proposed by Bondy et al. (2004) merged a detailed physiological model with the framework of the articulation index (French and Steinberg 1947). While this metric incorporated spike-timing information, there was no exploration of its contribution to the predictive accuracy relative to the mean-rate information. Zilany and Bruce (2007a) modified the Spectro-Temporal Modulation Index (STMI) of Elhilali et al. (2003) to incorporate a spiking auditory periphery model, but the version of the STMI that they implemented did not take spike-timing information into account. The STMI only considers information conveyed by modulations in the mean rate up to 32 Hz; one approach to make the STMI sensitive to spike-timing is to incorporate a lateral inhibitory network (LIN) between the auditory peripheral model and the cortical modulation filters to convert spike-timing cues into mean-rate cues (Shamma and Lorenzi 2013). However, quantitative predictions of speech intelligibility were not conducted in Shamma and Lorenzi (2013). An alternative predictor, the Neurogram SIMilarity measure (NSIM) developed by Hines and Harte (2010, 2012), has versions that explicitly include or exclude spike-timing cues. In Hines and Harte (2010), they showed that both the spike-timing and mean-rate representations were degraded by simulated hearing loss, but no quantitative predictions of human data were included. Hines and Harte (2012) provided quantitative predictions of consonant-vowel-consonant (CVC) word perception in normal-hearing listeners as a function of presentation level. Most of the assessment was done in quiet, but they did include one background noise condition. Overall, there was no substantial difference in the accuracy of the predictions including or excluding spike-timing information. However, it is unclear as to whether this is because the spike-timing cues are not necessary or if it is because of a general degradation of both types of cues due to background noise or inaudibility at low presentation levels. This motivates the use of manipulations of the acoustic features of speech signals that will lead to more independent degradation of mean-rate and spike-timing cues.

There are numerous signal processing approaches that have been used to manipulate the envelope (ENV) and temporal fine structure (TFS) of speech. A large class of these are referred to as vocoders (Drullman 1995; Dudley 1939; Flanagan 1980), where the broadband speech is divided into a set of frequency channels and the narrowband signals are decomposed into the corresponding ENV and TFS components. A speech signal is then synthesized based on only some aspects of the ENV or TFS from the original speech, with artificial signals being used for the remaining aspects. A widely used example of this is the noise vocoder, in which the TFS within frequency sub-bands is replaced by a noise signal (Shannon et al. 1995). A generalization of vocoded speech, referred to as “speech chimaeras,” was proposed by Smith et al. (2002), in which the ENV of one signal is mixed with the TFS of another within each sub-band. The general conclusion reached from studies such as Shannon et al. (1995) and Smith et al. (2002) is that ENV cues primarily support speech intelligibility in quiet and that narrowband TFS cues play a minimal role under such conditions. However, in a study by Lorenzi et al. (2006), it was argued that normal-hearing listeners were able to learn over several sessions to understand consonants in nonsense vowel-consonant-vowel (VCV) words where the speech information was conveyed primarily by narrowband TFS cues.

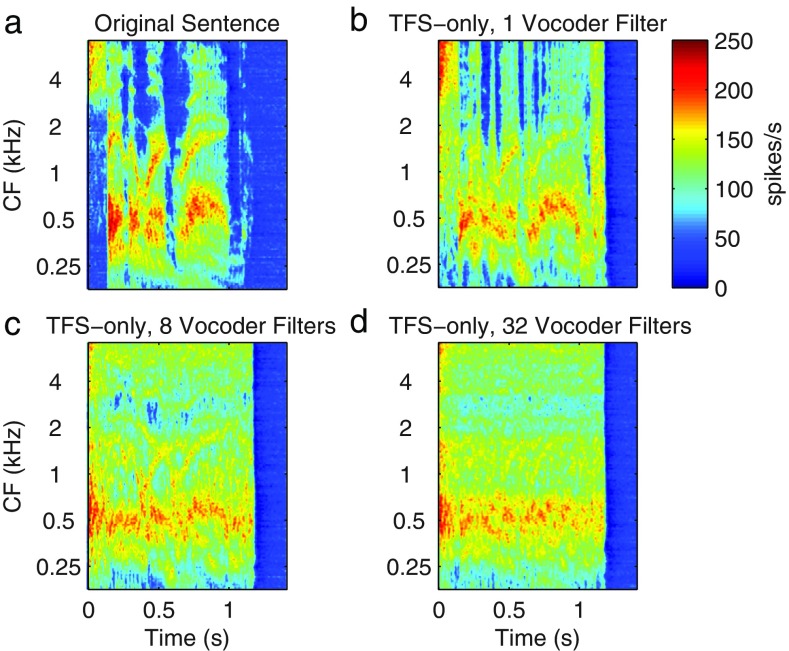
A significant concern regarding the evidence for TFS contribution to speech understanding is that these results may be influenced by residual ENV cues in the acoustic signals (due to imperfect processing) and/or reconstruction of ENV cues from the TFS due to cochlear filtering. Under band-limited conditions, the ENV and TFS of a signal are inherently linked to each other via fundamental modulation principals (Logan 1977; Rice 1973; Voelcker 1966) and thus allows the reconstruction of the ENV by narrowband filtering of the TFS by the cochlea (Ghitza 2001; Gilbert and Lorenzi 2006; Gilbert et al. 2007; Heinz and Swaminathan 2009; Hopkins et al. 2010; Ibrahim and Bruce 2010; Léger et al. 2015a, b; Shamma and Lorenzi 2013; Sheft et al. 2008; Swaminathan et al. 2014; Zeng et al. 2004). Figure 1 displays an example to illustrate the idea of ENV recovery from a speech TFS signal generated using a sample word from the NU-6 list used in this study. The figure shows neurograms at the output of the auditory periphery model of Zilany et al. (2009, 2014) modified to match the human cochlear tuning estimates of Shera et al. (2002). Ibrahim and Bruce (2010) have shown that sharper cochlear tuning will lead to a greater amount of ENV restoration. The output neurogram in Figure 1a shows the extent of the ENV detected by the model for intact speech, while the remaining three panels display the ENV recovery from the test word processed to keep only TFS cues (flat envelope). The processing is done with variable number of vocoder filters (1, 8, and 32) to examine the effect of the width of the generation filters on the quality of ENV recovery. As expected, the figure shows that as the number of filters increases, the quality of ENV recovery deteriorates. In addition, it can be observed that flattening the ENV over time leads to amplification of recording noise in the “silent” sections of a sentence, which itself will affect speech intelligibility (Apoux et al. 2013).

FIG. 1.

Observing the envelope recovery from the output neurograms of the human auditory periphery model when the input signal is a intact speech, b a Speech TFS with Flat ENV chimaera obtained using one vocoder filter, c eight vocoder filters, and d 32 vocoder filters. As the number of analysis vocoder filters applied increases, the quality of ENV recovery deteriorates in the case of Speech TFS signals.

Several recent studies using acoustic reconstruction of ENV cues from the TFS of nonsense VCVs (Léger et al. 2015a, b; Swaminathan et al. 2014) have argued that the ENV reconstruction likely explains all of the consonant intelligibility observed in their studies and the earlier work of Lorenzi et al. (2006). However, Swaminathan and Heinz (2012) found in a combined speech perception and physiological modeling study that, despite the overall dominance of ENV cues at a range of signal-to-noise ratios (SNRs), some TFS cues may be used in concert with ENV cues at low SNRs for consonant perception in nonsense VCVs. Furthermore, in a study of ENV and TFS contributions to both vowel and consonant perception in real words, Fogerty and Humes (2012) found evidence that TFS does contribute more to vowel recognition. This motivates an investigation of the neural mean-rate and spike-timing cues to convey both vowel and consonant information.

In this study, we conducted a speech intelligibility experiment in normal-hearing listeners using Speech ENV and Speech TFS chimaeras (Smith et al. 2002) for real consonant-nucleus-consonant (CNC) words from the NU-6 speech corpus (Tillman and Carhart 1966). We then used the auditory periphery model of Zilany et al. (2009, 2014) to simulate AN fiber responses to the same speech chimaera stimuli and quantified the mean-rate and spike-timing information that characterize, respectively, the short-term rate of neural firing and the level of synchronization due to phase-locking (Joris and Yin 1992; Rose et al. 1967) or onset responses to speech transients (Delgutte 1997). In addition to quantifying the mean-rate neural information using the STMI, we investigate the viability of the NSIM to quantify spike-timing cues and as an alternative measure of the mean-rate information. We also examined and quantified the effects of LIN processing on the STMI predictions, which was not done by Shamma and Lorenzi (2013). To quantify the accuracy of the different intelligibility predictors, we examined several linear regression models using the perceptual scores as the dependent variable and the neural predictors as the independent variables (cf., Heinz and Swaminathan 2009; Swaminathan and Heinz 2012). The results indicate that a large degree of phoneme perception for real words in quiet can be explained by information from mean-rate cues, but combining spike-timing information with mean-rate cues does substantially improve predictions of chimaeric speech intelligibility.

MATERIALS AND METHODS

Terminology

One complication with studies of vocoder processing is the diverse terminology that has been used in the literature to describe different aspects of acoustic speech signals and their neural representation. Rosen (1992) proposed a taxonomy that divided temporal information in speech signals into three fluctuation ranges. He defined fluctuations in the range of approximately 2–50 Hz as ENV, those in the range of 50–500 Hz as periodicity, and those in the range of 500 Hz to 10 kHz as fine structure. When considering a wideband speech signal over a short time window, the high-frequency features in the acoustic waveform can be considered as spectral fine structure. Alternatively, when considering the frequency modulations over time within a narrow frequency band of speech, it is common to refer to the high-frequency information as the TFS. However, in many cases, the distinction between spectral and temporal fine structures is not explicitly made. Furthermore, a large number of studies do not treat periodicities in the range of 50–500 Hz as a separate class. These are grouped in with either the ENV or the TFS, or are split between them at some cutoff frequency within this range, depending on the type of acoustic processing that is performed. Further complicating the terminology is the fact that there is not a one-to-one correspondence between the acoustic features and their neural representation (Heinz and Swaminathan 2009; Shamma and Lorenzi 2013), because of the time-frequency analysis performed by the cochlea. Shamma and Lorenzi (2013) proposed the terminology of amplitude modulation (AM) and frequency modulation (FM) for the acoustic signals, reserving the terminology of ENV and TFS for the neural representation. Similarly, Hines and Harte (2010, 2012) used the terminology of ENV and TFS neurograms and ENV and TFS NSIM values, and Swaminathan and Heinz (2012) referred to ENV and TFS neural correlation coefficients. However, this is somewhat at odds with the widespread use of ENV and TFS to refer to acoustic signals, as well as the historical usage of mean-rate and spike-timing in the physiological literature, and the possibility of confounding acoustic cues and their neural representation if ENV and TFS are used to describe both, even though they do not have a one-to-one mapping. Therefore, in our study we will use ENV and TFS when referring to the acoustic signals, and the cutoff frequency between these two will depend on the bandwidth of the frequency sub-bands used for the acoustic signal processing, following the methodology of Smith et al. (2002). Spectral features that are supported by a neural rate-place code and temporal fluctuations in these up to a rate of approximately 78 Hz will be referred to as mean-rate information, and temporal fluctuations in neural firing at rates higher than 78 Hz and precise timing of spike occurrences due to acoustic transients will be referred to as spike-timing information. Thus, we will refer to the ENV neurograms and NSIM measures of Hines and Harte (2010, 2012) as mean-rate (MR) neurograms and NSIMs in this study. Because the TFS neurograms and NSIM measures of Hines and Harte (2010, 2012) convey both mean-rate and spike-timing information, we will refer to them as fine-timing (FT) neurograms and NSIMs.

Speech Recognition Experiment

Chimaera Processing

Speech chimaeras were constructed by processing two acoustic waveforms using a vocoder consisting of a bank of band-pass filters followed by the Hilbert transform to generate ENV-only and TFS-only versions of the signals (Smith et al. 2002). To be consistent with the processing methodology of Smith et al. (2002), the ENV signal was not smoothed by a low-pass filter, in contrast to some more recent studies. In each band, the envelope of one waveform was multiplied by the TFS of the other waveform. The products were then summed across frequency bands to construct the auditory chimaeras, which were generated with one waveform being the speech signal and the other being a noise waveform. The noise waveform was chosen to be either white Gaussian noise (WGN) or matched-noise (MN) with the purpose of suppressing any remaining ENV or TFS cues in the stimulus. Matched-noise was generated from the Fourier transform of the signal by keeping the magnitude and randomizing the phase. Intelligibility results with WGN auditory chimaeras were compared to those obtained with matched-noise chimaeras in order to achieve a better understanding of the matched-noise effect on speech recognition scores. Matched-noise has been used in previous experiments (e.g., Smith et al. 2002) with the goal of suppressing some of the speech cues. However, Paliwal and Wójcicki (2008) carried out a study where they constructed speech stimuli based on the short-time magnitude spectrum (this is equivalent to the matched-noise signal generation in the case of relatively short-duration speech signals). They investigated the effect of the analysis window duration on speech intelligibility, and their results showed that speech reconstructed from the short-time magnitude spectrum can be quite intelligible for time windows up to around 500 ms in duration, which suggests that the MN signals used by Smith et al. (2002) have the potential to add to the speech intelligibility rather than to detract from it. In contrast, the WGN signal should not contribute to the overall intelligibility.

The test sentences (described below) were processed to remove any silence before and after the end of the sentence, and the resulting sentences were then filtered with a variable number of 6th-order Butterworth band-pass zero-phase filters. There were seven different processing cases, where the number of frequency bands was changed to be either 1, 2, 3, 6, 8, 16, or 32. For each set of frequency bands, the cutoff frequencies span the range from 80 to 8820 Hz and their values were calculated based on the Greenwood function for humans (Greenwood 1990) using equally spaced normalized distances along the human cochlea (nearly logarithmic frequency spacing). The filter overlap is 25 % of the bandwidth of the narrowest filter in the bank (the lowest in frequency). In each band, the signal envelope was extracted using the Hilbert transform and the TFS signal was computed by dividing the filtered signal by its envelope. Auditory chimaeras were then generated by combining the Speech ENV with the noise TFS or the Speech TFS with the noise ENV and summing over all bands. The conflicting noise was chosen here to be WGN or MN and was added to suppress any remaining ENV or TFS cues in the stimulus. The matched-noise signal was generated by applying the fast Fourier transform (FFT) to each speech signal individually, retaining the magnitude spectrum, uniformly randomizing the phase (preserving the anti-symmetry property of the phase spectrum), and then taking the real part of the inverse FFT. Moreover, a Speech TFS-only (Speech TFS with Flat ENV) stimulus was generated by taking only the TFS from all frequency bands. Note that this Flat ENV chimaera differs somewhat from the “TFS speech” of Lorenzi et al. (2006) in which the relative signal power across frequency bands was maintained. Hence, we have five different types of chimaeras:

where the colors here match the color scheme used in all of the figures except Figure 8.

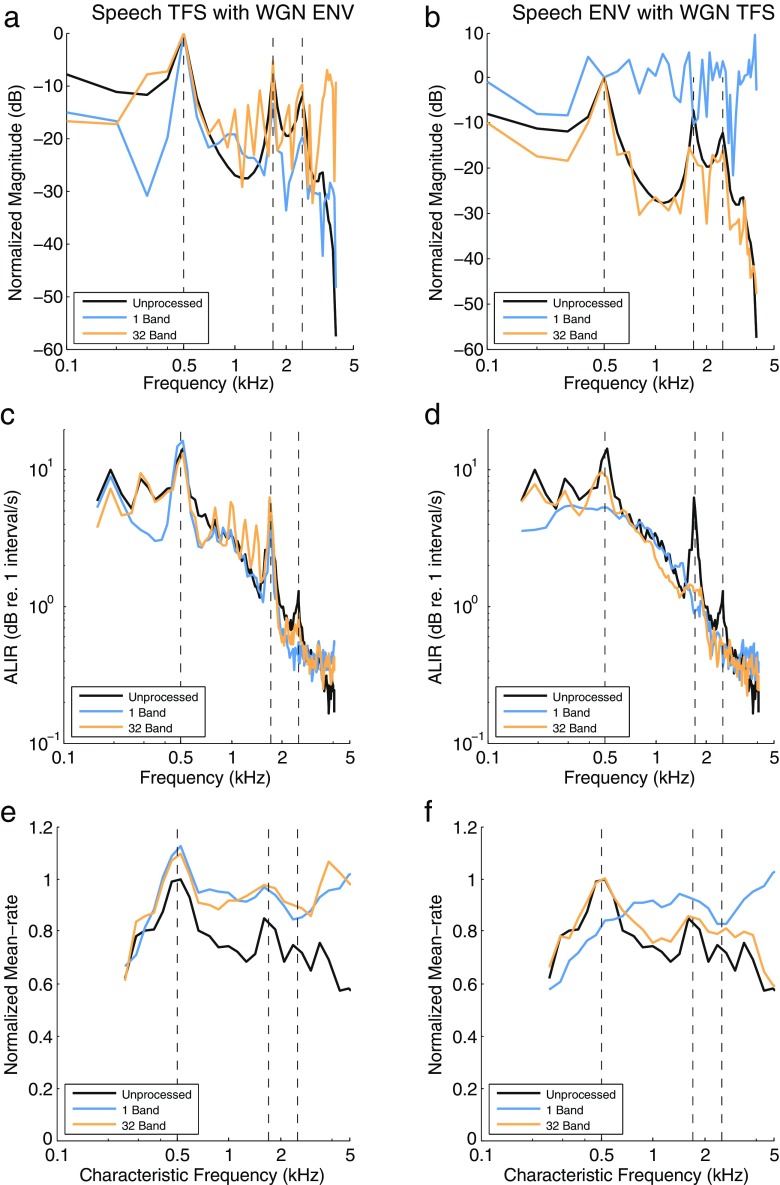
FIG. 8.

The effect of Speech TFS with WGN ENV (left column) and Speech ENV with WGN TFS (right column) vocoding on the acoustic (a, b) and neural (c–f) representations of the synthesized vowel /ε/. The vowel has a fundamental frequency of 100 Hz and five formant frequencies of 0.5, 1.7, 2.5, 3.3, and 3.7 kHz (see Miller et al. 1997). The frequencies of the first three formants are shown by the vertical dashed lines in all panels. a, b The spectral envelope for each chimaera type compared to the unprocessed vowel. c, d The average localized interval rate (ALIR) profiles, in units of decibels re. 1 interval per second, showing the degree of synchrony of AN fibers whose CFs are within 0.5 octave of each frequency sample in the stimulus. e, f The mean-rate discharge profiles as a function of CF for the time period of the unprocessed vowel.

Subjects and Speech Material

A word recognition experiment was conducted on five normal-hearing subjects aged 18–21 with English as their first language, who were paid for their participation. The subjects were asked to identify the final word in the sentence “Say the word (test word).” where the test words were chosen from the NU-6 word list (Tillman and Carhart 1966), which contains a total of 200 monosyllabic CNC words, and were recordings spoken by a native American English male speaker (Auditec, St. Louis). While Tillman and Carhart (1966) used the terminology of “nucleus” to describe the central phonemes because they include diphthongs as well as vowels, to simplify the description of our results, we will use the term “vowel” to refer to the central phoneme. The test sentences had all undergone auditory chimaera processing as described above.

Procedure

Subjects were tested in a quiet room. All signals were generated with a high-quality PC sound card (Turtle Beach—Audio Advantage Micro) at a sampling rate of 44,100 Hz. The sound was presented to the subjects via a Yamaha HTR-6150 amplifier and Sennheiser HDA 200 headphones. The signals were calibrated through a B&K 2260 Investigator sound analyzer (Artificial Ear Type 4152) to adjust the target speech to a presentation level of 65 dB SPL (i.e., re. 20 μPa). The test was done without prior training and was completed over five 1-h sessions for each subject. The five different chimaera types were each tested in a different session, and the order of the chimaera types was randomized for each subject. The chimaera types were blocked in this fashion to allow the participants to quickly become familiar with each type of processing, as the Speech ENV and Speech TFS chimaeras can sound very different.

For each chimaera type, seven sets of vocoder frequency bands were used. For each set of frequency bands, 50 test words were generated. These 50 test words were randomly selected from the 200 available words of the NU-6 list, resulting in 1750 test words that were used in this study. This word set was presented to the subjects using the following procedure:

• Randomly select one of 350 available words (50 words for each of the 7 filter sets) for the chimaera type being tested in that session.

• Ask the subject to repeat the word as they perceived it.

• Voice record the subject’s verbal response as well as a written record.

Subjects were told that they might not be able to understand all of the test words because the speech processing made some of them unintelligible. In the cases where a subject could not recognize a test word, they were asked to guess to the best of their ability. No feedback was provided.

Scoring

Several scoring methods were adopted, with the phonemic representation being the main scoring scheme. With phonemic-level scoring, each word was divided into its phonemes such that subjects could be rewarded for partial recognition. This scoring mechanism provides a closer comparison to the neural-based intelligibility predictors described below, particularly the STMI. Scores for consonant and vowel recognition were also reported.

Auditory Periphery Model

The auditory periphery model of Zilany et al. (2009) can produce AN fiber responses that are consistent with physiological data obtained from normal and impaired ears for stimuli intensities that span the dynamic range of hearing. The model has been used previously to study hearing-aid gain prescriptions (Dinath and Bruce 2008), for optimal phonemic compression schemes (Bruce et al. 2007), and for the development and assessment of the NSIM (Hines and Harte 2010, 2012). The model was established using single-unit auditory nerve data recorded in cat (Zilany and Bruce 2006, 2007b; Zilany et al. 2009), but recent changes have attempted to improve the model, including increased basilar membrane frequency selectivity (Ibrahim and Bruce 2010) to reflect revised (i.e., sharper) estimates of human cochlear tuning (Joris et al. 2011; Shera et al. 2002), human middle-ear filtering (Pascal et al. 1998), and some other updated model parameters (Zilany et al. 2014). Note that the threshold tuning of the model is based on Shera et al. (2002), but the model is non-linear and incorporates physiologically appropriate changes in tuning as a function of the stimulus level (Zilany and Bruce 2006, 2007b).

It is worth noting that there is an ongoing debate regarding the accuracy of the estimates of the human cochlear tuning. Ruggero and Temchin (2005) argued that the estimates provided by Shera et al. (2002) are not accurate due to some theoretical and experimental assumptions. However, more recent studies have refuted some of the criticisms and provided additional support for sharper cochlear tuning in humans (Bentsen et al. 2011; Shera et al. 2010), although the debate is not fully resolved (Lopez-Poveda and Eustaquio-Martin 2013). Thus, we chose in this study to use the sharper estimates of Shera et al. (2002), as a maximal role of ENV restoration would be expected in this case (Ibrahim and Bruce 2010).

Neurogram Generation

For every speech signal of the chimaera corpus, the auditory periphery model was used to compute a set of AN post-stimulus time histograms (PSTHs) at 128 logarithmically spaced characteristic frequencies (CFs) from 180 to 7040 Hz at a sampling rate of 100 kHz. The 10-μs bin size PSTH responses characterize the neural activity of a healthy cochlea and are “stacked” across CFs to create a spectrogram-like representation called a “neurogram.” Prior to applying each speech signal to the auditory model, it was preprocessed to incorporate typical hearing functionality and meet the processing requirements of the model: the head-related transfer function of Wiener and Ross (1946) was applied to simulate outer-ear frequency tuning characteristics; envelope transients at the beginning and end of the signal were removed to avoid potential ringing responses of the auditory filters; the stimulus was scaled to a 65-dB SPL presentation level; and the signal was up-sampled to the 100-kHz sampling rate of the auditory periphery model. Each preprocessed speech signal was then applied to the auditory periphery model of Zilany et al. (2014).

The PSTH response at each CF was generated by adding together the individual PSTH responses for a set of 50 AN fibers: 30 high spontaneous-rate (>18 spikes per second), low-threshold fibers; 15 medium spontaneous-rate (0.5 to 18 spikes per second) fibers; and 5 low spontaneous-rate (<0.5 spikes per second), high-threshold fibers, a distribution that is in agreement with past studies (Jackson and Carney 2005; Liberman 1978; Zilany et al. 2009).

Additional processing was then carried out on these unmodified neurograms to derive the alternate forms that separately and explicitly characterized the inherent mean-rate and spike-timing neural cues. The objective speech intelligibility measures examined in this work were then applied to only the CVC target-word region of the modified neurograms. The STMI, the STMI LIN, and the NSIM are discussed in the following sections.

Spectro-Temporal Modulation Index

The STMI quantifies the differences in spectral-temporal modulations found between a clean speech signal and its associated chimaeric speech signal using a physiologically-based cortical model (Chi et al. 1999; Elhilali et al. 2003), and it is only sensitive to mean-rate, or average, neural activity. A schematic illustration of the STMI is shown in Figure 2.

FIG. 2.

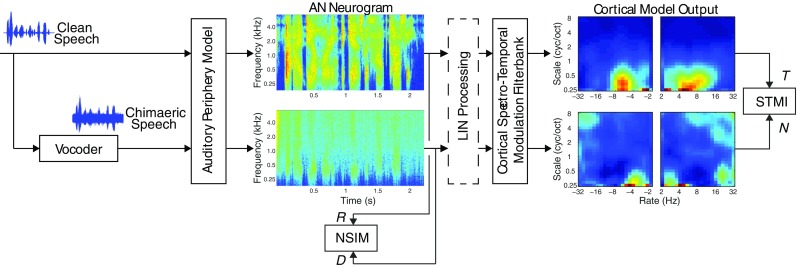
A schematic illustration of the STMI based on the processing of AN neurograms by a bank of cortical spectro-temporal modulation filters producing clean “template,” T, and “noisy”, N, auditory cortex outputs. The NSIM is also illustrated and is based on the clean “reference,” R, and “degraded,” D, neurograms. In this study, unprocessed speech signals are applied to the models to produce the “reference” neurograms and “template” cortical responses, and chimaeric speech signals are applied to the models to obtain the “degraded” neurograms and “noisy” cortical responses. The optional LIN processing extracts additional information from the neurograms by accounting for phase offsets in the AN fiber responses.

The STMI can quantify the effects of non-linear compression and phase distortions, as well as the effects of background noise and reverberations (Elhilali et al. 2003). The equation for the STMI is

$$\mathrm{\text{STMI}}=1-\frac{{‖T-N‖}^2}{{‖T‖}^2}$$ 1

where ‖·‖ is the Euclidean-norm operator, i.e., $‖\mathit{X}‖=\sqrt{{\sum }_{k=1}^n{\left|X_k\right|}^2}$ for a matrix X with n elements indexed by k, T is a token representing the cortical response for a clean speech signal, and N is a token representing the cortical response for the associated chimaeric 270 speech signal. The T and N tokens each reflect the difference between the cortical response of a speech signal and its matched-noise signal, or base-spectrum in the terminology used by Elhilali and colleagues (Elhilali et al. 2003). The T token is determined by subtracting the cortical response of the clean speech matched-noise signal from the cortical response of the clean speech signal. The N token is computed in the same manner using the chimaeric speech signal. The associated matched-noise representations were generated by applying the FFT to each speech signal individually, retaining the magnitude spectrum, uniformly randomizing the phase (preserving the anti-symmetry property of the phase spectrum), and then taking the real part of the inverse FFT. This is the same processing that was used to generate the matched-noise signal for the creation of the chimaera signals. The matched-noise subtraction operation is necessary in order to minimize non-critical modulations that might mask the important modulation information measured by the STMI. The STMI produces a scalar value, theoretically bound between 0 and 1, with larger values indicating better speech intelligibility.

To calculate the STMI, each neurogram was composed using PSTHs at 128 CFs (128 CFs logarithmically spaced from 180 to 7040 Hz provides about 5.2 octaves along the tonotopic axis, sufficient sampling to support the spectral and temporal modulation filters used by the STMI), as noted above. Each CF PSTH in the CVC target-word region was then convolved with a 16-ms rectangular window at 50 % overlap, yielding an effective sampling rate of 125 Hz and thereby eliminating TFS phase-locking characteristics from the neurogram. This processing was used on the clean speech signal, the chimaeric speech signal, and their respective matched-noise representations.

A set of spectro-temporal response fields (STRFs), in the form of a spectro-temporal Gabor function (Chi et al. 1999), derived as a function of ripple peak-frequency and drifting velocity, were applied to each pair of neurograms to produce respective four-dimensional, complex-valued matrices. The dimensions of these four-dimensional matrices are as follows: scale (0.3, 0.4, 0.5, 0.7, 1.0, 1.4, 2.0, 2.8, 4.0, 5.6, 8.0 cycles per octave); rate (±2.0, 2.8, 4.0, 5.7, 8.0, 11.3, 16.0, 22.6, 32.0 Hz), where positive values indicate a downward frequency-sweep sensitivity of the response field and negative values indicate an upward frequency-sweep sensitivity); time (seconds); and characteristic frequency (Hz). With a maximum best modulation rate of 32 Hz, the STMI only considers temporal modulations that are well within the range of ENV cues as defined by Rosen (1992). Prior to computing the cortical differences, the magnitudes of the complex-valued elements in each matrix were computed. The four-dimensional, real-valued T token was determined by subtracting the matched-noise cortical response from the clean speech cortical response and setting any resulting negative values to zero. The N token was computed in the same manner using the associated chimaeric cortical responses.

The STMI was computed using Eq. 1, with all scales, rates, times, and characteristic frequencies equally weighted. However, only the portion of the neurogram corresponding to the duration of the target-word was used. The numerator Euclidean result was calculated by subtracting N from T, setting any negative values to zero, squaring each value, and summing all values. The denominator was calculated by squaring each value of T and summing all values. The rationale for setting negative difference values in the numerator to zero is that negative values can arise because of spurious modulations occurring in the “noisy” cortical response N that are not present in the “template” cortical response T due to the stochastic behavior of the AN model used in this study. These are unlikely to degrade the perceptual intelligibility to the same degree that a large loss of speech-conveying modulations will, which corresponds to positive values for T-N. In this study, we found that the quantitative accuracy of the predictions were improved when this rectification was done, as was also the case for the previous study of Zilany and Bruce (2007a).

Following Zilany and Bruce (2007a), the template has been chosen as the output of the normal-hearing model to the unprocessed stimulus at 65dB SPL (conversational speech level) in quiet. In contrast to Elhilali et al. (2003), we keep the time and CF indices in the cortical outputs for the template and test signal in the same manner as suggested in Zilany and Bruce (2007a). This is important because the STMI scored in this way will be a good measure of the partial matches between the template and test signals and reflect the phonemic-level scoring of each subject’s verbal response to each CVC target-word (Mesgarani et al. 2008). If the cortical outputs are averaged over time as in Elhilali et al. (2003), the STMI will not be able to detect reconstruction of ENV cues at particular times and CFs.

STMI with Lateral Inhibition

As described earlier, ENV cues can be recovered from the interaction of TFS speech with the cochlear filters, which are then transduced into corresponding mean-rate neural cues. In addition to this peripherally located process, there are likely more centrally located auditory processes, such as LINs, that may convert spike-timing cues into mean-rate cues (Shamma and Lorenzi 2013). To investigate the process of how mean-rate neural cues are recovered from spike-timing cues and how this might impact predicted speech intelligibility, a simple LIN was applied to both the clean speech and chimaeric speech neurograms prior to calculating the STMI cortical responses (see Fig. 2). By itself, the STMI processing is sensitive only to mean-rate neural cues. However, with the addition of the LIN, it can assess the spike-timing cues to the extent that the LIN can convert the information from those cues into corresponding mean-rate cues (Shamma and Lorenzi 2013).

A spatial, or tonotopic, first-order difference network using neighboring AN channels was implemented to sharpen the overall neural representation, enhance formant structures and harmonics present in the neurograms, and convert spike-timing information into mean-rate cues (Shamma 1985, 1998).

The LIN was applied prior to the rectangular windowing operation in the following manner. Each constituent AN fiber PSTH response of the unprocessed clean speech neurogram, and its corresponding matched-noise neurogram, was filtered using a 32-sample Hamming window. At a 100-kHz auditory model sampling rate, this results in a lowpass filtering operation with a frequency response capturing the spectral extent of AN phase-locking (Johnson 1980). The first-order difference LIN was then applied to the smoothed neurograms, with the lower-CF response subtracted from the higher-CF response and any negative results set to zero (Shamma and Lorenzi 2013; Shamma 1985). The respective pair of neurograms for the chimaeric speech were processed in the same manner. The STMI metric was then calculated using these modified neurograms as described earlier. These processing steps were applied to all of the sentences in the speech corpus.

STMI Empirical Bounds

For both variations of the STMI, estimates of the average lower and upper bounds were determined empirically using 350 clean speech CVC target-words. Lower-bound estimates were calculated using the clean speech sentences as the unprocessed signal (producing cortical reference token, T, of Eqs. 1 and Fig. 2) and white-Gaussian noise (WGN) as the test signal (producing cortical noise token, N, of Eq. 1 and Fig. 2). Under this condition, the cortical responses are theoretically orthogonal and, with respect to Eq. 1, result in a minimum value of 0. However, due to the stochastic nature of auditory model responses and WGN generation, spurious correlations artificially inflate this expected minimum value. Upper-bound estimates were calculated using the same procedure, but clean speech was used for both the unprocessed and test signals (producing reference token, T, and noise token, N, respectively). In this case, the theoretical cortical responses would be equal, producing a maximum value of 1. However, the estimated upper bound is lower because of the stochastic effects mentioned previously.

Neurogram Similarity

The NSIM quantifies differences in neural spectro-temporal features using an image-based processing model (Hines and Harte 2010, 2012; Wang et al. 2004). Like the STMI, the NSIM can quantify informational cues linked to mean-rate neural activity, but it can also be used to quantify informational cues that reside in spike timing. In both cases, the NSIM compares a clean speech neurogram, R, and a corresponding chimaeric speech neurogram, D, as shown in Figure 2.

In the auditory model AN fiber responses, mean-rate and spike-timing neural information coexist in the same PSTH. To investigate the relative contribution by each type of information to speech intelligibility, the clean speech and chimaeric speech neurograms were processed to produce neurograms that reflect the respective cues from each source: a mean-rate neurogram averages spike-events across a set of PSTH bins, while a fine-timing neurogram retains most of the original spike-event temporal coding.

A mean-rate neurogram was produced from the CVC target-word region of an unmodified neurogram by rebinning the constituent AN fiber PSTH responses to 100-μs bins and convolving with a 128-sample Hamming window at 50 % overlap, which yields an effective upper modulation frequency limit of 78 Hz. This excludes most of the modulation frequencies due to the temporal fine structure (i.e., the harmonics of the vowels). The corresponding fine-timing neurogram was produced from the same unmodified target-word region by retaining the 10-μs bin size produced by the auditory periphery model and convolving each PSTH with a 32-sample Hamming window at 50 % overlap. In this case, the effective upper modulation frequency limit is 3125 Hz, which preserves spike-timing and phase-locking information. The convolution of each PSTH with its respective Hamming window produces a response that is more representative of a response from a larger population of AN fibers, which is a more general response than the 50-AN fiber response used here. For the NSIM metric, only 29 CFs, logarithmically spaced from 180 to 7040 Hz, are used (cf., Hines and Harte 2010, 2012), unlike the 128 CFs required by the STMI. The general equation for the NSIM is

$$\mathrm{N}\mathrm{S}\mathrm{I}\mathrm{M}(R,D)={\left(\frac{2{\mu }_R{\mu }_D+C_1}{{\mu }_R^2+{\mu }_D^2+C_1}\right)}^{\alpha }\cdot {\left(\frac{2{\sigma }_R{\sigma }_D+C_2}{{\sigma }_R^2+{\sigma }_D^2+C_2}\right)}^{\beta }\cdot {\left(\frac{{\sigma }_{RD}+C_3}{{\sigma }_R{\sigma }_D+C_3}\right)}^{\gamma }$$ 2

and is applied to each pair of mean-rate neurograms and each pair of fine-timing neurograms (Hines and Harte 2012). To compute the NSIM, a three-by-three kernel was moved across the complete target-word region of the clean speech and chimaeric speech neurograms and a local NSIM value was calculated at each position. The left-hand term of Eq. 2 characterizes a “luminance” property that quantifies the average intensity of each kernel, where the terms μ _R and μ _D are the means of the nine respective kernel elements for the “reference” and “degraded” neurograms, respectively. The middle term characterizes a “contrast” property for the same two kernels, where σ _R and σ _D are the standard deviations. The right-hand term characterizes the “structural” relationship between the two kernels and is conveyed as the Pearson product-moment correlation coefficient. C ₁, C ₂, and C ₃ are regularization coefficients that prevent numerical instability (Wang et al. 2004). A single scalar value for the overall NSIM is computed by averaging the positionally dependent, or mapped, NSIM values.

The influence of the weighting powers (α , β , γ) on phoneme discrimination using CVC word lists was investigated by Hines and Harte (2012). They optimized these powers and found that the “contrast” term (β) had little to no impact on overall NSIM performance. They further examined the influence of setting the “luminance” (α) and “structural” (γ) terms to unity and the “contrast” (β) term to zero and found the results produced under these conditions had comparable accuracy and reliability as those computed using the optimized values. They concluded that using this set of powers simplifies the NSIM and establishes a single computation for both the mean-rate and fine-timing neurograms (Hines and Harte 2012).

As was the case for the STMI and the STMI LIN, these processing steps were applied to all of the sentences in the chimaeric speech corpus.

Scaling of the NSIM Neurograms

The computation of the NSIM uses a three-by-three kernel (CFs on the ordinate and discrete-time values on the abscissa) that compares highly localized regions of the clean speech and chimaeric speech neurograms. For the fine-timing neurograms, which retain a large degree of temporal coding in the AN fiber responses, there are large regions in each neurogram without any neural activity. As a result, each NSIM kernel value in these areas approaches unity because the regularization coefficients (C ₁ and C ₃ based on the weighting parameters mentioned in the previous section) are defined by the [0, 255] scaling restriction (Hines and Harte 2010, 2012; Wang et al. 2004). The contribution of these particular values to the overall NSIM, which is the average of all the local NSIM results, effectively “swamps out” the local NSIM values from areas with neural activity that are correctly quantifying the differences between the two neurograms. Mean-rate neurograms are not affected by this behavior because their timescale is such that the vast majority of time-CF bins have some level of neural activity.

During the course of this study, we determined that the undesired effect associated with scaling the neurograms to [0, 255] could be avoided by simply not scaling them to this range and computing the localized NSIM values using neurograms in units of spikes per second (the regularization coefficients C ₁ and C ₃ were still based on the [0, 255] range). This revised scaling method has resulted in improvements in predicted outcomes in another recent study using this approach (Bruce et al. 2015).

NSIM Empirical Bounds

As with the STMI and STMI LIN, estimates of the average lower and upper empirical bounds for the mean-rate and fine-timing NSIM measures were determined experimentally. Lower-bound estimates were calculated using clean speech sentences as the unprocessed signal (producing the clean speech neurogram, R, of Eq. 2 and Fig. 2) and WGN noise as the test signal (producing the degraded neurogram, D, of Eq. 2 and Fig. 2). With these conditions, the right-hand term of Eq. 2 weighs the NSIM measure towards 0 because of the small correlations, on average, between the respective kernels of the R and D neurograms. Like the STMI, the lower bound can be non-zero due to the stochastic nature of the auditory model responses and the WGN noise. Upper-bound estimates were calculated using the same procedure, but clean speech was used for both the unprocessed and test signals (the R and D neurograms, respectively). In this case, the contribution of the “structural” term is closer to unity because of the larger correlations, on average, between the two kernels. The theoretical upper bound of the NSIM value is unity, but in practice it will be lower because of the stochastic character of the auditory model responses.

Results

Perception of Chimaeric Speech

The results of a three-way analysis of variance (ANOVA) on the phoneme scores of the main effects of subject number, number of filters, and chimaera type plus three two-factor interactions are shown in Table 1. All three factors are statistically significant, but the number of filters and chimaera type are much stronger factors than the subject number. The small but significant difference in performance of the different subjects is consistent with the results of Lorenzi et al. (2006), in which they found that some subjects had higher initial “TFS speech” perception scores than others, a difference that largely remained even after substantial training. The interactions between subject number and chimaera type and between the number of filters and chimaera type are significant, but the interaction between the subject number and number of filters is not significant.

TABLE 1.

Significance of subject number, number of filters, and chimaera type and three two-factor interactions obtained with three-way ANOVA on Phoneme Perception Data

Source	Sum sq.	d.f.	Mean sq.	F	Prob>F
Subject no.	0.83	4	0.2073	3.57	0.0064
No. of filters	72.44	6	12.073	208.14	<0.0001
Chimaera type	60.83	4	15.2074	262.18	<0.0001
Subject × no. of filters	1.8	24	0.0748	1.29	0.1553
Subject × chimaera type	3.85	16	0.2405	4.15	<0.0001
No. of filters × chimaera type	380.46	24	15.8527	273.31	<0.0001
Error	502.95	8671	0.058
Total	1023.15	8749

The intelligibility results from the speech experiment are plotted in Figures 3 and 4. The percent correct scores based on the phonemic-level scoring scheme is presented in Figure 3, while the percent correct vowels and consonants’ scores are compared in Figure 4.

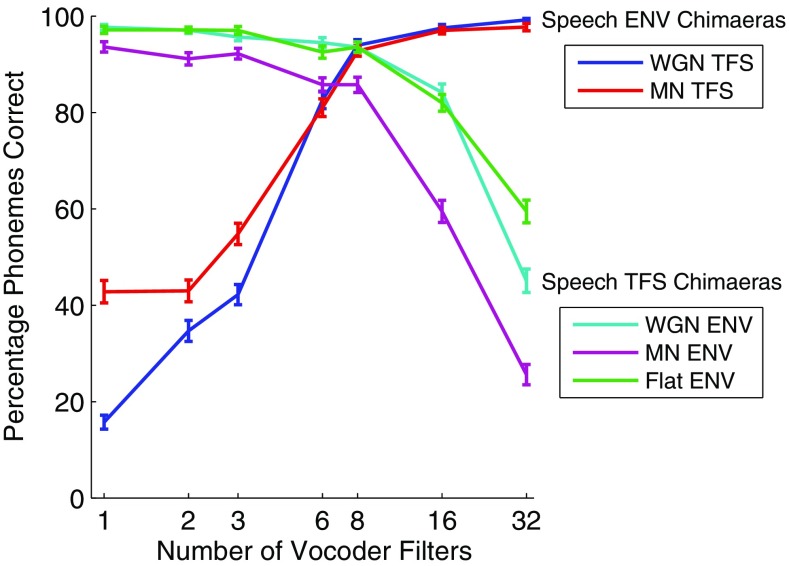
FIG. 3.

Phoneme perception scores from the listening experiment as a function of the number of vocoder filters, averaged over the words and listeners. Error bars show ± 1 standard error of the mean (SEM). Speech ENV chimaeras retain the ENV of the original speech signals and are combined with WGN or MN TFS. Speech TFS chimaeras retain the TFS of the original speech signals and are combined with WGN, MN, or Flat ENV.

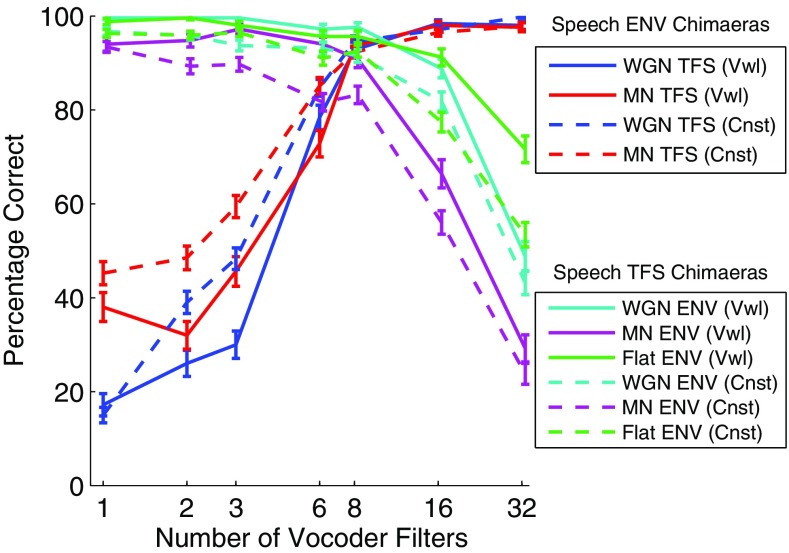
FIG. 4.

Vowel (solid lines) and consonant (dashed lines) perception scores from the listening experiment. Error bars show ± 1 SEM. As in Figure 3, Speech ENV chimaeras retain the ENV of the original speech signals and are combined with WGN or MN TFS, while the Speech TFS chimaeras retain the TFS of the original speech signals and are combined with WGN, MN, or Flat ENV.

For the Speech ENV chimaeras, subjects performed better when the number of frequency bands increased. The reverse is true for the Speech TFS chimaeras, where perceptual performance is better when the number of analysis filters used in the generation of the auditory chimaeras is decreased. These results are consistent with Smith et al. (2002).

We observe in Figure 4 that for Speech ENV chimaeras the percentage of correctly recognized consonants is higher than that of vowels when the number of vocoder filters is less than six (above which performance saturates for both consonants and vowels), whereas for Speech TFS chimaeras the vowel recognition performance is better than that of consonants in most cases. The higher scores for vowels with the Speech TFS chimaeras may be explained by the fact that they have more harmonic structure to be conveyed by TFS than consonants. This will be explored further in the modeling section below.

It can also be seen that the percentage of phonemes correctly recognized is higher for the Speech ENV chimaeras with MN TFS compared to WGN TFS (the red curve versus the blue curve in Fig. 3) for chimaeras with fewer than six vocoder filters, whereas for the Speech TFS chimaeras the MN ENV produces a reduction in phoneme recognition compared to the WGN ENV and Flat ENV cases. This suggests that the use of a noise signal matched to the individual sentence, as we have done following the methodology of Smith et al. (2002), can have quite different effects for Speech ENV versus Speech TFS chimaeras. The possible causes of these behaviors will be explored in the “Discussion” section.

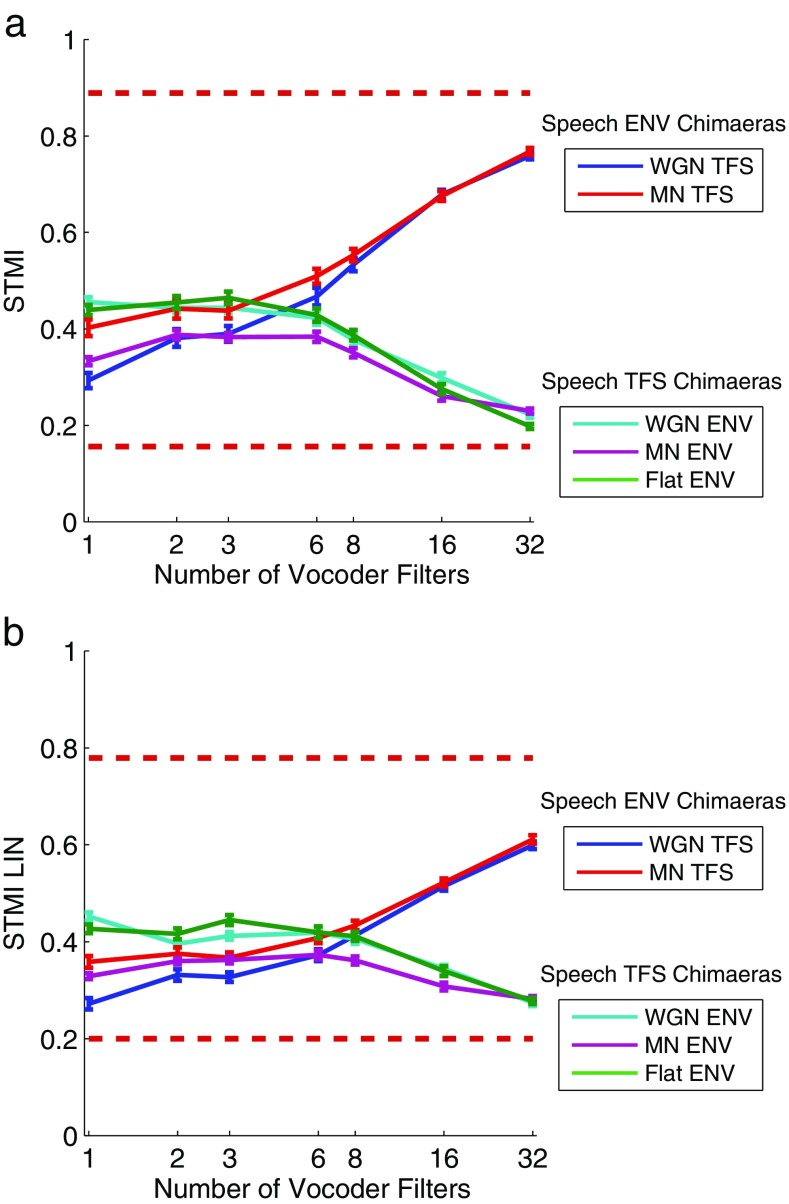
STMI Predictions of Chimaeric Speech Intelligibility

Figure 5 shows the average STMI and STMI LIN values versus the number of vocoder filters for the Speech ENV and Speech TFS chimaeras. The STMI and STMI LIN capture the general shape of the perceptual response curves shown in Figures 3 and 4.

FIG. 5.

Average STMI and STMI LIN values (error bars ± 1 SEM) as a function of the number of vocoder filters. The horizontal dashed lines in each panel show the empirically determined lower and upper metric bounds. a Average STMI values. The lower bound is 0.16 and the upper bound is 0.89. b Average STMI LIN values. The lower bound is 0.20 and the upper bound is 0.78.

For the Speech ENV chimaeras, both the STMI and the STMI LIN demonstrate less noticeable asymptotic character than the perceptual response curves. This difference is more drastic under narrowband conditions (i.e., large number of vocoder filters) where the curves are more linear and both measures fail to capture the strong perceptual performance, from just below 20 % to almost 100 %, despite smaller value ranges which are shown with the estimated empirical bounds for each measure. Both measures produce larger values for the MN TFS type relative to the WGN TFS type under broadband conditions (significant difference at one band for both measures; one-sided paired t test at p = 0.01), which is consistent with the perceptual results shown in Figure 3. With increasing numbers of vocoder bands, the difference between the curves gradually decreases and both measures produce similar values at eight or more bands. In the perceptual data, the predictions for the WGN TFS and MN TFS converge at six bands. The STMI had lower and upper empirical bounds of 0.16 and 0.89, respectively, and produced higher values than the STMI LIN for larger numbers of vocoder filters. The STMI LIN had lower and upper empirical bounds of 0.20 and 0.78, respectively.

For the Speech TFS chimaeras, both measures again capture the same relative placement of the three Speech TFS chimaera types as the perceptual responses, but again demonstrate only a mild asymptotic behavior across a decreased range of values. An important difference between the curves in Figure 5 and the perceptual responses shown in Figure 3 is that the STMI predictions for the MN ENV chimaera converge with those for the other two chimaera types as the number of filters increases above 8. STMI values for the WGN ENV and Flat ENV types are larger than the MN ENV type across all vocoder bandwidths, except at 32 bands (for both the STMI and the STMI LIN, the MN ENV type is significantly different than the WGN ENV type at one band and significantly different than the Flat ENV type at one, two, three, and eight bands at p = 0.01 for all cases). As with the Speech ENV chimaeras, the STMI and STMI LIN produce values within their respective lower and upper empirical bounds, but have a smaller range than the perceptual responses, with the predicted maximum intelligibility for the Speech TFS chimaeras being noticeably less than the predicted maximum intelligibility for the Speech ENV chimaeras. These results suggest that the STMI is able to assess the original and recovered ENV cues conveyed by the Speech TFS chimaeras (Heinz and Swaminathan 2009; Ibrahim and Bruce 2010), but the mean-rate representation as measured by the STMI cannot fully explain the perceptual responses.

NSIM Predictions of Chimaeric Speech Intelligibility

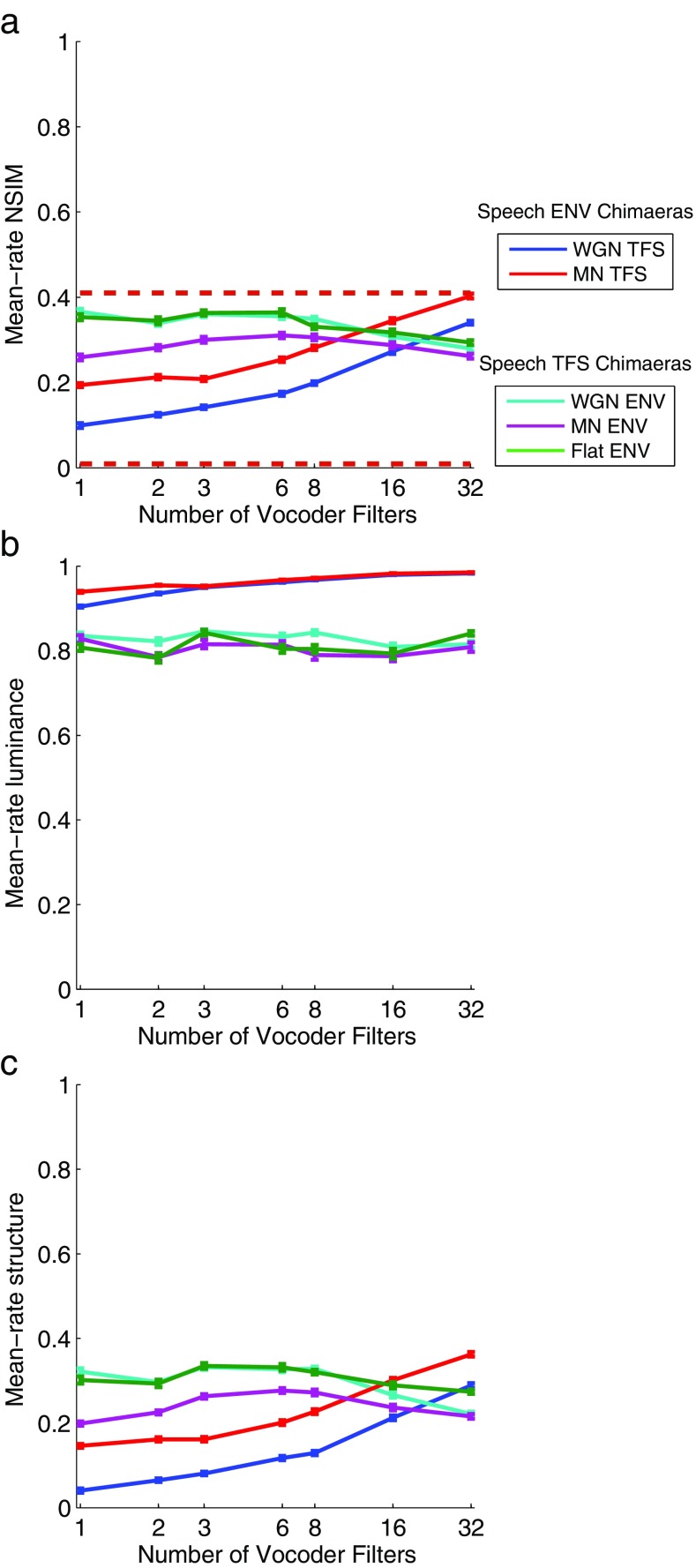
Figures 6 and 7 show the average mean-rate and fine-timing NSIM values (Figs. 6a and 7a) for the chimaeric speech corpus as a function of the number of vocoder filters, respectively, along with the constituent “luminance” (Figs. 6b and 7b) and “structure” values (Figs. 6c and 7c) that are multiplied to obtain the NSIM value according to Eq. (2).

FIG. 6.

a Average mean-rate NSIM values as a function of the number of vocoder filters. The horizontal dashed lines show the empirically determined lower and upper bounds. The lower bound is 0.0090 and the upper bound is 0.41. Each mean-rate NSIM value is the product of the “luminance” term and “structure” term as given in Eq. (2). Averages of the mean-rate luminance and structure values for the different conditions are plotted in b, c, respectively. Error bars ± 1 SEM.

FIG. 7.

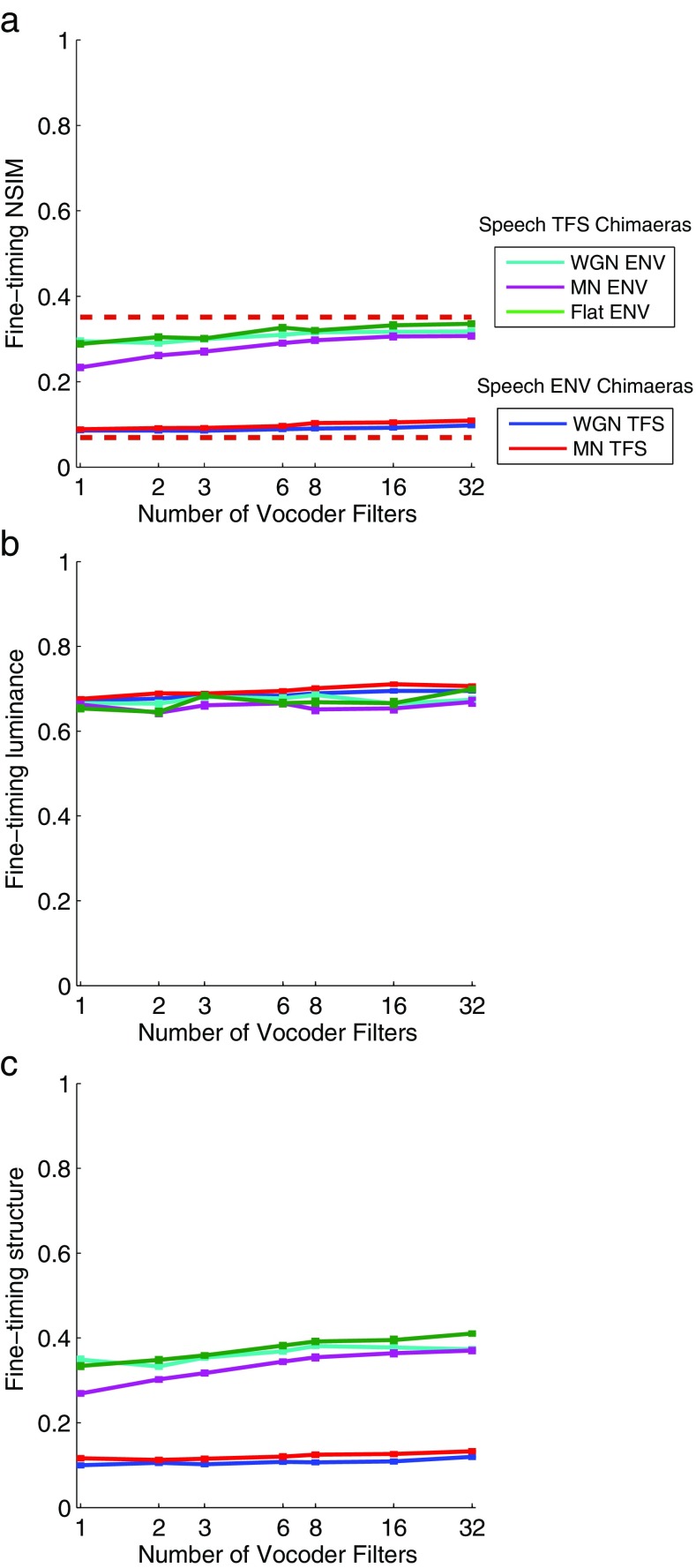
a Average fine-timing NSIM values as a function of the number of vocoder filters. The horizontal dashed lines show the empirically determined lower and upper bounds. The lower bound is 0.069 and the upper bound is 0.35. Each fine-timing NSIM value is the product of the “luminance” term and “structure” term as given in Eq. (2). Averages of the fine-timing luminance and structure values for the different conditions are plotted in b, c, respectively. Error bars ± 1 SEM.

Mean-Rate NSIM

Figure 6a shows the average mean-rate NSIM values for the chimaeric speech corpus. For the Speech ENV chimaeras, the mean-rate NSIM correctly predicts the higher perceptual scores for the MN TFS chimaera type relative to the WGN TFS chimaera type when one, two, or three vocoder bands are used. However, it fails to predict the convergence in perceptual performance as the number of vocoder bands increases (cf. Fig. 3). The predictions for the Speech TFS chimaeras correctly predict the lower intelligibility of the MN ENV chimaera type compared to the WGN ENV and Flat ENV chimaera types, but the predictions do not reflect the large decrease in perceptual performance that was found with an increase in the number of vocoder bands (cf. Fig. 3). Overall, the mean-rate NSIM predictions are just slightly better than the STMI predictions, which may be due to the slightly higher maximum modulation rate considered by the mean-rate NSIM. Jørgensen et al. (2013) and Kates and Arehart (2014) have also utilized maximum modulation rates greater than 32 Hz in their intelligibility predictors. One other major difference between these metrics that could be particularly important for vocoder and chimaeric processing is that the NSIM values will be affected by spectral flattening, whereas the STMI inherently compensates for long-term spectral flattening by including a base-spectrum operation that subtracts an estimate of the long-term spectrum prior to computing the cortical response of the metric.

Figure 6b, c respectively illustrate how the “luminance” and “structure” terms of Eq. (2) each contribute to the MR NSIM values for these predictions. The higher luminance values for the Speech ENV chimaeras compared to the Speech TFS chimaeras indicate that the overall magnitudes of the discharge rates for the Speech ENV chimaeras are closer to those for the unprocessed reference neurograms than are the discharge rates for the Speech TFS chimaeras. However, the main effects of the number of vocoder filters and the chimaera type that are observed in the MR NSIM values are seen to be driven by the structure term.

Fine-Timing NSIM

Figure 7a shows the average fine-timing NSIM values for the chimaeric speech corpus. In general, the fine-timing NSIM does not exhibit any strong dependence on the number of vocoder bands for any of the chimaera types. The fine-timing NSIM should also be somewhat dependent on mean-rate cues; however, as was observed for the mean-rate NSIM predictions, it appears that spectral flattening introduced by the chimaera vocoder distorts the NSIM’s representation of mean-rate cues. The fine-timing NSIM values for the Speech TFS chimaera types are notably larger and located near the upper empirical bound, while the fine-timing NSIM values for the Speech ENV chimaera types are smaller and are located near the lower empirical bound.

Figure 7b, c show how the constituent luminance and structure values each contribute to the FT NSIM values. The number of vocoder filters and the chimaera type are seen to produce very little difference in the luminance values when using the very small time bins of the FT neurogram. Thus, the effects of the number of vocoder filters and the chimaera type that are observed in the FT NSIM values are caused entirely by the structure term.

In conjunction with its ability to differentiate the Speech ENV and Speech TFS chimaeras and capture the spread of empirical values, the fine-timing NSIM captures a weak dependence on the number of vocoder bands for the Speech TFS chimaera types. Unlike the associated perceptual results shown in Figure 3, the Speech TFS fine-timing NSIM values are easily seen to become larger, not smaller, as the number of vocoder filters increases. To understand how this could occur, we examined how vocoder processing changed the acoustic and neural representations of the synthetic vowel /ε/. We replaced the CVC target-word with the vowel in an unprocessed sentence in order to retain the contextual cues and used it to construct 1-band and 32-band versions of the Speech TFS with WGN ENV and Speech ENV with WGN TFS chimaeras. These sentences were then preprocessed and applied to the auditory periphery model to produce the corresponding neurograms. We used the spectral envelopes to examine the signals in the acoustic domain, along with the average localized interval rate (ALIR; Sachs and Young 1980; Voigt et al. 1982) and mean-rate profiles in the neural domain. The ALIR is a quantitative measure that characterizes the strength of phase-locking in spike-timing activity to the spectrum of a speech signal. It produces an average “interval rate” value for all AN fibers whose CFs lie within 0.5 octave of each frequency sample and thereby indicates the strength of the tonotopically appropriate phase-locking representation of each frequency component present in the stimulus. The ALIR is similar to the better-known average localized synchronized rate (ALSR; Young and Sachs 1979) but is based on the interval histogram rather than the period histogram and is thus more suited to stimuli that are not perfectly periodic such as whispered vowels as studied by Voigt et al. (1982) or the Speech ENV with noise TFS chimaeras in the present study. In healthy auditory nerves, both the ALIR and the ALSR exhibit sharp peaks at the formant frequencies of vowels below 4 kHz (Sachs and Young 1980; Young and Sachs 1979), a phenomenon that is referred to as synchrony capture. For whispered vowels, the peaks in the ALIR are still present at the formant frequencies but are less pronounced (Voigt et al. 1982). The mean-rate profile is the mean-rate activity across time as a function of CF for the duration of the synthetic vowel. Figure 8 shows the acoustic spectral envelope plots and the ALIR and mean-rate profiles for the Speech TFS with WGN ENV (left column) and the Speech ENV with WGN TFS (right column) vowel chimaeras compared to the unprocessed vowel.

Figure 8a shows the acoustic spectral envelopes for the Speech TFS with WGN ENV chimaeras and the unprocessed vowel. Apart from the alternation of harmonic magnitudes above 700 Hz, the 32-band chimaera compares more favorably to the unprocessed vowel than the 1-band chimaera. The second and third formant magnitudes for the 32-band chimaera are slightly amplified compared to the magnitudes for the unprocessed vowel. In contrast, the 1-band chimaera still clearly shows all three formants, but the magnitudes for the second and third formants are attenuated. Below the first formant, the amplitudes of all the harmonics for the 1-band chimaera are noticeably smaller, especially at 300 Hz, which indicates a decreased level of low-frequency TFS. The harmonic amplitudes for the 1-band and 32-band chimaeras are larger than the unprocessed vowel spectrum between the first and second formants. The ALIR analysis shown in Figure 8c indicates that strong levels of synchrony are still present in response to the first and second formants for the 1-band and 32-band chimaeras, while the synchrony at the third formant is weakened somewhat for the 32-band chimaera and totally lost for the 1-band chimaera. This indicates that the level of neural synchrony to vowels is somewhat independent of the number of vocoder bands for the Speech TFS chimaeras, but the level of synchrony is slightly larger at second and third formants for the 32-band chimaera compared to the 1-band chimaera. This is consistent with the fine-timing NSIM curves shown in Figure 7, where the curves for the Speech TFS chimaeras increase as the number of vocoder filters increases. Figure 8e shows the mean-rate profiles for the vowel. With the use of the static vowel, there is very little to no ENV reconstruction occurring due to cochlear filtering for either the 1-band or the 32-band chimaeras, and thus the mean-rate representation is degraded for both the 1-band and the 32-band Speech TFS vowel chimaeras.

Figure 8b shows the acoustic spectral envelopes for the Speech ENV with WGN TFS chimaeras and the unprocessed vowel. The 1-band chimaera envelope is elevated across all of the harmonic frequencies compared to the 32-band chimaera, and the unprocessed vowel and the formants are not clearly represented. In contrast to the 1-band chimaera, the spectral envelope for the 32-band chimaera is well defined and it agrees well with the unprocessed vowel. However, the second and third formant magnitudes are slightly attenuated and the magnitudes of harmonic frequencies below 500 Hz are somewhat smaller. The ALIR results for the Speech ENV vowel chimaeras plotted in Figure 8d show that the level of synchrony is severely degraded when a noise TFS is used in the chimaera. There is little to no synchrony capture at the second and third formants for both the 1-band and 32-band chimaeras, although a small peak is present at the second formant for the 32-band chimaera. At the 200- and 300-Hz harmonics and the first formant, the 32-band chimaera produces some phase-locking that is effectively eliminated for the 1-band chimaera. This is consistent with the fine-timing NSIM results shown in Figure 7, where the Speech ENV chimaeras have very low fine-timing NSIM values, almost at the empirical lower bound, and a very slight increase in values is observed for increasing numbers of vocoder filters. Figure 8f shows the mean-rate profiles for the Speech ENV with WGN TFS vowel chimaeras. For the 32-band chimaera, there is good agreement with the unprocessed vowel, but the profile for the 1-band chimaera is severely degraded. This is consistent with the STMI behavior (see Fig. 5a) and the mean-rate NSIM behavior (see Fig. 6a), where there are low values under broadband conditions (small numbers of vocoder filters) and higher values under narrowband conditions (large numbers of vocoder filters).

From these results, we can see that the fine-timing NSIM values should be larger for the 32-band chimaera relative to the 1-band chimaera (due to a greater level of similarity between the ALIR for the 32-band chimaera and the ALIR for the unprocessed vowel), which is consistent with the fine-timing NSIM behavior shown in Figure 7 for the Speech TFS versions of the NU-6 phonemes.

The neural measure predictions suggest that the STMI is the most suitable measure for quantifying the original speech ENV cues that are conveyed by the AN mean-rate representation and the recovered ENV from cochlear filtering of the TFS speech, while the fine-timing NSIM is able to independently quantify the TFS speech cues conveyed by the AN spike-timing representation. However, an important issue is that the spike-timing representation does not vary strongly with the number of vocoder filters, so the contribution of the FT NSIM in explaining the perceptual data will be limited to the effects of chimaera type. Based on these results, regression models will be explored in the following section that quantify the accuracy of the different predictors, as well as a combined STMI and fine-timing NSIM predictor.

Correlations Between Neural Predictions and Perception of CVC Words

Each regression model was computed using 35 data points that were aggregated across all 5 chimaera types, with 7 data points coming from each chimaera type (350 sentences per chimaera type, with phoneme scores averaged across the 5 normal-hearing listeners and the 50 sentences for each of the 7 vocoder filter sets and neural measures averaged across the 50 sentences for each of the 7 vocoder filter sets).

Prior to computing the linear regression coefficients for each model, the neural measures were normalized to a percentage of their respective empirical range. As characterized in the plots for each neural measure, the range defined by the lower and upper empirical bounds is reduced compared to the perceptual data. The reasons why the ranges are relatively narrow is because of the size of the time bins and the number of fibers being simulated, and the overall responses are still relatively random due to the stochastic nature of auditory nerve firing. With the normalization, predictions can span those ranges.

Each metric value was normalized using the expression

$$\mathrm{M}{\mathrm{V}}_{\mathrm{\text{normalized}}}=\frac{\left(\mathrm{MV}-\mathrm{M}{\mathrm{V}}_{\mathrm{\text{lowerbound}}}\right)}{\left(\mathrm{M}{\mathrm{V}}_{\mathrm{\text{upperbound}}}-\mathrm{M}{\mathrm{V}}_{\mathrm{\text{lowerbound}}}\right)}·100$$ 3

where MV is an unnormalized data point, MV_lowerbound and MV_upperbound are the empirically determined lower and upper bounds for a given measure, and MV_normalized is the normalized data point used in the regression calculations.

Several first-order linear regression models were constructed using the normalized neural measures and the perceptual scores, using the general form of

$$\mathrm{RAU}\left(\mathrm{PC}\right)=\mathrm{b}0+\mathrm{b}1·M_1+\mathrm{b}2·M_2+\mathrm{b}3·M_1·M_2$$ 4

where RAU(PC) are the average rationalized arcsine transformed (RAU; Studebaker 1985) fractional phonemic-level scores for the CVC target-words, and M ₁ and M ₂ correspond to normalized versions of two neural measures. The RAU transform is a method used in speech research to mitigate the floor and ceiling effects commonly observed in perceptual performance data. For models using a single neural predictor measure, M ₂ is set to zero. For models with more than two neural measures, each measure had its own term and was combined with each of the remaining measures in two-term product interaction terms (i.e., no interaction terms with more than two predictors were included). Table 2 summarizes the linear regression models investigated in this study and shows the respective adjusted R ² value and corrected Akaike information criterion (AICC) ratios (Burnham and Anderson 2002) for each model. The AICC ratio for each model is computed relative to the STMI and fine-timing NSIM (spikes per second) with interaction model (gray row in Table 2). We will justify our reasons for doing this below.

TABLE 2.

Summary of regression models

Except where indicated, the STMI is calculated for best modulation rates up to 32 Hz and all NSIM measures are computed using 29 CF neurograms

STMI spectro-temporal modulation index without lateral inhibitory network, STMI LIN spectro-temporal modulation index with lateral inhibitory network, MR NSIM mean-rate neurogram similarity measure, FT NSIM fine-timing neurogram similarity measure

p < 0.001 for all fits except as noted

^aThe adjusted R ² is the proportion of variation in the response variable accounted for by the model regressors. However, unlike the R ², it only increases when an increase in explained response variation is more likely than chance when additional regressors have been added to the model

^bThe corrected Akaike information criterion ratio (Burnham and Anderson 2002) is adjusted for a finite sample size. The sample size is 35, which corresponds to the number of average RAU-transformed perceptual scores and data points for each neural measure. An AICC ratio smaller than 0.5 indicates that the model is less likely than the “best” model (gray row of table) to minimize information loss, while an AICC ratio larger than 0.5 indicates that the model is more likely than the “best” model to minimize information loss

STMI Regressions

We examined two regression models based on the STMI. For the STMI as the single predictor, the adjusted R ² value for the predicted CVC target-word identification scores is 0.292 (significant at p value <0.001). The adjusted R ² value increases to 0.507 (significant at p value <0.001) when the neurograms are conditioned using the spatial, first-order difference LIN prior to the computation of the STMI. The LIN converts a portion of spike-timing cues to mean-rate cues, thereby characterizing aspects of auditory processing that produce centrally recovered mean-rate cues as proposed by Shamma and Lorenzi (2013). Table 3 summarizes the regression coefficients and statistics for the STMI and STMI LIN models computed using the corresponding scale-normalized measures.

TABLE 3.

Summary of the STMI regression models using scale-normalized values

STMI		STMI LIN
b1 (STMI)	0.83 (<0.001)	b1 (STMI LIN)	1.47 (<0.001)
Adj. R 2	0.292	Adj. R 2	0.507
p value	<0.001	p value	<0.001

The b1 coefficient of Eq. 4 is shown with its p value in parenthesis. The adjusted R ² value, indicating the overall goodness of fit, and p value for each model are also shown

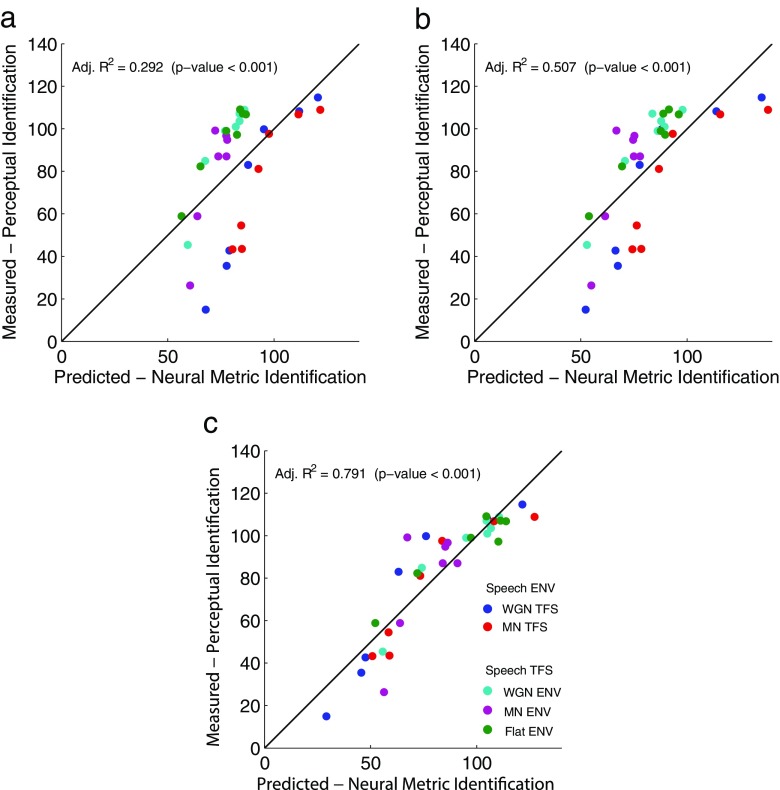
Figure 9a, b shows the RAU-transformed average phoneme scores from our human subjects plotted versus the predicted perceptual scores for the STMI and STMI LIN models, respectively. The diagonal lines indicate perfect prediction. As shown in Figure 9a, b, the STMI-based models overpredict the Speech ENV chimaeras and underpredict the Speech TFS chimaeras, but inclusion of the LIN does improve the predictions, reflected in a tighter clustering around the diagonal line and a higher adjusted R ² value. These results demonstrate that neural coding of mean-rate information, coming from the original mean-rate cues, the peripherally recovered mean-rate cues as indicated by the conversion of spike-timing cues to mean-rate cues by the LIN, and centrally recovered mean-rate cues (Shamma and Lorenzi 2013), are important contributors to phonemic-level identification (Shamma and Lorenzi 2013; Swaminathan and Heinz 2012).

FIG. 9.

Predictions of the RAU-transformed subjective scores using the linear regression models. a STMI, b STMI LIN, and c STMI and fine-timing NSIM with interaction. The adjusted R ² value and p value for each regression are shown in the upper lefthand corner of its respective panel. The diagonal line represents a one-to-one correspondence between the perceptual scores and the associated predictions; for points lying under the line, the model prediction is higher than the perceptual score, while for points above the line the prediction is lower.

NSIM Regressions

We examined several models that included the mean-rate and fine-timing NSIM measures independently, as well as their combination. Table 4 summarizes the regression coefficients and statistics for the NSIM models. Like the STMI models, the NSIM models were computed using the scale-normalized values.

TABLE 4.

Summary of the NSIM linear regression models

MR NSIM		FT NSIM		MR NSIM and FT NSIM
b1 (MR NSIM)	0.959 (<0.001)	b1 (FT NSIM)	0.185 (0.157)	b1 (MR NSIM)	1.0916 (<0.001)
				b2 (FT NSIM)	−0.953 (0.0570)
				b3 → b1 × b2	0.00769 (0.166)
Adj. R 2	0.563	Adj. R 2	0.0312	Adj. R 2	0.652
p value	<0.001	p value	0.157	p value	<0.001

The b1, b2, and b3 coefficients of Eq. 4 are shown with the respective p value in parenthesis. The adjusted R ² value and p value for each model are also shown

When compared to the STMI and the STMI LIN models, the mean-rate NSIM model performs well in predicting the variability of the CVC target-word identification scores, having a slightly higher adjusted R ² value of 0.563 (significant at p value <0.001). Although the STMI LIN and mean-rate NSIM have comparable adjusted R ² values, their behavior for the different chimaera types are not identical (compare Fig. 5b to Fig. 6a), suggesting that each measure might be representing different aspects of the neural representation of the speech but equally well.

Unlike the mean-rate NSIM, when the fine-timing NSIM is used as the single regressor variable, it is unable to account for any noteworthy level of variability in the CVC target-word identification scores. The adjusted R ² value is 0.0312 with a p value of >0.05. Thus, the fine-timing NSIM on its own is not a viable measure to predict the perception of chimaeric speech, which is consistent with the observations of Swaminathan and Heinz (2012).

The combination of the mean-rate NSIM and the fine-timing NSIM with an interaction term leads to somewhat improved predictions with an adjusted R ² value of 0.652 (significant at p value <0.001). The fine-timing NSIM coefficient is almost significant at a level of p = 0.05, while the mean-rate NSIM coefficient is significant. However, the interaction term is not significant at a p value of 0.166. With the removal of the interaction term, the fine-timing NSIM coefficient becomes significant (the mean-rate NSIM remains significant), but the adjusted R ² value decreases to 0.641. These results indicate that combining informational cues from the mean-rate and fine-timing neural measures can produce strong predictions of chimaeric speech.

STMI with NSIM Regressions

We examined several models that combined the STMI and the NSIM measures. The STMI and mean-rate NSIM quantify mean-rate neural cues, but each measure does it in a different way. The STMI, with its base-spectrum subtraction operation, quantifies localized spectro-temporal modulations, while the mean-rate NSIM is influenced by the global spectral shape. We did examine the use of base-spectrum subtraction in the mean-rate NSIM, but found that it did not have a large influence. Additionally, the mean-rate NSIM will have some redundancy with the STMI (because they are both quantifying rate-place information) and with the fine-timing NSIM (because they are using the same mathematical framework).

Table 5 summarizes the regression coefficients and statistics for the combined STMI and NSIM models. Combining either the mean-rate NSIM or the fine-timing NSIM in a regression model with the STMI produces greatly improved predictions compared to any of the predictors considered above. The resulting adjusted R ² value for these two models is around 0.8. However, there are some principled reasons why the combination of the fine-timing NSIM with the STMI could be a better choice than the mean-rate NSIM. The regression model with the mean-rate NSIM leads to a significant interaction term, which makes it somewhat difficult to interpret. This is likely caused by the redundant representation of mean-rate information between the STMI and mean-rate NSIM, as noted above. In contrast, combining the fine-timing NSIM with the STMI produces an interaction term that is not significant. Removing the interaction term in the regression only makes the adjusted R ² and AICC ratio values drop very slightly (see Table 2). Thus, the STMI and the fine-timing NSIM can be considered to be contributing complementary mean-rate and spike-timing information, respectively, to the overall intelligibility for this speech chimaera corpus.

TABLE 5.

Summary of the STMI with NSIM linear regression models

STMI and MR NSIM		STMI and FT NSIM
b1 (STMI)	2.907 (<0.001)	b1 (STMI)	1.357 (<0.001)
b2 (MR NSIM)	1.767 (<0.001)	b2 (FT NSIM)	0.444 (<0.05)
b3 → b1 × b2	−0.0257 (<0.001)	b3 → b1 × b2	0.00598 (p = 0.139)
Adj. R 2	0.803	Adj. R 2	0.791
p value	<0.001	p value	<0.001

The b1, b2, and b3 coefficients of Eq. 4 are shown with the respective p value in parenthesis. The adjusted R ² value and p value for each model are shown

Figure 9c shows the predictions for the STMI and fine-timing NSIM with interaction model. The predictions from this model are more accurate overall compared to the STMI and STMI LIN models, and the residual errors are more balanced than the predictions of the STMI and STMI LIN models. For the Speech ENV chimaeras, the combined model slightly overpredicts the behavioral data under broadband and narrowband vocoding conditions, but slightly underpredicts for more moderate vocoding bandwidths. For the Speech TFS chimaeras, the combined model somewhat underpredicts the Flat ENV type and slightly overpredicts the MN ENV type in broadband vocoding conditions, but somewhat overpredicts the Flat ENV type and underpredicts the MN ENV type in narrowband vocoding conditions. The predictions of the WGN ENV are evenly distributed about the diagonal line.

We also examined a number of other regression models including different combinations of the STMI and NSIM metrics, as well as some variants on these metrics such as the original neurogram scaling used by Hines and Harte (2010, 2012) and altering the number of CFs used in the NSIM to match the number used in the STMI. However, all of these alternatives produced poorer predictions as quantified by the adjusted R ² value and/or the AICC value (Wirtzfeld 2017). Thus, the most accurate model while remaining readily interpretable is that combining the STMI and fine-timing NSIM with or without an interaction term, which is still able to account for approximately 78–79 % of the variance in the phoneme perception data.

DISCUSSION

Our intelligibility results (Figs. 3 and 4) qualitatively match the results of Smith et al. (2002), where it was observed that speech reception improves as the number of vocoder bands is increased for the Speech ENV chimaeras but degrades for the Speech TFS chimaeras. When a matched-noise is used for the TFS in Speech ENV chimaeras, the intelligibility improves relative to the intelligibility for the chimaeras with a WGN TFS (see Figs. 3 and 4) for vocoders with fewer than six filter bands. The STMI is able to predict this effect (see Fig. 5a), suggesting that even with the phase randomization used to create the MN TFS, there is still some amount of ENV restoration from this TFS occurring at roughly the correct time, enough to boost intelligibility somewhat. In contrast, when MN is used for the ENV of the Speech TFS chimaeras, the intelligibility scores are decreased relative to those obtained with the Flat ENV or WGN ENV (see Figs. 3 and 4). Again, the STMI is generally able to predict this behavior (see Fig. 5a). In this case, it appears that the reduction in intelligibility can be explained by the MN ENV having a strong spectral tilt that degrades the rate-place representation more so than does the flattening of the overall spectrum for the Flat ENV and WGN ENV chimaeras. These differing effects of using MN for the Speech ENV and Speech TFS chimaeras suggest that it would be better to use WGN for speech-noise chimaeras in future studies. However, any issues with using MN in the Smith et al. (2002) study may have been smaller than observed in the present investigation because the length of the sentences that they used compared to the primer-phrase plus NU-6 word utterances used here. Note that the noise type (MN versus WGN) primarily influences the STMI for the Speech ENV chimaeras but has an effect on both the STMI and the fine-timing NSIM for the Speech TFS chimaeras (compare Fig. 5 to Fig. 7).

Consonant recognition scores indicate significant intelligibility (approximately 80 %) for the Speech TFS with Flat ENV stimuli when using 16 vocoder filters (see Fig. 4). This is in agreement with Lorenzi et al. (2006) and Gilbert and Lorenzi (2006), who have reported consonant recognition of approximately 90 % after repeated training in response to nonsense VCV stimuli processed to contain only TFS information. In Lorenzi et al. (2006), 5-min training sessions were used and most of the normal-hearing subjects reached stable performance after about three sessions. In our case, although separate training sessions were not provided, analysis of the scores as a function of time within the 1-h session indicates that the subjects’ recognition performance improves over time. The improvement in the second half of the session was relatively small, which suggests that the perceptual performance may be approaching its asymptote within the first half hour of the session. This means that instead of having many short-duration training sessions, experiments can use a single relatively long-duration test session knowing that the recognition performance is likely to stabilize within approximately half an hour. Moore (2008) indicated the need for training in order to achieve significant recognition scores because the auditory system is not attuned to processing TFS cues in isolation from envelope cues. Further, TFS cues in processed stimuli are distorted compared to unaltered speech, which again could demand training. The results of Swaminathan et al. (2014) further suggest that there may be a complex interaction when learning of chimaeras with speech TFS is interleaved with learning of chimaeras lacking speech TFS. The patterns of learning experienced in our study may have been simplified because the different chimaera types were blocked into separate sessions. Furthermore, the subjects in our study may have been assisted by listening to the processed version of the primer phrase “Say the word…” ahead of each NU-6 target word. Davis et al. (2005) have shown that intelligibility of vocoded speech is increased if a known utterance is provided first with the specific vocoder processing, suggesting that the primer phrase in our NU-6 test material could provide a top-down lexical context for each target word.

The higher vowel recognition scores for the Speech TFS chimaeras may be explained by the fact that they have more harmonic structure that is conveyed by TFS compared to consonants (see Fig. 4). On examination of the ALIR profiles for the Speech TFS with WGN ENV chimaera of the synthetic vowel, which is shown in Figure 8c, the first, second, and third formants of the vowel are well represented. The level of synchrony at the first formant for the 1-band chimaera is larger compared to the 32-band chimaera. However, the level of synchrony for the 32-band chimaera is higher at the second and third formants, which supports the higher fine-timing NSIM values under narrowband conditions as shown in Figure 7. In contrast to the robust harmonic representation of vowels by the Speech TFS chimaeras, the Speech ENV chimaeras degrade the harmonic structure of vowels. In Figure 8d, which shows ALIR profiles for the Speech ENV with WGN TFS chimaera of the vowel, the formants are not well represented by the synchronized response. This is consistent with the perceptual results for Speech ENV chimaeras shown in Figure 4, where the subjects in our study exhibited poorer vowel intelligibility compared to consonant intelligibility for Speech ENV chimaeras.

The predictive accuracy of the regression modeling results for a combined model with the STMI and fine-timing NSIM (with interaction) suggests that, as Swaminathan and Heinz (2012) concluded for consonant perception in nonsense VCV words, phoneme perception in real CVC words is achieved primarily through spectro-temporal modulations in the mean rate of AN fibers, but spike-timing information does assist in representing the TFS of voiced speech. This conclusion is slightly at odds with the results of Swaminathan et al. (2014) and Léger et al. (2015a), both of which suggested that perhaps all of the consonant perception of their Speech TFS VCVs could be explained by ENV reconstruction. One difference is due to how the envelope was reconstructed, with their 40-channel filterbank versus our use of the Zilany et al. (2009, (2014) auditory periphery model. A larger difference, however, could be that our study included vowel perception and the TFS and spike-timing cues for vowels appear to be quite resistant to chimaera processing (see Fig. 8). This importance of TFS and spike-timing information for vowels is consistent with the conclusions of Fogerty and Humes (2012).

While the best explanation of the chimaera perception data appears to be obtained when spike-timing cues are included, there are some alternative possibilities worth discussing. Inclusion of the LIN processing in the STMI computation improved the accuracy of its speech chimaera predictions. There are general areas of perception where lateral inhibition networks are believed to play an important role, such as sharpening spatial input patterns to highlight their edges and peaks, which could be particularly useful in background noise, and to sharpen the temporal changes in the input (Hartline 1974). This latter property might potentially counteract the spread of excitation exhibited in the cochlea for speech presented at conversational levels. In Shamma and Lorenzi (2013), they hypothesize that a LIN is one possible approach to regenerate an ENV neurogram using spike-timing information associated with the phase-locking response to TFS, and it is this property that we have focused on in the present study. On the other hand, the combined model of the STMI without the LIN and the fine-timing NSIM provides more accurate predictions of the chimaera data, suggesting that the spectral representation of the STMI without the LIN is sufficient and that the LIN extracts some amount, but not all, of the spike-timing information contained in a given neurogram. Another possibility is that the STMI does not accurately capture all of the mean-rate information contained in the AN responses. The STMI computation is based on a normalized difference between spectro-temporal modulations in the AN mean-rate representation (see Eq. 1), whereas alternative intelligibility predictors have instead measured the correlation between the ENV representations of template and test speech signals (Kates and Arehart 2014; Swaminathan and Heinz 2012). Comparison of these alternative neural ENV computation methods, along with some recently published intelligibility metrics (Hossain et al. 2016; Jassim and Zilany 2016), warrants future investigation. Alternative measures of spike-time coding could also be evaluated. One issue with the fine-timing NSIM is that its use of 3 × 3 CF-time windows makes it very sensitive to phase distortion or delays in acoustic stimuli. Some forms of phase distortion or delay can affect intelligibility (Elhilali et al. 2003), but many do not. In this study, we dealt with this issue by using zero-phase filtering in our chimaera processing, but avoiding or compensating for phase delays introduced by realistic acoustic signal processing algorithms is not always straightforward. Therefore, spike-timing metrics that do not depend on the absolute phase of the spike-timing responses (Kates and Arehart 2014; Swaminathan and Heinz 2012) may be better suited in these cases. Also of interest is how the results of this study would be affected by the presence of background noise—will the spike-timing cues representing voiced speech be robust to background noise, as indicated by Sachs et al. (1983), such that they play a stronger role at low SNRs?

While it may be more parsimonious to have a single prediction framework, rather than the combined STMI and fine-timing NSIM regression model with different numbers of CFs and different formulations for computing the measure values, we believe that this hybrid approach is not inconsistent with the diversity of cell types and circuitry located in the cochlear nucleus that produce quite different spectro-temporal representations and thus enhance different aspects of sound information (Joris et al. 2004; Young and Oertel 2003). In regards to the NSIM predictor, we find that our results do not support the statement in Hines and Harte (2012) that the values of the regularization coefficients relative to the scaling of the neurograms have negligible impact on NSIM values. Further, this alternative neurogram scaling approach has been found to produce greatly improved predictions in complementary studies (Bruce et al. 2013; Bruce et al. 2015).

CONCLUSIONS

The goals of this paper were to establish a methodological approach for predicting the intelligibility of chimaeric speech in quiet and use it to establish novel insights into how mean-rate and spike-timing cues contribute more generally to speech perception. Chimaera vocoder processing was used to modify the ENV and TFS of CVC words in a lexical context and thereby the levels of associated neural mean-rate and spike-timing representations. In particular, we found that the number of vocoder bands for the Speech TFS chimaeras does not greatly affect the spike-timing representation of the TFS. This behavior has achieved our original goal of using chimaera processing to create more independent degradation of mean-rate and spike-timing cues than that caused by background noise or hearing impairment. However, because the mean-rate representation changes as a function of both the number of vocoder bands and the chimaera type, while the spike-timing representation changes mainly as a function of chimaera type and only weakly as a function of number of vocoder bands, the mean-rate predictions play the primary part in the regression analysis and the spike-timing predictions only a secondary role. Therefore, a future research direction would be to investigate different forms of signal processing that have the potential to produce a more continuous parametric degradation of the spike-timing information while keeping the mean-rate cues relatively constant.

The use of real words in a lexical context provided a realistic scenario to assess the importance of spike-timing cues, while some past studies used nonsense VCV words and measured only consonant perception. Using the neurograms for these chimaeric presentations, we quantified neural information using the STMI (Elhilali et al. 2003; Zilany and Bruce 2007a) and the mean-rate and fine-timing NSIM measures (Hines and Harte 2010, 2012). These measures allowed us to examine spike-time coding in more general terms, whereas recent similar studies looked specifically at stationary aspects of neural responses (Swaminathan and Heinz 2012). Indeed, it allowed us to demonstrate that the NSIM is a viable measure of the variations in mean-rate and spike-timing responses. We also demonstrated that a lateral inhibition network makes the STMI sensitive to some spike-timing information as speculated by Shamma and Lorenzi (2013).

By combining different measures of mean-rate and spike-timing cues, possibly reflecting the parallel processing mechanisms within the cochlear nucleus, we found that the STMI with fine-timing NSIM with interaction regression model provides better predictions of chimaeric speech in quiet than either of the two models that considered only mean-rate information. The model was simple and readily more intuitive than the other complex combinations of neural predictors examined. The regression models looked at in this work are based on perception of a chimaerically vocoded dataset by normal-hearing listeners and likely will not apply directly to all other listening conditions, but the results support the idea that both mean-rate and spike-timing neural cues are important for speech intelligibility. Swaminathan and Heinz (2012) have shown evidence that spike-timing cues can play a supporting role for consonant perception in background noise, and the physiological data of Sachs et al. (1983) suggests that spike-timing cues may play a similar, or even greater, role for vowel perception in background noise.

The results of this work motivate the development of better signal processing schemes for hearing aids and cochlear implants to facilitate the use of TFS cues. Current speech processing schemes for cochlear implants do not efficiently deliver TFS cues (Lorenzi et al. 2006; Moore 2008; Nie et al. 2005, 2008; Sit et al. 2007). Some speech processing schemes for hearing aids have been proposed to encode TFS cues by improving the spectral contrast of the speech (Baer et al. 1993; Lyzenga et al. 2002; Simpson et al. 1990; Stone and Moore 1992). However, multiband compression, which is needed to compensate for reduced cochlear compression, tends to flatten the speech spectrum diminishing any benefits of some spectral expansion schemes (Franck et al. 1999) but not others (Bruce 2004). The neural-based intelligibility predictors explored in this paper should provide a useful tool in optimizing such hearing aid and cochlear implant processing strategies.

Future research must investigate several questions: (1) How will the relative contributions of mean-rate and spike-timing neural cues be altered for normal-hearing listeners in the presence of noise? How will they differ for hearing-impaired listeners under the same conditions? (2) How will the contributions be affected by different forms of cochlear pathology?

Compliance with Ethical Standards

Conflict of Interest

The authors declare that they have no conflict of interest.