Attractor Dynamics of Spatially Correlated Neural Activity in the Limbic System

Abstract

Attractor networks are a popular computational construct used to model different brain systems. These networks allow elegant computations that are thought to represent a number of aspects of brain function. Although there is good reason to believe that the brain displays attractor dynamics, it has proven difficult to test experimentally whether any particular attractor architecture resides in any particular brain circuit. We review models and experimental evidence for three systems in the rat brain that are presumed to be components of the rat’s navigational and memory system. Head-direction cells have been modeled as a ring attractor, grid cells as a plane attractor, and place cells both as a plane attractor and as a point attractor. Whereas the models have proven to be extremely useful conceptual tools, the experimental evidence in their favor, although intriguing, is still mostly circumstantial.

ATTRACTOR NETWORKS: GENERAL CONCEPTS

Attractor neural networks have occupied a prime place in the theoretical and computational literature on systems neuroscience. The elegance and explanatory power of these models are matched, unfortunately, by the ambiguity of the experimental evidence that any particular brain circuit actually incorporates attractor network architecture and dynamics. In this review, we describe the basic types of attractor networks and then evaluate the evidence for attractors in three components of the rat limbic spatial-navigation system: the head-direction (HD) circuit, the grid-cell circuit, and the place-cell circuit.

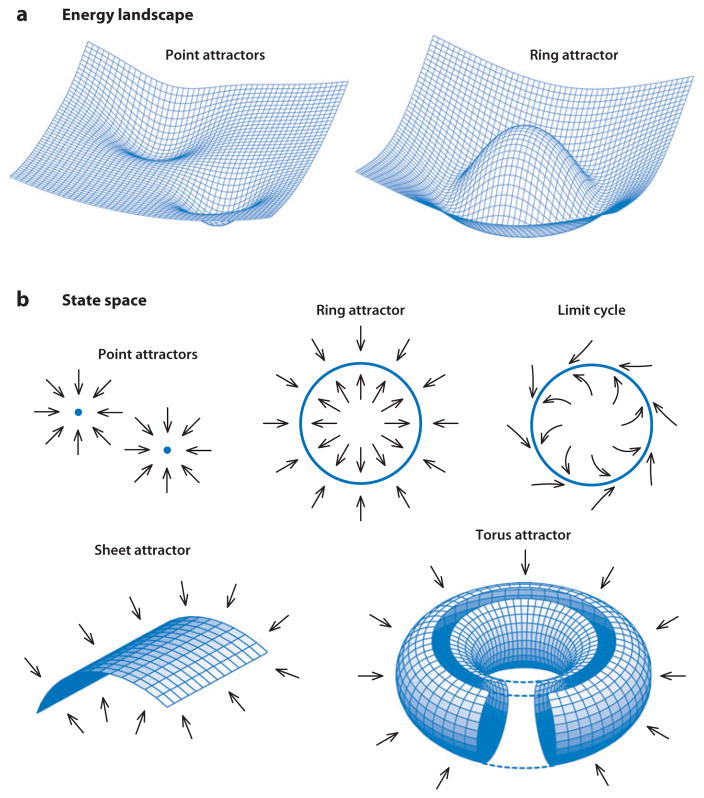
An attractor is a convenient general concept for describing the stability of a dynamical system, whose state evolves in time (Milnor 1985, Amit 1989). In intuitive terms, an attractor refers to a collection of states that will eventually attract neighboring states toward that collection, as if it were a magnet. This concept is illustrated by the simplest type of attractor, the point attractor, which is a single, stable, equilibrium state of the system (Figure 1). The basin of attraction for an attractor refers to the collection of all neighboring states that will eventually be drawn toward that attractor.

Figure 1.

(a) In a neural network with an energy function, the state of the network goes spontaneously downhill and eventually settles into some attractor states, which correspond to local energy minima. Neural networks with symmetric connections (equal reciprocal connections between neurons) always allow an energy function (Lyapunov function) (Hopfield 1982, Cohen & Grossberg 1983, Hopfield 1984). (b) Schematic examples of various attractors in neural network models, with the arrows indicating how the state of a network changes. Some attractors, such as a limit cycle, cannot be described by an energy function. Connecting the opposite edges of a sheet attractor can lead to a torus attractor, which has no boundary.

Many types of attractors have been studied in computational neuroscience. A well-known example is a Hopfield network, which allows multiple point attractors, each corresponding to a stored memory pattern (Hopfield 1982). The model has several interesting properties, such as robustness against damage to the synaptic connections (structural stability), pattern completion (recall of a stored representation from partial or noisy inputs), and pattern separation (divergence toward different stable states). Pattern completion occurs when different initial states belong to the basin of attraction of the same attractor, whereas pattern separation occurs when similar initial states actually fall into the basins of different attractors.

A limit cycle is an attractor that represents a stable periodic oscillation. It is a stable, closed trajectory in the state space, but it does not contain any equilibrium states. Starting from different initial states, the system will eventually approach the same oscillation or the same trajectory in the state space. Examples of a limit cycle in a network are central pattern generator circuits that produce periodic rhythms (Kopell & Ermentrout 1988, Rand et al. 1988, Marder & Bucher 2001).

A relatively new type of attractor, often called a continuous attractor, allows a continuum of stable equilibrium states, or at least closely related states that approximately form a continuum. The simple examples are the one-dimensional cases of a line attractor and a ring attractor. The line attractor can represent a variable that has a minimum value and a maximum value, such as the orbital position of the eye in one dimension (Robinson 1989, Seung 1996, Major et al. 2004). The ring attractor is suitable for representing a variable without boundary values (Dunin-Barkowski & Osovets 1995), such as azimuth heading direction (Skaggs et al. 1995, Blair 1996, Redish et al. 1996, Zhang 1996). Both examples can be used as a velocity integrator; that is, they can be used to integrate velocity over time to produce a position signal (eye position, head direction). The continuous attractor model has also been used to model other neural systems, such as orientation tuning in visual cortex (Ben-Yishai et al. 1995, Somers et al. 1995, see also Ferster & Miller 2000), binocular rivalry (Laing & Chow 2002), and perceptual decision making (Brody et al. 2003, Machens et al. 2005, Wang 2008).

An extension of the one-dimensional line or ring attractor to two dimensions is called a plane (or sheet) attractor. This type of attractor is well-suited to representing two-dimensional variables, such as location in a room. Plane attractors have been used to account for place cells in the rat hippocampus (Samsonovich & McNaughton 1997) and view cells in the monkey hippocampus (Stringer et al. 2005). Transforming the topology of the plane into a torus allows for the periodic spatial-activity patterns demonstrated by grid cells (see below) (McNaughton et al. 2006).

These types of attractors are not mutually exclusive, in that multiple types of attractors can be embedded in the same networks. For example, continuous attractors and point attractors can be stored in the same network (Rolls et al. 2002), allowing both continuous variables, such as spatial information, and discrete variables, such as the names of individuals, to be stored.

It is important to note that attractor states refer to states of activity in the network. This does not imply that there is an anatomical correspondence between attractor states in the network and locations in the physical brain. In effect, nearby cells on a ring attractor do not need to be located next to each other anatomically. Neighboring HD cells, for example, recorded on the same electrode, can have widely different preferred firing directions (Muller et al. 1996). The connectivity between neurons, not their physical proximity, allows different topologies of attractor states.

HEAD-DIRECTION CELLS AND RING ATTRACTORS

HD cells fire whenever the rat’s head is pointed in a particular direction in an allocentric coordinate frame (Ranck Jr. 1985; Taube et al. 1990a,b). These cells are sensitive to HD only in the horizontal plane (y axis); are insensitive to HD relative to the body axis; and fire continuously at a high rate whenever the rat’s head is pointed in its preferred direction, with little adaptation. Rotation of salient landmarks causes a corresponding rotation of the preferred firing direction of the HD cell (Taube et al. 1990b, Taube 1998, Taube 2007), thus demonstrating that visual landmarks exert powerful control over the HD cells. However, visual input is not necessary for robust HD firing, as the cells maintain their directional selectivity (at times with a change in preferred direction) even in total darkness (Mizumori & Williams 1993, Chen et al. 1994, Goodridge et al. 1998).

Models

Most models of the HD system are variations on a basic theme developed by a number of investigators in the mid-1990s (McNaughton et al. 1991, Skaggs et al. 1995, Blair 1996, Redish et al. 1996, Zhang 1996). To explain how HD cells could fire in the same direction across multiple environments, maintain their preferred firing in the dark, yet be controlled by rotation of salient visual landmarks, McNaughton and colleagues (McNaughton et al. 1991) proposed that the HD signal was primarily updated by an angular head velocity signal. That is, if the animal is facing west, HD cells that encode that direction would be active. A head turn 90° clockwise would activate cells that respond to clockwise motion, via presumed afferents from the vestibular system. In turn, these cells would cause the cells encoding west to become silent and cause the cells that encode north to become active, via an intermediate layer of cells that encoded the combination of a particular starting direction and a particular change in direction. This conceptual model was originally implemented as a look-up table. Subsequent work incorporated the architecture of a ring attractor to implement this idea in plausible brain circuitry (Skaggs et al. 1995, Blair 1996, Redish et al. 1996, Zhang 1996, Goodridge & Touretzky 2000, Stringer et al. 2002, Xie et al. 2002). The HD cells are conceptualized as being arrayed in a circle, with the location of each cell on the circle representing the preferred firing direction of that cell. Nearby cells are connected by strong excitatory synapses, with the strength of excitation proportional to the angular distance between the cells on the ring. Cells that are far apart on the ring are connected with inhibitory synapses. If the strength of excitation and inhibition is appropriately tuned, such an architecture exhibits attractor dynamics. From a starting condition of random excitation, stochastic fluctuations cause one part of the ring to have slightly greater excitation than other parts. The excitatory circuitry reinforces activity of other nearby cells, whereas the inhibitory connections force cells further away to be silent. The symmetric connectivity results in a localized, self-sustaining “bump” or “hill” of activity on the ring, the cells outside of which are silent.

If the location of the bump of activity was made to follow the momentary changes in the HD of the animal, such a network could form the basis of the HD signal. To accomplish this, an asymmetry in the connectivity matrix of the attractor is required to turn the ring attractor into a limit cycle and, thus, move the bump of activity around the ring. Different models added this asymmetry in different ways, but the key component was adding velocity modulation to the HD cells. With proper tuning of the weights, this asymmetry would cause the bump of activity to move in concert with the animal’s HD. This circuit, dependent on self-motion cues to update the location of the activity bump, is susceptible to cumulative error. That is, if there is an error in the calculation of the angular head velocity, the bump will be offset by a certain amount from the animal’s true HD. This offset would be reflected as a global shift in each HD cell’s preferred firing direction. To correct for such errors, the models incorporate input from stable landmarks. Thus, the moment-by-moment updating of the activity bump is governed by the angular head velocity signals, with calibration by the stable, external landmarks to keep the bump of activity stable relative to the external world.

It is thought that the HD signal emerges as an interaction between neurons in the lateral mammillary nucleus and the dorsal tegmental nucleus of Gudden (Taube 1998, Sharp et al. 2001a), both of which contain cells that encode HD and angular head velocity (Blair et al. 1998, Stackman & Taube 1998, Bassett & Taube 2001, Sharp et al. 2001b). Thus, these nuclei contain the major components of the ring attractor models. One problem for the ring attractor models, however, is that these nuclei do not appear to contain the recurrent excitatory circuitry required for the self-sustaining activity bump. Song & Wang (2005; see also Boucheny et al. 2005) showed that a network without excitatory connections among the HD cells could drive the activity bump, as long as there was a source of tonic, excitatory drive onto the cells. The source of this tonic drive was not known. However, an intriguing possibility comes from the discovery of a cellular mechanism that enables graded, persistent activity. In these slice experiments, in which synaptic transmission was blocked, an injection of depolarizing current caused a cell to fire persistently at a tonic rate. Additional current injections caused the cell to fire at a higher rate, which persisted indefinitely. Changing the polarity of the current caused a decrement in the tonic, persistent firing rate. This type of activity has been demonstrated in a number of brain areas (Morisset & Nagy 2000; Egorov et al. 2002, 2006; Fransen et al. 2006; Winograd et al. 2008), including the anterodorsal nucleus of the thalamus (Kulkarni et al. 2011) and post-subiculum (Yoshida & Hasselmo 2009), two key components of the HD circuit. Although the firing rate of this persistent activity tends to be slower than that of many HD cells, and the time course for changing the firing rates is slower than typical head movements, these cells may still play a role in promoting the stability of the attractor states. Thus, it is conceivable that the persistent activity of HD cells derives in part from intrinsic cellular mechanisms, not recurrent excitatory circuitry, and the attractor properties may be derived from the inhibitory connections modeled by Song & Wang (2005) and Boucheny et al. (2005).

Experimental Evidence

What is the experimental evidence in favor of the ring attractor models of HD cells? With the discovery of intracellular mechanisms for persistent activity, some properties of HD cells that initially inspired the formulation of the ring attractor models can no longer be considered as strong evidence in favor of attractor dynamics in the circuit. These properties include the persistent activity of these cells, with little or no adaptation while the rat remains stationary facing the cell’s preferred direction, and the continued activity of these cells in the dark. Nonetheless, the ring attractor models still provide a large amount of explanatory power to a number of known properties of the HD cell system. (a) The models require cells that encode both HD and angular head velocity, and such cells have been discovered in the system (McNaughton et al. 1991, Blair et al. 1998, Stackman & Taube 1998, Bassett & Taube 2001, Sharp et al. 2001b). (b) The HD cell tuning curves can drift relative to external landmarks, demonstrating that the signal can be purely “inside the rat’s head,” independent of any external sensory cue (Knierim et al. 1995, 1998; Yoganarasimha & Knierim 2005). (c) Strong attractor circuitry would result in a system in which individual HD cells maintain the same preferred firing directions relative to each other, even when the preferred directions drift relative to an external sensory framework. Studies that recorded multiple HD cells simultaneously have confirmed that the preferred firing directions of these cells are rigidly coupled to each other (Taube & Burton 1995, Zugaro et al. 2001, Yoganarasimha et al. 2006). (d) The models predict that self-motion input is the primary drive that updates the HD signal; external landmarks play a powerful, but secondary, role of correcting or preventing drift. In agreement, disruption of the vestibular system severely disrupts the HD circuit (Stackman & Taube 1997). In particular, plugging the semicircular canals causes the loss of a directional signal; nonetheless, simultaneously recorded cells in the anterodorsal nucleus of the thalamus still fire bursts in predictable sequences corresponding to clockwise and counterclockwise turns, as if the internal ring circuitry is still intact, but the update mechanism from the vestibular system causes the bump of activity to move around the ring in ways that bear no relationship to the animal’s actual HD in the world (Muir et al. 2009). (e) External landmarks are required to keep the system calibrated relative to the external world as well as to reset the system to its “correct” orientation when the animal reenters a familiar environment. The attractor dynamics cause the correction to be either a continuous change (as the HD activity bump moves continuously to a new direction) or an abrupt shift (as the activity bump disappears at one location while reappearing at the new location). Whether the correction is continuous or abrupt depends both on the angular magnitude of the correction and on the strength of the embedded attractors (Zhang 1996, Song & Wang 2005). Consistent with the models, Knierim and colleagues (Knierim et al. 1998) showed that small angular deviations were more likely to be corrected than were large deviations, whereas Zugaro and colleagues (Zugaro et al. 2003) showed that large deviations could be corrected in a very fast, abrupt manner (80 ms).

GRID CELLS AND TWO-DIMENSIONAL CONTINUOUS ATTRACTORS

Grid cells are spatially tuned neurons that fire in multiple locations in an environment (Hafting et al. 2005). Each firing location is at the vertex of a triangular (or hexagonal) grid that tiles the entire surface of the environment. These cells, originally discovered and most prominent in the dorsocaudal medial entorhinal cortex (MEC), are also found in the presubiculum and parasubiculum (Boccara et al. 2010). In the MEC, neighboring grid cells have the same orientation and scale, differing only in phase (i.e., locational shift) (Hafting et al. 2005). In more ventral parts of the MEC, the scale of the grids increases (Hafting et al. 2005). Similar to HD cells, grid cells have a number of properties that are amenable to modeling with attractor networks. Grid cells can be controlled by salient cues and boundaries, yet they maintain their grid-like firing patterns even in total darkness (Hafting et al. 2005). Thus, a self-motion signal appears to be a key component of updating the system. Also similar to HD cells, grid cells of the same scale appear to be rigidly coupled (Fyhn et al. 2007, Hargreaves et al. 2007), although it is not known whether this rigidity extends to grid cells across all spatial scales and across hemispheres.

Attractor versus Oscillatory Interference Models

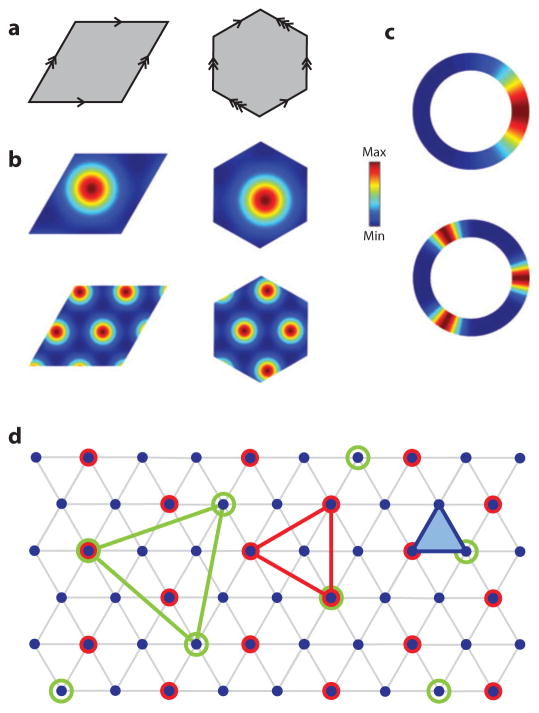
Many computational models of grid cells have now been proposed, and the large majority of them fall into two classes: oscillatory interference (OI) models and attractor models. OI models propose that the grid pattern arises from the beat frequencies that form from several oscillators with slightly different frequencies centered around the theta frequency (Blair et al. 2007, Burgess et al. 2007, Hasselmo et al. 2007, Monaco et al. 2011, Welday et al. 2011). The key requirement is that the frequency be modulated by the animal’s velocity (speed and direction) (Geisler et al. 2007, Welday et al. 2011). Under appropriate conditions, the beat frequencies of the interference patterns cause a cell to reach firing threshold whenever the rat is at the vertex of the grid. In contrast, attractor models are basically two-dimensional extensions of the ring attractor models of HD cells (Fuhs & Touretzky 2006, McNaughton et al. 2006, Guanella et al. 2007, Burak & Fiete 2009). Rather than a ring, however, the neurons are arranged conceptually on a two-dimensional plane, with appropriate excitatory connections among neighbors and global inhibition to cause a two-dimensional bump of activity to form at a location on the plane. Similar to the ring attractor, each location on the plane is a stable state, and the bump can move in a continuous manner from one stable state to another, driven by asymmetric input from cells that encode linear velocity. In one mechanism, the periodically repeating pattern of grid cells comes from the toroidal architecture of the attractors (McNaughton et al. 2006). That is, just as a line attractor is made into a ring attractor by connecting the ends of the line to form a ring, a plane attractor is made into a toroidal attractor by connecting the edges of the plane to each other to form a torus (Figure 1b). The simplest example of this is a square sheet of paper for which two opposing sides are joined together to form a cylinder and the ends of the cylinder are joined to form a torus (i.e., a doughnut). The movement of the bump of activity along this torus would be bounded, but if tied to the movement of the animal, it would produce a periodic, repeated pattern of activity resembling a grid cell, but with a square grid. To get a hexagonal grid, one could make the shape of the paper a rhombus (McNaughton et al. 2006) or a hexagon (in which case the resulting topology is called a twisted torus) (Guanella et al. 2007) (Figure 2a). Alternatively, one could set up a center-surround excitation-inhibition connectivity scheme (e.g., a Mexican-hat function) that will naturally cause cells to fire in a hexagonal grid (the optimal packing density of circles) (Fuhs & Touretzky 2006), which is the pattern that emerges in a Turing mechanism of pattern formation (Turing 1953). Finally, it is worth mentioning that although attractor and OI models appear radically different, they actually satisfy the same general mathematical conditions for exact path integration (Issa & Zhang 2012).

Figure 2.

(a) Connecting the opposite edges of a sheet of cells shaped as a rhombus (left) or a hexagon (right) yields a torus or a twisted torus, respectively. Both networks can generate hexagonal firing fields if the activity bump moves according to the velocity of the animal’s movement. A sheet of cells without toroidal connectivity can also support multiple activity peaks and hexagonal firing fields (Fuhs & Touretzky 2006). (b) Activity pattern in a torus network may have either a single peak (top) or multiple peaks (bottom), depending on the connectivity of the network. Note that these figures show the activity pattern on the attractor sheet, not the spatial firing-rate map of individual units. In all cases, recordings from a single unit would display grid-like firing fields as the bump(s) move across the attractor sheet. (c) Activity pattern in a ring network, showing a single peak (top) or multiple peaks (bottom). In a head-direction ring attractor model, if the speed at which the multiple bumps moves around the ring is one-third the speed of the single bump, then individual units in each attractor would show identical, single-lobed directional tuning curves.

(d) Consistency of grid fields of different sizes may require special geometric arrangements. Let the blue dots indicate a base hexagonal grid whose spacing is given by the side length of the filled blue triangle. The spacing of a large hexagonal grid (red circles) consistent with the base grid will be $\sqrt{3}=1.73$ times as large, with an orientation offset of 30°. Several larger grids are also consistent with the base grid. For instance, the spacing of the grid indicated by the green triangle is $\sqrt{7}=2.65$ times as large.

Experimental Evidence

Similar to HD cell models, the attractor models of grid cells are elegant and account for many properties of grid cells, but the experimental evidence that the system is organized as such an attractor is indirect and circumstantial. The evidence for these models is perhaps best evaluated in comparison with the evidence for the most popular alternative, the OI models, which have a number of bases of support (Hasselmo 2011). The OI models naturally account for the presence of theta phase precession in grid cells (Hafting et al. 2008) as a necessary consequence of the OI mechanism, whereas attractor models, although consistent with phase precession, do not intrinsically explain the phenomenon. OI models have some experimental support, such as the change in the resonant frequency of neurons from dorsal to ventral MEC that corresponds with the increased scale of grids along that axis (Giocomo et al. 2007). Again, attractor models can be consistent with this finding, and incorporating it into the models allows the simulated grid cells to show phase precession and scaling, but the models do not require it to produce the spatial grid patterns (Navratilova et al. 2011). Inactivation of the medial septum, which disrupts theta rhythm, abolishes the grid-like firing patterns of grid cells, in accordance with predictions of the OI theory (Brandon et al. 2011, Koenig et al. 2011). However, this result must be interpreted cautiously: The septal inactivation does more than just disrupt the rhythmic firing of the cells. It undoubtedly has other effects that may cause the disruption of grid cells. For example, the persistent cellular firing discussed above requires cholinergic input (Egorov et al. 2002), and the medial septum is a major source of cholinergic input into the MEC (Witter & Amaral 2004). Furthermore, bats have been reported to display grid cells in the absence of obvious theta oscillations (Yartsev et al. 2011), which does not disprove the OI models but presents them with a serious challenge.

Some of the attractor models naturally account for the fact that all grids within an animal appear to be of the same orientation—a necessary consequence of the toroidal architecture. The attractor map also predicts that different grid scales must come about through distinct attractor modules (McNaughton et al. 2006), and evidence suggests that this prediction is true (Barry et al. 2007). However, it is possible that OI models also require such discrete steps in grid scale to ensure that the grids stay stable relative to each other. The geometry of the grid may constrain the relative orientation and scales of grids along the dorsal-ventral axis of the MEC (Figure 2d). Both models have difficulty in justifying the somewhat artificial mechanisms employed to impose the hexagonal structure on the grid. OI models have to postulate that the HD cells that provide the directional component of the velocity vector are restricted to representing only three angles, 120° apart. There is currently no strong evidence that HD cells are so organized. Toroidal attractor models have to postulate a priori that the sheet is either a rhombus or a hexagon to obtain the proper grid geometry. Although there are good arguments for why the grids should be arranged as a hexagonal lattice, on the basis of arguments of optimal packing density and natural formation of patterns from reaction-diffusion-type equations and center-surround excitation-inhibition connectivity (Fuhs & Touretzky 2006, McNaughton et al. 2006), the models still need to build this into their architecture somewhat artificially. Thus, the jury is still out on the relative merits of these classes of models. OI models have been criticized because they appear to require temporal precision greater than is observed in biological systems (Welinder et al. 2008), but newer versions have devised methods with the potential to overcome this problem (Zilli & Hasselmo 2010). Continuous attractor models are also subject to structural instability, with any small damage or disturbance capable of changing them to point attractors (Zhang 1996, Tsodyks 1999, Renart et al. 2003). As a result, the grid cells may combine aspects of both types of models. At the cellular level, OI may bootstrap the cells to fire in a grid-like manner. However, attractor dynamics may then be required to keep the system stable and to correct errors imposed by temporal noise in the oscillators. It will be of interest to see if future modeling efforts can make use of both mechanisms to create more robust models that conform closely to the biological data. (For a more detailed review of the different models of grid cells, see Giocomo et al. 2011.)

PLACE CELLS AND CONTINUOUS VERSUS POINT ATTRACTORS

The hippocampus has been modeled both as a point attractor neural network and as a continuous attractor network (Treves & Rolls 1994, Levy 1996, Samsonovich & McNaughton 1997, Battaglia & Treves 1998, Tsodyks 1999, Conklin & Eliasmith 2005, Touretzky et al. 2005, Monaco et al. 2007). In particular, the CA3 region has been the focus of such models, as its extensive system of excitatory recurrent collaterals endows it with an anatomical substrate conducive to the formation of attractor states. The discrete attractor models derive from ideas put forward by Hebb and Marr. Hebb (1949) postulated that coactive populations of neurons form, through plasticity, cell assemblies that have many of the properties now described as signatures of attractor networks. Marr (1971) formulated the idea that such a network is capable of pattern completion. That is, if a memory is stored in a recurrent network as a distributed pattern of synaptic weights, such a network is capable of reinstating the full activity pattern even if the original input pattern is incomplete, degraded, or corrupted. An attractor network is a prime candidate mechanism to perform this function. Complementary to the idea of pattern completion is pattern separation, i.e., two similar input patterns are stored as more dissimilar patterns to reduce the probability of errors in recall. The putative attractor dynamics of CA3 will promote a sigmoidal relationship between changes in the inputs to CA3 and changes in the CA3 output representation (O’Reilly & McClelland 1994). When changes are small, the CA3 attractor dynamics tend to cause CA3 to converge to the original attractor basin, such that the CA3 outputs are less different than the inputs. When changes are larger, however, the CA3 representation may form in a region of state space away from the attractor basin, making the CA3 outputs less similar than the inputs. Under these conditions, it is hypothesized that a new attractor basin will form far away from (orthogonal to) the original attractor basin. (For reviews of various computational models of the hippocampus, see Burgess 2007 and Hasselmo 2011.)

Pattern Completion and Pattern Separation

A number of experiments in recent years have tested the pattern completion/separation hypotheses in different components of the hippocampal formation. A set of studies published nearly simultaneously from three different laboratories provided evidence for the sigmoidal relationship between input and output changes in the CA3 region. Lee and colleagues (Lee et al. 2004) rotated a local reference frame (a circular track with salient cues) counter to a global reference frame (salient landmarks on the curtained walls of the environment) and found that, compared with CA1 place cells, CA3 place cells responded in a more coherent fashion to the cue-mismatch (Figure 3). They interpreted this as reflecting the pattern-completion functions of CA3, as the conflicting input regarding local and global cues was resolved in favor of the local cues at each location on the track, in contrast to the split representations seen in CA1. Leutgeb and colleagues (Leutgeb et al. 2004) recorded CA3 and CA1 cells in an experiment in which the rat was transported into two completely different rooms. In contrast to the findings of Lee et al. (2004), CA3 place fields under these conditions were completely independent in the two situations, even though CA1 place fields maintained some degree of similarity. Leutgeb et al. (2004) concluded that under these conditions CA3 showed pattern separation, as presumed similarities in the input representations (as reflected by the similarities in the feedforward CA1 network) were erased in CA3. The trade-off between pattern completion seen by Lee et al. (2004) and pattern separation seen by Leutgeb et al. (2004) was confirmed in a single study utilizing the immediate early gene Arc by Vazdarjanova & Guzowski (2004). Under conditions in which changes to the environment were small, CA3 showed a greater overlap in Arc expression than did CA1; conversely, when the changes to the environment were larger, CA3 representations overlapped less than those of CA1. Taken as a set, these three studies provide strong evidence for the nonlinear, attractor-like behavior of CA3 versus CA1 when environmental inputs are altered in a graded fashion (Guzowski et al. 2004).

Figure 3.

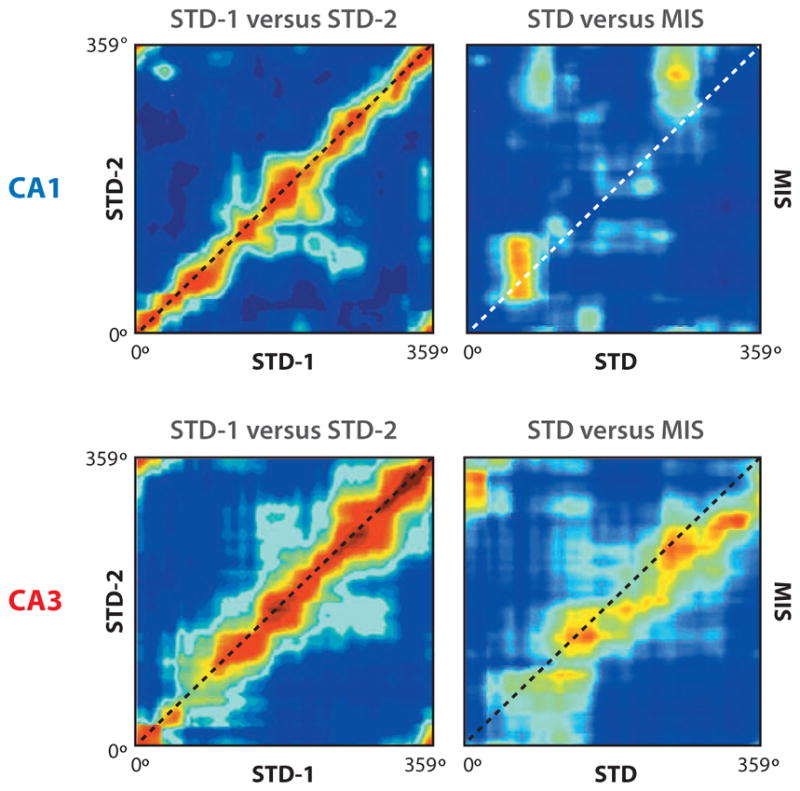
Spatial correlation matrices for population vectors of CA1 and CA3 place fields. Location along a standard track (session 1: STD-1; session 2: STD-2) or along a track with mismatched reference frames (MIS) is plotted along the axes. (Left) The red diagonal band signifies that the representations of both CA1 and CA3 were highly similar across two standard sessions. (Right) The band of high correlation remains in CA3 but is absent in CA1. This result demonstrates that CA3 responds more coherently to the mismatch than does CA1, consistent with pattern completion (or generalization) properties expected if CA3 incorporated attractor dynamics. Modified from Lee et al. (2004).

Nakazawa et al. (2002) tested the effects of selective deletion of the NR1 subunit of the NMDA receptor in CA3 by recording from the downstream CA1 region during a classic test of pattern completion. When a subset of the visual landmarks in a room was removed, perhaps degrading the spatial representations that provide input to CA3 and CA1, normal mice showed similar place fields between the full-cue and partial-cue environments. In contrast, mice lacking normal NMDA receptors in CA3 showed degraded place fields in CA1 in the partial-cue environments, consistent with the hypothesized role of CA3 in pattern completion.

Wills et al. (2005) recorded CA1 place fields as the geometry of an environment was gradually morphed in four stages from a circle to a square. They found that place fields in the square-like morph geometries matched the place fields of the true square, whereas place fields in the circle-like geometries matched the place fields of the true circle. The transition between square-like and circle-like place fields was sharp, which the authors interpreted as evidence for attractor dynamics in the hippocampus, presumably in the CA3 region upstream of CA1. In contrast, though employing a similar experiment, Leutgeb and colleagues (2005a) showed a gradual change in place fields as the box geometry was morphed. Place fields mostly stayed in the same locations in both the circle-and square-like environments, but the firing rate within each place field gradually changed. Insight into the discrepancy between the studies comes from Fyhn et al. (2007), who recorded from MEC grid cells and CA1 place cells when the CA1 place fields remapped. Global remapping [i.e., that seen by Wills et al. (2005)] was accompanied by shifts in the MEC grids relative to the environmental boundaries, whereas rate remapping [i.e., that seen by Leutgeb et al. (2004)] was accompanied by a stable relationship between the grids and the boundaries. It is conceivable that the Wills study caused the MEC grids to shift abruptly at the transition between the most ambiguous circle-like shape and the most ambiguous square-like shape, causing the abrupt global remapping between these two similar shapes. In contrast, because of the way the rats were pretrained and the experimental sessions were run, the grids may have remained stable in the Leutgeb experiments promoting gradual rate remapping (Leutgeb et al. 2005b).

Colgin et al. (2010) tested a similar idea by showing that CA3 and CA1 place fields displayed rate remapping when the path-integration coordinates thought to align the MEC grids were kept stable across two environments. In contrast, the place fields displayed global remapping when the path-integration coordinates between the two environments were distinctly different, which would tend to cause a shift in the grid relative to the environments. Colgin et al. (2010) interpreted these results as evidence in favor of the path-integration-based, plane attractor models of the hippocampal formation, as opposed to the single-point attractor models that were associated with notions of pattern completion and separation.

Continuous versus Point Attractor Dynamics

How does one reconcile the interpretation put forth by Colgin et al. (2010) with earlier work that interpreted the place-field data in terms of pattern completion and separation? More generally, do any of the experiments described above provide compelling, direct (rather than circumstantial) evidence in favor of attractor dynamics in the hippocampus? Because the hippocampus is an intricately connected network of multiple areas, with external input and feedback connections that can have strong influences on how the cells behave, this question has become somewhat intractable. Whereas the inputs can be turned off and the pure attractor dynamics observed in a simple computer model, this is difficult, if not impossible, to do in the biological system. Thus, even if strong attractor dynamics exist in the system, almost any experimental manipulation designed to expose those dynamics will produce results that are a hybrid between attractor dynamics and external drive onto the attractor. To test for true attractor dynamics, it is necessary to remove the external drive, as was attempted in studies of the visual cortex by Akrami et al. (2009). This is difficult to do in the hippocampus, as experimentalists do not have direct control over the highly processed sensory and cognitive representations that compose the inputs to the hippocampus (activity during sleep may help, but does not obviate, this problem). Moreover, different parts of the system may display different types of attractor dynamics. Thus, the continuous attractor dynamics supported by Colgin et al. (2010) may be present in the MEC inputs to the hippocampus. The output of the MEC attractor would then be an external input to the CA3 attractor and under most conditions would likely be a strong drive on the activity of CA3 cells. CA3 could still contain classic, point attractor dynamics, yet its place fields would also reflect the continuous attractor dynamics of its MEC inputs. If the roles of these inputs include aligning the path-integration framework with the external world and incorporating external information about the world onto this framework in support of episodic memory (perhaps via its lateral entorhinal inputs) (Knierim et al. 2006, Deshmukh & Knierim 2011), such a hybrid system may reflect properties of both the classic, discrete attractor models and the continuous attractor models.

FUTURE DIRECTIONS

Attractor models hold great sway across a number of brain systems, owing to the computational power they bring to various problems that the brain has to solve. In addition to the properties described above for limbic regions, attractor networks are useful for solving optimization problems, such as the traveling-salesman problem (Hopfield & Tank 1985). A continuous attractor network can be used to estimate signal hidden in noise, with near-optimal statistical efficiency (Pouget et al. 1998, Latham et al. 2003, Wu et al. 2008). Evidence is accumulating that the brain displays attractor dynamics in its processing; However, it is exceedingly difficult to test quantitatively any particular model of attractors in a particular brain circuit. Nonetheless, these models have proven extremely useful in providing a conceptual framework for understanding experimental data that defy simple, feedforward circuitry explanations. We finish this review by describing interesting questions for future research.

Learning the Weights of an Attractor Map

One of the major unsolved problems in attractor theory is how a neural system can learn through self-organization the synaptic-weight matrix required to form stable attractors (Kali & Dayan 2000, Stringer et al. 2005). This problem is particularly difficult with continuous attractors, which are hard to learn even in a simulation and hard to maintain because of their structural instability (any small damage or disturbance can change a continuous attractor to point attractors). The lack of anatomical topography of high-order brain systems complicates neural learning rules. Some have suggested that the weights can be learned through a developmental process in which topographically organized representations are initially present to serve as a teacher to the attractor and then disappear (McNaughton et al. 2006). The feasibility of these ideas may be tested in experiments that measure the developmental onset of place, grid, and directional signals (Martin & Berthoz 2002, Langston et al. 2010, Wills et al. 2010, Scott et al. 2011). However, there is as yet no consensus theory or model of self-organization of weights of an attractor map, and such a model would help guide interpretation and analysis of the experimental results.

Anatomical Measurement of a Connectivity Matrix

Attractor theory predicts how different neurons should be connected into a network. A main problem has been the lack of effective experimental methods for directly measuring the connectivity-weight matrix of a real network. The stable activity pattern on the attractor sheet may have either a single peak or multiple peaks, depending on the connectivity and exact values of the parameters. For example, the grid-cell model of Fuhs & Touretzky (2006) has multiple peaks of activity (arranged as a hexagonal grid) on the attractor sheet, whereas the model of McNaughton et al. (2006) has a single activity peak on a torus attractor (Figure 2b). If one “records” from a unit in both models, the unit would appear as a grid cell, regardless of whether there is a single peak or multiple peaks in the activity pattern of the attractor. Similarly, if there were multiple peaks in an HD ring network, each individual cell could still appear as a normal HD cell (Figure 2c). It is not known whether the single-peak or the multiple-peak case is closer to the real biological situation, although the two cases can imply different patterns of synaptic connectivity. The ultimate test would be direct measurement of the synaptic-connection patterns in the brain, which may directly reveal a toroidal pattern of weights in the MEC, for example. The recent advance of high-throughput connectomics may eventually provide data to address this question (Chklovskii et al. 2010, Seung 2011).

Multiple Stable States

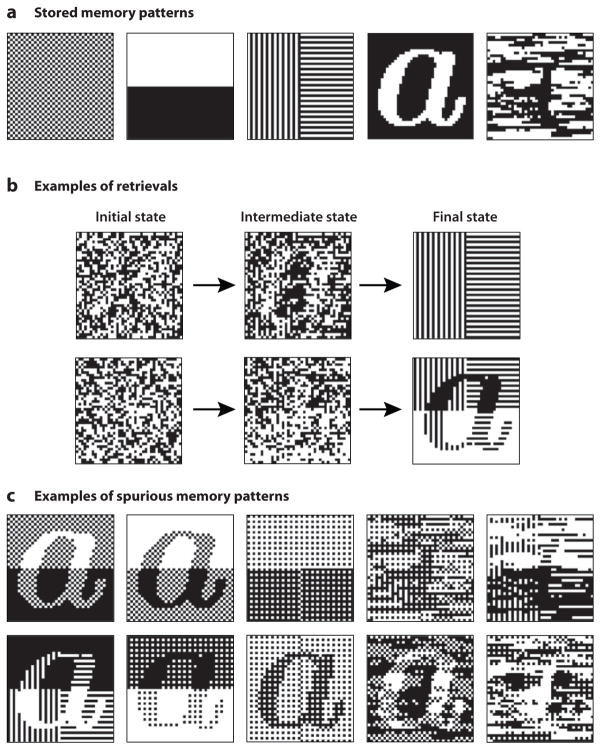
Although rat hippocampal place cells tend to be stable for a long time in a stable environment, they are notoriously fickle in their responses to environmental or behavioral changes, displaying various forms of “remapping” and partial remapping (Knierim 2003). A theoretical explanation for the vagaries of partial remapping remains poorly understood. The ability of multiple stable states to be simultaneously active in an attractor may help explain some of these phenomena, including the existence of “split” place fields that occur in reference-frame mismatch experiments (Knierim 2002, Lee et al. 2004). One concept that may help researchers develop a theory of partial remapping is the notion that “spurious” attractors can arise in an attractor network (Amit 1989); that is, stable activity states can form that were not explicitly encoded in the network. To illustrate this concept, Figure 4 shows a simulation of spurious attractors, in which we embedded five memory patterns in a Hopfield attractor network (Figure 4a) and then ran a number of simulations in which we let the network evolve to a stable state after starting out with random input patterns. Although the system sometimes settled on one of the stored patterns (Figure 4b, top row), it more often settled into a spurious, stable state (Figure 4b, bottom row; Figure 4c). Note that each spurious state in Figure 4 is a mixture of several stored memory patterns. This mixture is not a simple, linear combination or superposition because different subregions of the image can combine different memory patterns in different ways, resulting in a rich variety of possible spurious states. It will be of interest to pursue whether investigation of spurious attractors may impart some insight into the sometimes seemingly capricious nature of place-cell remapping.

Figure 4.

Spurious attractors. (a) Five memory patterns stored in a Hopfield network are shown as images, with each pixel corresponding to the state of a unit in the network. The last pattern is the “Loch Ness monster.” (b) Starting from a random initial state, the network eventually settles to either a stored memory pattern or a spurious equilibrium state, which is some mixture of multiple memory patterns (sometimes with flipped polarity). (c) Some examples of the spurious states showing the diversity of the mixtures.

Glossary

HD

head direction

MEC

medial entorhinal cortex

OI

oscillatory interference