Abstract
This article shows how the COLTRIMS (Cold Target Recoil Ion Momentum Spectroscopy) or the "reaction microscope" technique can be used to distinguish between enantiomers (stereoisomers) of simple chiral species on the level of individual molecules. In this approach, a gaseous molecular jet of the sample expands into a vacuum chamber and intersects with femtosecond (fs) laser pulses. The high intensity of the pulses leads to fast multiple ionization, igniting a so-called Coulomb Explosion that produces several cationic (positively charged) fragments. An electrostatic field guides these cations onto time- and position-sensitive detectors. Similar to a time-of-flight mass spectrometer, the arrival time of each ion yields information on its mass. As a surplus, the electrostatic field is adjusted in a way that the emission direction and the kinetic energy after fragmentation lead to variations in the time-of-flight and in the impact position on the detector.
Each ion impact creates an electronic signal in the detector; this signal is treated by high-frequency electronics and recorded event by event by a computer. The registered data correspond to the impact times and positions. With these data, the energy and the emission direction of each fragment can be calculated. These values are related to structural properties of the molecule under investigation, i.e. to the bond lengths and relative positions of the atoms, allowing to determine molecule by molecule the handedness of simple chiral species and other isomeric features.
Keywords: Chemistry, Issue 126, Coulomb Explosion Imaging, chirality, Absolute Configuration, femtosecond laser, COLTRIMS, coincidence, mass spectrometry, molecular beam, photoionization
Introduction
Chirality is a feature of our nature that has been fascinating researchers for more than 150 years. In the 19th century, Pasteur, van't Hoff and others discovered that molecules can occur in two mirror image structures that are not super-imposable - like our left and right hands. This property was termed 'chiral', from the Greek word for 'hand'.
So far, no difference in thermodynamic properties or in energy levels of left- and right-handed forms (the two 'enantiomers') has been found. In order to analyze the handedness of a given sample and to separate the enantiomers, interaction with other chiral molecules can be used, as is for example done in various chromatographical approaches.1 Chiroptical methods such as (vibrational) circular dichroism, (V)CD, and optical rotatory dispersion, ORD, are routinely employed to distinguish between enantiomers.2
When it comes to the determination of the microscopic structure, these techniques require additional information, e.g. from quantum-chemical calculations. The only technique that is widely accepted to directly determine the absolute configuration is anomalous X-ray diffraction.3
It has recently been shown that the absolute configuration of simple chiral species can be determined by Coulomb Explosion Imaging.4,5 In this approach, molecules in the gas phase are multiply ionized so that the remaining cores strongly repel each other. This repulsion leads to fast fragmentation ('explosion') of the molecules. The direction and the magnitude of the fragment momenta correlate to the structure of the molecule – for small molecules, the momentum directions correspond surprisingly well to the bond axes. Coulomb Explosion for molecular structure determination has been pioneered using molecular ion beams from an accelerator.6 This beam foil technique has recently also been applied for chiral recognition.7
Contrary to anomalous X-ray diffraction, the sample must not be crystalline but provided in the gas phase. This makes the Coulomb Explosion approach ideal for volatile species and thus complementary to X-ray diffraction. In certain cases, the handedness can even be determined for individual molecules.
In practice, the exact reconstruction of the molecular structure has proven difficult even for methane derivatives, e.g. molecules with a central carbon and different substituents. This is attributed to the fact that the interaction between the fragments is not exactly Coulombic and that not all bonds break simultaneously. In order to obtain stereochemical information, especially to distinguish between enantiomers, this reconstruction is fortunately not necessary. Instead, the momentum vectors of different fragments can be correlated to yield a quantity that is distinct for the left- and right-handed molecules. To get reliable results, at least four fragment momenta have to be recorded.
In order to measure this momentum information, the fragments from one – and only one – molecular break-up have to be detected in a single measurement step. This condition is usually referred to as 'coincident detection'. In addition, the emission directions have to be analyzed, which amounts in practice to record the time and the position of the fragment impact in a list-mode data format.
In atomic and molecular physics, techniques have been developed that implement this approach of measurement by employing electrostatic spectrometers for mass separation and time- and position-sensitive multi-hit detectors. The most prominent example is the COLTRIMS (Cold Target Recoil Ion Momentum Spectroscopy) setup – also known as Reaction Microscope.8,9 A sketch for this kind of experiment is given in Figure 1. Contrary to a standard COLTRIMS that can record electrons as well, Coulomb Explosion Imaging requires only the ion detector.
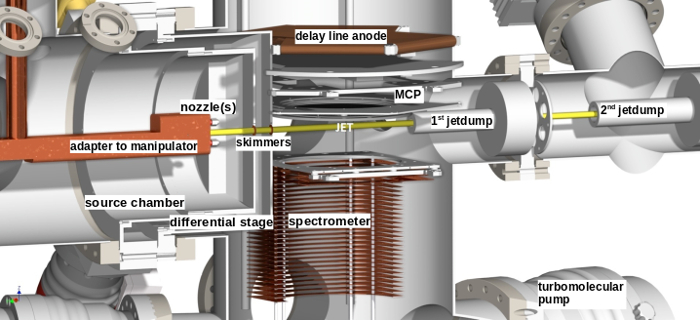
Spectrometer and detector are mounted under ultra-high vacuum (<1 x 10-9 hPa) to avoid creation of ions from residual gas. Single molecules of the sample are provided via a gaseous free molecular jet created by supersonic expansion: By virtue of the vapor pressure, the molecules expand through a small nozzle (around 50 µm diameter) into the vacuum. This part of the experiment, the source chamber, is separated from the interaction region by usually two skimmers and differentially pumped stages. An additional differentially pumped section is located behind the interaction region to dump the gas jet and thus avoid background gas in the interaction region.
The ionizing radiation intersects with the molecular jet under 90°. Most laboratories nowadays use femtosecond laser pulses, although synchrotron radiation, fast ions or electron impact are possible 'projectiles' to induce Coulomb Explosion.
The following protocol makes the assumption that a running setup for coincident imaging of ions and a femtosecond laser are available in the lab. The peak intensity needed to induce Coulomb Explosion into four or even five fragments must be on the order of 6 x 1014 W/cm2. To avoid exceedingly long measurements, the repetition rate of the laser should be 10 kHz or more. This is crucial because, on the one hand, coincident detection can only be ascertained if the probability for fragmentation in the laser focus is significantly below 1 per laser pulse (ideally not more than 10%). The total fragmentation rate, on the other hand, should not be lower than a few kHz because the share of relevant multifragmentation pathways is usually less than 10-4. As encouraging fact, it should be mentioned that in principle already a single fragmentation event is sufficient to identify the configuration of an enantiopure sample, and that detection of a few hundred allows to determine the abundance of the enantiomers in a sample of unknown enantiomeric composition.
Protocol
Caution: Make sure to be familiar with all possible hazards connected with the experiment and in the laboratory. The procedure below includes class-IV lasers, high voltage and vacuum. Consult the material safety data sheet (MSDS) for the species to be investigated.
1. Preparation
- Preparatory considerations NOTE: Before the actual experiment starts, two main choices have to be made; the first regarding the possible species under investigations and the second the electric field in the spectrometer. It is assumed here that the setup has been used previously for other experiments and that the spectrometer itself will not be remodeled.
- Choice of sample
- Choose a sample where fragmentation pathways can be expected that carry signature of the handedness or the structural feature to be investigated. Keep in mind that hydrogen atoms are often released as neutral fragments; functional groups that differ only by the number of hydrogen atoms can probably not be distinguished. Start with simple (maybe achiral) species such as halomethanes or haloethanes.
- Check that at least 0.02 mol of the sample is available as this is the minimal amount used in successful experiments so far.
- Verify that a sufficient vapor pressure is achievable with the sample. Depending on the design of the apparatus, vapor pressures >5 hPa are necessary for a sufficient jet density for laser experiments. If the vapor pressure is significantly lower, examine if the required vapor pressures can be reached by heating the sample. This can be possible for both liquid and solid samples, by virtue of sublimation for the latter. If heating is required, it is necessary to have a positive temperature gradient along the path of the gas in the delivery system (with the nozzle being the hottest part) to avoid condensation. More advanced sample preparation schemes like pick-up by a carrier gas might be considered.
- Choice of electric field strength in the spectrometer NOTE: A value of 50 to 100 V/cm has proven reasonable for Coulomb Explosion Imaging. The optimum value, however, depends on the geometry of the spectrometer. The steps below show how to optimize the electric field strength.
- Estimate the time-of-flight of the expected cationic fragments. If the spectrometer consists only of a homogeneous field region with length s and electric field strength E, the mean time-of-flight of a particle with mass m and charge q is simply given by
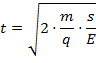
- Estimate the spread x of the fragment cations with mass m on the detector by using the time-of-flight t calculated above and the formula
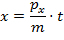 Ions will gain momenta px of up to 400 atomic units of momentum (protons up to 150 atomic units).
Ions will gain momenta px of up to 400 atomic units of momentum (protons up to 150 atomic units). - If the spatial spread x of the lightest ion species is larger than the detector radius, increase the electric field strength in the calculation until the spread is a few millimeters smaller than the detector size. The field strength should not be much higher as this leads to a lower resolution for heavier fragments that are spread out less on the detector.
- Check of experimental set-up NOTE: Before proceeding to the actual measurement, it has to be checked that the experimental setup is well prepared.
- Check that the vacuum in the interaction chamber is <1 x 10-9 hPa. If this is not the case, the residual gas will lead to a high background rate. In case of doubt about the vacuum conditions, continue until step 2.2.1 where the ionization rate of the residual gas is determined. If the pressure is too high, perform a leak-check. If no leak is apparent, bake the chamber for a few days.
- Verify the connections for the voltage supply and the detector signals according to the manual or experiment description.
- Check that the data acquisition software on the measurement computer is able to record and analyze at least four ions. Make sure that the dead time of the electronic modules and the pulse width of the signals is below 30 ns.
- Prepare sample delivery
- Verify that the sample delivery tubes are clean and the connections tightened. If the sample is corrosive (e.g. acidic) make sure that all components in the delivery system and the roughing pumps of the vacuum chamber are compatible with the chosen sample. Pump the sample delivery system with a roughing pump, open the valves and verify that the pressure in the experimental chamber is not increasing.
- Clean and prepare the sample recipient. An ultrasonic bath with acetone or a usual laboratory glassware washer are sufficient.
- Prepare the heating of reservoir and sample delivery system if the sample needs to be heated (cf. 1.1.1.3). The most convenient way is to use adjustable heating circuits, each one made up of a heating wire, a temperature sensor and a temperature controller.
- If the sample has a very low vapor pressure, or if it tends to form clusters (e.g. acids), use different approaches for pick-up or copropagation with inert gases. Modify the design of the gas lines depending on these requirements.
- Check that the molecular jet is well aligned. For that purpose, use a rare gas sample (e.g. Argon) so that a dense jet can be achieved (roughly 1 bar absolute pressure should be sufficient for a 50 µm nozzle). Maximize the pressure in the jet dump section by moving the manipulator to which the nozzle is mounted.
- Provide femtosecond laser pulses NOTE: The ionizing pulses are provided by a femtosecond laser system. Describing such a laser and its use in detail is beyond the scope of this protocol. If a commercial laser system is used, consult the manual.
- Switch on the laser and check the laser beam profile at the output.
- Check and correct (if necessary) the beam path to the entrance window of the experiment by adjusting the respective mirrors.
- If necessary, align the focusing mirror inside the experimental chamber by using the respective manipulator. Center the reflection of the focusing mirror with respect to the incoming beam.
- Insert filters or a rotatable polarizer in the beam path to achieve a peak intensity of roughly 6 x 1014 W/cm2. For normal Coulomb Explosion Imaging, use linear polarization. If dichroism effects are to be investigated, change the polarization by a quarter-wave plate just before the entrance window.
- Insert a photodiode in a place where it can record a reliable replica of the laser pulse (e.g. a reflection or the transmission through an alignment mirror). Connect the output of the photodiode to an oscilloscope and verify that the diode produces clean pulses with the repetition rate of the laser.
- Always block the beam when not in use.
2. Turning on Spectrometer and Detectors
NOTE: This part of the protocol slightly depends on the actual implementation of the spectrometer and detector system. The description here is valid for a standard COLTRIMS setup with a hexagonal delay line detector (HEX75).10 In this implementation, a detector has 7 output channels: one for the microchannels plates (MCPs) and two for each of the three layers of the anode.
- Turn on power supplies.
- Switch off vacuum gauges in the interaction chamber as they might produce ions that are seen by the detector.
- Connect the amplified signal output (using a fast amplifier with amplification ≈100) of the MCP to a fast (preferably analogue) oscilloscope. Set the oscilloscope to 5 or 10 ns per division on the time scale and 100 mV per division on the signal scale. Verify that the electronic noise is below 30 mV.
- Switch on the high-voltage power supply for the detector. For a typical ion detector, the voltage is -2,000 V for the front side and 300 V for the anode side. The voltage depends on the age of the MCPs and should be set such that the analog signals are maximal but do not saturate. Check the current. It depends on the resistance of the MCPs in the detector but should not exceed 50 µA. On the oscilloscope trace, a few signals per second with a signal height of several hundred mV should be visible ('dark counts').
- Tune the power supply for the spectrometer to the value established in step 1.1.2.
- Check detector signals via ionization of residual gas NOTE: A detailed description of the detector start-up can also be found in the respective manuals.11,12
- Attenuate the laser intensity to an estimated value below 1014 W/cm2 in the focus. Unblock the laser and watch the oscilloscope trace. If this leads to a rate exceeding 5% of the laser repetition rate, the amount of residual gas in the chamber is too high or the laser beam touches the spectrometer. Fix this problem before continuing. If the count rate is significantly lower than 5% of the laser repetition rate, gradually increase the laser intensity.
- Have a closer look at the signals. They should only show one peak of several hundred mV and no 'ringing' (oscillations after the actual pulse). The width of the MCP signal should not exceed 10 ns (FWHM).
- Look at the oscilloscope trace of all six anode signals. The signals are broader here (20-30 ns), and usually a bit lower in voltage. Check again that no disturbances of signal are present. If all anode signals are below 100 mV, increase the voltage (step 2.1.3) in steps of 50 V. Tuning the amplifier gain can help to get the same pulse height for all channels.
- Convert these analogue signals to standard NIM signals (Nuclear Instrumentation Module) of -0.8 V by a Constant Fraction discriminator (CFD). Check the settings of the CFD before each experimental run. For a detailed description, refer to a manual available on the internet.12 Feed the NIM pulses into a Time-to-Digital Converter (TDC) that records the arrival time of the pulses with high resolution (usually 25 ps). These time signals are the input for the data acquisition and analysis software.
- Turn on the data acquisition software and start recording data. Look at the hit distribution for each channel - the histograms should be similar for all channels. If that is not the case for some channels, check the CFD settings (step 2.2.4) for these channels. Check the settings by additionally inspecting the sum of the signal run times for each of the detector layers as described in the detector manual. If necessary, correct the settings of the CFDs.
- Display a detector image in the data acquisition software. The detector should be displayed as a circle with a diffuse spot (image of the laser focus) in the center. The extension of the spot is mainly due to the thermal velocity of the residual gas that gets ionized.
- Feed the signal of the laser diode (step 1.5.5) into the data acquisition, preferably in the same way as the detector signals. Display a time-of-flight spectrum in the software. Relate the observed peaks residual gas species (H2, H2O, possibly N2, O2, CO2) by calculating their expected time-of-flights from the spectrometer geometry (step 1.1.2.1).
- Try to minimize the laser pulse duration by maximizing the count rate, using the dispersion correction of the laser system. A shorter pulse (and thus a higher peak intensity) will lead to a significant increase of the rate.
- If the background pressure is so low that the rate is not sufficiently high to perform the above steps, turn on the gas jet (see step 2.3) and perform steps 2.2.1 until 2.2.8. The time-of-flight spectrum in step 2.2.7 should then obviously be dominated by the species in the jet.
- Find out the absolute orientation of the detector. In order to do so, move the focusing mirror so that the image of the laser focus moves visibly in the detector image in the software. Note the direction of the movement (used in step 5.1.1). This step is important for measurement of absolute configuration because it enables to avoid inversion of the measured momenta with respect to the real laboratory space.
- Find overlap of gas jet and laser.
- Turn on the gas jet as described in step 1.3.5.
- If the rate increases and a very narrow spot ('jet spot') is visible on the detector image in the data acquisition program, ensure that the molecular jet and laser beam overlap at least partially. In this case, tune the manipulator for the focusing mirror carefully to maximize the counts in the jet spot. At optimal overlap, they should exceed the number of counts from the residual gas (step 2.2) by orders of magnitude. It might be necessary to decrease the laser intensity because the MCP count rate should not exceed 30 kHz. If the background due to the ionization of the residual gas is too high compared to the signal from the gas jet, consider to expand the laser beam outside the chamber to reach a more narrow focus.
- If no jet spot is visible on the detector image, tune the manipulator for the focusing mirror in larger steps to find the overlap, and continue then with step 2.3.2.
3. Sample Delivery
Prepare well all tools, recipient gaskets and other items needed, as the exposure of the sample to the environment should be minimized.
Fill the sample into the recipient that will be connected to the experiment. If the sample has a high vapor pressure, cool the recipient and sample beforehand to reduce evaporation losses in this step.
Connect the sample cylinder to the jet system and tighten the connection vacuum-proof. Cool the cylinder (to avoid sample losses) and pump for a few seconds to remove air.
Open the valve to the nozzle. The pressure in the source chamber should increase to at least several 10-5 hPa.
Verify that a jet spot is visible (step 2.3.2) and identify the most prominent peaks in the time-of-flight spectrum.
Optimize experimental conditions (adjust temperature, laser intensity, pressure of copropagating gas…) to maximize the ionization rate from the sample. Keep in mind that heating leads to thermal expansion of the components so that adjustment of the jet manipulator (step 1.4.5) might be necessary.
4. Measurement
NOTE: The following steps are performed in the data acquisition software.
- Check mass spectrum and coincidence spectrum.
- Plot a time-of-flight spectrum and assign the different peaks to masses that can occur in the fragmentation (parent mass, abundant fragments).
- Plot the time-of-flight of the first ion on the x-axis and the time-of-flight of the second ion on the y-axis. Regions with many counts indicate two fragments emitted in coincidence. Sharp diagonal lines indicate a break-up into two charged fragments.
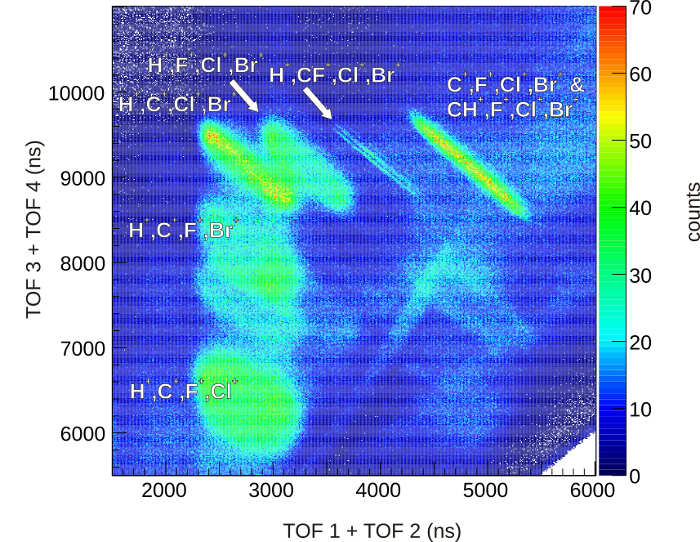
- Plot a similar histogram for more particles, e.g. the sum of the time-of-flights for the first two ions on the x-axis and the sum of the time-of-flights for the third and fourth ion on the y-axis. An example of such a multicoincidence spectrum is shown in Figure 2.
- Try to identify the different break-ups in the four-particle or five-particle spectrum and check if there is a break-up that could yield the structural information under investigation.
- Estimate measurement time.
- Let the experiment run for roughly 1 h and check the number of counts for the chosen channel. Be careful not to count background events.
- Multiply this number with the expected time available for the experiment. The total number of counts in the relevant channel should be at least a few thousands.
- If the number of counts in the chosen channel is significantly below this number, increase the laser intensity and repeat steps 4.2.1 and 4.2.2. Be careful that the rate is still low enough for coincident detection (see Introduction).
5. Data Analysis
NOTE: Data analysis in a Coulomb Explosion Imaging experiment is a complex, yet rewarding task because many parameters can be fine-tuned after the experiment and a multitude of correlations between the measured momenta can be explored. All following steps are usually performed after the experiment in the data analysis software.
- Calibrate experimental parameters NOTE: In a first step, ensure that the position and time information reconstructed from the detector is correct. Similar to the tuning of the electronics (step 2.2), the exact procedure depends on the specific implementation, in this case on the data analysis software. Thus, only some general advice can be given.
- Plot images of the detector. Check that for all three anode layers, the size of the detector image corresponds to the actual size of the MCP and that the detector image is centered at 0. Verify that all combinations of the three layers yield the same detector image. If necessary rotate or flip the detector such that the coordinate system of the detector image corresponds to the laboratory frame (use the measurements of step 2.2.10).
- Identify different masses in the time-of-flight spectrum and fit the spectrometer function (step 1.1.2.1) to these values. The important parameter in this step is the time-of-flight offset t0 that all time-of-flight values have to be corrected for.
- Have a look at the coincidence spectra (cf. Step 4.1.4) and identify promising break-up channels. It is recommended to put a gate on the time-of-flight values of a few 100 ns around the interesting patterns and only select the events within these windows for the further steps. Otherwise, the amount of unnecessary events is too large and will slow down the analysis.
- Store the corrected values for x,y,t for further analysis.
- Calculate ion momenta and energies.
- Use the experimental parameters and the assumed mass-to-charge ratios to calculate the momentum components px, py and pz. Use these to calculate the kinetic energies of the fragments and their sum, the kinetic energy release (KER).
- Use the coincidence spectrum (step 4.1.4) for fine-tuning the electric field strength E and the spectrometer length s and a plot of impact position vs. time-of-flight to determinethe position offsets x0 and y0 and the velocity vjet of the gas jet. If a precision calibration is necessary, use N2 and O2 fragmenting into two singly charged species with very narrow and well characterized vibrational progressions in the kinetic energy release (see Ref. 13 and references therein).
- Plot px vs py etc. and tune the parameters so that the momenta are distributed on a sphere in momentum space (e.g. on a circle in the two-dimensional plots) and centered at 0. This is due to the fact that the kinetic energy should not depend on the emission direction of the ion fragment.
- Plot the sum momentum of all fragments from a molecular break-up. For a complete break-up, the distribution should be narrow (typically <10 atomic unit momentum) and centered at 0.
- Select relevant events and investigate properties of the molecular system.
- Separate the actual break-up events from the background by setting constraints in the sum momentum around the observed peaks (usually less than 20 atomic units in each direction).
- For these events, use vector arithmetic to construct quantities that contain the structural information to be investigated. An example for the differentiation between left- and right-handed stereoisomers is given in the following section.
Representative Results
In this part, we show results obtained for halomethanes. These species are ideal for proof-of-principle experiments due to their simplicity and high vapor pressure. In the meantime, the more complex species halothane has been investigated using single soft-x-ray photons from a synchrotron source to induce multiple ionization.14
CHBrClF
Bromochlorofluoromethane (CHBrClF) is a textbook example for chiral molecules with a stereogenic carbon atom. It is also the ideal candidate for Coulomb Explosion Imaging due to its simple structure and the high vapor pressure (around 600 hPa at room temperature). Unfortunately, the species is not available commercially; for the experiment presented here, a racemic mixture was synthesized by reacting CHBr2Cl with HgF2 according to reference15. Enantio-enriched samples are difficult to obtain in the quantities needed so that only results for racemates have been obtained so far.
For the results presented here the sample was cooled to around 240 K to obtain an appropriate target density with the given nozzle (10% of ionization probability per pulse). The peak intensity of the laser was estimated to be 6 x 1014 W/cm2. The measurement at 100 kHz laser repetition rate took 11 h.
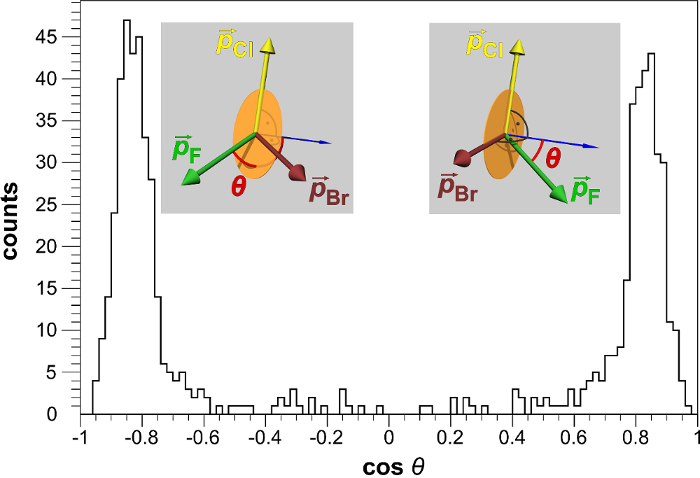
In order to distinguish R and S-enantiomers, a normalized triple product is calculated from the momentum vectors of the three halogens fluorine, chlorine, and bromine. Geometrically, this quantity can be interpreted as the cosine of the angle between the fluorine momentum and the plane of the chlorine and bromine momenta.
![]()
Figure 3 shows cosθ for the isotope CH79Br35ClF, together with the geometric definition. Two clear peaks are visible, indicating the enantiomers. The position of the peaks is consistent with a classical molecular dynamics simulation. As almost no background is present, the assignment of handedness works on a single molecule level.
CHBrCl2
The chirality of CHBrCl2 occurs only if the both isotopes 35Cl and 37Cl are present in the same molecule. A sample with natural abundance of isotopes thus contains chiral and achiral molecules. Two additional complications arise here: Firstly, the time-of-flight distributions of the chlorine and bromine isotopes overlap respectively due to the small mass difference. This is particularly relevant for chlorine as the determination of handedness depends on the correct assignment of the isotopes. Secondly, the chiral species CH79Br35Cl37Cl has (within the setup's accuracy) the same total mass as the achiral species CH81Br35Cl2. The investigation of this species can thus be seen as a benchmark test for the method.
With the spectrometer used (spectrometer length s = 60.5 mm, electric field strength E = 57.1 V/cm), the data for the chiral isotope CH79Br35Cl37Cl could be selected via the total momentum, using an algorithm suggested by reference16 to assign which of the hits belongs to which isotope.
Geometrical considerations lead to the conclusion that there can be orientations of the molecule in space where the two chlorine isotopes have the same time-of-flight; in this case, they cannot be distinguished as a matter of principle. A procedure to sort out these events has been described in the supplementary materials reference4. As a result, the configuration even of isotopically chiral molecules can be determined with high reliability.
Figure 1: View into a COLTRIMS Setup. Molecules enter the setup through the nozzle and pass through a pair of skimmers. In the interaction chamber, the laser pulses cross with the molecular jet under 90°. Ions are guided by the electric field of the spectrometer to the detector (top). For better visibility, not all spectrometer plates are shown. The remaining molecules are dumped in a differentially pumped section (jet dump) to keep the background pressure in the interaction region as low as possible. Figure modified from reference17 with permission by G. Kastirke. Please click here to view a larger version of this figure.
Figure 2: Four-Particle Coincidence Spectrum. This histogram is an extension of a time-of-flight mass spectrum to four particles: The sum of the time-of-flights for the first and second hit on the detector are plotted on the x-axis, the sum for the third and fourth hit on the y-axis. The center of the peaks allows to identify the masses of the four detected fragments. The shape of the structures contains additional information: If the momenta of the fragments add up to zero, the events are contained in a narrow line (H, CF, Cl, Br). If an undetected fragment carries momentum, the non-zero total momentum of the measured particle leads to a broadening of the features. For illustration purposes, data from synchrotron, not laser, measurements are used here due to higher statistics. Figure reproduced from reference5 with permission by Wiley-VCH. Please click here to view a larger version of this figure.
Figure 3: Distinction of enantiomers in the five-particle break-up of CHBrClF via the chirality parameter cosθ as defined in the text. The peak at positive values corresponds to the R-enantiomer, the peak at negative values to the S-enantiomer. The inset illustrates cos θ geometrically. The low background allows for an assignment of handedness for individual molecules. Figure reproduced from reference4 with permission by AAAS. Please click here to view a larger version of this figure.
Discussion
Due to the variety of components, a COLTRIMS setup requires a rather high level of technical expertise, especially in the areas of vacuum technique, particle detection, fast electronics and data analysis. Before turning to the investigation of complex species, it should thus be thoroughly checked if the setup is running properly, e.g. by performing and analyzing a measurement on a diatomic or triatomic species.
Optimizing the intensity and duration of the laser pulses and the overlap with the molecular jet is essential to achieve as many multiple ionization events as possible. As the momentum distribution might broaden due to sequential ionization during different cycles of the laser pulse, the pulse duration should ideally not exceed 40 fs. During the measurement, it is crucial to obtain sufficient statistics. On the positive side, the determination of absolute configuration does not require a particularly high precision compared to other coincidence experiments, i.e. the procedure is rather robust to fluctuations in the laser or jet intensity and to electric field distortions in the spectrometer.
The most fundamental limitation of the technique concerns its applicability to larger molecules. One must keep in mind that the results represent the momenta of fragments, not the structure of the molecules in real space. For complex bio-molecules, the relation between measured momenta and molecular structure is not expected to be as straightforward as for the molecules presented here. In addition, complex molecules can produce many break-up channels that do not carry information on the configuration, possibly decreasing the yield of relevant channels. Theoretical modeling of the fragmentation, control of break-up patterns and more sophisticated analysis procedures will be needed if the technique is to be extended to molecules with three or more carbon atoms. At the current stage, it seems not possible to investigate the configuration of proteins or molecules of similar complexity, but the actual limitations have still to be determined.
Another limitation of the current setup is the relatively high sample consumption due to the molecular jet. It can be reduced by implementing a recycling mechanism (e.g. cold traps in the vacuum foreline). Nevertheless, it would be beneficial to test other sample preparation methods such as effusive jets, thermodesorption18 or laser desorption techniques19 that have been successfully applied for studying bio-molecules in the gas phase.
Coulomb Explosion Imaging is a destructive method, i.e. molecules that have been fragmented for determination of configuration cannot be used further. However, only a small fraction is actually ionized (which is one of the reasons for the high sample consumption mentioned in the previous paragraph). It might thus be possible to use the recycled molecules for subsequent application.
As the measurement of momenta allows to create an 'aligned' data set of the molecules and to select certain spatial directions, the coincidence technique opens new perspectives for the investigation of asymmetry effects in chiral molecules This is in particular the case if the momenta of the electrons are measured in coincidence which can be achieved by using a complete COLTRIMS setup. Pump-probe techniques additionally allow to study the structural dynamics of chiral species.
Very recently, Coulomb Explosion Imaging has also been used to determine the absolute geometries of cis and trans-isomers,20 adding a new class of possible species and questions to be addressed. As the investigation of stereochemistry with coincidence spectroscopy is still in its infancy, the authors hope that this article helps to inspire researchers working in the directions outlined in the preceding paragraphs to new experiments.
Disclosures
The authors declare no competing interests.
Acknowledgments
We thank Robert Berger (Philipps-Universität Marburg, Germany) for inspiring discussions about the interpretation of our data and molecular chirality in general. We are grateful to Julia Kiedrowski, Alexander Schießer and Michael Reggelin from TU Darmstadt (Germany), as well as Benjamin Spenger, Manuel Mazenauer and Jürgen Stohner from ZHAW Wädenswil (Switzerland) for providing the sample.
The project was supported by the Hessen State Initiative for Scientific and Economic Excellence under the focus ELCH (Electron dynamics of chiral systems) and the Federal Ministry of Education and Research (BMBF). MS acknowledges financial support by the Adolf Messer foundation.
References
- Gübitz G, Schmid MG. Chiral Separation by Chromatographic and Electromigration Techniques. A Review. Biopharm. Drug Disposition. 2001;22:291–336. doi: 10.1002/bdd.279. [DOI] [PubMed] [Google Scholar]
- Berova N, Polaravapu PL, Nakanishi K, Woody RW, editors. Comprehensive Chiroptical Spectroscopy. Hoboken: Wiley; 2012. [Google Scholar]
- Bijvoet JM, Peerdeman AF, van Bommel AJ. Determination of the Absolute Configuration of Optically Active Compounds by means of X-rays. Nature. 1951;168(4268):271–272. [Google Scholar]
- Pitzer M, et al. Direct Determination of Absolute Molecular Stereochemistry in Gas Phase by Coulomb Explosion Imaging. Science. 2013;341(6150):1096–1100. doi: 10.1126/science.1240362. [DOI] [PubMed] [Google Scholar]
- Pitzer M, et al. Absolute Configuration from Different Multifragmentation Pathways in Light-Induced Coulomb Explosion Imaging. Chem Phys Chem. 2016;17(16):2465–2472. doi: 10.1002/cphc.201501118. [DOI] [PubMed] [Google Scholar]
- Vager Z, Naaman R, Kanter EP. Coulomb Explosion Imaging of small molecules. Science. 1989;244(4903):426–431. doi: 10.1126/science.244.4903.426. [DOI] [PubMed] [Google Scholar]
- Herwig PH, et al. Imaging the Absolute Configuration of a Chiral Epoxide in the Gas Phase. Science. 2013;342(6162):1084–1186. doi: 10.1126/science.1246549. [DOI] [PubMed] [Google Scholar]
- Dörner R, et al. Cold Target Recoil Ion Momentum Spectroscopy: a 'momentum microscope' to view atomic collision dynamics. Physics Reports. 2000;330:95–192. [Google Scholar]
- Ullrich J, et al. Recoil-ion and electron momentum spectroscopy: reaction-microscopes. Rep. Prog. Phys. 2003;66(9):1463–1545. [Google Scholar]
- Jagutzki O, et al. Multiple Hit Readout of a Microchannel Plate Detector With a Three-Layer Delay-Line Anode. IEEE Trans Nucl Sci. 2002;49(5):2477–2483. [Google Scholar]
- RoentDek GmbH MCP Delay Line Detector Manual. 2017. http://www.roentdek.com/manuals/MCP%20Delay%20Line%20manual.pdf.
- RoentDek GmbH The RoentDek Constant Fraction Discriminators CFD8c, CFD7x, CFD4c, CFD1c and CFD1x. 2017. http://www.roentdek.com/manuals/CFD%20Manual.pdf.
- Zeller S, et al. Imaging the He2 quantum halo state using a free electron laser. PNAS. 2016;113(51):14651–14655. doi: 10.1073/pnas.1610688113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitzer M, et al. Stereochemical configuration and selective excitation of the chiral molecule halothane. J. Phys. B.: At. Mol. Opt. Phys. 2016;49(23):234001. [Google Scholar]
- Hine J, Dowell AM, Singley JE. Carbon Dihalides as Intermediates in the Basic Hydrolysis of Haloforms: IV Relative Reactivities of Haloforms. J. Am. Soc. Chem. 1956;78:479–482. [Google Scholar]
- Wales B, et al. A coincidence detection algorithm for improving detection rates in coulomb explosion imaging. Nucl. Instr. Meth. in Phys. Res. A. 2012;667:11–15. [Google Scholar]
- Kastirke G. Konstruktion und Aufbau einer UHV-tauglichen COLTRIMS-Kammer. Goethe-University Frankfurt; 2014. Master Thesis. [Google Scholar]
- Calegari F, et al. Charge migration induced by attosecond pulses in bio-relevant molecules. J. Phys. B.: At. Mol. Opt. Phys. 2016;49(14):142001. [Google Scholar]
- Gaie-Levrel F, Garcia GA, Schwell M, Nahon L. VUV state-selected photoionization of thermally-desorbed biomolecules by coupling an aerosol source to an imaging photoelectron/photoion coincidence spectrometer: case of the amino acids tryptophan and phenylalanine. Phys. Chem. Chem. Phys. 2010;13:7024–7036. doi: 10.1039/c0cp02798g. [DOI] [PubMed] [Google Scholar]
- Ablikim U, et al. Identification of absolute geometries of cis and trans molecular isomers by Coulomb Explosion Imaging. Sci. Rep. 2016;6:38202. doi: 10.1038/srep38202. [DOI] [PMC free article] [PubMed] [Google Scholar]


