The two-phase flow IPTT method for measurement of nonwetting-wetting liquid interfacial areas at higher nonwetting saturations in natural porous media

Abstract

Interfacial areas between nonwetting-wetting (NW-W) liquids in natural porous media were measured using a modified version of the interfacial partitioning tracer test (IPTT) method that employed simultaneous two-phase flow conditions, which allowed measurement at NW saturations higher than trapped residual saturation. Measurements were conducted over a range of saturations for a well-sorted quartz sand under three wetting scenarios of primary drainage (PD), secondary imbibition (SI), and secondary drainage (SD). Limited sets of experiments were also conducted for a model glass-bead medium and for a soil. The measured interfacial areas were compared to interfacial areas measured using the standard IPTT method for liquid-liquid systems, which employs residual NW saturations. In addition, the theoretical maximum interfacial areas estimated from the measured data are compared to specific solid surface areas measured with the N₂/BET method and estimated based on geometrical calculations for smooth spheres. Interfacial areas increase linearly with decreasing water saturation over the range of saturations employed. The maximum interfacial areas determined for the glass beads, which have no surface roughness, are 32±4 and 36±5 cm⁻¹ for PD and SI cycles, respectively. The values are similar to the geometric specific solid surface area (31±2 cm⁻¹) and the N₂/BET solid surface area (28±2 cm⁻¹). The maximum interfacial areas are 274±38, 235±27, and 581±160 cm⁻¹ for the sand for PD, SI, and SD cycles, respectively, and ~7625 cm⁻¹ for the soil for PD and SI. The maximum interfacial areas for the sand and soil are significantly larger than the estimated smooth-sphere specific solid surface areas (107±8 cm⁻¹ and 152±8 cm⁻¹, respectively), but much smaller than the N₂/BET solid surface area (1387±92 cm⁻¹ and 55224 cm⁻¹, respectively). The NW-W interfacial areas measured with the two-phase flow method compare well to values measured using the standard IPTT method.

1. Introduction

The interface between nonwetting and wetting fluids is of great importance for numerous multiphase fluid flow applications, such as oil and gas extraction, geologic CO₂ sequestration, transport of organic contaminants in subsurface systems, and water recharge through the vadose zone. The interfacial partitioning tracer test (IPTT) method is one of the few methods by which to measure fluid-fluid interfaces in the laboratory for 3D porous-media systems. This method has been used to measure NW-W interfacial areas for various porous media including glass beads, silica sands, and natural soils [Saripalli et al., 1997, 1998; Kim et al., 1997, 1999; Anwar et al., 2000; Schaefer et al., 2000a, 2000b; Jain et al., 2003; Chen and Kibbey, 2006; Dobson et al., 2006; Brusseau et al., 2007, 2008, 2010; Narter and Brusseau., 2010].

The standard methods used for measuring air-water interfacial areas (aqueous tracer tests under steady unsaturated flow; gas-phase tracer tests) allow measurements over a wide range of wetting-phase saturations. Conversely, the standard IPTT technique for liquid-liquid interfacial area measurement is based on establishing trapped (residual) NW saturation conditions. However, NW liquid saturations are likely to be higher than residual for many applications of interest, and for these cases the impact of multiphase flow conditions on interfacial area would be of critical importance. The relationship between liquid-liquid interfacial area and fluid saturation has not been investigated to a significant extent due to the limitation of the standard IPTT method. An alternative IPTT method that can measure interfacial area at higher-than-residual NW liquid saturations is based on implementing a simultaneous two-phase flow regime [Jain et al., 2003]. This method, however, has been tested to date only for an ideal glass-beads medium [Jain et al., 2003]. Given the need to examine NW-W liquid interfacial-area functional behavior at higher NW saturations, it is crucial to test the viability of the modified IPTT method for natural porous media.

The objective of this study is to test the two-phase flow method for measuring liquid-liquid interfacial area over a range of NW saturations. Experiments are conducted for three porous media, including two natural porous media, a quartz sand and a soil, with glass beads used as a reference medium. The effect of hysteresis on the interfacial area was also investigated. Interfacial areas measured with the two-phase flow method are compared to values measured using the standard IPTT method (employing residual NW saturation). In addition, the theoretical maximum interfacial areas estimated from the measured data are compared to the specific solid surface area determined in two ways, based on geometrical calculations for smooth spheres and as measured with the N₂/BET method.

2. Materials and Methods

2.1 Materials

Three porous media were used in this study: 1-mm diameter glass beads, a well-sorted natural, commercially available 45/50-mesh silica sand (Accusand, Unimin Co.), and a natural soil (Vinton) that was collected at a site in Pima County, AZ. The volume-normalized specific solid surface areas were obtained using two methods. For the first method, the areas were estimated based on geometric considerations, assuming that the solids have smooth surfaces (Table 1). The geometric-based surface areas do not include the influence of surface roughness. The N₂/BET method was used to measure the surface areas. This method captures the influence of surface roughness. Relevant properties of the porous media are presented in Table 1. Tetrachloroethene (PCE) was used as the representative NW fluid and water as the W fluid. All chemicals were reagent grade (Sigma-Aldrich Co.).

Table 1.

Physical Properties of Porous Media

Porous media	Bulk density (g/cm3)	Ua	Median grain diameter (d50, mm)	Geometric solid surface area (cm−1)b	N2/BET solid surface area (cm−1)c
Glass beads	1.35	1.0	1.16	31±2	28±2d
Sand-45/50	1.69	1.1	0.35	107±8	1387±92e
Vinton soil	1.56	2.4	0.234	152±8	55224f

^aU = uniformity coefficient (d₆₀/d₁₀), d_i is the ith percent of grains by mass that are smaller than a given sieve size.

^bGeometric specific solid surface area with 95% confidence interval is calculated using the equation [= 6(1 - n)/d₅₀, where the porosity (n) obtained in our prior studies and this study were used (Brusseau, et al., 2006, 2007, 2008, 2009, 2010; Narter and Brusseau, 2010)].

^cMeasured with the N₂/BET method by Quantachrome Instruments (Boynton Beach, FL) and Micromeritics Corporation (Norcross, GA).

^dCalculated from data in Narter et al., 2010.

^eCalculated from data in Brusseau et al., 2008.

^fCalculated from data in Brusseau et al., 2010.

The columns used for the tracer tests are stainless steel, with a length of 15 cm and inner diameter of 2.2 cm. One cap of the column was modified to have two inlet ports. This cap was always used for fluid injection. Porous plates were placed at each end of the column. All tubing, porous frits, and connectors are constructed of stainless steel.

Sodium dodecyl benzenesulfonate (SDBS) (35mg/L) was used as the interfacial partitioning tracer, and bromide (Br⁻, 10 mg/L) in the form of NaBr was used as the nonreactive tracer. The tracer solution containing both SDBS and Br⁻ was prepared with deionized water and was used for all column experiments. The interfacial tension between the aqueous surfactant solutions (including Br⁻) and PCE liquid was measured using a ring tensionmeter (Fisherscientific, Surface Tensiomat 21). The interfacial partition coefficient (K_i) of SDBS was determined by interfacial tension as a function of SDBS concentrations [e.g., Kim et al., 1997; Saripalli et al., 1997; Jain et al., 2003], which is 1.13×10⁻³ cm at the SDBS concentration of 35 mg/L (Figure S1, supporting information (SI)).

2.2 Methods

Multiple tracer tests were conducted over a range of saturations for the sand and glass beads under two wetting scenarios of primary drainage (PD, defined as initial drainage of a water-saturated system) and secondary imbibition (SI, defined as imbibition from an initial condition of low wetting-fluid saturation (i.e., after primary drainage)). In addition, tracer tests were conducted under secondary drainage (SD, drainage step following secondary imbibition) for the sand. A limited set of experiments with a single PD and SI step were conducted for the soil to provide an initial evaluation of method feasibility for a physically and geochemically heterogeneous medium. Tracer tests were conducted for each medium before emplacement of PCE liquid to verify that the column was packed uniformly and to measure the adsorption coefficient of SDBS (K_d). The series of two-phase flow tests were then initiated, using different ratios of PCE/water (fractional) flow to attain different saturations. The tracer test was conducted once conditions stabilized at a set PCE/water ratio. The columns were dry packed and then flushed with CO₂. The column was then oriented vertically and de-aerated water was injected from the bottom of the column using a HPLC pump (Gilson, Acuflow series II). The column was removed and weighed periodically until the weight was constant, which indicated saturation of the column. The saturated column was then oriented horizontally for the IPPTs, with the two inlets on the cap of fluid entry lined up vertically. The same column was used for a series of tracer tests to obtain a range of PCE saturations under drainage/imbibition cycles (Table S1, SI). Water and PCE liquid were pumped simultaneously into the column to start two-phase flow conditions. Water was injected into the top inlet of the cap by a HPLC pump (Gilson, Acuflow series II), and PCE was injected into the bottom inlet by a high-precision, valveless pump (FMI, QG6). The total flow rate of water and PCE was maintained at approximately 1 mL/min (Darcy velocity (q) was 0.26 cm/min) during the experiments. Effluent samples were collected continuously and weighed for the total water and PCE mass discharge. The PCE liquid was then removed from the sample vials using a pipette and the samples were weighed again for the volume of water. The weight of the column was measured (precision of 0.01g). Steady-state two-phase flow was considered to be established when the difference in fractional flow rates between the influent and effluent varied by less than 2% and the weight of the column varied by less than 0.02 g.

After establishing steady flow conditions, the aqueous-phase influent was switched from water to the tracer solution to initiate the IPTT. After injection of the tracer solution for at least 3.5 aqueous-phase pore volumes (PVs) for glass beads and sand or 20 PVs for Vinton soil, the aqueous-phase influent was switched back to water to elute the tracer solution. After the elution was completed, the column was weighed again. Aliquots of the aqueous samples were set in a hood for a week to allow the dissolved PCE to volatilize. The samples were weighed before and after volatilization to account for water evaporation. The samples were then analyzed by UV-Vis spectrophotometry (Shimazu, Model 5150) at wavelength of 223 nm for SDBS and by an ion-selective electrode for bromide.

During primary drainage conditions, the water-PCE flow-rate ratio was decreased to increase PCE saturation to approximately 50%. Then the water-PCE ratio was increased to initiate secondary imbibition. As the water-PCE ratio increased to 100% water, residual PCE saturation in the column was established and another tracer test was conducted under this condition. The capillary number calculated for this displacement condition was 1 × 10⁻⁶, which is in the range of the values typically associated with formation of a stable distribution of discontinuous (residual) nonwetting liquid [e.g., Wardlaw and McKellar, 1985; Brusseau et al., 2008]. After this, the water-PCE ratio was decreased again to effect secondary drainage. After each tracer test at a given PCE saturation was completed, the influent water-PCE flow-rate ratio was adjusted instantaneously and a new steady-state PCE saturation was established. The weight of the column was measured before and after each tracer test (a BTC curve), and these data were used to calculate water saturations. Although the difference between the two water saturations was very small, the mean was used and the error was calculated as the difference between measured value and the mean (see Table S1, SI).

2.3 Data Analysis

The saturations of water (S_w) and PCE (S_n) in the column were obtained from mass balance calculation

$$S_{\mathrm{w}}+S_{\mathrm{n}}=1$$ (1)

$${\rho }_w{V}_{\mathrm{c}}n{S}_{\mathrm{w}}+{\rho }_{\mathrm{n}}{V}_{\mathrm{c}}n{S}_{\mathrm{n}}=m_2-m_1$$ (2)

where ρ_w is the density of water (0.998 g/mL at 20 °C), ρ_n is the density of PCE (1.622 g/mL at 20 °C), V_c is the bulk volume of porous media in the column, n is the porosity, m₁ is the weight of the column with dry porous media, and m₂ is the weight of the column with porous media saturated by both water and PCE liquid.

The volume normalized specific NW-W interfacial area (interfacial area normalized by the porous-medium volume, A_nw, cm⁻¹) was obtained using equation 3:

$$R=1+K_{\mathrm{d}}{\rho }_{\mathrm{b}}/{\theta }_{\mathrm{w}}+K_{\mathrm{i}}{A}_{\mathrm{n}\mathrm{w}}/{\theta }_{\mathrm{w}}$$ (3)

where R is the retardation factor obtained by moment analysis of the full SDBS breakthrough curves, [Narter and Brusseau, 2010]. K_d is the equilibrium sorption coefficient, ρ_b is bulk density, θ_w is the volumetric water content determined as θ_w = nS_w, and K_i is the interfacial partition coefficient of SDBS. The contribution of adsorption of SDBS by the solid surfaces is subtracted from the total R in the determination of A_nw.

3. Results and Discussion

3.1 Water Saturation and Water-PCE Flow Ratio

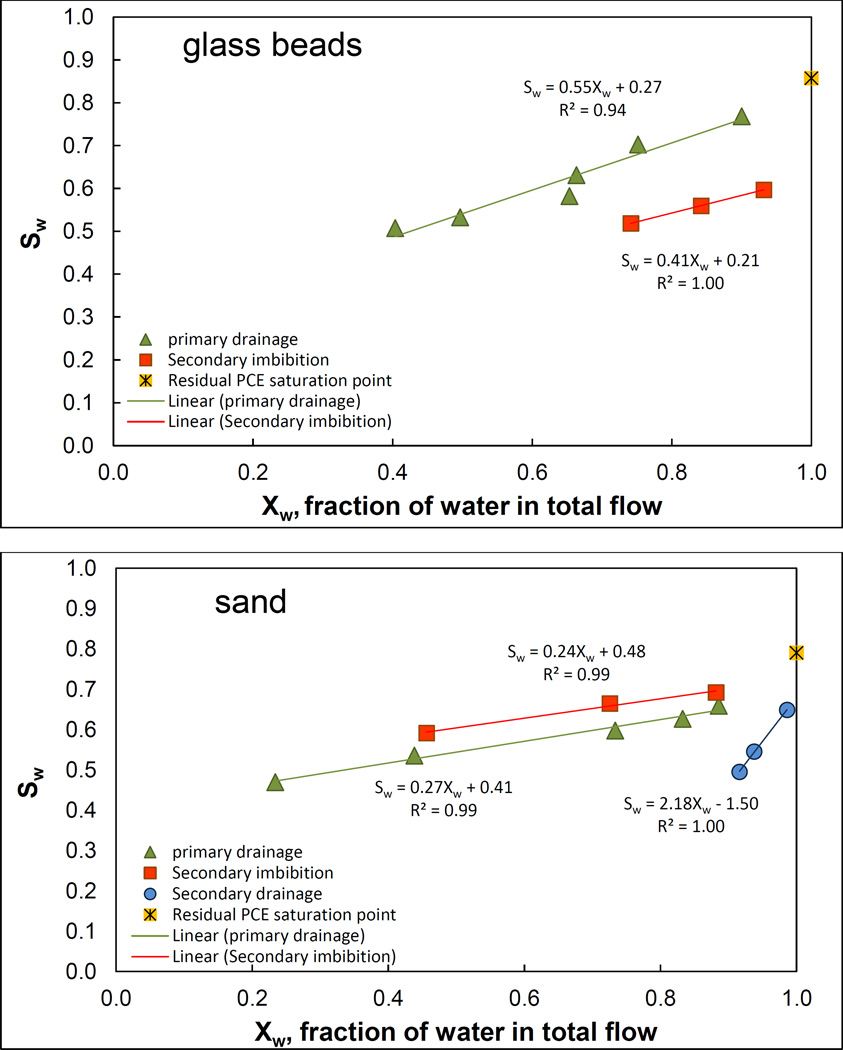
A summary of the conditions for the tracer experiments is presented in Table S1, SI. The total flow rate of the fluids ranges from 0.7 to 1.2 mL/min, and the water-PCE flow-rate ratio ranges from 1:0 to 1:3. The water saturation decreases with a reduction in the water-PCE ratio during drainage, and increases with an increase in the ratio during imbibition. A linear relationship is observed between water saturation and the fraction of water in the total flow (Figure 1).

Figure 1.

Relationship between water saturation (S_w) and water fraction of total flow (X_w) under steady-state two-phase flow conditions (See Table S1 in Supporting Information for details).

The slopes are similar between primary drainage and secondary imbibition for both glass beads and sand. However, the slope is significantly greater for the secondary drainage data for the sand. Thus, decreasing the water–flow fraction during secondary drainage causes a more pronounced reduction of water saturation than for primary drainage. The observed increased sensitivity of water saturation to the water-PCE flow ratio is consistent with hysteresis effects typically observed for two-fluid-phase systems. This behavior is likely due to the formation of trapped, disconnected PCE bodies at the end of the secondary imbibition cycle (i.e., residual saturation), and their impact on fluid distribution and displacement.

3.2 NW-W Interfacial Area and Water Saturation

All of the breakthrough curves for the conservative tracer, Br⁻, are symmetrical and exhibited no retardation, indicating that the transport is ideal under the experiment conditions. The breakthrough curves for SDBS transport are retarded compared to those of Br⁻ (see Figure S2, SI). The SDBS retardation factors obtained for the water-saturated column tests are close to 1 for the glass beads (~1.1, K_d ~0.03 cm³/g) and the sand (~1.3, K_d ~0.07 cm³/g), indicating that adsorption of the tracer by these two porous media is minimal. Greater SDBS adsorption was observed for Vinton soil, with a retardation factor of 3.5 (K_d ~0.5 cm³/g). The SDBS retardation factors increase significantly with the presence of NW saturation, ranging from 1.1 to 1.3 for glass beads, 1.3 to 3.7 for the sand, and 3.4 to 9.8 for Vinton soil over the range of saturations examined (Table S1, SI). No emulsions were observed in the effluent, indicating that the presence of SDBS did not emulsify PCE.

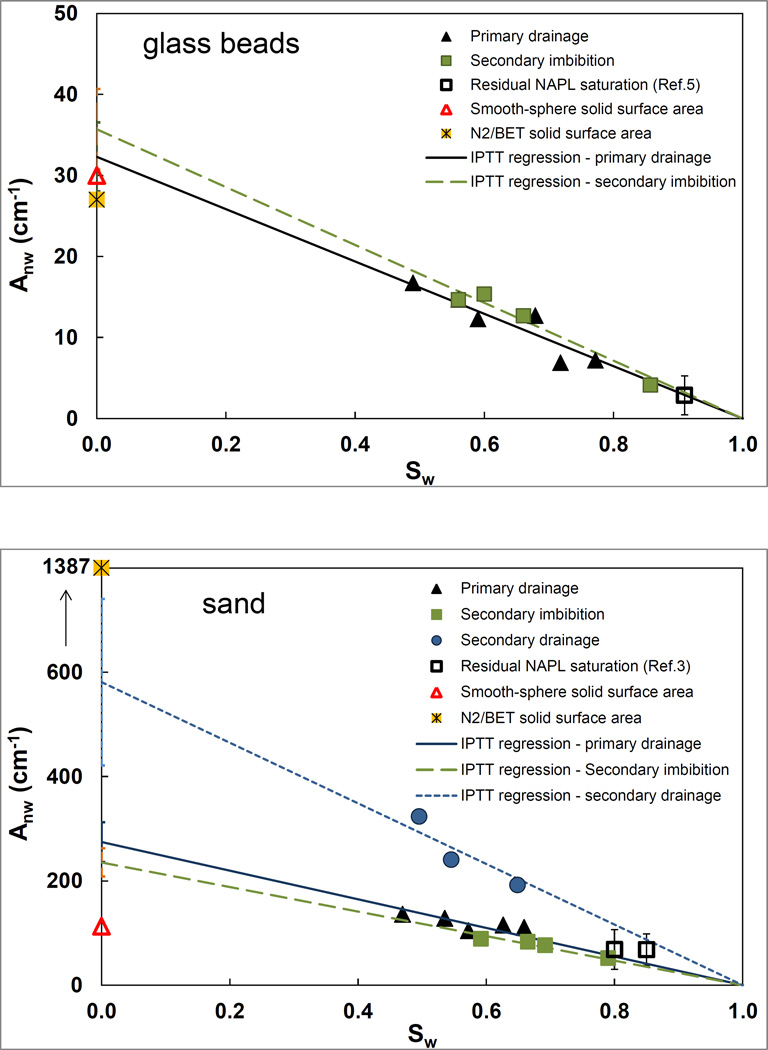
Specific PCE-water interfacial areas as a function of water saturation obtained from the IPTTs are presented in Figure 2. The areas increase as water saturation decreases for the glass beads and sand over the range investigated. This is consistent with the results of prior studies for liquid-liquid systems using X-ray microtomography [Brusseau et al., 2009; Porter et al., 2010] or IPTTs [Jain et al., 2003; Schaeffer et al., 2000a]. This is also consistent with prior microtomography and IPTT studies for measurement of air-water interfacial areas in porous media [Kim et al., 1997, 1999; Anwar et al., 2000; Schaefer et al., 2000b; Costanza-Robinson and Brusseau, 2002; Peng and Brusseau, 2005; Brusseau et al., 2006, 2007]. Single A_nw values of 1575 cm⁻¹ (S_w = 0.21) and 1330 cm⁻¹ (S_w = 0.17) were obtained for primary drainage and secondary imbibition, respectively, for the soil (Table 2).

Figure 2.

Specific NW-W interfacial area (A_nw) as a function of water saturation (S_w). Also included are (i) the geometric specific solid surface area, (ii) the specific solid surface area measured with the N₂/BET method (note the expanded maximum values for the y-axis for the sand), and (iii) data obtained using the standard IPTT method with residual NW saturation (references [Brusseau et al., 2008, 2010; Narter and Brusseau, 2010]).

Table 2.

Comparison of the study results to literature data

Porous media	Porosity	Flow scenarios	Sna	Anwb (cm−1)	Amc (cm−1)	Calculation method	Source of data
Glass beads	0.42	PDd	0.23–0.51h	6.9–16.7	32.3±4i (R2=0.99)j	Linear regressionk	This study
	0.42	SIe	0.44-0.14	15.3–4.1	35.7±5 (R2=0.99)	Linear regression	This study
	0.38	Residualg	0.09±0.02	2.9±2.4	35.0±30	Mean of 4 replicates	Narter et al., 2010
Sand-45/50	0.37	PD	0.34–0.53	105–136	274±38 (R2=0.99)	Linear regression	This study
	0.37	SI	0.41–0.21	89–52	235±27 (R2=0.99)	Linear regression	This study
	0.37	SDf	0.35–0.51	192–323	581±160 (R2=0.99)	Linear regression	This study
	0.37	Residual	0.20	68±19	341±96	Mean of 4 replicates	Brusseau et al., 2008
	0.40	Residual	0.15	68±15	455±102	Mean of 4 replicates	Brusseau et al., 2008
Vinton soil	0.39	PD	0.21	1575	7629	Single runl	This study
	0.39	SI	0.17	1330	7623	Single run	This study
	0.42	Residual	0.14	1098±501	8075±3794	Mean of 4 replicates	Brusseau et al., 2010

^aS_n = saturation of organic liquid.

^bA_nw = interfacial area calculated employing equation (3) in text.

^cA_m = the extrapolated maximum interfacial area employing equation A_nw=A_mS_n.

^dPD = primary drainage.

^eSI = secondary imbibition.

^fSD = secondary drainage.

^gResidual NW saturation created during secondary imbibition.

^hminimum and maximum values.

ⁱ95% confidence interval by using the uncertainty for the regression slope variable.

^jR = Correlation coefficient of linear regression A_nw=A_mS_n.

^kFit A_nw=A_mS_n to the data points of various S_n

^lA_m obtained using A_nw=A_mS_n assumption

Good linear correlations are observed between interfacial area and water saturation for the glass beads and the sand. They can be described with the equation A_nw = A_m(1-S_w), where A_m is the estimated theoretical maximum specific interfacial area obtained by extrapolating the regression to S_w = 0. The results are reported in Table 2. While A_m values are recognized to have associated uncertainty, partly due to the assumption of a linear A_nw-S_w correlation, they are useful for comparison of interfacial-area data obtained at different saturations, and for comparison to related system variables such as specific solid surface area.

The A_m values determined for the glass beads, which have no microscopic surface roughness, are 32±4 and 36±5 cm⁻¹ for primary drainage and secondary imbibition cycles, respectively. These values are similar to the calculated geometric specific solid surface area (31±2 cm⁻¹) and to the measured N₂/BET specific solid surface area (28±2 cm⁻¹) (Table 1). The A_m represents the extrapolated maximum interfacial area at an infinitesimally low water saturation, wherein the remaining water exists as a vanishingly thin film covering the solids. Under these conditions, the NW-W interfacial area is anticipated to be essentially identical to the solid surface area (minus the effect of grain-grain contacts). The similarity of the A_m values to the two independently determined specific solid surface areas indicates that the IPTT method provided accurate measurements of the NW-W interfacial area in this study. This is further supported by comparison to the results reported by Narter and Brusseau [2010], who used X-ray microtomography to measure interfacial area between PCE and water for the same glass beads used herein. They reported an A_m value of 30 (±2 cm⁻¹), which is statistically identical to the IPTT-determined value obtained in this study.

The A_m values for the sand are 274±38, 235±27, and 581±160 cm⁻¹ for primary drainage, secondary imbibition, and secondary drainage cycles, respectively. The A_m values for Vinton soil are 7629 and 7623 cm⁻¹ for primary drainage and secondary imbibition, respectively (Table 2). The A_m values for the sand and Vinton soil are significantly greater than the respective geometric specific solid surface areas, 107±8 cm⁻¹ and 152±8 cm⁻¹ (Table 1). This observation is consistent with the results of prior studies and supports the contention that the aqueous IPTT method characterizes some fraction of film-related interfacial area associated with solid surface roughness [Brusseau et al., 2007, 2008, 2010]. However, the A_m values for both the sand and the soil are much smaller than the N₂/BET solid surface areas (1387±92 cm⁻¹ and 55224 cm⁻¹, Table 1). This disparity would be anticipated given two primary factors, one that a large portion of surface roughness is likely masked by thick water films at the relatively high range of S_w tested, and second that hydraulic accessibility of some interfaces to the tracer may be limited. Such disparity was also observed in prior studies using the aqueous-phase IPTT method for air-water systems [Kim et al., 1999; Schaefer et al., 2000b; Brusseau et al., 2007]. These results are supported by the results obtained with the gas-phase IPTT method, wherein air-water interfacial area is observed to increase exponentially, rather than linearly, as S_w decreases in the low range of S_w [Kim et al., 1999; Costanza-Robinson and Brusseau, 2002; Peng and Brusseau, 2005; Brusseau et al., 2007]. Finally, it is observed that the A_nw and A_m values for the soil are much larger than those for the sand, which in turn are much larger than those for the glass beads, and that the values correlate approximately with magnitudes of surface roughness, consistent with Brusseau et al. [2010].

3.3 Effect of Drainage/Imbibition Conditions on Interfacial Area

Both the specific interfacial areas and A_m values are similar for primary drainage and secondary imbibition for all three porous media (Figure 2, Table 2). It has been observed that hysteresis occurring in drainage/imbibition cycles influences the magnitude of the capillary-associated air-water interfacial area. For example, employing microtomographic methods, Culligan et al. [2004, 2006] and Porter et al. [2010] observed that capillary NW-W interfacial areas measured under imbibition were smaller than those for drainage for glass beads, reflecting differences in wetting-nonwetting phase configuration between drainage and imbibition conditions. Similar results were reported by Brusseau et al. [2007] for microtomographic measurement of air-water interfacial area for the Vinton soil (same soil as used herein). This observed behavior is consistent with the results of numerous pore-scale modeling analyses using various approaches. Conversely, total specific interfacial areas measured with microtomography were similar for primary drainage and secondary imbibition conditions for glass beads [Porter et al., 2010] and the Vinton soil [Brusseau et al., 2007], and for multiple drainage-imbibition cycles for an acrylic bead pack [Landry et al., 2011]. Similar air-water interfacial areas were obtained for primary drainage and primary imbibition with the standard IPTT method for the same sand and soil used in the present study [Brusseau et al., 2015].

The total interfacial areas obtained with the IPTT and microtomography methods include interfacial area associated with films in addition to capillary domains. The film-associated interfacial area usually comprises a major fraction of total interfacial area [e.g., Or and Tuller, 1999; Costanza-Robinson and Brusseau, 2002; Brusseau et al., 2006, 2007]. For ideal conditions (e.g., strongly wetting surfaces, minimal wettability alterations), this film-associated interfacial area is anticipated to be unaffected by hysteresis effects, as the wetting films remain present independent of flow conditions. Conversely, capillary interfacial area is typically influenced by flow conditions.

The interfacial areas measured under secondary drainage for the sand are significantly larger than those obtained under primary drainage and secondary imbibition (Figure 2b and Table 2). The larger interfacial areas observed for secondary drainage are hypothesized to result at least in part from an increase in the magnitude of capillary-associated area. This is attributed to the impact of changes in NW fluid distribution and configuration as related to the hysteresis effects typically observed for multi-phase flow. Specifically, the presence of capillary-trapped residual NW fluid formed at the end of the secondary imbibition cycle may influence the distribution and displacement of fluids during the secondary drainage sequence. For example, the presence of the NW residual may cause some fraction of the NW fluid newly introduced during secondary drainage to enter and displace through smaller-diameter pores compared to primary drainage. This change in distribution of NW fluid would affect fluid surface and interfacial areas. Differences in populations of pore-sequences active in displacement may be expected among multiple cycles particularly for natural media such as the sand, with its significant surface roughness and grain angularity. The results of a pore-network modeling analysis for Berea sandstone showed capillary interfacial areas for secondary drainage to be larger than those for primary drainage over the W saturation range of 0.4 – 0.6 [Raeesi and Piri, 2009].

It is also possible that the larger interfacial areas observed for secondary drainage are in addition influenced by invalidity of the assumption that film-associated interfacial area is unaffected by hysteresis. First, the potential occurrence of surface-wettability alterations after multiple PCE floods, and their subsequent impact on fluid distribution and displacement, cannot be ruled out. Second, it is recognized that the IPTT method produces effective measures of interfacial area in that factors such as interface accessibility mediate the magnitude of interfacial area characterized. It is possible that significant changes in fluid distribution and configuration may alter interface accessibility between cycles, resulting in measurement of different effective interfacial areas. The observation that the SDBS BTCs consistently reached plateaus at C/C₀ < 1 for the secondary drainage experiments may reflect the impact of significant changes in fluid distribution and configuration.

3.4 Comparison with the Standard IPTT Method

Liquid-liquid interfacial areas obtained from prior IPTTs conducted with the standard technique (residual NW saturation) are plotted in Figure 2 along with the results of this study. Inspection of Figure 2 shows that the interfacial areas measured with the two-phase flow method are similar to those obtained with the standard IPTT method. In addition, the maximum interfacial areas obtained in this study compare well to those reported in prior studies using the standard method for all three porous media (Table 2). These results indicate that the two-phase flow method provides measurements that are comparable to those obtained with the standard IPTT method.

It is of interest to note that, for the current study, the residual saturation condition was attained after many pore volumes of surfactant solution had been injected into the column. In contrast, residual saturation of NW is typically established prior to introduction of surfactant tracer for the standard IPTT method (as was done for the literature data used herein). The residual PCE saturation ranges from 0.08 to 0.12 for the glass beads and from 0.14 to 0.20 for the sand in the prior standard-IPTT studies. The residual S_ns for glass beads and sand in the present study are 0.14 and 0.21, respectively. The values are comparable to those obtained in the prior studies. This indicates that the presence of the SDBS tracer had minimal effect on the magnitude of residual S_n. The similarity of the A_nw and A_m values measured with the two methods further indicates that prior presence of the surfactant tracer had no measurable impact on configuration of the non-wetting phase. This is consistent with the results reported by Brusseau et al. [2008], who used x-ray microtomography to examine the impact of SDBS addition on organic-liquid/water systems. The results showed that the addition of SDBS solution had minimal impact on NW configuration or NW-W interfacial area under the conditions typically employed for standard IPTTs.

Comparison of the methods should include evaluation of potential impacts of method-specific differences on uncertainties associated with IPTT measurements. One issue of general concern for IPTT methods is the potential for the tracer solution upon its introduction to cause changes in fluid configuration or distribution due to changes in interfacial tension. While this issue has been shown to impact the standard aqueous-based method for measuring air-water interfacial area under certain conditions [Chen and Kibbey 2006; Costanza-Robinson et al., 2012], it has been shown to be negligible for the standard liquid-liquid IPTT method [Brusseau et al., 2008] and for the standard air-water IPTT method with strong flow control [Brusseau et al., 2007, 2015]. The mass of PCE and water in each effluent sample was monitored throughout each IPTT test for the present study. A small increase in the mass of water, and a corresponding decrease in PCE mass, was observed for the first 2–3 samples collected after injection of the tracer solution for the glass-bead system. The masses then re-stabilized to values consistent with those before tracer injection. This phenomenon is likely caused by the change in interfacial tension upon introduction of the tracer solution. This effect was minimal for the sand and soil systems, consistent with their lower permeabilities.

Another issue is the potential impact of fluid-fluid interface mobility on retardation of the interfacial tracer, and thus on measured interfacial areas. This was evaluated by Kim et al. [1999] who estimated that the velocity of the air-water interface was 23–36% of the bulk pore-water velocity, based on comparison of interfacial areas measured with gas-phase versus aqueous-phase IPTT methods. This range should be considered as a maximum estimate given that they were determined based on an assumption that both methods accessed identical interfacial domain. However, it is likely that the gas-phase method has greater accessibility for the mid and lower range of water saturations employed in the study [Costanza-Robinson and Brusseau, 2002; Brusseau et al., 2007]. It should be noted that Kim et al.’s evaluation was for the standard air-water aqueous IPTT method, wherein the aqueous solution is mobile and the gas phase is essentially immobile. Conversely, the non-wetting fluid is mobile as well for the two-phase flow method employed herein. In any event, the similarity in interfacial areas obtain with the two-phase flow method to those obtained with the standard liquid-liquid IPTT method (for which the NW fluid is immobile) indicates that any potential difference in impacts of interface mobility are small. In addition, the fact that the A_nw and A_m values obtained for the glass beads were essentially identical to independent measures of interfacial area and specific solid surface area, respectively, suggests that interface-mobility effects were negligible, at least for the glass-bead system.

A third potential issue is the distribution of the fluids for the two-phase flow method compared to the standard methods. For the standard fluid-fluid IPTT method, the NW fluid is present at residual saturation and displacement of the aqueous tracer solution (W fluid) occurs under single-phase flow conditions. Similar conditions are present for the standard air-water aqueous IPTT method, except that the NW fluid may be present at higher-than-residual saturations. There may be some question as to whether fluid distributions attained for the two-phase flow method, with simultaneous concurrent flow of the two fluids, would be similar to that of the other methods. For example, would flow stratification occur and limit fluid distribution. This issue was examined by Prodanovic et al. [2006], who used x-ray microtomography to characterize fluid displacement for two methods of generating multiphase systems, the standard incremental displacement of one fluid with another fluid, and a simultaneous two-fluid flow regime with changing fractional flow (as used herein). They observed that fluid distributions and interfacial areas were similar for the two systems, indicating that the two-phase flow approach generates fluid distributions consistent with the standard approach. Furthermore, the similarity in interfacial areas obtained herein with the two-phase flow method to those obtained with the standard liquid-liquid IPTT method indicates that any potential differences in fluid distribution are small for the system used in the present study.

4. Conclusions

The standard IPTT method for measuring fluid-fluid interfacial area is used for systems with residual NW saturation. An alternative to the standard IPTT method, based on two-phase flow, was used to measure liquid-liquid interfacial areas over a wider range of NW saturations. The results of this study show that measurements obtained with the two-phase flow method are comparable to those measured with the standard IPTT method. In addition, the validity of measurements obtained with the two-phase flow method was evaluated by comparison to independent benchmarks. The two-phase flow method appears to be a viable alternative for measuring NW-W interfacial area in circumstances for which the NW saturation is higher than residual. Application of this method will allow examination of the change in interfacial area as a function of changes in fluid saturation, information critical for understanding and simulating multi-phase flow.

Key Points.

1. NW-W interfacial area at above-residual S_n is successfully measured using a two-phase-flow IPTT method.

2. NW-W interfacial area increases linearly with increasing S_n for the range of S_n tested.

3. The measured interfacial areas compare well to values measured using the standard IPTT method.