Modeling the Response of Exogenously Crosslinked Tissue to Cyclic Loading: The Effects of Permanent Set

Abstract

Bioprosthetic heart valves (BHVs), fabricated from exogenously crosslinked collagenous tissues, remain the most popular heart valve replacement design. However, the life span of BHVs remains limited to 10–15 years, in part because the mechanisms that underlie BHV failure remain poorly understood. Experimental evidence indicates that BHVs undergo significant changes in geometry with in vivo operation, which leads to stress concentrations that can have significant impact on structural damage. These changes do not appear to be due to plastic deformation, as the leaflets only deform in the elastic regime. Moreover, structural damage was not detected by the 65 million cycle time point. Instead, we found that this nonrecoverable deformation is similar to the permanent set effect observed in elastomers, which allows the reference configuration of the material to evolve over time. We hypothesize that the scission-healing reaction of glutaraldehyde is the underlying mechanism responsible for permanent set in exogenously crosslinked soft tissues. The continuous scission-healing process of glutaraldehyde allows a portion of the exogenously crosslinked matrix, which is considered to be the non-fibrous part of the extracellular matrix, to be re-crosslinked in the loaded state. Thus, this mechanism for permanent set can be used to explain the time evolving mechanical response and geometry of BHVs in the early stage. To model the permanent set effect, we assume that the exogenously crosslinked matrix undergoes changes in reference configurations over time. The changes in the collagen fiber architecture due to dimensional changes allow us to predict subsequent changes in mechanical response. Results show that permanent set alone can explain and, more importantly, predict how the mechanical response of the biomaterial change with time. Furthermore, we found is no difference in permanent set rate constants between the strain controlled and the stress controlled cyclic loading studies. An important finding we have is the collagen fiber architecture has a limiting effect on the maximum changes in geometry that the permanent set effect can induce. This is due to the recruitment of collagen fibers as the changes in geometry due to permanent set increases. This means we can potentially optimize the BHV geometry based on the predicted the final BHV geometry after permanent set has largely ceased. Thus, we have developed the first structural constitutive model for the permanent set effect in exogenously crosslinked soft tissue, which can help to simulate BHV designs and reduce changes in BHV geometry during cyclic loading and thus potentially increasing BHV durability.

1. Introduction

1.1. Background and clinical significance

Heart valve treatment is a common cardiovascular surgical procedure with over 100,800 done annually in the U.S. alone [1] and 275,000 to 370,000 in developed nations [2]. Almost all contemporary heart valve replacement designs use exogenously crosslinked (EXL) collagenous soft tissues (e.g. bovine pericardium) to manufacture leaflets for bioprosthetic valves (BHVs) [3, 4]. BHVs have advantages in immunogenicity and hemodynamics over other designs, but also have a limited life span of 10–15 years. As a recent development in BHV technology, transcatheter valve interventions [5, 6] reduce surgical risk and make valve replacement more feasible for those who cannot tolerate full surgical interventions. However, this new technology also presents additional design challenges, including complex folding and compression during delivery. As a result, the leaflets are required to be significantly thinner than in traditional BHVs, which increases the leaflet stress and potentially the rate of failure. Existing data on transcatheter aortic valve interventions suggest a 2-year mortality rate of 33.9% overall [1] and over 68% when specifically replacing stenotic aortic valves [7]. As such, this further accentuates the need to develop an approach to improve BHV durability.

1.2. Mechanisms of BHV failure

The causes of BHV failure can be divided into two broad categories, mineralization and structural damage, with both processes occurring in parallel or independently [8]. Mineralization is the accumulation of mineral deposits, mainly calcium phosphate, within the BHV leaflets [9]. This disrupts the underlying microstructure preventing the proper mechanical function of BHVs, increasing the likelihood of tearing, and reducing flexibility (preventing normal opening and closing motions, and induce valve stenosis). This process is exacerbated by the presence of exogenous crosslinkers, such as glutaraldehyde (GLUT), where the phosphates from the devitalized endothelial cells bind with the calcium in blood to form deposits. The causes of calcification and associated anti-calcification treatments are extensively studied in literature [10–12]. On the other hand, structural damage includes the collagen fiber damage and breakdown of the non-fibrous part of extracellular matrix (ECM), which we will refer as simply the matrix. Fourier transform infrared spectroscopy(FTIR) results have shown changes in the collagen fiber molecular structure after 50 million cycles [13], which suggests that some collagen fiber damage has occurred during this period. However, its effect on the mechanical response of BHVs was not detectable. Nevertheless, it is important to maintain the structural integrity of the BHV, as this will help to improve BHV durability.

1.3. Response to long-term cyclic loading

The current process for evaluating BHV designs is an expensive and time consuming three-stage process: 1) accelerated wear testing(AWT), 2) large animal studies, and 3) clinical trials. AWT is performed by cycling BHVs in sterile saline at 10 to 20 times the normal heart rate. It is currently the only way to evaluate BHV durability in a feasible amount of time (months instead of years). However, the loading conditions and environment during AWT are not physiological and the only durability information currently used is the presence of visible damage. Designs which show promise are then put through costly large animal studies, which still do not fully duplicate the human native environment. The final and most important stage is clinical evaluations. This is the only stage in evaluation process that can provide true indications of the in vivo performance of BHV designs. However, this is the final, most difficult, most expensive and most time consuming stage. Clearly, current methods of evaluating BHV designs are not feasible for advancing the BHV technology in a timely manner. Computational simulations have been presented as an effective approach to this problem[4]. To be effective, we need better a understanding of the underlying mechanisms of structural damage.

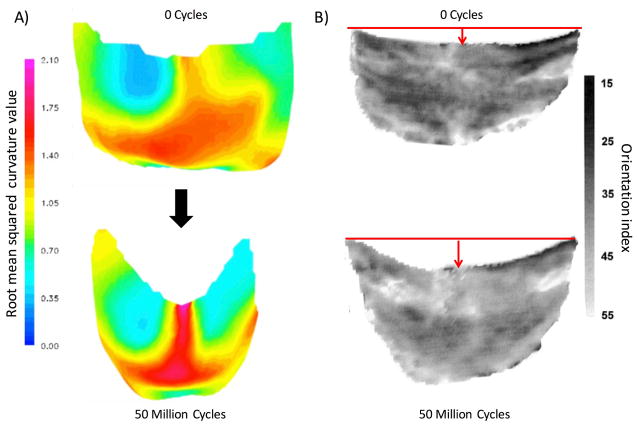
However, these mechanisms are poorly understood, especially for how they affect the mechanical response of the exogenously crosslinked tissues used to construct the BHV leaflets. The most significant change in response to cyclic loading is the change in geometry of the BHV leaflets. In a study on the porcine aortic BHVs [14], Smith et al. found significant changes in the unloaded geometry of BHVs after AWT, especially in the belly region of the leaflets (Fig. 1A). By changing the unloaded reference configuration, the shape of the leaflets and their mechanical response will change as well. Further analysis shown that significant structure damage occurred within the belly region as compared to other regions of the leaflet, where the stress significantly increased [15]. Interestingly, Smith et al. also found most the most significant changes in BHV leaflet geometry to occur within first 50 million cycles [14]. Moreover, Sacks and Smith [16] also found that there were minimal structural damage in this early stage (Fig. 1B). This is further supported by another study by Wells et al [17], where they found minimal structural changes during the first 50 million cycles for the pressure fixed BHVs, with most significant change observed in the first million cycles. Clearly, there is a non-damage based mechanism at play that changes the geometry of the material, with significant impact on the early stage of cycling and the rate of fatigue in later stages.

Figure 1.

A) The 3D unloaded geometry a BHV leaflet before and after cyclic loading, with the color indicating the local root mean squared curvature. The most significant change in geometry is in the belly region. B) BHV leaflet collagen fiber architecture, showing that the collagen fiber architecture are convected by the dimensional changes. The grayscale scale bar shows the orientation index (OI), which is angle containing 50 % of fibers. The lack of changes in the OI suggests that minimal damage to the collagen fiber architecture has occurred.

1.4. The effect of exogenous crosslinking

Bovine pericardium (BP) is a dense collagenous tissue composed mostly of collagen type I fibers with some elastin, GAGs, cells and vasculature. Collagen fibers are complex protein structures at the 2 – 10 μm scale, composed of tightly bundled collagen fibrils, which are approximately 50 nm in diameter. Much of what we know about the use of GLUT to exogenously crosslink collagenous tissue is from Nimni et al.[18–24]. GLUT, which is an aldehyde based crosslinker, aggressively crosslinks free amines in proteins. This suppresses immunogenicity by crosslinking all cell membrane protein remnants, but also forms polymeric networks (at the nm scale) which allow for long range crosslinks to the nearby tissue microstructures. We previously found that exogenous crosslinking increases the bending stiffness of the matrix by four time the original stiffness [25]. We also tested the mechanical response of exogenously crosslinked BP before and after crosslinking, and developed the first constitutive model for exogenously crosslinked soft tissue [26]. Interestingly, we also found that exogenously crosslinking does not increase the collagen fiber modulus, but significantly increases the interactions between collagen fibers [26], which is responsible for up to 30% of the stress in the fully loaded state.

The GLUT crosslinking process involves a Schiff-base reaction. Importantly, the molecular bonds formed from Schiff-base reactions are known to be unstable at room and temperatures [27, 28]. Thus, although GLUT is highly reactive and aggressively crosslinks extracellular matrix proteins, any resulting crosslinks will also readily undergo hydrolysis at body temperature [27]. As a result, under cyclic loading in-vivo, exogenous ECM crosslinks will constantly break and reform. This continual process will cause the reference configuration to evolve towards the current loaded state. We thus hypothesize that this scission-healing behavior could be linked to the mechanisms that underlie how the BHV leaflet geometry evolves over time.

This damageless change in the BHV geometry has many similarities to the permanent set (PS) mechanisms observed in elastomers. Permanent set is an irreversible deformation that remains after a structure or material has been subjected to external stresses and then released. It does not involve damage to the constituents of the material, but instead changes the referential configuration. Although the outcomes may be similar, this form of permanent set is not a plastic deformations, as they are entirely within the elastic regime. In particular, it has been used to model the scission-healing reactions of elastomers that occur when stretched, heated, cooled, then unloaded. This results in some of the materials to change in referential configuration to the loaded state. In this process, permanent set does not damage the polymeric fibers but is a result of the change in configuration of the underlying polymeric fiber network. Some works on constitutive models of this process include the works of Rajagopal and Wineman [29], Andrews and Tobolsky [30], and Rottach et al. [31–33]. However, there are little known studies on the permanent set effect in soft tissues or soft tissue derived exogenously crosslinked biomaterials.

Based on the above considerations, we hypothesize that the initial time evolving BHV geometry and mechanical response can be predicted by permanent set mechanisms. Rather than heating and cooling, we assume that permanent set in exogenously crosslinked tissue occurs continuously at body temperature due to the GLUT, allowing the reference configuration of the exogenously crosslinked matrix (EXL matrix) to evolve over time. As a result, the reference configuration of BHVs will change while not affecting the intrinsic material properties of their constituents such as collagen fibers and the EXL matrix. Since the BHVs deform into a new configuration (Fig. 1), there may develop regions of stress concentrations. The high stresses will increase the rate of structural damage and thus accelerate the rate of BHV failure. Thus, by compensating for the permanent set effects, it may be possible to reduce the BHV leaflet stresses and thus reduce structural damage to BHVs during in vivo operation after implant. Therefore, constitutive models that can predict the effects of permanent set are crucial for the simulation of BHVs.

1.5. Constitutive models for the permanent set effect for soft tissues

The only work in the simulation of the permanent set effect in native or exogenously crosslinked soft tissues is the pioneering study of Martin and Sun [34], who developed a time dependent constitutive model for uniaxial cyclic loading of GLUT exogenously crosslinked BP strips using a damage analog. Briefly, to model the uncycled mechanical response, they used the Fung hyperelastic model for the strain energy density function, Ψ₀. The time dependent stress softening was then described using a modification to the strain energy function as Ψ_PS = (1−D_s)Ψ₀−Ψ₀(E_PS). Here the strain energy of the material after permanent set (Ψ_PS) is reduced from Ψ₀ in accordance with a scaled damage function D_s and the same strain energy function evaluated at the current amount of permanent set (E_PS). Martin and Sun then measured the maximum permanent set deformation that occurs for each specimen, and used that to set the maximum bound of E_PS. Additionally, Martin and Sun set two parameters, a lowerbound below which no permanent set occurs, and an upperbound above which the tissue fails. In the intermediate region, D_s and E_PS simply increase linearly with the number of cycles. The number of cycles needed to reach the maximum permanent set deformation was then described using an inverse exponential like function of the maximum strain applied, which is an analogous to the stress versus cycles (SN) curve used to describe the fatigue behavior of traditional engineering materials. However, such approaches have the following limitations: 1) they are not predictive as there are no underlying mechanisms in the model. A damage-like model can mimic the results of permanent set but cannot explain nor predict the mechanisms responsible in exogenously crosslinked tissue, and 2) there is no way to extrapolate for predicting into unmeasured regimes using the Fung hyperelastic model. Therefore, there is a need for a more predictive constitutive model that utilizes the underlying mechanisms.

1.6. A new approach for modeling the permanent set effect in exogenously crosslinked soft tissues

We utilize a structural constitutive modeling approach, which integrates information on tissue composition and structure for material characterization [35]. In principal, using structural models we only need to perform parameter estimation for the intrinsic material properties, such as collagen fiber modulus and EXL matrix modulus, to predict the mechanical response using the quantified tissue microstructure. This mechanism based approach allows us to predict the mechanical response at strains outside of the strain range of the experimental data used for parameter estimation [36, 37]; a feat not possible using purely phenomenological approaches. In addition, by using a structural modeling approach coupled with the permanent set mechanism to predict the collagen fiber architecture after cyclic loading, we can also predict the mechanical response of the soft tissue at higher cycle numbers. Thus, we use 1) the structural model parameters obtained in the uncycled mechanical state and 2) the permanent set mechanisms to predict how the mechanical response of the exogenously crosslinked tissues evolves with cyclic loading. The key aspects of our approach include:

1. Model the change in mechanical response entirely as a kinematic change in the underlying microstructure; no actual change in mechanical properties (damage)

2. Predict the change in geometry from the loading history and the permanent set mechanism

3. Validate the permanent set mechanism under both strain and stress controlled loading conditions

4. Develop a time dependent implementation with an evolving loaded configuration under stress control

2. Overall modeling approach

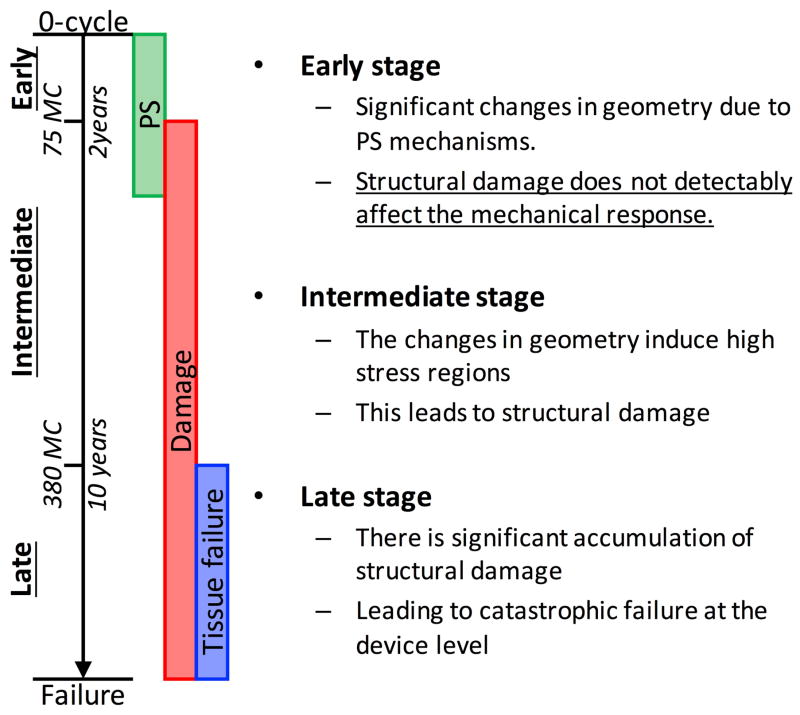
We hypothesize that permanent set and structural damage are two separate and largely sequential mechanisms that underlie the mechanical response of BHVs. Thus, the life span of BHVs can by separated into three stages: early (up to 2–5 years), intermediate (up to 10 years), and late stage (up to failure) (Fig. 2). In the early stage, permanent set induces significant changes in BHV geometry while structural damage does not play a detectable role. This leads to increased stress and structural damage in the intermediate term which leads to failure in the late term. Thus, by compensating for the effect of permanent set on the geometry, we hypothesize that we can extend the life span of BHVs. We focus our model on the early stage of cyclic loading and build a solid foundation for modeling and simulating the later stages.

Figure 2.

We speculate that the progression of structural damage and permanent set of BHV leaflets progress during long term cyclic loading can be separated into three stages: early, intermediate, and late.

We assume that permanent set is driven by the scission-healing behaviors of the GLUT polymer network in the non-fibrous EXL matrix, allowing for fractions of it to change in reference state (Fig. 3A). The formation of aldehyde bonds during crosslinking, as well as the occasional hydrolysis of the aldehyde bonds follows first order molecular kinetics [27]. Since this process drives the scission-healing of GLUT polymers and thus permanent set, we hypothesize that permanent set also follows first order kinetics. In addition, we note that the length scale of crosslinks formed by GLUT polymers (nm) in the EXL matrix is several orders of magnitude smaller than that of the collagen fibers (μm). Thus, we assume that the collagen fiber architecture does not undergo scission-healing like the EXL matrix. Instead, the collagen fibers remain intact during cyclic loading. Rather, the collagen fiber architecture is convected by the changes in geometry that occurs with permanent set in the EXL matrix (Fig. 3B). We refer to this mechanism as structural convection, which is defined as applying a permanent deformation (elongation and rotation of collagen fibers, Fig. 4) to the collagen fiber architecture based on the change in the reference configuration. Previously, we have shown that dense collagenous tissues deform under affine kinematics [38]. Since deformations during cyclic loading are in the elastic regime and cyclic loading (second) is on a time scale much shorter than that of permanent set (weeks), the only change in collagen fiber architecture on a cycle to cycle period is also under affine kinematics. Therefore, we also assume that the convection of collagen fiber architecture due to permanent set is under affine kinematics as well. Thus, our approach is based on using the permanent set effect to model the evolving properties of the EXL matrix, determine the change in reference configuration and convect collagen fiber architecture, which then allows us to determine the change in mechanical response of the collagen fibers using structural models.

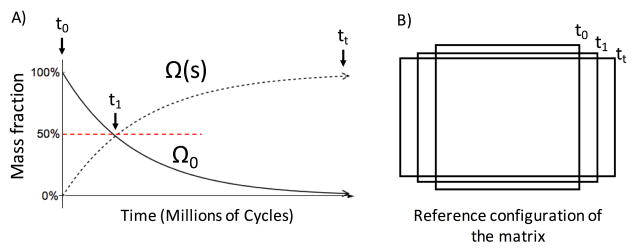
Figure 3.

Illustration of the permanent set effect under cyclic uniaxial loading. A) There is a transfer of mass fraction of the EXL matrix to the loaded configuration Ω(s) from the original state Ω₀. B) This results in changes in the unloaded geometry of the tissue.

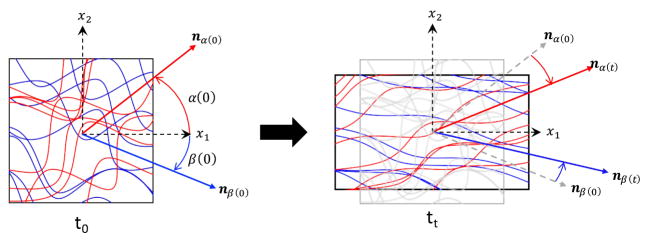
Figure 4.

An illustration of how the collagen fiber architecture is convected by changes in the dimension of the bulk tissue. The left figure shows the origin geometry of the tissue at t₀ in figure 3 while the right figure shows the geometry of the tissue at t_t. Structural convection includes the rotation and straightening of the collagen fiber ensembles.

To develop the constitutive model form, we start by modeling the exogenously crosslinked tissue under cyclic loading as parts of a mixture of materials with the same properties but different evolving reference states. The reference state of each part of the EXL matrix is updated according the strain history (Fig. 3A). The response of each part are then summed together for the bulk-level mechanical response of the EXL matrix. The new bulk level mechanical response is then used to determine the new unloaded state (Fig. 3B). The change in the EXL matrix from its uncycled state is then used to convect the collagen fiber architecture(Fig. 4). The new mechanical response of the EXL matrix is summed with the fiber ensemble interactions and collagen fiber response predicted from the new collagen fiber architecture to determine the full tissue-level mechanical response. Thus, how the collagen fiber architecture (CFA) is convected by the EXL matrix is crucial to our model. We start developing our constitutive model by 1) modeling and parameter estimation for the native uncycled mechanical response of the exogenously crosslinked tissue. Then 2) develop the model form for the time evolving mechanical response based on the permanent set mechanism and cyclic loading data. The basic assumptions of our models are:

1. There is no structural damage to the collagen fibers or the EXL matrix

2. The crosslinking process that induce permanent set follows first order kinetics

3. We are only modeling permanent set under physiological conditions and the process is thus isothermal

4. Permanent set occurs in the isotropic EXL matrix, so that its rate constant is directionally independent

5. The permanent set rate constant is strain-level independent in the physiological range

6. Permanent set occurs over a time scale much longer than a single cardiac cycle

7. The tissue is functionally elastic, and thus viscoelastic effects are ignored

8. The convection of the collagen fiber architecture follows affine kinematics

9. collagen fibers do not bare load or interact until they are straightened [38]

3. Extant experimental data

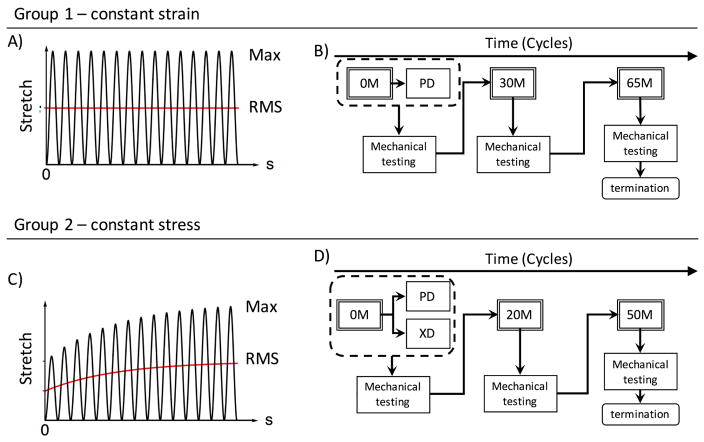
We utilized data from the following two extant studies, which differ by their loading conditions and specimen orientations. In the study by Sun et al.[13], exogenously crosslinked BP patches were cycled along the preferred collagen fiber direction (PD) at a peak strain of 16% and maintained for up to 65 million cycles (Fig. 5A&B). The reference configurations of the exogenously crosslinked BP were tracked using fiducial markers attached to the center of the specimens[39]. The mechanical cycling was stopped at 30 and 65 million cycles for mechanical testing with multiple protocols and different loading paths. It was found that there were significant extensions in the direction of loading (7.1%), PD, and contractions in the cross direction (−7.7%). In addition, the collagen fiber crimp period increased from 40.6μm to 45.24μm which is consistent with the convection of the collagen fiber architecture that would occur as collagen fiber straighten (Fig. 4). The mechanical response also changed accordingly. The compliance in the PD decreased over time while the compliance in the cross direction of the tissue increased.

Figure 5.

We utilize two extant databases in this study. The first is strain controlled, with A) constant strain level and is B) sorted for orientation along the preferred direction then put through cyclic loading and mechanical testing. The second is with C) constant strain but evolving strain level. The specimens are then D) sorted for orientation along both the preferred direction and cross-preferred direction, then put through cyclic loading and mechanical testing.

In the study by Sellaro et al.[40], the same exogenously crosslinked BP patches were cycled at 500kPa for up to 50 million cycles (Fig. 5C&D). In this case, the specimens were separated into two groups: with stress controlled loading along the 1) PD and 2) orthogonal to the PD (XD). Similarly, the reference states of the exogenously crosslinked BP specimens were tracked, with cycling stopped at 20 and 50 million cycles for mechanical testing. Analysis of the results showed interesting differences between the PD and XD cycled specimens. For both the PD and XD cycled specimens, we observed significant elongation in the direction of loading and contraction in the orthogonal direction with cycling. Additionally, the effective stiffness in the direction of loading increased over time, whereas the orthogonal direction decreased over time. In addition, we also studied how the collagen fiber architecture of the tissue changed with cyclic loading. For the PD cycled specimens, it was observed that the collagen fiber orientation distribution became more aligned, and the collagen fiber crimp period increased from 24 μm to 28μm. On the other hand, for the XD cycled specimens, it was observed that the collagen fiber orientation distribution became more spread, and the collagen fiber crimp period remained unchanged. This findings on the structural changes with direction of cyclic loading are consistent with the structural convection that we hypothesizes with permanent set and lend further support to our model (Fig. 4).

4. Constitutive model for uncycled exogenously crosslinked tissue

4.1. Constitutive model for exogenous crosslinking

We have previously developed the first constitutive model for exogenously crosslinked collagenous tissues [26] and determined the following three contributors to the mechanical response: collagen fibers, EXL matrix and fiber-fiber interactions, where the total strain energy density function is given by

$$\mathrm{\Psi }={\varphi }_{\text{col}}[{\mathrm{\Psi }}_{\text{col}}+{\mathrm{\Psi }}_{int}]+{\varphi }_m{\mathrm{\Psi }}_m$$ (1)

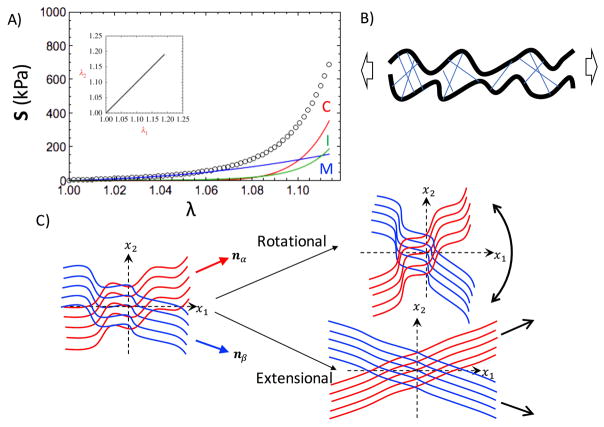
In particular, we found the fiber ensemble interaction term (ϕ_colΨ_int) to be especially important in modeling exogenously crosslinked tissues, accounting for approximately 30% of the stress in the fully loaded state (Fig. 6A). To determine the model form of the interaction component, we used the remaining stress after subtracting the collagen fiber response and EXL matrix response from the mechanical response of the tissue after exogenous crosslinking (Fig. 6A). In that study, we consider three possible forms of interactions: intra-fiber ensemble (Fig. 6B) (an ensemble being a family of fibers sharing a common orientation), ensemble-ensemble rotations, and ensemble-ensemble relative extensions (Fig. 6C&D). We found that intra-fiber ensemble and ensemble-ensemble rotations were not consistent with the experimental data, whereas ensemble-ensemble extensional interactions were able to explain all of the remaining stress.

Figure 6.

A) The mechanical response of exogenously crosslinked BP, which is composed of 3 parts: (C)ollagen in Red, (M)atrix in Blue, and the fiber ensemble (I)nteractions in Green. B) Illustration for intra-ensemble interactions due to crosslinking is shown. C) The inter-ensemble interactions could be separated into rotational effects and extensional effects.

The interaction model form, Ψ_int, was developed utilizing the pseudo invariant I₈, which is a function of the stretch and angle between two fiber ensembles oriented along the angle α and β directions in the tissue (Fig. 4), and then separated it into its rotational and extensional components[26] (Fig. 6C&D),

$$\begin{gathered} I_8={\mathbf{n}}_{\alpha }·\mathbf{C}·{\mathbf{n}}_{\beta }={\lambda }_{\alpha }{\lambda }_{\beta }cos(\alpha -\beta ), \\ {I}_8^{\text{ext}}={\lambda }_{\alpha }{\lambda }_{\beta },I_8^{\text{rot}}=cos(\alpha -\beta )=\frac{I_8}{{\lambda }_{\alpha }{\lambda }_{\beta }}, \end{gathered}$$ (2)

where n_α and n_β are vectors pointing along α and β, respectively, λ_α and λ_β are the stretches of the collagen fiber ensembles oriented along α and β, respectively, $I_8^{\text{ext}}$ is the pseudo invariant for ensemble-ensemble extensions, and $I_8^{\text{rot}}$ is the pseudo invariant for ensemble-ensemble rotations. From this, we established the model form for the interactions to be

$${\mathrm{\Psi }}_{int}=\frac{d_0}{4}\underset{\alpha }{\int }\underset{\beta }{\int }\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\beta )\left[e^{d_1{({\lambda }_{\alpha }{\lambda }_{\beta }-1)}^2}-1\right]\mathrm{d}\alpha \mathrm{d}\beta ,$$ (3)

where Γ is the fiber orientation distribution (ODF), and d₀ and d₁ are material constants. However, this model form is still essentially phenomenological. Specifically, while it is sufficient to model the mechanical response in the range of the acquired experimental data, we have no method for predicting how it will change with changes in dimensions with cyclic loading. Thus, an extension to this model component is necessary.

4.2. Extension of the structural derivation of the fiber-fiber interactions term

The key to our approach in the constitutive model for the permanent set effect is to use the change in the collagen fiber architecture to predict the new mechanical response. Thus, having a full structural model, including a full structural derivation of the fiber-fiber interactions, is crucial. As in the previous model form [26], we will only keep the extensional component $I_8^{\text{ext}}$. In addition, since collagen fibers do not bear stress until fully straightened [4], we also assume that collagen fibers do not play a role in the interactions of the fiber ensembles until they are straightened. Following the same approach common in structural models, we first define the stretch of the collagen fibers after it’s straightened, which is also the true fiber stretch (λ_t) defined in Zhang et al. [36], to be λ_t = λ_ens/λ_s, where λ_ens is the stretch of the collagen fiber ensemble and λ_s is the slack stretch required to straighten the collagen fiber crimp. We assumed that interactions do not occur until the fibers are straighten, so the extensional invariant should be a function of the true stretch of the individual fibers, λ_t, rather than the stretch of the whole fiber ensembles as defined in equation 2,

$$I_8^{\text{ext}}=\frac{{\lambda }_{\alpha }{\lambda }_{\beta }}{{{}_{\alpha }\lambda }_s{{}_{\alpha }\lambda }_s},$$ (4)

where _αλ_s and _βλ_s are the slack stretches of the two ensembles oriented along α and β in the reference configuration, respectively. This invariant is then integrated only for fibers with λ_t > 1, i.e. fibers which are straightened. To develop the form for the interactions, we start from the strain energy. At the ensemble level, we integrate the invariant over the slack stretch (λ_s) of both the fiber ensembles orienting along α and β, weighted by the probability distribution function of the proportion of collagen fibers with that specific slack stretch D(λ_s),

$${\mathrm{\Psi }}_{int}^{\text{ens}}=\frac{{\eta }_I}{2}\underset{1}{\overset{{\lambda }_{\alpha }}{\int }}\underset{1}{\overset{{\lambda }_{\beta }}{\int }}D(x_{\alpha })D(x_{\beta }){\left(\frac{{\lambda }_{\alpha }{\lambda }_{\beta }}{x_{\alpha }{x}_{\beta }}-1\right)}^2\mathrm{d}{x}_{\alpha }\mathrm{d}{x}_{\beta }.$$ (5)

We refer to D(λ_s) as the recruitment function, which is defined in Zhang et al. [36]. The ensemble-level model is then integrated with respect to the fiber ODF, Γ, for all possible pair of collagen fiber ensemble to give the tissue-level model

$${\mathrm{\Psi }}_{int}=\frac{{\eta }_I}{2}\underset{\alpha }{\int }\underset{\beta }{\int }\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\beta )\underset{1}{\overset{{\lambda }_{\alpha }}{\int }}\underset{1}{\overset{{\lambda }_{\beta }}{\int }}D(x_{\alpha })D(x_{\beta }){\left(\frac{{\lambda }_{\alpha }{\lambda }_{\beta }}{x_{\alpha }{x}_{\beta }}-1\right)}^2\mathrm{d}{x}_{\alpha }\mathrm{d}{x}_{\beta }\mathrm{d}\alpha \mathrm{d}\beta .$$ (6)

The second Piola Kirchhoff stress, using $\mathbf{S}=2\frac{\partial \mathrm{\Psi }}{\partial \mathbf{C}}$, is

$$\begin{gathered} {\mathbf{S}}_{int}={\eta }_I\underset{\alpha }{\int }\underset{\beta }{\int }\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\beta )[\left\{\underset{1}{\overset{{\lambda }_{\alpha }}{\int }}\underset{1}{\overset{{\lambda }_{\beta }}{\int }}\frac{2{\lambda }_{\beta }D(x_{\alpha })D(x_{\beta })}{x_{\alpha }{x}_{\beta }}\left(\frac{{\lambda }_{\alpha }}{x_{\alpha }}\frac{{\lambda }_{\beta }}{x_{\beta }}-1\right)\mathrm{d}{x}_{\alpha }\mathrm{d}{x}_{\beta }+\underset{1}{\overset{{\lambda }_{\beta }}{\int }}D(x_{\beta }){\left(\frac{{\lambda }_{\beta }}{x_{\beta }}-1\right)}^2\mathrm{d}{x}_{\beta }\right\}\frac{{\mathbf{n}}_{\alpha }\otimes {\mathbf{n}}_{\alpha }}{{\lambda }_{\alpha }}+ \\ \left\{\underset{1}{\overset{{\lambda }_{\alpha }}{\int }}\underset{1}{\overset{{\lambda }_{\alpha }}{\int }}\frac{2{\lambda }_{\beta }D(x_{\alpha })D(x_{\beta })}{x_{\alpha }{x}_{\beta }}\left(\frac{{\lambda }_{\alpha }}{x_{\alpha }}\frac{{\lambda }_{\beta }}{x_{\beta }}-1\right)\mathrm{d}{x}_{\alpha }\mathrm{d}{x}_{\beta }+\underset{1}{\overset{{\lambda }_{\alpha }}{\int }}D(x_{\alpha }){\left(\frac{{\lambda }_{\alpha }}{x_{\alpha }}-1\right)}^2\mathrm{d}{x}_{\alpha }\right\}\frac{{\mathbf{n}}_{\beta }\otimes {\mathbf{n}}_{\beta }}{{\lambda }_{\beta }}]\mathrm{d}\alpha \mathrm{d}\beta . \end{gathered}$$ (7)

This model form has only one constant η_I to account for all interactions. The remaining mechanisms are all based on the collagen fiber architecture, which is determined through a convection using dimensional changes.

5. Permanent set model

5.1. Kinematics

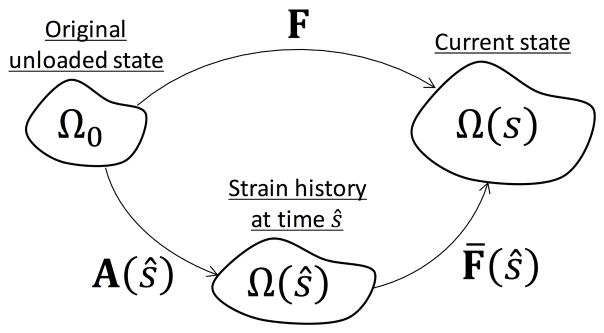
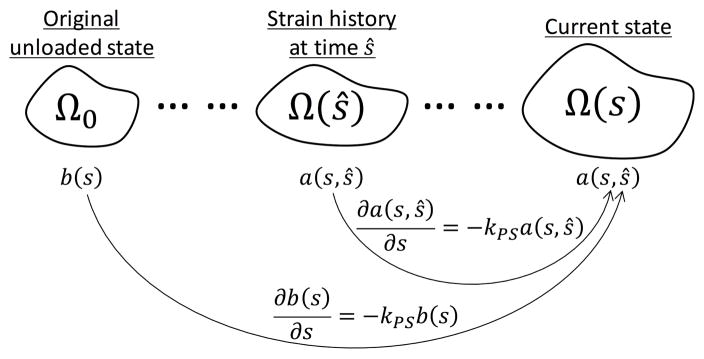
For the bulk tissue level mechanical response, consisting of the EXL matrix, the collagen fibers, and fiber ensemble interactions, we first consider the EXL matrix alone. Permanent set occurs in the EXL matrix, and is the main driver for the evolving mechanical response and structural changes in the tissue. As such the permanent set model is our starting point (section 2), which then can be used to convect collagen fiber architecture and predict the remaining collagen fibers and fiber ensemble interactions components of the mechanical response. To model the EXL matrix under permanent set, many reference states need to be considered. Due to scission-healing, the reference configuration of the EXL matrix is the configuration at its time of formation. For this we first introduce the following definition for the for the evolution of the configurations involved (Fig. 7):

Figure 7.

The relation between the reference configurations during cyclic loading.

1. The original unloaded configuration Ω₀

2. The evolving loaded configuration is Ω(s), where s is the current time.

3. We also make the distinction between ŝ, the intermediate time for which the EXL matrix is formed, and s. As the reference configuration of the EXL matrix evolves, there needs to be a distinction between the configuration for which the EXL matrix formed by the scission-healing reaction at time ŝ, referenced to Ω(ŝ), and the current loaded configuration Ω(s). In this way, ŝ is also suitable as an variable of integration.

4. The strain history, A(s), which is a deformation gradient tensor as a function of time s, that maps between the original configuration Ω₀ to the loaded configuration Ω(s) at which the EXL matrix is formed

5. We define B̃(s) = AA^⊤ to be left Cauchy Green tensor of the strain history A(s), which should not be confused with the left Cauchy Green tensor of the deformation applied to the tissue

6. We define the deformation gradient tensor from the intermediate loaded state Ω(ŝ) to the current loaded state Ω(s) to be F̄(ŝ), where the following relation is assumed (Fig. 7)

   $$\begin{gathered} \mathbf{F}=\overline{\mathbf{F}}(\widehat{s})\mathbf{A}(\widehat{s}), \\ \overline{\mathbf{F}}(\widehat{s})=\mathbf{F}·\mathbf{A}{(\widehat{s})}^{-1}. \end{gathered}$$ (8)

7. The evolving unloaded reference configuration after permanent set is Ω_PS(s) with F_PS(s) mapping from the original configuration Ω₀ to Ω_PS(s)

We also note the following important considerations:

• The original reference configuration Ω₀ is important as it is the configuration for which the mechanical response of the original material as well as the collagen fiber architecture is referenced. Similarly, we track the loaded configuration (Ω(s)) using A(s) and the unloaded configuration (Ω_PS(s)) using F_PS from Ω₀.

• We also note that under cyclic loading, the exogenously crosslinked tissue is not held at the constant loaded configuration, it is put through a range of deformation each cycle. Because permanent set happens at a time scale much longer than a single cycle, we define the loaded configuration Ω(s) as the root mean squared configuration, which is the time averaged deformation for a single loading cycle.

• We note that the tissue is never fully unloaded during cyclic loading. Thus, to simulate cyclic loading, the stresses are still referenced to the origin configuration Ω₀. The unloaded geometry is determined a posteriori from Ω_PS(s) for when cyclic loading is stopped for mechanical testing.

Thus the right Cauchy Green tensor when referenced to the strain history Ω(ŝ) is given by C̄(ŝ) = F̄(ŝ)^⊤F̄(ŝ). This also has the following relation to the applied deformation F,

$$\begin{gathered} \overline{\mathbf{C}}(\widehat{s})={(\mathbf{F}·\mathbf{A}{(\widehat{s})}^{-1})}^{\top }(\mathbf{F}·\mathbf{A}{(\widehat{s})}^{-1}) \\ =\mathbf{A}{(\widehat{s})}^{-\top }({\mathbf{F}}^{\top }\mathbf{F})\mathbf{A}{(\widehat{s})}^{-1} \\ =\mathbf{A}{(\widehat{s})}^{-\top }·\mathbf{C}·\mathbf{A}{(\widehat{s})}^{-1}. \end{gathered}$$ (9)

Our material model for the EXL matrix is an isotropic model of Ψ_m = Ψ_m(I₁), where I₁ is the first invariant of C. For this, we can define the first invariant Ī₁(ŝ) for the right Cauchy Green tensor C̄(ŝ) as

$${\overline{I}}_1(\widehat{s})=\text{Trace}(\overline{\mathbf{C}}(\widehat{s}))=\text{Trace}({\mathbf{A}}^{-\top }(\widehat{s})·\mathbf{C}·{\mathbf{A}}^{-1}(\widehat{s})).$$ (10)

With this, the stress of the EXL matrix is given by

$${\overline{\mathbf{S}}}_m=2\frac{\partial \overline{\mathrm{\Psi }}}{\partial \mathbf{C}}-p\mathbf{I}=2\frac{\partial \overline{\mathrm{\Psi }}}{\partial {\overline{I}}_1(\widehat{s})}\frac{\partial {\overline{I}}_1(\widehat{s})}{\partial \mathbf{C}}-p\mathbf{I},$$ (11)

where p is the Lagrange multiplier enforcing incompressibility. The partial derivative of Ī₁(ŝ) is

$$\frac{\partial {\overline{I}}_1}{\partial \mathbf{C}}=\frac{\partial {\overline{I}}_1}{\partial \overline{\mathbf{C}}(\widehat{s})}\frac{\partial \overline{\mathbf{C}}(\widehat{s})}{\partial \mathbf{C}}=\frac{\partial \mathbf{A}{(\widehat{s})}^{-\top }·\mathbf{C}·\mathbf{A}{(\widehat{s})}^{-1}}{\partial \mathbf{C}}=\mathbf{A}{(\widehat{s})}^{-\top }\mathbf{A}{(\widehat{s})}^{-1}=\stackrel{\sim }{\mathbf{B}}{(\mathbf{A}(\widehat{s}))}^{-1},$$ (12)

which is the inverse of the left Cauchy Green tensor of the strain history A(s).

5.1.1. Kinematics for updating the reference configuration

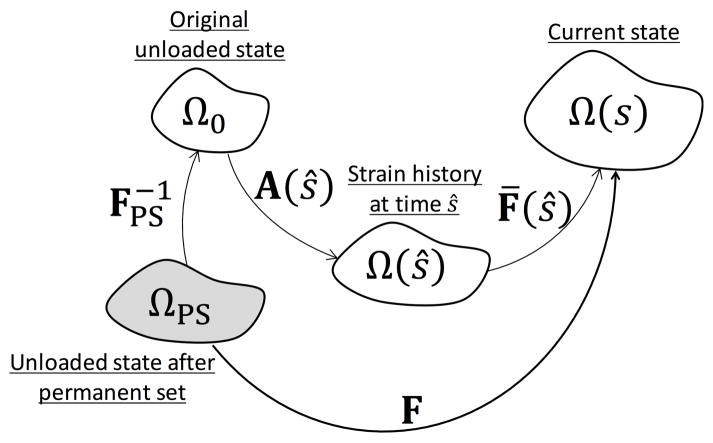
As the unloaded configuration changes due to permanent set, we need to be able to express the stresses with the new reference configuration. Since all configurations are referenced to Ω₀, the deformation from the new reference configuration Ω_PS to the current loaded state Ω(s) is given by (Fig. 8)

Figure 8.

Modification of the relation between the different reference configurations when the unloaded configuration changes.

$$\mathbf{F}=\overline{\mathbf{F}}(\widehat{s})·\mathbf{A}(\widehat{s})·{\mathbf{F}}_{\text{PS}}^{-1}.$$ (13)

Following the same derivation as equations 8–10, we have

$$\begin{gathered} \overline{\mathbf{F}}(\widehat{s})=\mathbf{F}·{\mathbf{F}}_{\text{PS}}·\mathbf{A}{(\widehat{s})}^{-1}, \\ \overline{\mathbf{C}}({\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}))=\mathbf{A}{(\widehat{s})}^{-\top }·{\mathbf{F}}_{\text{PS}}^{\top }·\mathbf{C}·{\mathbf{F}}_{\text{PS}}·\mathbf{A}{(\widehat{s})}^{-1}, \\ {\overline{I}}_1({\mathbf{F}}_{\text{PS}},\mathbf{A}(s))=\text{Trace}(\mathbf{A}{(\widehat{s})}^{-\top }·{\mathbf{F}}_{\text{PS}}^{\top }·\mathbf{C}·{\mathbf{F}}_{\text{PS}}·\mathbf{A}{(\widehat{s})}^{-1}). \end{gathered}$$ (14)

and the new inverse of the left Cauchy Green tensor of the strain history is given by

$$\begin{gathered} \stackrel{\sim }{\mathbf{B}}{({\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}))}^{-1}=\frac{\partial \overline{\mathbf{C}}({\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}))}{\partial \mathbf{C}}=\frac{\mathbf{A}{(\widehat{s})}^{-\top }·{\mathbf{F}}_{\text{PS}}^{\top }·\mathbf{C}·{\mathbf{F}}_{\text{PS}}·\mathbf{A}{(\widehat{s})}^{-1}}{\partial \mathbf{C}} \\ =\mathbf{A}{(\widehat{s})}^{-\top }·{\mathbf{F}}_{\text{PS}}^{\top }·{\mathbf{F}}_{\text{PS}}·\mathbf{A}{(\widehat{s})}^{-1}. \end{gathered}$$ (15)

5.2. Extension to the EXL matrix model for changes in reference configuration

We start by extending the EXL matrix model from our previous model [26]. The strain energy is a modified form of the Yeoh model, which exhibits the following stress-strain relation,

$$\begin{gathered} {\mathrm{\Psi }}_m=\frac{{\eta }_m}{2}\left(\frac{1}{\alpha }{(I_1-3)}^{\alpha }+\frac{r}{\beta }{(I_1-3)}^{\beta }\right), \\ \text{with}1<\alpha <\beta ,\alpha \beta <2,0\le r. \end{gathered}$$ (16)

Here η_m is the EXL matrix modulus, α, β are the exponent and r is the relative weight between the two terms which is typically between 10 to 20. To modify the model form to reference the configuration at the time of formation Ω(ŝ), we make the substitution for Ī₁(F_PS,A(ŝ)) (Eqn. 10),

$${\overline{\mathrm{\Psi }}}_m(\mathbf{C},\mathbf{A}(\widehat{s}))=\frac{{\eta }_m}{2}\left(\frac{1}{\alpha }{({\overline{I}}_1({\mathbf{F}}_{\text{PS}},\mathbf{A}(s))-3)}^{\alpha }+\frac{r}{\beta }{({\overline{I}}_1({\mathbf{F}}_{\text{PS}},\mathbf{A}(s))-3)}^{\beta }\right),$$ (17)

The derivative of the strain energy with respect to the invariant Ī₁ is

$$\frac{\partial \overline{\mathrm{\Psi }}}{\partial {\overline{I}}_1}=\frac{{\eta }_m}{2}\left({({\overline{I}}_1({\mathbf{F}}_{\text{PS}},\mathbf{A}(s))-3)}^{\alpha -1}+r{({\overline{I}}_1({\mathbf{F}}_{\text{PS}},\mathbf{A}(s))-3)}^{\beta -1}\right).$$ (18)

After solving for the Lagrange multiplier p, with S̄_m,33 = 0, we have

$${\overline{\mathbf{S}}}_m({\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}),\mathbf{C})={\mu }_m\left({({\overline{I}}_1({\mathbf{F}}_{\text{PS}},\mathbf{A}(s))-3)}^{\alpha -1}+r{({\overline{I}}_1({\mathbf{F}}_{\text{PS}},\mathbf{A}(s))-3)}^{\beta -1}\right)\times \left(\stackrel{\sim }{\mathbf{B}}{({\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}))}^{-1}-{\stackrel{\sim }{B}}_{33}^{-1}({\mathbf{F}}_{\mathbf{PS}},\mathbf{A}(\widehat{s}))C_{33}{\mathbf{C}}^{-1}\right).$$ (19)

5.2.1. Extension of the EXL matrix for the permanent set effect

Next, we developed the model form for the EXL matrix after permanent set. This approach is based on the work by Rajagopal and Wineman [29], where we assume that the response of the full EXL matrix to be

$${\varphi }_m{\mathbf{S}}_m=b(s){\overline{\mathbf{S}}}_m^{\text{existing}}+\underset{0}{\overset{s}{\int }}a(s,\widehat{s}){\overline{\mathbf{S}}}_m^{\text{new}}\mathrm{d}\widehat{s},$$ (20)

where b(s) is the remaining amount of the existing material, a(s, ŝ) is the remaining amount of the new material formed during the strain history (A(s)) at time ŝ, ${\overline{\mathbf{S}}}_m^{\text{existing}}$ is the stress of the existing material and ${\overline{\mathbf{S}}}_m^{\text{new}}$ is the stress of the new material. Assuming first order kinetics with the permanent set rate constant k, we have for the material remaining (Fig. 9)

Figure 9.

The mass fractions of the EXL matrix change over time, assuming first order kinetics.

$$\frac{\partial b(s)}{\partial s}=-k·b(s),\frac{\partial a(s,\widehat{s})}{\partial s}=-k·a(s,\widehat{s}).$$ (21)

Given that the total amount of EXL matrix (ϕ_m) has not changed, $b(s)+{\int }_0^{s}a(s,\widehat{s})\mathrm{d}\widehat{s}={\varphi }_m$, and we have

$$b(s)={\varphi }_m\text{Exp}[-k·s],a(s,\widehat{s})={\varphi }_{m}k\text{Exp}[-k(s-\widehat{s})].$$ (22)

Substitution into equation 20, we have the mechanical response of the EXL matrix after permanent set,

$${\varphi }_m{\mathbf{S}}_m={\varphi }_m\left[\text{Exp}[-k·s]{\overline{\mathbf{S}}}_m({\mathbf{F}}_{\text{PS}},\mathbf{A}(0),\mathbf{C})+\underset{0}{\overset{s}{\int }}k·\text{Exp}[-k(s-\widehat{s})]{\overline{\mathbf{S}}}_m({\mathbf{F}}_{\text{PS}},\mathbf{A}(\overline{s}),\mathbf{C})\mathrm{d}\widehat{s}\right].$$ (23)

The final form for the EXL matrix component of the permanent set model is thus,

$$\begin{gathered} {\varphi }_m{\mathbf{S}}_m({\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}),\mathbf{C})={\varphi }_m{\mu }_m[\text{Exp}[-k·s]\left({({\overline{I}}_1({\mathbf{F}}_{\text{PS}},\mathbf{A}(0))-3)}^{\alpha -1}+r{({\overline{I}}_1({\mathbf{F}}_{\text{PS}},\mathbf{A}(0))-3)}^{\beta -1}\right) \\ \times \left(\stackrel{\sim }{\mathbf{B}}{({\mathbf{F}}_{\text{PS}},\mathbf{A}(0))}^{-1}-{\stackrel{\sim }{B}}_{33}{({\mathbf{F}}_{\text{PS}},\mathbf{A}(0))}^{-1}{C}_{33}{\mathbf{C}}^{-1}\right) \\ +\underset{0}{\overset{s}{\int }}k·\text{Exp}[k(s-\widehat{s})]\left({({\overline{I}}_1({\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}))-3)}^{\alpha -1}+r{({\overline{I}}_1({\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}))-3)}^{\beta -1}\right) \\ \times \left(\stackrel{\sim }{\mathbf{B}}{({\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}))}^{-1}-{\stackrel{\sim }{B}}_{33}{({\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}))}^{-1}{C}_{33}{\mathbf{C}}^{-1}\right)\mathrm{d}\widehat{s}]. \end{gathered}$$ (24)

5.3. Convection of the collagen fiber architecture

Now that the model form for the EXL matrix under permanent set is established, we need to consider how the collagen fiber architecture is convected by the change in reference configuration. The convection of the collagen fiber architecture is done through two parts: the ODF and the recruitment function. This is done by assuming that the collagen fiber architecture is convected under the affine assumption[38]. The form of the ODF and the recruitment distribution was previously described in Zhang et al. [36], and the operation used to convect the collagen fiber architecture is given in Sacks et al. [26]. Briefly, the convected ODF Γ₁ is determined from the ODF in the 0-cycle state Γ₀ and the deformation ${}_0{}^1\mathbf{F}$ by the conservation of the number of fiber Γ(θ₀)dθ₀ = Γ(θ₁)dθ₁ (Fig. 10A). This is given by

Figure 10.

The effects of convecting the collagen fiber architecture show A) gradual alignment of collagen fibers, B) changes in the probability distribution of collagen fiber lack stretches and C) its effect on the mechanical response.

$$\begin{array}{c}{\mathrm{\Gamma }}_1({}_0{}^1\mathbf{F},{\theta }_1)={\mathrm{\Gamma }}_0({\theta }_0({}_0{}^1\mathbf{F},{\theta }_1))\frac{{}_0{}^1\lambda {({\theta }_0)}^2}{{{}_0{}^{1}J}_{2\mathrm{D}}},\\ {}_0{}^1\lambda ({\theta }_0)=\sqrt{{\mathbf{n}}_{{\theta }_0}·{{}_0{}^1\mathbf{F}}^{\top }{}_0{}^1\mathbf{F}·{\mathbf{n}}_{{\theta }_0}},{{}_0{}^{1}J}_{2\mathrm{D}}=det({}_0{}^1\mathbf{F}),\end{array}$$ (25)

where n_θ is a unit vector for the orientation θ. The distribution of slack stretch needed to straighten collagen fiber crimp after convection, in other words the recruitment distribution D₁(λ_s) (Fig. 10B), is given by

$$\begin{array}{c}{D}_1({}_0{}^1\mathbf{F},{\lambda }_s)=\{\begin{array}{ll}\frac{\mathrm{B}[{\gamma }_0,{\gamma }_1](y)}{{{}_1\lambda }_{\text{ub}}-{{}_1\lambda }_{\text{lb}}}\hfill & {{}_1\lambda }_{\text{ub}}<y<{{}_1\lambda }_{\text{lb}}\hfill \\ 0\hfill & \text{else}\hfill \end{array},\\ {{}_1\lambda }_s=\frac{{\lambda }_s}{{}_0{}^1\lambda (\theta )},y=\frac{{{}_1\lambda }_s-{{}_1\lambda }_{\text{lb}}}{{{}_1\lambda }_{\text{ub}}-{{}_1\lambda }_{\text{lb}}}.\end{array}$$ (26)

where ${}_0{}^1\lambda ({\theta }_0)$ is defined in equation 25, (₁λ_lb, ₁λ_ub) are the new bounds of the distribution after being convected, and (γ₀, γ₁) are the shape parameters of the beta distribution function B. The model form for collagen fibers in exogenously crosslinked BP after being convected by a change in geometry is previously presented in Sacks et al. [26] and can also be used for the convection of the collagen fiber architecture due to the permanent set effect. The model form for the fiber ensemble interactions is given by equation 7, where equations 25 and 26 are substituted in for the ODF and recruitment distribution function for the mechanical response after permanent set.

5.4. Further considerations of the permanent set mechanism

In addition to the above considerations, we explored the the following as a means to validate the mechanisms we proposed for permanent set. This was done by performing an analysis on predicting the mechanical response after cyclic loading using only the convection of the collagen fiber architecture by the measured F_PS. The analysis takes the following steps: 1) Material model parameter estimation for the 0-cycle data for the strain controlled data. This is done using the approach from Sacks et al.[26], with the constitutive model for collagen fibers and the EXL matrix from the same study, and the interaction model from equation 7. 2) Use equations 25 and 26 (Sec.5.3) to convect the collagen fiber architecture (Fig. 4 and Fig. 10). The deformation used to convect the collagen fiber architecture is determined from the fiducial markers. 3) We compare the new convected exogenously crosslinked mechanical response to the experimental data.

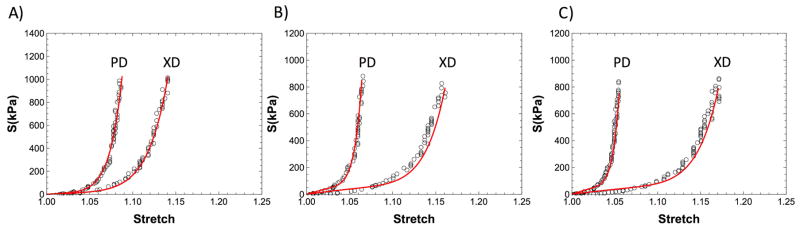
We used this approach to examine both the strain (n = 3) and stress controlled specimens (n = 5), and tested the hypothesis that there is a significant different between the mechanical response predicted from structural convection and the experimentally measure data, in other words, our model is not sufficient to explain the change in mechanical response. We take the maximum stress of each specimen under equibiaxial strain, and compared the difference between the model and the experimental data using student t-test. For the strain control specimens, we found that there is no statistical significant difference between the convected mechanical response and the experimental data, where the average p-value of the PD and XD for both after 30 million cycle and after 65 million cycle is p = 0.37 (minimum p > 0.07). Likewise, we also found no statistical significant differences between the convected response and the experimental data for the stress controlled specimens, where the average p-value is 0.57 (Fig. 11). These results suggest that 1) the underlying collagen fiber architecture, including collagen fiber crimp and orientation, is convected affinely according to the permanent set in the EXL matrix. This indicates that our approach to model permanent set is realistic, and the underlying mechanism for permanent set is likely to be correct. 2) Structural damage to the collagen fiber architecture was not detectable at this stage (up to 65 million cycles). These important results indicate that permanent set alone is sufficient to capture the response to cyclic loading up to 50–65 million cycles.

Figure 11.

The equibiaxial mechanical response of an exogenously crosslinked BP specimen after 50 million cycles and the mechanical response determined from structural convection (Red) using the measured F_PS

5.5. Full model form

Combining all three components, we have the final model form as a function of the permanent set rate constant k, the permanent set deformation F_PS, the strain history A(s), and the material parameters of the constitutive model in the uncycled state. The input of the model is the applied deformation C referenced to the current unloaded state Ω_PS, given by the deformation F_PS from Ω₀. The full form is

$$\mathbf{S}=\mathbf{S}(k,{\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}),\mathbf{C})={\varphi }_{\text{col}}[{\mathbf{S}}_{\text{col}}+{\mathbf{S}}_{int}]+{\varphi }_m{\mathbf{S}}_{\mathrm{m}},$$ (27)

where the collagen contribution is

$${\varphi }_{\text{col}}{\mathbf{S}}_{\text{col}}(k,{\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}),\mathbf{C})={\varphi }_{\text{col}}{\eta }_C\underset{\theta }{\int }{\mathrm{\Gamma }}_1({\mathbf{F}}_{\text{PS}},\theta )\left\{\underset{1}{\overset{{\lambda }_{\theta }}{\int }}\frac{D_1({\mathbf{F}}_{\text{PS}},x)}{x}\left(\frac{1}{x}-\frac{1}{{\lambda }_{\theta }}\right)\mathrm{d}x\right\}{\mathbf{n}}_{\theta }\otimes {\mathbf{n}}_{\theta }\mathrm{d}\theta ,$$ (28)

where ${\lambda }_{\theta }=\sqrt{{\mathbf{n}}_{\theta }·\mathbf{C}{\mathbf{n}}_{\theta }}$ is the stretch of the fiber ensemble oriented along θ, the fiber ensemble interactions is

$$\begin{gathered} {\varphi }_{int}{\mathbf{S}}_{int}(k,{\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}),\mathbf{C})={\varphi }_{\text{col}}{\eta }_{int}\underset{\alpha }{\int }\underset{\beta }{\int }{\mathrm{\Gamma }}_1({\mathbf{F}}_{\text{PS}},\alpha ){\mathrm{\Gamma }}_1({\mathbf{F}}_{\text{PS}},\beta ) \\ \times \left[\right\{\underset{1}{\overset{{\lambda }_{\alpha }}{\int }}\underset{1}{\overset{{\lambda }_{\beta }}{\int }}\frac{2{\lambda }_{\beta }{D}_1({\mathbf{F}}_{\text{PS}},x_{\alpha })D_1({\mathbf{F}}_{\text{PS}},x_{\beta })}{x_{\alpha }{x}_{\beta }}\left(\frac{{\lambda }_{\alpha }}{x_{\alpha }}\frac{{\lambda }_{\beta }}{x_{\beta }}-1\right)\mathrm{d}{x}_{\alpha }\mathrm{d}{x}_{\beta } \\ +\underset{1}{\overset{{\lambda }_{\beta }}{\int }}{D}_1({\mathbf{F}}_{\text{PS}},x_{\beta }){\left(\frac{{\lambda }_{\beta }}{x_{\beta }}-1\right)}^2\mathrm{d}{x}_{\beta }\}\frac{{\mathbf{n}}_{\alpha }\otimes {\mathbf{n}}_{\alpha }}{{\lambda }_{\alpha }} \\ +\{\underset{1}{\overset{{\lambda }_{\alpha }}{\int }}\underset{1}{\overset{{\lambda }_{\alpha }}{\int }}\frac{2{\lambda }_{\beta }{D}_1({\mathbf{F}}_{\text{PS}},x_{\alpha })D_1({\mathbf{F}}_{\text{PS}},x_{\beta })}{x_{\alpha }{x}_{\beta }}\left(\frac{{\lambda }_{\alpha }}{x_{\alpha }}\frac{{\lambda }_{\beta }}{x_{\beta }}-1\right)\mathrm{d}{x}_{\alpha }\mathrm{d}{x}_{\beta } \\ +\underset{1}{\overset{{\lambda }_{\alpha }}{\int }}{D}_1({\mathbf{F}}_{\text{PS}},x_{\alpha }){\left(\frac{{\lambda }_{\alpha }}{x_{\alpha }}-1\right)}^2\mathrm{d}{x}_{\alpha }\left\}\frac{{\mathbf{n}}_{\beta }\otimes {\mathbf{n}}_{\beta }}{{\lambda }_{\beta }}\right]\mathrm{d}\alpha \mathrm{d}\beta , \end{gathered}$$ (29)

and the EXL matrix is

$$\begin{gathered} {\varphi }_m{\mathbf{S}}_{\mathrm{m}}(k,{\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}),\mathbf{C})={\varphi }_m{\eta }_m[\text{Exp}[-k·s]\left({({\overline{I}}_1({\mathbf{F}}_{\text{PS}},\mathbf{A}(0))-3)}^{\alpha -1}+r{({\overline{I}}_1({\mathbf{F}}_{\text{PS}},\mathbf{A}(0))-3)}^{\beta -1}\right) \\ \times \left(\stackrel{\sim }{\mathbf{B}}{({\mathbf{F}}_{\text{PS}},\mathbf{A}(0))}^{-1}-{\stackrel{\sim }{B}}_{33}^{-1}({\mathbf{F}}_{\text{PS}},\mathbf{A}(0))C_{33}{\mathbf{C}}^{-1}\right) \\ +\underset{0}{\overset{s}{\int }}k·\text{Exp}[-k(s-\widehat{s})]\left({({\overline{I}}_1({\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}))-3)}^{\alpha -1}+r{({\overline{I}}_1({\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}))-3)}^{\beta -1}\right) \\ \times \left(\stackrel{\sim }{\mathbf{B}}{({\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}))}^{-1}-{\stackrel{\sim }{B}}_{33}^{-1}({\mathbf{F}}_{\text{PS}},\mathbf{A}(\widehat{s}))C_{33}{\mathbf{C}}^{-1}\right)\mathrm{d}\widehat{s}]. \end{gathered}$$ (30)

5.6. Determining permanent set deformation and loaded state

To solve for the permanent set deformation (F_PS), and for the deformation (A(s)) to the new loaded state after permanent set (Ω(s)) when under an applied stress of Ŝ, we need to use optimization as the permanent set constitutive model has no analytical inverse form. Specifically,

$$\begin{gathered} {\mathbf{F}}_{\text{PS}}=\underset{\mathbf{F}}{argmin}\Vert \mathbf{S}(k,\mathbf{I},\mathbf{A}(\widehat{s}),\mathbf{C}={\mathbf{F}}^{\top }\mathbf{F})-0\Vert , \\ \mathbf{A}(s)=\underset{\mathbf{F}}{argmin}\Vert \mathbf{S}(k,\mathbf{I},\mathbf{A}(\widehat{s}),\mathbf{C}={\mathbf{F}}^{\top }\mathbf{F})-\widehat{\mathbf{S}}\Vert . \end{gathered}$$ (31)

5.7. Modeling approach and parameter estimation

5.7.1. Strain controlled cycling

Our goal using the strain controlled data is to validate the constitutive model form and perform parameter estimation. Since the loaded state never changes, the permanent set model can be simplified into a two-state model, with the loaded state (Ω(s)) being the root mean square strain. Specifically, the EXL matrix can be simplified to

$$\begin{gathered} {\varphi }_m{\mathbf{S}}_m={\varphi }_m\left[\text{Exp}[-k·s]{\overline{\mathbf{S}}}_m({\mathbf{F}}_{\text{PS}},\mathbf{I},\mathbf{C})+\underset{0}{\overset{s}{\int }}k·\text{Exp}[-k(s-\widehat{s})]{\overline{\mathbf{S}}}_m({\mathbf{F}}_{\text{PS}},\mathbf{A},\mathbf{C})\mathrm{d}\widehat{s}\right] \\ ={\varphi }_m[\text{Exp}[-k·s]{\overline{\mathbf{S}}}_m({\mathbf{F}}_{\text{PS}},\mathbf{I},\mathbf{C})+(1-\text{Exp}[-k·s]){\overline{\mathbf{S}}}_m({\mathbf{F}}_{\text{PS}},\mathbf{A},\mathbf{C})]. \end{gathered}$$ (32)

Of the 3 time points (0, 30, and 65 million cycles), we fit the first two time points (0 and 30 million cycles) and use the results to predict the response to cycling at 65 million cycles as a way to validate our model (Fig. 12A). We note that the mounted configuration of the specimen for mechanical testing and cyclic loading are not the same, thus there is a small rigid body rotation of the specimen between the two testing configurations. We will compensate for this during the parameter estimation, which is done as followed

Figure 12.

Our parameter estimation approach for the A) strain controlled cyclic loading data, B) stress controlled data cycled in the cross-preferred direction and C) in the preferred direction

1. Determine the 0-cycled mechanical response using the methods of Sacks et al.[26]

2. Fit the permanent set deformation F_PS and the mechanical response at the same time for the 30 million cycles time point

   1. choose a k

   2. choose a mounting direction θ_mount

   3. compute ${\mathit{err}}_{\text{PS}}={\mathbf{F}}_{\text{PS}}-{\mathbf{F}}_{\text{PS}}^{\text{data}}$ error at 30 million cycles

   4. compute ${\mathit{err}}_{\mathbf{S}}={\mathbf{S}}^{max}-{\mathbf{S}}_{\text{data}}^{max}$

   5. compute the weighted error err_PS + W_Serr_S, where the weight W_S =max strain in the direction of loading/ ${\mathbf{S}}_{\text{data}}^{max}$

   6. update k and θ_mount using the Quasi-Newton method [41]

3. Predict F_PS and the mechanical response at 65 million cycles

5.7.2. Stress controlled cycling

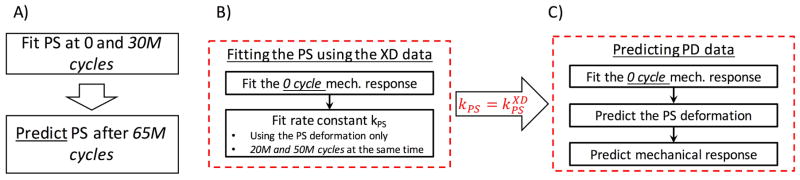
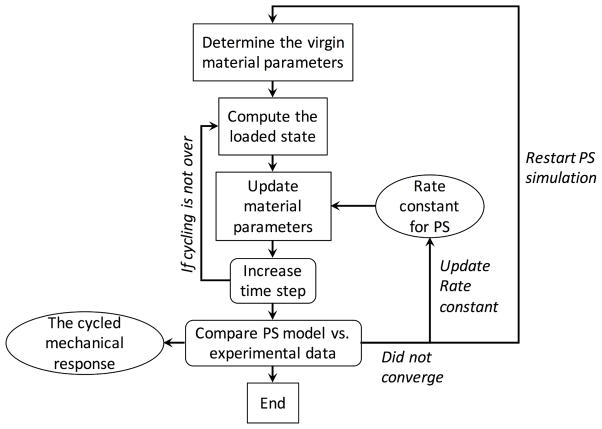
The parameter estimation for the stress controlled specimens is more complicated than the strain controlled specimens as we do not know the strain history a priori. This becomes a dynamic simulation, and we need to use optimization to determine the strain history (Eqn. 31) at each time point. Thus, this data set is well suited to validate the full model using time dependent simulations. Since we have data for both PD-loading and XD-loading, we can fit the XD-loading data and used the resulting rate constant k to predict the PD-loading data. First, we discretized the problem as followed

$${\varphi }_m{\mathbf{S}}_m={\varphi }_m\left[\text{Exp}[-k·n·\mathrm{\Delta }s]{\overline{\mathbf{S}}}_m({\mathbf{F}}_{\text{PS}},\mathbf{I},\mathbf{C})+\sum _{i=1}^n(k\mathrm{\Delta }s)\text{Exp}[-k(n\mathrm{\Delta }s-i\mathrm{\Delta }s)]{\overline{\mathbf{S}}}_m({\mathbf{F}}_{\text{PS}},\mathbf{A}(i\mathrm{\Delta }s),\mathbf{C})\right].$$ (33)

After each time step Δs, we compute the new loaded state A(iΔs) using optimization(Eqn. 31, Fig. 13). Through preliminary trials, the most optimal resolution in time is Δs = 1 million cycles when considering both time to run the simulations and accuracy of the results. We note that since an additional optimization is added to the parameter estimation process, we can no longer fit both the permanent set deformation F_PS and the mechanical data at the same time. Our attempts at fitting both at the same time were not able to converge. Thus, we choose to predict the mechanical data as a way to validate our results. The parameter estimation process for the XD-loading data is

Figure 13.

Implementation of the full model with updates in time.

1. Determine the 0-cycled mechanical response

2. Fit the permanent set deformation F_PS

   1. choose a k

   2. choose a mounting direction ${\theta }_{\text{mount}}^{20}$ for cycling up to 20 million cycles

   3. compute ${\mathit{err}}_{\text{PS}}={\mathbf{F}}_{\text{PS}}-{\mathbf{F}}_{\text{PS}}^{\text{data}}$ error at 20 million cycles

   4. choose a mounting direction ${\theta }_{\text{mount}}^{50}$ for cycling from 20 to 50 million cycles

   5. compute ${\mathit{err}}_{\text{PS}}={\mathbf{F}}_{\text{PS}}-{\mathbf{F}}_{\text{PS}}^{\text{data}}$ error at 50 million cycles

   6. update k, ${\theta }_{\text{mount}}^{20}$, and ${\theta }_{\text{mount}}^{50}$ using Quasi-Newton

3. Predict the mechanical response

Next we, used k from the XD-loading data to predict the PD-loading data.

1. Determine the 0-cycled mechanical response

2. Compute Fit the permanent set deformation F_PS

   1. set k from XD-loading data

   2. choose a mounting direction ${\theta }_{\text{mount}}^{20}$ for cycling up to 20 million cycles

   3. compute ${\mathit{err}}_{\text{PS}}={\mathbf{F}}_{\text{PS}}-{\mathbf{F}}_{\text{PS}}^{\text{data}}$ error at 20 million cycles

   4. choose a mounting direction ${\theta }_{\text{mount}}^{50}$ for cycling from 20 to 50 million cycles

   5. compute ${\mathit{err}}_{\text{PS}}={\mathbf{F}}_{\text{PS}}-{\mathbf{F}}_{\text{PS}}^{\text{data}}$ error at 50 million cycles

   6. update ${\theta }_{\text{mount}}^{20}$ and ${\theta }_{\text{mount}}^{50}$ using Quasi-Newton

3. Predict the mechanical response

5.8. Parametric studies

Next, we performed an parametric study using the stress-controlled PD data. The same material parameters and rate constant, k, from parameter estimation results above was used. We simulated one specimen by extending the cycle duration to 100 million cycles to examine how the changes in geometry due to permanent set respond to an extended cycling period.

6. Permanent set model results

6.1. Model fit and predictive capabilities

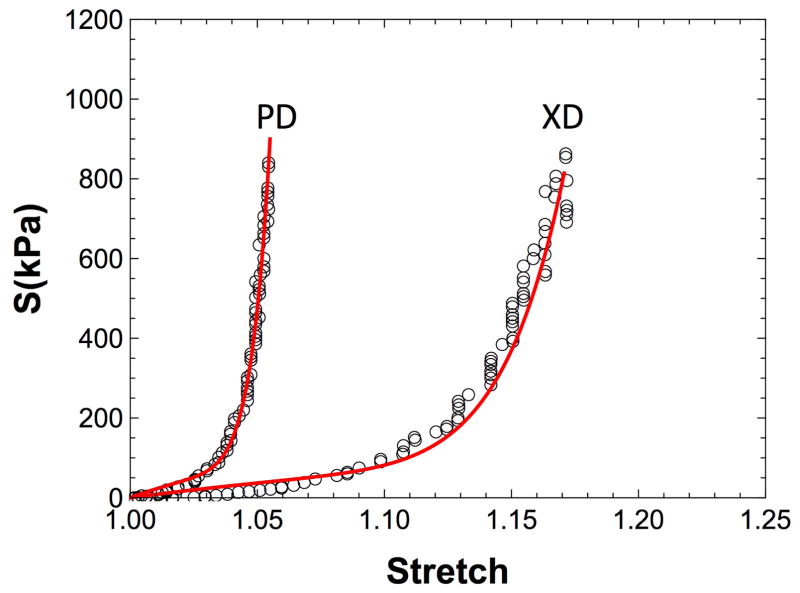
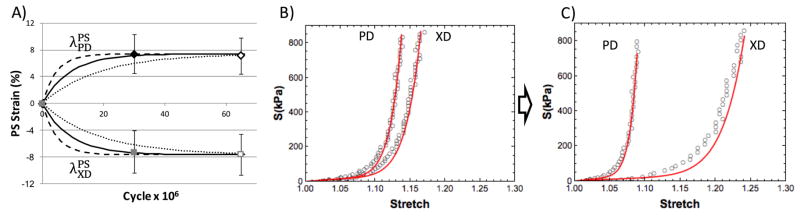
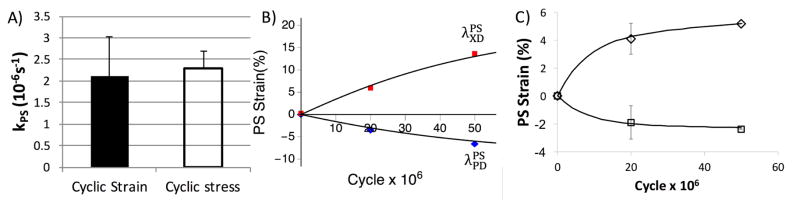
For the strain control specimens, we found that we were able to fit the permanent set deformations very well (R² = 0.96) (Fig. 14A). We were able to predict the mechanical response of the strain controlled specimens at 65 million cycles (R² = 0.83) (Fig. 14B&C). For the stress controlled specimens, we found we were able to fit the permanent set deformations for the XD specimens (R² = 0.93)(Fig. 15B), as well as predict the PD specimens very well (R² = 0.97) (Fig. 15C). The resulting rate constant from both data sets shown no statistical difference (p > 0.98)(Fig. 15A). The mechanical response for the stress controlled XD specimens did not match as well in terms of the R² value(R² = 0.72). However, given none of the mechanical data was involved in the parameter estimate this was nevertheless a very good prediction. For example, when comparing the model to the experimental data by extrapolating the loading path of the equibiaxial protocol and finding the peak strain at 1MPa, the R² value increases to 0.93. One the other hand, the predicted mechanical response for the PD controlled data were very good (R² = 0.95) (Fig. 16), suggesting that our model was able to capture the underlying mechanisms. These results agree with our hypothesis that the initial changes in the mechanical response (in the first 50 million cycles) can be predicted by the change in collagen fiber architecture alone, and that structural damage is low at this stage.

Figure 14.

Results of the strain controlled cycling data, shown how the A) model fits the permanent set deformation at 30 million cycles and predicts the 65 million cycles time point (hollow points). The dotted line shows the model prediction with 0.5k and the dashed line shows the model prediction with 2k and C) Shows how the model predicts the mechanical response at 65 million cycles using material parameters from the B) 0 cycle time point.

Figure 15.

) Comparison of the permanent set rate constant between the strain controlled and stress controlled specimens. B) The model fit for the permanent set deformation at both 20 and 50 million cycles for the stress controlled XD cycled specimens. C) The predicted permanent set deformation for the PD cycled specimens using the rate constant from fitting the XD cycled specimens.

Figure 16.

A) Best fit of the mechanical response at 0 cycle for the material parameters (r² = 0.98). The predicted mechanical response for the representative PD cycled specimen at B) 20 (r² = 0.87) and C) 50 million cycles. (r² = 0.82)

6.2. Parametric study results

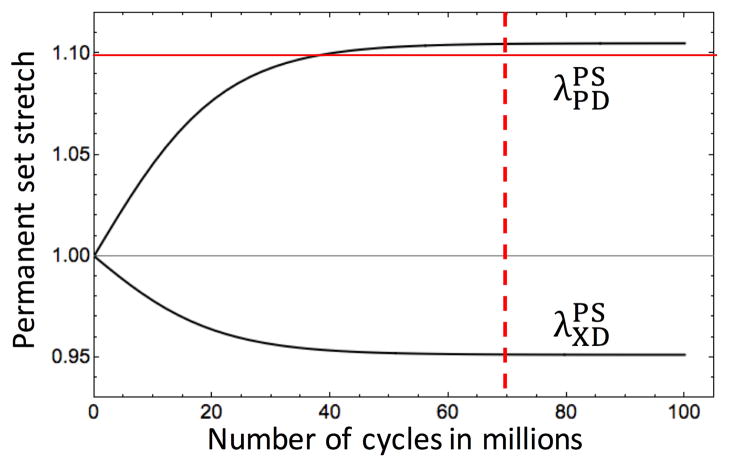
By extending the cycling duration in the parametric study, we found that the permanent set deformation reaches an assymptote after approximately 70 million cycles when loading along the PD. This threshold slightly exceeds the lower bound for collagen recruitment. We estimate that around 2.6% of collagen fiber are recruited when the permanent set deformation reaches this threshold (Fig. 17). This suggests that collagen fibers are limiting the maximum change in geometry that can occur, and that the lower bound of the collagen fiber recruitment can serve as an estimated bound for the changes in geometry due to the permanent set effect in BHVs. Once this bound is exceed, some collagen fibers can exist perennially in an extended state. This could be a potential mechanism in exacerbating the rate of damage to the collagen fiber architecture. This can have significant implications in optimizing BHV design. By optimizing the BHV geometry for the post permanent set state, we can minimize the stresses in for the BHV for the majority of the BHV life span, minimizing structural damage and potentially increasing BHV durability.

Figure 17.

The results of the parametric study. The red solid line shows the lower bound for the collagen fiber slack stretches and the red dashed line show the approximate cycle when the permanent set stretches reach an assymptote.

7. Discussion

7.1. Permanent set is sufficient to describe early stages of BHV cycling

The most important result from this study is that a permanent set mechanism in the EXL matrix alone is sufficient to explain the responses due to cyclic loading in the range of 0 to 65 million cycles. This further suggests that there is no detectable damage to the collagen fiber architecture, and that the overall collagen fiber architecture stays intact and convected under affine kinematics. This is not unexpected, as we previously found dense collagenous tissues to behave affinely when deforming in the physiological range [38]. Although the permanent set effect is very noticeable in the early stages of the cyclic loading, it still takes millions of cycles; in other words, years. Due to the time scale difference between the opening and closing of heart valves versus permanent set, BHVs always deforms quasi-statically, which means it always follows affine kinematics. It follows that any structural changes in the collagen fiber architecture is affine as well. This is all extremely important, as this allows us to completely separate permanent set from other cyclic loading effects and independently determine the permanent set rate constant just from the cyclic loading data in the early stage.

7.2. Lack of detectable structural damage

We have observed that there are molecular conformation changes in the collagen fiber during this early stage [13, 40]. This suggests that while effects of collagen fiber damage are not detectable at the bulk level, it remains an ongoing but much slower process in comparison to permanent set. Significant tearing and delamination have been observed after 500 million cycles [16], but this corresponds to the late stage (Fig. 2), for which we do not have extant mechanical data. There are no other existing experimental data quantifying the intrinsic structural damage in BHVs during cyclic loading. This is not surprising as actual structural damage is difficult to distinguish from other processes such as permanent set. The relation between molecular changes and mechanical response is not well understood. The most promising way of quantifying structural damage is through constitutive modeling and simulations. Structural models can separate structural damage and permanent set, but we do not have sufficient data at high cycle numbers where structural damage is detectable. This remains an important extension for the model in the future.

7.3. Permanent set is driven by the scission-healing of the EXL matrix

One important assumption in our model is that permanent set only occurs in the EXL matrix due to scission-healing. Based on our theory for permanent set, the process is driven entirely by the first order kinetics of the crosslinking reactions of GLUT leading to scission-healing, as well as the kinematics involved in the reference state evolution. Our results indicate that these mechanisms and permanent set can indeed explain the response to cyclic loading. This highlights the importance of understanding the effects of GLUT crosslinks and their role in the cyclic loading response of BHVs. The use of GLUT was originally intended for suppressing immunogenicity by crosslinking antigen within BP xenographs, but also has the fortunate consequence of stiffening the mechanical response of the BHV. Unfortunately, the scission-healing behavior of GLUT also plays a major role in the cyclic loading of BHVs. By severely changing the geometry of the BHV in the first 1–2 years, it strongly influences the cyclic loading response of BHVs at latter stages. It may be possible to design BHVs to accommodate permanent set deformations caused by GLUT’s scission-healing. Alternative exogenous crosslinking chemistry [42, 43] may be an important area for technological advancement of BHVs. Protecting the optimal mechanical response of the BHVs by reducing the impact of permanent set can significantly limit the peak stress on BHVs and protect the underlying tissue microstructure.

7.4. Collagen fiber recruitment can limit the maximum change in geometry due to permanent set

One of the most important finding from our permanent set model is that collagen fibers may play a significant role in limiting the changes in BHV geometry due to the permanent set effect. Our parametric study results shows that the permanent set deformation eventually reaches a threshold asymptotically (Fig. 17). This is due to the different parts of the EXL matrix as well as the collagen fibers separating into different reference configurations due to the permanent set effect. Although the bulk tissue as a whole is at a stress free equilibrium, there exists some internal stress between the different parts of the EXL matrix and the collagen fibers as a result of the different reference states. If the changes in geometry is sufficiently large, some collagen fibers will be recruited and exert compressive stress on the EXL matrix. However, since the stiffness of collagen fibers is over three magnitudes higher than the EXL matrix, the deformation of collagen fibers due to the internal stress is insignificant. As such, the recruitment of collagen fibers can resist against further changes in the geometry of the tissue due to permanent set. In addition, we generally found significant collagen fiber structural reserve in collagenous tissue [36]. From the parametric study, no more than 2–4% of collagen fibers are straightened under physiological loading levels (up to 1 MPa) due to permanent set. Coupled with the exponentially increased cumulative stiffness of the collagen fibers with strain, significant structural reserved implies that loading stresses several orders of magnitudes higher than the physiological loading level is necessary to further deform the collagen fibers. Also, taking into account the rapid recruitment of native collagen fibers (collagen fibers do not extend by more than 5–8% strain before breaking [44]), the collagen fiber architecture serves as a barrier in limiting the changes in geometry due to permanent set. This potentially gives us a way of predicting the final stress free BHV geometry after permanent set has largely ceased. This can have significant impact on the design BHVs as we can optimize the BHV geometry based on these results to minimize the leaflet stresses. Since the permanent effect is most significant during the first 40 to 50 million cycles (Fig. 17), which approximates to the first 8–9 month after implant, BHVs will operate in the post permanent set geometry during the majority of its life span (Fig. 2, when structural damage the accumulation of structural damage is most significant. Thus predicting the post permanent set geometry can have significant implications on the durability of BHV designs.

7.5. Effects on the durability of BHVs

Our findings suggests that this that the permanent set mechanism has great potential in predicting the non-biological driven changes in the BHVs in the first 2–5 years. As such, the permanent set mechanism can greatly aid the use of computational simulations in exploring BHV designs and the impact of permanent set at the valve-level. Specifically, computational models can be used to adjust the initial geometry to tailor for optimal stress distribution in the valve leaflets after permanent set. Thus, the permanent set mechanism can help us explain why stress concentrations develop, which will accelerate structural damage, and help to create designs which can mitigate this effect. High stress regions have been linked to regions with high structural damage which have significant impact on the long-term behavior of BHVs. By quantifying factors such as how the peak stress and stress distribution change due to permanent, we can predict the increased likelihood of structural damage in the leaflet due to permanent set and how it impact BHV durability.

7.6. Limitations

Our available cyclic loading data for exogenously crosslinked BP is limited in terms of cycled duration, multitude of strain levels, the rate of cyclic loading and number of specimens. However, it is important to note that our goal was to develop the constitutive model form for exogenously crosslinked tissue under cyclic loading, not to obtain a population of material parameters for statistical testing and simulations. The extant experimental data we used for parameter estimation was sufficient for this purpose, which have specimens under both constant strain level and time evolving strain level, and with loading along the preferred collagen fiber direction and more rigorous loading orthogonal to preferred collagen fiber direction. We note that some modification may be necessary, such as extending the model for the rate constant as a function of strain level and rate of cycling. However, the permanent set mechanism described was able to explain the effects of cyclic loading in the early stage. The lack of cyclic loading data beyond 65 million cycles, especially up to 100 or 200 million cycles, means that we are not able to incorporate structural damage into our constitutive model at this point. Although, based on what we observed, structural damage does not appear to play an observable 65 million cycles.

8. Summary and Future Directions

We have developed the first structural-based constitutive model for the time evolving properties of exogenously crosslinked collagenous soft tissues under cyclic loading. We focused on permanent set as the mechanism for the geometry changes in the early stage of cycling and developed our constitutive model based on the underlying scission-healing reaction of the GLUT crosslinked matrix. Permanent set allows the reference configuration of the exogenously crosslinked matrix to evolve over time and convect the collagen fiber architecture through the change in geometry. The results show that permanent set alone is sufficient to explain all changes in the early stage of BHV cycling, and more importantly predict how the shape and reference configuration evolve during this stage. Moreover, structural damage does not play a detectable role up to 65 million cycles. Our model also indicates that the collagen fiber architecture can play a role in limiting the permanent set effect, where the straightening of collagen fibers prevents further changes in geometry. Thus, accounting for the permanent set effect is especially important in the design of BHVs to better improve their performance and durability.

In addition to the exogenously crosslinked tissue applications addressed herein, we have observed permanent set like phenomenon in mitral valve tissue during pregnancy [45]. In that study, our results suggested that much of the growth and remodeling in the MV leaflet does not begin immediately, but rather undergoes mostly passive leaflet enlargement until these parameters reach a critically low level, at which point growth and remodeling are triggered. This initial tissue distension process is very similar in behavior to the permanent set mechanism outlined in the present work. Thus, the current approach could be applied to these types of the early phases soft tissue remodeling, where non-failure mechanisms occur before the onset of growth of tissue growth and remodeling. In addition, although the permanent set model we described only include the remodeling of the matrix due to scission-healing, the same concept can be extended by separating the rate constant into growth and resorption to simulate growth and remodeling of the matrix. Furthermore, the frame work outlined in section 5 can also be extended for the remodeling of the collagen fiber architecture, given further studies on mechanisms for how the collagen fiber architecture grows once the critical level observed in Rego et al [45] is exceeded. This is the advantage for the structural-based approach to modeling permanent set, which allows us to describe the mechanical response based on real physically measure-able quantities. We can further extend the more toward effects such as structural damage are the fiber-level, proteolytic degradation, and growth based on how this effects affect the components of the permanent set model layed out herein.

9. Nomenclature

Matrix

Non-fibrous part of the extracellular matrix

EXL

Exogenously crosslinked

PS

Permanent set, an irreversible deformation that remains in a structure or material after it has been subjected to stress

Damage

Loss of mechanical properties

Fatigue

Weakening of a material caused by repeated loading

Plastic deformation

Deformation of a material undergoing irreversible change in shape in response to applied forces

Structural convection

A permanent deformation of the collagen fiber architecture based on the change in the reference configuration

BP

Bovine pericardium

CFA

Collagen fiber architecture

BHV

Bioprosthetic heart valve

AWT

Accelerated wear testing

GLUT

Glutaraldehyde

TVI

Transcatheter aortic intervention

PD

Preferred direction

XD

Cross-preferred direction

ODF

Orientation distribution function

Recruitment

Probability distribution function describing the strain at which a collagen fiber’s crimp is straightened

Fiber ensemble

A group of fibers which share a common orientation

Ψ

Strain energy

Ψ_col, Ψ_int, Ψ_m

Strain energy of the collagen fiber, ensemble-ensemble interactons, and matrix components respectively

D

Collagen fiber recruitment distribution function

λ_s

The slack stretch, the stretch needed to straighten the collagen fiber crimp

Γ

Collagen fiber orientation distribution function

ϕ

Mass fraction

η_C, η_m, η_I

The modulus of collagen, EXL matrix and fiber-fiber interactions

I

Identity tensor

F

An arbitrary deformation gradient tensor applied to the tissue, referenced to the original uncycled stress free state

C

Right Cauchy-Green strain tensor, referenced to the original uncycled stress free state

E

Green Lagrange strain, referenced to the original uncycled stress free state

λ

Stretch

n_α

A vector pointing at the angle α

${\lambda }_{\alpha }=\sqrt{{\mathbf{n}}_{\alpha }·\mathbf{C}{\mathbf{n}}_{\alpha }}$

The applied stretch at the fiber ensemble-level in the direction α

_αλ_s

The slack stretch of a collagen fiber oriented with the angle α

S

Second Piola Kirchhoff tensor, referenced to the original uncycled stress free state

I₁

First invariant

I₈

Eighth pseudo invariant

$I_8^{r}ot$

The rotational component of I₈

$I_8^{e}xt$

The extensional component of I₈

k

Rate constant for permanent set

s

The current time in seconds

ŝ

The intermediate time when the EXL matrix is formed by the scission-healing process

Ω₀

The original unloaded configuration of the tissue before any cyclic loading

Ω(s)

The current loaded configuration of the tissue during cyclic loading

A(s)

Strain history, which is the root mean square strain of each cycle as a function of time

B̃(s) = AA^⊤

Left Cauchy Green tensor of the strain history

F̄(ŝ)

Deformation gradient tensor applied to the tissue, referenced to the strain history A(ŝ) at time ŝ

C̄(ŝ)

The right Cauchy Green strain tensor applied to the tissue, referenced to the strain history A(ŝ) at time ŝ

Ī₁

Modified first invariant, referenced to the strain history A(ŝ) at time ŝ

Ψ̄_m

Strain energy of the matrix as function of Ī₁

S̄_m

Stress of the matrix as function of Ī₁

Ω_PS(s)

The current unloaded configuration due to changes in geometry caused by permanent set

F_PS(s)

The deformation from Ω₀ to the current unloaded configuration (Ω_PS) due to permanent set

b(s)

The proportion of the existing amount of material remaining

a(s, ŝ)

The proportion of the material newly formed at time ŝ remaining

${}_0{}^1\mathbf{F}$

The deformation gradient from Ω₀ to some arbitrary state Ω₁, most commonly Ω₁ = Ω_PS

${}_0{}^1\lambda ({\theta }_0)$

The stretch of an ensemble oriented along θ₀ in Ω₀ deformed from Ω₀ to some arbitrary state Ω₁

D₁

The collagen fiber recruitment distribution function convected from Ω₀ to to some arbitrary state Ω₁

Γ₁

The collagen fiber orientation distribution function convected from Ω₀ to to some arbitrary state Ω₁

Ŝ

The applied stress during cyclic loading