Experimental study and mathematical modeling of toxic metals combined action as a scientific foundation for occupational and environmental health risk assessment. A summary of results obtained by the Ekaterinburg research team (Russia)

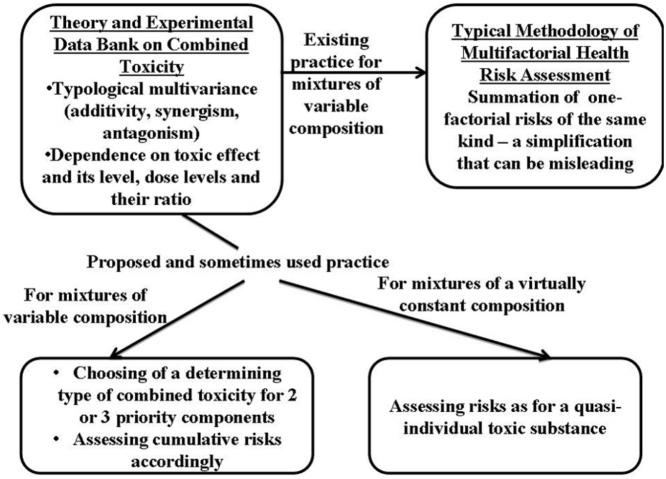
Graphical abstract

Highlights

• •Cumulative health risks assessment should be based on toxicology of mixtures.
• •Some principal discrepancies between these domains are discussed by the authors.
• •While simplification of the theory is inevitable, its vulgarization should be avoided.
• •Our contribution to this theory and its practical applications is summarized here.

Abstract

Assessment of cumulative health risks associated with the widely observed combined effects of two or more metals and their compounds on the organism has the toxicology of mixtures as its scientific basis although there is no full match between such assessment and this basis while some of the contradictions between them are of a fundamental nature. This state of things may be explained not only by simplifications characteristic of the generally recognized methodology of risk assessment but also by extreme complexity of the theory of combined toxicity, the most essential issues of which are considered by authors on the basis of literary and, mostly, their own previously published data.

1. Introduction

Human health risks due to exposure to toxic metals are associated, as a rule, with multiple factors. Such technologies as steel making (alloyed steels especially), electric arc welding, pyrometallurgy of heavy nonferrous metals (particularly copper smelting and refining), and electroplating bring about multicomponent (polymetallic) pollution of workroom and ambient air and of other compartments of the environment including foodstuffs produced in contaminated areas. Nevertheless, risk assessment experts tended to focus or still focus on certain isolated risks from exposure to hazardous metals that are considered (on more or less serious grounds) as a priority in a specific industrial or environmental context. The typical examples are studies conducted to assess the adverse effects of environmental pollution with lead on children’s health and development in areas around a copper smelter or the toxic impact of manganese on the CNS in arc welders.

At the same time, it is well known that these environments are actually contaminated with other elements as well (in particular, arsenic, copper, cadmium and zinc in copper smelting, or chromium, nickel, iron and silicon in arc welding). This may not seem to create any particular problems since the generally accepted methodology implies the possibility of assessing health risks individually for each of the factors operating in a combination with subsequent summation of risks of the same type. However, does the science of toxicology indeed provide sufficiently reliable and uniformly understood grounds for such a seemingly simple solution? As an analysis of the state of the art carried out by our group a few years ago [25] showed, answering this question is a challenge, and the answer itself is more likely to be negative.

Generally speaking, modern toxicology usually characterizes combined toxicity using the term “additivity” along with two other terms to describe some departure from it: superadditivity (or “synergism”), and subadditivity (or “antagonism”). The exact meaning of each of these terms can, however, vary broadly depending on which paradigm of combined adverse action is meant, even if not explicitly, by a researcher (e.g. [5], [28], [9], [10], [8] or, by an Agency (e.g. the US EPA or the ACGIH).

The so-called independence paradigm assumes that a similar effect of two or more substances is due to their action at different biological sites, and so the net effect of one chemical is independent of the presence of another chemical. The best known mathematical expression of this paradigm for the case of exposure to two toxicants is the so-called Bliss independence assumption [2], which, however, is strictly applicable only to indices that have the meaning of probability of a certain event.

For estimating the type of a combined impact in cases where its result is estimated by a quantitative shift in this or that index for the status of the organism compared with the baseline or the control value (which approach dominates in experimental toxicology), the central assumption is that of additivity of effects.

For a combination of two toxicants, this assumption is expressed by the equation:

[E(A,B) − E(0,0)] = [E(A,0) − E(0,0)] + [E(0, B) − E(0,0)] −

where E(A,B) is the value of an index under exposure to a combined effect of two toxicants; E(A,0) and E(0,B) are the values of the same index in response to the effect of one of the toxicants alone; and E(0,0) is the baseline or control value of the same index in the absence of both toxicants [8]. If the actually observed effect of a combination (A + B) is higher or lower than the expected effect E(A,B), this may be due to a non-zero interaction between the effects, and thus we deal with “synergy” or “antagonism”, respectively.

An alternative paradigm, the so-called “Loewe additivity”, assumes that two or more chemicals impact on the same biological site by the same mechanisms of action, being different in their potency only [13]. Thus A and B assumingly act as one and the same substance and, consequently, do not enter into any interaction between them. If DA and DB are isoeffective doses of these chemicals, one and the same effect of their combination in actual doses dA and dB can be obtained only where dA/DA + dB/DB = 1.0.

Where this sum is >1.0 or <1.0, it points to subadditivity (antagonism) or superadditivity (synergism), respectively. It is very popular to represent this paradigm with a graphic analogue called Loewe isobole or isobologram.

The official definitions of the terms «additive», «more than additive (potentiation, synergy)» and «less than additive (antagonism)» for combined action developed by a special Expert Committee [27], fully complied with the paradigm of effect additivity. However, later on the so-called Saariselkä Agreement recommended the use of both (effect additivity and dose additivity) models [6]. More recently, the report of a WHO/IPCS International workshop on “Assessment of combined exposures to chemicals” [14] virtually repeated this duality, also reproducing the widespread concept of a fundamental mechanistic difference between these two models.

Meantime, some researchers have demonstrated that the conformability of experimental data with this or that mathematical model of combined toxicity based on different paradigms depends essentially on the shape of the dose–effect curve for an isolated effect of each substance and on which segment of this curve the added effect of the second substance is considered [21], [9], [28]. Moreover, the type of combined toxicity may essentially differ depending on which of the components prevails in the combination quantitatively. In particular, this dependence gives biphasic Loewe isoboles, an example of which (for combined LD50 of sodium fluoride and manganese chloride in both mice and rats) was presented in Katsnelson [9] and Katsnelson et al. [10]. In this case, the combination proved subadditive where fluoride prevailed but superadditive where manganese did.

Tajima et al. [23] also came to the conclusion that the type of combined action of two toxicants depends on their dose ratio. Rozman et al. [20] evaluated the complex interaction between different doses and time–response using equations showing a sigmoid dose–response at a constant time and a sigmoid and sigmoid time–response at a constant dose.

It was also postulated that the type of combined action can depend on the organ or the system of the organism to which the effect considered pertains, as well as on the character of the effect [9]. Later on, the same conclusion was made in the ATSDR [1] overview document1 stating that “the predicted direction of interaction for the effects of these mixtures (Pb–As and Pb–Cd) is not consistent across endpoints. This observation is most striking for the effects of cadmium on the toxicity of lead. The predicted direction is greater than additive for the neurological effects (the critical effect) and testicular effects (a less sensitive effect), less than additive for renal and hematological effects, and additive for cardiovascular effects.”

Analysis of epidemiological data on combined cadmium–lead nephrotoxicity for children dwelling in industrially polluted areas led us, for the first time, to the conclusion that effect additivity vs. dose additivity should be regarded as two methods for estimating combined toxicity rather than two fundamentally different types of the latter [10]. This hypothesis was in conformity with the theoretical conclusion of Sühnel [21], who had proved analytically that any variant of combined action could be well described by isobolograms or, if this approach were to be generalized to take into account different dose levels, by response surfaces.

Vyskocil et al. [26] developed a practical approach to the identification of potential interactive effects of chemical mixtures and created a database comprising the results of 675 studies covering 209 binary mixtures of toxic substances acting in what the authors called “realistic exposure concentrations”. Their web-based computer tool allows the user to determine whether there is potential additivity or interaction among the components of a mixture. Stressing the lack of actual toxicological data in the primary literature, these authors generally adopt in such cases the additivity as a default hypothesis rather than as a proven fact.

We should underline in this connection that practical applications of the issue of combined toxicity (or “mixture toxicology”) to health risk assessment and to permissible exposure level setting, have to be, and are indeed straightforward and unavoidably simplified circumventing all the above-mentioned uncertainties of the theory. Nevertheless, we maintain that such a practical approach (which we discuss in detail in the concluding part of this paper) would not be just simplified but would also be rather deceptive if inferred from an oversimplified and uncertain theory, especially if the latter is formulated muddily and is not understood uniformly.

This general statement served as a starting point for a new series of experimenting and mathematical modeling [25], [18], [19], [11], [12], [16], the main results of which we propose to synthesize here.

2. Generalized design of our studies

2.1. Animal experiments

The first stage of the studies under consideration aimed to reveal some general patterns of combined action of toxic elements at systemic-organismic level disregarding the features associated with their chemical species, physical form, nature of exposure and the site of a toxicant’s entry into the body. At the same time, we restricted the scope of research by excluding acute intoxications from it, since the field of occupational and environmental health currently faces a much more important challenge of assessing the long-term effects of relatively low doses. We chose as a sufficiently close approximation the experimental model of subchronic intoxication induced by daily intraperitoneal injections during 5–7 weeks of salt solutions in doses typically equivalent to 1/20 of preliminarily estimated LD50. To minimize the probability of direct chemical interaction between the combined substances in the solution, they were drawn into separate syringes, and injections were made at a certain time interval.

This approach to modeling systemic intoxication (which in real conditions can be induced by long term exposure of humans to toxic substances, either inhaled or engulfed with contaminated water and food, or absorbed through the skin) may be justified by the consideration that the intraperitoneal animal model circumvents interspecies differences in main sites and kinetics of toxicant entry associated with anatomical, functional and behavioral peculiarities. At the same time, it is adequate enough when one wants to look into the body distribution and elimination of a toxicant, and into organism’s responses to it after they have penetrated into the blood – directly under a ‘natural’ exposure such as mentioned above or from either primary or secondary deposits. Like any model (a necessary simplification of a complicated system deliberately omitting some sub-systems and some material or informational flows and feedbacks), it has both drawbacks and virtues. One of the latter is the fact that dosing by injection is much more accurate, reliable and reproducible compared with more “natural” experimental exposures (a consideration of high importance where experimental results serve as a foundation for mathematical modeling).

In each subchronic experiment, groups of rats exposed to a toxic combination (binary or triple) were investigated parallel to groups of rats receiving separate injections of corresponding toxicants or normal saline. In this way, we studied the binary combinations: Pb-Cd, Pb-F, Cr-Ni, Cr-Mn, Ni-Mn; and three-factorial combination Cr-Ni-Mn [25], [18], [11], [12]

The same experimental model with some modifications was used at the second stage of our studies focusing on the combined toxicity of metal oxide nanoparticles, which are of special interest in the light of health risk assessment and management challenges because, along with engineered metallic NPs (Me-NPs) there usually is a substantial fraction of nanoscale (“ultrafine”) particles of the same substances in the particle size distribution of condensation aerosols generated by arc-welding and metallurgical technologies.

However extensive the advancements and developments in general and specific nanotoxicology have been over the recent decade, there was a virtually complete lack of studies devoted to combined toxicity of different substances in the nanoscale range. Meanwhile, the broader the use of nanomaterials in various industries, science and medicine, the higher the probability that humans would be exposed, either simultaneously or successively, to the multi-component impact of these materials. It is even more so when one considers not only purposely engineered Me-NPs but also those generated as by-products in many traditional technologies. Indeed, Me-NPs generated by arc-welding, alloyed steel metallurgy, copper smelting and so on and contaminating workroom and ambient air usually have a complex chemical composition comprising oxides of iron, manganese, nickel, chrome, vanadium, silicon or of copper, lead, zinc, arsenic and other elements. Both the chemical identity of these NPs and quantitative relationships between them vary broadly depending on a specific technology or its phase, the composition of the alloy being molten or welded and of the welding electrodes being used, the melting temperature, etc. Hence the urgent need to assess not only the comparative toxicity of various Me-NPs but also their combined effects. Our own research in this area published up to now [15], [16] has dealt with combinations of NiO-NP + Mn3O4-NP; PbO-NP + CuO-NP; PbO-NP + ZnO-NP; ZnO-NP + CuO-NP; PbO-NP + CuO-NP + ZnO-NP.

Upon the exposure period, both exposed and sham-exposed (control) rats went through the following procedures: body weighing; estimation of the CNS ability to perform temporal summation of sub-threshold impulses in a variant of the withdrawal reflex and its facilitation by repeated electrical stimulations in an intact, conscious rat; recording of the number of head-dips into the holes of a hole-board, which is frequently used for studying the behavioral effects of toxicants and drugs; collection of daily urine for analysis of its density, urine output, and coproporphyrin, delta-aminolevulinic acid (δ-ALA), creatinine and relevant toxic element contents.

Then the rats were killed by decapitation and their blood was collected by exsanguination. The liver, spleen, kidneys, and brain were weighed. The blood biochemical indices studied usually included total serum protein, albumin, globulin, triglycerides, cholesterol, high and low density lipoproteins, bilirubin, ceruloplasmin, reduced glutathione (GSH), malonyldialdehyde (MDA), alkaline phosphatase, alanine- and asparate-transaminases (ALT, AST), catalase, gamma glutamyl transferase, creatinine, and, in some experiments, also thyrotropic hormone of hypophysis, thyroxin, and triiodothyronine, follicle-stimulating and luteinizing hormones, progesterone, dehydroepiandrosterone, estradiol, and neuron-specific enolase. We used an MYTHIC-18 auto-hematology analyzer for determining the hemoglobin content, hematocrit, thrombocrit, mean erythrocyte volume, and RBC, WBС and thrombocyte counts. The proportion of reticulocytes was counted using the routine technique. Cytochemical determination of succinate dehydrogenase (SDH) activity in lymphocytes was based on the reduction of nitrotetrazolium violet to formazane, the number of granules of which in a cell was counted under immersion microscopy. Genomic DNA fragmentation was assessed in cells of several tissues using the RAPD test.

In all experiments, histological changes were described and estimated morphometrically in the liver, spleen and kidneys; and additionally in the brain in the experiments with copper, lead, manganese and nickel oxide NPs and in rat lungs after chronic inhalation exposure to iron oxide NPs. Thin sections of different organs were prepared for histological examination by hematoxilin-eosine stain and, where necessary, PAS, Nissl and Perl’s stains. We used a planimetric ocular grid for the morphometry of the spleen and an image recognition programmed system for that of the liver, kidneys and brain.

The total number of quantitative indices shifts in which served as indicators of toxicity thus amounted to 30–50.

The metal content of the liver, spleen, kidneys and brain was determined by atomic emission or atomic absorption spectrometry (AES, AAS) and, for iron, nickel, manganese, also by the electron paramagnetic resonance (EPR) method.

For estimating both isolated and combined effect of Me-NPs we used one more experimental model for organism’s response [15], [16]. A single-shot intratracheal (i.t.) instillation of 1 ml of 0.2 mg Me-NP water suspension (or of sterile de-ionized water from the same batch, without any particles) served as an experimental model for the response of the lower airways to particle deposition. It is well known that important qualitative and quantitative patterns of the response displayed by the pulmonary free cell population (in particular, its dependence on the cytotoxicity of deposited particles) observed in inhalation exposures to different mineral dust particles are essentially the same as in the case of their i.t. administration. As for Me-NPs, we saw the same homology when comparing the pulmonary responses to the i.t. instillation and low-level inhalation exposures of Fe2O3-NPs in a nose-only inhalation chamber [22].

At the same time, the i.t. model provides cellular material for assessing the in vivo phagocytic activity of pulmonary macrophages and polymorphonuclear leukocytes, as well as intracellular localization of Me-NPs engulfed by them and ultrastructural damage caused to the cell by those NPs. The results thus obtained may be compared with the data reported by researchers experimenting with NP-exposed cell cultures, being a valuable addition to the latter because in vivo interaction between cells and particles occurs in a microenvironment which is not completely reproducible by artificial cell culture media and, besides, under the influence of many direct and feedback cellular interactions.

A cell population of bronchoalveolar lavage fluid (BALF) obtained 24 h after intratracheal instillation of NP or MP suspensions to rats was studied with optical (OM), transmission electron (TEM) and semi-contact atomic force microscopy (sc-AFM). Besides, some biochemical indices were determined in the BALF and its cell-free supernatant with the special attention to lysosomal enzymes activity.

2.2. Mathematical modeling

In our first study [25], we analyzed experimental results using different mathematical models based on (a) ANOVA and (b) Mathematical Theory of Experimental Design, which correspond to the well-known paradigms of effect additivity and dose additivity (Loewe additivity), respectively (see Introduction). Having proved that assignment of type to combined toxicity is model-insensitive, in our further studies beginning from Panov et al. [18] we used mostly the Response Surface Methodology, which generalizes these traditional paradigms [24], [4], [3], [17]. In this methodology, an Eq. (1) describing the response surface Y = Y(x1, x2) can be constructed by fitting its coefficients to experimental data.

$$Y=f\left(x_1,x_2\right),$$ (1)

where Y is a quantitative effect (outcome) of a toxic exposure; x1 and x2 are the doses of the toxicants participating in the combination; f(x1,x2) is a regression equation with some numeric parameters. In the case of two-level exposures (even if one of the levels is equal to zero), the response surface may have one possible shape, namely hyperbolic paraboloid [19].

It is inferred that agents produce a unidirectional effect on response Y if both one-way response functions Y(x1, 0) and Y(0, x2) either increase or decrease with an increase in x1 or x2. On the contrary, two agents are assumed to be acting contra-directionally (oppositely) if one function increases while the other decreases. This mathematical model enables one to predict the magnitude of response Y for any combination of toxicant doses within the experimental range for each of them (rather than at two factual points only). The sectioning of the response surface on different levels corresponding to different meanings of the outcome Y or of the doses x, provides a family of Loewe isoboles that may have the same or a different form and/or different slopes and thus render the interpretation of binary combined toxicity types both easy and illustrative. Below we therefore discuss the results of analysis presented just in this form (see Section 3).

3. Main results of data analysis

3.1. Binary combinations of toxic metals

In all cases of binary toxic combinations that we have considered so far, analysis of subchronic experimental data led us to the following principal postulates:

• (1)the above-mentioned paradigms of effect additivity and dose additivity are virtually interchangeable and so they might be regarded as different methods for modeling combined toxicity rather than as concepts reflecting fundamentally differing processes;
• (2)within both paradigms, there exist more than three traditionally recognized types of combined toxicity (additivity, subadditivity and superadditivity), and we have found at least 10 variants of it depending on exactly which effect is considered and what its level is, as well as on dose levels and their ratios;
• (3)when one gives multiple-outcome characterization of combined intoxications, both unidirectional (additive, subadditive or superadditive) and oppositely directed action of one and the same pair of toxics in the sense determined above (see Subsection 3.2) is usually found in respect to even one and the same effect but at different dose or effect levels;
• (4)thus, toxicological antagonism can manifest itself either in hidden form (as a subadditivity) or explicitly (as a contra-directional action which is algebraically additive or departs from additivity in this or that direction).

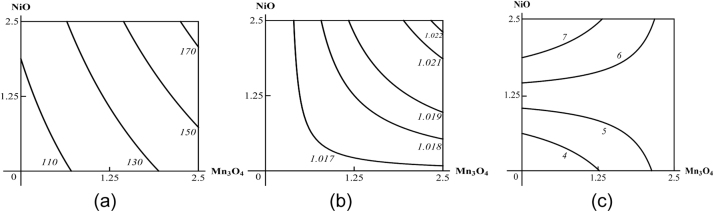
In all the above respects, there is no difference between metals acting in molecular-ionic form or in the form of metal oxide nanoparticles. We therefore illustrate these postulates only by isobolograms pertaining to Me-NP combined toxicity since the latter is more important from the industrial toxicologist’s point of view. These isobolograms are reproduced from our team’s papers originally published in “Food and chemical toxicology” (Fig. 1) [11] or in “Toxicology” (Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7 ) [16].

Fig. 1.

Examples of isoboles characterizing NiO-NP + Mn3O4-NP combined subchronic toxicity: (a) for uric acid concentration in blood serum (additivity); (b) for urine density (synergism at low effect levels and additivity at high effect levels); (c) for akaryotic hepatocyte percentage (subadditivity of unidirectional action at low effect levels and oppositely directed action at high effect levels). The doses of Mn3O4 and NiO are plotted on the axes in mg per rat. The numbers at the lines of the isoboles show the values of the effect Y (uric acid in mcMol/L).

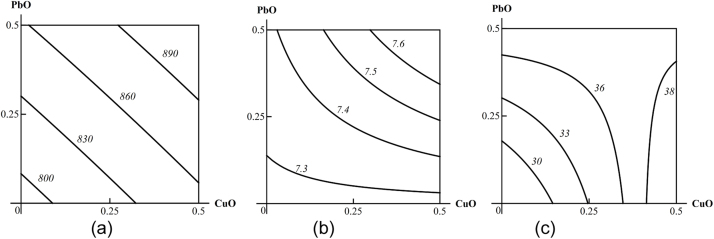
Fig. 2.

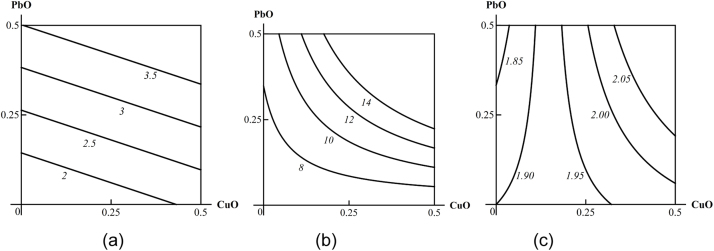
Examples of isoboles characterizing CuO-NP + PbO-NP combined subchronic toxicity: (a) for thrombocyte count (additivity); (b) for erythrocytes (synergism at low effect levels and additivity at high effect levels); (c) for diuresis subadditivity of unidirectional action at low effect levels and oppositely directed action at high effect levels. The doses of CuO and PbO are plotted on the axes in mg per rat. The numbers at the lines of the isoboles show the values of the effect Y (thrombocytes *109/L; erythrocytes *1012/L; diuresis in mL per 24 h).

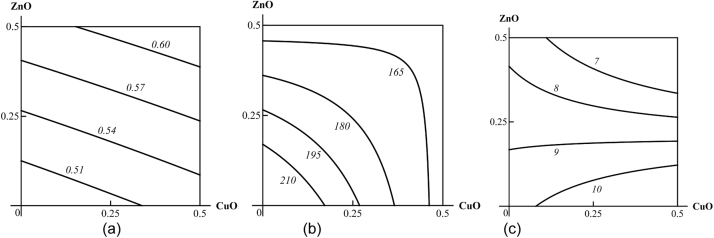
Fig. 3.

Examples of isoboles characterizing CuO-NP + ZnO-NP combined subchronic toxicity: (a) for thrombocrit (additivity); (b) for alkaline phosphatase (AF) in blood serum (subadditivity); (c) for testosterone (superadditivity of unidirectional action at low effect levels and oppositely directed action at high effect levels). The doses of CuO and ZnO are plotted on the axes in mg per rat. The numbers at the lines of the isoboles show the values of the effect Y (AF in IU/L; testosterone in nMol/L).

Fig. 4.

Examples of isoboles characterizing CuO-NP + PbO-NP combined pulmonary toxicity: (a) for BALF total cell count (additivity); (b) for BALF supernatant amylase activity (superadditivity); (c) for BALF albumin content (oppositely directed action at a low effect and superadditivity of unidirectional action at a high effect). The doses of CuO-NP and PbO-NP are plotted on the axes in mg per rat. The numbers at the lines of the isoboles show the values of the effect Y (cell counts in *106, amylase in IU/L, albumin in g/L).

Fig. 5.

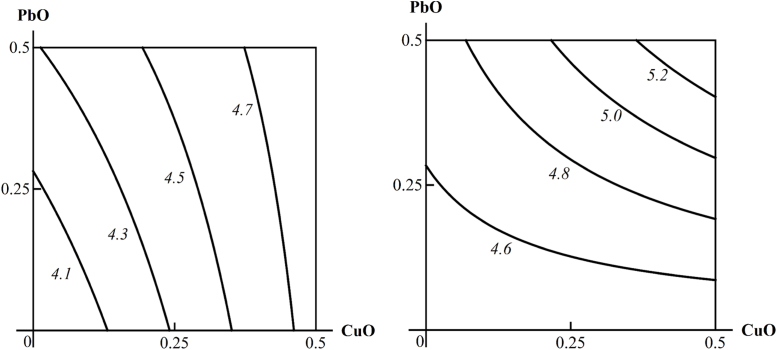
An example of three-factorial toxicity effects classified as “A”: an additive action of PbO-NP and CuO-NP on the De Ritis coefficient in the absence of any other toxic exposure is transformed into the synergism of the same two Me-NPs against concomitant background exposure to ZnO-NP. The doses of PbO and CuO are plotted on the axes in mg per rat. The numbers at the lines of the isoboles show the values of the effect.

Fig. 6.

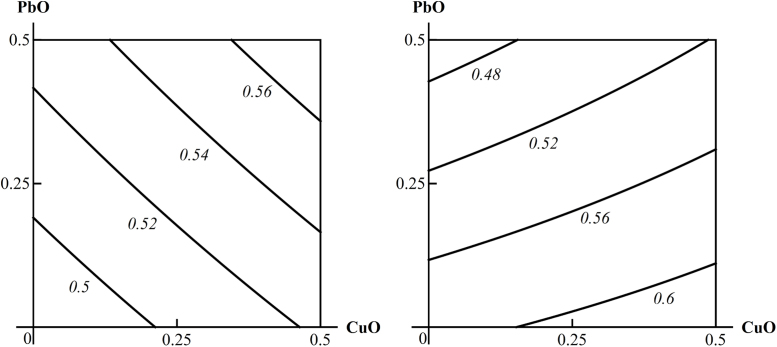
An example of three-factorial toxicity effects classified as “B”: the additivity of a PbO-NP and CuO-NP unidirectional action on the thrombocrit index in the absence of any other toxic exposure transforms into a contra-directional action of the same two Me-NPs against concomitant background exposure to ZnO-NP. The doses of PbO and CuO are plotted on the axes in mg per rat. The numbers at the lines of the isoboles show the values of the effect.

Fig. 7.

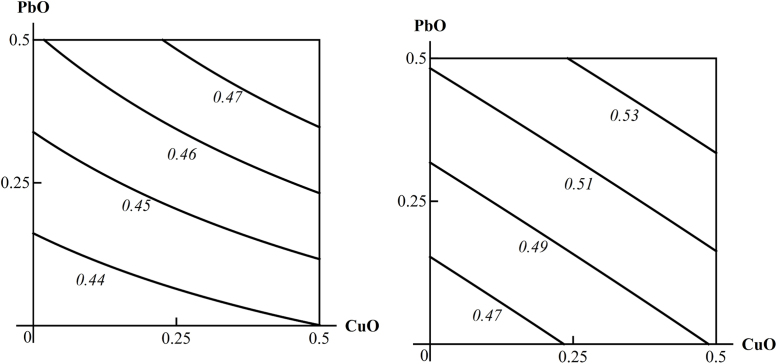
An example of three-factorial toxicity effects classified as “C”: the additivity of a PbO-NP and CuO-NP unidirectional action on the DNA fragmentation coefficient both with and without concomitant background exposure to ZnO-NP. The doses of PbO and CuO are plotted on the axes in mg per rat. The numbers at the lines of the isoboles show the values of the effect.

Essentially the same effect-dependent diversity of binary combined toxicity types was revealed when analyzing acute pulmonary responses to Me-NPs instilled i.t. as illustrated in Fig. 4.

3.2. Three-component combinations of toxic metals

As concerns the combined toxicity of three metals acting together, we [12] were the first to propose a health risk-oriented approach based on the consideration whether the addition of a third toxic to the other two leads to the type of binary combined action becoming either more or less adverse (Сlasses A and B, respectively) or remaining basically unchanged (Сlass C). This approach was successfully tested first with reference to subchronic intoxication with nickel, chromium and manganese salts. We revealed some stable patterns of classification fully or partly reproducible when considering various metals, one by one, as the third component of the combination. The classification was found to be inherently consistent for the absolute majority of outcomes. The same approach was then proved to be adequate for analyzing three-factorial Me-NP toxicity as well [16]. Examples of isobolograms typical of each class are given in Fig. 5, Fig. 6, Fig. 7.

3.3. Criteria for choosing the main type of combined toxicity

An analysis of the variety of combined action types for the same pair of toxic substances provides important information for understanding and forecasting the clinical presentation of corresponding intoxications. But for this information to be practically useful for health risk assessment and management (see Section 5), the ultimate assessment of each combination studied should be more or less unequivocal. However, as we stressed it in Introduction, we should aspire to achieve such unequivocal assessment not by theoretical simplification, which is fraught with serious errors, but on the basis of as comprehensive an understanding of its complexity as possible. The solution to this problem may be greatly facilitated by introduction of an additional concept of “principal” or “determining” type of combined toxicity.

The choice of the principal type of combined action out of all identified in an experiment with a specific binary combination of toxic substances can be based on a number of criteria:

• (1)the prevailing value of the type of combined action that is characteristic of low doses;
• (2)in cases where the combination considered occurs in real contexts mainly in a narrow range of ratios between its components, the prevailing value of the combined action type which is characteristic of this range;
• (3)in cases where one knows the organs and systems of the organism playing the greatest role in the toxicodynamics and/or toxicokinetics of given combined intoxication, the prevailing value of the type which is characteristic of the effects associated with the impact on these organs and systems;
• (4)in cases where at least one of the substances in a combination is regarded to be highly hazardous (particularly if it is genotoxic, carcinogenic or reproductively toxic), the prevailing value of the type of combined action which is characteristic of corresponding effects.

We suggest using basically the same criteria for choosing the principal class of three-factorial toxicity. However, as soon as the number of factors increases to 4 or more, this approach to combined toxicity typology would not be feasible. We are convinced that in relation to such multi-factorial mixtures it would be more reasonable to give up attempting to characterize as a whole the very complex picture of interactions among all the factors and, given a relatively constant ratio between the components, it would be more reasonable to consider each practically significant mixture as an individual substance and assess its effects on the organism, their dependence on dose, safe exposure levels, etc. just for this quasi-individual substance. Note that this approach was actually used in Soviet toxicological practice a long time ago. The same very rational position of “studying toxicology of chemical mixtures, instead of their individual constituents” is maintained by Hernàndez and Tsatsakis [7], who also emphasize the need to combine toxicological experiments with well designed and conducted epidemiological studies”.2

However, this approach is inapplicable to multicomponent mixtures of variable composition in which ratios between components may be substantially different (as is often the case with combined pollution of industrial and other environments), and we would recommend identifying a priority two- or three-component sub-combination of the most toxic and hazardous substances in such mixtures for experimental and mathematical analysis of combined toxicity patterns using the approach briefly described above in this paper.

4. What may be regulatory and risk assessment inferences from the combined toxicity analysis?

As is well known, the widely used methodology of health risk assessment originally developed by the US Environmental Protection Agency (US EPA) recommends summing risks up where we deal with risks of the same adverse health outcome. When we so summarize risks expressed as a probability of cancer or as a number of cancer or any other disease cases in a population, we proceed explicitly from the paradigm of effect (or, rather, response) additivity.

However, for characterizing cumulative non-carcinogenic risks, use is also made of summation of so-called hazard quotients (HQ) of separate toxicants (i.e. of ratios of their estimated doses to respective reference doses, RfD). This approach may seem similar to dose additivity assuming that RfDs for different toxics are isoeffective, which they are definitely not. It is even more important that if this sum (the so-called hazard index – HI) is not equal to 1.0, it cannot be interpreted as testifying to any kind of deviation from additivity.

Thus, even though the standard methodology of cumulative health risk assessment is based on the concept of additivity, which is pivotal to the ideology of combined toxicity analysis, the similarity in the usage of this concept in the above methodology and in quantitative toxicology is superficial.

Essentially the same may be said about some regulatory decisions, which are supposed to provide criteria for estimating not only exposure but also multi-factorial risks and serve as targets for efficient risk management scenarios. In the same country, the American Conference of Governmental Industrial Hygienists (ACGIH) has for decades evaluated concentrations of mixtures of several substances of similar toxicological effect as meeting the threshold limit values (TLVs) established for each of the substances where their actual concentrations (Ci) meet the condition:

C1/TLV1 + C2/TLV2 + C3/TLV3 + …….+ Cn/TLVn = or < 1.0.

A similar approach to «same-effect substances» is also adopted in the Russian law-enforceable standards for maximum permissible concentrations of harmful substances in the air. It is easy to see that this approach seemingly complies with the paradigm of dose additivity (Loewe additivity) but, again, only if one assumes that TLVs established for different substances are really isoeffective (which they are not either, being established based on different criteria and with different safety margins).

The more or less justified and not always correctly used assumption of additivity (either of effects or of doses) is nevertheless accepted by default for health risk assessment and risk management decisions. Meanwhile, the possibility of antagonism or synergism is virtually neglected even if proclaimed. We believe that a knowledgeable expert should bear this in mind to be more confident or make sure that additional safety margins are built into those decisions.

In other words, even when assessing a multifactorial risk by the standard method of summation of single-factor risks, the expert should take into consideration that where toxicological studies have provided evidence of synergism between the toxic impacts of two factors in relation to effects that may be identified as principal for determination of binary toxicity type (see Subsection 3.3) or where in an assessment of three-factorial toxicity such principal effects fall into class A (see Subsection 4.2), the standard approach of simple addition would definitely underestimate the total risk. If the principal type of binary toxicity is explicit and/or implicit antagonism and if the principal effects of triple toxicity fall into class B, simple summation of one-factorial risks would quite likely overestimate, more or less, the multifactorial risk.

In the first case it is recommended that proposed risk management scenarios be even more radical and reliable where practicable. Thus, for example, air exchange calculations for industrial premises and other inhalation exposure reducing technologies based on the dose additivity assumption should allow for an additional safety margin. As for the second case, it allows one to rely on the safety margins already integrated into the preventive measures taken to protect against additive toxicity (but, in our opinion, it does not provide grounds for relaxing them).

5. Conclusion

There is no doubt that cumulative health risk assessment of combined exposures to toxic substances, metals and their compounds in particular, has the science of mixture toxicology as its ideological basis. However, there is no direct match between such assessment and this ideology, which is explained not only by some simplification of the theory of combined toxicity characteristic of the generally accepted methodology of risk assessment but also by the extreme complexity of this theory, to which our group has hopefully made a significant contribution but which certainly needs further development.