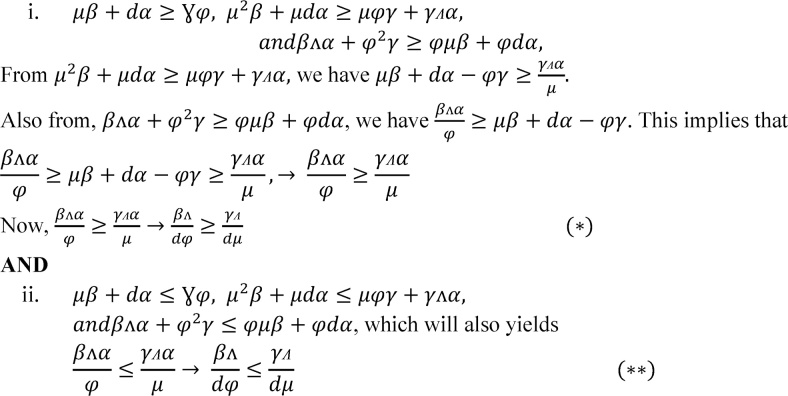Modelling the dynamics of toxicity associated with aflatoxins in foods and feeds

Highlights

• •Aflatoxins toxicity model has been developed.
• •Tracing aflatoxins concentration in foods and feeds at various stages is shown.
• •The need to use experimental data is suggested.
• •Satisfactory harmonization of acceptable threshold levels of aflatoxins in foods and feeds could be drawn.

Abstract

In this paper, we developed a mathematical model to describethe dynamics of Aflatoxins in plants, animals, and humans. Fourequilibrium points were found, and their stability analyses wereconducted using threshold quantities. If both are less than one, thestandardized toxic limit is not exceeded, while if both are greater thanone it is exceeded in both animals and humans. Standardized toxic limitis exceeded in a relevant host (animals or humans) when their respectivethreshold quantity is greater than one. Numerical simulations werecarried out to support the analytic results. The need to use experimentaldata in the model is also shown. This could ease satisfactoryharmonization of acceptable standards and facilitate international tradeof food and feeds.

1. Introduction

It is generally accepted that food products are naturally safe. However, it is evident that humans suffered from the vast number of toxic substances in foods, which could be natural (such as mycotoxins, allergens, chemical factors, and plant toxins), or artificial (pesticide and veterinary drug residues, and food additives) [1], [2], [3]. Mycotoxins are among the natural toxicants of particular importance as far as public health is concern.This is due to their widespread distribution in foods and feeds, and the resulting array of severe clinical conditions they posed to humans and animals. The resulting diseases from mycotoxins are referred to as mycotoxicoses, characterized by carcinogenic, genotoxic, teratogenic, nephrotoxic, hepatotoxic, immunotoxic, amongst other debilitating clinical conditions [4], [5] and even possible death in times of high exposure [6], [7].

Once food is contaminated by mycotoxins, decontamination may be a tedious process, or even impossible to achieve. This is due to the resistance of many known mycotoxins to extreme environmental conditions as well as to physical and biological treatments specifically designed for their inactivation/detoxification [8]. Hence, when they accumulate in the body of humans or animals they could produce toxicological effects.

At the moment, more than 400 mycotoxins have been identified and presented in the literature [9]. However, aflatoxins (produced by the genus Aspergillus), fumonisin, trichothecenes, zearalenone, and deoxynivalenol(produced by the genus Fusarium), patulin (produced by the genera Aspergillus, Byssochlamys and Penicillium), ochratoxin (produced by the genera Aspergillus and Penicillium) and ergotamine (produced by the genera Aspergillus, Claviceps, Penicilliumand Rhizopus) are the most significant in terms of the severity of the health consequences they posed to humans and animals [4].

In all the different kind of mycotoxins, aflatoxins (AFs) are the principal and most challenging in foods and animal feeds due to high prevalence, associated toxicity (in particular mutagenicity, carcinogenicity and teratogenicity) [10]; [11], [4], and high temperature and heat resistance during food processing [12].

Aflatoxin is a designation from “a”, “fla” and “toxin” for Aspergillus, flavus and toxin (resulting poison) respectively [13]. These toxins were discovered in the past six decades in an outbreak involving poultry (turkeys) and farm animals in the United Kingdom. The suspected cause of the outbreak was contaminated peanuts imported from Brazil, resulting in the death of hundreds of thousands poultry and farm animals. The incidence is correlated with Aspergillus flavus contamination levels.

Aspergillus species (A. flavus and A. parasiticus) are the dominant producers of AFs.Presently there are 18 various types ofaflatoxins, the most important ones are Blue (B1and B2), Green(G1 and G2), B1Metabolite (M1), B2Metabolite (M2), B2A and G2A (Stroka and Anklam 2000; [14]; Bennett and Klich 2003; [15]. Blue and Green are referred to their characteristic fluorescence lights emitted during the course of separation with thin-layer chromatography.For M-types, these compounds are normally not found on crops, but their metabolites are found in meat,eggs and dairy and their productsof animals fed with contaminated feedstuffs [16], [6].

Both Aflatoxins B- and G-types are Group 1 mutagenic compounds, in IARC classification, whereas AF-M1 is in Group 2B (The International Agency for Research on Cancer, [17]. Accordingly, high AFs exposure is attributed to high liver cancer incidence [18], [19]. Other debilitating clinical conditions associated AFs include alteration and impairment of child growth, enhancement of edema and kwashiorkor in malnourished adults and children respectively [20], [21], [22], [23].

The occurrence and level of AFs contamination is influenced by the kind of Aspergillus species present, farming system,handling and storage practices, and several other factors [7], that may contribute to the occurrence and severity of these toxins humans for example, genetic make-up, drying or evapo-transpiration, soil nature, moisture deficit, and insect infestations [24].

Nowadays, there has been substantial increase in the toxicity associated with the consumption of AFs in foods and feedstuffs [19]. As a result, numerous studies have been conducted showing toxicological effects in humans and animals, depending on the rate of contamination and exposure to AFs [25], [6]. In addition, AFs contamination in foods and feeds affects crop and animal production thereby causing significant economic losses.

For almost two decades, the European Union is committed setting up standards based on toxicological examination. The allowable limit of contamination of foods is governed by the principle of as low as reasonably achievable “ALARA”. However, during that time, similar approaches have been recommended for the establishment of safe limits of certain mycotoxins [26]. Measures have been set up by the relevant authorities in many countries and some international organizations to contain AFs levels [27], especially for agricultural products from countries with hot climates to satisfactorily harmonize foods and feeds trade. The recommended maximum level of aflatoxins in human foods is 4 ppb according to European Community and Codex Alimentarius [28], and Iranian maximum tolerated level is 15 ng/g (=ppb) for total aflatoxin [29]. Currently, maximum tolerable levels and guideline levels have been established for aflatoxins (AFs), ochratoxin (OTA), zearalenone (ZEN) and deoxynivalenol (DON) ranging from ppb to ppt for various food and feed products [30], [31], [28], [32].

The standardised safe limit of AFs in foods intended for human consumption ranges from 4 to 30 ug/kg. Hence, when strictest limits will be adopted worldwide, foods and feeds from tropical and subtropical countries will face both economic losses and additional costs related to meeting those standards. Likewise when the allowable limits are not so strong, there might be high exposure to these toxins.

Although, epidemiological studies of human populations can provide direct evidence of adverse health effects of toxins in humans, the issue of combating the concentrations of AFs in foods could be a difficult task considering the cloud of uncertainties which might arise with respect to levels of exposure, constrains inprocuring representative samples of food from subsistence farmers, multiple vulnerable crops and other relevant confounding risk factors which may mask or otherwise obscure any effects of the putative causative agent within food supply chain [33], [34].

Consequently, this situation requires numerous and sound approaches to set up the possible limits which may prevent or reduce toxicological effects to humans, taking into account the natural occurrence and effects of handling and food processing methods to the quantities of aflatoxins from the initial stages of contamination to post-harvest stages (from farm to fork), since respective limits are under debate for other mycotoxins [35].

Scientific evidence and legislation for AFs limits which are toxicologically acceptable are needed to estimate the exposure to these important mycotoxins; these actions are usually carried out in the agricultural practice, storage of products and control of the products intended for human or animal consumption [36], [37], [38].

Mathematical models of process dynamics along with simulation and optimization gained considerable attention in the agriculture and food industry as they can portray the real processes and significantly reduce the overall time for dealing with food safety issues [39], [40], [41].

The principle of modeling is based on having a set of mathematical equations that can adequately characterize the system. In particular, the solution of these equations must allow description or prediction of the process parameters as a function of time at any point in the food supply chain based on the initial concentrations. Thus, the model can be used to address and fulfill the needs of new and strategic approaches, and other innovations in the agriculture and food industry [42], [43], [44].

In this paper, we developed mathematical model of the SIR (Susceptible − Infected − Removed) form to describe the dynamics of AFs concentration in foods and feeds, animals, and human beings. It is in our interest to compute a threshold quantity which measures the consumption limit of the AFs in humans.Stability analysis of the model was also carried out and the conditions for the stability are given. Numerical simulations were carried out to support the analytic result.

2. Formulation of the model

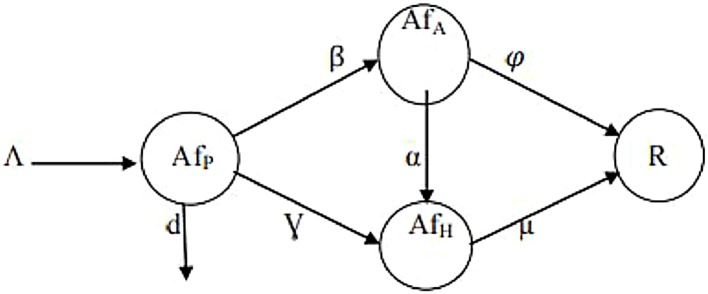
We take as our model, the dynamics of aflatoxins in food and feeds to animals/humans and consequently from animals to humans. Fig. 1 is the flow chart of the Aflatoxins in various hosts, and Table 1 gives the description of the parameters used in the model.

Fig. 1.

Transfer diagram of Aflatoxin concentration.

Table 1.

Parameter descriptions of the model.

Parameters	Description
AfP	Aflatoxin concentration in plants
AfA	Aflatoxin concentration in animals
AfH	Aflatoxin concentration in humans
R	Removed (natural death/decontamination technologies, etc)
β	Transmission rate of aflatoxins from plants to animals
Ɣ	Transmission rate of aflatoxins from plants to humans
Α	Transmission rate of aflatoxins from animals to humans
μ	Removal rate of aflatoxins from humans
$$\phi$$	Removal rate of aflatoxins from animals
Λ	Natural birth rate/rate of occurrence of aflatoxins
d	Death rate (natural/decontamination technologies, etc)

The Model is described by the following system of ordinary differential equations.

$$\begin{array}{l}\frac{dA{f}_P}{dt}=\Lambda -\beta A{f}_{P}A{f}_A-\mathrm{Ɣ}A{f}_{P}A{f}_H-dA{f}_P\\ \frac{dA{f}_A}{dt}=\beta A{f}_{P}A{f}_A-\phi A{f}_A-\alpha A{f}_{A}A{f}_H\\ \frac{dA{f}_H}{dt}=\mathrm{Ɣ}A{f}_{P}A{f}_H-\mu A{f}_H+\alpha A{f}_{A}A{f}_H\\ \frac{dR}{dt}=\phi A{f}_A+\mu A{f}_H\\ A{f}_P\left(0\right)>0,A{f}_A\left(0\right)=0,A{f}_H\left(0\right)=0,R\left(0\right)=0\end{array}$$ (1)

2.1. Assumptions

• 1)Initial concentration of aflatoxins in animals and humans are assumed to be zero for convenience.
• 2)The occurrence of aflatoxins into the plant is assumed to be constant.
• 3)The total concentration of aflatoxins in the process is equal to sum of all the equations at any stage.
• 4)We assume there is no degradation of aflatoxins at any other stage than in plants
• 5)Concentration of aflatoxins in humans is greater than that of animals since in most cases humans consume both plant and animal products.

2.2. Existence of equilibrium points

Equating Eq. (1) to zero and solving simultaneously we get the equilibrium points. The equilibrium points are biologically meaningful when they are positive. There are four equilibrium points;

1. Plants equilibrium point

$$E_0=\left\{\frac{\Lambda }{d},\mathrm{0,0}\right\}\text{,}$$

This equilibrium always exists, without any restriction.

2. Plants and humans equilibrium point

$$E_1=\left\{\frac{\mu }{\gamma },0,\frac{\mathrm{\Lambda }\gamma -d\mu }{\mu \gamma }\right\},$$

• •E₁ exists only if Λγ > dμ.

This means, the product of birthrate/occurrence rate and transmission rate to humans is greater than the product of death rate and removal rate. That is there is more consumption of AFs in humans than its removal.

3. Plant and animals equilibrium point

$$E_2=\left\{\frac{\phi }{\beta },\frac{\mathrm{\Lambda }\beta -d\phi }{\phi \beta },0\right\},$$

• •E₂ exists only if Λβ > dφ

This means, the product of birthrate/occurrence rate and transmission rate to animals is greater than the product of death rate and removal rate. That is there is more consumption of AFs in animals than its removal.

4. Interior equilibrium point

$$E_3=\left\{\frac{\mathrm{\Lambda }\alpha }{\mu \beta -\gamma \phi +d\alpha },\frac{-\gamma \mathrm{\Lambda }\alpha +{\mu }^2\beta -\mu \phi \gamma +\mu d\alpha }{\alpha \left(\mu \beta -\gamma \phi +d\alpha \right)},\frac{\beta \mathrm{\Lambda }\alpha -\phi \mu \beta +{\phi }^2\gamma -\phi d\alpha }{\alpha \left(\mu \beta -\gamma \phi +d\alpha \right)}\right\}.$$

• •E₃ exists only if

Therefore, $\left(*\right)\mathrm{and}\left(**\right)$ implies $\frac{\beta \mathrm{\Lambda }}{d\phi }=\frac{\gamma \mathrm{\Lambda }}{d\mu }$. Hence, the interior equilibrium exists only if

$$\frac{\beta \mathrm{\Lambda }}{d\phi }=\frac{\gamma \mathrm{\Lambda }}{d\mu }\mathrm{.}$$

2.3. Computation of threshold quantity (R₀)

The threshold quantity here is analogous to that of Mathematical epidemiology, a quantity called basic reproduction ratio. Basic reproduction ratio is the number of secondary infections caused by a single infective individual in a population of completely susceptible population. Here if the quantity is greater than one, it means the quantity of the toxins in the human body or in the animal body exceeds the carrying capacity limit hence there might be a problem. However, if the quantity is less than one, then there is no problem. The established safe limit of AFs for human consumption ranges from 4 to 30 μg/Kg [10].

We applied the next generation matrix to calculate the threshold quantity as,

$$F=\left[\begin{array}{cc}\hfill \beta A_P\hfill & \hfill 0\hfill \\ \hfill \alpha A_H\hfill & \hfill \gamma A_p+\alpha A_A\hfill \end{array}\right],V=\left[\begin{array}{cc}\hfill \phi +\alpha A_H\hfill & \hfill \alpha A_A\hfill \\ \hfill 0\hfill & \hfill \mu \hfill \end{array}\right]$$

$$V\left(E_0\right)=\left[\begin{array}{cc}\hfill \phi \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \mu \hfill \end{array}\right]F\left(E_0\right)=\left[\begin{array}{cc}\hfill \frac{\beta \Lambda }{d}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{\gamma \Lambda }{d}\hfill \end{array}\right]$$

$V^{-1}=\left[\begin{array}{cc}\hfill \frac{1}{\phi }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{1}{\mu }\hfill \end{array}\right]$. Therefore, $F{V}^{-1}=\left[\begin{array}{cc}\frac{\beta \mathrm{\Lambda }}{d\phi }& 0\\ 0& \frac{\gamma \mathrm{\Lambda }}{d\mu }\end{array}\right].$

The basic reproduction number is the spectrum radius of the matrixFV⁻¹,

$$R_0=\rho \left(F{V}^{-1}\right)$$

This implies $R_{01}=\frac{\beta \mathrm{\Lambda }}{d\phi }$ or $R_{02}=\frac{\gamma \mathrm{\Lambda }}{d\mu }.$

If R₀₁ > 1, then βΛ > dφ. This means, the product of birthrate/occurrence rate and transmission rate to animals is greater than the product of death rate and removal rate. That is there is more consumption of AFs in Animals than its removal. It also implies the threshold quantity will be exceeded.

If R₀₂ > 1, then γΛ > dμ. This means, the product of birthrate/rate of occurrence and transmission rate to humans is greater than the product of death rate and removal rate. That is there is more consumption of AFs in humans than its removal. It also implies the threshold quantity will be exceeded.

3. Stability analysis of the equilibria

Here we carry out the local stability analysis of the equilibrium points. From our model, we form the following Jacobian matrix. If all the eigenvalues of the Jacobian matrix are negative the equilibrium is locally asymptotically stable.

$$J=\left[\begin{array}{ccc}-\beta A{f}_A-\gamma A{f}_H-d& -\beta A{f}_P& -\gamma A{f}_P\\ \beta A{f}_A& \beta A{f}_P-\phi -\alpha A{f}_H& -\alpha A{f}_A\\ \gamma A{f}_H& \alpha A{f}_H& \gamma A{f}_P-\mu +\alpha A{f}_A\end{array}\right]$$ (2)

Theorem 1

The Plant equilibriumE₀ is locally asymptotically stable if R₀₁ < 1 and R₀₂ < 1.

Proof

From (2), we have the following

$$J\left(E_0\right)=\left[\begin{array}{ccc}\hfill -d\hfill & \hfill -\frac{\beta \Lambda }{d}\hfill & \hfill -\frac{\gamma \Lambda }{d}\hfill \\ \hfill 0\hfill & \hfill \frac{\beta \Lambda }{d}-\phi \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\gamma \Lambda }{d}-\mu \hfill \end{array}\right]$$

The eigenvalues of $J\left(E_0\right)$ are given by:

$${\lambda }_1=-d<0\text{,}$$

$${\lambda }_2=\frac{\beta \mathrm{\Lambda }-d\phi }{d}=\frac{d\phi \left(\frac{\beta \mathrm{\Lambda }}{d\phi }-1\right)}{d}=\phi (R_{01}-1)<0,if{R}_{01}<1.$$

$${\lambda }_3=\frac{\gamma \mathrm{\Lambda }-d\mu }{d}=\frac{d\mu \left(\frac{\gamma \mathrm{\Lambda }}{d\mu }-1\right)}{d}=\mu (R_{02}-1)<0,if{R}_{02}<1.$$

Hence, E₀ is stable if R₀₁ < 1 and R₀₂ < 1.

Theorem 2

The equilibrium E₁ is locally asymptotically stable ifR₀₂ > 1 and R₀₂ > R₀₁.

Proof

From (3.1), the matrix J(E₁) is given by

$$J(E_1)=\left[\begin{array}{ccc}-\frac{\mathrm{\Lambda }\gamma }{\mu }& -\frac{\beta \mu }{\gamma }& -\mu \\ 0& \frac{\beta {\mu }^2-\phi \mu \gamma -\alpha \mathrm{\Lambda }\gamma +\alpha d\mu }{\mu \gamma }& 0\\ \frac{\mathrm{\Lambda }\gamma -d\mu }{\mu }& \frac{\alpha \left(\mathrm{\Lambda }\gamma -d\mu \right)}{\mu \gamma }& 0\end{array}\right]$$

The eigenvalues of J(E₁) are given by:

$${\lambda }_1=\frac{\beta {\mu }^2-\phi \mu \gamma -\alpha \mathrm{\Lambda }\gamma +\alpha d\mu }{\mu \gamma }=\frac{\mu \left(\beta \mu -\phi \gamma \right)+\alpha d\mu \left(1-\frac{\mathrm{\Lambda }\gamma }{d\mu }\right)}{\mu \gamma }=\frac{\left(\beta \mu -\phi \gamma \right)+\alpha d\left(1-R_{02}\right)}{\gamma }$$

Now, λ₁ < 0 if R₀₂ > 1 and

βμ < φγ which implies $\frac{\beta \mu \mathrm{\Lambda }}{d}<\frac{\phi \gamma \mathrm{\Lambda }}{d}\to \frac{\beta \mathrm{\Lambda }}{d\phi }<\frac{\gamma \mathrm{\Lambda }}{d\mu }\to R_{01}<R_{02}.$ Hence, R₀₂ > 1 and R₀₂ > R₀₁.

For ${\lambda }_2=\frac{-\Lambda \gamma +\sqrt{{\left(\gamma \Lambda \right)}^2+4d{\mu }^3-4{\mu }^2\Lambda \gamma }}{2\mu }$, if ${\left(\gamma \Lambda \right)}^2+4d{\mu }^3<4{\mu }^2\Lambda \gamma ,$ then λ₂ is a complex root and $\mathrm{Re}\left({\lambda }_2\right)<0\text{.}$ But if ${\left(\gamma \Lambda \right)}^2+4d{\mu }^3>4{\mu }^2\Lambda \gamma$, then λ₂ is a real root and negative if

$$\Lambda \gamma >\sqrt{{\left(\gamma \Lambda \right)}^2+4d{\mu }^3-4{\mu }^2\Lambda \gamma }\to {\left(\gamma \Lambda \right)}^2>{\left(\gamma \Lambda \right)}^2+4d{\mu }^3-4{\mu }^2\Lambda \gamma \to$$

4μ²Λγ > 4dμ³ ↔ R₀₂ > 1. Therefore, ${\lambda }_2\langle 0\mathrm{if}{R}_{02}\rangle 1\text{.}$

For ${\lambda }_3=\frac{-\Lambda \gamma -\sqrt{{\left(\gamma \Lambda \right)}^2+4d{\mu }^3-4{\mu }^2\Lambda \gamma }}{2\mu }\text{,}$ if ${\left(\gamma \Lambda \right)}^2+4d{\mu }^3>4{\mu }^2\Lambda \gamma \text{,}$ then λ₃ is a real root and hence negative.

If ${\left(\gamma \Lambda \right)}^2+4d{\mu }^3<4{\mu }^2\Lambda \gamma \text{,}$ then λ₃ is a complex root and has negative real part. Hence, E₁ is locally asymptotically stable if R₀₂ > 1 and R₀₂ > R₀₁.

Theorem 3

The equilibrium point E₂ is locally asymptotically stable if R₀₁ > 1andR₀₂ < R₀₁

Proof

Similar to Theorem 2.

Theorem 4

The equilibrium point E₃ is locally asymptotically stable if R₀₁ − R₀₂ > 1 and .

Proof

Using (2), we have the following matrix

$$J(E_3)=\left[\begin{array}{ccc}\frac{2\beta \mu \phi \gamma -{\mu }^2{\beta }^2-{\phi }^2{\gamma }^2-d^2{\alpha }^2}{\mu \beta +d\alpha -\phi \gamma }& \frac{-\beta \mathrm{\Lambda }\alpha }{\mu \beta +d\alpha -\phi \gamma }& \frac{-\gamma \mathrm{\Lambda }\alpha }{\mu \beta +d\alpha -\phi \gamma }\\ \frac{-\beta \mathrm{\Lambda }\gamma \alpha +{\mu }^2{\beta }^2-\mu \beta \phi \gamma +\beta \mu d\alpha }{\mu \beta +d\alpha -\phi \gamma }& 0& \frac{\gamma \mathrm{\Lambda }\alpha -{\mu }^2\beta +\mu \phi \gamma -\mu d\alpha }{\mu \beta +d\alpha -\phi \gamma }\\ \frac{\gamma \beta \mathrm{\Lambda }\alpha -\gamma \phi \mu \beta +{\gamma }^2{\phi }^2-\gamma \phi d\alpha }{\mu \beta +d\alpha -\phi \gamma }& \frac{\beta \alpha \mathrm{\Lambda }-\phi \mu \beta +{\phi }^2\gamma -\phi d\alpha }{\mu \beta +d\alpha -\phi \gamma }& 0\end{array}\right]$$

To check the stability of the equilibrium point, we use the Ruth-Hurwitz criteria [45], which says;given the following characteristic equation,

$${\lambda }^3+a_1{\lambda }^2+a_2\lambda +a_3=0\text{,}$$

all roots have negative real part if,

$$a_3>0,a_1>0,a_1{a}_2>a_3\mathrm{.}$$

From the characteristics equation of the above matrix, we have the following:

$$a_1=\phi \gamma +d\alpha -\mu \beta ,a_2=\mathrm{\Lambda }\gamma +\beta \mathrm{\Lambda }-\phi \mu -\alpha \mathrm{\Lambda },a_3=\left(\mathrm{\Lambda }\alpha -\mu \phi \right)\left(\mu \beta +d\alpha -\phi \gamma \right).$$

• •Now, a₁ > 0 if $\frac{\mathrm{\Lambda }\gamma }{d\mu }+\frac{\alpha \mathrm{\Lambda }}{\phi \mu }\ge \frac{\beta \mathrm{\Lambda }}{d\phi }(*)\mathrm{.}$
• •
  a₃ > 0 implies $\left(\mathrm{\Lambda }\alpha -\mu \phi \right)\left(\mu \beta +d\alpha -\gamma \phi \right)>0.$ For the condition to be satisfied, we have the following two cases:

  • i.
    $\left(\Lambda \alpha -\mu \phi \right)>0$ and $\left(\mu \beta +d\alpha -\gamma \phi \right)>0$, which yields $\frac{\Lambda \alpha }{\phi \mu }>1$ and$\frac{\mathrm{\Lambda }\gamma }{d\mu }+\frac{\alpha \mathrm{\Lambda }}{\phi \mu }\le \frac{\beta \mathrm{\Lambda }}{d\phi }\left(**\right).$ OR
  • ii.
    $\left(\Lambda \alpha -\mu \phi \right)<0$ and $\left(\mu \beta +d\alpha -\gamma \phi \right)<0$.

$From(*)and\left(**\right)wehave\frac{\mathrm{\Lambda }\gamma }{d\mu }+\frac{\alpha \mathrm{\Lambda }}{\phi \mu }=\frac{\beta \mathrm{\Lambda }}{d\phi }$ which implies $R_{01}-R_{02}=\frac{\alpha \Lambda }{\phi \mu }\text{.}$ (***)

• •a₁a₂ > a₃ implies 2φμ > Λγ + αΛ.

Now, from (***) and $\frac{\Lambda \alpha }{\phi \mu }>1$, we have R₀₁ − R₀₂ > 1. Therefore, we haveR₀₁ − R₀₂ > 1 and 2φμ > Λγ + αΛ. Hence the proof.

4. Numerical simulations

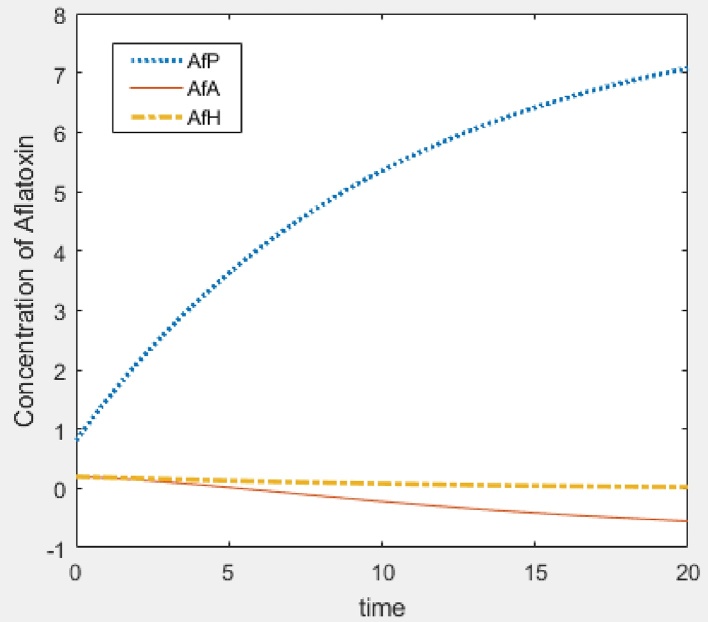
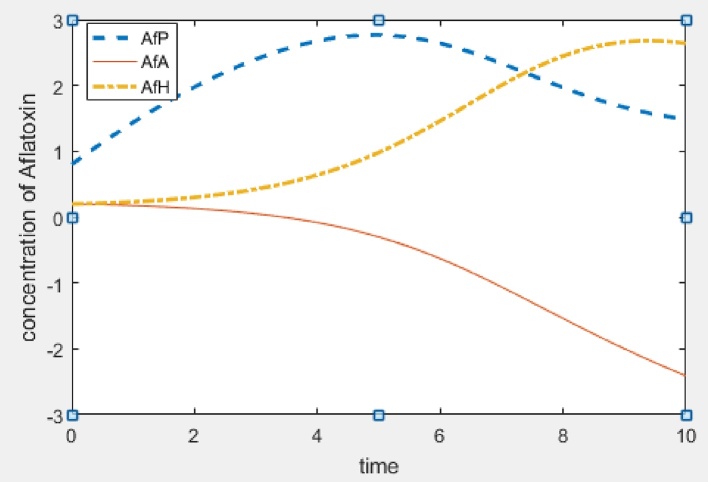
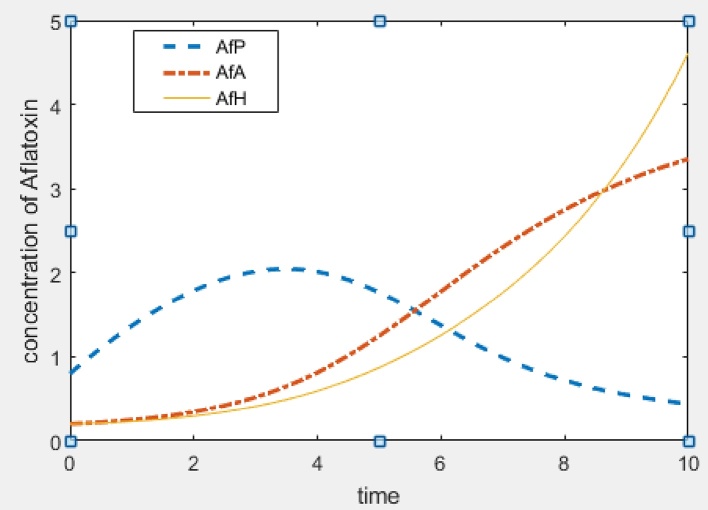
In this section, we give numerical simulations examples to support the analytic results and to show how our model works. Fig. 2 shows the stability result of E₀, that is when R₀₁ < 1 and R₀₂ < 1. Fig. 3 and Fig. 4 show the stability result of E₁ when R₀₁ > 1 and E₂ when R₀₂ > 1 respectively. Fig. 5 is the numerical stability result of E₃ when R₀₁ > 1 and R₀₂ > 1.

Fig. 2.

Plant equilibrium (aflatoxins concentration in human and animals is below toxic limit): Λ = 0.8, β = 0.003, γ = 0.002, d = 0.1, α = 0.1, μ = 0.1, φ = 0.08, R₀₁ = 0.3, R₀₂ = 0.16.

Fig. 3.

Plant and Animal equilibrium (aflatoxins concentration in humans is below toxic limit): Λ = 0.8, β = 0.3, γ = 0.002, d = 0.1, α = 0.1, μ = 0.1, φ = 0.08, R₀₁ = 30, R₀₂ = 0.16.

Fig. 4.

Plant and human equilibrium (aflatoxins concentration in animals is below toxic limit): Λ = 0.8, β = 0.003, γ = 0.2, d = 0.1, α = 0.1, μ = 0.1, φ = 0.008, R₀₁ = 0.3, R₀₂ = 16.

Fig. 5.

Interior equilibrium (aflatoxins concentration in humans and animals reaches toxic limit):Λ = 0.8, β = 0.03, γ = 0.2, d = 0.1, α = 0.1, μ = 0.1, φ = 0.08, R₀₁ = 30, R₀₂ = 16.

5. Summary and conclusions

We formulated a mathematical model which shows the dynamics of aflatoxins from plants (feeds) to animals, plants (plant foods) to humans, and animals to humans (carry-over effects). Stability analysis of the equilibrium points is determined using threshold quantities R₀₁ and R₀₂ . It is shown (analytically and numerically) that if R₀₁ < 1 and R₀₂ < 1 then AFs concentrations in animals and plants will not reach toxic limit. If R₀₁ > 1 the AFs concentration in animals will reach toxic limit and that of humans will not. IfR₀₂ > 1 then the aflatoxins concentration in humans will reach toxic limit and that of animals will not. Finally, if R₀₁ > 1 and R₀₂ > 1, the AFs concentrations in both animals and humans will reach toxic limit.

From the above results, it can be understood that the entire dynamics depends on the numerical values of the threshold quantity. Hence, to control the toxicity limits, food toxicologists and relevant authorities should put more emphasis on the parameter values of the threshold quantity by ensuring the denominator values in each case are greater than the numerators (βΛ < dφandγΛ < dμ). This can be achieved by employing various control measures like biological control and/or decontamination technologies. The model can be used as a framework in tracing the dynamics of concentration of aflatoxins and other mycotoxins from farm to fork.

Future work in this area should concentrate on studying these models using experimental data, to test the predictivity of the method and its utility in controlling contamination below acceptable limits.