Comprehensive and Automated Linear Interaction Energy Based Binding-Affinity Prediction for Multifarious Cytochrome P450 Aromatase Inhibitors

Abstract

Cytochrome P450 aromatase (CYP19A1) plays a key role in the development of estrogen dependent breast cancer, and aromatase inhibitors have been at the front line of treatment for the past three decades. The development of potent, selective and safer inhibitors is ongoing with in silico screening methods playing a more prominent role in the search for promising lead compounds in bioactivity-relevant chemical space. Here we present a set of comprehensive binding affinity prediction models for CYP19A1 using our automated Linear Interaction Energy (LIE) based workflow on a set of 132 putative and structurally diverse aromatase inhibitors obtained from a typical industrial screening study. We extended the workflow with machine learning methods to automatically cluster training and test compounds in order to maximize the number of explained compounds in one or more predictive LIE models. The method uses protein–ligand interaction profiles obtained from Molecular Dynamics (MD) trajectories to help model search and define the applicability domain of the resolved models. Our method was successful in accounting for 86% of the data set in 3 robust models that show high correlation between calculated and observed values for ligand-binding free energies (RMSE < 2.5 kJ mol^–1), with good cross-validation statistics.

Introduction

Cytochrome P450 aromatase (CYP19A1; EC 1.14.14.1) is a member of the Cytochrome P450 (CYP) superfamily of mono-oxygenases. This enzyme catalyzes a key step in estrogen biosynthesis, i.e., aromatization of androgens such as androstenedione and testosterone to estrone and 17β-estradiol, respectively.¹⁻⁷ Common to most CYPs, CYP19A1 can bind a variety of low molecular weight compounds, but it has a high catalytic specificity toward steroid substrates due to the distribution of polar and nonpolar residues within the binding site.^8,9

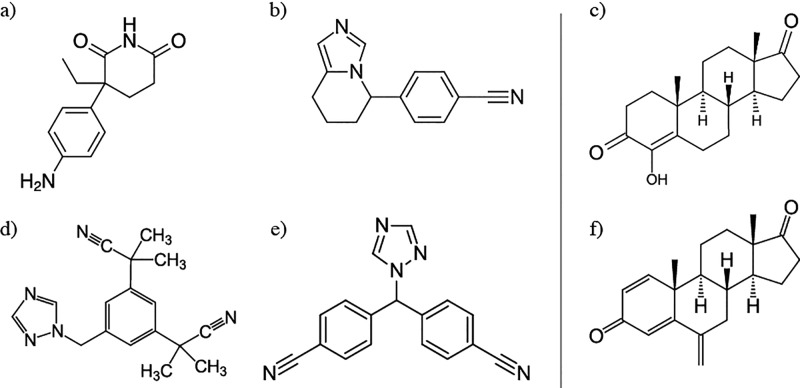
Overexpression of aromatase in tumor tissue was identified to play a key role in the development of estrogen receptor positive breast cancer, endometrial cancer and endometriosis.^1,3,5 Around 50–80% of breast cancers have been found to be estrogen-dependent, where estrogen binding to receptor stimulates tumor cell proliferation.¹⁰⁻¹³ Because the aromatization reaction catalyzed by CYP19A1 is rate limiting, it serves as an ideal target for the development of selective and potent inhibitors that decrease the levels of circulating estrogen.^14,15 This has led to the development of four generations of aromatase inhibitors (AIs) in clinical use over the last three decades (Figure 1).^14,16,17 Most AIs are nonsteroidal in nature (NSAIs) and derived from aminoglutethimide-like molecules, imidazole/triazole derivatives, or flavonoid analogs.^17,18 They act by means of competitive and reversible inhibition (type I) or quasi-irreversible inhibition by coordination with the heme iron (type II).^19,20 Steroidal inhibitors are typically based on the adrostenedione scaffold with various chemical substituents at varying positions, which can be functional groups responsible for mechanism based inhibition (e.g., Exemestane, Figure 1f).²¹

Figure 1.

Members of four generations of clinical steroidal (c,f) and nonsteroidal (a,b,d,e) aromatase (CYP19A1) inhibitors. First generation: aminoglutethimide (a, Cytadren, Novartis).⁹⁹⁻¹⁰¹ Second generation: Fadrozole (b, Afema, Novartis),⁹⁹⁻¹⁰¹ and Formestane (c, Lentaron, Novartis).¹⁴ Third generation: Anastrozol (d, Arimidex, AstraZeneca),¹⁰² Letrozole (e, Femara, Novartis),^103−105 and Exemestane (f, Aromasine, Pfizer).¹⁰³

Despite their clinical success, current AIs are associated with various drug related side-effects,^22,23 including effects due to inhibition of other members of the CYP family²⁴ that can lead to drug–drug interactions (DDI).²⁵ Therefore, the search for a next generation of AIs with improved potency, higher selectivity and reduced toxicity is still ongoing, and both synthetic as well as natural product derived alternatives such as coumarin, lignin and flavonoids have been explored over the years.^17,26−30

The widened search spectrum for AI lead compounds increases the need for effective methods to screen the inhibitory potential and modes of interaction for both the target protein and other CYPs. In particular, the use of in silico methods for the prioritization of compound ideas throughout the lead discovery and optimization stages potentially offers an attractive alternative for extensive use of in vitro methods.^31,32 However, especially for CYPs it remains a challenge to train generally applicable predictive models for protein binding due to their substrate promiscuity, catalytic site malleability, different modes of inhibition, and ability to bind the same ligand in multiple orientations.^19,25,33,34 The flexibility in both the structural and interaction dimensions limits the applicability of QSAR (Quantitative Structure–Activity Relationship) methods based on molecular descriptors only.^33,35,36 The addition of structural information such as in 3D-QSAR, molecular docking or extensive pharmacophore methods has increased predictive capacity, typically yielding local models for structurally similar binders.^33,36,37 However, these methods have difficulties dealing with the dynamic nature of the CYP catalytic site and substrate binding modes, providing a limited, static view of protein–substrate interactions.³⁸

On the other hand, molecular dynamics (MD) based free energy calculation methods have the potential to provide an accurate estimate of the binding affinity, even for very flexible systems such as CYP enzymes.³⁹⁻⁴¹ They are valuable methods in the design stage of drug discovery but due to their high CPU costs many of the pathway-based methods (including, e.g., Free Energy Perturbation (FEP) and Thermodynamic Integration (TI)) are unattractive for use in high-throughput settings especially when having to deal with multiple protein and/or ligand conformations that may contribute to binding (as in case of several CYPs).^41,42 Alternatively, end-point methods such as Linear Interaction Energy (LIE) theory may provide a trade-off between accuracy and speed by estimating the solvation free energy between the two end points using linear response theory instead of multiple intermediate steps along a pathway.^34,43−45 LIE requires empirical calibration of its scaling parameters. An advantage is that the sampling issue can be effectively and efficiently addressed using an iterative version of LIE⁴¹ that uses (re)weighted results from multiple short simulations starting from different ligand⁴¹ and protein conformations⁴⁰ as obtained, e.g., by molecular docking.

The LIE method has been applied extensively over the last two decades in the prediction of protein–ligand binding affinities.^45,46 Most LIE models have been trained using relatively small and curated data sets ranging from as few as 10–15 up to approximately 50 compounds, yielding predictive affinity models for compounds that are structurally similar or diverse but engage in similar interactions with the target protein.^{39,40,47−52} However, this situation may differ notably to the much larger data sets obtained in a typical industrial lead development and optimization project. Apart from their size, these compound libraries are often sparse and designed to increase possibilities to discover novel active ligands or scaffolds. It can become a challenge to create predictive LIE models with well-defined applicability domains³⁹ for these data sets and, with high-throughput in mind, to do so in an automated fashion.

In the current study, we present a system of three quantitative binding affinity prediction models for CYP19A1. The models were trained using a data set of 132 putative CYP19A1 inhibitors with known inhibition constants obtained from a lead discovery study by Bayer AG that is subject to the same challenges described above in terms of compound size and chemical diversity. As an additional challenge, we aim here for a comprehensive approach for LIE model inference, parametrization and applicability assessment based on simulation and calibration data only, without the need for data set prefiltering by the user based on other information from experiment such as type of binding, which is not always available a priori. We have dealt with these challenges by developing an automated machine learning workflow that uses a stochastic approach to explore LIE-model parameter landscape. The iterative LIE (iLIE) method is used as a cost function in this search to prioritize the relative contribution of a binding orientation among a series of independent simulations of possible binding orientations. This approach allows to efficiently deal with flexible proteins (such as CYPs) that are able to bind ligands in multiple orientations. The probability of a compound to be part of a particular model is defined by a Bayesian approach that determines the maximum a posteriori estimates for the α and β parameters of the iLIE equation for a set of compounds, in order to maximize the number of explained compounds in one or more LIE models with predefined quality of the correlation between calculated and experimentally observed values for the ligand-binding free energies (in terms of RMSE and r²). We subsequently used protein–ligand interaction profiling to define the applicability domain of the resolved models in terms of protein–ligand interactions.

We show that our machine learning workflow is able to explain 86% of the employed CYP19A1 data set in three fully cross-validated LIE models with distinct combinations of α and β model parameters and an error margin below 3.0 kJ mol^–1 of the experimentally observed binding free energy (i.e., within typical experimental accuracy⁵³). Using simulation data only, steroid inhibitors were separated from nonsteroidal inhibitors, and the presented system of binding affinity models together with their protein–ligand interaction profiles provide a comprehensive means of predicting the binding affinity of unknown ligands for CYP19A1.

Methods

Molecular Dynamics (MD) averaged protein–ligand interaction energies for LIE affinity prediction were obtained using our previously published (semi)automated iterative LIE workflow.^39,54,64 The methodological details on the protein and ligand structure preparation, molecular docking and MD simulation stages of this workflow are described below, together with the model calibration and validation strategies developed in this study.

Structure Preparation

The crystal structure of CYP19A1 with PDB ID 3EQM(55) was used after removal of the 4-androstene-3-17-dione (ASD) molecule, water oxygen atoms (none in the catalytic cavity) and crystallization buffer additives.

A data set of inhibition constants (K_i) for 132 putative CYP19A1 inhibitors with known stereochemistry (Tables S1 and S4, Supporting Information) was provided by Bayer AG, Berlin. Six of the 132 compounds entered the data set as duplicate (Table S1) but with independently measured K_i values. These compounds were used as internal validation in the study; and indeed most of the duplicates were found within the same (local) model, Table S1. K_i values were determined using the ³H₂O release assay with [1β-³H]androstenedione as substrate⁵⁶ in human placental microsomes according to FDA and UP guidelines, and were used to derive experimental binding free energies ΔG_obs (Table S1). Assumptions taken in directly deriving ΔG_obs from these inhibition data were supported by the obtained correlations for our final LIE models.

The initially minimized 3D structures for these compounds in their neutral form were generated from their canonical SMILES string using Molecular Operating Environment (MOE) version 2012.10,⁵⁷ and the MMFF94 force field.⁵⁸ Subsequent optimization and generation of MD topology and parameter files was performed using the Automated Topology Builder (ATB) server version 1.0.⁵⁹

Docking and Clustering

Ligands were docked into the active site of CYP19A1 using the PLANTS (Protein–Ligand Ant System) docking software version 1.2.⁶⁰ The target binding site was defined at the approximate center of the protein active site, at a position 0.7 nm distal to the heme iron center perpendicular to the heme plane, and with a size defined by a sphere with a radius of 1.1 nm. Docking poses were generated with speed 1 settings and evaluated using the ChemPLP⁶¹ scoring function. A maximum of 300 docked poses with mutual Root-Mean-Square Deviations (RMSDs) in atomic positions of more than 0.2 nm were retained and clustered using Principle Component Analysis (PCA), using the heavy atom positions as variables. After dimensionality reduction, the scores obtained were used for subsequent k-means clustering.⁶² During this analysis, an additional component or cluster was taken into account in case it would have led to a further increment of at least 5% of the explained variance in the space of the coordinates or scores, respectively. The medoids of the clusters obtained (4 to 8 per ligand) were chosen as representative binding conformations of the ligand in the CYP19A1 active site.

MD Simulations

The MD simulations for every representative binding pose obtained after docking and clustering were carried out using the GROMACS 4.5.4 package⁶³ and an adapted version⁶⁴ of the automated MD workflow script obtained from the GROMACS web server.⁶⁵ The GROMOS 54A7 force field⁶⁶ was applied to describe the protein and heme group in simulation. Ligand topologies were obtained with ATB⁵⁹ as described above (see Structure Preparation subsection).

Each complex was energy minimized in a vacuum using steepest descent minimization and solvated in a simulation box with a Near-Densest Lattice Packing (NDLP) optimized volume^67,68 (∼6300 solvent molecules) where water was described by the SPC model.⁶⁹ 7 Cl^– ions were added to neutralize the system. The system was energy minimized (steepest-descent) and gradually heated up to 300 K in four NvT simulations of 20 ps, in which harmonic potentials were used for heavy-atom positional restrains in the sequence: 100/1000, 200/5000, 300/50 and 300/0 for temperature (K) and positional restraint force constant (kJ mol^–1 nm^–2), respectively, together with a Berendsen thermostat⁷⁰ with a separate solute and solvent coupling time of 0.1 ps. Subsequently, three 20 ps equilibration runs were performed at NpT, using heavy-atom positional restraints on the solute with decreasing force constants of 1000, 100 and 10 kJ mol^–1 nm^–2. To further stabilize the system (as shown to be required before⁷¹), a short 500 ps unrestrained NpT simulation preceded the 2 ns production NpT simulation. A leapfrog algorithm⁷² was employed for integrating the equations of motion. Heavy hydrogens (with a mass of 4.032 amu)⁷³ were used and all bonds were constrained using the LINCS algorithm,⁷⁴ allowing a time-step of 4 fs. In all NpT simulations, a Berendsen thermostat⁷⁰ was employed to maintain the temperature of the system close to its reference value of 300 K, using separate temperature baths for the solvent and solute degrees of freedom, with a coupling time of 0.1 ps. A Berendsen barostat⁷⁰ with a coupling time of 0.5 ps and an isothermal compressibility of 7.5 × 10^–4 [kJ mol^–1 nm^–3]⁻¹ was used to maintain the pressure close to its reference value of 1.013 25 bar during NpT simulations. Van der Waals and short-range electrostatic interactions were explicitly evaluated every time step for pairs of atoms within a 0.9 nm cutoff, and a grid-based neighbor list was used and updated every 2 time steps. Long-range electrostatic interactions were included using a twin-range cutoff (0.9/1.4 nm) with reaction field correction.⁷⁵ The relative dielectric constant for the medium outside the reaction field was set to 61. Center of mass motion removal was applied to both the solute rotation and translation components every 10 steps. Interaction energies and atomic coordinates were stored every 2 ps.

To evaluate average ligand interaction energies of the unbound ligands in water, each ligand was solvated in a NDLP optimized simulation box filled with approximately 625 SPC water molecules. No counterions were added. The MD protocol was identical to the one described for the simulations of the protein–ligand complex.

Iterative Linear Interaction Energy (iLIE) Method

In LIE, the predicted free energy of binding for a ligand in pose i to a protein (ΔG_predⁱ) is estimated from MD-averaged electrostatic ⟨V_lig–surr⟩ and van der Waals interaction energies ⟨V_lig–surr^vdw⟩ between the ligand and its surrounding as obtained in complex with the protein (bound,i) and free in solution (free). Following LIE theory,^43,76

1

Values for the empirical LIE model parameters α and β are obtained by parametrization against a training set of compounds with experimentally determined binding affinities using linear regression analysis. An optional constant γ may be considered and has been used by others to account, e.g., for hydrophobicity of the binding site.^76,77

In the iterative version of eq 1,⁴¹ the predicted protein–ligand binding free energy ΔG_pred is calculated by combining results from N multiple short MD simulations starting from different ligand poses in the protein binding site that represent local minima on the potential energy surface of the protein–ligand complex, using a weighted sum (Σ_i^NW_i). The relative weight (W_i) of each simulation (i) entering the sum is calculated according to its probability using⁷⁸

2

with k_B Boltzmann’s constant, T the temperature of the simulation system and N the number of independent simulations. Extending eq 1 by including the weighted sum of multiple short simulations yields⁴¹

3

The dependencies of the ΔG_predⁱ on α and β requires eq 3 to be solved iteratively.⁴¹

Automated iLIE Binding Affinity Model Inference

LIE models can be trained automatically for an unknown data set of sufficient size by clustering ligands based on similarity in ΔV^vdW and ΔV^el energy patterns (defined as ⟨V_lig–surr^vdw⟩_bound (,i) – ⟨V_lig–surr⟩_free and ⟨V_lig–surr^el⟩_bound (,i) – ⟨V_lig–surr⟩_free), respectively) as a function of α and β model parameters (and possibly an optional constant γ) using the iLIE equation as a cost function in an iterative regression analysis. This is under the assumptions that (i) ΔV^vdw and ΔV^el in the data set show multivariate normality and low heteroscedasticity, (ii) there is similarity in the physio-chemical nature of the ligands and their interaction with the protein,^76,79 and (iii) the analysis leads to a single model.

Our machine learning workflow expands this automatic training approach with the aim of finding the a posteriori estimates for the α and β parameters of the iLIE equation (eq 3) for a set of compounds that maximizes the number of explained compounds in one or more LIE models within predefined RMSE and r² margins (RMSE ≤ 5 kJ mol^–1 and r² ≥ 0.6). The workflow (Figure 2) consists of a data curation and filtering stage to deal with assumption (i) (A in Figure 2), the main stochastic sampling routine using a Bayesian inference approach for parameter estimation (B), and a clustering stage where final LIE models are created (C). The latter two stages explore the existence of multiple (independent) models each describing a part of ligand physio-chemical/interaction space (assumptions (ii) and (iii)). The methods used in each of these stages are explained in more detail below.

Figure 2.

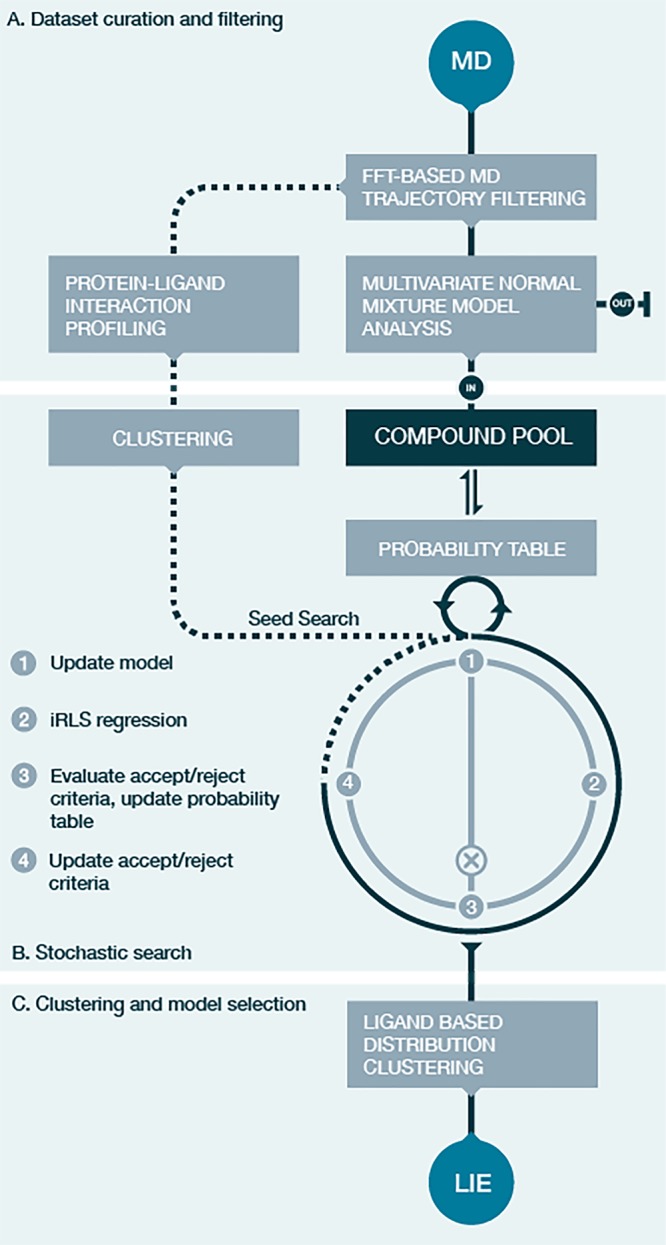
Schematic overview of the automated machine learning workflow aimed at finding the a posteriori estimates for one or multiple combinations of α and β parameters of the iLIE equation for a set of compounds, which maximize the number of explained compounds in one or more LIE models with predefined RMSE and r² cutoffs. The “data set curation and filtering” stage (A) uses FFT based MD trajectory filtering to obtain stable average values of ΔV^vdW and ΔV^el. Ligand poses with average ΔV^vdW/ΔV^el pairs outside a 97.5% confidence interval (Figure S2) identified using multivariate normal mixture model analysis are labeled as outlier (out). Protein–ligand interaction profiling is performed on the FFT based stable energy trajectories (dashed lines). Ligand groups identified by the clustering of the interaction profiles are used as input to the stochastic search (B). The existence of LIE models for these clusters is explored during an iterative four-step stochastic search in which compounds are added to the evolving model from the global compound pool, according to a progressively updated probability using the iRLS weights of the added compounds at every iteration. The charted model landscape is clustered during the last workflow stage (C) and final models are selected.

MD Trajectory Filtering

To enforce the independence of the multiple simulations performed per ligand,^78,80 average values ⟨V_lig–surr^el⟩_bound (,i) and ⟨V_lig–surr⟩_bound (,i) are used in eq 3 as obtained from segments of the interaction energy trajectories that are constant in time within a predefined cutoff. For that purpose, Fast Fourier Transform (FFT) filtering was carried out followed by spline fitting.⁸⁰ FFT smoothens the trajectory using a band-pass filter keeping the first 15 elements around the average in the frequency domain followed by inverse FFT to the original time domain (complex elements are discarded). Double spline fitting on the smoothened energy trajectory followed by gradient analysis identifies transitions when the absolute change in gradient is larger than 0.2 kJ mol^–1 ps^–1. The gradient was calculated using second-order central differences in the interior and first-order differences at the boundaries. For every protein–ligand MD simulation, the first continuous series of interaction energy data points with a minimum length of 100 ps is used in which both ⟨V_lig–surr^vdw⟩_bound and ⟨V_lig–surr⟩_bound do not show fluctuations (i.e., gradients) larger than the above given cutoff value. Simulations for which no such series could be identified were discarded from further analysis. This event occurred once for a total of 688 CYP19A1 MD simulations performed during this study.

Multivariate normal mixture model analysis deploying the expectation maximization algorithm^81,82 was used to identify (possibly multiple) normal distributed subpopulations in the dependent variables (ΔV_i^vdw, ΔV_i). We used the algorithm implemented in the sklearn.mixture Python library for this purpose with a “full” covariance type. Individual simulations were labeled as outlier and left out from further analysis if they have variable pairs outside a 97.5% confidence interval of the fitted χ²-distributions for all of the identified populations (out in Figure 2). When applicable, multiple subpopulations are treated as independent data sets in the remainder of the workflow.

Separation of Simulations

The use of multiple poses in iLIE to start short MD simulations allows the ligand to interact with the protein in multiple conformations. To guard the efficiency of the stochastic search when using multiple simulations per compound, a filtering step was performed based on an initial estimate of the α/β model parameter space by sampling a grid of predefined α/β parameters. This allowed to (i) discard results from simulations with low W_i representing poses unlikely to contribute to binding, and (ii) separate the combination of simulations with high W_i values in different regions of sampled α/β model parameter space into unique cases, to increase the chance for related cases to be grouped together in the same regression model. A square grid for the iLIE α and β model parameters was defined between a value of 0 and 1 with a grid spacing of 0.01. To compute ΔG_pred and the W_i values, the iLIE equation (eq 3) was evaluated at each grid point using all poses for a given ligand.

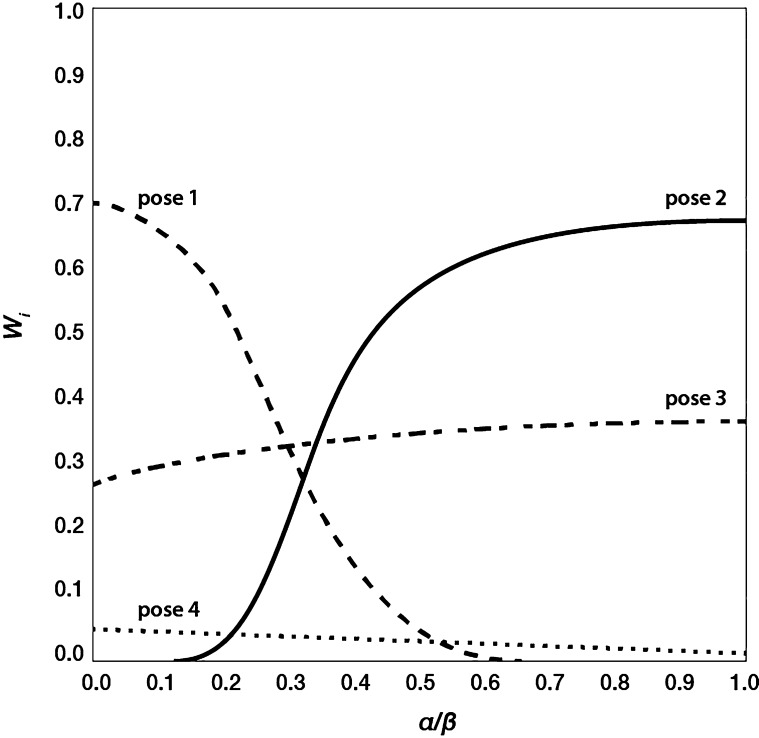
Minima in model parameter space were defined as regions in which the deviation of ΔG_pred from experiment is within ±5 kJ mol^–1 (1.2 kcal mol^–1), which equals about one pK_i log unit.⁵³ The propagation of the W_i’s for the independent simulations as a function of the model parameters in the defined region were analyzed and categorized as constant across minima or variable (illustrated in Figure 3). If in the latter case there was more than one simulation for which the gradient in W_i propagation is of opposite sign (Figure 3, poses 1 and 2), these are labeled as separate cases, together with a copy of the simulations of the same ligand for which W_i was identified to be constant with significant value (>0.1) across minima (Figure 3, pose 3). Simulations with W_i < 0.1 across minima were discarded for further analysis (Figure 3, pose 4). The separation of poses following this procedure was only used during the stochastic search.

Figure 3.

Propagation of weights W_i for four poses of a compound as a function of α or β model parameter, as obtained by solving the iLIE equation on a fixed grid of α and β parameters and focusing on the grid region where the difference between ΔG_pred and experimentally observed ΔG_obs is smaller than 5 kJ mol^–1.

Stochastic Sampling

A stochastic approach was used to assess a posteriori estimates for combinations of α and β parameters for clusters of compounds in the data set, which together maximize the number of explained compounds in a minimum number of LIE models with predefined RMSE and r² cutoffs. The stochastic search was seeded with subsets of compounds from every node in the hierarchical cluster tree obtained from protein–ligand interaction profile clustering (see the following). This approach increases the probability to identify predictive LIE models for compounds having similar protein–ligand interaction profiles. The compounds belonging to each node are first filtered for regression outliers according to the same protocol used during the stochastic search (step 3 in the following) to ensure that the start set is of maximum quality from a regression statistics point of view. Each stochastic search is an iterative process (Figure 2, middle pane) that consists of four steps:

• 1.Increase the current compound set by 20% with a random sample from the main compound pool according to probability p defined as the probability of a compound (c) to be part of a model as p = 1 – (|{c|c ∈ R}|/|R|). R is the set that maintains a counter of the number of times each ligand was labeled as outlier according to the maximum likelihood estimates (weights) of the iterative Reweighted Least Squares regression (iRLS) while iterating (step 3). The probability table is initiated with a probability of 1 for each ligand.
• 2.α and β model parameters for the new set of compounds are obtained from iRLS using ΔG_obs values for the compounds as dependent variable. Andrew’s Wave was used as maximum likelihood estimator.⁸³
• 3.Use the iRLS weights to determine regression outliers (<0.75) and inliers (≥0.75). Update the global table of outlier counts (R) for each compound and re-evaluate the probability table (p, step 1). Evaluate the model with respect to the ΔG_obs/pred RMSE and coefficient of determination r² and accept the model if statistics are within 10% deviation of the previous model and the α and β parameters are within the range 0 to 1.
• 4.If accepted, store the new model and start a new iteration until there are no more ligands to be added, statistics constraint limits are reached (5 kJ mol^–1 RMSE, 0.6 r²), or no successful ligand addition could be made during 50 consecutive trials.

Model Clustering

The stochastic sampling yields a collection of models describing the probability of ligands and individual poses to occur together with respect to the LIE model parameters and within the predefined statistical model quality. For every ligand in the data set, we collected the iRLS regression weights of the models in which the ligand occurs, normalized by the RMSE of the respective model and summed over individual poses. These values where visualized in a heat map by clustering them with respect to α and β model parameters, illustrating the distribution of ligands over LIE models. The heat map was used to visually select the ligand sets that maximize the number of explained compounds in one or more LIE models. The final models best representing the data set were trained using the iLIE equation (eq 3) with the ligand sets selected from the heat map. Representative simulations for each compound were selected by first training a model using all poses, after which we selected the simulations within a range of 0.2 of the most dominant simulation according to their weights W_i (eq 2). These simulations were used for retraining the final model.

Protein–Ligand Interaction Profiling

Protein–ligand interactions in all MD frames for all ligand poses were analyzed using in-house python software. The software aims to identify protein–ligand contacts as belonging to the following eight interaction types using rule-based protocols that are described in the Supporting Information: hydrogen bonded contacts (hb-ad, hb-da), water mediated hydrogen-bonded contacts (wb-da, wb-ad), halogen-bonded contacts (xb), salt bridging contacts (sb-np, sb-pn), cation-π interactions (pc), aromatic π- (ps) or T-stacking (ts), hydrophobic interactions (hf) and heme-coordination (hm, which is not explicitly accounted for during our classical simulations). Interaction subcategories include donor–acceptor (da), acceptor–donor (ad), negative–positive (np) and positive–negative (pn), for ligand and protein residue, respectively.

Relationships between the interaction profiles within pairs of MD simulations were evaluated by encoding the ligand-protein interaction profile data for each independent simulation as a structured key and by building a pairwise similarity matrix based on them using the following protocol:

• 1.Discard all protein–ligand interactions that occur for less than 10% of the simulation time, to reduce noise in further analysis due to infrequent interactions.
• 2.Normalize the frequency of occurrence of the interaction types by their relative abundance in the full data set, to prevent abundant hydrophobic interactions to have an artificially large influence on the final similarity metric.
• 3.Collect the unique protein residues involved in protein–ligand interactions from all filtered profiles after step 2.
• 4.
  Collect the resulting (sorted) residue numbers form the primary slots of the structured key. Each slot is divided in 2 × 12 registers subsequently containing:

  • a.
    The frequency with which any of the 12 interaction types (comprising the 8 main groups and their subcategories mentioned above) occur between the ligand and the given residue over the course of the simulation.
  • b.
    A list of ligand SYBYL atom types involved in the interaction in the corresponding first 12 registers (4a).
• 5.
  The similarity between two structured keys is evaluated as the sum of similarities between each register, normalized by key length (number of residues). The similarity is calculated differently for the two registry types mentioned in step 4:

  • a.
    For every residue interaction frequency (4a), the similarity is assigned 1 if they are identical, 0 if any of the registers equals 0, and the minimum frequency of occurrence otherwise.
  • b.
    Similarity is defined as the percentage of similarity in SYBYL atom types involved in the interaction (4b), multiplied by the frequency of occurrence of the corresponding type in the first 12 registers (4a). This multiplication ensures that the weight of similarity in SYBYL atom types for a given interaction type in the final similarity metric is never larger than that of the interaction type itself.

The resulting pairwise similarity matrix is used as input for a hierarchical agglomerative cluster analysis as implemented in the Python scipy.cluster.hierarchy(84) to identify groups of (independent) ligand simulations that show similar interaction profiles, which were used as seeds for the stochastic approach for iLIE model regression described above.

Results and Discussion

The 132 compounds in the data set (Tables S1 and S4 of the Supporting Information) were selected in a lead discovery study as promising AI candidates. The 12 steroid and 121 nonsteroid compounds can be classified as resembling the second to fourth generation of clinical AI’s (Figure 1) including Letrozole (compound 2), Anastrazole (compound 9) and Fadrozole (compound 13). All nonsteroid compounds have one azole ring of which the basic nitrogen atoms (mostly imidazole or triazole) have the potential to apically coordinate the heme iron.⁸⁵⁻⁸⁹ Most of them have an aryl or apolar cyclic moiety mimicking the steroid ring of the substrate, and one or two nitrile groups. Apart from these common features there is considerable structural diversity among the ligands with respect to the topological arrangement and chemical nature of the functional groups.

We initially attempted to train a single iLIE model for our data set of 132 compounds (using all docked poses and a 3/4 test-to-train set ratio), which resulted in models with negative r² values and RMSE values higher than 7.0 kJ mol^–1. Subsequent attempts to group compounds based on their molecular structures into iLIE binding affinity prediction models (i.e., based on SAI/NSAI compound groups or using structurally similar compounds derived from a chemical fingerprinting and clustering analysis) yielded local models with <10 ligands when using all ligand poses, leaving most of the data set unexplained. An initial estimate of optimum α/β parameter ranges was obtained by solving the iLIE equation for every ligand individually, taking into account all poses, on a grid of fixed α/β parameters. The range corresponding to a prediction error in ΔG_pred of less than 5 kJ mol^–1 for a maximum number of compounds is located in α and β ranges between 0 and 0.5 and 0.55–0.95, respectively, Figure 4. In this broad region, even the most densely populated area of model parameter combinations comprises no more than 50% of the ligands. Furthermore, 101 of the 132 ligands have at least two different dominant binding poses in different parts of this region based on the change in the distribution of weighted propensities W_i for the independent simulations. These observations illustrate the challenges mentioned before associated with LIE model development for diverse and large sets of training compounds with respect to their physicochemical variation, the possibility of ligands to bind in multiple orientations, and the unlikely existence of a single predictive model with sufficient coverage.

Figure 4.

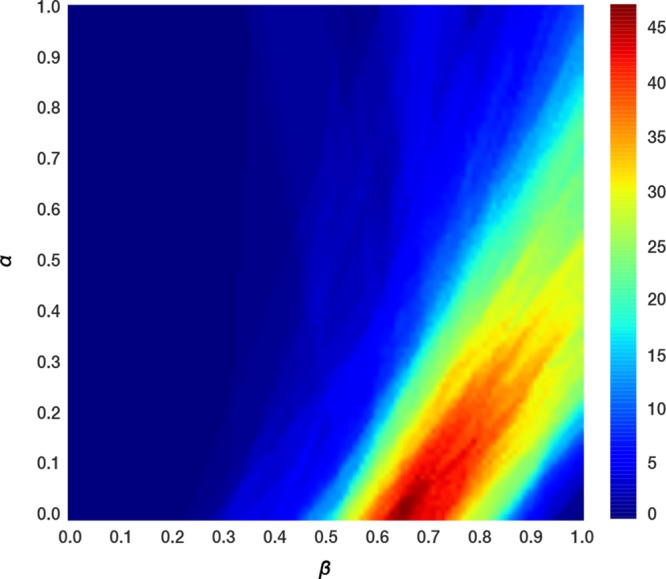
LIE α and β model parameter scan performed on each of the 132 ligands individually by solving the iLIE equation (eq 3), for every point on a square grid of α and β model parameters between a value of 0 and 1 with a grid spacing of 0.01. The color gradient highlights the percentage of ligands having a ΔG_pred value within 5 kJ mol^–1 of ΔG_obs for a given combination of α and β.

To explore the existence of a small subset of iLIE models that cover a substantially larger part of the data set and that have a well-defined protein–ligand interaction profile we developed a machine learning workflow using information extracted from the MD-trajectories only. The philosophy behind the method (see Methods section for details) is described below together with the results obtained after applying it to the data set of aromatase inhibitors.

Data Set Curation and Filtering

⟨V_lig–surr^el⟩ and ⟨V_lig–surr⟩ derived from the independent MD simulations used for iLIE are assumed to be averages over well-separated parts of the protein–ligand interaction energy surface.⁷⁸ Progressive changes in interaction energy values during a simulation may indicate an unstable system or a conformational transition of the ligand away from its initial position. As a remedy, constant interaction energy trajectories were obtained by filtering the MD energy trajectories for large fluctuations using a spline-fitting procedure on the FFT filtered time series.⁸⁰ Convergence of interaction energy terms is illustrated for a randomly picked subset of simulations in Figure S1 of the Supporting Information.

Subsequently, we performed a multivariate normal distribution analysis to identify possible multiple independent and/or partly overlapping normal distributed subpopulations in the dependent variables (i.e., ΔV^vdW and ΔV^el derived after FFT filtering, Tables S2 and S3). Using a 97.5% confidence interval, 18 protein–ligand simulations (29 without FFT filtering) were found to be not part of the single identified distribution (Figure S2, Supporting Information), which included all simulations for ligands 156 and 189. These two compounds were therefore not included in further analyses.

From Figure S2, detected outliers (which were left out from further analyses) involve among others the combinations of the ΔV values for compounds 156, and poses 2 of compounds 69 and 300, and pose 3 of compound 148. In these cases, the interaction profiles obtained from simulation indicated ligand interactions with protein residues located near the entrance channel to the catalytic cavity (between β-sheet 4 and helix F) instead of the protein residues and heme group located around the center of the catalytic cavity as defined for docking (see Methods section). Ligands 189 and 233 were found to interact with both regions. From the substantially different average energies and interaction profiles of the simulations involving these ligands, both can be labeled as outliers with respect to the simulations of other ligands in the data set and were left out from further analyses as well.

Stochastic Sampling

The stochastic sampling stage of our machine learning workflow (Methods section and Figure 2C) was initiated with the filtered and curated data set described above and seeded with ligand pose clusters derived from hierarchical clustering of the protein–ligand interaction profiles obtained from the MD trajectories (described in the following).

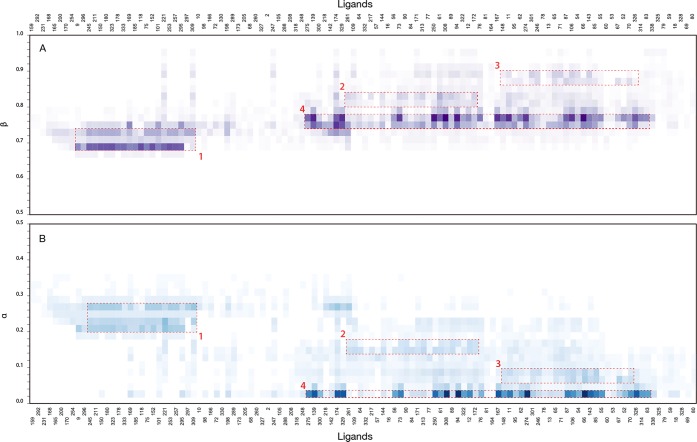
For the system considered, the full workflow is completed in ∼10 min on one core of a 4 core 2,2 GHz Intel Core i7 desktop machine. The results are visualized as a α and β heat map (Figure 5) showing clusters of ligands with an associated likelihood (color gradient) of constituting a model together for the respective combinations of sampled α and β model parameters. 12 of the 130 ligands used in the search (compounds 159, 166, 182, 194, 210, 220, 223, 232, 233 and 324) could not be placed in any model with a probability larger than 0.5 and are not shown in the heat maps. The ligand sets used to train the final representative models were visually selected based on the clusters in the heat map. This selection is the only manual step within our otherwise automated machine learning workflow.

Figure 5.

Results of the stochastic sampling of α and β model-parameter space for the data set of 132 CYP19A1 inhibitors. The likelihood for a compound (labeled by ID on the x-axis) to be part of a model in a given β (panel A) and α (panel B) range is shown as a heat map. The color gradient is a dimensionless measure of the likelihood calculated as the summed iRLS regression weights of a ligand in each of the sampled models of the stochastic search divided by the Root-Mean-Square Error (RMSE) of the model. The measure of likelihood is plotted as a function of the model α and β parameters with a bin size of 0.02. Regions of highest density used to train the final models are labeled as models 1 to 4 (red dashed rectangular boxes).

Selection of Representative LIE Binding Affinity Models Containing More Than 10 Compounds

The machine learning workflow sampled combinations of α/β model parameters that fall within the broad model-parameter region identified in the grid scan (Figure 4). The workflow identified four posterior distributions (clusters) with centers containing more than 10 components (Figure 5, red dashed rectangular boxes labeled 1 to 4). These four clusters served as training set for representative LIE binding affinity models (Table 1).

Table 1. Final Set of Representative LIE Binding Affinity Models Derived from the Stochastic Approximate Inference of Model Parameters for the Data Set of 132 Putative Aromatase Inhibitors^a.

Model	n	α	β	γ	RMSE	r2	q2LOO	SDEPLOO	r2bstr	RMSEbstr
1, center	16	0.203	0.663		1.30	0.95	0.94	1.47	0.960.01	1.100.17
1, center	16	0.200	0.627	–2.59	1.27	0.95	0.93	1.56	0.930.10	1.410.72
1, full	31	0.233	0.675		2.36	0.86	0.83	2.57	0.870.03	2.230.22
1, full	31	0.226	0.576	–7.32	2.11	0.89	0.85	2.41	0.890.04	1.980.23
2, center	13	0.161	0.796		1.69	0.89	0.82	2.14	0.900.03	1.540.28
2, center	13	0.162	0.830	2.45	1.69	0.89	0.78	2.38	0.900.03	1.480.32
2, full	52	0.107	0.748		2.59	0.76	0.76	2.59	0.730.03	2.710.10
2, full	52	0.101	0.696	–2.54	2.55	0.77	0.74	2.69	0.750.02	2.650.07
3, center	15	0.134	0.893		1.47	0.93	0.91	1.69	0.930.02	1.460.16
3, center	15	0.125	0.838	–3.23	1.42	0.93	0.86	2.11	0.940.05	1.300.12
3, full	31	0.108	0.868		1.68	0.92	0.91	1.80	0.920.02	1.620.17
3, full	31	0.110	0.877	0.495	1.68	0.92	0.90	1.89	0.920.02	1.660.11

^aModel statistics are reported for three representative LIE binding affinity models trained with and without γ parameter (kJ mol^–1) for ligands belonging to the full model cluster (full) and the cluster center only (center, within 75% confidence interval). Root-Mean-Square Error (RMSE, kJ mol^–1) and coefficient of determination (r²) model statistics are reported for the model, as well as for the bootstrap cross-validated model (bstr) and Leave-One-Out (LOO) cross-validated model (as Standard Error in Prediction (SDEP, kJ mol^–1) and cross-validated r² (q²)). Bootstrap cross validation was performed using a 20-fold random sampling with a training set of 75% of the model data set.

Model 1 with a cluster center of 16 ligands is able to account for a total of 31 ligands and shows little overlap with the other models in terms of α/β model parameter values. Cluster center 4 is able to account for 61% of the ligands not accounted for by model 1, with an r² of 0.75 and RMSE of 3.3 kJ mol^–1. Compared to cluster center 1, the ligands that are part of the area sampled by cluster center 4 show considerably more variation in the values for model parameters that can constitute a predictive model, in particular for α. With α close to 0, the predictive capacity of the model is mostly determined by the electrostatic component of the LIE equation. Furthermore, the dense population of ligands in cluster center 4 is predominantly determined by models with statistics in the less predictive half of the predefined RMSE and r² margins (with 0.6 ≤ r² < 0.8 and 3.0 < RMSE ≤ 5 kJ mol^–1).

However, the method did resolve two less populated clusters (Figure 5, cluster centers 2 and 3) that show little overlap but are contained within cluster 4. The models derived from these two centers have more favorable statistics than model 4 and together explain 95% of the ligands not explained by model 1. Model 2 and 3 cannot be combined without significantly worsening model statistics (r²= 0.59, RMSE = 3.5 kJ mol^–1 for the combined model, versus r² = 0.76, RMSE = 2.6 kJ mol^–1 and r² = 0.92, RMSE = 1.7 kJ mol^–1 for models 2 and 3, respectively; Table 1). Bootstrap analysis confirmed the two models to be derived from partly overlapping but distinct clusters (Figure S3, Supporting Information).

The relatively low values for γ when including an offset parameter (Table 1) indicates that the binding affinity can be modeled in terms of α and β only. Note that β values are higher than the theoretical value⁴³ of 0.5 and than the range of values previously reported for CYP LIE models (0.0–0.5),^{39−41,54,90} whereas α values are relatively low compared to the corresponding range of values (0.2–0.6),^{39−41,54,90}Table 1. The low α and high β values suggest that the binding represented by the models is mostly determined by electrostatic interactions.

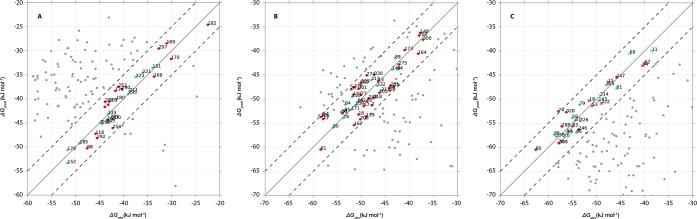
On the basis of the above, models 1, 2 and 3 were selected as representative models. Together, they cover 86% of the original data set with a RMSE between experimental and calculated binding free energy below 2.6 kJ mol^–1, which is well within the typical experimental error.⁵³ The LIE models are robust from a statistical point of view shown, e.g., by Leave-One-Out and bootstrap cross-validation, Table 1. Although presented as three separate models, there is overlap in the distributions they were derived from, in particular for models 2 and 3. This becomes evident from the ΔG_pred values and errors in prediction (Figure 6, Figure S4 Supporting Information) when making predictions for the same compound using each of the three models. The relationship is also reflected in the protein–ligand interaction profiles of the compounds used to train the models (see below).

Figure 6.

Correlation between the predicted (ΔG_pred) and observed (ΔG_obs) binding free energies in three models (panels A to C for models 1 to 3, respectively) that were trained using the results from stochastic sampling. The solid diagonal lines indicate ideal correlation and the dashed lines indicate upper and lower error margins of 5 kJ mol^–1. Blue filled circles correspond to compounds belonging to the cluster centers as indicated by the red boxes 1–3 in Figure 5, and red filled circles correspond to remaining compounds in that cluster, and gray filled circles correspond to the remaining compounds of the data set as predicted by the model. Blue and red filled crosses in panel C indicate low-affinity Fadrozole-like compounds.

Protein–Ligand Interaction Profiling

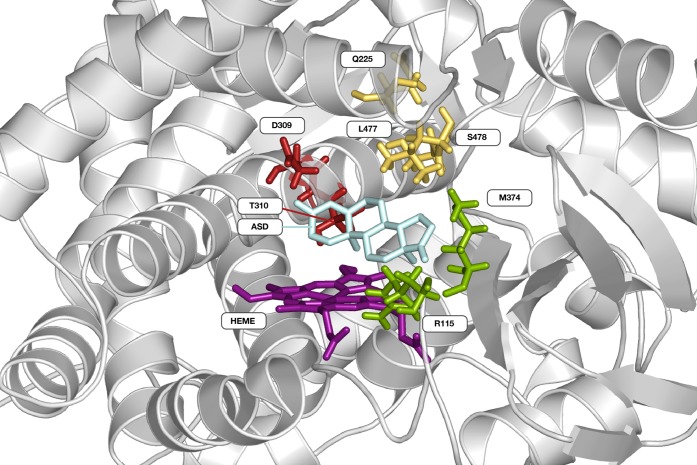
The classification of ligand-amino acid interactions occurring for more than 50% of the simulation time for all ligands identified 4 polar interaction sites (“hotspots”, Figure 7) comprising (i) R115 and M374; (ii) Q225; (iii) D309 and T310; and (iv) L477, S478 and the heme prosthetic group (497); and 3 apolar contact sites: (i) I133, F134; (ii) V370; and (iii) F221, W224. This particular combination between apolar and polar interaction sites has also been identified in previous crystallographic, mutagenesis and computational studies on CYP19A1.^{55,71,91−93} Below, we describe the dominant protein–ligand interactions observed in the simulations used for models 1–3 introduced above, starting with the dominant interactions for models 1 and 3, respectively.

Figure 7.

Cartoon representation of Cytochrome P450 19A1 (PDB code 3EQM(55)) with the natural substrate 4-androstene-3-17-dione (ASD, cyan stick representation) bound. Protein residues (stick representation) involved in polar protein–ligand interactions in more than 50% of the simulation time are grouped in four hotspots (indicated in red, yellow, green and purple), including the heme group (HEME).

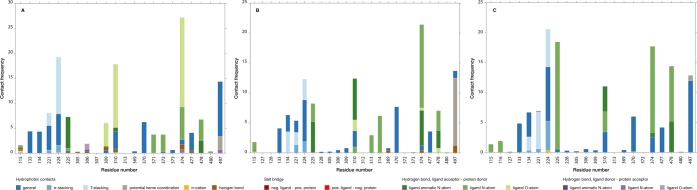
Model 1: The steroid based aromatase inhibitors, except ligand 210, form the basis of model 1. The starting poses for the simulations with highest W_i values for these ligands are similar to the natural substrate ASD with respect to binding orientation (i.e., as in the X-ray structure PDB ID 3EQM) and interaction profile,⁵⁵ cf. Figure S5 of the Supporting Information. Figure 8, panel A shows that hydrogen-bonded contacts dominate the polar interactions, between two carbonyl groups of the steroid (position A3 and D17) and residues M374 and D309 or T310, although not necessarily simultaneously. These findings are in line with previous biochemical studies on steroid binding to CYP19A1.⁹⁴⁻⁹⁶ Steroid 210 has a bulky trifluoride group hindering formation of both hydrogen bonds, resulting in a binding orientation similar to the natural substrate but resulting in a prediction error of 19.0 kJ mol^–1 by model 1. Interestingly, 82% of the NSAI ligands that are uniquely described by this model 1 form hydrogen-bonded interactions with M374 and/or D309/T310 as well (forming these interactions in on average 40% of simulation time). They predominantly do so using a carbonyl O atom or N atom acceptor part of a nitrile group and/or azole ring. In particular the presence of a nitrile group allows for simultaneous hydrogen-bond interactions with the aforementioned protein residues. In addition, there are hydrophobic contacts between residues F221 and W224 and aromatic or cyclic apolar ligand groups, and hydrogen bonding interactions with Q225 (Figure 8A). Figure 8 also illustrates that potential heme-coordinating poses of the NSAI ligands are observed less frequently in model 1 in comparison to the other two models.

Figure 8.

Protein–ligand interaction profiles for the compounds in models 1–3 (Table 1) derived from the stochastic approximate inference. The relative interaction frequencies for each protein residue–ligand interaction are represented by vertically stacked bars where the bar colors correspond to a specific interaction type as listed in the graph legend. Hydrophobic contact frequencies are divided by 10 because of their relative abundance with respect to the other classified interactions.

Model 2 and 3 exclusively contain NSAIs. The contact profiles include hydrogen-bonded interactions to the same residues of the protein as in model 1 but the hydrogen bond types and frequencies differ, Figure 8.

Model 3: Hydrogen bonding to residues Q225, M374 as well as S478 predominantly involves the (single) nitrile group of the compounds. The compounds almost exclusively contain imidazole groups of which the N atoms can be involved in hydrogen bonding to T310 and in heme coordination (cf. Figure 8).

22 of the 33 compounds have a Letrozole (Figure 1e) like topology with one imidazole group, one nitrile containing aryl group and a variable apolar moiety. This topology is complementary to the active site and enables contacts with various interaction hotspots simultaneously (Figure 8C). The Letrozole-like compounds can adopt multiple binding orientations due to rotational symmetry, thereby preserving interactions. This is confirmed by the finding that per ligand, several simulations contribute to the calculated binding free energy (Table S1, last column). The importance of interactions for the (predicted) affinity becomes apparent when comparing the compounds in model 3 in the low-affinity region of the correlation plot (Figure 6C, crosses) with those in the high-affinity region. The low-affinity compounds are almost exclusively Fadrozole (Figure 1b) like compounds with either an imidazole or imidazopyridine group that is unable to interact with as many hotspots simultaneously as the Letrozole-like compounds that are in the high-affinity region.

Model 2 shows more variation in the scaffold and functional groups of the compounds included when compared to model 3. Differences are the presence of halogens, carbonyl and hydroxyl groups in model 2 compounds and the replacement of the imidazole by a triazole group, the replacement of the variable apolar moiety by an aryl or thiophene group, and the replacement of a nitrile group by a halogen or keto group. Although the compounds belonging to the cluster center of model 2 are unique to it from a statistical point of view (in terms of α/β combination and other model statistics, Table 1 and Figure S3, Supporting Information), the compounds of the model that are under- and overpredicted are more model 3- and model 1-like, respectively, in terms of topology (Table S1) and interaction profile. As such, model 2 positions itself in between model 1 and 3 as shown by the interaction profile (Figure 8B) and model statistics (Table 1).

In conclusion, the interaction profiles of the MD trajectories provide a basis for understanding and establishing the applicability domain of the resolved models in terms of observed protein–ligand interactions. These differences in interactions can explain why similar compounds fall into different models. For example, compounds 333, 318 and 246 only differ by small variation in their benzylic para-substituent but they are part of models 1, 2 and 3, respectively (Table S1). The p-acetylated compound 318 was found to contribute to model 2 with four different binding poses and accordingly it interacted with a variety of protein residues. In contrast, the slightly larger compound 333 and the nitril containing compound 246 only contributed with a single pose, which mutually differed in terms of binding orientation and interacting residues (310 for compound 246 vs 115 and 309 for compound 333). As another example, a Cl-substituted letrozole analogue (compound 139) contributed to model 2, with its poses differing from the pose that contributed most (to model 1) and that showed the F- and Br-substituents of counterpart compounds 200 and 98 on a distance from methionine 374 suited for halogen-bonding interactions, Table S1.

We note that MD sampling was found to be necessary for the purpose of establishing applicability domains: when performing interaction profiling based on the docked MD starting conformations only, we could, e.g., not classify interaction profiles for models 2 and 3. Despite the diversity in the data set, our machine-learning workflow was successful in grouping together compounds with a steroid scaffold in model 1 and compounds with a Letrozole like topology composed out of an imidazole group, one nitrile containing aryl group, and a variable apolar moiety in model 3. In addition, other compounds present in these models that do not share the same topology show similar interaction profiles in terms of interaction hotspots. These structural characteristics and corresponding interaction profile define the applicability domain for models 1 and 3, which is beneficial for developing predictive LIE models as illustrated by their good model statistics. In contrast, model 2 is more diverse with topologically similar compounds being represented by small subsets (≤5) of compounds. The key protein residues interacting with the compounds comprised in model 2 are the same as for model 3. This could explain e.g. why compounds 78 and 80 fall in models 2 and 3, respectively (Table S1). However, the type of hydrogen-bond acceptors is different (Figure 8), which positions model 2 in between model 1 and 3 in terms of LIE parameters. The diversity in molecular structures covered by the three models is illustrated by a selection of compounds from the models as presented in Figure S6 of the Supporting Information.

Protein–ligand interaction profile results illustrate that the number and type of polar protein–ligand interactions are determinative for the LIE empirical parameters and that the variation in the data set results in a system of three overlapping but distinct models rather than one global model. The importance of polar contacts is shown by the consistent value for α between 0.10 and 0.24 as frequently reported before^79,97,98 and a β value as a function of the ligand functional groups^97,98 rather than the theoretical value of 0.5.⁴³ With values markedly larger than 0.5, the ligand functional group dependent value for β found in this study are different than those previously proposed for other systems,^97,98 which may well be due to choices in the force field and system set up⁸⁰ and which is in line with spread in LIE parameters previously reported among a variety of other CYPs.^39−41,54

All nonsteroidal ligands have one azole ring of which the basic nitrogen atoms have the potential to apically coordinate the heme iron. Despite the inability of commonly used force fields to accurately account for the energetics of heme coordination, a considerable number of compounds in model 2 and 3 adopted a potential coordinating pose during simulation based on interaction profile data (Figure 8, gray bars).

Conclusions

In this work, we present binding affinity prediction models for steroidal and nonsteroidal inhibitors of CYP19A1 aromatase using our automated LIE workflow.^39,54,64 The data set of 132 compounds used for training LIE models was acquired from a lead discovery study and poses challenges to the calibration of empirical free energy models because of the sparsity of and large structural diversity within the data set and due to the catalytic site malleability and the substrate and interaction promiscuity of the CYP protein. Nevertheless, it is a data set representative for training of LIE or other models in industrial or other applied settings. In spirit of our automated iLIE approach, we developed an automated machine learning workflow aimed at exploring the model parameter landscape and at maximizing the number of data set compounds explained in one or few LIE models. The method was successful in accounting for 86% of the data set in 3 models showing high correlation between calculated and observed values for binding free energy (r² of 0.86, 0.76, 0.92; RMSE of 2.36, 2.59, 1.68 kJ mol^–1 for the three models, respectively). The use of a maximum likelihood estimator and Bayesian inference maximize the chance of identifying posterior predictive distributions describing the data set and limiting the chance of overfitting of the LIE models. The robustness of the models is illustrated by small variations after bootstrap analysis (segmentation cross validation) and by good leave-one-out cross validation statistics (q²_LOO of 0.83, 0.73, 0.92; SDEP_LOO of 2.57, 2.59, 1.80 kJ mol^–1, respectively). The ligand clusters leading to the final set of models are visually selected from the heat map (Figure 5). In a future iteration of the software we aim to also automate this final step of our workflow, thereby completing its automation.

The resolved clusters, from which the three models were derived separate the data set into a SAI model and two NSAI models that have distinct α and β model parameters. With respect to polar interactions, compounds in model 1 predominantly interact with D309/T310 and/or M374 by hydrogen-bonded interactions with carbonyl oxygens as ligand acceptors, which is common for steroids interacting with CYP19A1.^{55,71,94−96} On the other hand, compounds in model 3 interact with Q225, M374 and S478 via hydrogen bonding involving the nitrile nitrogen, and with T310 by hydrogen bonding via an imidazole N atom. Rotationally symmetric binding conformations of these compounds that preserve the overall interaction profile are frequently included in the binding affinity prediction. This underlines the flexible nature of the CYP19A1 catalytic cavity and the ability of the iLIE approach to account for this.

Using our machine learning workflow, we have been able to calibrate LIE binding affinity prediction models with a protein–ligand interaction based applicability domain that explains 86% of the data set using experimental affinity data and information extracted from MD only. The detailed structure and interaction based applicability domain provides a frame of reference for the user to determine if a model, and which model, can be used for binding affinity prediction of a novel compound based on the protein–ligand interaction profile and provides an estimate of the reliability of the prediction. The automated nature of the workflow allows it to be used together with our automated iLIE workflow, together creating a pipeline to apply LIE in high-throughput settings.

Glossary

Abbreviations:

AI

Aromatase Inhibitor

ASD

4-Androstene-3-17-dione

ATB

Automated Topology Builder

CYP

Cytochrome P450

DDI

Drug–Drug Interaction

FEP

Free Energy Perturbation

iRLS

Iteratively Reweighted Least Squares

LIE

Linear Interaction Energy

MD

Molecular Dynamics

NSAI

Non-Steroidal Aromatase Inhibitor

QSAR

Quantitative Structure–Activity Relationship

RMSD

Root-Mean-Square Deviation (in atomic positions)

RMSE

Root-Mean-Square Error

TI

Thermodynamic Integration

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jcim.7b00222.

• Description of the rule based protocol for resolving 8 types of protein–ligand interactions used for the interaction profiling analysis described in this work, a selection of time series of V_lig–surr^el and V_lig–surr (Figure S1), multivariate normal distribution analysis of ΔV^vdW and ΔV^el energy values (Figure S2), bootstrap cross-validation results for the combined model 2 and 3 (Figure S3), ΔG_pred error values (residuals) for each compound when compared to experiment and when calculated using model 1, 2 or 3 (Figure S4), stick representation of the dominant binding pose of 10 steroidal aromatase inhibitors explained by LIE binding affinity prediction model 1 (Figure S5), molecular structures of compounds in models 1, 2 and 3 (Figure S6), data set of 132 putative aromatase inhibitors with experimentally determined inhibition constants, provided by Bayer AG (Table S1), averaged difference in the Coulomb component of the nonbonded protein–ligand interaction energy for up to 8 selected docking poses for the data set of 132 putative aromatase inhibitors (Table S2), averaged difference in the van der Waals component of the nonbonded protein–ligand interaction energy for up to 8 selected docking poses for the data set of 132 putative aromatase inhibitors (Table S3) (PDF)

• Excel spreadsheet containing data from Table S1 together with the canonical SMILES string for all ligands (Table S4) (XLSX)

The authors declare no competing financial interest.