Statistical Analysis on the Performance of Molecular Mechanics Poisson–Boltzmann Surface Area versus Absolute Binding Free Energy Calculations: Bromodomains as a Case Study

Abstract

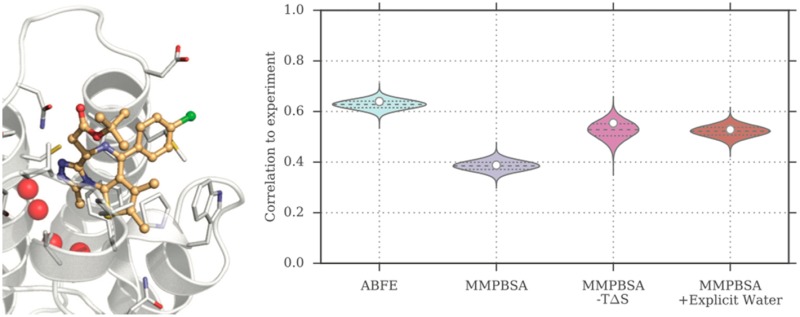
Binding free energy calculations that make use of alchemical pathways are becoming increasingly feasible thanks to advances in hardware and algorithms. Although relative binding free energy (RBFE) calculations are starting to find widespread use, absolute binding free energy (ABFE) calculations are still being explored mainly in academic settings due to the high computational requirements and still uncertain predictive value. However, in some drug design scenarios, RBFE calculations are not applicable and ABFE calculations could provide an alternative. Computationally cheaper end-point calculations in implicit solvent, such as molecular mechanics Poisson–Boltzmann surface area (MMPBSA) calculations, could too be used if one is primarily interested in a relative ranking of affinities. Here, we compare MMPBSA calculations to previously performed absolute alchemical free energy calculations in their ability to correlate with experimental binding free energies for three sets of bromodomain–inhibitor pairs. Different MMPBSA approaches have been considered, including a standard single-trajectory protocol, a protocol that includes a binding entropy estimate, and protocols that take into account the ligand hydration shell. Despite the improvements observed with the latter two MMPBSA approaches, ABFE calculations were found to be overall superior in obtaining correlation with experimental affinities for the test cases considered. A difference in weighted average Pearson (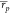) and Spearman (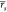) correlations of 0.25 and 0.31 was observed when using a standard single-trajectory MMPBSA setup (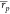 = 0.64 and 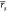= 0.66 for ABFE; 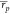= 0.39 and 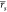= 0.35 for MMPBSA). The best performing MMPBSA protocols returned weighted average Pearson and Spearman correlations that were about 0.1 inferior to ABFE calculations: 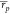= 0.55 and 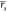= 0.56 when including an entropy estimate, and 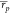= 0.53 and 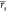= 0.55 when including explicit water molecules. Overall, the study suggests that ABFE calculations are indeed the more accurate approach, yet there is also value in MMPBSA calculations considering the lower compute requirements, and if agreement to experimental affinities in absolute terms is not of interest. Moreover, for the specific protein–ligand systems considered in this study, we find that including an explicit ligand hydration shell or a binding entropy estimate in the MMPBSA calculations resulted in significant performance improvements at a negligible computational cost.

Introduction

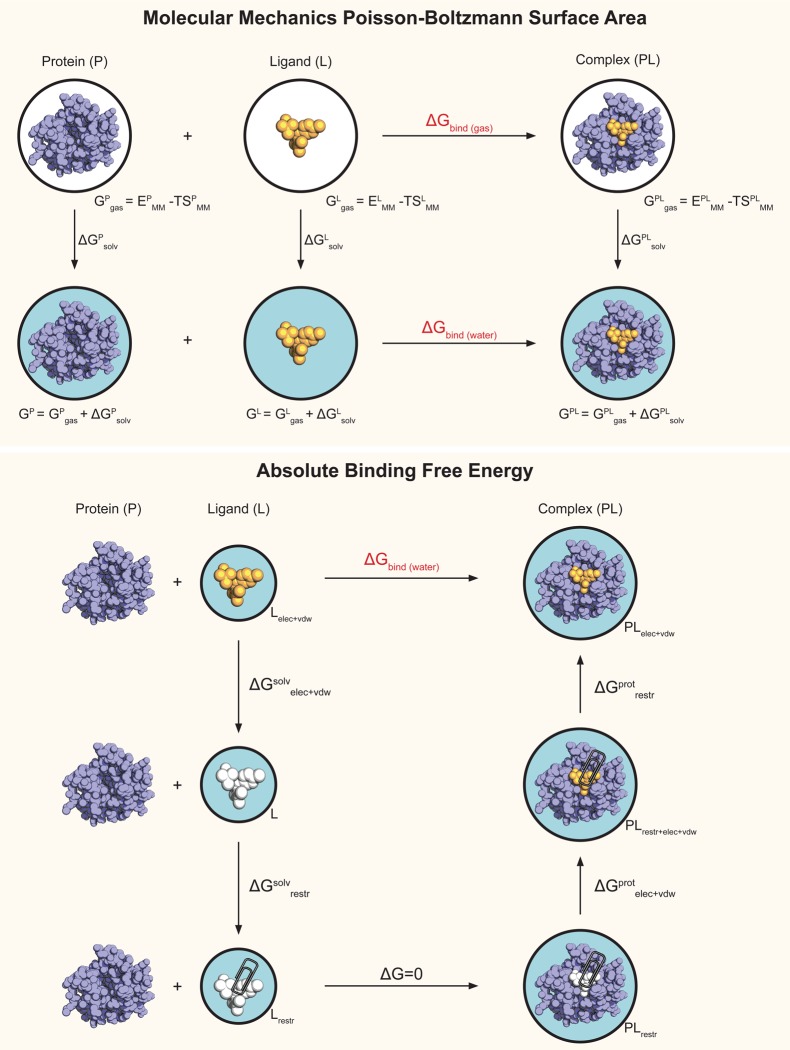
Binding affinity predictions that make use of molecular dynamics (MD) simulations are becoming increasingly popular as the computational cost of such calculations keeps decreasing thanks to continuous advances in hardware and algorithms.^1,2 Among these approaches are end-point methods,^3,4 such as the molecular mechanics Poisson–Boltzmann surface area (MMPBSA) method,^5,6 which are based on the postprocessing in implicit solvent of a number of frames extracted from a MD simulation. With MMPBSA, a binding energy estimate can be obtained from a single simulation of the protein–ligand complex, or from separate simulations of the complex as well as the free ligand and protein in solution.^5,7 A binding free energy estimate may also be obtained by calculating the entropic contribution to the reaction. Other approaches for the estimate of binding affinity include pathway methods, in which multiple simulations are used to calculate the free energy along the path that connects the two thermodynamic states of interest, the ligand in its bound and unbound states.⁸⁻¹³ The path can be physical with, for instance, the intermediate states being the ligand at different distances from the binding pocket, but it can also be nonphysical, as in alchemical free energy calculations where in the intermediate states the ligand is coupled to the rest of the system in various ways. Figure 1 provides an overview of the thermodynamic cycles and the terms involved in both MMPBSA and alchemical absolute binding free energy (ABFE) calculations. Pathway methods, including alchemical free energy calculations, are theoretically rigorous and generally perceived as more accurate than end-point methods; however, they also are computationally much more expensive.¹⁴ Although rigorous free energy calculations have a smaller number of empirical constants⁵ to be adjusted in a system-dependent fashion as compared to MMPBSA, currently they also tend to have a less automated and more complex setup, and a number of potential pitfalls.^15,16 Choosing which approach to employ for a specific system and problem at hand can therefore be difficult, as one has to consider whether the additional human and computational cost will be rewarded by a more accurate result.

Figure 1.

Overview of the thermodynamic cycles used in MMPBSA and ABFE calculations. A white background indicates a system being in a vacuum, and a light blue background indicates a systems being in aqueous solution. An orange ligand indicates it is fully interacting with the environment, whereas a white ligand indicates it is not interacting with the environment (decoupled state). In the ABFE cycle, a paper clip indicates the presence of restraints.

Although many notable studies on the performance of end-point approaches are present in the literature,¹⁷⁻²⁴ only a few have compared them to more rigorous pathway approaches and, to our knowledge, none to ABFE calculations. Genheden et al.²⁵ calculated the relative binding free energy (RBFE) of nine inhibitors binding to factor Xa with thermodynamic integration (TI) and molecular mechanics Generalized Born surface area (MMGBSA), concluding that MMGBSA provided overall slightly better agreement to experiment than TI, although the correlation coefficient was poor in both cases (r² = 0.2–0.3) and the performance of TI was negatively affected by an alchemical transformation involving a net-charge change of the system.²⁶ Wang et al.²⁷ have compared the performance of RBFE calculations to MMGBSA for a set of 6 cyclin-dependent kinase 2 (CDK2) ligands, reporting the higher performance of the alchemical RBFE approach. Homeyer et al.²⁸ evaluated the performance of MMPBSA, linear interaction energy (LIE) and TI for three sets of 25, 29, and 29 ligands binding to, respectively, factor Xa, CDK2, and the mineralcorticoid receptor. The performance observed was dependent on the details of the protocol used and the subsets considered; nevertheless, the authors concluded that both MMPBSA and TI could provide valuable predictions when taking into account certain data set-specific features, contrary to LIE. The Pearson correlation coefficients ranged from 0.00 to 0.62 for MMPBSA, and from 0.02 to 0.58 for TI. Recently, Wang et al.²⁹ performed a large retrospective test of RBFE calculations encompassing 199 ligands and 8 protein systems, where the resulting weighted average correlation coefficient for the calculations was 0.75, whereas it was found to be 0.35 for their MMGBSA protocol. A similar study evaluated the performance of the same free energy protocol and MMGBSA calculations on 96 fragments targeting 8 proteins, reporting a weighted average correlation of 0.65 for the alchemical pathway and of 0.41 for the end-point approach.³⁰ All these studies evaluated the performance of the methods in ranking the affinities of series of chemically similar ligands. However, there are scenarios where it would be beneficial to be able to rank any ligand–protein pair, independently of the similarity of the ligands within the set. At the lead discovery stage, one might want to rank sets of very different ligands; if a crystal structure of the complex is not available, it would be useful to accurately rescore docking poses in order to identify the most likely orientation of the ligand; if selectivity (or promiscuity) is of interest, one might want to predict the affinity of the ligand for multiple protein targets. Despite the challenges of such applications, they can in principle be tackled by end-point methods such as MMPBSA, which can approximate the binding energy or free energy, and ABFE calculations (Figure 1). However, to our knowledge, the performance of these two methodologies in drug discovery scenarios has not been directly compared yet. The more rigorous calculations tend to be perceived as more accurate; however, this hypothesis, despite reasonable, does not appear to having been supported by instances in the literature yet. Even though more rigorous methods should return a better performance in theory, this is not necessarily the case in practice. In fact, for end-point methods it has often been observed how theoretically less rigorous approaches (such as the use of a single rather than separate trajectories, the neglect of the entropic term, or the use of the Generalized Born model) returned more precise calculations that also showed better correlation with experiment.^{5,19,23,31−33}

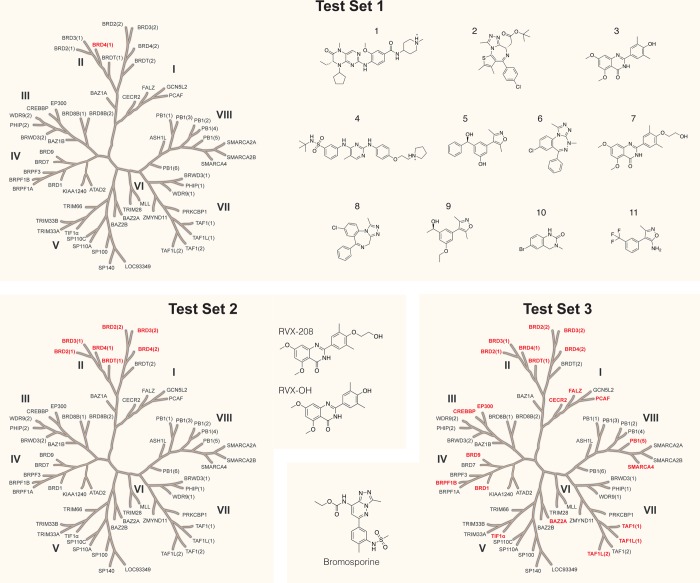
Recently, we reported on the performance of ABFE calculations for the prediction of the binding affinity of 11 ligands binding to the first bromodomain of bromodomain-containing protein 4 (BRD4(1)) (Figure 2, test set 1), both when using the structures of the protein–ligand complexes and when docking the ligands into an apo structure.³⁴ We also investigated the ability of ABFE calculations to predict the selectivity profile of two similar compounds binding to the bromodomain and extra-terminal (BET) family of bromodomains (BRDs) (Figure 2, test set 2), and that of a broad-spectrum inhibitor binding to 22 different BRDs (Figure 2, test set 3).³⁵ Here, we evaluate the performance of MMPBSA on the same test sets, thus being able to directly compare its performance to the alchemical ABFE approach. The following four test cases, based on the three test sets in Figure 2, were thus considered: (1a) prediction of the affinities of 11 diverse (i.e., not a chemical series) ligands binding to BRD4(1), assuming knowledge of their holo crystal structures;³⁴ (1b) prediction of the affinities of 11 diverse ligands binding to BRD4(1), after ranking their poses as returned by docking into an apo structure of the protein;³⁴ (2) prediction of the different selectivity profiles of RVX-OH and the closely related RVX-208 for 7 BET BRDs;³⁵ (3) prediction of the selectivity profile of bromosporine, a broad-spectrum BRD inhibitor, for 22 different BRDs.³⁵ This amounts to a total of 47 experimental affinities, primarily measured by isothermal titration calorimetry (ITC), across all test cases. A summary of these four test cases is in Table 1, with a more detailed description in Table S1.

Figure 2.

Overview of the proteins and ligands considered in this study. Three test sets were considered: test set 1 contains 11 different ligands binding to one specific protein; test set 3 contains one ligand binding to 22 different proteins; test set 2 sits in the middle, with two ligands binding to seven proteins. From test set 1, two test cases originate: one that uses the X-ray structures of the protein–ligand complexes (test case 1a) for the simulations, and one that uses ligand poses docked into an apo X-ray structure of the protein (test case 1b). Table S1 summarizes this information in table format.

Table 1. Summary of the Four Test Cases Considered in This Study^a.

Test Case No.	No. Ligands	No. Proteins	No. Complexes	Starting Structures	Simulations length
1a	11	1	11	X-ray	10 ns
1b	11	1	11	Docking	10 ns
2	2	7	14	Docking	15 ns
3	1	22	22	Docking	15 ns

^aTable S1 provides more detailed information on the systems studied.

Here, we focus on the ability of the calculations to correlate with experimental affinity values as measured by the Pearson and Spearman correlation coefficients. The ability of end-point methods to reproduce absolute affinity values is generally acknowledged to be poor, and when using these methods one is usually interested in the relative ranking of the values returned. We will, however, briefly comment on the performance of the two methods in this respect too. The MD trajectories used for the MMPBSA calculations were the same that had been used for the alchemical free energy calculations. Therefore, the same force field parameters for protein and ligands were employed and both calculations used the same ensemble, so that potential issues relating to sampling or the accuracy of the physical model would affect both calculations in a way that does not impair a fair comparison of the approaches. In the scenario of a perfectly accurate physical representation of the chemical systems and infinite sampling, the better performance of rigorous calculations as compared to MMPBSA would be the consequence of the approximations of the end-point method. However, given limited sampling of protein and ligand conformations, and inaccuracies in the force fields, it is not to be excluded that the approximations in MMPBSA might result in the cancellation or reduction of errors and eventually better correlation with experimental values.

In the first instance, a standard single-trajectory MMPBSA protocol was adopted, neglecting the solute entropic contribution. This contribution is typically estimated through quasi-harmonic or normal-mode analysis.^5,36 However, this term is often disregarded, as the full sampling of the free energy landscape required by these approaches is computationally demanding and the benefits of including the term are controversial.^{21,31−33,37,38} Nonetheless, Duan et al.³⁹ have recently proposed a computationally simple and efficient approach for the estimation of the binding entropy based on the fluctuations of protein–ligand interaction energies. It was therefore decided to evaluate the effect of including this term on the performance of the calculations. In addition, a number of studies have suggested that the inclusion of an explicit hydration shell during the calculations may lead to improved agreement with experiment.^33,40−43 As BRDs are furthermore known to contain structural waters in their cavity, bridging the binding of their inhibitors, we decided to test this approach as well. Thus, in this study, we compared the predictive ability (in terms of correlation) of ABFE calculations to that of (a) a standard single-trajectory MMPBSA protocol, (b) a protocol that includes an estimate of the entropic term, and (c) protocols that include an explicit ligand hydration shell of different size. Overall, as measured by the weighted average Pearson and Spearman correlation coefficients, and for the systems considered, it was observed that ABFE calculations provided a better performance than any of the MMPBSA protocols tested. In particular, ABFE calculations returned Pearson and Spearman correlations that were, respectively, 0.25 and 0.31 higher than the standard MMPBSA protocol, and ∼0.1 higher than the best performing MMPBSA protocols (Table 2), which involved either an estimate of the entropic term or the inclusion of an explicit ligand hydration shell.

Table 2. Overview of the Results Obtained with ABFE and MMPBSA Calculations, in Terms of Pearson and Spearman Correlation to Experimental Binding Free Energies^a.

Pearson Correlation
Test Case No.	Weight	ABFE	W0	W0e	W10	W20	W30	W40	W50
1a	5.5	0.87 [0.73, 0.92]	0.71 [0.61, 0.76]	0.73 [0.31, 0.85]	0.77 [0.62, 0.86]	0.82 [0.75, 0.86]	0.83 [0.79, 0.87]	0.83 [0.79, 0.86]	0.83 [0.79, 0.86]
1b	5.5	0.78 [0.67, 0.84]	0.79 [0.75, 0.82]	0.67 [0.56, 0.76]	0.89 [0.85, 0.91]	0.90 [0.86, 0.92]	0.88 [0.85, 0.91]	0.87 [0.83, 0.89]	0.86 [0.83, 0.89]
2	14	0.75 [0.67, 0.80]	0.05 [−0.06, 0.17]	0.63 [0.46, 0.72]	0.44 [0.32, 0.54]	0.50 [0.37, 0.60]	0.10 [−0.05, 0.25]	–0.14 [−0.29, 0.01]	–0.23 [−0.37, −0.08]
3	22	0.48 [0.41, 0.53]	0.42 [0.38, 0.46]	0.43 [0.31, 0.51]	0.36 [0.30, 0.43]	0.38 [0.32, 0.44]	0.39 [0.34, 0.44]	0.35 [0.30, 0.40]	0.34 [0.29, 0.39]
Weighted Average		0.64 [0.56, 0.69]	0.39 [0.32, 0.45]	0.55 [0.39, 0.64]	0.50 [0.41, 0.57]	0.53 [0.45, 0.59]	0.42 [0.34, 0.49]	0.32 [0.24, 0.39]	0.29 [0.21, 0.36]

Spearman Correlation
Test Case No.	Weight	ABFE	W0	W0e	W10	W20	W30	W40	W50
1a	5.5	0.85 [0.69, 0.94]	0.72 [0.62, 0.83]	0.61 [0.17, 0.82]	0.57 [0.50, 0.82]	0.77 [0.67, 0.85]	0.83 [0.74, 0.86]	0.83 [0.74, 0.85]	0.79 [0.73, 0.85]
1b	5.5	0.78 [0.55, 0.85]	0.79 [0.72, 0.85]	0.75 [0.47, 0.82]	0.79 [0.75, 0.85]	0.85 [0.78, 0.89]	0.85 [0.77, 0.87]	0.83 [0.75, 0.85]	0.83 [0.75, 0.85]
2	14	0.78 [0.64, 0.85]	–0.05 [−0.15, 0.20]	0.57 [0.38, 0.74]	0.31 [0.24, 0.53]	0.46 [0.25, 0.60]	0.11 [−0.06, 0.36]	0.02 [−0.19, 0.23]	–0.05 [−0.28, 0.18]
3	22	0.50 [0.41, 0.62]	0.41 [0.36, 0.52]	0.50 [0.35, 0.61]	0.48 [0.40, 0.59]	0.48 [0.37, 0.56]	0.48 [0.40, 0.57]	0.45 [0.35, 0.53]	0.41 [0.34, 0.51]
Weighted Average		0.66 [0.53, 0.75]	0.35 [0.28, 0.50]	0.56 [0.35, 0.70]	0.48 [0.40, 0.63]	0.55 [0.42, 0.64]	0.45 [0.35, 0.58]	0.41 [0.28, 0.52]	0.37 [0.25, 0.49]

^aIn square brackets are the 95% confidence intervals of the statistics. W0 refers to the single-trajectory MMPBSA protocol that did not include a binding entropy estimate or explicit water molecules; W0e refers to the protocol that included a binding entropy estimate (but no explicit water molecules); W10 to W50 refer to the protocols that included an explicit ligand hydration shell composed of 10 to 50 water molecules (but no binding entropy estimate).

Methods

Molecular Dynamics Simulations

The MD trajectories for the protein–ligand complexes considered here have been taken from two previous studies that focused on the performance of absolute binding free energy calculations.^34,35 The details of the systems setup and the free energy calculations are reported in the respective publications.^34,35Table S1 summarizes all proteins and ligands considered, the Protein Data Bank (PDB) structures used, the number of docking poses considered for each ligand (when applicable), and the references for the experimental affinity values.

From the multiwindow free energy calculations, the simulation of the protein–ligand complex at λ = 0, where the ligand is unrestrained and fully coupled to the system, were taken for the MMPBSA calculations. Each simulation was either 10 or 15 ns long, and was performed starting from either a crystal pose or docking pose as reported in Table 1. All simulations were carried out using Gromacs 4.6 or 5.0.⁴⁴⁻⁴⁶ The solvated protein–ligand systems were energy minimized with a steepest descent algorithm for 10 000 steps. The systems were then simulated for 0.5 ns in the canonical ensemble with harmonic position restraints applied to the solute heavy atoms with a force constant of 1000 kJ mol^–1 nm^–2. Temperature was coupled using Langevin dynamics^47,48 with 298.15 K as the reference temperature. A 1 ns position restrained run in the isothermal–isobaric ensemble was then performed using the Berendsen weak coupling algorithm.⁴⁹ 10 or 15 ns unrestrained production runs (as reported in Table 1 and previous publications) were finally performed using Hamiltonian-exchange⁵⁰ Langevin dynamics with a 2 fs time-step in the NPT ensemble with the Parrinello–Rahman pressure coupling scheme.⁵¹ The particle mesh Ewald (PME) algorithm⁵² was used for electrostatic interactions with a real space cutoff of 12 Å, a spline order of 6, a relative tolerance of 10^–6 and a Fourier spacing of 1.0 Å. The length of covalent bonds to hydrogen atoms was constrained using the P-LINCS algorithm.⁵³ Swaps attempts between any state pair along the alchemical pathway were allowed every 1000 time steps. The resulting trajectory at λ = 0, used for the MMPBSA calculations, is thus different from the trajectory one would normally obtain from a standard MD simulation. It may be thought as being composed of many short simulations of variable length and starting from different structures, rather than being a single linear trajectory. For all test cases, a single MD simulation was performed and used for the prediction of each protein–ligand affinity, except for test case 1a, for which three separate simulations were performed.

MMPBSA Calculations

All MMPBSA calculations were performed using the set of scripts provided with GMXPBSA 2.1.1.⁵⁴ Protein–ligand conformations were extracted from the MD simulation every 20 ps, from 5 to 15 ns, for a total of 501 snapshots, for the calculations with 15 ns windows. For the free energy calculations that employed 10 ns windows, conformations were extracted from 2 to 10 ns every 16 ps, for same number of total snapshots. To evaluate the effect of including explicit waters, we repeated the calculations on the same frames while retaining the N closest water molecules to the ligand, where N = [10, 20, 30, 40, 50], similarly to what was done by Maffucci and Contini.⁴² The MD trajectories were processed with the Python library MDAnalysis(55) in order to extract the N water molecules closest to any atom in the ligand for each of the 501 frames. During the MMPBSA calculations, the explicit water molecules were considered as being part of the protein.

Although a more extensive explanation of the terms involved in MMPBSA calculations can be found elsewhere,^5,36,56,57 we provide a brief summary here:

1

2

3

4

where G_x is the free energy of system x, that being the ligand, the protein, or the complex; E_MM is the potential energy in vacuum as defined by the molecular mechanics (MM) model, which is composed of the bonded energy terms (E_bonded) and nonbonded Coulombic (E_coul) and Lennard-Jones (E_LJ) terms; S_MM is the entropy; ΔG_solv is the free energy of solvation, composed by a polar (G_polar) and nonpolar (G_nonpolar) term; T is the temperature and angle brackets represent an ensemble average. Molecular mechanics energies for E_LJ were calculated with Gromacs 5.0,^44,46 whereas the coulomb tool in APBS 1.3⁵⁸ was employed for E_coul; note that ΔE_bonded = 0 as the single trajectory method was adopted. G_polar and G_nonpolar were calculated with APBS 1.3.⁵⁸ For the polar solvation energy contribution, the nonlinear Poisson–Boltzmann equation was solved using a value of 80 for the exterior dielectric constant, and a value of 2 for the solute dielectric constant (ε). A value of ε = 2 (rather than ε = 1 as in the original MMPBSA approach)⁶ was used as it is default in the GMXPBSA program,⁵⁴ but also because it has been suggested that values of ε = 2–4 tend to provide best results, in particular when studying several different proteins.^5,19,59,60 The temperature was set to 298.15 K and the salt concentration to 0.15 M to match the setup of the ABFE calculations. The nonpolar term was considered proportional to the solvent accessible surface area (SASA), G_nonpolar = γ · SASA, where γ = 0.0227 kJ mol^–1 Å ^–2. A probe radius of 1.4 Å was used to define the dielectric boundary, whereas the radii of the solutes were taken by GMXPBSA from the force field (Amber99SB-ILDN/GAFF)^61,62 using the editconf tool in Gromacs⁴⁴ generating the PQR files.

Entropy Calculations

The entropic contribution was estimated as recently proposed by Duan et al.,³⁹ based on the fluctuations of protein–ligand interaction energies:

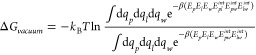5

6

7

8

where k_b is the Boltzmann constant, β = 1/k_bT, and angle brackets represent an ensemble average; E_p, E_l, and E_w are the internal energies of the protein, ligand, and solvent, respectively; E_pl^int,E_pw, and E_pw^int are the protein–ligand, protein–solvent, and ligand-solvent interaction energies. Following eq 2, the vacuum binding free energy using the single trajectory approach, where ΔE_MM = E_pl, corresponds to

9

Combining eq 9 and 8, the following result observed by Duan et al.³⁹ is obtained:

10

where

The interaction entropy was calculated on the 501 frames extracted from the simulations. When explicit water molecules were present, they were considered as being part of the protein, consistently with what was done for the other MMPBSA terms. The short-range Lennard-Jones and Coulombic interaction energies (cutoff of 12 Å) were calculated via the gmx energy command in Gromacs 5.0^44,46 for the 501 frames extracted from the original trajectories. Note that, in principle, E_pl^int corresponds to E_coul + E_LJ used for calculating E_MM (eq 3). In practice, there is a small discrepancy between the two due to the use of cut-offs for the entropy estimate.

Data Analysis

The ΔG_MMPBSA values reported are the mean of the values obtained for all snapshots analyzed. As described above, 501 snapshots were extracted from each simulation. Where repeated calculations were performed (test case 1a), the uncertainty of the ΔG_MMPBSA estimate was taken as the sample standard deviation of the repeated calculations. In all other cases the standard error was estimated by bootstrap:^63,64 10⁵ bootstrap samples were generated through random resampling with replacement of the 501 free energy values, and the standard deviation of the resulting sampling distribution was taken as the uncertainty of the mean. This bootstrap procedure was employed also to estimate the uncertainty in the entropic term when a single simulation repeat was used. We note, however, that in this case this is a crude approximation of the uncertainty given that, contrary to ΔG_MMPBSA, the distributions of bootstrap samples for −TΔS (obtained by resampling the interaction energies) are not always Gaussian or even unimodal. Nonetheless, it provides a rough estimate of the uncertainty of the entropy term that would otherwise be neglected and that can be easily compounded with the uncertainty of ΔG_MMPBSA as the root sum squared to provide a more realistic picture of the precision of MMPBSA calculations that included this term.

Correlation to experimental values was evaluated using the Pearson (r_p) and Spearman (r_s) correlation coefficients. 95% confidence intervals (CIs) for the correlations were obtained by percentile bootstrap:^63,64 first, 10⁵ samples were built by random sampling from the distributions of experimentally measured affinity values assuming normality; then, 10⁵ samples of the predicted affinities (by ABFE or MMPBSA) were built in the same fashion based on the mean and standard error of the calculations. From the resulting distribution of 10⁵ correlation coefficients, the α/2 and 1−α/2 percentiles of the bootstrapped coefficients were taken as the confidence interval, where α = 0.05 for a 95% CI. We will report the correlation coefficient of the original sample in front of the 95% CI in square brackets.

The distribution of the difference in correlation between ABFE and MMPBSA calculations was then obtained by subtracting the values of the 10⁵ bootstrapped coefficients for the two approaches. Note that the bootstrap correlation coefficients for ABFE and MMPBSA calculations are paired, because each coefficient was calculated with respect to a particular bootstrap sample of experimental affinities. The probability density functions (PDFs) resulting from subtracting the bootstrap distribution of ABFE correlation values from the distribution of MMPBSA correlation values gives an indication of the significance for the difference observed. The fraction of the PDF above/below zero can be interpreted as a one-tailed p-value, and a two-tailed p-value if multiplied by two. This approach does not assume any distribution of the sampling distributions for the correlations, and shows the estimated range of possible difference in correlation values between ABFE and MMPBSA. All distributions will be shown as Gaussian kernel density estimates.

Weighted averages of the statistics were obtained by assigning a weight proportional to the number of protein–ligand systems present within a test set, and distributing the weight between multiple sets of calculations if more than one was carried out for a certain test set. Thus, the same weight of one was assigned to each protein–ligand pair, which also means that more weight was then given to larger test sets. If multiple calculations were carried out on a test set (e.g., starting from X-ray and then docking structures), the weight of the test set was distributed equally between the different sets of calculations. In such a way, double counting of repeated calculations on the same test set (which is composed of the same protein–ligand systems and affinities) is avoided, because this can skew the overall performance to the one obtained for a particular test set. This procedure effectively corresponds to averaging the performance of multiple sets of calculations done on a test set (if any), before averaging the performance across the different test sets with weights proportional to the size of the different test sets. In the work here presented, two sets of calculations were performed on test set 1: starting from X-ray and docking structures (test case 1a and 1b, respectively). As both sets of calculations (i.e., test case 1a and 1b) refer to the same test set, the weight for this test set (11, because test set 1 contains 11 protein–ligand systems and affinities) was split between the two test cases (5.5 each). This means that each binding free energy prediction in test case 1a and 1b carried a weight of 0.5, rather than 1, effectively averaging their performance. Accordingly, test case 2 was assigned a weight of 14, and test case 3 a weight of 22, as per the number of protein–ligand systems and ITC affinities they contain. The analysis was performed via scripts written in Python 2.7 using the matplotlib and seaborn libraries for plotting, and pandas, numpy and scipy for data handling and statistics.

Results

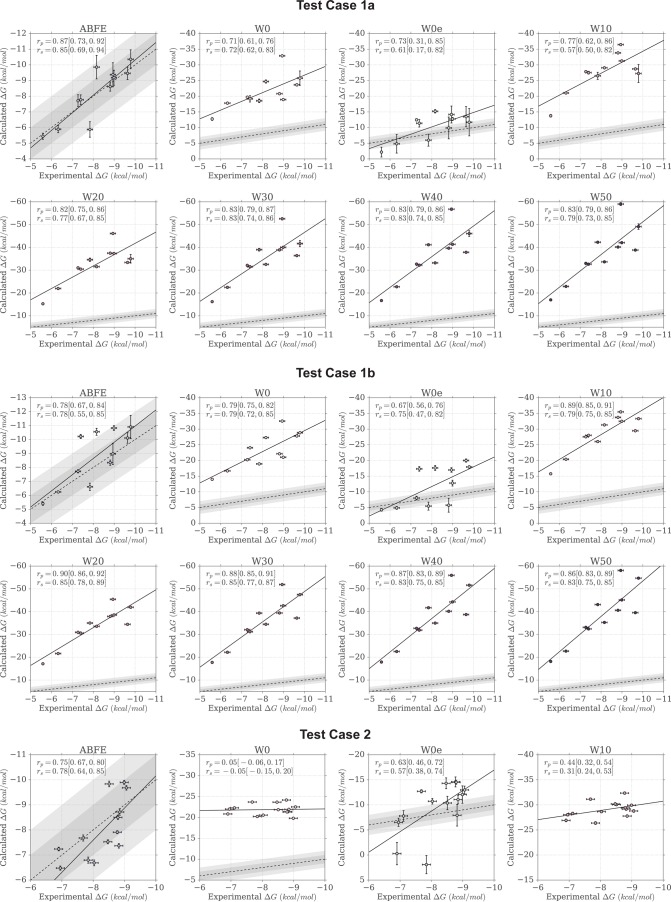
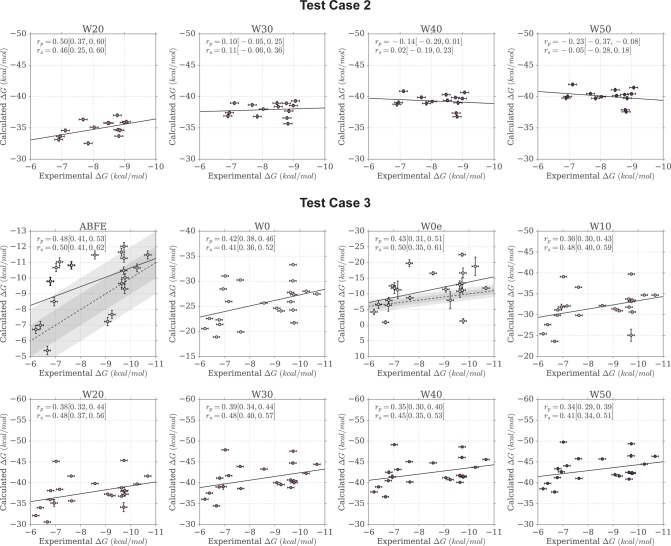
Here we report the performance of the different MMPBSA protocols tested, with particular attention to comparing the results to what had previously been attained with ABFE calculations.^34,35 We primarily discuss performance as measured by the Pearson correlation coefficient (r_p), because similar results were observed for the Spearman correlation (r_s). Both correlation coefficients are however reported in Table 2. The quality of the correlations can also be visually assessed by looking at Figure 3, where the predicted versus measured binding free energies are plotted by test case.

Figure 3.

Scatter plots of calculated versus experimental binding free energies. The areas shaded in gray indicate the 1 and 2 kcal/mol error boundaries. A linear fit to the data is shown as a black line, whereas a dashed line shows the identity line representing a perfect linear fit between experiment and calculations.

Standard MMPBSA Calculations

As a first comparison, we adopted a widely used protocol in which a single MD trajectory of the protein–ligand complex is employed to represent both the bound and unbound ensembles. In addition, the configurational entropy contribution to the binding free energy was ignored. These two approximations are commonly used in end-point calculations as they result in computationally cheaper calculations,⁵ and have often been found to improve the convergence and in some cases the correlation to experiment of the predictions.^32,33,37,65 Because this MMPBSA protocol also does not consider any water molecule explicitly, we label it “W0”. Among the protocols tested, this is the simplest but also the most widely used.

Table 2 summarizes the performance of this protocol under the column “W0”, as well as the performance of ABFE calculations. From a glance at the weighted average correlations (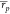 and 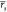) it is possible to see how ABFE calculations returned more reliable results (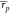 = 0.64, 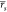= 0.66) than the MMPBSA protocol (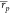 = 0.39, 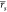= 0.35). When looking more in detail at the performance for each individual test cases, it becomes evident that MMPBSA particularly struggled with case 2, effectively returning no correlation with experimental ITC data (r_p = 0.05, r_s = −0.05). This test case is quite challenging, as it involves two similar ligands binding to seven similar BRDs, yet showing a different selectivity profile. In fact, RVX-208 displays a slight selectivity for three of these seven BRDs, whereas RVX-OH does not, due to the fact the ligand can bind the pockets in two different orientations. Both orientations were considered in the ABFE and MMPBSA calculations. There is then also the additional challenge for the computational method to correctly predict the binding mode of RVX-OH first, which we will discuss later in the text. A more detailed explanation of these systems can be found in Picaud et al.⁶⁶ and Aldeghi et al.³⁵

Note that the ABFE correlation coefficients shown here for test cases 1a and 1b slightly differ from the coefficients reported in Aldeghi et al.⁴ This is simply due to a different way of handling the data. Here, we report the correlation obtained for the original sample whereas we use bootstrap only to estimate the 95% CI. In our previous publications, we reported the mean correlation coefficient of the bootstrap samples. However, the distribution of correlation coefficients obtained via bootstrap might not be normally distributed; for instance, when the original sample has r_p close to one, the sampling distribution of r_p has a longer tail toward lower values because r_p is bound at one. The long tail thus skews the mean of the bootstrap samples toward lower correlation values than the value of the original sample. We deem the approach used here to be more appropriate, and we updated the r_p values for test cases 1a and 1b for a consistent analysis.

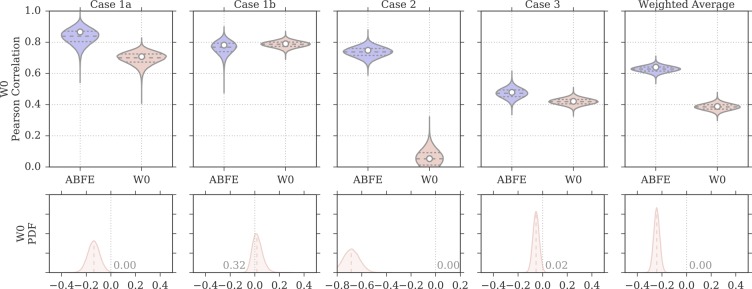
Figure 4 compares the ABFE and MMPBSA distribution of Pearson correlation values (as obtained by bootstrap) for all four test cases, and for the weighted average results (the same plots but for the Spearman correlation are in Figures S1–3). The violin plots thus provide a visual estimate of the uncertainty in r_p based on the precision of the ITC measurements and the computational predictions. Note that the bootstrap data is paired, as each r_p value for the different approaches refer to a single bootstrap sample of experimental affinities; this means that although the experimental uncertainty contributes to the spread of r_p observed in the plots, the effects it has on the bootstrapped r_p values of the different approaches are not independent. The 95% confidence intervals reported in Table 2 were derived from these distributions. The plots at the bottom of the same figure show instead the probability density functions (PDFs) resulting from subtracting the bootstrap distribution of ABFE r_p values from the distribution of MMPBSA r_p values (note again that the subtraction was done so to preserve the pairing of r_p values between the different approaches). Thus, positive values indicate better correlation with experiment for MMPBSA calculations, whereas negative values indicate better correlation with experiment for ABFE calculations. In these plots, the fraction of the PDF above or below zero is also reported; this provides an estimate of the significance for the difference observed, effectively representing a one-tailed p-value, and a two-tailed p-value if multiplied by 2. A small number thus indicate that the difference observed is unlikely to have been caused by chance. Rather than choosing an arbitrary cutoff (such as p < 0.05) that defines the significance of the difference, we show the distribution and its p-value for each pair of MMPBSA and ABFE calculations, giving the opportunity to the reader to independently judge the reliability and importance of the differences observed. This partly because there is additional and not quantified uncertainty in the error estimates that is not taken into account; furthermore, considering there are cases where the p-value is close to the commonly used threshold of 0.05, categorizing those differences as significant if p = 0.04 but not if p = 0.06 (a difference that it is itself likely nonsignificant) seems arbitrary and assigns trustworthiness to the results in a binary fashion. Overall, however, in most instances the fraction of the PDF area greater or smaller than zero is below 0.025, suggesting the difference would be significant at an α = 0.05 level, and when considering all test cases together in the weighted averages, it is well below 0.01. In this case, as shown in Figure 4, ABFE calculations displayed r_p distributions considerably shifted toward higher values for case 1a and 2, slightly shifted toward higher values for case 3, and almost equivalent to the MMPBSA distribution for case 1b. Overall, according to the weighted average difference, ABFE calculations provided a correlation to experiment that can be confidently considered to be higher than the W0 protocol.

Figure 4.

Distributions of Pearson correlation values for the protocol W0 and for ABFE calculations, obtained by bootstrap and based on the uncertainties of the experimental affinity measurements and computational predictions. In the violin plots, the white circle represents the r_p value of the original sample, whereas the dashed horizontal lines the first, second, and third quartiles of the bootstrap distribution. The probability density on the bottom row show the distribution of r_p for ABFE subtracted from the distribution of r_p for MMPBSA. The fraction of the area above or below zero is reported on the plots, the median is shown as a dashed line, and a difference value of zero is marked with a vertical gray dotted line.

As anticipated above, in some test cases, and specifically cases 1b and 2, the computational methods also had to score different docking poses for the protein–ligand pairs (Table S1). ABFE and MMPBSA calculations were performed on the alternative poses, and the pose returning the highest affinity (lowest binding free energy) would be considered the most stable pose. In test case 1b, docking poses for 10 ligands binding to BRD4(1) were considered (one of the ligand does not have a resolved X-ray complex structure); each ligand had between one and five possible poses suggested by the docking. In test case 2, two alternative poses were evaluated for the ligand RVX-OH, which binds with one pose to BRD2(1), BRD3(1), BRD4(1), and BRDT(1), and with another pose to BRD2(2), BRD3(2), and BRD4(2); both poses were tested for all seven BRDs (both with ABFE and MMPBSA) and the one with lowest predicted binding free energy was considered to be the most stable one. Details of docking protocol and poses can be found in the publications where the results of the ABFE calculations are reported.^34,35 Because of the limited number of poses tested for each protein–ligand pair, it is expected that on average, by chance, half of the poses would be correctly identified. Figure 5 shows the number of ligand-protein complexes for which the ABFE and MMPBSA calculations managed to identify the crystallographic binding mode as the one predicted to have highest affinity. It is possible to see that ABFE calculations correctly identified 9/10 poses for case 1b, and 7/7 poses for case 2. The W0 protocol, instead, correctly identified only 3/10 poses for case 1b, and 3/7 for case 2.

Figure 5.

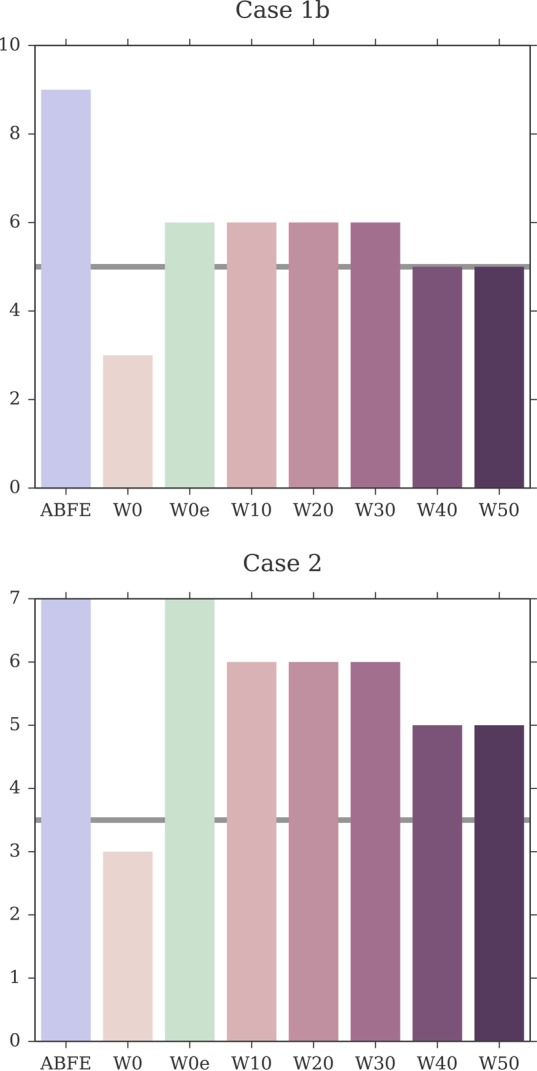
Number of correct X-ray binding modes recovered from sets of docking poses by the different approaches. In test case 1b, a variable number of alternative possible poses were evaluated for 10 ligands. In test case 2, two alternative binding modes were evaluated for RVX-OH binding to seven different protein; the ligand is known to bind to four of these proteins with a certain pose, and to the three in a different with a different orientation. The thick horizontal gray line represents the number of X-ray poses expected to be correctly identified on average by chance.

The Supporting Information reports the predicted binding free energies for all protein–ligand pairs studied in this work. These data are also summarized visually by Figure 3 as scatter plots. In these tables and plots, it is possible to notice how most standard errors in the MMPBSA calculations for test cases 1b, 2, and 3 tend to fall in the range of 0.2–0.3 kcal/mol. These uncertainties were obtained from a single calculation repeat via bootstrap. On the other hand, the standard errors for test case 1a were derived from three repeated calculations, resulting in an uncertainty estimate that, to a certain extent, takes finite sampling issues into account. The resulting standard errors in test case 1a were, on average, two-to-three times larger than those obtained by bootstrap and a single repeat (mean uncertainty of 0.6 kcal/mol), yet they were still reasonably small in most cases. In fact, these uncertainties did not impact noticeably the distribution of r_p values obtained by bootstrap for case 1a, which shows a spread that is similar to the other three test cases. This suggests that the length of the simulations and number of snapshots considered were sufficient to obtain reasonably converged MMPBSA results. The fact that the uncertainty of MMPBSA results based on a single repeat was two-to-three times smaller than that for calculations based on three repeats may be due to the presence of correlated samples, which would result in the bootstrap approach underestimating the true uncertainty. However, it is likely that the largest contribution to this discrepancy is due to limited sampling, i.e., the repeats explore slightly different ensembles of conformations, which then return different distributions of ΔG_MMPBSA values.

MMPBSA Calculations with an Entropy Estimate

As an addition to the previous MMPBSA protocol, we decided to test the effect of including an estimate of the entropic contribution to the binding free energy. This is usually done via quasi-harmonic or normal-mode analysis. However, the benefits of including this term has been subject of debate, in particular when considering the additional computational cost.^5,32,33,65 Recently, Duan et al.³⁹ proposed an alternative method that is computationally cheap and easy to apply by simple postprocessing of the simulation trajectories. The authors also showed how the method returned an improved mean unsigned error as compared to normal-mode analysis for a set of 15 protein–ligand systems. Although the performance of such an approach, also in terms of impact on correlation, still needs to be further validated, its simplicity is very attractive. Thus, we decided to use this interaction entropy method proposed to test whether the MMPBSA calculations of the W0 protocol could be improved, and how would compare to ABFE calculations. Because this protocol included zero explicit water molecules, but an estimate of the entropic term, we refer to it as the “W0e” MMPBSA protocol.

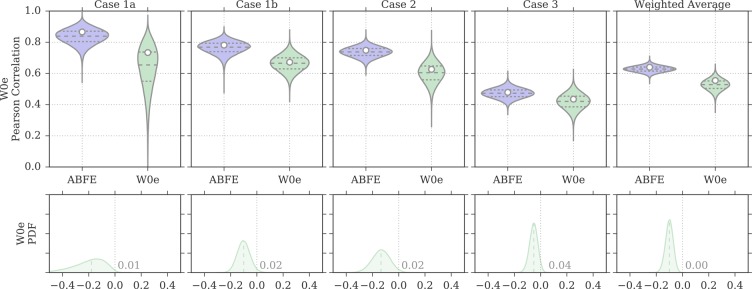
Overall, the addition of the entropic term resulted in a stark improvement of the agreement with ITC data with respect to the W0 protocol. In fact, the weighted average correlation values raised to 0.55 [0.39, 0.64] and 0.56 [0.35, 0.70], for the Pearson and Spearman coefficients, respectively (Table 2). A closer look indicates that this was driven by a recovered positive correlation for test case 2. The W0e protocol also managed to correctly identify the pose of RVX-OH in case 2 for all seven complexes (Figure 5). In case 1b too, the number of correctly identified poses improved to 6/10, just slightly better than random. Despite the improvements over W0, the performance of this MMPBSA protocol was still inferior to that of ABFE calculations, by 0.09 and 0.11 in terms of Pearson and Spearman weighted average correlation. Indeed, Figure 6 shows how for test cases 1a, 1b, and 2, the distribution of W0e r_p values is shifted toward lower values; for test case 3 there is more overlap between the two distributions, despite ABFE calculations still being more likely to return a higher correlation.

Figure 6.

Distributions of Pearson correlation values for the protocol W0e and for ABFE calculations, obtained by bootstrap and based on the uncertainties of the experimental affinity measurements and computational predictions. In the violin plots, the white circle represents the r_p value of the original sample, whereas the dashed horizontal lines the first, second, and third quartiles of the bootstrap distribution. The probability density on the bottom row show the distribution of r_p for ABFE subtracted from the distribution of r_p for MMPBSA. The fraction of the area above or below zero is reported on the plots, the median is shown as a dashed line, and a difference value of zero is marked with a vertical gray dotted line.

The estimate of the uncertainty for the entropic term was based on three independent samples (i.e., repeats) for test case 1a, and on bootstrap resampling for the other cases. For case 1a, a large uncertainty was observed for the entropic calculations: the average standard error in the −TΔS estimate for the 11 protein–ligand pairs was 1.9 kcal/mol, driving the average standard error for the overall ΔG_MMPBSA for W0e to 2.1 kcal/mol. Although the uncertainties derived by bootstrap for cases 1b, 2, and 3 are smaller, they still result in considerably less precise calculations than for protocol W0. In fact, when considering these other three test cases together, the average standard error for the overall ΔG_MMPBSA was of 1.1 kcal/mol. The impact of the larger uncertainties on the spread of possible correlation values for all cases can be seen in Figure 6, and in the 95% CI for the r_p in Table 2: the probability density for the r_p values is wider, in particular for test cases 1a, allowing for both strong and weak correlations. Therefore, despite the addition of the entropy estimate had resulted in a better correlation to ITC data for the tests cases considered here, the precision of this term still appears to be problematic.

Given these larger uncertainties, one might wonder whether the improvement observed over the protocol W0 for case 2 might be due to chance. However, the difference in performance between the two protocols is much larger than their respective uncertainty, so that even assuming the uncertainties were underestimated the improvement would still be significant. For instance, adding Gaussian random noise to the W0 and W0e bootstrap samples of r_p so to triplicate the spread of their distributions still results in a difference of r_p (using the same approach as done for the comparison of MMPBSA to ABFE) that would be significant at α = 0.05.

MMPBSA Calculations with an Explicit Ligand Hydration Shell

It has been previously shown by different authors how the inclusion of an explicit ligand hydration shell can in some instances lead to an improved correlation between calculated binding energies and experimental affinities.^33,40−43 Furthermore, bromodomains are known to have a conserved network of water molecules at the bottom of their binding pockets that interact with the small molecule binders. For these reasons, we decided to test this approach too and we repeated the MMPBSA calculations while including a different number of explicit water molecules around the ligand, using the same approach employed by Maffucci and Contini.⁴² We ran five different sets of calculations, which included the 10, 20, 30, 40, and 50 closest water molecules to the ligand in each of the frames extracted from the MD simulations. We will thus refer to these protocols as “W10”, “W20”, “W30”, “W40”, and “W50”.

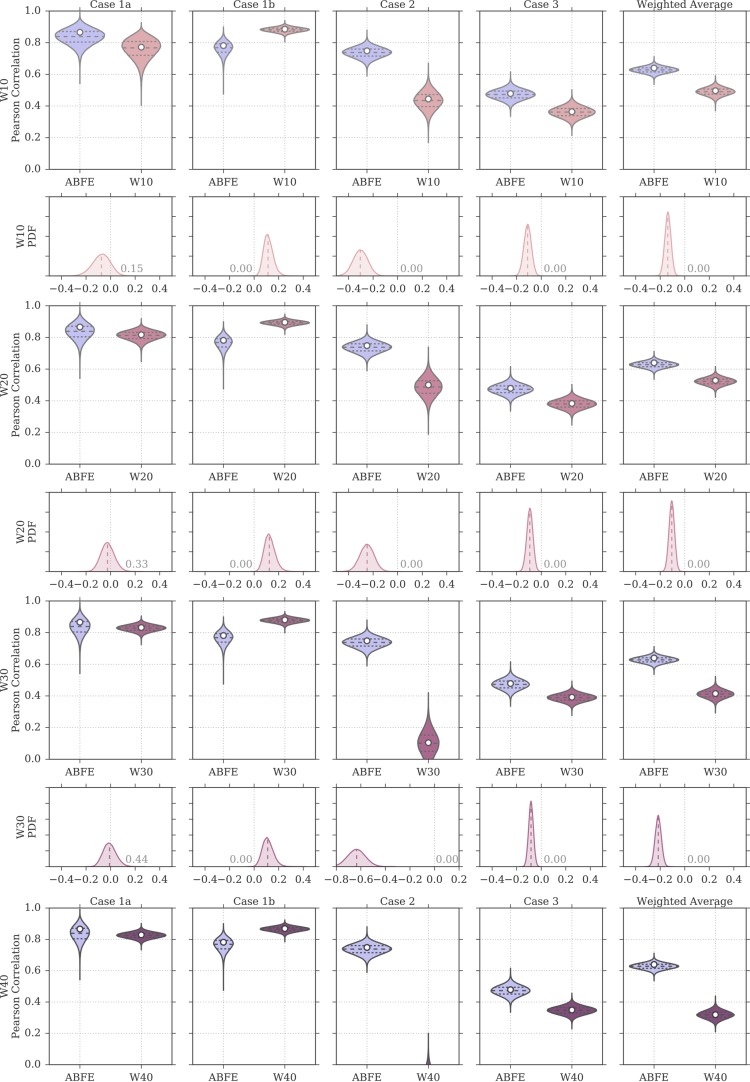
Figure 7 provides an overview of how the correlation between calculated and measured affinities changed when including a larger number of explicit water molecules in the MMPBSA calculations. The numerical data are available also in Table 2. For test case 1a, r_p increased between W0 and W20 (r_p = 0.82 [0.75, 0.86]), and reached its peak value at W30 with r_p = 0.83 [0.79, 0.87], after which it leveled off. For test case 1b too, r_p increased when including a small number of explicit water molecules, with the peak correlation being achieved by W20 (r_p = 0.90 [0.86, 0.92]), after which r_p seemed to deteriorate only marginally. Case 2 showed the strongest dependence on the presence of explicit water molecules in the MMPBSA calculations. In fact, although the W0 protocol returned no correlation to the ITC data, the inclusion of 10 or 20 water molecules managed to recover a moderate correlation (r_p = 0.44 [0.32, 0.54] for W10, and r_p = 0.50 [0.37, 0.60] for W20). However, the inclusion of a larger number of explicit water molecules resulted in no (or negative) correlation with the ITC data. In test case 3 instead, the inclusion of an explicit ligand hydration shell seemed to result in a minor deterioration of the Pearson correlation. Overall, because of cases 1a, 1b, but in particular case 2, the performance of the approach (measured as weighted average Pearson correlation) improved markedly when including a small number of explicit water molecules (up to 20), but deteriorated again at higher numbers.

Figure 7.

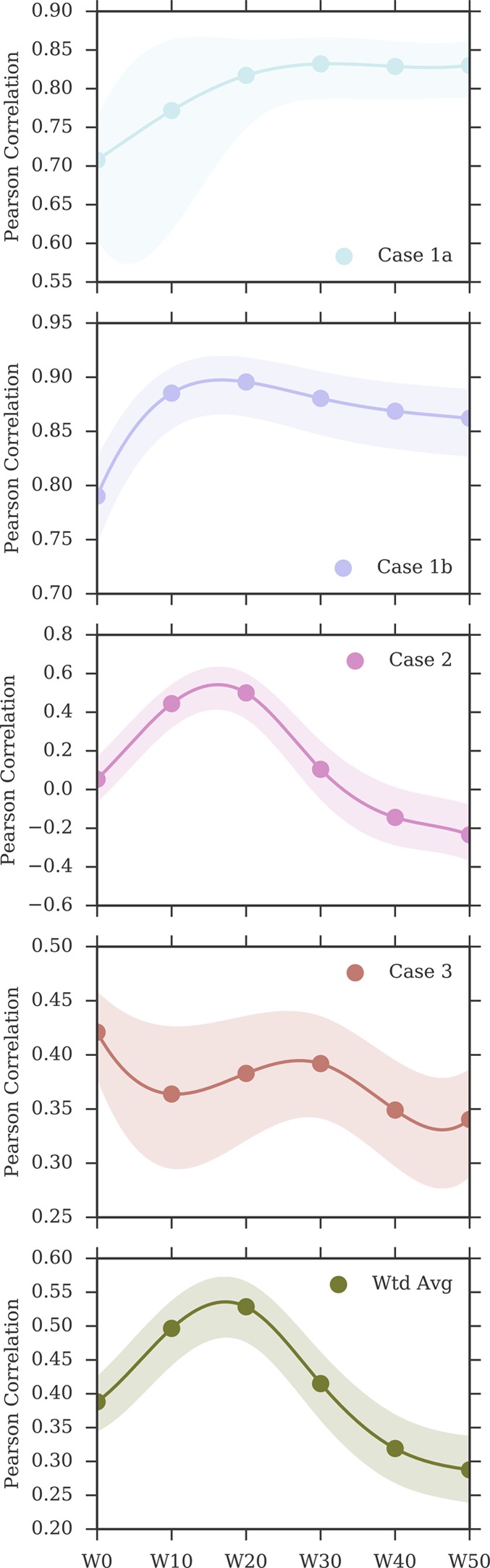
Change in Pearson correlation with the inclusion, in the MMPBSA calculations, of larger numbers of explicit water molecules representing the ligand hydration shell. The shaded area represents the 95% CI of the Pearson coefficient. The discrete data points (at W0, W10, W20, W30, W40, W50) have been interpolated with a cubic spline only for visualization purposes. Note the different scales on the y-axis.

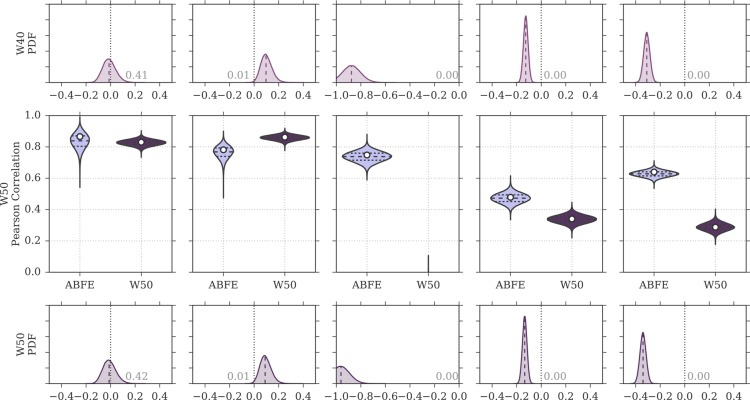
Figure 8 shows a comparison of the r_p distributions observed for ABFE calculations and for the MMPBSA protocols that included an explicit ligand hydration shell (W10 to W50). Focusing on W20, the protocol that achieved highest overall performance (r_p = 0.53 [0.45, 0.59], r_s = 0.55 [0.42, 0.64]) among the ones discussed in this section, it is possible to see that the difference in correlation to ABFE is still significant. Looking at each test case more specifically, for test case 1a the distribution of r_p was similar to that obtained by ABFE calculations. For test case 1b, MMPBSA returned higher correlation to experiment than ABFE. Surprisingly, MMPBSA calculations behaved oppositely to ABFE, in that the end-point approach returned better (rather than worse) correlation to ITC data when starting from docked poses rather than X-ray structures; this trend was conserved across all MMPBSA calculations that did not include the interaction entropy estimate. Looking more in detail at the individual results for all ligands in case 1a and 1b, it was noticed that the largest average difference in binding free energy between the two test cases was associated with ligand 1 (the dual kinase-BRD inhibitor BI-2356).⁶⁷ This ligand is also the one with highest affinity for BRD4(1) among the ones considered, but in case 1a its affinity is slightly underestimated (in relative terms with respect to the other ligands; see Figure 3). In case 1b, however, there is a docking pose that deviates from the X-ray pose (RMSD of 8.4 Å) only because the solvent-exposed tail of the ligand adopts a more extended conformation, whereas the core of the ligand interacting with the protein maintains a correct binding orientation. This more extended pose is scored higher (lower binding free energy) by MMPBSA (protocols W10–W50) than the pose closest to the X-ray (with RMSD of 3.2 Å), so that the ligand affinity is ranked more appropriately (despite the “wrong” pose being identified as the most stable), in turn positively impacting the correlation to the experimental data. This is the largest contributing factor to the unexpected improvement in correlation between test case 1b and 1a that we have identified. Excluding this ligand, protocol W20 would return a Pearson correlation of 0.85 [0.82, 0.88] for test case 1a and of 0.88 [0.84, 0.91] for test case 1b (a difference that is not significant anymore). For case 2, despite the net improvement as compared to W0, the distribution of r_p was still shifted toward lower values as compared to ABFE. The same was noticed for test case 3, which was expected, because in this test case the inclusion of an explicit hydration shell did not improve the correlation to ITC affinities. Overall, the performance of the W20 protocol was comparable to that of W0e, with W20 performing better on test set 1 (case 1a and 1b, where 11 ligands bind to one protein with a range of affinities), and W0e performing better on test sets 2 and 3 (where single ligands bind to multiple proteins).

Figure 8.

Distributions of Pearson correlation values for the protocols W10 to W50 and for ABFE calculations, obtained by bootstrap and based on the uncertainties of the experimental affinity measurements and computational predictions. In the violin plots, the white circle represents the r_p value of the original sample, whereas the dashed horizontal lines the first, second, and third quartiles of the bootstrap distribution. The probability density on the even rows show the distribution of r_p for ABFE subtracted from the distribution of r_p for MMPBSA. The fraction of the area above or below zero is reported on the plots, the median is shown as a dashed line, and a difference value of zero is marked with a vertical gray dotted line.

The inclusion of explicit water molecules in the MMPBSA calculations also resulted in a higher ability to identify the correct ligand binding mode from the set of docking poses (Figure 5). In test case 1b, protocols W10, W20, and W30 correctly identified the X-ray binding pose for 6/10 ligands. Despite this being only slightly better than chance with this set of protein–ligand complexes and docking poses, it is double the number of correctly identified poses that of the standard MMPBSA protocol (W0) adopted here and discussed previously. For the same test case, however, the recovery of correct binding modes decreased to 5/10 for protocols W40 and W50. In test case 2, the improvement was more noticeable. Although W0 predicted RVX-OH to bind in the same orientation to all seven BET BRDs, thus identifying only 3/7 correct orientations, W10, W20, and W30 allowed for the two possible orientations of RVX-OH to be predicted as more stable in different BRDs. As a consequence, these protocols recovered 6/7 correct binding modes for RVX-OH, with BRDT(1) being the only BRD for which the pose was not correctly predicted. Also in this instance, the number of correct binding poses recovered decreased slightly, to 5/7, for protocols W40 and W50.

Given the performance improvements observed for both the MMPBSA protocol including an estimate of the binding entropy and the protocol including an explicit ligand hydration shell, the two approaches were also combined in order to test whether further gains in correlation could be achieved. However, this did not result in higher correlations than those obtained with protocols W0e and W20 (Supporting Information Table 2). It is possible that, because the entropy estimate here employed depends on the interaction energy between the ligand and the protein (with the solvent, if present, being considered as part of the protein), the inclusion of explicit water molecules may add noise to the estimate given that many water molecules included in the ligand hydration shell are exposed to bulk and are nonstructural. Assuming prior knowledge of the presence and location of conserved water molecules important for binding, it would also be possible to selectively choose a specific set of water molecules to be retained during the MMPBSA calculations, as opposed to defining a hydration shell around the ligand as done in this work. Although we have not investigated this approach, and as such the following is speculative, it is conceivable that such a strategy might too be able to return improved agreement with experiment over standard MMPBSA approaches that do not include any explicit water molecule in the calculations. It is also plausible that, if only structural water molecules relevant for the ligand-binding event are included in the MMPBSA calculations, then adding a binding entropy estimate (similarly to protocols W10e to W50e) may result in further accuracy gains because highly localized bridging water molecules would be included as part of the protein structure, whereas bulk-exposed, mobile, noise-inducing water molecules would not.

Discussion

When the interest is in the relative ranking of affinities of very diverse ligands or of a ligand for multiple proteins, MMPBSA calculations are an alternative to computationally more demanding ABFE calculations. Given the lack of direct comparisons between the two techniques, it is informative to observe the performance of these on the same systems, using the same physical models and MD trajectories. When running end-point calculations, several different options are available to the user. Here, one of the most widely employed MMPBSA procedures was first adopted; that is, the single-trajectory approach with neglect of the binding entropy. Then, the effect of including a computationally efficient estimate of the binding entropy was evaluated. Furthermore, protocols that included an explicit ligand hydration shell of different size were considered too. Importantly, the MMPBSA calculations were carried out on frames extracted from the simulations used for the ABFE calculations. Hence, a similar ensemble of conformations was used in both computations, as well as the same physical model, so that potential sampling or force field issues would affect both sets of predictions. The affinity predictions were evaluated based on four test cases, which included a total of 47 experimental affinity data points (43 of which were obtained with ITC, one with SPR, and three with AlphaScreen), where either the protein target or the ligand of interest were kept constant. These scenarios are amenable to both MMPBSA and ABFE calculations. On the other hand, because of large differences within the set of either ligands or proteins considered, RBFE calculations would be impractical and, at the moment, unfeasible in such cases.

Table 2 reports the Pearson and Spearman correlations for all ABFE and MMPBSA setups here considered. The performance of the four test cases (two of which on the same test set) as well as their weighted averages are shown. Overall, when considering all test cases, ABFE calculations were more reliable and returned moderate or strong correlation with experimental affinities in all four cases. Consequently, the achieve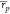d and 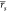were of 0.64 [0.56, 0.69] and 0.66 [0.53, 0.75], respectively. Nonetheless, the best MMPBSA protocols achieved overall correlations that were only about 0.1 points worse than ABFE, despite needing about 5% of the compute time. For an ABFE calculation, 42 simulations (each 10 or 15 ns long) of the protein–ligand complex were performed; on the other hand, for a MMPBSA calculation, only one such simulation was used, followed however by a set of three Poisson–Boltzmann calculations. To provide an idea of the difference in computational cost, each ABFE calculation with 15 ns long windows took about 2 days on 504 cores (42 CPUs, Intel Xeon E5-2697 v2 2.7 GHz), whereas the simulation needed for a MMPBSA calculation took the same time but on 12 cores (1 CPU) because it corresponded to only one of the 42 windows simulating the protein–ligand complex. Then, the MMPBSA postprocessing for each 501-frame trajectory with GMXPBSA 2.1⁵⁴ and APBS 1.3⁶⁸ took about 2 days and 9 h on 8 cores (AMD Opteron 2378 processor). There can be, however, substantial differences in the efficiency of different MD and MMPBSA codes,^69,70 and the performance of different hardware. Furthermore, in our previous ABFE studies we did not optimize the protocol for computational efficiency, so that the relative cost of ABFE versus MMPBSA reflects the details of the setup we employed, but it is by no means general. On one hand, it is likely possible to optimize the ABFE protocol so to obtain similar accuracy with lower cost,^25,71 and on the other hand the use of different MMPBSA protocols, like ensemble approaches, would involve a considerably larger number of MD simulations and thus higher cost.^18,72 Ultimately, the applicability of ABFE versus MMPBSA depends on the computer resources one is willing or able to assign to a specific problem. Thus, in practice, large computational screens might be more amenable to cheaper MMPBSA calculations, whereas ABFE calculations could be employed for a more accurate re-evaluation of some binding free energies. On the other hand, if only a relatively small number of protein–ligand complexes are of interest, and accuracy is of primary importance, ABFE calculations should be the method of choice.

Here, the best performing MMPBSA protocols overall were W0e and W20, the former including an estimate of the entropic term, and the latter including an explicit ligand hydration shell comprising 20 water molecules. W0e returned 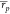= 0.55 [0.39, 0.64] an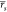d = 0.56 [0.35, 0.70], whereas W20 returned 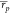= 0.53 [0.45, 0.59] and 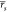= 0.55 [0.42, 0.64]. Interestingly, W20 performed particularly well in test cases 1 and 2, whereas W0e was superior in test cases 3 and 4. It should be kept in mind that although it was possible to retrospectively identify the MMPBSA protocols returning the best correlation to experiment in these specific test cases, it would not be possible to do this prospectively, unless one has an indication of which protocol is most likely to perform best based on previous experience and testing on the specific system. This system-dependence of the most suitable protocol can be a nuisance for MMPBSA calculations,^65,73,74 whereas such uncertainty is not present to the same extent in ABFE calculations where the appropriateness of the protocol adopted tends to be less dependent on the system under investigation. For instance, the use of more thorough protocols (e.g., using replica exchange to enhance sampling,^50,75 or restraints to improve convergence,^76,77 or correcting for the use of cut-offs,⁷⁸ or for artifacts related to the treatment of electrostatics²⁶) may not provide any improvement in some cases, but also is unlikely to be detrimental. This is not to say that the performance of ABFE calculations is not system-dependent, but that there is a smaller number of setup variables that can affect the results in ways that are hard to predict. Although the performance of ABFE is too ultimately system dependent, given the rigorous nature of the calculations this dependence should only be due to the underlying physical model used (assuming convergence), and not to other setup choices.

Note that although we tried to test different MMPBSA protocols, these were not by any means exhaustive. Parameters such as solute dielectric constant and salt concentration could be tuned, the GB rather than PB model could be employed, and other approaches to the estimate of the binding entropy could be adopted. It is conceivable that a protocol that is overall superior to the ones considered here exists. However, our principal aim was a fair comparison between ABFE and MMPBSA, rather than the identification of the best MMPBSA protocol. This is also in light of the fact that, as mentioned previously, in a prospective scenario one would choose a protocol without prior knowledge of its performance. The protocols here used thus reflect the choices the authors would have made in such scenario, and the necessary compromises made in order to achieve a direct comparison to ABFE calculations (e.g., length and number of MD simulations, force fields, etc.). Furthermore, given that ABFE calculations were known to perform well for the test cases here described (aside test case 3, for which they returned modest correlations), there might be a bias against MMPBSA calculations in the sense that they would have had to perform particularly well in order to be found superior or equivalent to ABFE. On the other hand, we did not select the literature for positive ABFE results, but rather reanalyzed all our previous data. In the future, it would be interesting to consider cases where MMPBSA has performed well and test whether ABFE could achieve similar results, or cases where ABFE is known to fail and test whether MMPBSA could succeed instead. As it may also be the case for different protein systems, it cannot be excluded that opposite results in terms of performance may be found in such scenarios.

In this paper, we have not focused on the ability of MMPBSA to reproduce affinities in absolute terms as compared to ABFE calculations. This because it is generally accepted that obtaining agreement in absolute terms is problematic for MMPBSA.^5,36 However, this is one of the benefits of ABFE calculations. In fact, the results obtained here confirmed this notion about ABFE versus MMPBSA methods (Table 3). For the ABFE calculations, the weighted average root-mean-square error (RMSE) for the four test cases was of 1.5 kcal/mol, whereas the best weighted average RMSE for MMPBSA was of 5.3 kcal/mol, obtained with the W0e protocol. Without the entropy estimate, the standard W0 protocol returned an overall RMSE of 15.7 kcal/mol, but this is not surprising given the neglect of entropy contributions upon binding. Therefore, in Table 3 only the RMSE for the results of the protocols including an estimate of the entropic term (W0e to W50e) are showed. In all cases, in fact, the addition of the entropy estimate significantly reduces the RMSE with respect to the MMPBSA calculations without this term (e.g., W20e versus W20). Nonetheless, with larger numbers of explicit water molecules included in the calculations, larger errors are observed. Therefore, among all MMPBSA protocols, W0e is still the best performing in terms of absolute errors, with a RMSE (5.3 kcal/mol) that is however about 3.5 times larger than that of ABFE.

Table 3. Overview of the Results Obtained with ABFE and MMPBSA Calculations, in Terms of Root Mean Square Error As Compared to Experimental Binding Free Energies^a.

Root Mean Square Error (kcal/mol)
Test Case No.	Weight	ABFE	W0e	W10e	W20e	W30e	W40e	W50e
1a	5.5	0.85 [0.64, 1.32]	3.94 [3.61, 5.86]	7.09 [6.38, 9.40]	12.52 [11.50, 13.90]	15.39 [14.33, 16.73]	17.36 [16.02, 19.26]	18.38 [17.02, 20.13]
1b	5.5	1.37 [1.25, 1.64]	6.46 [6.34, 6.60]	7.88 [7.29, 8.70]	14.12 [13.66, 14.64]	17.25 [16.81, 17.73]	18.86 [18.31, 19.48]	19.68 [19.03, 20.43]
2	14	0.95 [0.87, 1.05]	4.68 [4.57, 4.80]	7.02 [6.58, 7.82]	12.74 [12.24, 13.65]	16.18 [15.59, 16.89]	17.93 [17.39, 18.54]	18.54 [17.99, 19.16]
3	22	2.13 [2.03, 2.26]	5.70 [5.60, 5.80]	8.70 [8.24, 9.47]	15.54 [15.08, 16.17]	18.69 [18.23, 19.23]	19.82 [19.32, 20.42]	20.62 [20.13, 21.20]
Weighted Average		1.54 [1.43, 1.72]	5.28 [4.86, 6.23]	7.92 [7.41, 8.88]	14.18 [13.65, 14.97]	17.39 [16.82, 18.07]	18.86 [18.24, 19.62]	19.63 [19.00, 20.38]

^aIn square brackets are the 95% confidence intervals of the statistics.

The present study is in agreement with the previous observations of improved correlation with experiment when an explicit ligand hydration shell is included in the MMPBSA calculations.^42,43 However, for the bromodomain systems considered it was observed that correlation improved after including a small number of explicit waters (up to 20) and then leveled or decreased at higher numbers (30 to 50). The same effect was observed by Maffucci and Contini,^42,43 who suggested that the inclusion of additional and unnecessary solvent molecules around the ligand introduces noise while not contributing anymore to capturing discrete solvent effects upon binding. Addition of the binding entropy estimate too resulted in an improved overall performance as compared to the standard MMPBSA protocol here referred to as W0. In addition, the inclusion of the entropic term largely improved the agreement with experimental free energies in absolute terms. Nonetheless, the larger uncertainties obtained for this protocol raise concerns with respect to the precision of calculations making use of this term, in particular when its uncertainty is not estimated.

Considering the small data set of docking poses in the present study, it is difficult to confidently determine the best rescoring approach. Nonetheless, ABFE calculations appeared to provide the best recovery rate of X-ray poses, followed by the MMPBSA protocols that included either an entropy estimate (W0e) or a small explicit hydration shell (W10, W20, and W30), which is consistent with their improved correlations as compared to the more standard MMPBSA protocol (W0).

As for all studies focusing on a specific protein family, the question of whether or to what extent the results and observations made are transferable to other systems arises. Given the small number of protein–ligands pairs studied and the focus on BRDs, the transferability of the results observed for ABFE and MMPBSA to other systems is not guaranteed. Nonetheless, one might speculate that at least for protein systems with similar characteristics, such as a rigid structure and a solvent-exposed binding pocket, similar observations about the relative performance of ABFE and MMPBSA will apply. In addition, we would also expect the observation of improved agreement with experiment for the MMPBSA protocols that included a number of explicit water molecules to be true for other protein systems with either solvent-exposed binding pockets or bridging water molecules. On the other hand, it is conceivable that for protein targets with enclosed and dry binding pockets the inclusion of explicit water molecules might have less of a positive effect, which might mean the advantage of explicit solvent ABFE calculations may be diminished too.

Conclusions

In summary, and on the basis of the data described in this work, which are contingent on the test cases considered, the following observations can be made. (1) Overall, ABFE calculations appeared to be more robust than MMPBSA ones in the ability to correlate to experimental affinities. However, this came at high computational price. (2) Certain MMPBSA protocols, namely the ones that included either an estimate of the binding entropy or an explicit ligand hydration shell, still achieved reasonable correlation with experimental affinities at a much lower computational cost than ABFE calculations. (3) The inclusion of a small explicit ligand hydration shell resulted in improved correlation with experiment. (4) The inclusion of the binding entropy term, calculated as proposed by Duan et al.,³⁹ was also beneficial for improving the correlation with experiment. However, this term appeared to be more sensitive to the simulated ensemble than the rest of the MMPBSA terms, thus potentially affecting the precision of the calculations. (5) Perhaps unsurprisingly, MMPBSA did not provide quantitative agreement with experimental binding free energies in absolute terms, contrary to ABFE. The incorporation of the entropic term largely improved the absolute errors, yet the RMSE achieved with MMPBSA was still about 3.5 times larger than the one achieved with ABFE calculations.

Finally, we stress the fact that the present analysis was based on a limited number of protein–ligands pairs and a single protein family, such that the transferability of the above observations to other systems is not guaranteed. Nonetheless, the study provides a first glance at how MMPBSA and ABFE compare to each other in their ability to correlate with ligand binding affinities. As ABFE calculations become more affordable and widespread, it will be possible to gather a more general picture of their performance and to compare them to established computational methods like MMPBSA.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jcim.7b00347.

• Full details of the test cases, summary of the MMPBSA calculations in terms of Pearson and Spearman correlation to experimental binding free energies, violin plots of Spearman correlation values for the different protocols (PDF)

Author Present Address

^⊥ Department of Computational and Theoretical Biophysics, Max Planck Institute for Biophysical Chemistry, D-37077 Göttingen, Germany

The authors declare no competing financial interest.