A Feasibility Study on Ribs as Anatomical Landmarks for Motion Tracking of Lung and Liver Tumors at External Beam Radiotherapy

Abstract

At external beam radiotherapy for some tumors located at thorax region due to lack of information in gray scale fluoroscopic images tumor position determination is problematic. One of the clinical strategies is to implant clip as internal fiducial marker inside or near tumor to represent tumor position while the contrast of implanted clip is highly observable rather than tumor. As alternative, using natural anatomical landmarks located at thorax region of patient body is proposed to extract tumor position information without implanting clips that is invasive method with possible side effect. Among natural landmarks, ribs of rib-cage structure that result proper visualization at X-ray images may be optimal as representative for tumor motion. In this study, we investigated the existence of possible correlation between ribs as natural anatomical landmarks and various lung and liver tumors located at different sites as challenging issue. A simulation study was performed using data extracted from 4-dimensional extended cardiac-torso anthropomorphic phantom that is able to simulate motion effect of dynamic organs, as well. Several tumor sites with predefined distances originated from chosen ribs at anterior–posterior direction were simulated at 3 upper, middle, and lower parts of chest. Correlation coefficient between ribs and tumors was calculated to investigate the robustness of ribs as anatomical landmarks for tumor motion tracking. Moreover, a consistent correlation model was taken into account to track tumor motion with a rib as best candidate among selected ribs. Final results represent availability of using rib cage as anatomical landmark to track lung and liver tumors in a noninvasive way. Observations of our calculations showed a proper correlation between tumors and ribs while the degree of this correlation is changing depends on tumor site while lung tumors are more varied and complex with less correlation with ribs motion against liver tumors.

Introduction

The purpose of radiation therapy at each treatment modality is killing all cancerous cells of planning tumor volume, while minimizing the received dose by surrounding normal tissues at the same time. In recent years, many efforts have been done on the following 2 substantial challenging issues of radiotherapy to enhance treatment quality: (1) tumor localization and delineation during treatment planning system and (2) dose delivery technique at beam irradiation system.¹ The degree of a success treatment is strongly depending on the accuracy of tumor localization as a main component of treatment planning process. This issue will be a serious concern while tumors located at thorax region move semi-irregularly due to breathing phenomena. This error known as intrafractional organs motion error may lead to a significant uncertainty of tumor localization and therefore a great amount of over-under dosage is happened onto tumor and healthy surrounding tissues that is far away from prescribed dose.^2–7 Several strategies have been proposed to compensate the effect of tumor motion error on planned dose such as breath-holding, respiratory motion-gating, and real-time tumor tracking techniques.^8–15

In breath-holding technique, the goal is to immobilize the tumor by asking the patient to keep breathing in a specific level. Breath-holding technique requires cooperating patients that is problematic for patients with noncontrolled breathing.^8,10 Respiratory-gated radiotherapy was proposed as another method to save normal surrounding tissue against additional high dose by irradiating the therapeutic beam only in a predefined phase of the breathing cycle.^11,12 In real-time tumor tracking technique, the irradiation beam is continuously repositioned dynamically to trace tumor motion in real time. In this method, the beam is always ON during a treatment fraction. In order to implement 2 latter techniques, tumor position information must be extracted as function of time during treatment. Among several strategies proposed for tumor motion monitoring, some of clinically available techniques range from continuous X-ray imaging (ie, fluoroscopy) to the use of external surrogates radiotherapy.^16–29

In an ideal form, the tumor motion would be observed continuously using fluoroscopic imaging system at external beam radiotherapy. While tumor contrast is not proper during imaging by fluoroscopy, a fiducial marker is implanted near or inside tumor volume representing a given point of tumor. During each irradiation fraction, implanted fiducial is traced by means of fluoroscopy imaging system, providing 3-dimensional (3D) coordinates at usually 30 frames per second. The tumor motion information is then utilized to turn the beam ON while the tumor is in the desired place at radiotherapy based on motion gated. Apart from some advantageous points of using fluoroscopy imaging, this method would deliver too much imaging dose mainly at hypofractionated radiotherapy and radiosurgery. As solution, using external surrogates technique, the patient is kept away additional imaging dose versus fluoroscopy-based tumor motion monitoring.

In radiotherapy with both continuous imaging and external surrogates techniques for motion monitoring, since some tumors located at special sites have not enough visibility at images taken by fluoroscopy and stereoscopic X-ray systems (due to low contrast); internal clips are implanted inside or near tumor to represent tumor position with a 3D spatial point shown by x(t), y(t), and z(t) over time.¹⁴

Implementing internal clips raise some concerns as (1) side effects of invasive procedure of clip implantation inside or near tumor, (2) marker migration, and (3) risk of pneumothorax for lung cancers.³⁰

Taking into account these limitations, getting any strategy to track tumor motion without using internal artificial markers can be strongly helpful to minimize patient difficulties and also treatment costs. In this study, we are interested in investigating the representative role of internal anatomical landmarks belonging to patient organs at thorax region instead of implanted fiducial markers at radiotherapy guided by fluoroscopy X-ray imaging system. While tumor position is unclear in images taken by fluoroscopy imaging, relevant moving structures around tumor volume with proper contrast can be considered as anatomical landmarks to produce internal motion signals, 3 dimensionally.^31,32 Chosen natural landmarks must include 2 major characteristics: (1) proper visualization at X-ray images to be tracked precisely and (2) certain correlation with tumor motion. Assuming first property is available, in this work we are investigating to find the existence of possible linear or nonlinear relationship between anatomical landmark motion and tumor motion. By proving certain and reliable this correlation, as next step, the motion data of anatomical landmark are correlated with tumor motion using a consistent correlation model. Therefore, tumor motion tracking is performed properly without implementing clips.

Several works have been done to predict tumor motion using surrogate anatomic features in the images such as diaphragm and lung boundary.^32,33 In this study, we investigated the role of ribs (from rib-cage structure) to be used as natural internal markers for lung and liver tumors. To do this, several inner points of different ribs were taken into account as natural anatomical landmark with 2 groups of lung and liver tumors located at different positions to complete our assessment. In order to clarify the procedure of our work, we tested all the possible correlations between anatomical landmarks motion with assumed tumors motion at different distances inside lung and liver regions during breathing cycles.

To implement ribs as anatomical landmark for tumor tracking, there are several concerns that must be addressed. The most challenging issue is the distance between supposed tumor and determined anatomical landmarks on different ribs. In fact, the validity and reliability of configured correlation model must be considered as responsible to correlate any superficial and deep tumors with given points at various ribs of rib cage. For more clarifying, the performance of ribs as anatomical natural landmark is compared with diaphragm at the same condition on a group of predefined tumors. Moreover, we are interested in finding optimum ribs to be tracked for most lung and liver tumors.

In order to address these challenging issues, a simulation study was performed using 4-dimensional extended cardiac-torso (4DXCAT) anthropomorphic phantom developed by Dr Segars et al.³⁴ Using this phantom, internal organs at thorax region such as liver and lung are easily accessible to define any arbitrary tumors at different sites regarding with ribs position where there is no option in real condition to conclude the proposed method with reasonable uncertainty error.

After determining phantom parameters according to motion information of real patients treated with Cyberknife Synchrony system, the motion pattern of tumors and anatomical landmarks of the ribs were extracted for finding possible correlation among them. Moreover, in this work, an adaptive neuro-fuzzy-based correlation model was used to predict tumor motion from rib motion as output. Based on our previous studies,^35–37 this model may be optimal for correlating the rib cage motion with internal tumor motion due to a high degree of uncertainty and time-varying characteristics of breathing phenomena.

Apart from the differences between motion pattern of different tumors and ribs, final analyzed results represent that ribs are robust to be used as anatomical landmarks for lung and liver tumors. It has been proven comparing the ribs as anatomical landmark with diaphragm using the same database at the same condition in this work. Correlation coefficient parameter utilized in this work and the performance of utilized correlation model realized that choosing the best rib as anatomical landmark for tumor motion depends highly on the location of tumor. As clinically, selecting the best rib that is most correlated with an assumed tumor and then generating a proper correlation model to predict tumor position must be done at pretreatment step. Then, the model is ready to track tumor motion using only rib motion information during treatment. Moreover, as shown tumors located at liver organ have better correlation with the ribs in comparison with lung tumors in the same condition.

Materials and Methods

XCAT Anthropomorphic Phantom and Database Extraction

As mentioned, since contrast parameter of ribs is satisfied at fluoroscopy images we are interested in using its possible correlation with lung and liver tumors as representative. To do this, a simulation study was accomplished using 4DXCAT anthropomorphic phantom. This validated phantom that is commercially available has been developed to simulate the shapes and structures of complex organs in human body along with motion of dynamic organs such as respiratory system.³⁴ As XCAT phantom is hybrid between the realism of pixel-based and the flexibility of geometry-based phantoms, it can model dynamic process better than other available cases.³⁸

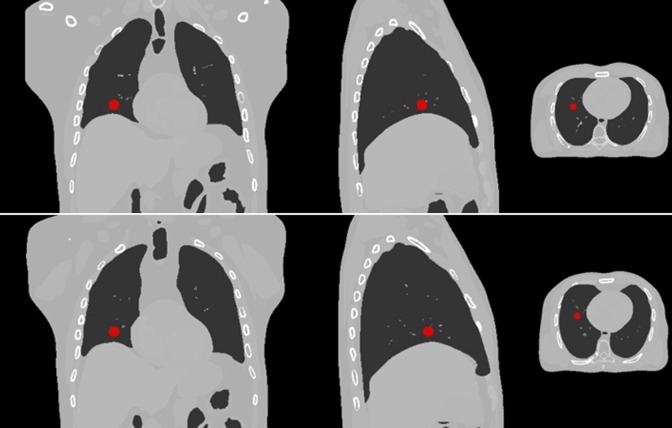
The XCAT consists of detailed whole-body models for the standard male and female adult and also motion modeling of the cardiac and respiratory systems. In this phantom, nonuniform rational b-splines (NURBS) surfaces were utilized to construct the organ shapes using the 3D anatomical computational tomography data set. Deformable registration map can also be extracted from the spline-based representation approach. Figure 1 shows typical visual application of images extracted from XCAT phantom with a lung tumor at 2 different breathing phases.

Figure 1.

Computed tomography (CT) images extracted from XCAT phantom at 2 inhale (upper images) and exhale (lower images) respiratory phases. A typical lung tumor is shown in pictures. Left, middle, and right images are coronal view, sagittal view, and transverse view of extended cardiac-torso (XCAT) phantom, respectively.

Table 1 shows 6 different breathing cycles with their characteristics generated by this phantom to mimic real respiratory pattern. For better simulation accuracy, the required parameters of XCAT phantom was defined according to motion information of real patients. For instance, maximum anterior–posterior (AP) expansion of chest wall and time of respiratory period were determined using amplitude and frequency of respiratory motion signals of real patients treated with Cyberknife Synchrony System at Georgetown University medical center (Washington, District of Columbia). This table shows the implemented breathing information in combination with inserted lung and liver tumors utilized in this work.

Table 1.

Characteristics of 6 Different Respiratory Cycles Created by XCAT Phantom.

Breathing Cycle Number	Time of Respiratory Period, Seconds	Maximum Diaphragm Motion, cm	Maximum Anterior–Posterior Expansion of Chest Wall, cm
1	5	2	1.2
2	5	1.7	0.7
3	4	1.2	0.5
4	6	2.2	1.3
5	5.5	1.8	1
6	3.5	1	0.5

Abbreviation: XCAT, extended cardiac-torso.

It should be noted that required motion database is extracted by means of vector generator mode of XCAT phantom. This mode generates displacement vector field (DVF) of real-time motion tracking of internal anatomical landmarks (ribs) and assumed lung and liver tumors predefined at different distances versus ribs position. Similar to deformable image registration, DVFs include motion information for each voxel of one frame to another frame without uncertainty errors raise due to deformable image registration strategies.

For extracting the location of tumors and desired landmark points of ribs, time interval between data acquisition step required for each frame was assumed to be 25 ms. Totally, 6 ribs were chosen equally from left and right sides of the rib-cage structure as anatomical landmarks for lung and liver tumors. Behind each rib, a tumor was assumed to be located at several specific points of a line from superficial areas toward lung depth at AP direction. Tumors volume was assumed to be 268 mm³. During respiration, the relation between motions data of assumed tumor at specific distance from a given rib is considered with motion data of an inner point of that rib as anatomical landmark, in a synchronized fashion. This strategy is repeated for all predefined lung and liver tumors at 6 supposed lines at left and right sides of lung region. By this way, the effect of distance on relation between rib-based anatomical landmarks and assumed tumors is tested. As metric tool, correlation coefficient is utilized as mathematical analysis to find how tumors motion are correlated with synchronized ribs motion for each point concerning lung tumors, separately. The same calculation was also implemented for liver tumors taking into account 2 ribs were chosen as anatomical landmarks. As another issue, we are also interested in finding a rib that has the most correlated with a group of distributed tumors in specific regions. For this purpose, the correlation coefficient parameter between right rib number 3 and a lung tumor located at different distances behind this rib were taken into account versus other given ribs.

To identify anatomical landmarks, paired ribs with number 2, 3, and 5 in right and left sides of chest wall were chosen. Ribs with these numbers represent upper, middle and lower parts of anatomical regions for lung tumors. For liver tumors, paired 7 and 8 ribs were selected with same aim. By this way, 6 anatomical landmarks in lung (left upper, left middle, left lower, right upper, right middle, and right lower) and 2 anatomical landmarks in liver (upper and lower) were taken into account with corresponding lung and liver tumors.

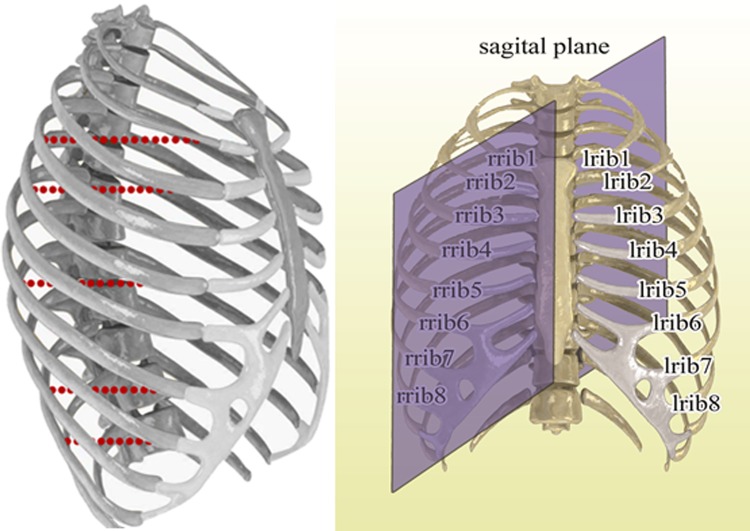
Behind each rib, an assumed tumor was considered to be located at several predefined points on a line at each simulation process. This line is started from rib toward a specific depth of lung and liver regions at AP direction. The aim is to simulate several tumor sites with specific distance in AP direction from chosen ribs at different parts. Figure 2 shows typically ribs as anatomical landmarks and tumors center at different simulation process for right ribs.

Figure 2.

Left side: ribs of rib cage as anatomical landmarks and simulated tumors behind right ribs in front of lung and liver. Right side: rib numbering and location of sagittal plane compared to rib cage.

During respiration, the relation between motion data of each tumor at specific distance from a given rib is considered with motion data of our anatomical point (landmark) of given rib in a synchronized form. This strategy is repeated for all predefined tumors at 6 supposed lines of left and right sides of lung region and 3 supposed lines of liver region.

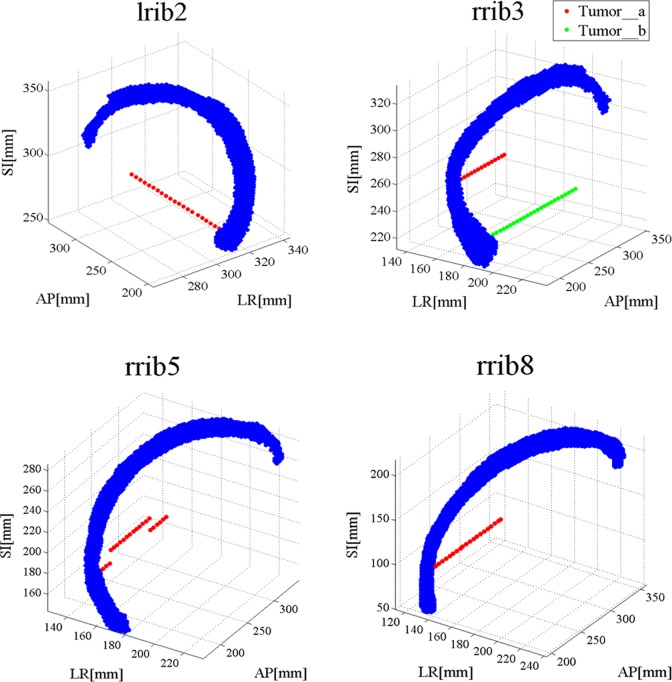
For right rib no. 3 (rrib3), 2 points in rib and 2 groups of tumors behind corresponding points were considered to investigate the location effect of desired point on rib in correlation between rib and tumor. Figure 3 shows relative anatomical location between ribs and corresponding tumors in simulating lung and liver tumors respectively with anatomical landmarks as described previously.

Figure 3.

Some of ribs and tumors in lung and liver. Blue points represent rib cage and red and green points represent simulated tumors behind ribs in extended cardiac-torso (XCAT) phantom.

In order to measure an affine relationship between the motion of rib and tumor, the correlation coefficient was calculated to investigate the ability of ribs to be used as anatomical landmarks for lung and liver tumor tracking. The correlation coefficient parameter between the rib and tumor motion signals was calculated as follow:

$$\begin{array}{l}r=\frac{{\displaystyle \sum _i{\displaystyle \sum _j(A_{\mathit{\text{i}}j}-\overline{A})(B_{\mathit{\text{i}}j}-}}\overline{B})}{\sqrt{\left({\displaystyle \sum _i{\displaystyle \sum _j{(A_{\mathit{\text{i}}j}-\overline{A})}^2}}\right)\left({\displaystyle \sum _i{\displaystyle \sum _j{(B_{\mathit{\text{i}}j}-\overline{B})}^2}}\right)}}\\ \overline{A}=\frac{{\displaystyle \sum _{i=1}^I{\displaystyle \sum _{j=1}^J\mathit{\text{A}}i\mathit{\text{j}}}}}{I\times J}\hspace{0.17em}\overline{B}=\frac{{\displaystyle \sum _{i=1}^I{\displaystyle \sum _{j=1}^J\mathit{\text{B}}i\mathit{\text{j}}}}}{I\times J}\end{array}$$ 1

where r is the correlation coefficient between 2 matrices with the same size, A and B are 2D matrices with 3 columns representing rib and tumor motion in 3 dimensions, respectively. Aij is ith rib motion data point from jth motion dimension of a given rib and Bij is ith tumor motion data point form jth motion dimension of an assumed tumor. Ā and B̄ are the average of A and B matrices, respectively.

The Performance of Adaptive Neuro-Fuzzy Correlation Model

While using implanted clip or anatomical landmark as representative for moving tumors, a model must be utilized to correlate tumor motion with clip or natural landmark. Using correlation models is mandatory at both fluoroscopy-based and also external surrogate radiotherapy. In latter case, tumor position information can be obtained by correlating motion data of tumor with motion data of some external markers located on chest and/or abdomen by means of a consistent correlation model.^39–47 It should be considered that the output of each utilized correlation model at tumor motion estimation is always with an uncertainty error that may affect on model performance accuracy. The various correlation models differ in terms of performance accuracy and complexity and range from simple linear correlation to nondeterministic models. In this study, we utilized a correlation model based on an adaptive neuro-fuzzy inference system (ANFIS) to correlate tumor motion with the motion of a selected rib as representative in fluoroscopy-based radiotherapy. This model is able to combine the abilities of fuzzy systems with numeric power of neural adaptive network systems in model configuration for accurate prediction of tumor motion. Due to a high degree of uncertainty and time-varying characteristics of breathing phenomena, an adaptive neuro-fuzzy model may be optimal for correlating the rib cage motion with internal tumor motion as a crucial issue in external beam radiotherapy.

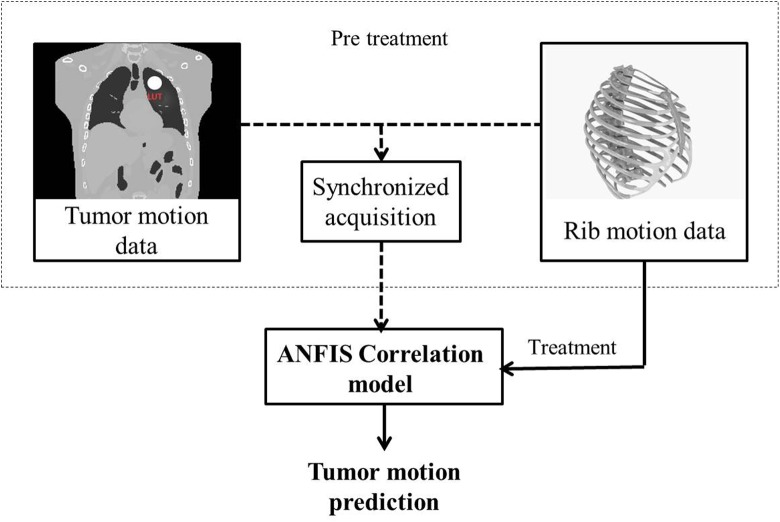
Since, ANFIS correlation model works on the basis of learning process, the model must be configured in pretreatment step before irradiating therapeutic beam using training data (Figure 4, dashed rectangular). Training data include rib motion data in x, y, and z directions as input of the model and the corresponding internal tumor motion data as model output in a synchronized form. In this step, internal tumor motion is correlated with rib cage data by classifying, model learning, and rule extraction. When ANFIS is built, the model is ready to track tumor motion as output versus time using only 3D rib motion data (Figure 4, solid black line). In the implemented ANFIS algorithm, input data collected from rib was shown in a matrix with 3 columns, where columns represent the x(t), y(t), and z(t) of rib position. Among 6 breathing cycles utilized in this work, ANFIS is configured using the information of 4 cycles and the rest of them are used for model test. Moreover, for quantitative investigation on ANFIS model performance the root mean square error (RMSE) parameter was utilized in this work. The RMSE gives the difference between predicted and corresponding observed values that are each squared and then averaged over the sample. Finally, the square root of the average is taken.

Figure 4.

Flowchart of a typical tumor motion prediction by adaptive neuro-fuzzy inference system (ANFIS) using ribs of rib cage structure.

In our utilized ANFIS, tuning the nonlinear premise parameters is done iteratively and this process is controlled proportional with the error value in correlating input–output data set in the fuzzy inference system section. In this model, fuzzy inference method is on the basis of Sugeno type, utilized Membership functions are in Gaussian and if-then rules (that are equal to the number of clusters) are connected with AND (minimum selection criteria) operator in antecedent and consequent parts of fuzzy inference system. Defuzzification as final step is also achieved by centroid calculation method.

Results

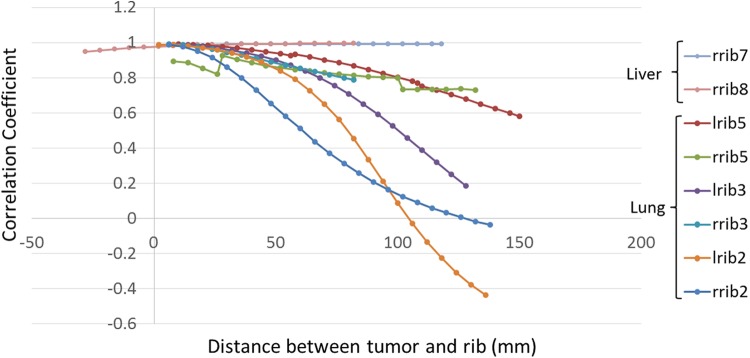
Final results of correlation coefficient between ribs and tumors are shown in Figure 5. For lung tumors according to this figure, by increasing the distance between tumor and rib in AP direction, the correlation coefficient between them has been decreased. For tumors that located behind right rib no. 2 (rrib2) and left rib no. 2 (lrib2), with distance increment toward a specific depth inside lung region, the correlation coefficient is decreased to zero, but after this depth, by increasing the distance, the absolute value of correlation coefficient has been increased as shown. As resulted, the distance effect is more remarkable for lrib2 and its corresponding tumor while correlation coefficient reach faster to zero regarding the other ribs, especially at depth from 60 to 80 mm.

Figure 5.

Correlation coefficient between ribs and tumors behind them that located in lung and liver. Horizontal axis shows the distance between tumor and corresponding rib. Vertical axis shows the correlation coefficient between tumor and corresponding rib.

In Figure 5, for tumor located behind left rib no. 5 (lrib5) and right rib no. 5 (rrib5), there are 2 discontinuities as prompt shift down-to-ups at 56 and 26 mm depth and up-to-down at 108 and 100 mm depth, respectively, in the curves. The first shift belongs to the place which the distance between tumor and diaphragm has been increased and therefore the correlation coefficient between tumor and rib has been increased. Second is belong to the place which tumor is closed to the diaphragm and therefore the correlation coefficient has been increased. Because of a more shift of tumor located behind rrib5 (12 mm in superior–inferior [SI] direction) in comparison with lrib5 (6 mm in SI direction), these changes are more noticeable for rrib5.

As seen in Figure 5, with the exception of rrib5, the starting point of other curves for tumors close to the rib, the correlation coefficient parameter is near 1. This means the maximum correlation is happening between ribs and superficial tumors near them.

Considering correlation coefficient between ribs and corresponding liver tumors, for a given tumor located at different sites behind right rib no. 8 (rrib8), while the distance increases in AP direction, the calculated correlation coefficient is increased. But, this the curve slope increment is very slow in regard with lung tumors. For right rib no. 7 (rrib7) at first with distance increasing, the correlation coefficient has been increased till a specified depth and then it has been almost constant. As resulted, the correlation between ribs and tumors located in liver is not remarkably influenced by distance increment.

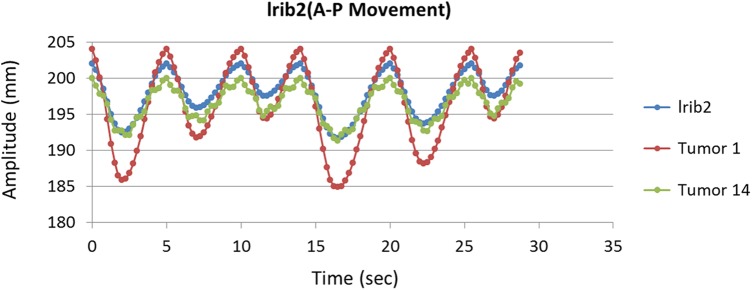
Figure 6 shows 1-dimentional motion of lrib2 with 2 assumed tumors at 2 close (tumor no. 1) and far (tumor no. 14) distances away from this rib on AP direction as function of time. As shown in this figure, both tumors motion have same phase with rib motion while deeper tumor (no. 14) motion may disturbs mainly at inhalation–exhalation peaks against superficial tumor that is due to heart bit (no. 1). As seen in this figure, motion amplitude of rib is 10.34 mm while this value is 19.14 and 8.7 mm on AP direction for superficial and deep tumors, respectively.

Figure 6.

One-dimensional motion of lrib2 and 2 assumed tumors at close (tumor no. 1) and far (tumor no. 14) distances away from this rib on AP direction as a function of time.

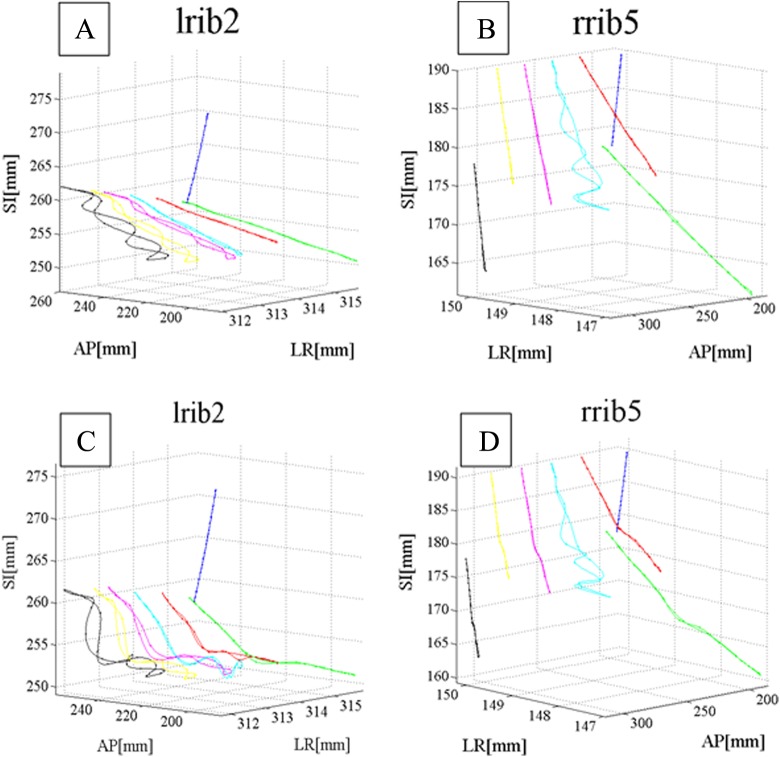
Figure 7 shows 3D real (A and B) and predicted (C and D) motion data of 2 given ribs and an assumed tumor at different sites. In this figure, 2 chosen ribs are lrib2 and rrib5 belonging to ventral part of lung (blue line) and assumed tumor is located at different distance behind these ribs (green, red, cyan, magenta, yellow, and black lines). Tumor motion was predicted using ANFIS correlation model using only ribs motion database as input. As seen, there is a close correlation between actual and predicted motions database depends on tumor site.

Figure 7.

Three- dimensional (3D) real (A and B) and predicted (C and D) motion data of 2 given ribs and an assumed tumor at different sites.

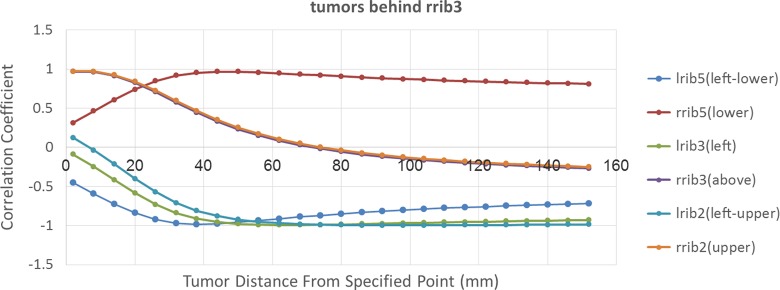
In order to discover the best rib as anatomical landmark to track tumor motion, the correlation coefficient between 3D motion of all ribs located on the ventral part of lung and an assumed tumor located at different sites behind rrib3 has been taken into account. The results of this calculation were shown in Figure 8. According to this figure correlation mode between tumors and ribs can be categorized into 2 groups. The first group including lrib5, left rib no. 3 (lrib3), and lrib2 have a negative correlation with tumors located at right side of the lung as opposed direction with these ribs. In should be noted that all of these ribs are located on the ventral part of left lung. Moreover, correlation behavior of rrib5 located at the bottom of assumed tumors is similar with 3 mentioned left ribs, but in positive mode. By increasing the distance between tumor and rib in AP direction, the correlation coefficient between them has been increased to near −1¹ until a specific depth and then, it has been decreased. The second group includes rrib3 and rrib2 located in front and at the top of the assumed tumors, respectively. For these ribs, by increasing the distance between tumor and rib, the correlation coefficient is decreased to zero until specific depth and then it will be increased. These 2 groups have an opposite behavior. Finally, depending on where the tumor is located, we can find the best rib to be correlated with that tumor. For instance, in this case lrib2 is the best option to be correlated with a tumor located at 12 cm depth with 99% correlation coefficient.

Figure 8.

The correlation coefficient between tumors that located behind rrib3 and all ribs that located on the ventral of lung. Vertical axis shows the correlation coefficient between mentioned tumor and all ribs. Horizontal axis shows the distance between tumor and fixed point on rrib3.

The performance of each rib in correlation with each tumor position was taken into account and the rib with best correlation was chosen. Figure 9 shows the role of each rib in correlation with assumed tumors located at different distances from specific point using ANFIS correlation model. As seen in this figure the best ribs are rrib2, lrib5, lrib3, and lrib2, respectively, while tumor position is going toward depth. Therefore, the rib with best correlation is changing based on tumor position.

Figure 9.

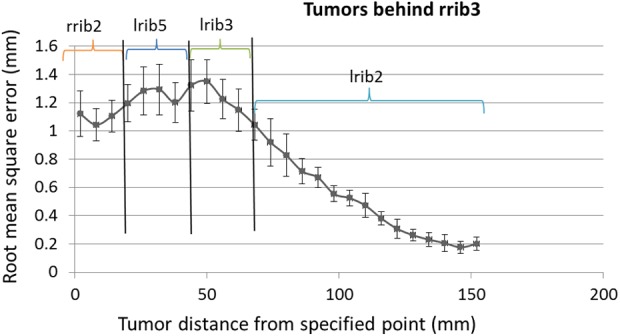
Root mean square error (RMSE) of prediction of tumors located in ventral of rrib3 using adaptive neuro-fuzzy inference system (ANFIS) model by means of best correlated ribs from Figure 8.

To investigate the effect of chosen point as landmark of a rib on its correlation with assumed tumor the correlation coefficient between 2 groups of tumors located behind rrib3 and corresponding predefined points were taken into account (Figure 10). The point of interests on rrib3 and predefined tumor motion lines are already shown in Figure 1. By comparing this figure with Figure 10, it is emerged that while a desired point of a rib is close to the sagittal plane in left–right (LR) direction (Figure 1), its correlation with tumor decreases. In Figure 10, the correlation coefficient between tumor_a with rib_a is more than rib_b; this is also correct for tumor_b. It should be noted that the desired point of rib_b is closer to sagittal plane than desired point of rib_a. As resulted from Figure 10, when tumor becomes close to the sagittal plane in LR direction, its correlation with rib landmark decreases. In Figure 10, the correlation curve between rib_a and tumor_a is superior to rib_a and tumor_b.

Figure 10.

The correlation coefficient between 2 groups of tumors, behind rrib3 (tumor_a and tumor_b) with 2 corresponding point on rrib3 (rib_a and rib_b). Four possible ways to make a correlation between tumors and points have been showed in these curves.

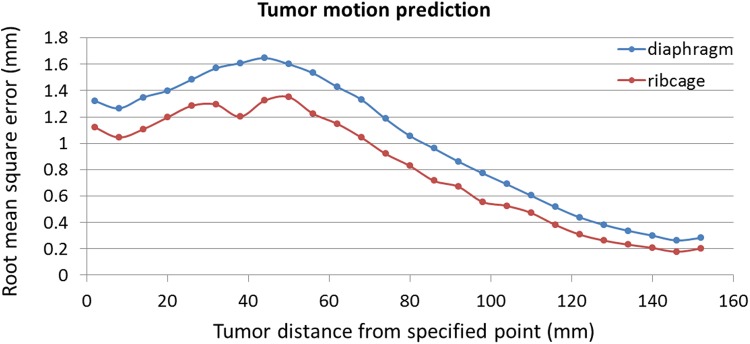
In Figure 11, a comparative assessment has been shown between ribs and diaphragm motions data representative as anatomical landmarks correlated with an assumed tumor located at each position at lung and liver organs. As resulted from this figure, the average RMSE is 1 mm and 0.8 while diaphragm and ribs are, respectively, considered as anatomical landmark in correlation with assumed tumors. Therefore, ribs may perform as representative better than diaphragm as natural anatomical landmark.

Figure 11.

Comparison of tumor motion prediction using diaphragm and ribs signals as anatomical landmarks, by adaptive neuro-fuzzy inference system (ANFIS) model.

Discussion

In radiation treatment of moving tumors located at thorax region, in order to compensate the effect of motion error on prescribed dose several strategies were proposed such as gated and real-time tumor tracking during therapeutic beam irradiation. In these strategies, tumor motion information must be captured to enhance treatment quality by delivering the beam, controllably. One of the applicable strategies for tumor motion monitoring is using continues X-ray imaging such as fluoroscopy as real time. In this method, an internal fiducial marker may be implanted inside tumor volume for better tracing while tumor is not visual at fluoroscopy images due to lack of information in gray scale fluoroscopic images. Implanting fiducial markers is invasive procedure and caused several side effects such as increasing risk of pneumothorax and also treatment costs for patients. As alternative, using internal anatomical landmarks can be taken into account for this issue. For this aim, recognizable anatomical landmarks that are high contract at fluoroscopy images must be utilized that also have reasonable correlation with a given tumor. In previous literatures, diaphragm and lung boundary were introduced as natural anatomical landmarks instead of using artificial clips. In this study, rib cage was proposed as appropriate landmark due to its high contrast at fluoroscopy images. The most challenging issue in using ribs as landmark is the existence of reliable correlation between rib and tumor motions pattern that we investigated in this work, comprehensively.

For this aim, at first the correlation coefficient parameter between several ribs chosen from upper, middle, and lower parts of lung and assumed tumors were calculated, separately. Calculations were done through simulation studies by means of 4DXCAT anthropomorphic phantom which models motion of dynamic organs to mimic real respiratory pattern. This validated phantom has been widely utilized at several research activities ranging from nuclear medicine to radiation treatment of moving tumors.^48–50 Since, this phantom simulating different dynamic organs with detailed information and also breathing motion issues are not exactly same as real patient body due to phantom simplification, some concerns may raise during phantom performance. In order to address this issue, motion simulation parameters were defined using breathing data of real patients treated with Cyberknife Synchrony module to minimize uncertainty error of phantom performance. Eight points of ribs as anatomical landmarks (6 points located at ribs covering lung and 2 point located at ribs covering liver) with several tumors behind each rib were defined to produce required database. Correlation coefficient between each rib and corresponding tumor that moves on a line at AP direction toward lung and liver depth was calculated separately to investigate the effect of distance between landmark point and tumor. Furthermore, in order to find the most correlated rib with a group of lung and liver tumors, correlation coefficients between assumed tumors (located behind rrib3) and lung ribs were calculated. According to information of Table 1, six different respiratory patterns representing different possible breathing patterns of a typical patient were utilized, but in reality patients are highly individual and results obtained over 6 respiratory patterns on average may arise some uncertainty errors; so, there is need to investigate more patients. Moreover, in order to taking into account the uniqueness of each patient we can select best rib in an adaptive manner. Moreover, in addition to tumor location several variables including tumor volume, type, and so forth affect tumor motion which didn’t consider in this study and must be considered in future study on real patients.

Final analyzed results confirmed the ribs are robust to be used as natural anatomical landmarks representative for motion tracking of lung and liver tumors due to their availability around most of dynamic tumors and high contrast. As the most important outcome emerged from correlation coefficients, the distance between tumor and rib has the most effect on the correlation between them. The motion pattern of assumed tumors differs from superficial toward depth in comparison with motion pattern of each rib that is due to tumor type (lung, liver, pancreas, etc), respiration, and heartbeat motion. Initial results showed that superficial tumors near ribs are in close correlation with ribs with correlation coefficient close to unity but this result is not extended to all tumors while liver tumors seem have more stability with less dependence to their location versus lung tumors. This is due to breathing phenomena variability that has different influence on motion pattern of lung tumors against liver tumors. It is also worth mentioning that liver tumors are less deformed regarding with lung tumors due to respiration. According to obtained motion information of ribs, it should be noted that the motion of all ribs are not in a same fashion, while the pattern of their motion at upper part of chest wall is changing to lower part. As next challenging issue that is clinically important is choosing the best rib that has most correlation with a given tumor. Therefore, it is necessary to determine an appropriate rib as anatomical landmark for a given tumor depending on its specification in the pretreatment session before therapeutic beam irradiation. We assessed ANFIS as prediction model that could accurately estimate tumor position as function of time according to rib motion. The model output was compared with real tumor motion as benchmark that is accessible at our utilized database to verify model performance accuracy. This part (finding the best rib correlated with a tumor and configuring correlation model) should be done at pretreatment step of radiotherapy session at clinical situation.

As concluded from total results, the less degree of proposed correlation between some of lung tumors and corresponding ribs is due to several effects as (1) phase difference between the rib and tumor motions versus time, (2) changing of relative amplitude of tumors motion very irregularly in comparison with rib motion, (3) perturbing tumor position by the heartbeat with high degree of variability, and (4) uncertainty error of utilized correlation model output.

The results presented here represent availability of using rib cage as anatomical landmark to track lung and liver tumors in a noninvasive way, with high accuracy. However, to achieve this goal several developments are required. Though the study here implemented using XCAT phantom, the proposed idea can be implemented on real patient data at our future studies. This strategy is also applicable for external surrogate radiotherapy as another treatment modality.

In this study, one point into the rib was considered as anatomical landmark but by taking averages over large numbers of measurements the correlation between tumor and anatomical landmark motions may be increased. Furthermore, we compared the performance of ribs as anatomical landmark with diaphragm as conventional natural marker assessed before and based on our calculated results around 20% improvement was achieved in the accuracy of rib performance against diaphragm.

Conclusion

In radiation treatment of moving targets as alternative for implanting fiducial marker, natural anatomical landmarks located at thorax region of patient body is introduced to extract tumor position information as representative. In this work, ribs of rib-cage structure were proposed as optimal anatomical landmark due to high-density property of this tissue that causes proper visualization in fluoroscopy images. We investigated the possible existence of proper correlation between different ribs at upper, middle, and lower parts of rib cage structure and various lung and liver tumors located at different sites, using 4DXCAT anthropomorphic phantom. Correlation coefficient and ANFIS correlation model performance as final results represented the abilities of ribs of rib cage as anatomical landmark to track lung and liver tumors in comparison with diaphragm. Observations of several measurements on correlations showed an appropriate correlation between tumors and ribs while the degree of this correlation is changing depends on tumor type and its site. We conclude that the lung tumors are a more varied and complex against liver tumors in correlation with ribs motion pattern.

Future studies will investigate further types of tumors at 3 AP, SI, and LR directions 3 dimensionally in correlation with ribs using real patient database at both fluoroscopy-based and external surrogates-based radiotherapy as another treatment modality. Since the best rib representative tumor motion varies tumor by tumor, so selecting the best rib can be done adaptively on a patient by patient basis using for instance feature selection algorithms.

Abbreviations

3D

3-dimensional

4D

4-dimensional

ANFIS

adaptive neuro-fuzzy inference system

AP

anterior–posterior

DVF

displacement vector field

LR

left–right

SI

superior–inferior

lrib2

left rib no. 2

lrib3

left rib no. 3

lrib5

left rib no. 5

rrib2

right rib no. 2

rrib3

right rib no. 3

rrib5

right rib no. 5

rrib7

right rib no. 7

rrib8

right rib no. 8

RMSE

root mean square error