Abstract
Studies of reproductive physiology involve rapid sampling protocols that result in time series of hormone concentrations. The signature pattern in these times series is pulses of hormone release. Various statistical models for quantifying the pulsatile release features exist. Currently these models are fitted separately to each individual and the resulting estimates averaged to arrive at post-hoc population level estimates. When the signal-to-noise ratio is small or the time of observation short (e.g., 6 hours) this two-stage estimation approach can fail. This work extends the single subject modelling framework to a population framework similar to what exists for complex pharamacokinetics data. The goal is to leverage information across subjects to more clearly identify pulse locations and improve estimation of other model parameters. This modelling extension has proven difficult because the pulse number and locations are unknown. Here we show that simultaneously modelling a group of subjects is computationally feasible in a Bayesian framework using a birth-death Markov chain Monte Carlo (BDMCMC) estimation algorithm. Via simulation we show that this population based approach reduces the false positive and negative pulse detection rates and results in less biased estimates of population level parameters of frequency, pulse size and hormone elimination. We then apply the approach to a reproductive study in healthy women where approximately 1/3 of the 21 subjects in the study did not have appropriate fits using the single subject fitting approach. Using the population model produced more precise, biologically plausible estimates of all model parameters.
Keywords: hierarchical models, birth-and-death MCMC, Bayesian, luteinizing hormone, reproductive hormones
1. Introduction
This work is motivated by recent collaborative studies of reproductive fitness and obesity [1, 2]. Female obesity is associated with decreased reproductive fitness: irregular ovulation and menses, subfertility, and harmful metabolic programming in the offspring [3–6]. However, the mechanisms of reproductive dysfunction in obesity are not well understood. To identify potential mechanisms, time series of concentrations of reproductive hormones [e.g. luteinizing hormone (LH)] are collected. The goal is to quantify the hormone secretion patterns and identify differences in secretion between groups.
Reproductive hormones are a class of hormones that are secreted intermittently in pulses [7, 8]. In the observed data, pulsatile secretion is observed as a fairly sharp increase in blood hormone concentration followed by a steady decrease in concentration as the hormone is eliminated from the blood (Figure 1). Because elimination is always occurring, pulsatile secretion is not directly observed. This means the observed concentration is a convolution of secretion and elimination and that the pulse locations are unknown. The major features of clinical interest are the pulse frequency, average amount of hormone secreted in a pulse, and basal concentration (i.e., amount of non-pulsing secretion). The current analysis approach is to fit a statistical model of pulsatile hormone concentration separately for each subject [9–17]. Fitting each individual series is often two-staged where first a set of pulse locations are identified using a threshold criterion and then conditional on these locations, the other parameters are estimated using maximum likelihood. More recently a Bayesian approach using birth-and-death MCMC has been developed for fitting a single subject’s hormone series [15]. This approach allows for simultaneous estimation of the number of pulses and the other parameters and improves estimation in single subject analysis [18]. Here we extend the model and estimation approach to simultaneously fit a population of subjects and show that fitting a population of subjects provides even further improvements in estimation.
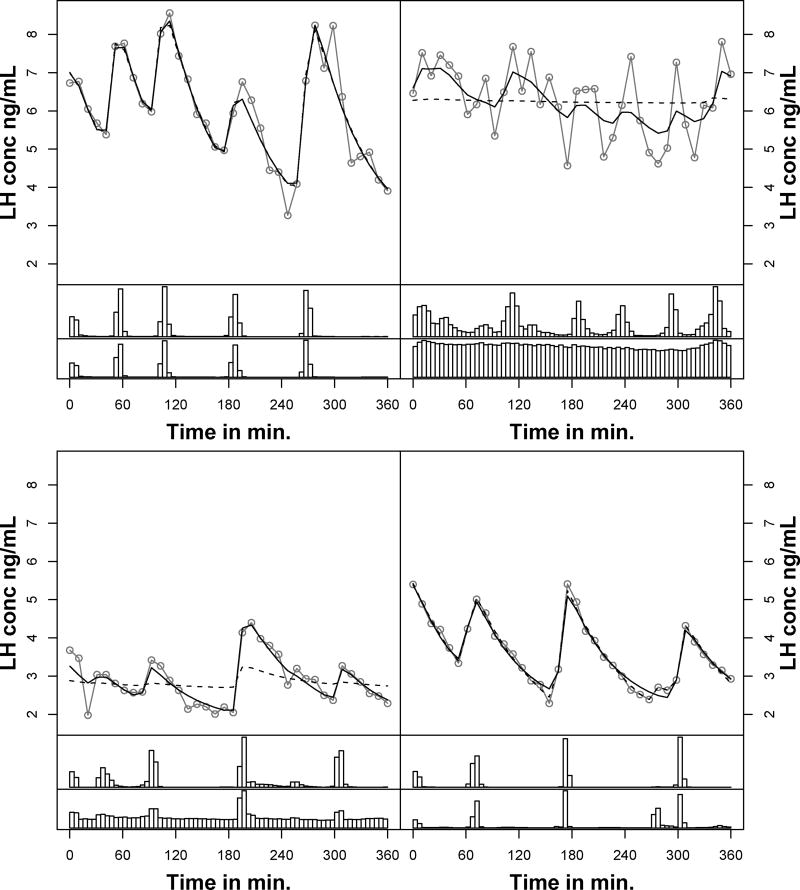
Figure 1.
Observed hormone concentration profiles and posterior predictive fits of four of the ten healthy normal weight women pre-treatment. The observed hormone concentrations are in grey circles and the black lines represent posterior predictive fits (solid - population model, dashed - single subject). The top histogram under each hormone profile is the posterior distribution of pulse locations from the population model and the bottom histogram from the single-subject model.
In our motivating studies, women had blood sampled every 10 minutes for 6 hours, once before treatment with an estrogen patch and once after one month of using an estrogen patch. This was a shorter collection length compared to a more typical 12-hour design. In preliminary analysis using the Bayesian deconvolution model [15], we were unable to characterize the pulsatile secretion in all of these subjects. We hypothesized that the existing single subject approach had poor identifiability of pulse secretion in some series given the lower signal-to-noise ratio and shorter length of observation. We and others [14, 15, 17, 18] further hypothesized that simultaneously fitting all subjects together and leveraging the information across subjects would improve estimation. Simultaneously fitting a population of subjects has proved useful in other problems involving complex models for individual subjects (e.g., pharmacokinetic data [19, 20]). Moving to a population approach has been computationally infeasible given the computational issues with model selection that exist with two stage approaches. We show that the Bayesian birth-and-death MCMC algorithm allows us to overcome these computational issues.
This paper is organized as follows. In Section 2, we first extend the deconvolution model of pulsatile hormones from a model of a single subject to a population of subjects, developing notation and highlighting the new primary parameters of interest. We then show in Section 3 how the Bayesian single subject birth-and-death MCMC estimation approach [15,21] can be extended to our population model in a computationally feasible manner. This continues to allow for simultaneous estimation of pulse locations and the other model parameters. We use the deconvolution modeling framework due to its biologic plausibility, existing Bayesian development using this model [22], and its common use in the clinical literature. However, extending other single subject statistical models of pulsatile hormone data would also be plausible. In Section 4, via simulation, we show situations when the population modeling approach results in improved estimation of sample characteristics compared to fitting each subject separately. We then show that the population based modeling approach improves estimation for the motivating LH data in Section 5. Discussion is provided in Section 6.
2. The Population Bayesian Deconvolution Model
2.1. Overview
The deconvolution model [10] is a convolution integral defining how the independent hormone secretion and elimination components interact over time to produce a profile of observed hormone concentrations. There are three levels of parameters: 1) pulse specific parameters; 2) subject specific parameters, which define features that are common across pulses within an individual; and 3) population level parameters, which define features that are common across subjects. The model and parameters are defined further in Table 1 for continued reference. Below we define the likelihood of the time series of hormone concentrations and then define the priors for the three levels of parameters.
Table 1.
Notation Dictionary
| Hormone Concentration Model | ||
|
| ||
| yij | Observed hormone concentration at time tj for subject i | |
| N | Number of subjects | |
| m | Number of observations on a subject | |
| S(t) | Pulsatile secretion function | |
| E(t) | Elimination function | |
| εij | Model error for log hormone concentration | |
| Pulsatile Secretion Function, S(t) | ||
|
| ||
| Ns,i | The number of secretion events (pulses) for subject i | |
| θs,i,k = (αik, ωik, τik) | Log pulse mass and width and location for pulse k, subject i | |
| μs,i = (μα,i, μω,i) | Mean log pulse mass and width for subject i | |
| μs = (μα, μω) | Mean log pulse mass and width | |
| ϒs | Pulse-to-pulse variation in log pulse mass and width (i.e., within subject variation) | |
| Σs | Subject-to-subject variation in mean log pulse mass and width | |
| Elimination Function E(t) | ||
|
| ||
| θh,i | Half-life for subject i | |
| μh | Mean half-life | |
|
|
Subject-to-subject variation in the half-life | |
| Baseline Concentration, B(t) | ||
|
| ||
| θb,i | Baseline for subject i | |
| μb | Mean baseline | |
|
|
Subject-to-subject variation in the baseline | |
| Model Error | ||
|
| ||
|
|
Model error variance | |
2.2. The Likelihood
Let yi(tij) be the observed hormone concentration for subject i at observation time tij where i = 1, …, N and j = 1, …, mi. N is the number of subjects defining the population under study. Each subject has mi observations. In practice, the observation times are common across subjects. Thus, in future notation, tij = tj and mi = m.
Let Cij be the true hormone concentration for subject i at time tj. The following statistical model links the observed and true hormone concentrations: log[yij] = log[Cij] + εij, where and εij represents technical and biologic variation. We model observed concentration on the log scale because hormone concentrations are constrained to be positive and error increasing with concentration is biologically plausible [23]. Cij, the true concentration, is defined by the following convolution integral:
| (1) |
B(t; θb,i) models the non-pulsatile, baseline concentration, S(t; θs,i) models pulsatile secretion, and E(t; θh,i) models hormone elimination. For this work, the mathematical forms defining B, S, and E are the same across subjects. However, B and E are defined by a set of subject specific parameters, θb,i and θh,i. S is defined by a set of subject and pulse specific parameters , where Ns,i is the number of pulses observed over the period of observation for subject i and each θs,i,k is a set of pulse specific parameters.
The baseline concentration, B(t; θb,i) is assumed constant over time and defined by θb,i, i.e., B(t; θb,i) = θb,i. The pulse secretion function, S(t; θs,i), is modeled as the superposition of pulse secretion events, i.e., , where Ns,i is unknown. The secretion shape function, p, is a user defined non-negative time dependent function that further depends on pulse specific parameters θs,i,k. In practice, p is often assumed Gaussian in shape and then scaled by the mass of the pulse, i.e. . This means that each pulse is defined by a location, τi,k, a mass (amount of hormone secreted), αi,k, and a duration, ωi,k, i.e., θs,i,k = (τi,k, αi,k, ωi,k)′. The elimination function is a single exponential decay defined by half-life, θh,i, i.e., , which can be generalized to a double exponential decay as necessary. Thus, the decay is constant across pulses within an subject but allowed to vary across subjects.
2.3. Priors
The pulse and subject specific parameters are linked to population parameters through a hierarchical prior specification. The full prior factorizes as follows:
| (2) |
| (3) |
| (4) |
| (5) |
where Eq. (2) is pulse specific priors with the corresponding subject and population specific hyper-priors, Eq. (3) is the subject specific prior for the baseline with the corresponding population specific hyper-priors, Eq. (4) is the subject specific prior for the half-life with the corresponding population specific hyper-priors, and Eq. (5) is the subject specific priors for the model error variance. Although the prior distributions chosen will be problem specific, below we define the priors for our application and simulations. The population parameters are entirely new in this work. They are the main quantities of interest in pulse analyses, but in current analysis platforms are estimated post-hoc by averaging parameter estimates from single subject analyses. This model extension focuses on improving estimation of all the parameters by expanding the model hierarchy to directly estimate the population level quantities of interest and leveraging the population information when estimating the subject level parameters.
2.3.1. The hierarchical prior for the pulse specific parameters (2)
Recall, the pulse secretion model is a superposition of Gaussians, each defined by its location, mass and duration {θs,i,k = (τi,k, αi,k, ωi,k)′}.We assumed (log αi,k, log ωi,k)′ ~ MV N(μs,i, ϒs), a multivariate normal defined by a subject specific mean and a variance that is assumed common across all subjects. The log normal was chosen given the positivity constraints on pulse masses and widths. As in previous work [15, 21, 22], we assumed the set of pulse locations conditioned on the number of pulses, Ns,i, was distributed as the 3rd order statistic of (3Ns,i + 2) Unif[a, b], i.e. , where a and b are chosen by the user to be slightly outside the range of observation in the study. This prior reduces the chance that a single biologic secretion will be modeled by more than one Gaussian component. The subject specific mean log pulse mass and width were assumed bivariate normal, μs,i ~ N(μs, Σs) and the population mean log pulse mass was assumed bivariate normal μs ~ N(ms,Vs). In the variance-covariance matrices (ϒs and Σs) the components were assumed uncorrelated and the standard deviations of each component, σα, σω, υα and υω, were each assumed Uniform. Finally, the number of pulses was Poisson, Ns,i ~ Poi(r), where r is chosen by the user.
2.3.2. The hierarchical prior for the baseline parameters (3)
We assumed the subject specific baselines had Gaussian priors centered around a common mean, . The prior on the population mean, μb was also assumed Gaussian, μb ~ N(mb, υb) and σb was assumed to have a Unif(0, c] prior where mb, υb, and c are user specified values. In practice, the baselines are far from zero; however, in cases where they may be near zero, a log normal prior could be specified.
2.3.3. The hierarchical prior for the elimination parameters (4)
The framework for the half-life was similar to the baseline. We assumed the subject specific half-lives had Gaussian priors centered around a common mean, . The prior on the population mean, μh was also assumed Gaussian, μh ~ N(mh, υh) and the standard deviation, σh, was assumed to have a Unif(0, d] prior where mh, υh and d are user specified values. In practice, the half-lives are also far from zero. In cases where they may be near zero, a log normal prior could be specified.
The prior for the model error (5) is assumed common across all subjects, , where e and f are chosen by the user.
2.3.4. Single subject model
In the single subject model the pulse specific priors are as in the population model. The subject specific parameters have the same form as the subject specific priors specified above but the population parameter values are user specified instead of having a further hierarchical specification. The pulse specific standard deviations, σα,i and υω,i were Uniform. For the prior was the same for all subjects.
3. Estimation and Implementation: Birth-and-death MCMC
3.1. Population model
The number of pulses for each subject was unknown, thus, we used an estimation algorithm that allows the number of parameters to differ from iteration to iteration. Examples of algorithms that handle such cases include reversible jump MCMC [24] and birth-and-death MCMC [21]. Given success with the birth-and-death MCMC for single subject models [15, 22], we developed a birth-and-death MCMC (BDMCMC) algorithm for this problem. In brief, a single iteration of BDMCMC occurred in two stages. First, the number of components for each subject was simulated using a set of birth-death processes. Next, conditional on the number of pulses for each subject, the remaining pulse, subject and population level parameters were drawn using a traditional Gibbs within Metropolis-Hastings sampler [25]. One iteration occurred as follows:
For subject i, update (Ns,i, {θs,i,k}) by running the birth-death process. Repeat for all subjects.
Update each population level parameter (μs, μb, μh, Σs,ϒs, ) using a Gibbs sampler [26] or a random walk Metropolis-Hastings algorithm [25], as appropriate.
For subject i, update each subject level parameter (θb,i, θh,i, μs,i) using a Gibbs or Metropolis-Hastings algorithm, as appropriate. Repeat for each subject. Note, the mean in the prior on pulse number, r, is not updated.
For subject i, update each pulse level parameter in {θs,i,k} using random walk Metropolis-Hastings algorithms. Repeat for each subject. This step is not necessary for convergence but improves mixing [21].
For subject i, update the model error precision using a Gibbs sampler. Repeat for each subject.
In implementation, each chain was run for 200,000 iterations (simulations) and for 2 million iterations (application). Every 50th iteration was stored. The first 10% of the iterations were ignored as a burn-in period. For parameters drawn using a random walk Metropolis-Hastings algorithm, we used a Gaussian proposal distribution centered on the current value of the parameter. The starting proposal variance was adaptively updated every 500th iteration for the first 25,000 iterations to achieve an acceptance rate between 25%–50% [25]. Mixing and convergence were assessed visually using trace plots (Supplementary Material Figures 1 and 2). One population of subjects (144 observed values on each subject for 10 subjects for 200,000 interations) was completed in approximately 50 minutes on a laptop with an Intel Core i5 2.40 GHz processor, making this algorithm usable on a personal computer. Two-million iterations on 6 hours of data for 10 subjects (36 observed values per subject) completed in a similar amount of time.
When setting the priors, the means were set to values based on previous analysis or existing clinical knowledge. The variances were set to be vague. The mean pulse number was set to 5. The mean log pulse mass was 1 log concentration unit, the mean log pulse width was 3 log min2, the mean half-life was set to 45 minutes and the mean baseline was 2.6 concentration units. The variances were set to 100 with the exception of the half-life, which was set to 1000.We initialized the pulse to pulse variation of the log masses and widths to 10 units2. The upper bound of the Uniform distributions for the pulse-to-pulse and subject-to-subject standard deviations was set to 10. The parameters in the model error prior were both set to 0.0001. We initialized the algorithm with the means of the priors. As discussed in [15], with the exception of pulse number, starting values in a biologically plausible range produce similar results. Pulse number was initialized at a value less than the mean pulse number because convergence from below reduces the chance that a single biological pulse is modeled with two Gaussian components.
The population model can be implemented by compiling a set of custom coded C programs. This approach was chosen to reduce computation time. The code and example input and data files are available at https://github.com/BayesPulse/poppulsepaper.
3.2. Single subject model
Each subject was fitted separately. One iteration of the subject level birth-and-death MCMC algorithm occurred as follows:
Update (Ns,i, {θs,i,k}) by running the birth-death process.
Update each subject level parameter, (θb,i, θh,i, μs,i, υα,i, υω,i), using a Gibbs or Metropolis-Hastings algorithm, as appropriate. Note, the mean in the prior for pulse number is not updated.
Update each pulse level parameter in {θs,i,k} using a random walk Metropolis-Hastings algorithm.
Update the model error precision using a Gibbs sampler.
The implementation was as in the population model. The values for the parameters in the priors for the subject level parameters were the same as the values for the population level parameters in the population model. The population level parameters were estimated post-hoc by averaging the posterior means of the subject level parameters. Subject-to-subject variance estimates were obtained by calculating the sample variance of the parameters at each iteration. The single subject approach can be implemented through an R package that calls a set of custom coded C programs and is available for download at https://github.com/BayesPulse/pulsatile.
4. Simulation
We simulated various scenarios to investigate when a population model would provide improvements in estimation compared to the single subject approach. Across the simulations we varied the population mean pulse frequency, mass, and half-life. This covered high and low signal-to-noise settings. Typical designs have 12 to 24 hours of data sampled every 10 minutes. Our motivating study had a short sampling duration of only 6 hours. Thus, we simulated 6 hours and 24 hours of hormone concentration data sampled every 10 minutes. For each scenario we generated 100 sets of samples with 10 subjects per sample. For each population, we simulated each hormone concentration series one subject at a time. We first simulated the subject level parameters (mean mass and width on the log scale, baseline and half-life) from their population distributions, which were the distributions specified above. Next, we simulated pulse locations for each subject using a renewal process [27]. Given the pulse locations and subject level parameters, the mass and width for each individual pulse was simulated from the pulse specific distributions specified above. The logs of the true hormone concentrations were then calculated using the deconvolution model, (1) in Section 2.2. Model error at each observation was drawn independently from a normal distribution with mean 0 and variance 0.005 log concentration units2. The model error was added to the log of true hormone concentration for each time point and the result was back transformed to the natural scale. The values at all observed points were recorded as the vector of observed hormone concentration.
Five scenarios were investigated. Throughout the scenarios, mean pulse width and variability of pulse width were the same (μw = 3.0 minutes2, ). For all scenarios, the mean and variance of baseline were μb = 2.6 units and . As in previous work [18, 28], the minimum interpulse interval for the renewal process was set at 40 minutes to prevent pulses from being too close together in time.
The first scenario was a reference scenario with a high signal-to-noise ratio. In this scenario, mean pulse mass, μa, was 1.25 and the subject-to-subject, , and pulse-to-pulse variability, , were each 0.5 units2. Subjects had a mean half-life of 45 minutes with low subject-to-subject variability . There was an average number of 12 pulses over the 24 hour period of observation (mean interpulse interval of 120 minutes). We simulated a high interpulse variability (variance of interpulse interval of 4000) so that different subjects would have a varied pulse number. In the second scenario we reduced the sampling length to 6 hours but kept the other parameters the same. The third scenario reduced the pulse frequency over the 24 hour period to 6 (mean interpulse interval of 240 minutes and a high variation of 10000 minutes2). All other parameters remained the same. For the last two scenarios the signal-to-noise was reduced by reducing the average log pulse mass to 0 log concentration units. We increased the subject-to-subject variability of the mean pulse mass and investigated a half-life of 45 minutes and 60 minutes. The longer half-life was investigated because it reduces the number of observation points that occur before the next pulse, which can make half-life more difficult to investigate in single subject analyses.
One assumption when fitting a population model is that biologically all subjects had pulsatile release of the hormone during the study period. To investigate sensitivity to this assumption, we simulated data where no subjects had pulsing. The log hormone concentration was simulated from a Normal(4.5, 0.052), which results in average concentration levels similar to the pulsing series. We also created populations of 10 subjects where 80% were pulsing according to the reference model and 2 subjects were simulated from the random Normal distribution.
4.1. Methods of evaluation
The population and single subject models were compared based on the following metrics:
False Positive rate (FP): This is 100 times the number of estimated pulses that are not within 20 minutes of a true pulse location divided by the number of pulses that were estimated. The false positives were identified for each iteration and the percentage calculated by summing the false positives across all iterations and dividing by the total number of pulses across all iterations. Sensitivity to thresholds between 10 and 30 minutes were also investigated and the patterns were similar (data not shown).
False Negative rate (FN): This is 100 times the number of true pulses that have no estimated pulse within 20 minutes divided by the number of pulses that were simulated. The false negatives were identified for each iteration and the percentage calculated by summing across all iterations and dividing by the total number of simulated pulses times the number of iterations.
Average Bias: This is the average of the bias (estimated posterior mean minus the true parameter value) for each of the 100 simulated sets of concentration profiles.
95% Coverage: This was the percentage of simulations, or subjects depending on the parameter, where the true parameter value was included in the 95% equal tails credible interval.
5. Results
5.1. Simulation
5.1.1. Reference case
In the reference scenario, the signal-to-noise ratio was relatively large. The pulses were reasonably identifiable and variability in the pulse mass and pulse width between and within subjects was small. Variability in number of pulses across subjects was large, but the variation across subjects in baseline and half-life was small. For this scenario, we expected the population model and the single subject model to perform similarly. Compared to the single subject approach, the population approach resulted in a small improvement in the false positive (FP) and false negative (FN) rates and small reductions in the bias of most mean parameters when using the population approach (Table 2). The bias reduction was greater for the subject-to-subject variance estimates (Table 3). The largest gains were in the coverage probabilities for the variance estimates. These findings are consistent when the pulse frequency decreases (Scenario 3).
Table 2.
False positive and negative rates of pulse detection and bias and coverage of population means
| False Positive Rate (SE) | False Negative Rate (SE) | |||
|---|---|---|---|---|
| Model | Population | Single subject | Population | Single Subject |
| Reference | 7.1% (0.9%) | 9.0% (1.1%) | 5.7% (1.4%) | 6.0% (1.4%) |
| Short Series | 16.4% (0.4%) | 30.3% (0.5%) | 10.0% (0.4%) | 16.9% (0.6%) |
| Slow Pulsing | 4.1% (0.8%) | 6.1% (1.0%) | 1.9% (0.7%) | 2.3% (0.9%) |
| Small Mass | 27.6% (3.1%) | 30.2% (3.2%) | 30.8% (3.8%) | 33.6% (4.1%) |
| Multia | 27.9% (4.3%) | 31.8% (4.4%) | 27.2% (4.6%) | 31.6% (5.0%) |
| Bias and Coverage of Population Means | ||||||||||
|
|
||||||||||
| Pulse Mass, μa | Pulse Width, μw | |||||||||
| Population | Single Subject | Population | Single Subject | |||||||
| Model | Truth | Biasb (SE) | Cov.c | Bias (SE) | Cov. | Truth | Bias (SE) | Cov. | Bias (SE) | Cov. |
|
| ||||||||||
| Reference | 1.25 | −0.05 (0.02) | 96 | −0.08 (0.03) | 60 | 3 | −0.1 (0.026) | 98 | −1.0 (0.06) | 55 |
| Short Series | 1.25 | −0.09 (0.03) | 95 | −1.18 (0.06) | 100 | 3 | −0.30 (0.05) | 99 | −2.44 (0.08) | 87 |
| Slow Pulsing | 1.25 | −0.09 (0.03) | 97 | −0.6 (0.03) | 54 | 3 | −0.05 (0.03) | 96 | −1.2 (0.07) | 72 |
| Small Mass | 0 | −0.03 (0.04) | 97 | −1.0 (0.09) | 93 | 3 | −0.3 (0.06) | 94 | −1.9 (0.09) | 89 |
| Multia | 0 | −0.28 (0.06) | 92 | −1.5 (0.1) | 88 | 3 | −0.27 (0.05) | 99 | −1.9 (0.10) | 92 |
| Baseline, μb | Half-life, μh | |||||||||
| Population | Single Subject | Population | Single Subject | |||||||
| Model | Truth | Bias (SE) | Cov. | Bias (SE) | Cov. | Truth | Bias (SE) | Cov. | Bias (SE) | Cov. |
|
| ||||||||||
| Reference | 2.6 | −0.001 (0.02) | 94 | −0.01 (0.02) | 30 | 45 | −0.2 (0.09) | 97 | 0.5 (0.1) | 93 |
| Short Series | 2.6 | 0.03 (0.02) | 95 | 0.03 (0.02) | 74 | 45 | −0.74 (0.23) | 98 | 2.77 (0.30) | 95 |
| Slow Pulsing | 2.6 | −0.03 (0.02) | 95 | −0.04 (0.02) | 9 | 45 | −0.3 (0.09) | 99 | 0.1 (0.1) | 96 |
| Small Mass | 2.6 | 0.04 (0.02) | 94 | 0.05 (0.02) | 21 | 45 | −0.4 (0.2) | 99 | 2.4 (0.2) | 96 |
| Multia | 2.6 | 0.006 (0.02) | 98 | 0.02 (0.02) | 19 | 60 | −1.1 (0.3) | 94 | −2.3 (0.3) | 98 |
Low mass and frequency with a longer half-life;
average bias of the posterior means;
Cov.=Coverage of the 95% credible interval
Table 3.
Bias and coverage of estimates of subject-to-subject variation for pulse mass and width, baseline and half-life
| Bias and Coverage of subject-to-subject variation | ||||||||||
| Pulse Mass, σa | Pulse Width, σw | |||||||||
| Population | Single Subject | Population | Single Subject | |||||||
| Model | Truth | Biasb (SE) | Cov. | Bias (SE) | Cov. | Truth | Bias (SE) | Cov. | Bias (SE) | Cov. |
|
| ||||||||||
| Reference | 0.71 | 0.08 (0.02) | 97 | 0.10 (0.02) | 77 | 0.71 | 0.13 (0.03) | 94 | 1.8 (0.1) | 22 |
| Short Series | 0.71 | 0.02 (0.03) | 98 | 2.7 (0.09) | 4 | 0.71 | 0.29 (0.04) | 98 | 5.6 (0.09) | 0 |
| Slow Pulsing | 0.71 | 0.16 (0.02) | 95 | 0.76 (0.03) | 32 | 0.71 | 0.15 (0.03) | 93 | 2.5 (0.1) | 6 |
| Small Mass | 1.4 | 0.30 (0.05) | 93 | 2.4 (0.1) | 49 | 0.71 | 0.37 (0.06) | 98 | 5.4 (0.1) | 0 |
| Multia | 1.4 | 0.41 (0.07) | 87 | 2.5 (0.1) | 34 | 0.71 | 0.41 (0.06) | 99 | 5.6 (0.1) | 0 |
| Baseline, σb | Half-life, σh | |||||||||
| Population | Single Subject | Population | Single Subject | |||||||
| Model | Truth | Bias (SE) | Cov. | Bias (SE) | Cov. | Truth | Bias (SE) | Cov. | Bias (SE) | Cov. |
|
| ||||||||||
| Reference | 0.5 | 0.09 (0.01) | 94 | 0.02 (0.01) | 42 | 2.1 | 0.6 (0.10) | 98 | 3.8 (0.2) | 3 |
| Short Series | 0.5 | 0.09 (0.02) | 92 | 0.27 (0.02) | 46 | 2.1 | 1.7 (0.10) | 100 | 13.8 (0.25) | 0 |
| Slow Pulsing | 0.5 | 0.05 (0.01) | 98 | −0.03 (0.01) | 19 | 2.1 | 0.2 (0.08) | 99 | 2.9 (0.1) | 12 |
| Small Mass | 0.5 | 0.08 (0.01) | 93 | 0.02 (0.01) | 37 | 2.1 | 1.2 (0.11) | 98 | 12.4 (0.3) | 0 |
| Multia | 0.5 | 0.04 (0.01) | 96 | −0.04 (0.01) | 24 | 5.5 | −0.1 (0.17) | 99 | 10.1 (0.3) | 3 |
Low mass and frequency with a longer half-life;
average bias of the posterior means;
Cov.=Coverage of the 95% credible interval
5.1.2. Decreasing number of observations per subject
The improvements in the FP and FN rates with the population model were greatest when the study was short (36 observations per subject). The false positive rate decreased to approximately 16% for the population model from 30% with the single subject model. The false negative rate decreased to 10% with the population model compared to 17% with the single subject model. The improvements in the bias for the population mean parameters were also greatest for this scenario (Table 2). The improvements in the estimates of subject-to-subject variation were greater than the reference case and similar to the lower signal-to-noise scenarios (Table 3). A comparison of population model and single subject results for one simulation are provided in Table 4. The mean pulse mass was close to truth using the population model. Using the single subject post-hoc approach results in an average mean pulse mass that is less than half of the true pulse mass. In addition, the over-estimation of the subject-to-subject variation using the single subject approach is visible. The number of pulses is more precisely estimated, exhibited by the narrower 95% credible intervals for the two subjects shown in Table 4. The improvement in the pulse locations is also show in Figure 2 in the bottom example series. The top histogram in the bottom panel is peaked with unique modes for the population model and diffuse for the single subject model (bottom histogram in bottom panel).
Table 4.
Estimates of parameters for a single simulation with 6 hours of sampling on each subject (N=10). Subject level estimates are provided for two randomly selected subjects of the 10 series.
| Population Level Parameters | ||||||
|
| ||||||
| Population Model | Single Subject Model | |||||
|
|
|
|||||
| Truth | PM | 95% C.I. | MPM | 95% C.I. | ||
| Population Means | ||||||
|
|
||||||
| Mass, μa | 1.25 | 1.4 | (0.7,2.1) | 0.4 | (−1.8,2.4) | |
| Width, μw | 3 | 2.9 | (1.9,3.8) | 1.1 | (−2.2,4.4) | |
| Baseline, μb | 2.6 | 2.8 | (2.4,3.1) | 2.7 | (2.4,2.9) | |
| Half-life, μh | 45 | 43.1 | (39.0,47.2) | 46.9 | (38.7,57.1) | |
| Subject-to-subject variation | ||||||
|
|
||||||
| Mass, σa | 0.7 | 0.9 | (0.4, 1.7) | 3.4 | (1.1,7.7) | |
| Width, σw | 0.7 | 1.0 | (0.1,2.4) | 6.1 | (2.8,10.5) | |
| Baseline, σb | 0.5 | 0.5 | (0.2,0.8) | 0.7 | (0.4,1.0) | |
| Half-life, σh | 2.1 | 2.5 | (0.2,7.8) | 16.6 | (8.4,27.4) | |
| Pulse-to-pulse variation | ||||||
|
|
||||||
| Mass, υa | 0.7 | 0.7 | (0.5,1.1) | 2.5 | (0.3,7.9) | |
| Width, υw | 0.7 | 0.7 | (0.1,1.6) | 3.9 | (0.2,9.3) | |
| Model Error | ||||||
|
|
||||||
|
|
0.005 | 0.006 | (0.0049, 0.007) | 0.009 | (0.004, 0.019) | |
|
| ||||||
| Subject Specific Parameters (Subject 4) | ||||||
|
| ||||||
| Population Model | Single Subject Model | |||||
|
|
|
|||||
| Truth | PM | 95% C.I. | PM | 95% C.I. | ||
| μai | 0.9 | 0.6 | (−0.3,1.4) | −4.7 | (−20.4,11.8) | |
| μwi | 2.7 | 2.4 | (−0.2,4.0) | 2.1 | (−17.6,22.1) | |
| θb,i | 2.4 | 2.5 | (2.3,2.7) | 3.1 | (2.5,3.3) | |
| θh,i | 49.8 | 42.0 | (32.3,48.1) | 45.5 | (6.2,103.9) | |
| Ns,i | 2 | 3 | (3,4) | 3 | (1,6) | |
|
| ||||||
| Subject Specific Parameters (Subject 8) | ||||||
|
| ||||||
| Population Model | Single Subject Model | |||||
|
|
|
|||||
| Truth | PM | 95% C.I. | PM | 95% C.I. | ||
| μai | 1.1 | 1.3 | (0.7,1.9) | 1.3 | (0.2,2.2) | |
| μwi | 1.9 | 2.8 | (1.5,3.7) | 2.4 | (−1.4,4.7) | |
| θb,i | 1.8 | 2.6 | (2.1,3.0) | 2.5 | (1.3,3.6) | |
| θh,i | 48.1 | 42.4 | (35.1,48.5) | 41.3 | (23.8,65.6) | |
| Ns,i | 5 | 5 | (5,6) | 5 | (4,7) | |
PM: Posterior Mean; 95% CI: 95% equal probability tails credible intervals; MPM: Mean of the posterior means.
Figure 2.
Observed hormone concentration profiles and posterior predictive fits of 2 simulated series of 6 hour length. Grey circles represent observed hormone concentrations, and black lines represent posterior predictive fits (solid - population model, dashed - single subject). In each series, the upper histogram shows the posterior distribution of pulse locations from the population model and the bottom histogram from the single-subject model.
5.1.3. Low signal-to-noise and higher subject-to-subject variation: small mass and multi cases
An example fit of two simulated series in one simulation is shown in Figure 2. As pulse size decreased both models had higher FP and FN rates; although the population model produces slightly lower rates. These increases did not change with a longer half-life. The biases in parameters related to pulse mass (μa, σa, νa) were smaller in the population model (Tables 2 and 3) and the coverage of the subject-to-subject variance estimates much higher using the population approach. This same pattern held for the pulse width parameters and the half-life. As pulse size decreased, estimation of pulse width in the single subject model became more erratic. This reflected the tendency of the single subject model to produce unusually large estimates of individual pulse widths when the pulses were relatively small (data not shown). As half-life increases there is less decay observed prior to another pulse occurring. However, the results were not influenced by half-life.
5.1.4. Sensitivity to presence of pulsing
When no series were pulsing, the model does not provide usable fits. The pulse masses of the one to two pulses detected are very small, the pulse widths very large, and the histograms of the locations are uniform over the period of observation (Supplementary Figure 4). In cases were most series are pulsing, the estimates of those with pulses were stable. One to two pulses were detected in those without pulses, but the masses were much smaller than the population average. The histograms of the pulse locations were less flat, making it somewhat harder to distinguish non-pulsing from series with just a few pulses.
5.2. Analysis of experimental LH data in normal weight women
We used our approach to investigate LH pulsatility in the obese and normal weight women described in the introduction. The obese and normal weight women and the pre-post observation periods were fitted separately for this application. The differences and similarities between the two approaches were similar for the 4 scenarios; for brevity, we show the results for the pre-treatment normal weight women (N=10). Notable features of these data are the large subject-to-subject variation in the concentrations and visual pulse characteristics (Supplementary Material Figure 3). In addition, not all subjects have clear visual pulses, indicating a lower signal-to-noise ratio for some. All subjects had normal menstrual cycles as an inclusion criterion and we confirmed ovulation by daily urinary hormonal secretion. Thus, it was presumed that all women had LH pulses needing identification because LH pulsing is required for normal menstrual cycling.
The average number of pulses fitted using the population approach was 5.3 compared to 5.0 for the single subject approach. The population mean pulse mass of the pulses was larger and more biologically plausible using the population model (Table 5; 1.1 log ng/ml vs. −2.0 log ng/ml). These values translate to pulse masses of approximately 3.0 vs 0.15 units on the natural scale. A pulse mass of 0.15 would be indistinguishable from noise visually. The subject-to-subject and pulse-to-pulse variation estimates were smaller using the population model compared to the single subject fits (Table 5). The half-life was approximately 13 minutes lower using the population approach (40 minutes vs. 53 minutes). Visual inspection of the posterior distributions for each subject shows clearer modes in the posterior distribution in the pulse locations in the population model (Figure 1).
Table 5.
Estimates of parameters for normal weight pre-treatment period (N=10) for both the population and single-subject models. Subject level estimates are provided for two randomly selected women.
| Population Level Parameters | |||||
|
| |||||
| Population Model | Single Subject Model | ||||
|
|
|
||||
| PM | 95% CI | MPM | 95% CI | ||
| Population Means | |||||
|
|
|||||
|
|
5.3 | (4.2, 6.4) | 5.0 | (3.9, 6.1) | |
| Mass, μa | 1.1 | (0.4, 1.7) | −2.0 | (−5.3, 1.4) | |
| Width, μw | 2.7 | (−1.1, 6.2) | 3.0 | (−1.8, 7.8) | |
| Baseline, μb | 2.7 | (1.5, 4.1) | 3.5 | (3.2, 3.8) | |
| Half-life, μh | 40.2 | (31.9, 50.1) | 53.1 | (41.3, 64.2) | |
| Subject-to-subject variation | |||||
|
|
|||||
| Mass, σa | 0.8 | (0.3, 1.6) | 6.0 | (2.6, 10.3) | |
| Width, σw | 3.7 | (0.1, 8.8) | 8.1 | (4.2, 12.7) | |
| Baseline, σb | 1.6 | (0.4, 3.2) | 3.3 | (2.9, 3.6) | |
| Half-life, σh | 4.2 | (0.2, 9.5) | 21.5 | (12.9, 31.9) | |
| Pulse-to-pulse variation | |||||
|
|
|||||
| Mass, υa | 0.5 | (0.3, 0.8) | 2.9 | (0.1, 9.3) | |
| Width υw | 0.9 | (0.1, 2.8) | 4.2 | (0.1, 9.7) | |
| Model Error | |||||
|
|
|||||
|
|
0.010 | (0.008, 0.013) | 0.018 | (0.0006, 0.058) | |
|
| |||||
| Subject Specific Parameters (Subject ID4) | |||||
|
| |||||
| Population Model | Single Subject Model | ||||
|
|
|
||||
| PM | 95% C.I. | PM | 95% CI | ||
| Ns,i | 5.5 | (4,8) | 4.5 | (1,9) | |
| μai | 0.4 | (−0.2,1.0) | −5.1 | (−21.2,11.6) | |
| μwi | 0.09 | (−9.0,1.3) | 3.2 | (−16.9,24.4) | |
| θb,i | 1.7 | (1.3,2.1) | 2.6 | (1.6,3.0) | |
| θh,i | 39.6 | (26.0,53.4) | 44.0 | (7.5,96.0) | |
|
| |||||
| Subject Specific Parameters (Subject ID8) | |||||
|
| |||||
| Population Model | Single Subject Model | ||||
|
|
|
||||
| PM | 95% C.I. | PM | 95% C.I. | ||
| Ns,i | 5.4 | (5,7) | 5.5 | (5,8) | |
| μai | 1.4 | (0.9,2.0) | 1.4 | (0.3,2.1) | |
| μwi | 2.7 | (−1.4,4.6) | 1.1 | (−11.9,5.5) | |
| θb,i | 2.4 | (1.3,3.3) | 1.6 | (0.1,3.4) | |
| θh,i | 40.6 | (29.6,53.7) | 51.8 | (28.1,77.9) | |
PM: Posterior Mean; 95% C.I.: 95% equal probability tails credible intervals; MPM: Mean of the posterior means.
N̄ is the mean of the posterior mean number of pulses for each individual.
6. Discussion
In this paper, we extended the Bayesian deconvolution model from analysis of a single subject analysis to simultaneous analysis of a population of hormone concentrations. The population model is able to simultaneously estimate the pulse locations on a population of subjects along with parameters defining each subject’s hormone profile. This extension formalizes in the model and estimation the population level effects that are of interest to clinical investigators. Compared to a single subject Bayesian deconvolution model, the population model results in improved parameter estimates of population level effects and pulse locations. The estimation has lower bias, higher coverage, and lower false positive and false negative rates for detecting pulses. Estimation of parameters related to baseline concentration (μb, σb and θb,i) was good in both the population and single subject models. The estimation of pulse width and half-life was better using the population model. We found that population level parameters were more well identified than subject specific parameters, which were more well identified than pulse specific parameters. For parameters that were poorly identified, the population model yielded more stable and less biased estimates, especially in the case of pulse mass. In cases where subjects had very small pulses, the single subject model produced poor estimates of pulse specific pulse width, ωik. In general, this did not occur with the population model.
Modest gains are made using the population model when there is high subject-to-subject variability. Additionally, if pulses are smaller, the population model appears useful, although the FP and FN rates are high for both approaches. The biggest improvement of the population model over the single subject model occurs when there are fewer observations per series. This was the case with our motivating study data, which used a shorter study length (6 hrs) compared to previous studies (12 or 24 hrs). Improvements in model fit were seen when analyzing these data with the population model when compared to the single subject model and the estimates of mean pulse mass were more biologically plausible. Also, the population model resulted in posterior distributions with much lower variability (more precise parameter estimates). This is partly due to the fact that in the single subject model, subject specific parameters are assigned non-informative priors. In the population model, these parameters are assigned distributions with parameters that are estimated from the data. These can be thought of as more informative prior distributions, resulting in estimates with less variability. We re-fit the single subject model on each individual series using parameter estimates obtained in the population model as informative priors (results not shown). In these cases, the single subject and the population models resulted in similar fits.
Conversely, when there are many observations per series and low subject-to-subject variability, the additional level of model complexity and computational burden of the population model seems unnecessary. However, when both models were fit to well-defined series, the results did not differ greatly between the population model and the ad-hoc measures of population effects from the single subject model. This shows that potentially overcomplicating the model did not introduce estimation issues. Thus, if one wants to use one approach to fitting data, the population model will work in more settings than the single subject approach without introducing problems in situations where the single subject model may be sufficient.
One challenge in the population model is getting each pulse to be modeled as a single Gaussian component so that pulse number has a clear biologic meaning. When fitting each subject separately, post-hoc processing has been used to combine Gaussian events that are close in time. This approach is less desirable in the population model because the post-processing would destroy the meaning of the population level pulse parameters (e.g., pulse mass). This means in practice careful selection of the prior on pulse number is important. We also recommend a sensitivity analysis with a few choices of pulse number. One model based solution to this problem could be to assign a prior that formally restricts the distance between two pulses.
Additionally, under the prior structure for pulse number and location used in this paper, all subjects in a population have the same prior mean for number of pulses. If number of pulses differs greatly between subjects, the result is misfitting (either increased false positives or false negatives). We recommend applying a subject specific prior mean for number of pulses or exploring different structures for the pulsing process.
Based on our sensitivity analysis it is important when implementing the population approach that there is a priori information that indicates all subjects should be pulsing. In the case of the motivating LH study, all women had evidence of ovulation. Since LH pulsing is required for ovulation, the assumption that all subjects were pulsing was reasonable.
This work focused on comparing the gains of analyzing a population of subjects all within the Bayesian deconvolution modeling framework. This comparison was chosen because 1) in previous work the single subject Bayesian approach had improved pulse detection and parameter estimation compared to other approaches [18] and 2) an extension to a population framework in non-Bayesian approaches [29,30] presents with several computational issues when trying to simultaneously estimate the number of pulses for all subjects along with other model parameters. Work by Liu and Wang (2007) was conducted at a population level. Their model of hormone concentration differed from the deconvolution model in that pulse secretion and elimination did not simultaneously occur. In addition, the emphasis of their population extension focused on estimating a common circadian rhythm in the pulse location model across subjects. The Liu and Wang approach was novel in that estimation of the pulse location model occurred without actually estimating the pulse locations. Given the differences in the modeling framework and the limited software that exists for implementation, we focused on investigating whether gains in estimation could be made within the deconvolution modeling framework. In future work, it may be interesting to develop a Bayesian extension to Liu and Wang’s work and assess whether one approach results in better estimates of the population pulse masses and pulse frequency.
This paper shows that a population model extension is computationally feasible in a Bayesian deconvolution framework and has estimation benefits in short designs or noisy hormones.
Supplementary Material
Acknowledgments
Contract/grant sponsor: Supported by NIH/NCATS Colorado CTSI Grant Number KL2 TR000156, NIH/NIMH R21 MH094994, NIH/NCHID R01 HD081162. Contents are the authors sole responsibility and do not necessarily represent official NIH views.
References
- 1.Al-Safi ZA, Liu H, Carlson NE, Chosich J, Lesh J, Robledo C, Bradford A, Gee N, Phang T, Santoro N, et al. Estradiol priming improves gonadotrope sensitivity and pro-inflammatory cytokines in obese women. The Journal of Clinical Endocrinology and Metabolism. 2015;100(11):4372–4381. doi: 10.1210/jc.2015-1946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Al-Safi ZA, Liu H, Carlson NE, Chosich J, Harris M, Bradford AP, Robledo C, Eckel RH, Polotsky AJ. Omega-3 fatty acid supplementation lowers serum FSH in normal weight but not obese women. The Journal of Clinical Endocrinology and Metabolism. 2016;101:324–33. doi: 10.1210/jc.2015-2913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lake JK, Power C, Cole TJ. Women’s reproductive health: the role of body mass index in early and adult life. International Journal of Obesity and Related Metabolic Disorders: Journal of the International Association for the Study of Obesity. 1997;21:432–38. doi: 10.1038/sj.ijo.0800424. [DOI] [PubMed] [Google Scholar]
- 4.Stothard KJ, Tennant PWG, Bell R, Rankin J. Maternal overweight and obesity and the risk of congenital anomalies. The Journal of the American Medical Association. 2009;301:636–50. doi: 10.1001/jama.2009.113. [DOI] [PubMed] [Google Scholar]
- 5.Smith GC, Shah I, Pell JP, Crossley JA, Dobbie R. Maternal obesity in early pregnancy and risk of spontaneous and elective preterm deliveries: a retrospective cohort study. American Journal of Public Health. 2007;97:157–62. doi: 10.2105/AJPH.2005.074294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Heerwagen MJR, Miller MR, Barbour LA, Friedman JE. Maternal obesity and fetal metabolic programming: a fertile epigenetic soil. American Journal of Physiology - Regulatory, Integrative and Comparative Physiology. 2010;299:R711–R722. doi: 10.1152/ajpregu.00310.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Schally AV, Arimura A, Kastin AJ, Matsuo H, Baba Y, Redding TW, Nair RM, Debeljuk L, White WF. Gonadotropin-releasing hormone: one polypeptide regulated secretion of luteinizing and follicle-stimulating hormones. Science. 1971;173:1036. doi: 10.1126/science.173.4001.1036. [DOI] [PubMed] [Google Scholar]
- 8.Sherwood L. Fundamentals of Human Physiology: A Human Perspective. 3. Brooks-Cole; Belmont, CA: 2005. [Google Scholar]
- 9.O’Sullivan FO, O’Sullivan J. Deconvolution of episodic hormone data: an analysis of the role of season on the onset of puberty in cows. Biometrics. 1988;44:339–353. [PubMed] [Google Scholar]
- 10.Veldhuis JD, Johnson ML. Deconvolution analysis of hormone data. Methods in Enzymology. 1992;210:539–575. doi: 10.1016/0076-6879(92)10028-c. [DOI] [PubMed] [Google Scholar]
- 11.Keenan DM, Veldhuis JD. Stochastic model of admixed basal and pulsatile hormone secretion as modulated by a deterministic oscillator. American Journal Physiology. 1997;273:R1182–R1192. doi: 10.1152/ajpregu.1997.273.3.R1182. [DOI] [PubMed] [Google Scholar]
- 12.Keenan DM, Veldhuis JD, Yang R. Joint recovery of pulsatile and basal hormone secretion by stochastic nonlinear random-effects analysis. American Journal Physiology. 1998;275:R1939–R1949. doi: 10.1152/ajpregu.1998.275.6.R1939. [DOI] [PubMed] [Google Scholar]
- 13.Keenan D, Chattopadhyay S, Veldhuis JD. Composite model of time-varying appearance and disappearance of neurohormone pulse signals in blood. Journal of Theoretical Biology. 2005;236:242–55. doi: 10.1016/j.jtbi.2005.03.008. [DOI] [PubMed] [Google Scholar]
- 14.Guo W, Wang Y, Brown MB. A signal extraction approach to modeling hormone time series with pulses and a changing baseline. Journal of the American Statistical Association. 1999;94:746–756. [Google Scholar]
- 15.Johnson TD. Bayesian deconvolution analysis of pulsatile hormone concentration profiles. Biometrics. 2003;59:650–660. doi: 10.1111/1541-0420.00075. [DOI] [PubMed] [Google Scholar]
- 16.Johnson TD. Analysis of pulsatile hormone concentration profiles with nonconstant basal concentration: a Bayesian approach. Biometrics. 2007;63:1207–1217. doi: 10.1111/j.1541-0420.2007.00809.x. [DOI] [PubMed] [Google Scholar]
- 17.Liu A, Wang Y. Modeling of hormone secretion-generating mechanisms with splines: a psuedo-likelihood approach. Biometrics. 2007;63:201–208. doi: 10.1111/j.1541-0420.2006.00672.x. [DOI] [PubMed] [Google Scholar]
- 18.Carlson NE, Horton KW, Grunwald GK. A comparison of methods for analyzing time series of pulsatile hormone data. Statistics in Medicine. 2013;32:4624–4638. doi: 10.1002/sim.5882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Davidian M, Gallant A. Smooth nonparametric maximum likelihood estimation for population pharmacokinetics, with application to quinidine. Journal of Pharmacokinetics and Biopharmaceutics. 1992;20:529–56. doi: 10.1007/BF01061470. [DOI] [PubMed] [Google Scholar]
- 20.Davidian M, Giltinan DM. Nonlinear Models for Repeated Measurement Data. Chapman and Hall/CRC; London: 1995. [Google Scholar]
- 21.Stephens M. Bayesian analysis of mixture models with an unknown number of components-an alternative to reversible jump methods. The Annals of Statistics. 2000;28:40–74. [Google Scholar]
- 22.Carlson NE, Johnson TD, Brown MB. A Bayesian approach to modeling associations between pulsatile hormones. Biometrics. 2009;65:650–659. doi: 10.1111/j.1541-0420.2008.01117.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rodbard D, Rayford PL, Ross GT. Statistical quality control. In: McArthur J, Colton T, editors. Statistics in Endocrinology. The MIT Press; Cambridge, Massachusetts: 1970. pp. 411–429. [Google Scholar]
- 24.Green PJ. Reversible jump MCMC computation and Bayesian model determination. Biometrika. 1995;82:711–732. [Google Scholar]
- 25.Tierney L. Markov chains for exploring posterior distributions. The Annals of Statistics. 1994;22:1701–1762. [Google Scholar]
- 26.Geman S, Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Transaction on Pattern Analysis and Machine Intelligence. 1984;6:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- 27.Daley D, Vere-Jones D. An Introduction to the Theory of Point Processes, Volume 1: Elementary Theory and Methods. Springer; New York: 2003. [Google Scholar]
- 28.Mauger DT, Brown MB, Kushler RH. A comparison of methods that characterize pulses in a time series. Statistics in Medicine. 1995;14:311–325. doi: 10.1002/sim.4780140309. [DOI] [PubMed] [Google Scholar]
- 29.Johnson ML, Pipes L, Veldhuis PP, Farhy LS, Nass R, Thorner MO, Evans WS. AutoDeconv: a robust numerical method for the quantification of pulsatile events. Methods in Enzymology. 2009;454:367–404. doi: 10.1016/S0076-6879(08)03815-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yang Y, Liu A, Wang Y. Detecting pulsatile hormone secretions using nonlinear mixed effects partial spline models. Biometrics. 2006;62:230–238. doi: 10.1111/j.1541-0420.2005.00403.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.