Lawful relation between perceptual bias and discriminability

Significance

We present a law of human perception. The law expresses a mathematical relation between our ability to perceptually discriminate a stimulus from similar ones and our bias in the perceived stimulus value. We derived the relation based on theoretical assumptions about how the brain represents sensory information and how it interprets this information to create a percept. Our main assumption is that both encoding and decoding are optimized for the specific statistical structure of the sensory environment. We found large experimental support for the law in the literature, which includes biases and changes in discriminability induced by contextual modulation (e.g., adaptation). Our results imply that human perception generally relies on statistically optimized processes.

Abstract

Perception of a stimulus can be characterized by two fundamental psychophysical measures: how well the stimulus can be discriminated from similar ones (discrimination threshold) and how strongly the perceived stimulus value deviates on average from the true stimulus value (perceptual bias). We demonstrate that perceptual bias and discriminability, as functions of the stimulus value, follow a surprisingly simple mathematical relation. The relation, which is derived from a theory combining optimal encoding and decoding, is well supported by a wide range of reported psychophysical data including perceptual changes induced by contextual modulation. The large empirical support indicates that the proposed relation may represent a psychophysical law in human perception. Our results imply that the computational processes of sensory encoding and perceptual decoding are matched and optimized based on identical assumptions about the statistical structure of the sensory environment.

Perception is a subjective experience that is shaped by the expectations and beliefs of an observer (1). Psychophysical measures provide an objective yet indirect characterization of this experience by describing the dependency between the physical properties of a stimulus and the corresponding perceptually guided behavior (2).

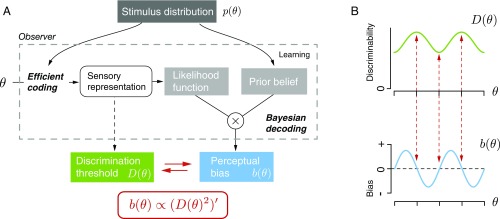
Two fundamental measures characterize an observer’s perception of a stimulus. Discrimination threshold indicates the sensitivity of an observer to small changes in a stimulus variable (Fig. 1A). The threshold depends on the quality with which the stimulus variable is represented in the brain (2) (i.e., encoded; Fig. 1B); a more accurate representation results in a lower discrimination threshold. In contrast, perceptual bias is a measure that reflects the degree to which an observer’s perception deviates on average from the true stimulus value. Perceptual bias is typically assumed to result from prior beliefs and reward expectations with which the observer interprets the sensory evidence (1), and thus is determined by factors that seem not directly related to the sensory representation of the stimulus. As a result, it has long been believed that there is no reason to expect any lawful relation between perceptual bias and discrimination threshold (3).

Fig. 1.

Psychophysical characterization and modeling of perception. (A) Perception of a stimulus variable (e.g., the angular tilt ${\theta }_0$ of the leaning tower of Pisa) can be characterized by an observer’s discrimination threshold and perceptual bias. Discrimination threshold specifies how well an observer can discriminate small deviations around the particular stimulus orientation ${\theta }_0$ given that there is noise in perceptual processing (green arrow). Perceptual bias specifies how much, on average, the perceived orientations over repeated presentations (thin lines) deviate from the true stimulus orientation (blue arrow). (B) Modeling perception as an encoding–decoding processing cascade. Discriminability is limited by the characteristics of the encoding process, i.e., the quality of the internal, sensory representation $\stackrel{\sim }{m}$. Perceptual bias, however, also depends on the decoding process that typically involves cognitive factors such as prior beliefs and reward expectations. Both discrimination threshold and perceptual bias can be characterized with appropriate psychophysical methods (indicated by dashed arrows).

However, here we derive a direct mathematical relation between discrimination threshold $D(\theta )$ and perceptual bias $b(\theta )$ based on a recently proposed observer theory of perception (4, 7). The key idea is that both the encoding and the decoding process of the observer are optimally adapted to the statistical structure of the perceptual task (Fig. 2A). Specifically, we assume encoding to be efficient (8, 9) such that it maximizes the information in the sensory representation about the stimulus given a limit on the overall available coding resources (10). The assumption implies a sensory representation whose coding resources are allocated according to the stimulus distribution $p(\theta )$. This results in the encoding constraint

$$p(\theta )\propto \sqrt{J(\theta )},$$ [1]

where the Fisher information $J(\theta )$ represents the coding accuracy of the sensory representation (4, 11–13). Fisher information provides a lower bound on the discrimination threshold irrespective of whether the estimator is biased or not, which can be formulated as $D(\theta )\ge c/\sqrt{J(\theta )}$, where $c$ is a constant (5, 6). Rather than assuming a tight bound, we make the weaker assumption that the bound is equally “loose” over the range of the stimulus value $\theta$. Using the encoding constraint (Eq. 1) above, we can express discrimination threshold in terms of the stimulus distribution as

$$D(\theta )\propto 1/p(\theta ).$$ [2]

Similarly, we have shown that the perceptual bias of the Bayesian observer model (Fig. 2A) can also be expressed in terms of the stimulus distribution (4, 7). Assuming that uncertainty in the perceptual process is dominated by internal (neural) noise and that the noise is relatively small, we can analytically derive the observer’s bias as

$$b(\theta )\propto (1/p{(\theta )}^2)\prime .$$ [3]

We can show that the expression holds independently of the details of the assumed loss function for a large family of symmetric loss functions (Supporting Information). Magnitude and sign of its proportionality coefficient, however, depend on several factors, including the noise magnitude and the loss function. Finally, by combining Eqs. 2 and 3, we obtain a direct functional relation between perceptual bias and discrimination threshold in the form of

$$b(\theta )\propto (D{(\theta )}^2)\prime ;$$ [4]

i.e., perceptual bias (as a function of the stimulus variable) is proportional to the slope of the square of the discrimination threshold (Fig. 2B).

Fig. 2.

Observer model that links perceptual bias and discrimination threshold. (A) Our theory of perception proposes that encoding and decoding are both optimized for a given stimulus distribution (4). Based on this theory, the encoding accuracy characterized by Fisher information $J(\theta )$ and the bias $b(\theta )$ of the Bayesian decoder are both dependent on the stimulus distribution $p(\theta )$. With Fisher information providing a lower bound on discriminability $D(\theta )$ (5, 6), we can mathematically formulate the relation between perceptual bias and discrimination threshold as $b(\theta )\propto {(D{(\theta )}^2)}^{\prime }$. (B) Arbitrarily chosen example highlighting the characteristics of the relation: Bias is zero at the extrema of the discrimination threshold (red arrows) and largest for stimulus values where the threshold changes most rapidly. Thus, the magnitude of perceptual bias typically does not covary with the magnitude of the discrimination threshold.

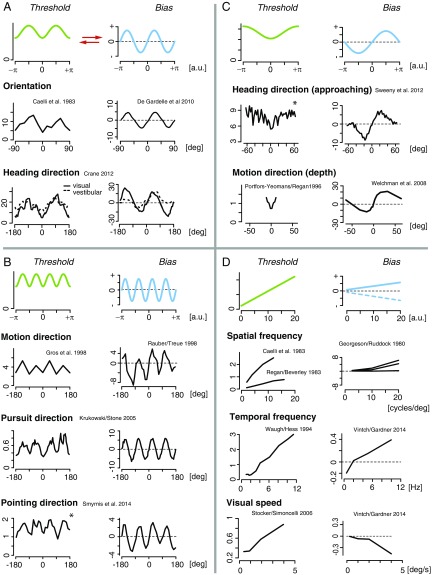
We tested the surprisingly simple relation against a wide range of existing psychophysical data. Figs. 3 and 4 show data for those perceptual variables for which both discrimination threshold and perceptual bias have been reported over a sufficiently large stimulus range. We grouped the examples according to their characteristic bias–threshold patterns. The first group consists of a set of circular variables (Fig. 3 A–C). It includes local visual orientation, probably the most well-studied perceptual variable. Orientation perception exhibits the so-called oblique effect (38), which describes the observation that the discrimination threshold peaks at the oblique orientations yet is lowest for cardinal orientations (14). Based on the oblique effect, Eq. 4 predicts that perceptual bias is zero at, and only at, both cardinal and oblique orientations. Measured bias functions confirm this prediction (15). Other circular variables that exhibit similar patterns are heading direction using either visual or vestibular information (16), 2D motion direction measured with a two alternative forced-choice (2AFC) procedure (17, 18) or by smooth pursuit eye movements (19), pointing direction (20), and motion direction in depth (21, 22). The relation also holds for the more high-level perceptual variable of perceived heading direction of approaching biological motion (human pedestrian) (23) as shown in Fig. 3C.

Fig. 3.

Predicted and measured bias–threshold patterns in perception. Data are organized into different groups. Green/blue curves represent the predicted discrimination threshold/bias. (A) Discrimination threshold (14) and bias (15) data for perceived orientation and heading direction (16) (solid lines for visual stimulation, and dashed lines for vestibular stimulation). (B) We found similar patterns for perceived motion direction [measured both with a 2AFC procedure (17, 18) or with smooth pursuit behavior (19)] and pointing direction [where subjects had to estimate the direction of a visually presented arrow (20)]. (C) The predicted relation also holds for perceived motion direction in depth (21, 22), as well as for the perception of higher-level stimuli such as the approaching heading direction of a person (23), although the quality of the available data is limited. (D) The bias–threshold relation is different for magnitude (i.e., noncircular) variables: Discrimination threshold is typically proportional to the stimulus value [Weber’s law (24)], and thus we predict that perceptual bias is also linear in stimulus value. Reported patterns for visually perceived spatial frequency (14, 25, 34), temporal frequency (26, 27), and grating speed (27, 28) match this prediction. All data curves are replotted from their corresponding publications, except bias data for orientation (15) and threshold data for visual speed (28), which both were derived by analyzing the original data. Stars (*) mark data that represent perceptual variability rather than discrimination thresholds (see also Figs. S2 and S3 for more details).

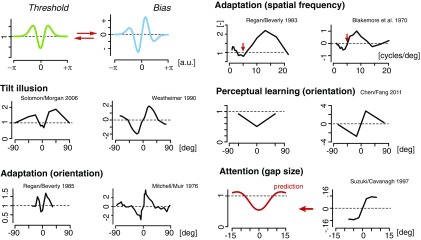
Fig. 4.

Predicted and measured bias–threshold patterns induced by various forms of contextual modulation. Spatial context as in the tilt illusion (29, 30) [or using motion stimuli (31)] and temporal context during adaptation experiments [orientation (32, 33), relative to adaptor orientation; spatial frequency (34, 35), red arrows indicating the value of the adaptor stimulus] induce similar biases and changes in thresholds that are qualitatively well predicted (relative to the unadapted condition). The predicted relation seems to also hold for perceptual changes induced by perceptual learning (36) and spatial attention. Spatial attention has been tied to repulsive biases (37) at the locus of attention and is also known for improvements in discriminability, although little is known about how discriminability changes with stimulus value. All data curves are replotted from the corresponding publications. All data represent biases and changes in threshold (ratio) relative to the corresponding control conditions (no surround; preadapt; prelearn; nonattended).

Fig. S3.

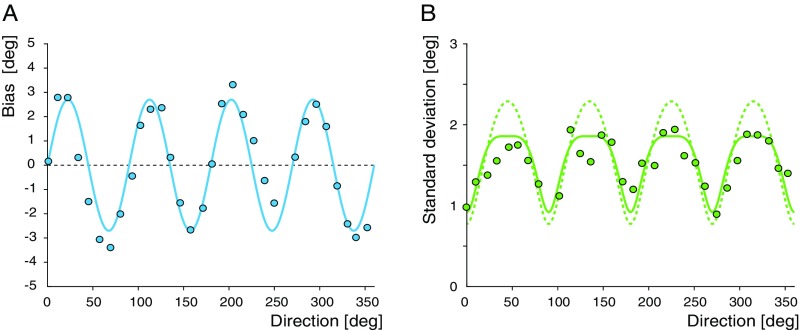
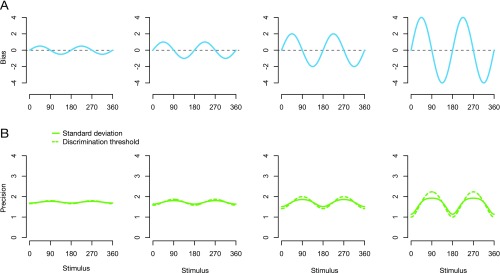
Variance prediction for pointing direction dataset (20). (A) Bias data and sinewave approximation (bold line). (B) Pointing variability $\widehat{\sigma }(\theta )$ (data) superimposed with the prediction (based on the sinewave approximation) according to Eq. S18 (bold line) and the prediction for discrimination threshold according to Eq. S15 (dashed line). Both predictions are made using the same values for their common free parameters $C_2$. See also Fig. S2.

The second group contains noncircular magnitude variables for which discrimination threshold (approximately) follows Weber’s law (24) and linearly increases with magnitude (Fig. 3D). We predict that these variables should exhibit a perceptual bias that is also linear in stimulus magnitude. Indeed, we found this to be true for spatial frequency [threshold (14, 34, 39), bias (25)] as well as temporal frequency [threshold (40), bias (27)] in vision. Visual speed is another example for which discrimination threshold approximately follows Weber’s law (28) and bias is also approximately linear with stimulus speed (27), although, in contrast to the other examples, with a negative proportionality coefficient. A possible explanation for the sign difference may be that speed perception is governed by a loss function that differs from the loss functions for the other variables. In perceiving the speed of a moving object, an observer’s emphasis might be on estimating the speed “just right” to maximize the chance to, e.g., successfully intercept the object. A loss function that approximates the “all-or-nothing” characteristics of the $L_0$ norm would serve that goal, and would also predict the negative sign of the proportionality coefficient (see Supporting Information). Finally, perceived weight, one of the classical examples for illustrating Weber’s law (24), also seems to be consistent with the proposed bias–threshold pattern (41).

The last group contains bias–threshold patterns that are not intrinsic to individual specific variables but are induced by contextual modulation (Fig. 4). Spatial context as in the tilt illusion can induce characteristic repulsive biases in the perceived stimulus orientation away from the orientation of the spatial surround (30). The corresponding change in discrimination threshold (29) well matches the predicted pattern based on our theoretically derived relation. A similar bias–threshold pattern has been reported when probing motion direction instead of orientation (31). Furthermore, similar patterns have been observed for temporal context, i.e., as the result of adaptation. Adaptation-induced biases and changes in discrimination threshold for perceived visual orientation (32, 33) and spatial frequency (34, 35) are qualitatively in agreement with the prediction. At a slightly longer time scale, perceptual learning is also known to reduce discrimination thresholds. We therefore predict that perceptual learning also induces repulsive biases away from the learned stimulus value. This prediction is indeed confirmed by data for learning orientation (36) and motion direction (42), albeit the existing data are sparse. Finally, attention has been known as a mechanism that can decrease discrimination threshold (43). We predict that this decrease should coincide with a repulsive bias in the perceived stimulus variable. Although limited in extent, data from a Vernier gap size estimation experiment are in agreement with this prediction (37) and are further supported by recent results (44). In sum, the derived relation can readily explain a wide array of empirical observations across different perceptual variables, sensory modalities, and contextual modulations.

Based on the strong empirical support, we argue that we have identified a universal law of human perception. It provides a unified and parsimonious characterization of the relation between discrimination threshold and perceptual bias, which are the two main psychophysical measures characterizing the perception of a stimulus variable. Only a very few quantitative laws are known in perceptual science, including Weber–Fechner’s law (2, 24) and Stevens’ law (45). These laws express simple empirical regularities which provide a compact yet generally valid description of the data. The law we have proposed here shares the same virtue. However, unlike these previous laws, our law is not the result of empirical observations but rather was derived based on theoretical considerations of optimal encoding and decoding (4). Thus, as such, it does not merely describe perceptual behavior but rather reflects our understanding of why perception exhibits such characteristics in the first place. Note that, without the theory, we would not have discovered the general empirical regularity between discrimination threshold and bias. It is conceivable that some of the theoretical assumptions we made in deriving the law may prove incorrect (see Fig. S1) despite the fact that the law itself is empirically well supported. It is difficult to imagine, however, how a lawful relation between perceptual bias and discrimination threshold could emerge without a functional constraint that tightly links the encoding and decoding processes of perception (Fig. 2A).

Fig. S1.

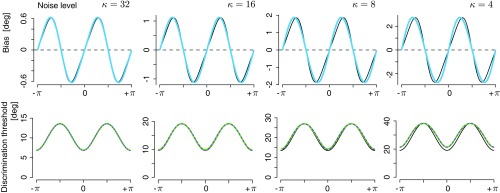
Bayesian observer model simulations vs. analytic approximations (Eqs. 2 and 3). Discrimination threshold and perceptual bias are shown for a given prior distribution $p(\theta )\propto 1/(3-\cos 2\theta )$ and four increasing levels of sensory (internal) noise. We assumed additive noise following a von Mises distribution whose concentration parameter $\kappa$ determined the noise magnitude (high $\kappa$ corresponds to low magnitude). Black lines represent the predicted curves according to Eqs. 2 and 3, and the colored lines represent the predicted curves according to numerical simulations of the full Bayesian observer model. Note that, while threshold and bias curves of the observer model show noticeable differences from the curves predicted by the analytic approximations, the lawful relation between the two still persists to an almost perfect extent. This is illustrated by how well the discrimination thresholds predicted by the law based on the numerically computed bias of the observer model (dashed purple lines) match the actual discrimination thresholds of the observer model (green lines).

The law allows us to predict either perceptual bias based on measured data for discrimination threshold or vice versa. One general prediction is that stimulus variables that follow Weber’s law should exhibit perceptual biases that are linearly proportional to the stimulus value as demonstrated with examples in Fig. 3D. Furthermore, because perceptual illusions are often examples of a strong form of perceptual bias induced by changes in context, we predict that these illusions should be accompanied with substantial threshold changes according to our law.

Perceptual biases can arise for different reasons, not all of which are aligned with the assumptions we made in our derivations. In particular, because we assumed that the uncertainty in the inference process is predominantly due to internal (neural) noise of the observer, we do not expect the proposed law to hold under conditions where stimulus ambiguity/noise is the dominant source of uncertainty. In this case, we expect discrimination threshold to be mainly determined by the stimulus uncertainty and not the prior expectations as we have assumed (Eq. 2).

It is worth noting that the law can also be expressed in terms of perceptual variance rather than discrimination threshold. This can be useful because some psychophysical experiments designed for measuring perceptual bias (e.g., by a method of adjustment) often record variance in subjects’ estimates as well. Using the Cramer–Rao bound on the variance ${\widehat{\sigma }}^2(\theta )$ of a biased estimator, we can rewrite Eq. 4 as

$$b(\theta )\propto {({\widehat{\sigma }}^2(\theta )/{(1+b\prime (\theta ))}^2)}^{\prime }.$$ [5]

For relatively small and smoothly changing biases, the predictions for variance and discrimination threshold are similar (see Supporting Information for details).

Last but not least, perhaps the most surprising finding is that the law seems to hold for bias and discriminability patterns induced by contextual modulation (Fig. 4). This implies not only that changes in encoding and decoding can happen immediately (e.g., spatial context), or at least on short time scales, but also that these changes are matched between encoding and decoding by relying on identical assumptions (i.e., prior expectations) about the structure of the sensory environment. This fundamentally contrasts with existing theories that assume mismatches between encoding and decoding (i.e., the “coding catastrophe”) to be responsible for many of the known contextually modulated bias effects (46). It also contrasts with findings that put the locus of perceptual learning either at the encoding (47) or at the decoding (48) level; we predict learning to occur at both levels. Whether these contextual priors actually match the stimulus distributions within these contexts or not is unclear and remains a subject for future studies. Data from spatial attention experiments (Fig. 4) at least suggest that they may reflect subjective rather than objective expectations. This would imply that the distinction is not relevant in the context of the observer model considered here (Fig. 2A) and that efficient encoding and Bayesian decoding are both optimized for identical prior expectations, irrespective of whether these expectations are subjective or objective. We believe that the proposed law and its underlying theoretical assumptions have profound implications for the computations and neural mechanisms governing perception, which we have just started to explore.

SI Text

This document consists of three parts: The first part provides derivations of all of the components (i.e., essentially Eqs. 1–3) used in expressing the relation between perceptual bias and the discrimination threshold. Note that most of these derivations have been described before, and we only include them here to make the paper self-contained. In the second part, we derive the relation between perceptual bias and variance (rather than discrimination threshold). Finally, in the last part, we prove that the proposed relation between discrimination threshold (or variance) and perceptual bias is not limited to the $L_2$ case but holds for a large class of symmetric loss functions.

Part 1: Relation Between Perceptual Bias and Discrimination Threshold.

Relation between Fisher information and stimulus distribution (prior).

A key assumption of the used observer model (4) is that encoding is efficient in the sense that it seeks to maximize the mutual information $I[\theta ,m]$ between a scalar stimulus variable $\theta$ and its sensory representation $m$ (9, 10). Fisher information $J(\theta )$, defined as

$$J(\theta )=\int {\left(\frac{\partial \ln p(m|\theta )}{\partial \theta }\right)}^{2}p(m|\theta )dm,$$ [S1]

can approximate mutual information in the regime of small Gaussian noise (11, 13) through

$$I[\theta ,m]=\frac{1}{2}\ln \left(\frac{S^2}{2\pi e}\right)-KL(p(\theta )||\frac{\sqrt{J(\theta )}}{S}),$$ [S2]

where $S={\int }_{\theta }\sqrt{J(\theta )}d\theta$ and $KL(||)$ represents the (always nonnegative) Kullback–Leibler divergence (49).

We have previously shown (4, 13) that, by imposing a constraint to bound the total coding resource of the form

$$S={\int }_{\theta }\sqrt{J(\theta )}d\theta \le c_1,$$ [S3]

where $c_1$ is a constant, maximizing mutual information requires the $KL(||)$ in Eq. S2 to be zero. This is the case if

$$p(\theta )\propto \sqrt{J(\theta )},$$ [S4]

i.e., if the limited coding resources as measured by Fisher information $J(\theta )$ are matched to the stimulus prior distribution $p(\theta )$. Several theoretical studies (4, 11, 12, 50) have previously derived and identified the constraint Eq. S4, which we refer to as the “efficient coding constraint.”

Relation between Fisher information and discrimination threshold.

Fisher information provides a lower bound on the discrimination threshold (5), including biased estimators (6). Below, we provide a shortened version of the derivation for the biased estimator according to ref. 6.

Consider two stimulus values ${\theta }_0-\delta \theta /2$ and ${\theta }_0+\delta \theta /2$. With the assumption $\delta \theta >0$, it follows that ${\theta }_2>{\theta }_1$. Signal detection theory (3) provides a formal description of how bias and variance for the estimates ${\widehat{\theta }}_1$, ${\widehat{\theta }}_2$ of the two stimulus values determine the probability that ${\widehat{\theta }}_2>{\widehat{\theta }}_1$, i.e., that the discrimination of the two stimulus values based on the estimates is correct. We can write

$$P_{\text{correct}}({\theta }_1,{\theta }_2)=\frac{1}{2}G\left(\frac{d({\theta }_1,{\theta }_2)}{2}\right),$$ [S5]

by making the assumption that both estimates are Gaussian distributed, where the function $G(.)$ is defined as

$$G(d)=\frac{2}{\sqrt{\pi }}{\int }_{-\mathrm{\infty }}^d\exp (-y^2)dy,$$ [S6]

and $d({\theta }_1,{\theta }_2)$ is the normalized distance (referred to as d-prime) between the distributions for the two estimates ${\widehat{\theta }}_1,{\widehat{\theta }}_2$. The distance $d({\theta }_1,{\theta }_2)$ can be expressed as

$$d({\theta }_1,{\theta }_2)=\frac{\widehat{\mu }({\theta }_2)-\widehat{\mu }({\theta }_1)}{\sqrt{\frac{{\widehat{\sigma }}^2({\theta }_2)+{\widehat{\sigma }}^2({\theta }_1)}{2}}},$$ [S7]

where $\widehat{\mu }({\theta }_i)$ and ${\widehat{\sigma }}^2({\theta }_i)$ denote the mean and the variance of each of the two Gaussian distributions.

By writing $\widehat{\mu }({\theta }_i)={\theta }_i+b({\theta }_i)$, where $b({\theta }_i)$ is the estimation bias at ${\theta }_i$, we can approximate $d({\theta }_1,{\theta }_2)$ for a small $\delta \theta$ as

$$d({\theta }_1,{\theta }_2)=d({\theta }_0-\delta \theta /2,{\theta }_0+\delta \theta /2)=\frac{\delta \theta +b({\theta }_0+\delta \theta /2)-b({\theta }_0-\delta \theta /2)}{\sqrt{\frac{{\widehat{\sigma }}^2({\theta }_2)+{\widehat{\sigma }}^2({\theta }_1)}{2}}}\approx \frac{\delta \theta (1+b\prime ({\theta }_0))}{\widehat{\sigma }({\theta }_0)},$$ [S8]

where, in the last step, we have exploited the assumption of small $\delta \theta$ by (i) approximating ${\widehat{\sigma }}^2({\theta }_1)$ and ${\widehat{\sigma }}^2({\theta }_2)$ as ${\widehat{\sigma }}^2({\theta }_0)$ and (ii) approximating $[b({\theta }_0+\delta \theta /2)-b({\theta }_0-\delta \theta /2)]/\delta \theta$ using $b\prime ({\theta }_0)$. For a given discrimination criterion $\alpha$ (measured in $P_{correct}$), the corresponding $d({\theta }_1,{\theta }_2)$ can be obtained via Eq. S5. We will refer to this $d$ value as $D_{\alpha }$. With Eq. S9, we then can express the discrimination threshold $\delta \theta$, which we will formally denote as $D(\theta )$, as

$$D(\theta )=\delta \theta =D_{\alpha }\frac{\widehat{\sigma }(\theta )}{1+b\prime (\theta )}.$$ [S9]

The Cramer–Rao bound for a biased estimator is given as

$${\widehat{\sigma }}^2(\theta )\ge \frac{{(1+b\prime (\theta ))}^2}{J(\theta )}.$$ [S10]

Strictly, the Cramer–Rao bound is only formulated for linear variables. However, for small noise levels, we can approximate circular variables as locally linear variables, and thus apply the Cramer–Rao bound. The approximation will break down for nonlocal problems, in which case the metrics and topology of the circular space also make the calculation of several key statistical quantities (e.g., mean, variance) substantially different from the way they are computed in the linear space. Rearranging Eq. S10, we get

$$\frac{\widehat{\sigma }(\theta )}{1+b\prime (\theta )}\ge \frac{1}{\sqrt{J(\theta )}}.$$ [S11]

By combining Eqs. S11 and S9, we find that the discrimination threshold is lower bounded by the Fisher information, i.e.,

$$D(\theta )\ge D_{\alpha }\frac{1}{\sqrt{J(\theta )}}.$$ [S12]

Finally, assuming that the Cramer–Rao bound is equally loose (not necessarily tight) for every $\theta$, we obtain the relation between Fisher information and discrimination threshold,

$$D(\theta )\propto \frac{1}{\sqrt{J(\theta )}}.$$ [S13]

Relation between perceptual bias and stimulus distribution (L₂ loss).

We have previously derived an analytic expression for perceptual $b(\theta )$ as a function of the stimulus distribution $p(\theta )$, assuming a Bayesian decoder that minimizes squared error ($L_2$ loss) (4). Assuming relative small noise and a smooth stimulus distribution, we found

$$b(\theta )\propto {\left(\frac{1}{p{(\theta )}^2}\right)}^{\prime }.$$ [S14]

As we show in Generalization to Different Loss Functions, this functional relation holds for a large family of symmetric loss functions, including some of the most commonly used loss functions (e.g., $L_p$ loss function). Thus there seems little use in rederiving Eq. S14 for the special case of mean squared error loss.

Putting it together: The relation between perceptual bias and discrimination threshold.

By combining Eqs. S4, S13, and S14, we obtain our main result, the proposed relation between perceptual bias and discrimination threshold,

$$b(\theta )\propto {(D{(\theta )}^2)}^{\prime }.$$ [S15]

In Generalization to Different Loss Functions, we will prove that this relation generalizes to a large class of symmetric loss functions of the Bayesian decoder.

Validation of the analytic expressions for discrimination threshold and perceptual bias.

The analytic expressions for both the discrimination threshold and the perceptual bias (Eqs. 2 and 3) relied on a set of assumptions and approximations (mostly with regard to the magnitude of the noise). To provide some insight into how these assumptions affect our results, we simulated the full Bayesian observer model (as briefly described in Generalization to Different Loss Functions and in more detail in ref. 4) for various sensory (internal) noise magnitudes, and then compared the bias and threshold curves of the observer model with those predicted by the two analytic expressions.

Fig. S1 shows this comparison for increasing levels of noise. As expected, the approximations are good under small noise conditions and smoothly degrade with increasing noise levels. The largest noise level shown ($\kappa =4$) corresponds to an estimation variance of a circular variable of approximately 30°. Importantly, while the numerically computed discrimination threshold and perceptual bias of the full Bayesian observer model are noticeably different from the curves given by the analytic expressions (Eqs. 2 and 3), they still almost perfectly obey the proposed law.

Part 2: Relation Between Estimation Bias and Variance.

The relation between discrimination threshold and bias can be rewritten in terms of estimation variance rather than threshold. This can be useful when trying to analyze datasets obtained with an estimation task (e.g., the method of adjustment). These datasets typically consist of a subject’s estimates over repeated trials, and thus allow the simultaneous estimate of perceptual bias and variance. While discrimination threshold and estimation variance are directly related, the reformulation in terms of variance results in a slightly more complex expression.

We start with the Cramer–Rao bound on the variance of a biased estimator, that is,

$${\widehat{\sigma }}^2(\theta )\ge \frac{{(1+b\prime (\theta ))}^2}{J(\theta )},$$ [S16]

where $J(\theta )$ is the Fisher information and $b(\theta )\prime$ is the derivative of the bias. Using the characteristic efficient coding constraint Eq. S4 of our Bayesian observer model, we can express the variance in terms of the prior expectation as

$${\widehat{\sigma }}^2(\theta )\propto \frac{{(1+b\prime (\theta ))}^2}{p{(\theta )}^2},$$ [S17]

where we again make the assumption that the bound is equally loose across the entire range of $\theta$. Combining Eq. S17 with the above derived dependency of the bias on the prior expectation Eq. S14, we find

$$b(\theta )\propto {\left(\frac{\widehat{\sigma }{(\theta )}^2}{{(1+b^{\prime }(\theta ))}^2}\right)}^{\prime }.$$ [S18]

Compared with the original expression Eq. S14, the formulation is identical for variance except that it is scaled by ${(1+b\prime (\theta ))}^2$. Given the bias $b(\theta )$, we can predict variance as

$$\widehat{\sigma }{(\theta )}^2\propto {(1+b\prime (\theta ))}^2\left(\int b(\theta )d\theta +c_0\right),$$ [S19]

while the reverse is generally not easy because it would involve solving a nonlinear differential equation. Obviously, when $b\prime (\theta )$ is constant, the relation simplifies to

$$b(\theta )\propto {(\widehat{\sigma }{(\theta )}^2)}^{\prime },$$ [S20]

and the predicted relation between the bias and variance has identical functional form to the one between the bias and discrimination threshold. This should be the case for magnitude variables (i.e., variables that follow Weber’s law), as the perceptual bias for these variables is approximately linear in the stimulus value $\theta$, and thus $b\prime (\theta )$ is constant (Fig. 3D). Similarly, for low noise levels, the biases become small and thus, assuming reasonably smooth bias curves, the term ${(1+b\prime (\theta ))}^2$ in Eq. S18 approximates 1. The relation between variance and bias again approximates Eq. S20. As the noise increases, the term ${(1+b\prime (\theta ))}^2$ becomes effective, and predictions for variance and squared discrimination threshold start to deviate from each other. Simulations shown in Fig. S2 demonstrate this effect.

Fig. S2.

Comparing the predictions for discrimination thresholds and variance (i.e., SD). (A) Perceptual bias is modeled as $b(\theta )=C_1\ast sin(2\theta )$, with four different $C_1$ values (0.5, 1, 2, 4). (B) A comparison between the predictions for discrimination threshold $D(\theta )$ (dashed lines) and the SD $\widehat{\sigma }(\theta )$ based on the bias curves in A. Discrimination threshold is modeled as $D(\theta )\propto \sqrt{C_2-0.5\ast C_1\ast cos(2\theta )}$. For SD, we use $\widehat{\sigma }(\theta )\propto \sqrt{C_2-0.5\ast C_1\ast cos(2\theta )}(1+2\ast C_1\ast cos(2\theta ))$. $C_2=3$ for all of the panels. When $b\prime (\theta )$ is small, the threshold and SD behave similarly (up to a scale factor, which we have set to be 1 here for simplicity). As $b\prime (\theta )$ increases, the difference between the two becomes larger.

The two predictions remain qualitatively similar, which was the reason for us to include the pointing direction dataset (20) in our collection of examples (Fig. 3) even though it reports estimation variance rather than discrimination threshold.

Part 3: Generalization to Different Loss Functions.

Below, we show that the expression for bias (Eq. S15) generalizes to a large class of symmetric loss functions. Therefore, the main result of the paper, the predicted relation between discrimination threshold (or variance) and perceptual bias, is general. We first focus on the family of $L_p$ loss functions and then consider the case of more general symmetric loss functions in the end.

Bayesian observer model with efficient sensory representation.

We consider a Bayesian observer model that relies on the efficient encoding of sensory information (4). Given a stimulus with value ${\theta }_0$, we assume the generative model for the encoding stage as

$$\stackrel{\sim }{m}=F({\theta }_0)+\delta ,$$ [S21]

where $\stackrel{\sim }{m}$ is the noisy sensory measurement, and $\delta$ represents the internal noise, which we assume is additive Gaussian with small variance ${\sigma }^2$. $F(\theta )$ represents the encoder (Fig. 1) and is a one-to-one mapping from stimulus space to an internal sensory space with units $\stackrel{\sim }{\theta }=F(\theta )$. This internal sensory space (and thus the mapping $F$) is defined as the space in which Fisher information is uniform (thus uniform discrimination threshold). For all following derivations, we use the notation $\stackrel{\sim }{(.)}$ to indicate any variable that is expressed in units of this space, e.g., $\stackrel{\sim }{m}=F(m)$.

Due to the efficient constraint Eq. S4 of the observer model, the mapping $F$ is defined as

$$F(\theta )={\int }_{-\mathrm{\infty }}^{\theta }p(\chi )d\chi ,$$ [S22]

which is the cumulative of the prior distribution $p(\theta )$.

With the above assumption of Gaussian noise, the posterior distribution can be expressed as

$$p(\theta |m)\propto p(\theta )e^{-\frac{{(F(\theta )-F(m))}^2}{2{\sigma }^2}}.$$ [S23]

Note that we formulate the inference problem in units of the stimulus space where a loss function has a clear physical interpretation. The $L_p$ loss function is defined as the norm

$$L_p(\theta ,\widehat{\theta })={|\theta -\widehat{\theta }|}^p$$ [S24]

between the estimate $\widehat{\theta }$ and the actual stimulus value $\theta$. The corresponding Bayesian estimate $\widehat{\theta }$ is the one that minimizes the Bayes risk

$$R={\int }_{\theta }{|\theta -\widehat{\theta }|}^{p}p(\theta )e^{-\frac{{(F(\theta )-F(m))}^2}{2{\sigma }^2}}d\theta .$$ [S25]

Below, we will derive how the bias of this estimate depends on the specifics of the loss function Eq. S24. Note that we have previously derived the bias for the $L_2$ loss (mean squared error estimate) (4).

L₁ loss.

The Bayesian estimate that minimizes the $L_1$ loss function corresponds to the median of the posterior distribution. Note that the median is invariant to the particular parametrization of the posterior based on the following mathematical fact: Assuming $x_0$ is the median of random variable $X$, for a one-to-one mapping $g$, $g(x_0)$ is the median of random variable $g(X)$. Because the posterior distribution for $\stackrel{\sim }{\theta }$ is Gaussian and centered around $F(m)$ (the prior is flat in the internal space), the median for $p(\stackrel{\sim }{\theta }|m)$ is simply $F(m)$. Mapping the value back to the stimulus space via $F^{-1}$, the median for $p(\theta |m)$ becomes $F^{-1}(F(m))=m$, and thus the estimate $\widehat{\theta }=m$. The bias then can be rewritten as

$$b({\theta }_0)=E[\widehat{\theta }]-{\theta }_0=E[m]-{\theta }_0.$$ [S26]

Note that the density of $m$ (with the inverse mapping of Eq. S22) follows

$$d(m)=\frac{1}{\sqrt{2\pi }\sigma }p(m)e^{-\frac{{(F(m)-F({\theta }_0))}^2}{2{\sigma }^2}},$$ [S27]

where $p(.)$ represents the prior distribution on $\theta$. Thus,

$$E[m]-{\theta }_0=\frac{1}{\sqrt{2\pi }\sigma }\int mp(m)e^{-\frac{{(F(m)-F({\theta }_0))}^2}{2{\sigma }^2}}dm-{\theta }_0=\frac{1}{\sqrt{2\pi }\sigma }\int F^{-1}(\stackrel{\sim }{m})e^{-\frac{{(\stackrel{\sim }{m}-{\stackrel{\sim }{\theta }}_0)}^2}{2{\sigma }^2}}d\stackrel{\sim }{m}-{\theta }_0,$$ [S28]

where we performed a change of variable from $m$ to $\stackrel{\sim }{m}=F(m)$. Assuming the prior density to be smooth, we expand $F^{-1}$ around ${\stackrel{\sim }{\theta }}_0$ up to the second order,

$$F^{-1}(\stackrel{\sim }{m})\approx F^{-1}({\stackrel{\sim }{\theta }}_0)+{(F^{-1})}_{\stackrel{\sim }{\theta }}^{\prime }({\stackrel{\sim }{\theta }}_0)(\stackrel{\sim }{m}-{\stackrel{\sim }{\theta }}_0)+\frac{1}{2}{(F^{-1})}_{\stackrel{\sim }{\theta }}^{″}({\stackrel{\sim }{\theta }}_0){(\stackrel{\sim }{m}-{\stackrel{\sim }{\theta }}_0)}^2.$$ [S29]

Note that, the derivative is taken with respect to $\stackrel{\sim }{\theta }=F(\theta )$, as indicated by the subscript $\stackrel{\sim }{\theta }$. Applying this expansion, we find that

$$E[m]-{\theta }_0\approx \frac{1}{\sqrt{2\pi }\sigma }\int \frac{1}{2}{(F^{-1})}_{\stackrel{\sim }{\theta }}^{″}({\stackrel{\sim }{\theta }}_0){(\stackrel{\sim }{m}-{\stackrel{\sim }{\theta }}_0)}^2{e}^{-\frac{{(F(m)-F({\theta }_0))}^2}{2{\sigma }^2}}d\stackrel{\sim }{m}=\frac{1}{2\sqrt{2\pi }\sigma }\int {\left(\frac{1}{p(F^{-1}({\stackrel{\sim }{\theta }}_0))}\right)}_{\stackrel{\sim }{\theta }}^{\prime }{(\stackrel{\sim }{m}-{\stackrel{\sim }{\theta }}_0)}^2{e}^{-\frac{{(F(m)-F({\theta }_0))}^2}{2{\sigma }^2}}d\stackrel{\sim }{m}=\frac{1}{2\sqrt{2\pi }\sigma }\int -\left(\frac{p_{\theta }^{\prime }({\theta }_0)}{p{({\theta }_0)}^3}\right){(\stackrel{\sim }{m}-{\stackrel{\sim }{\theta }}_0)}^2{e}^{-\frac{{(F(m)-F({\theta }_0))}^2}{2{\sigma }^2}}d\stackrel{\sim }{m}=\frac{1}{4\sqrt{2\pi }\sigma }\int {\left(\frac{1}{p{({\theta }_0)}^2}\right)}_{\theta }^{\prime }{(\stackrel{\sim }{m}-{\stackrel{\sim }{\theta }}_0)}^2{e}^{-\frac{{(F(m)-F({\theta }_0))}^2}{2{\sigma }^2}}d\stackrel{\sim }{m}=\frac{1}{4\sqrt{2\pi }\sigma }{\left(\frac{1}{p{({\theta }_0)}^2}\right)}^{\prime }\int {(\stackrel{\sim }{m}-{\stackrel{\sim }{\theta }}_0)}^2{e}^{-\frac{{(\stackrel{\sim }{m}-\stackrel{\sim }{{\theta }_0})}^2}{2{\sigma }^2}}d\stackrel{\sim }{m}=\frac{1}{4\sqrt{2\pi }\sigma }{\left(\frac{1}{p{({\theta }_0)}^2}\right)}^{\prime }\int y^2{e}^{-\frac{y^2}{2{\sigma }^2}}dy,$$ [S30]

where, in the last step, we have defined $y=\stackrel{\sim }{m}-{\stackrel{\sim }{\theta }}_0$ to simplify the notation. Evaluating the Gaussian integral $\int y^2{e}^{-\frac{y^2}{2{\sigma }^2}}dy$, we then find that

$$E[m]-{\theta }_0\approx \frac{1}{4}{\sigma }^2\left(\frac{1}{p{({\theta }_0)}^2}\right)\prime .$$ [S31]

It is important to note that this expression for $E[m]-{\theta }_0$ does not depend on the loss function of the decoder, because it does not involve the estimate $\widehat{\theta }$. It is determined merely by the encoding process. We will use this result again when we consider other loss functions. With Eqs. S26 and S31, we then can express the bias for any ${\theta }_0$ as

$$b({\theta }_0)=E[\widehat{\theta }]-{\theta }_0\approx \frac{1}{4}{\sigma }^2{(1/p{({\theta }_0)}^2)}^{\prime }.$$ [S32]

Therefore, $b(\theta )\propto (1/p{(\theta )}^2)\prime$.

L₀ loss (MAP estimate).

The Bayesian estimate that minimizes the $L_0$ loss corresponds to the mode of the posterior distribution. Computing the mode of the posterior Eq. S23 is equivalent to computing the mode of the logarithm of the posterior, thus

$$\frac{\partial \ln p(\theta |m)}{\partial \theta }=\frac{p\prime (\theta )}{p(\theta )}-\frac{1}{{\sigma }^2}(F(\theta )-F(m))F\prime (\theta ).$$ [S33]

Applying a first-order Taylor expansion on $F(\theta )$ around $m$, we obtain the approximation

$$F(\theta )-F(m)\approx F\prime (m)(\theta -m)=p(m)(\theta -m)$$ [S34]

and can reexpress Eq. S33 as

$$\frac{\partial \ln p(\theta |m)}{\partial \theta }\approx \frac{p\prime (\theta )}{p(\theta )}-\frac{1}{{\sigma }^2}p(m)(\theta -m)p(\theta ).$$ [S35]

Setting the left-hand side to zero, we find that the difference between the optimal Bayesian estimate $\widehat{\theta }$ and the measurement $m$ can be approximated by a constant related to $p({\theta }_0)$ and $p({\theta }_0)\prime$, i.e.,

$$\widehat{\theta }-m\approx {\sigma }^2\frac{p\prime (\widehat{\theta })}{p{(\widehat{\theta })}^{2}p(m)}\approx {\sigma }^2\frac{p\prime ({\theta }_0)}{p{({\theta }_0)}^3},$$ [S36]

where we approximated both $p(\widehat{\theta })$ and $p(m)$ by $p({\theta }_0)$ because $\sigma$ is assumed to be small. The expectation of this difference is

$$E[\widehat{\theta }-m]\approx {\sigma }^2\frac{p\prime ({\theta }_0)}{p{({\theta }_0)}^3}=-\frac{1}{2}{\sigma }^2{\left(\frac{1}{p{({\theta }_0)}^2}\right)}^{\prime }.$$ [S37]

With Eq. S31, we then can express the bias for the MAP estimator as

$$b({\theta }_0)=E[\widehat{\theta }-{\theta }_0]=E[\widehat{\theta }-m]+E[m-{\theta }_0]\approx -\frac{1}{4}{\sigma }^2{(1/p{({\theta }_0)}^2)}^{\prime }.$$ [S38]

Therefore, $b(\theta )\propto {(1/p{(\theta )}^2)}^{\prime }$. Note that the coefficient of proportionality is negative.

L_2q loss function ($\mathrm{\text{q}}\mathrm{>}1$, and q is an integer).

The Bayesian estimate under $L_{2q}$ loss cannot be expressed in closed form, in general. However, we can compute the leading term of the bias of this estimator when the noise variance is small.

Again, the goal is to find the estimator $\widehat{\theta }$, which minimizes the following Bayes risk:

$$R={\int }_{\theta }{(\widehat{\theta }-\theta )}^{2q}p(\theta )e^{-\frac{{(F(\theta )-F(m))}^2}{2{\sigma }^2}}d\theta .$$ [S39]

By examining the second-order derivative of $R$ with respect to $\widehat{\theta }$, we find that the problem is a convex optimization problem. Therefore, there exists one and only one solution. We begin by rewriting

$$\widehat{\theta }-\theta =(\widehat{\theta }-m)+(m-\theta )=(\widehat{\theta }-m)+(F^{-1}(\stackrel{\sim }{m})-F^{-1}(\stackrel{\sim }{\theta })).$$ [S40]

Applying a second-order Taylor expansion on $F^{-1}$ (Eq. S22) around $\stackrel{\sim }{m}$, we find

$$\widehat{\theta }-\theta =(\widehat{\theta }-m)+F^{-1}(\stackrel{\sim }{m})-F^{-1}(\stackrel{\sim }{\theta })\approx (\widehat{\theta }-m)+\frac{1}{p(m)}(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })+\frac{p\prime (m)}{2p{(m)}^3}{(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })}^2.$$ [S41]

To simplify notation, we define $r=\widehat{\theta }-m$ and $s=\frac{p\prime (m)}{2p{(m)}^3}$. Given these notations,

$$\widehat{\theta }-\theta =r+\frac{1}{p(m)}(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })+s{(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })}^2.$$ [S42]

Now the Bayes risk $R$ can be approximated as

$$R\approx {\int }_{\stackrel{\sim }{\theta }}{\left[r+\frac{1}{p(m)}(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })+s{(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })}^2\right]}^{2q}{e}^{-\frac{{(\stackrel{\sim }{\theta }-\stackrel{\sim }{m})}^2}{2{\sigma }^2}}d\stackrel{\sim }{\theta }.$$ [S43]

To find the estimate $\widehat{\theta }$ that minimizes $R$, we take the first-order derivative with respect to $\widehat{\theta }$ (which is equivalent to the first-order derivative with respect to $r$ because of the linear dependence on $\widehat{\theta }$), and set it to zero. We find that $r$ should approximately satisfy the following equation:

$${\int }_{\stackrel{\sim }{\theta }}{\left[r+\frac{1}{p(m)}(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })+s{(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })}^2\right]}^{2q-1}{e}^{-\frac{{(\stackrel{\sim }{\theta }-\stackrel{\sim }{m})}^2}{2{\sigma }^2}}d\stackrel{\sim }{\theta }=0.$$ [S44]

Denoting $x=\stackrel{\sim }{m}-\stackrel{\sim }{\theta }$, the above expression can be simplified as

$${\int }_x{\left[r+\frac{1}{p(m)}x+s{x}^2\right]}^{2q-1}{e}^{-\frac{x^2}{2{\sigma }^2}}dx=0.$$ [S45]

We expand the left-hand side, exploiting (due to the symmetry) the fact that

$$\int x^{2n-1}{e}^{-\frac{x^2}{2{\sigma }^2}}dx=0,$$ [S46]

where $n$ is an arbitrary integer, and obtain

$${\int }_x[B_0(x^{2q}s+o(x^{2q}s))+B_{1}r(x^{2q-2}+o(x^{2q-2}))+B_2{r}^2(x^{2q-2}s+o(x^{2q-2}s))+B_3{r}^3(x^{2q-4}+o(x^{2q-4}))+\mathrm{\dots }+B_{2q-2}{r}^{2q-2}(x^{2}s+o(x^2))+B_{2q-1}{r}^{2q-1}]e^{-\frac{x^2}{2{\sigma }^2}}dx=0,$$ [S47]

where $B_i$ are the corresponding coefficients which we didn’t explicitly express for simplicity. Using the Gaussian integral

$$\int x^{2n}{e}^{-\frac{x^2}{2{\sigma }^2}}dx=\sqrt{2\pi }(2n-1)!!{\sigma }^{2n+1},$$ [S48]

where $n$ is an arbitrary integer, we use the notation for double factorial $(2n-1)!!=(2n-1)\ast (2n-3)\ast \mathrm{\dots }\ast 3\ast 1$ and obtain

$$C_0({\sigma }^{2q+1}s+o({\sigma }^{2q+1}s))+C_{1}r({\sigma }^{2q-1}+o({\sigma }^{2q-1}))+C_2{r}^2({\sigma }^{2q-1}s+o({\sigma }^{2q-1}s))+C_3{r}^3({\sigma }^{2q-3}+o({\sigma }^{2q-3}))+\mathrm{\dots }+C_{2q-2}{r}^{2q-2}({\sigma }^{3}s+o({\sigma }^{3}s))+C_{2q-1}{r}^{2q-1}\sigma =0,$$ [S49]

where $C_i$ are the corresponding coefficients. Ignoring the high-order terms, we obtain

$$C_0{\sigma }^{2q}s+C_{1}r{\sigma }^{2q-2}+C_2{r}^2{\sigma }^{2q-2}s+C_3{r}^3{\sigma }^{2q-4}+\mathrm{\dots }+C_{2q-2}{r}^{2q-2}{\sigma }^{2}s+C_{2q-1}{r}^{2q-1}=0,$$ [S50]

which can be rewritten as

$${\sigma }^{2q-2}(C_0{\sigma }^{2}s+C_{1}r)+{\sigma }^{2q-4}{r}^2(C_2{\sigma }^{2}s+C_{3}r)+\mathrm{\dots }+r^{2q-2}(C_{2q-2}{\sigma }^{2}s+C_{2q-1}r)=0.$$ [S51]

It can be verified that the coefficients $C_i$ satisfy the following property:

$$q<\frac{C_{2k}}{C_{2k+1}}<q^2,k=\mathrm{0,1},\mathrm{\dots },q-1.$$ [S52]

The left-hand side of Eq. S51 is a continuous function of $r$ that we define as $f(r)$. We find that

$$f(-q{\sigma }^{2}s)f(-q^2{\sigma }^{2}s)<0.$$ [S53]

Due to the Intermediate Value Theorem, there must exist a solution for $f(r)=0$ in the interval $(-q{\sigma }^{2}s,-q^2{\sigma }^{2}s)$, and, because the problem is convex, this solution is unique. This tells us that $r\sim O({\sigma }^2)$. As a result, all of the terms on the left-hand side of Eq. S51 are of the order $o({\sigma }^{2q})$, except for the first term ${\sigma }^{2q-2}(C_0{\sigma }^{2}s+C_{1}r)$, which is of the order $O({\sigma }^{2q})$.

For small $\sigma$, the higher-order terms can be ignored, and the only relevant term left is ${\sigma }^{2q-2}(C_0{\sigma }^{2}s+C_{1}r)$. Thus, for small $\sigma$, we only need to solve the equation

$${\sigma }^{2q-2}(C_0{\sigma }^{2}s+C_{1}r)=0.$$ [S54]

With the constraint Eq. S52 on the coefficients $C_0,C_1$, this results in

$$r=-\frac{C_0}{C_1}{\sigma }^{2}s=-(2q-1){\sigma }^{2}s=-(2q-1){\sigma }^2\frac{p\prime (m)}{2p{(m)}^3}\approx \frac{(2q-1)}{4}{\sigma }^2{\left(\frac{1}{p{({\theta }_0)}^2}\right)}^{\prime },$$ [S55]

and thus

$${\widehat{\theta }}_0-m\approx \frac{(2q-1)}{4}{\sigma }^2{\left(\frac{1}{p{({\theta }_0)}^2}\right)}^{\prime }.$$ [S56]

The bias of the Bayesian estimator for any $L_{2q}$ loss function can then be approximated as

$$b({\theta }_0)=E[{\widehat{\theta }}_0-{\theta }_0]=E[{\widehat{\theta }}_0-m]+E[m-{\theta }_0]\approx \frac{(2q-1)}{4}{\sigma }^2{\left(\frac{1}{p{({\theta }_0)}^2}\right)}^{\prime }+\frac{1}{4}{\sigma }^2{\left(\frac{1}{p{({\theta }_0)}^2}\right)}^{\prime }=\frac{2q}{4}{\sigma }^2{(1/p{({\theta }_0)}^2)}^{\prime },$$ [S57]

where we have again used Eq. S31.

Therefore, $b(\theta )\propto \left(1/p{(\theta )}^2\right)\prime$.

L_2q−1 loss function ($\mathrm{\text{q}}\mathrm{>}1$, and q is an integer).

We can use techniques similar to those for the $L_{2q}$ case to compute the bias for an $L_{2q-1}$ loss function. The main difference is that we have now to consider an additional term $M$ that, however, as we show below, can be neglected. For an $L_{2q-1}$ loss, the Bayesian estimator $\widehat{\theta }$ minimizes the Bayes risk

$$R={\int }_{\theta }{|\widehat{\theta }-\theta |}^{2q-1}p(\theta )e^{-\frac{{(F(\theta )-F(m))}^2}{2{\sigma }^2}}d\theta .$$ [S58]

Similar to the $L_{2q}$ case, the optimization problem is convex and thus has one and only one solution. We solve for the extremum by setting $\partial R/\partial \widehat{\theta }=0$. Applying a Taylor expansion, we find

$$0={\int }_{\theta \ge \widehat{\theta }}{(\widehat{\theta }-\theta )}^{2q-2}p(\theta )e^{-\frac{{(F(\theta )-F(m))}^2}{2{\sigma }^2}}d\theta +{\int }_{\theta <\widehat{\theta }}-{(\widehat{\theta }-\theta )}^{2q-2}p(\theta )e^{-\frac{{(F(\theta )-F(m))}^2}{2{\sigma }^2}}d\theta ={\int }_{\theta \ge \widehat{\theta }}{(\widehat{\theta }-\theta )}^{2q-2}p(\theta )e^{-\frac{{(F(\theta )-F(m))}^2}{2{\sigma }^2}}d\theta +{\int }_{\theta <\widehat{\theta }}-{(\widehat{\theta }-\theta )}^{2q-2}p(\theta )e^{-\frac{{(F(\theta )-F(m))}^2}{2{\sigma }^2}}d\theta \approx {\int }_{\stackrel{\sim }{\theta }\ge \stackrel{\sim }{\widehat{\theta }}}{\left(r+\frac{1}{p(m)}(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })+s{(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })}^2\right)}^{2q-2}{e}^{-\frac{{(\stackrel{\sim }{\theta }-\stackrel{\sim }{m})}^2}{2{\sigma }^2}}d\stackrel{\sim }{\theta }+{\int }_{\stackrel{\sim }{\theta }<\stackrel{\sim }{\widehat{\theta }}}-{\left(r+\frac{1}{p(m)}(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })+s{(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })}^2\right)}^{2q-2}{e}^{-\frac{{(\stackrel{\sim }{\theta }-\stackrel{\sim }{m})}^2}{2{\sigma }^2}}d\stackrel{\sim }{\theta }={\int }_{\stackrel{\sim }{\theta }\ge \stackrel{\sim }{m}}{\left(r+\frac{1}{p(m)}(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })+s{(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })}^2\right)}^{2q-2}{e}^{-\frac{{(\stackrel{\sim }{\theta }-\stackrel{\sim }{m})}^2}{2{\sigma }^2}}d\stackrel{\sim }{\theta }+{\int }_{\stackrel{\sim }{\theta }<\stackrel{\sim }{m}}-{\left(r+\frac{1}{p(m)}(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })+s{(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })}^2\right)}^{2q-2}{e}^{-\frac{{(\stackrel{\sim }{\theta }-\stackrel{\sim }{m})}^2}{2{\sigma }^2}}d\stackrel{\sim }{\theta }+M,$$ [S59]

where the term $M$ is introduced without being explicitly spelled out. We will deal with this term later.

To simplify notation, we define $x=\stackrel{\sim }{m}-\stackrel{\sim }{\theta }$. It follows that

$$0\approx {\int }_{x\le 0}{(r+\frac{1}{p(m)}x+s{x}^2)}^{2q-2}{e}^{-\frac{x^2}{2{\sigma }^2}}dx-{\int }_{x>0}{(r+\frac{1}{p(m)}x+s{x}^2)}^{2q-2}{e}^{-\frac{x^2}{2{\sigma }^2}}dx+M.$$ [S60]

Let us define $g(r)={\int }_{x\le 0}{(r+\frac{1}{p(m)}x+s{x}^2)}^{2q-2}{e}^{-\frac{x^2}{2{\sigma }^2}}dx-{\int }_{x>0}{(r+\frac{1}{p(m)}x+s{x}^2)}^{2q-2}{e}^{-\frac{x^2}{2{\sigma }^2}}dx$. The goal then is to find the $r$ which satisfies $g(r)+M\approx 0$. We will take advantage of the fact that the problem has a unique solution.

We first deal with $g(r)$. Similar to the analysis performed for the $L_{2q}$ case, we can verify that, for small $\sigma$,

$$g(r)\approx {\int }_{x\le 0}[C_0{x}^{2q-1}s+C_1{x}^{2q-3}r]e^{-\frac{x^2}{2{\sigma }^2}}dx.$$ [S61]

By verifying the coefficients $C_0,C_1$, we find that $r=-(2q-2)s{\sigma }^2$ to first order approximately satisfies $g(r)=0$.

Furthermore, we find that $r=-(2q-2)s{\sigma }^2$ also satisfies $g(r)+M\approx 0$. The reason is that, for $r=-(2q-2)s{\sigma }^2$, $M\sim o({\sigma }^{2q})$ is of higher order than $g(r)$. Thus, $M$ can be ignored. Specifically, we can calculate the order of $M$ as

$$|M|=2{\int }_{\stackrel{\sim }{\theta }\in [\stackrel{\sim }{\widehat{\theta }},\stackrel{\sim }{m}]}{\left(r+\frac{1}{p(m)}(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })+s{(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })}^2\right)}^{2q-2}{e}^{-\frac{{(\stackrel{\sim }{\theta }-\stackrel{\sim }{m})}^2}{2{\sigma }^2}}d\stackrel{\sim }{\theta }\approx 2{\int }_{\stackrel{\sim }{\theta }\in [\stackrel{\sim }{\widehat{\theta }},\stackrel{\sim }{m}]}{\left(\frac{1}{p(m)}(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })\right)}^{2q-2}{e}^{-\frac{{(\stackrel{\sim }{\theta }-\stackrel{\sim }{m})}^2}{2{\sigma }^2}}d\stackrel{\sim }{\theta }\le 2{\int }_{\stackrel{\sim }{\theta }\in [\stackrel{\sim }{\widehat{\theta }},\stackrel{\sim }{m}]}{\left(\frac{1}{p(m)}(\stackrel{\sim }{m}-\stackrel{\sim }{\theta })\right)}^{2q-2}d\stackrel{\sim }{\theta }\sim O({\sigma }^{4q-2})\sim o({\sigma }^{2q}).$$ [S62]

We have assumed $\stackrel{\sim }{m}\ge \stackrel{\sim }{\widehat{\theta }}$ in the above calculation for the convenience of notation. The same technique applies and the result holds for the case of $\stackrel{\sim }{m}\le \stackrel{\sim }{\widehat{\theta }}$.

Thus, $r=-(2q-2)s{\sigma }^2$ is the only solution of $\partial R/\partial \widehat{\theta }=0$ when $\sigma$ is small. Similar to the case of the $L_{2q}$ loss function, we then can express the bias of the Bayesian estimate as

$$b({\theta }_0)\approx \frac{2q-1}{4}{\sigma }^2{(1/p{({\theta }_0)}^2)}^{\prime }.$$ [S63]

Therefore, $b(\theta )\propto {(1/p{(\theta )}^2)}^{\prime }$.

General symmetric loss function.

For an arbitrary symmetric loss function $L$ with $L$ being smooth except at $0$, the Bayesian estimator $\widehat{\theta }$ is the estimator that minimizes the Bayes risk

$$R={\int }_{\theta }L(|\widehat{\theta }-\theta |)p(\theta )e^{-\frac{{(F(\theta )-F(m))}^2}{2{\sigma }^2}}d\theta .$$ [S64]

Suppose that $L(|\widehat{\theta }-\theta |)\sim O({|\widehat{\theta }-\theta |}^k)$ where $k$ is an integer. Then the bias of the Bayesian estimator is approximately the bias of the Bayesian estimator corresponding to the $L_k$ loss function, which is what we have derived above.

We thus conclude that $b(\theta )\propto {(1/p{(\theta )}^2)}^{\prime }$ represents a general description of the bias for a large set of symmetric loss functions.