Osmotaxis in Escherichia coli through changes in motor speed

Significance

Bacterial taxis has been a subject of active investigation for over 100 years, serving as a model of both biological sensory transduction and self-propulsion. Consequently, chemotaxis of Escherichia coli is one of the best-understood biological networks. Nevertheless, the exact roles of taxis and motility in E. coli’s life cycle, particularly in host invasion, remain unknown, partly because of the complexity of its natural habitat. By looking at the response of both individual bacterial motors and a swimming population, we investigate E. coli’s response to changes in external osmolalities similar to those found in the human gastrointestinal tract. We find that, unlike chemotaxis, osmotic response changes the motor speed and discuss how the observation can lead to previously observed osmotaxis.

Abstract

Bacterial motility, and in particular repulsion or attraction toward specific chemicals, has been a subject of investigation for over 100 years, resulting in detailed understanding of bacterial chemotaxis and the corresponding sensory network in many bacterial species. For Escherichia coli most of the current understanding comes from the experiments with low levels of chemotactically active ligands. However, chemotactically inactive chemical species at concentrations found in the human gastrointestinal tract produce significant changes in E. coli’s osmotic pressure and have been shown to lead to taxis. To understand how these nonspecific physical signals influence motility, we look at the response of individual bacterial flagellar motors under stepwise changes in external osmolarity. We combine these measurements with a population swimming assay under the same conditions. Unlike for chemotactic response, a long-term increase in swimming/motor speeds is observed, and in the motor rotational bias, both of which scale with the osmotic shock magnitude. We discuss how the speed changes we observe can lead to steady-state bacterial accumulation.

Many bacterial species are able to not only self-propel (exhibit motility), but also direct their motion toward more favorable environments. This behavior, called taxis (1, 2), has long been a subject of scientific investigation, as it serves a variety of purposes: seeking out nutrients and avoiding toxic substances (3, 4) and identifying thermal (5) and oxygen (6) gradients, as well as aiding pathogenic species in infecting their hosts (7, 8). The understanding of bacterial taxis is not only important when it comes to bacterial motility and accumulation; it also serves as a model for biological signal processing. Of particular interest are the precision (9, 10), sensitivity (11), and robustness (12, 13) that can be achieved with biological networks and potentially used for human design purposes (14, 15). Specifically, bacterial chemotaxis, motion toward or away from specific chemicals (3), was first described over 120 years ago (16, 17). Since then, the systematic research efforts made it one of the best-studied topics in biology, especially regarding Escherichia coli.

E. coli swims by rotating a bundle of flagellar filaments (18, 19), each powered by a bacterial flagellar motor (BFM), a rotary nanomachine that spins in the clockwise (CW) or counterclockwise (CCW) direction (20). Each bacterium possesses several individual motors randomly distributed along the cell body (19, 21), which when rotating CCW enable formation of a stable filament bundle that propels the cell forward (22). When one or, most likely, a few motors switch to CW rotation, their respective filaments fall out of the bundle, leading to a tumble event (19). Forward swimming, likely in a different direction due to approximately random reorientation of the bacterial cell during the tumble event, resumes when motors switch back to the CCW direction and the bundle reforms (18, 19).

The probability of CW rotation increases with the intracellular concentration of phosphorylated CheY protein (CheY-P) that interacts with the rotor of the BFM (23). CheY-P is part of a feedback control circuit, the chemotactic network (3), which relays outside information to the motor and allows E. coli to direct its motion. Inputs of the circuit are the methyl-accepting chemotactic proteins (MCPs), transmembrane proteins that bind specific ligands in the cell exterior (3) and through a signaling cascade affect the CheY-P to CheY ratio. When sensing attractants or repellents in the nanomolar to micromolar range, the change in CheY-P to CheY ratio resets to the initial level within seconds, a characteristic feature of the network termed perfect adaptation (24). Thus, directionality in the net motion of the cell arises through transient tuning of motor switching frequency in response to external stimuli (3).

The majority of work on E. coli chemotaxis over the last 40 years has been performed in a minimal phosphate buffer [termed motility buffer (25)]. However, one of the primary habitats of E. coli is the gastrointestinal tract of humans and other warm-blooded animals (26, 27). This complex environment features not only various chemoattractants and repellents, but also spatial and temporal changes in osmolarity (28, 29, 30), which, in the stomach and intestine of humans, reach up to 500 mOsmol/kg. The exact composition and osmolarity depend on the meal, ingestion history, and location within the gastrointestinal tract (28, 31).

Sudden osmotic increases, termed hyperosmotic shocks or upshocks, cause cell volume shrinkage and require solute pumping and/or synthesis to reinflate the cell and reestablish osmotic pressure (32, 33). Bacterial movement in search of environments with optimal water content, termed osmotaxis, was discovered as early as 1889 (34). Nonspecific taxis away from sources of high concentrations has since been observed both in agar plate and in capillary assays (35–38). However, the behavior that leads to negative osmotaxis is less known (35, 36, 39, 40), and contradictory observations have been reported. Osmotic stimuli can send a signal down the network through mechanical stimulation of chemoreceptors (41); yet, free-swimming cells were observed to tumble in response to an osmotic stimulus even when completely devoid of all components of the chemotactic network (35, 40). Intriguingly, this tumbling was later attributed to CCW rotation of flagella that normally results in cell runs (40). The finding that osmotaxis on agar plates requires the presence of at least some chemosensors and all of the chemotactic signaling proteins further complicates the picture (35). Open questions thus remain about the nature of this motile behavior that drives spatial accumulation and its similarities, differences, and possible interactions with taxis toward chemicals.

To clarify the exact nature of the osmotactic response, we study the phenomenon on both single-cell and population levels, observing the rotation of individual flagellar motors under stepwise increases in osmolality and measuring the swimming speeds of a population of $\sim$10,000 bacteria after exposure to an osmotic shock. The shock magnitudes we administer are motivated by those encountered in the human gastrointestinal tract (28, 31). We find that a stepwise increase in osmolality results in an elevated, long-term CW bias. In addition, we observe osmokinesis after osmotic shock, i.e., significant changes in the motor and, consequently, swimming speeds of bacteria. Finally, for higher shock magnitudes, we observe a loss of motor speed immediately after shock, followed by a speed recovery. We discuss how the observed nonadaptive response and osmokinesis can lead to taxis.

Results

Single-Motor Response to an Osmotic Shock Is Complex.

We begin with the reasonable assumption that at least one component of the chemotactic network responds to an osmotic stimulus to generate previously observed osmotactic behavior (35). Then, the response should be evident in the output of the chemotactic network, the CW bias of a single BFM. CW bias is defined as the fraction of time the BFM spends rotating in the clockwise direction (42),

$$CWBias=\frac{N_{cw}}{N_{tot}},$$ [1]

where $N_{cw}$ is the number of data points corresponding to CW rotation and $N_{tot}$ is the total number of data points in a given time interval.

To compute the CW bias, we measured the speed of an individual BFM when exposed to a stepwise increase in the external osmolality. SI Appendix, Fig. S1 gives a schematic of the bead assay used for measuring the motor speed (25, 42). Briefly, we attach cells to the coverslip and attach a polystyrene bead, 0.5 $\mathrm{\mu }$m in diameter, to a short filament stub (25, 42). The rotation of the BFM-driven bead is recorded using back-focal-plane interferometry at a 10-kHz sampling rate (43–45). A representative single-motor rotation trace so obtained is shown in Fig. 1A. The shaded light-blue interval shows the motor speed and rotational direction before osmotic stimulus. Positive motor speed values represent CCW rotation and negative ones CW. Fig. 1B shows the histogram of the CW bias obtained from the motor speed trace in A (Materials and Methods). Before the stimulus, the motor switches from CCW to CW rotation approximately four times per minute at $\text{CW bias}=0.07$, agreeing with previous studies (42, 46).

Fig. 1.

(A) An example 30-min speed trace obtained from a single BFM. The cell was initially in VR buffer (Materials and Methods), indicated in light-blue shading, and exposed to an osmotic upshock of 488 mOsmol/kg at t = 5 min. The shock was delivered as a step increase by flowing in VRB containing an additional 400 mM sucrose, resulting in a shock magnitude of 488 mOsmol/kg. (B, Top) A histogram of CW bias computed by binning the trace in A into 30-s bins and dividing the time spent rotating CW by the bin length (Eq. 1 and Materials and Methods). B, Bottom shows the same histogram condensed into a color map, with an intensity scale to the right. (C) Single-motor speed trace of a $\mathrm{\Delta }CheY$ mutant exposed to the same osmotic upshock as in A.

At $t=5\text{min}$, the extracellular osmolality is elevated by delivering 400 mM sucrose, at a flow rate of $\sim 120\mathrm{\mu }\text{L}/\text{min}$ and local flow velocity $\sim 60\mathrm{\mu }\text{m}/\text{s}$ (47), causing an osmotic upshock of 488 mOsmol/kg. Immediately upon upshock, the motor stops switching rotational direction and speed drops. Then, a recovery phase begins (Fig. 1 A and B, unshaded time interval) with the motor speed gradually increasing while switching is absent. Postrecovery phase, which we define as the period after motor switching has resumed, is characterized by an increased switching frequency. Consequently, the CW bias is also elevated (to 0.16) and is maintained over at least 20 min, suggesting that, unlike chemotaxis, the osmotactic response does not exhibit perfect adaptation (10, 24). The color map in Fig. 1B, Bottom is a compact representation of the histogram in Fig. 1B, Top.

To determine whether CheY-P is necessary for the osmotic response observed in Fig. 1 A and B, we performed single-motor measurements on a strain lacking CheY [$\mathrm{\Delta }\mathrm{𝐶ℎ𝑒𝑌}$ mutant (48, 49)]. A representative trace is shown in Fig. 1C, and several more traces are given in SI Appendix, Fig. S2. The recovery phase of the $\mathrm{\Delta }CheY$ mutant is the same as observed in Fig. 1A for the chemotactic wild type. However, the postrecovery phase of the mutant shows no switching events, indicating that CheY-P is necessary for the elevated bias observed in Fig. 1 A and B.

Osmotic Response Does Not Exhibit Perfect Adaptation.

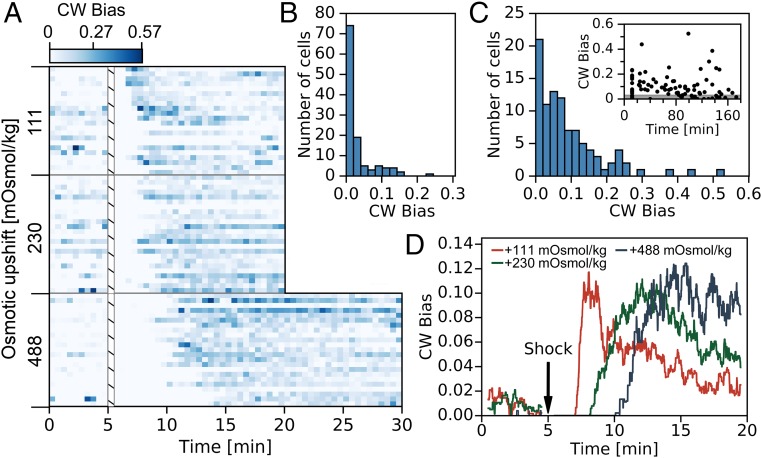
We analyzed 69 cells exposed to three upshock magnitudes to confirm the absence of perfect adaptation observed in postrecovery phase (Fig. 1 A and B). Upshocks were delivered as in Fig. 1, by exchanging volume recovery (VR) buffer (Materials and Methods) with the same buffer supplemented with 100 mM, 200 mM, and 400 mM sucrose, corresponding to osmotic shocks of 111 mOsmol/kg, 230 mOsmol/kg, and 488 mOsmol/kg [similar to osmolalities found in the human intestine (28, 31); see also SI Appendix, Table 1 for osmolality measurements of all our buffers].

Fig. 2A shows color map histograms of each individual single-motor bias trace, where darker color represents higher CW bias and white represents smooth swimming. The recovery phase, characterized by the zero CW bias period, scales with the shock magnitude. SI Appendix, Fig. S3A shows the duration of the recovery phase, $T_{rec,CW}$, against the shock magnitude, where for the highest shock administered $T_{rec,CW}\sim$ 5 min. The length of the recovery phase roughly corresponds to the time E. coli takes to recover its volume and osmotic pressure upon the hyperosmotic shock (50). Throughout the postrecovery phase, CW bias levels do not, on average, relax to their initial preshock values. In our measurements this phase lasts for $\sim$10–20 min, which is significantly longer than chemotactic adaptation times (10) even when saturating attractant concentrations are used (51).

Fig. 2.

(A) Stacked single-cell color maps (histograms) of CW bias for three different shock magnitudes (Left). Bin widths are 30 s. VRB was exchanged for the same buffer with the addition of sucrose at t = 5 min. The white hatched column represents the period of the media exchanged whose duration was $\sim$10–15 s. Twenty-two, 24, and 23 cells are given for the 111-mOsmol/kg, 230-mOsmol/kg, and 488-mOsmol/kg conditions, respectively. A, Top shows color map scale. (B and C) Histogram of CW bias for cells (B) before osmotic upshock (in VRB) and (C) after osmotic upshock, administered by exchanging VRB with VRB + 200 mM sucrose. Bin width is set to 0.020. A total of 120 motors (each on a different cell) were used to construct B and 96 motors to construct C. C, Inset plots these 96 single-motor biases against the time after their respective osmotic upshift. Gray shading represents the range between the 25th and the 75th percentile of the CW bias distribution in VRB given in B. (D) Median population CW bias in time, computed from cells given in A, for different shock magnitudes: 111 mOsmol/kg (red), 230 mOsmol/kg (green), and 488 mOsmol/kg (dark blue). Black arrow indicates the time at which hyperosmotic shock was administered.

Evidence for this assertion is shown in the CW bias histograms in Fig. 2B, which shows a distribution computed from 3-min recordings in VR buffer before shock, and Fig. 2C, which shows a distribution computed from 3-min intervals taken at various time points, 12 or more minutes after shock with 200 mM sucrose. A total of 120 single-motor recordings were used for the preshock condition and 96 recordings for after it. The median value of the population CW bias shifts from 0.01 preshock to 0.06 after addition of 200 mM sucrose. Fig. 2D shows the median CW bias in time for each of the three different shocks, calculated from the raw speeds of individual cells presented in Fig. 2A, using a 60-s-wide moving window. Here, only medians are shown for clarity and the means, together with the interquartile range for each shock magnitude, are plotted in SI Appendix, Fig. S3 B–D. While the CW bias shows some recovery in time, in particular for 111-mOsmol/kg and 230-mOsmol/kg shocks, it proceeds on a slow timescale and the median values at the end of our measurement time remain elevated with respect to the initial value.

A further corroboration of long-term increase in CW bias after osmotic shock comes from separating the CW bias values of Fig. 2B according to the time point at which they were measured, relative to the administration of the osmotic shock (t = 0). This is displayed in Fig. 2C, Inset and shows that the elevated CW bias persists over a timescale as long as 1 h.

Osmotic Response Shows Osmokinesis, That Is, Changes in Motor Speed.

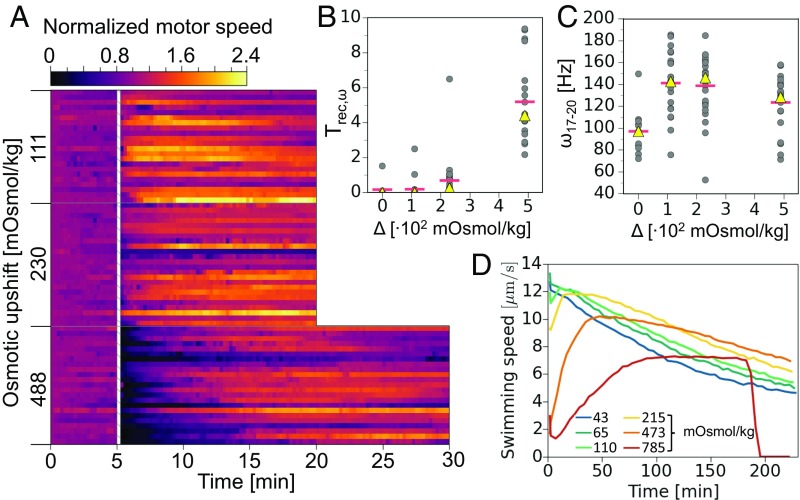
The response to an osmotic upshock includes not only CW bias dynamics, but also changes in motor and free-swimming speed. Fig. 3A shows a color map plot of normalized single-motor speeds of the same 69 cells presented in Fig. 2A. All cells were originally in VR buffer and subsequently exposed to an osmotic upshock, using 100 mM, 200 mM, or 400 mM sucrose, corresponding to upshifts of 111 mOsmol/kg, 230 mOsmol/kg, and 488 mOsmol/kg. BFM speeds were normalized with respect to the initial speed of each motor, i.e., to the average value of the first 15 s of the recording.

Fig. 3.

(A) Stacked single-motor (also single-cell) speed histograms, where the motor speed for each BFM is normalized to the average value of the first 15 s. Bin widths are 15 s and the color represents the bin height. Results are grouped by upshock magnitude, as indicated at Left. The white hatched column represents the point where an osmotic shock was performed by exchanging VRB for VRB + sucrose and the flow lasted for 10–15 s. Twenty-two, 24, and 23 cells are given for the 111-mOsmol/kg, 230-mOsmol/kg, and 488-mOsmol/kg conditions, respectively. A, Top shows the color map scale. (B) Time necessary to recover the average value of preshock speed. Red horizontal bars are mean, and yellow triangles are median values, and the graph contains 18, 22, 23, and 20 single-motor data points for the 0-mOsmol/kg, 111-mOsmol/kg, 230-mOsmol/kg, and 488-mOsmol/kg upshocks. One value for the 230-mOsmol/kg condition and three for the 488-mOsmol/kg condition have been excluded from the graph as these motors do not recover average initial speed in the course of recording. The 0-mOsmol/kg condition is a buffer-to-buffer control flush, where we used the same shocking protocol as for osmotic upshocks. (C) Single-motor speeds calculated as 3-min averages corresponding to a section between t = 17 min and t = 20 min in A. The graph contains 12, 22, 24, and 23 single-motor data points for the 0-mOsmol/kg, 111-mOsmol/kg, 230-mOsmol/kg, and 488-mOsmol/kg upshocks. The 0-mOsmol/kg condition contains 12 of 18 control flushes that were at least 20 min long. (D) DDM measurement of swimming speeds following an osmotic shock. Cells were shocked in microfuge tubes and brought into a microscope within 2 min. The key shows shock magnitudes and the mean speed is the average of swimming speeds obtained for each time point in a range of different length scales (Materials and Methods). The systematic error of our measurements is then calculated as the SD of the mean and falls within $\sim$5% of the mean value. Here it was not plotted for clarity.

Following the osmotic upshock, motors show two kinds of behavior. If a shock is of a large magnitude, such as 488 mOsmol/kg, the speed drops sharply and significantly, with a period of speed recovery that follows. As can be seen from Fig. 3 A and B, the speed recovery ($T_{rec,\omega }$) lasts $\sim$4.4 min on average (5.2 min median). This is of similar magnitude to $T_{rec,CW}$ (5.4 min mean, 5.0 min median; SI Appendix, Fig. S4) and likely corresponds to the time necessary to recover volume after an osmotic shock (50); however, $T_{rec,\omega }$ and $T_{rec,CW}$ for individual motors do not occur simultaneously (SI Appendix, Fig. S4). After recovery, the speed increase continues, leading to elevated levels compared with the preshock values (Fig. 3C). Weaker upshocks, 111 mOsmol/kg and 230 mOsmol/kg, are characterized by an increase in motor speed without a significant speed drop, as seen in Fig. 3 A–C. Elevated speed levels we observed are reversible. SI Appendix, Fig. S5 shows motor speeds of cells exposed to 100 mM sucrose upshock, which have been allowed to recover before transferring them back to VR buffer (VRB). Upon recovery to the downshock, motor speeds return to approximately the same initial levels.

To explore the population-level significance of our observation of osmokinesis in single cells, we next performed differential dynamic microscopy (DDM) (Materials and Methods) (52, 53). DDM is a fast, high-throughput method for measuring the distribution of swimming speeds in populations of a range of different self-propelled particles, averaging up to $\sim {10}^4$ particles at the same time. The technique is well suited for rapid scanning of parameter space, so that it also allowed us to extend the range of external osmolalities studied. DDM characterizes the motility of a population of particles (in our case E. coli) by analyzing the statistics of temporal fluctuations of pixel intensities in a sequence of low-optical resolution microscopy images, where the intensity fluctuations are caused by the variation in number density of particles. Specifically, we measure the differential image correlation function (DICF), which is effectively a power spectrum of the difference between two images taken at separate time points (52, 53). If a theoretical motility model exists, such as in the case of E. coli (22), the expected DICF can be calculated and fitted to experimental data (53), allowing accurate estimates of the distribution of free-swimming speeds of a large number of bacteria (52).

Before DDM measurements cells were kept in VRB and osmotically shocked in a microfuge tube. Upon the upshock cells were quickly placed into a capillary for DDM measurements and the capillary was sealed, resulting in a fixed amount of oxygen present during the experiment. Swimming speed recordings commenced within 2 min after the upshock (Materials and Methods) and are shown in Fig. 3D. The gradual decrease of swimming speed with time observed in Fig. 3D for all magnitudes of osmotic upshocks was previously characterized in motility buffer, where E. coli maintains proton motive force (PMF) using endogenous energy sources (54, 55). At fixed buffer composition, the time it takes to consume all available oxygen is inversely proportional to the cell concentration, and upon oxygen exhaustion a sudden “crash” in swimming speed occurs (55). Interestingly, we do not see such a crash in swimming speed for the lowest five values of the imposed upshock, but do see a crash when the upshock is at the highest value of 785 mOsmol/kg. Since the cell concentration is fixed, this implies that cells consume oxygen at a significantly higher rate at the highest osmotic shock.

The increase in BFM speed observed in single cells, Fig. 3A, translates to an increase in population swimming speed with increasing upshock magnitudes, Fig. 3D. Similarly, in agreement with Fig. 3A, for high shock magnitudes, in particular for 473-mOsm/kg and 785-mOsm/kg sucrose upshocks, a sharp speed drop is observed immediately upon upshock. We also see a period of speed recovery, with duration increasing with the shock magnitude.

To demonstrate that, on the timescales of our experiments, the speed increase is set by the external osmolality, in SI Appendix, Fig. S7, as well as administering a sharp step increase, we upshocked the cells to VRB with 200 mM sucrose in a series of 10 steps, each 12 s apart, lasting 2 min in total. The DDM measurements commenced $\sim$2 min after completion of the slower shock, and the slower shock shows identical speed behavior to that of the step increase.

Increasing sucrose concentrations results in the increased viscosity of the media, consequently increasing the drag coefficient on the motor (measured values of viscosity of our solutions are given in SI Appendix, Table 2). In Fig. 3 we show BFM speeds and cell swimming speeds uncorrected for this effect, as the actual speed of the cell will be relevant for taxis. The viscosity-corrected BFM speeds, calculated under the assumption that the motor torque does not change with the increasing viscosity, are shown in SI Appendix, Fig. S8.

Furthermore, we check for the presence of steps during single-motor speed recovery. To that end, in SI Appendix, Fig. S9 we show examples of BFM speeds during the recovery phase after 488-mOsmol/kg upshock, starting just after the osmotic shock was administered. The majority of the traces do not show obvious steps during the BFM speed recovery period.

Discussion

Origins of Osmotaxis.

With no external stimuli E.coli swims in an almost straight line and reorients every so often in a nearly random fashion, performing a random walk with an effective diffusion constant $D\sim v^2/\alpha$ (56, 57), where $v$ is the swimming speed and $\alpha$ the tumbling rate given by

$$\alpha =\frac{3(1-\cos {\varphi }_0)({\tau }_{\text{run}}+{\tau }_t)}{{\tau }_{\text{run}}^2}$$ [2]

with ${\tau }_{\text{run}}$ mean run time, ${\varphi }_0\backsim {71}^{\circ }$ mean reorientation angle following a tumble, and ${\tau }_t$ the duration of the tumble event (56, 58).

Upon sensing a sudden increase in attractant concentration, E. coli sharply elevates the CCW bias for $\sim$1 s and then slightly lowers it for $\sim$3 s, returning to the prestimulus level in $\sim$4 s (24). It is this characteristic impulse response of modulating the tumbling rate that allows E. coli to navigate toward a favorable environment. The detailed chemotactic performance and its origins have often been studied (56, 59–64).

The observation that a chemotactic mutant of E. coli (CheRCheB) lacking normal methylation and demethylation enzymes does not show chemotactic accumulation, but does respond to raised attractant concentrations by lowering the tumble rate without adaptation (10, 24), led researchers to calculate the consequences of spatially varying $\alpha (x)$ and $v(x)$ on steady-state bacterial density (56, 63). Similar calculations were performed for particles with $v$ and $\alpha$ dependent on the local density (57) or when studying diffusion of bacteria in porous media (65). These calculations offer possible explanations for previously observed negative osmotaxis, given the characteristic speed and bias response we here observed.

If we assume the simplest scenario, where there is no directional dependency of $\alpha (x)$ and $v(x)$, the steady-state E. coli density will be inversely proportional to its swimming speed (57):

$$\rho (x)\sim \frac{1}{v(x)}.$$ [3]

In Fig. 3C we show motor speeds, $\omega$, and in Fig. 4 mean CCW motor interval (${\overline{\tau }}_{CCW}$) and tumbling rate ($\alpha$) at a given osmolality. The $\omega$ and ${\overline{\tau }}_{CCW}$ were obtained from the last 3 min of measurements presented in Fig. 3A, which represent the long-term osmolality-dependent changes. We then calculated $\alpha$ from ${\overline{\tau }}_{CCW}$ and ${\overline{\tau }}_{CW}$ (Fig. 4 and SI Appendix, Fig. S10), using Eq. 2. The assumption was made that swimming speed $v$ and the mean run time ${\overline{\tau }}_{\text{run}}$ are proportional to the motor speed $\omega$ and the mean CCW interval ${\overline{\tau }}_{CCW}$, in agreement with previous studies (66) and our own DDM and motor measurements given in Fig. 3.

Fig. 4.

Mean CCW motor interval, corresponding to cell runs, as a function of osmotic upshift. The “0” condition box contains 96 mean run intervals, calculated by averaging interval lengths over 5 min before osmotic upshift. Subsequent conditions, osmotic upshifts of 111 mOsmol/kg, 230 mOsmol/kg, and 488 mOsmol/kg, contain 21, 20, and 22 single-motor values calculated by averaging interval lengths over the time span from t = 12 min to t = 15 min after an osmotic shock. Not all cells were used to obtain ${\overline{\tau }}_{CCW}$ as we note all cells had bound CCW intervals (SI Appendix, Fig. S11). In Inset, we calculate the tumbling rate $\alpha$ according to Eq. 2, approximating the run times with ${\overline{\tau }}_{ccw}$ and tumble times with ${\overline{\tau }}_{cw}$ given in SI Appendix, Fig. S10.

Thus, based on experimental results we present here and previous theoretical calculations (Eq. 3 and refs. 56 and 57) we would expect accumulation at lower osmolarities, equivalent to negative taxis previously observed (35). The changes in tumbling rates suggest differences in the time-dependent approach to steady state, but not the steady-state density distribution itself (56, 63).

The theoretical calculations we refer to make the assumption that spatial gradients of $v(x)$ and $\alpha (x)$ are small (56, 57), such that we do not expect local gradients in steady-state bacterial densities. For steeper osmotic gradients we expect a more complex osmotactic response, in particular since the recovery phases shown in Figs. 2 and 3 will no longer be vanishingly short, as we assumed above, which could explain some previous contradictory osmotactic observations (35, 40).

Our assumption that $\alpha (x)$ and $v(x)$ lack directional dependence in the case of osmotaxis could be satisfied if the observed changes in $\alpha$ are not due to signaling within the chemotactic network, but purely due to changes in the interaction of CheY-P with the rotor units of the motor. For example, previous observations indicate that at higher external osmolarities, osmotic pressure is kept the same (50). Thus, the crowding in an already crowded cytoplasm (67) increases, which can affect cytoplasmic interactions (68, 69) and the binding of CheY-P to the BFM, perhaps in a similar fashion to that observed at higher hydrostatic pressures (70).

However, it is also possible that the observed changes in ${\overline{\tau }}_{CCW}$ and $\omega$ are a consequence of signal processing by the chemotactic network. In particular, Vaknin and Berg (41) reported that osmotically induced changes in cell volume can perturb the chemoreceptors and that the signal could travel down some of the network components. In such a scenario, $\alpha (x)$ and $v(x)$ would be directionally dependent (as in chemotactic response) and steady-state cell density would need to be calculated, taking into account the directional dependency as well as the characteristic signal response we observed. Future work needs to investigate strains lacking specific parts of the network to determine the contribution of signaling and different components of the network to the osmotactic response.

Origins of Osmokinesis.

The large increase in motor speed after osmotic shock could be due to increases in PMF, possibly through alterations in cell metabolism, or, as an alternative explanation, due to the increase in number of stator units through mechanosensation (71, 72) or adaptive motor remodeling (12). The BFM has been shown to act as a mechanosensor, increasing the number of stator units in response to higher loads (71, 72). As the viscosity of the medium rises with addition of sucrose, the speed increase we observed could be due to the incorporation of additional stator units. In fact, at higher loads, an increase in the mean CW interval has been reported as well (71, 73). At our load, a 0.5-$\mathrm{\mu }\text{m}$ bead attached to the motor via a short filament stub, the motor is still expected to operate in the high-load, “plateau” region of the torque-speed curve (74, 75) with the estimated full number of stator units (75). In addition, we observe an average long-term 30-Hz increase in motor speeds even at our lowest osmotic shocks where the viscosity of the solution hardly changes (it increases by 1.057 times). Furthermore, free-swimming cells with the motor operating in the linear-torque regime, where motor remodeling due to increased load is more likely, do not increase the swimming speed at viscosities well above the highest viscosity used in our experiments, as measured using Ficoll (76). Therefore, it is less likely that additional stator unit incorporation or adaptive motor remodeling is the sole explanation for the speed increases we observe.

SI Appendix, Fig. S9 shows the motor speeds during the speed recovery phase for all of the BFMs recorded in the +488-mOsmol/kg condition. In the majority of the traces no obvious steps are observed, suggesting that the increase in motor speed could be due to the increase in PMF with the full set of stator units present. Here we note that the engagement of stator units with the rotor has been reported as torque dependent (72), where in the absence of torque stator units disengage from the rotor. We would then expect stator resurrection during the recovery phase shown in SI Appendix, Fig. S9. Absence of obvious stepwise increases indicates that volume shrinkage caused by the osmotic shock could affect motor dynamics and perhaps prevent, or slow down, stator disengagement.

The length of the motor speed recovery period observed in Fig. 3 is $\sim$5–10 min, in line with the volume recovery timescales observed previously after osmotic upshocks (33, 50). The timescales of speed recovery (at similar shock magnitudes) observed from DDM data in Fig. 3D are longer, with recovery lasting $\sim$40 min for the 473-mOsmol/kg upshock. Some variation in these timescales can be due to the difference between individual motor speed recovery and subsequent bundle formation. However, based on Fig. 3D, we suspect that greater contribution to the difference comes from alterations in oxygen consumption rate, which in turn shifts the time it takes to reach the maximum swimming speeds.

By looking at individual BFMs and population swimming speeds together, we reveal the main characteristics of E. coli’s motility response to step increases in external osmolarity. The response consists of long-term CW bias and motor rotation/cell swimming-speed increase. This is a unique observation of osmokinesis in E. coli. We discuss how such observed speed increases can lead to negative taxis previously reported. Our study emphasizes the importance of investigating bacterial motility in environments that are closer to natural habitats, in the effort to understand the role and evolutionary advantage swimming offers to bacterial cells (77–79).

Materials and Methods

E. coli Strains and Plasmids.

E. coli strains KAF84 and KAF95 (49) were used for BFM speed and bias and a highly motile MG1655 with an insertion sequence element inserted in the flhD operon regulatory region, which is the master operon for the expression of flagellar genes (80, 81), for DDM experiments. Both KAF84 and KAF95 carry the fliC726 allele (produce nonflagellate phenotypes) and contain a plasmid carrying an ampicillin-resistance and a ${\mathit{fliC}}^{sticky}$ gene (produces flagellar filaments that stick readily to surfaces). Additionally, KAF84 is a chemotactic wild type and KAF95 is a $\mathrm{\Delta }$CheY strain and therefore cannot perform chemotaxis, producing a smooth-swimmer phenotype. MG1655 is a K-12 strain and a chemotactic wild type.

E. coli Growth and Culturing.

KAF95, KAF84, and MG1655 cells were grown in Tryptone Broth (1% Bacto tryptone, 0.5% NaCl) at 30 °C while being shaken at 200 rpm (42, 52). KAF95 and KAF84 were supplemented with 100 $\mathrm{\mu }$g/mL of ampicillin and grown to ${\text{OD}}_{600}$ = 0.8–1.0 (Spectronic 200E Spectrophotometer; Thermo Scientific) and MG1655 to ${\text{OD}}_{600}$ = 0.6. We have calibrated the single scattering range of our spectrophotometer (SI Appendix, Fig. S12) and ensured we stay within that range during ${\text{OD}}_{600}$ readings by appropriately diluting the culture when needed (82). In SI Appendix, Fig. S12 we give the growth curves of the three strains we used for the experiments and indicate the ${\text{OD}}_{600}$ at the point of culture harvest. After growth cells were washed in VRB composed of modified motility buffer (MMB), which is 10 mM sodium phosphate buffer, pH 7.1 (an aqueous solution with 6.1 mM of ${\text{Na}}_2$${\text{HPO}}_4$, 3.9 mM of ${\text{NaH}}_2$${\text{PO}}_4$), and 0.01 mM of EDTA, with added glycine betaine, potassium chloride, and choline chloride to final concentrations of 10 mM, 20 mM, and 10 mM, respectively. These compounds act as osmoprotectants and allow the cell to recover volume after an osmotic shock. MMB is a variant of the motility buffer, commonly used in flagellar motor and chemotaxis experiments (25, 42), with sodium phosphates substituted for potassium phosphates. After washing, all of the experiments were performed in VRB. KAF95 and KAF84 cells were washed by centrifuging them into a pellet and exchanging solution, while MG1655 cells were washed by gentle filtration to preserve filaments (55) and experiments were performed in VRB as for motor speed measurements.

Sample Preparation and Osmotic Shock.

For BFM experiments flagellar filaments were truncated by passing a bacterial suspension through two syringes with narrow-gauge needles (26 gauge) connected with a plastic tube [“shearing device” (25, 42, 83)].

Subsequently, cells with truncated filaments were washed by centrifugation. Slides for BFM experiments were prepared as before (42, 83) by layering two parallel strips of double-sided sticky tape onto a microscope slide and covering them with a cover glass, forming a tunnel slide (SI Appendix, Fig. S1) of approximate volume of $\sim$8 $\mathrm{\mu }$L. One percent poly-L-lysine was loaded into the tunnel and extensively washed out after keeping it in for $\sim$10 s to allow glass coating. Cells with truncated filaments were loaded into the tunnel and incubated for 10 min in a humid environment to prevent evaporation. Subsequently, nonattached cells were washed out. Next, 0.5-$\mathrm{\mu }$m beads in diameter (Polysciences) were added and incubated for 10 min to allow sticking to the filaments and excess beads were washed out postincubation. Osmotic shocks were performed while the slide was in the microscope by adding 24 $\mathrm{\mu }$L of the shocking solution to one end and immediately bringing a piece of tissue paper to the other, resulting in flow and exchange of media. The flow duration was ∼10–15 s and the local flow velocity next to the attached bacterium was 60 $\mathrm{\mu }$m/s (47). The tunnel was sealed after the shock to prevent evaporation and thus potential further increase in osmolality throughout the course of the experiment. For DDM experiments an $\sim$400-$\mathrm{\mu }$m-deep flat capillary (Vitrocom) glass sample was filled with $\sim$150 $\mathrm{\mu }$L of bacterial suspension immediately after upshock and subsequently sealed to prevent evaporation during the experiment. Osmolalities of the solutions were measured with a freezing-point depression osmometer (Camlab) and are listed in SI Appendix, Table 1.

Microscopy and Data Collection.

For BFM experiments back-focal plane interferometry (43, 44) was performed using a custom-built microscope and an 855-nm laser (Blue Sky Research) which formed a weak optical trap. The rotating bead attached to a flagellar stub was brought into the focus of the laser and the back-focal plane of the condenser was imaged onto a position-sensitive detector (PSD Model 2931; New Focus). The voltage signal from the PSD was passed through an analog antialiasing filter (low pass, Bessel-type filter with a cutoff frequency of 2.5 kHz; Krohn-Hite Corporation) and sampled at 10 kHz (PCIE-6351 DAQ; National Instruments). For DDM experiments imaging within the glass capillary was performed at 100 $\mathrm{\mu }$m away from the bottom of the capillary to avoid any interaction with the glass wall. The imaging began within $\sim$2 min postupshock and consisted of a time series of phase-contrast images (Nikon TE300 Eclipse fitted with a Nikon Plan Fluor 10Ph1 objective, N.A. = 0.3, Ph1 phase-contrast illumination plate). Imaging was performed at a 100-Hz sampling rate [Mikrotron high-speed camera (MC 1362) and frame grabber (Inspecta 5, 1-GB memory)] for $\sim$40 s per movie duration and using 512 × 512 pixels field of view. Both DDM and BFM experiments were performed at room temperature (21 $\pm$ 1 °C).

Data Analysis.

Data collected during BFM experiments were analyzed in the following way. X and Y signals (obtained from voltages from the PSD) were passed through a moving-window discrete Fourier transform, where the window moves point by point and the window size was 1.684 s. Time traces of single motor speed obtained in such a way were processed to calculate the CW bias, using Eq. 1. CW biases were calculated for fixed interval sizes (30 s in Fig. 2A, 3 min in Fig. 2C, and 5 min in Fig. 2B) and using a 60-s-long moving window in Fig. 2D and SI Appendix, Fig. S3 B–E. To calculate ${\overline{\tau }}_{CCW}$ we first take a mean of the ${\tau }_{CCW}$ intervals belonging to each individual BFM rotation trace. We then pool so-obtained mean cell intervals into a distribution and obtain its mean (the same was done for ${\overline{\tau }}_{CW}$). We include only bounded CCW and CW intervals (SI Appendix, Fig. S11). In DDM experiments, the mean swimming speed was calculated from DDM movies as an average over $\sim$${10}^4$ cells/mL. Details of the image processing and data analysis were as before (52, 53, 55, 76). DDM allows the measurement of an advective speed, simultaneously, over a range of spatial-frequency q, where each q defines a length-scale L = 2*pi/q (for more details, see refs. 52 and 53). A mean swimming speed is extracted by averaging over q. Data plotted in Fig. 3D were obtained by averaging over the range 0.5 $\lesssim$ q $\lesssim$ 2.2 $\mathrm{\mu }$${\text{m}}^{-1}$, corresponding to a range in length-scale 3 $\lesssim$ L $\lesssim$ 13 $\mathrm{\mu }$m.