Significance
Nucleation is the process by which constituent building blocks first assemble to form a new substance. In the case of mineral formation from initially free ions in solution, the emergence of intermediary phases often determines the thermodynamics and kinetics of formation for the most stable phase. Our work on CaCO3 mineralization reevaluates a topic of intense discussion: Can nucleation be explained by theories established over a century ago, or should new physical concepts, as recently proposed, be adopted? Our data show that classical theories can indeed be used to describe complex mechanisms of crystallization. In addition, we provide information about the properties of intermediate phases, which will aid in the design of additives to control mineralization.
Keywords: calcium carbonate, nucleation, crystal growth, cryo-electron microscopy, molecular simulation
Abstract
Understanding and controlling nucleation is important for many crystallization applications. Calcium carbonate (CaCO3) is often used as a model system to investigate nucleation mechanisms. Despite its great importance in geology, biology, and many industrial applications, CaCO3 nucleation is still a topic of intense discussion, with new pathways for its growth from ions in solution proposed in recent years. These new pathways include the so-called nonclassical nucleation mechanism via the assembly of thermodynamically stable prenucleation clusters, as well as the formation of a dense liquid precursor phase via liquid–liquid phase separation. Here, we present results from a combined experimental and computational investigation on the precipitation of CaCO3 in dilute aqueous solutions. We propose that a dense liquid phase (containing 4–7 H2O per CaCO3 unit) forms in supersaturated solutions through the association of ions and ion pairs without significant participation of larger ion clusters. This liquid acts as the precursor for the formation of solid CaCO3 in the form of vaterite, which grows via a net transfer of ions from solution according to z Ca2+ + z CO32− → z CaCO3. The results show that all steps in this process can be explained according to classical concepts of crystal nucleation and growth, and that long-standing physical concepts of nucleation can describe multistep, multiphase growth mechanisms.
In the process of forming a solid phase from a supersaturated solution, nucleation is the key step governing the timescale of the transition. Controlling nucleation is an essential aspect in many crystallization processes, where distinct crystal polymorphism, size, morphology, and other characteristics are required. It is, therefore, important to obtain a fundamental understanding of nucleation mechanisms.
More than 150 years ago, a basic theoretical framework, classical nucleation theory (CNT) (1, 2), was developed to describe such nucleation events. CNT describes the formation of nuclei from the dynamic and stochastic association of monomeric units (e.g., ions, atoms, or molecules) that overcome a free-energy barrier at a critical nucleus size and grow out to a mature bulk phase. Calcium carbonate (CaCO3) is a frequently used model system to study nucleation (3–5); however, despite the many years of effort, there are still phenomena associated with CaCO3 crystal formation where the applicability of classical nucleation concepts have been questioned (6). These include certain microstructures and habits of biominerals formed by organisms (7), or geological mineral deposits with unusual mineralogical and textural patterns (8).
Three anhydrous crystalline polymorphs of CaCO3 are observed in nature: vaterite, aragonite, and calcite in order of increasing thermodynamic stability. In many cases, the precipitation of CaCO3 from solution is described as a multistep process, with amorphous phases first precipitated before transformation to more stable crystalline forms according to Ostwald’s rule of stages (9). Moreover, in biological systems, time-dependent spectroscopy measurements indicated that a hydrated amorphous calcium carbonate (ACC) is first deposited and then undergoes dehydration before crystallization (10). Liquid–liquid phase separation has been proposed to occur in CaCO3 solutions. Faatz et al. (11) presented the basis for a phase stability diagram including liquid–liquid phase separation. Wolf et al. (12) performed experiments in acoustically levitated droplets and observed the formation of emulsion-like structures in transmission electron microscopy (TEM), which were proposed to be a dense liquid phase (DLP). Bewernitz et al. (13) performed titration experiments at moderate pH levels, in which they supported the proposed emergence of a DLP by 13C nuclear magnetic resonance (NMR) T2 relaxation and 13C pulsed field gradient stimulated-echo self-diffusion NMR measurements. Later, Wallace et al. (14) developed the phase stability diagram to include regions for direct nucleation of solid CaCO3. They also performed lattice gas simulations, which showed that upon classical nucleation of a dense liquid close to the critical temperature, a wide distribution of cluster sizes could be found in dilute solution. Recently, Zou et al. (15) proposed a stability diagram for calcium carbonate with a metastable solution region—where mineral phases or dense liquids are able to nucleate from solution—bounded by a limit of solution stability at 3–4 mM calcium and carbonate concentrations (under standard conditions). At a limit of solution stability, dense liquids or solids and dilute ionic (“lean”) solution phases spontaneously phase separate (i.e., they undergo spinodal decomposition).
Transformations from free ions in solution to dense liquid or solid phases may occur according to classical concepts. However, recent studies have described so-called nonclassical nucleation pathways (16) involving thermodynamically stable, nanometer-sized prenucleation clusters (PNCs) (17, 18) that are already present in undersaturated solutions. In fact, ∼75% of bound calcium in solution was proposed to be present in PNCs in typical titration experiments (17). In this scenario, the first solid mineral phase is produced upon aggregation of PNCs, as indicated by an increase in the sedimentation coefficients for solution species in analytical ultracentrifugation (AUC) measurements (17).
Computer simulations indicate that PNCs are dynamically ordered liquid-like oxyanion polymers (DOLLOPs) with an average twofold cation–anion coordination (18). The loose binding of ions allows for a wide range of cluster configurations, and a limiting size to clusters was attributed to the pH dependence of bicarbonate incorporation. While the structural and dynamical properties of DOLLOPs may appear similar to nanodroplets of dense liquids, PNCs are defined as stable solutes, that is, they do not have a phase boundary with the surrounding solution (19). Recently, evidence from AUC (17) and cryogenic TEM (cryo-TEM) (20) reporting PNCs with well-defined (sub)nanometer sizes has been disputed (21). The role of PNCs in the nucleation process has also been questioned, considering that their proposed thermodynamic stability should increase the barrier to nucleation, relative to the one from ions in solution (22).
Attempts have been made to incorporate PNCs into pathways for liquid–liquid separation (13, 19); nevertheless, no direct evidence for these mechanisms have been provided. Computer simulations have shown that liquid–liquid separation provides the possibility for a wide distribution of cluster sizes in solution, but no special thermodynamic status for clusters of a well-defined size was demonstrated (14). Thus, an open debate remains about the involvement of stable PNCs in the nucleation of CaCO3.
In this work, a combined experimental and computational investigation of CaCO3 precipitation is reported using a titration setup with ion-selective electrodes (ISEs) as described by Gebauer et al. (17), and molecular-dynamics (MD) simulations of clusters and free ions in water with the force field reported by Demichelis et al. (18). This system is additionally studied using cryo-TEM with image analysis, TEM simulations, and dynamic light scattering (DLS). Our studies confirm that a significant fraction (>60%) of Ca2+ in solution is bound before nucleation, in agreement with earlier studies (17, 18). However, we find no evidence for the formation of PNCs. Before nucleation of solid CaCO3 in the form of vaterite, we find the emergence of a dense liquid calcium carbonate phase in both experiments and simulations. In titration experiments, the vaterite grows following nucleation via a net transfer of stoichiometric calcium and carbonate ions from solution, which eventually exhibits Ostwald ripening as determined from DLS measurements. All of the observed results can be completely explained within the concepts of classical nucleation in a multiple-step, multiple-phase reaction from predominantly free ions and ion pairs in solution.
Results
Prenucleation Species.
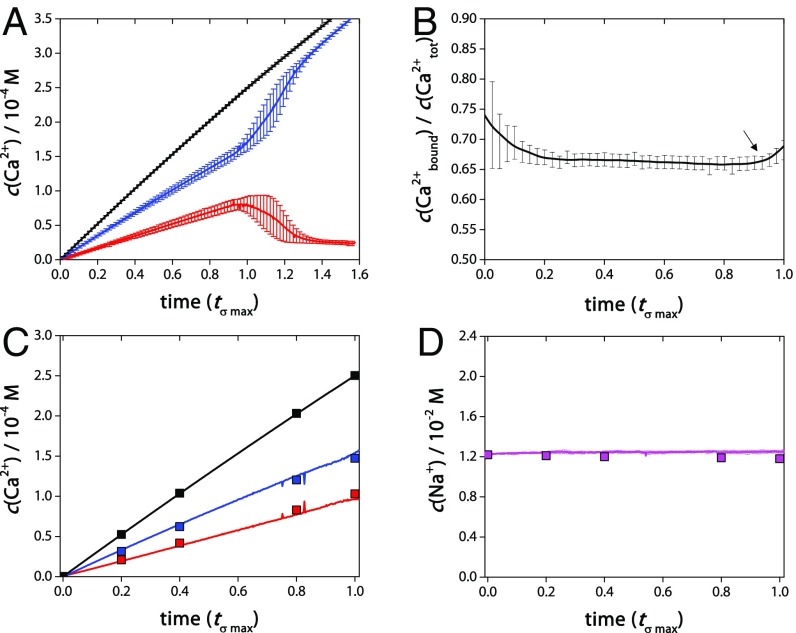
As in the report of Gebauer et al. (17), a typical LaMer curve (23) was obtained (Fig. 1A) with high reproducibility, which showed a steady increase in the concentration of free Ca2+, c(Ca2+free), followed by a sudden drop indicating the nucleation of a new phase. Following nucleation, c(Ca2+free) converged toward the equilibrium solution concentration of the newly formed solid phase. In the following, we used a dimensionless time, tσ max, normalized by the time of maximum c(Ca2+free) to account for the stochastic nature of nucleation. The high reproducibility of the experiments is then evident in Fig. 1.
Fig. 1.
(A) Titration curve for n = 10 experiments showing the average development of concentration of free Ca2+ ions as measured by the Ca2+-ISE [c(Ca2+free); red line] compared with the total average concentration of Ca2+ dosed [c(Ca2+tot); black line] as a function of time normalized with respect to the time of maximum c(Ca2+free): tσ max. The average concentration of bound Ca2+ [c(Ca2+bound) = c(Ca2+total) − c(Ca2+free)] is given by the blue curve. Error bars show SDs of the distribution. (B) Ratio of bound and total Ca2+ ion concentrations up until tσ max (intervals are 100 s). The arrow indicates nucleation at ∼0.90 tσ max, as the fraction of bound Ca2+ starts to increase compared with the constant ratio of c(Ca2+bound)/c(Ca2+tot) determined in the prenucleation stage (≲0.90 tσ max). The deviation of c(Ca2+bound)/c(Ca2+tot) at ≲0.1 tσ max is attributed to electrode signal instability during the calibration at very low ionic strength. Error bars are standard errors of measurement (SEMs). (C) MINTEQ model data for c(Ca2+free), c(Ca2+bound), and c(Ca2+total), shown as red, blue, and black squares, respectively, overlaid on the experimentally measured time-dependent concentration curves with the same color. (D) The concentration of free Na+ in solution c(Na+free) as determined by the MINTEQ speciation program (magenta squares) and the average c(Na+free) determined from n = 3 Na+-ISE measurements (magenta line), with corresponding SDs of the distribution.
The difference between the total concentration of titrated Ca2+, c(Ca2+tot), and c(Ca2+free), defines the concentration of bound Ca2+ in solution: c(Ca2+bound). Fig. 1B shows that, in accordance with previous data (17), on average 65–75 ± 1.0% (mean ± SE) of the Ca2+ was bound in solution before nucleation. During the prenucleation stage (≲0.90 tσ max), the activity ratio of bound to free calcium ions in solution (SI Appendix, Fig. S3), and concentration ratio of bound to total calcium ions in solution (Fig. 1B) was nearly constant until the nucleation point (the deviation at t ≲ 0.1 tσ max is attributed to electrode signal instability during the calibration at very low ionic strength, see SI Appendix, section 2.3). At the same time, during linear Ca2+ addition, the linear addition rate of NaOH to maintain the pH indicated a constant chemical composition of the reaction mixture in the prenucleation stage (SI Appendix, Fig. S4). It can be concluded from these considerations that the carbonate activity is virtually constant.
From the definition of the equilibrium for any prenucleation species of the type Cax(CO3)y, it follows that
This is true if over a large range of Ca2+ concentrations x = 1 (see SI Appendix, section 2.3.4, for more details), and suggests that bound calcium in solution is therefore present in single Ca2+-based ion association complexes, such as the classical ion pair CaCO30, similar to what was previously demonstrated for the case of calcium phosphate (24). Complexes with y = 2, 3… and containing bicarbonate would also agree with these data. An alternative that has been proposed could be the formation of polymeric assemblies of the type [ion association complex]n, where, using a multiple binding approach, the free energy of binding would be equal for all subsequent additions of monomeric units to n = 2, 3, 4… assemblies. Such polymeric assemblies were indeed proposed for [CaCO30]n on the basis of AUC (17) and molecular simulations (18), and for [Ca(HPO42−)3]n on the basis of titration experiments and cryo-TEM observations (24).
To verify whether the titration data could indeed be fully explained by the formation of classical species, the activities of all relevant ions (Ca2+, CO32−, HCO3–, Na+, Cl–, OH–) were calculated, taking into account the ionic strength at different time points, and entered into an equilibrium speciation model (Visual MINTEQ; SI Appendix, section 2.4). The model not only correctly described the experimentally determined concentrations of calcium (Fig. 1C) and sodium (Fig. 1D), but also requires that the only relevant species before nucleation are dissolved ions and the classical ion pairs CaCO30 and CaHCO3+ in a 96/4 ratio (SI Appendix, Table S4). This contrasts the suggestion that relatively large ionic assemblies are accessible to the system. Indeed, DLS did not indicate any significant population of nanoparticles in the prenucleation stage compared with the buffer background (SI Appendix, Fig. S5).
Cryo-TEM was used to investigate the presence of ionic assemblies of the type [CaCO30]n in the prenucleation stage. An example TEM image is shown in SI Appendix, Fig. S5, demonstrating that no such objects were found in any of the acquired images. At the applied imaging conditions, objects ≥0.9 nm (25) can be detected, which would permit the observation of polymeric prenucleation clusters for which average diameters of 2–3 nm have been proposed (19). The obtained images were also systematically analyzed using an in-house computational process (SI Appendix, section 1.9), but no prenucleation clusters were found to be present in solution. Specifically, at ≲0.90 tσ max, a significant population of clusters with sizes ≥0.9 nm, as proposed for PNCs (17, 26), was not observed in cryo-TEM, in good agreement with titration analysis and DLS measurements.
The lack of polynuclear assemblies contrasts with the proposed stability of DOLLOPs, which were shown to emerge spontaneously in computer simulations and proposed as the structural form for PNCs (18). For high Ca2+ concentrations (500 mM), 50- to 70-ns simulations identified DOLLOPs containing up to ∼60 ions at pH = 10. Using a speciation model incorporating the multiple binding assumption, Demichelis et al. (18) predicted that, at these pH levels and c(Ca2+) = 0.4 mM, around 25% and 75% of bound calcium would be present in ion pairs and DOLLOPs, respectively. To investigate cluster sizes at close-to-experimental concentrations, we performed similar simulations, generating trajectories of at least 20 ns and using total Ca2+ concentrations (20–30 mM) and pH values as close as computationally feasible to those used in the experiments (SI Appendix, Table S1).
At equilibrium, the concentrations of free calcium and (bi)carbonate were measured as 3–5 and 16–26 mM, respectively (SI Appendix, Table S1). In agreement with previous simulations (18), from an initial single cluster in water, polymeric chains with characteristics of DOLLOP were observed during the first few nanoseconds of simulation. However, upon continuing the simulation up to 10 ns, these polymers dissociated into free ions, ion pairs, and, occasionally, clusters of at most four ions in size with any reasonable probability (Fig. 2). A second series of simulations was initiated from random distributions of free ions (Materials and Methods). These equilibrated to the same cluster size distribution found with the first series (Fig. 2 and SI Appendix, section 3.1) and the frequencies for both ion attachment and detachment to/from clusters were equivalent. Furthermore, while density fluctuations in all simulations produced—albeit rarely—larger clusters, these quickly dissociated. While the system size may limit the size to which clusters can grow in solution, multiple simulations with varying total numbers of ions produced, qualitatively, the same exponential decay in cluster size distribution that is predicted by classical theories (SI Appendix, Fig. S12).
Fig. 2.
Simulations at low CaCO3 concentrations starting from (A–C) a preformed cluster and (D–E) a random distribution of ions in solution. Snapshots of (A) a cluster present at the beginning of a simulation (where the initial Ca2+ concentration was 32 mM), and (B) ionic species found at equilibrium in a 20-ns MD simulation. Calcium, carbon of carbonate, and carbon of bicarbonate are shown in yellow, purple, and blue, respectively. Green lines show carbon and calcium within 4.2 Å. (C) Time dependence of the relative probability for calcium to bind to one (black), two (blue), or three (red) (bi)carbonates. (D) Size probability distribution at equilibrium (in number of ions, Nions; Nions = 1 indicates free ions) for ionic species in water for a system with an initial Ca2+ concentration of 26 mM; averages were obtained from the final 2 ns of simulation. Inset is the probability of a Ca2+ ion coordinating to NCa-C carbon atoms (black) in associated species recorded over the same time window. Red and blue data are for binding to CO32− and HCO3−, respectively. Error bars represent 1 SD in the distribution. (E) Radius of gyration (Rg, in nanometers) probability densities for ionic species in solution at equilibrium for the simulation described in D. The peak at Rg = 0 is due to free calcium, which is modeled as a charged point mass.
In the present work, 60–65% of the bound calcium was found in ion pairs in the system where the pH at equilibrium was 8.3 ± 0.8, and we would expect this to be higher still for lower Ca2+ concentrations, in line with the speciation model data above. The affinities for calcium binding to carbonate or bicarbonate showed a preference for CaCO30 ion pairs in all simulations (Fig. 2D, Inset, and SI Appendix, section 3.1). In the random system at equilibrium, the same ionic species were also found, with 66% of the ion pairs being of the type CaCO30 (SI Appendix, Fig. S13). During the simulation, the pH decreased due to the preferred binding of Ca2+ to CO32−, which enriches the solution in HCO3−. Another simulation performed at higher initial pH (pH = 10.3) showed an increased preference for the formation of CaCO30 ion pairs (87%) and a further reduction of the larger clusters, with only 3% of the Ca2+ bound to two carbons (Fig. 2D, Inset). Values closer to the predicted 96/4 ratio for CaCO30/CaHCO3+ (SI Appendix, Table S4) are expected at higher equilibrium pH, but simulations very much larger in system size would be required to obtain statistically meaningful values.
The size of clusters was determined according to radius of gyration, Rg. Fig. 2E shows Rg probability densities for a simulation which started from a random distribution of ions. The distribution indicates a high probability to find clusters with Rg = 0.2 nm (ion pairs), while larger clusters (up to a maximum of Rg = 0.4–0.5 nm) were found with only very low probability. Thus, no larger clusters ≥0.9 nm could be found, entirely consistent with our cryo-TEM data.
As HCO3− limits DOLLOP growth, simulations at moderately basic pH could lead to an underestimation of equilibrium cluster sizes. Therefore, we investigated a series of cluster simulations from an initial (CaCO3)20 structure, where ionic coordination and ionic density were consistent with the structure of liquid-like clusters, at the limit of high pH and at 20–50 mM. These clusters dissociated at all concentrations, with the dissolution rate being highest at the lowest concentration. Here, ion pairs (70%) and a low probability of clusters containing four ions were found after 45 ns of simulation (SI Appendix, section 3.2 and Table S7). While some dissolution of clusters in water might be expected, the continued, gradual dissociation of smaller polymeric species over tens of nanoseconds is further suggestive of the instability of liquid-like clusters in homogeneous, low-salinity solutions.
Wallace et al. (14) showed the free energy of liquid-like clusters from a low-density calcium carbonate solution to consistently decrease with cluster size in replica exchange simulations sampling 300–400 K at 15 mM. While their all-atom approach is adequate to understand the energetics of cluster growth, it does not provide the equilibrium cluster size distribution at low concentrations.
To summarize, we do not observe larger nanometer-sized polymeric species at our experimental conditions in cryo-TEM, nor detect them by DLS, and additionally demonstrate that PNCs dissipate in solution via our simulations. Instead, MINTEQ calculations, titration data, and our simulations demonstrate that ion pair formation of the form of CaCO30 dominates calcium-bound species in solution. Therefore, we are confident that we can exclude the formation of PNCs to describe our data.
Nucleation of a DLP.
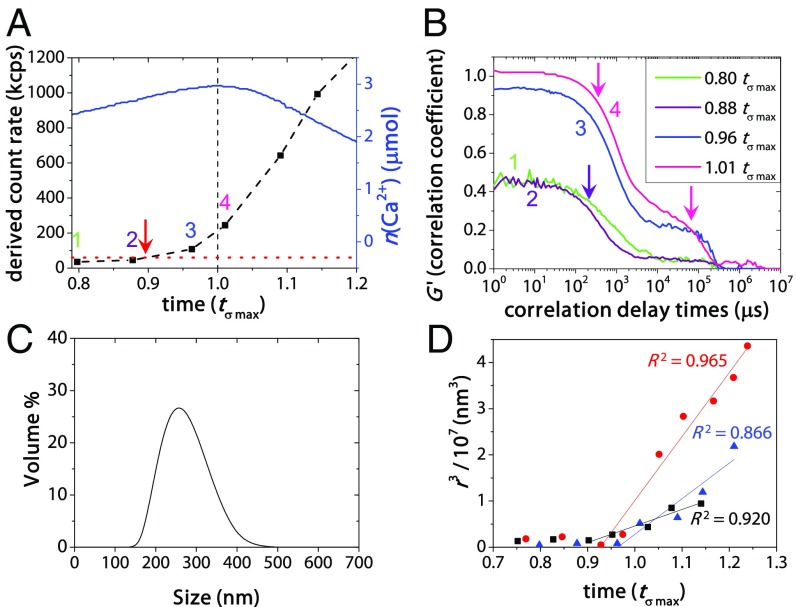
Before 0.96 tσ max, DLS showed an initial increase in the count rate starting from ≥0.90 tσ max, indicating the nucleation of a new phase (Fig. 3A). The associated correlation diagrams (Fig. 3B) indicated that around these time points (∼0.88–0.96 tσ max) objects with a size of ∼200–400 nm were present (Fig. 3C). DLS demonstrated that after 0.96 tσ max a further increase in count rate and particle size occurred (Fig. 3 A and B, and SI Appendix, Fig. S9) where the average particle radius, r, at time, t, scales approximately as r(t) ∼ t1/3 (Fig. 3D), which fits particle growth through coalescence by Brownian collisions (27) and through coarsening by Ostwald ripening (28, 29) (SI Appendix, section 2.7.2).
Fig. 3.
DLS results showing (A) evolution of the derived count rate (black dashed line) during 0.8–1.2 tσ max around the nucleation point at ∼0.90 tσ max (red arrow). The dotted red line indicates the average count rate in the prenucleation stage, while the blue curve represents the amount of free Ca2+ (right axis). (B) The correlation coefficient (G′) given for the time points 1–4 in A, showing a significant increase between measurement 2 and 3. The purple arrow indicates the single descent in curves 1 and 2, as also found for the carbonate buffer solution. Pink arrows point at two distinct descents in curves 3 and 4 indicating the presence of a populations of micrometer-sized particles (around 105 μs) alongside a population of smaller particles (at 102–103 μs) after 0.96 tσ max. The intercept G′ > 1 at 1.01 tσ max at 100 μs is indicative of sedimentation. (C) Volume size distribution of a typical DLS measurement between 0.88 and 0.96 tσ max (at 0.92 tσ max; bin size, 33 nm) demonstrating the presence of ∼200–400 nm particles in solution. (D) Rate of particle Ostwald ripening/coalescence as determined by DLS. The average radius r at time t scales with r(t) ∼ t1/3 from approximately ∼0.90–0.96 tσ max onward, as indicated by the linear fits with corresponding R2 for n = 3 measurements in red, blue, and black.
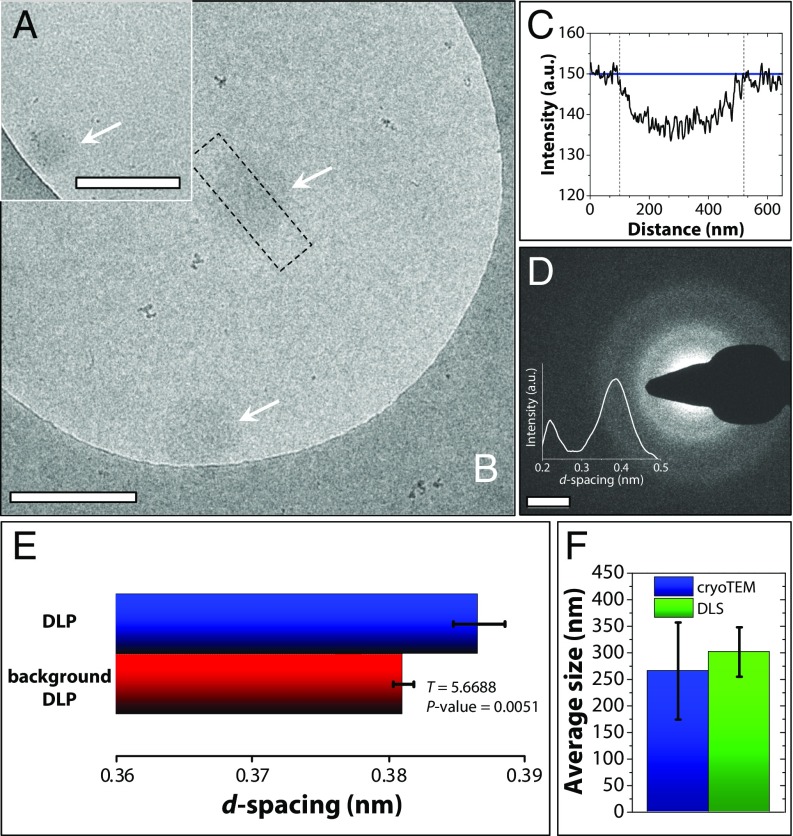
To investigate the evolution of morphology and structure of the formed CaCO3 in more detail, samples for cryo-TEM were taken from the titration experiment at time points close before tσ max and vitrified by plunge freezing (Materials and Methods). At >0.90 tσ max, cryo-TEM images showed the presence of round amorphous objects of ∼200–400 nm (Fig. 4 A, B, and D), with image contrast that was very low compared with what would be expected for solid CaCO3 particles of the same size (30). For this system, the observed low contrast implies a phase of low density, and therefore it is sensible to assume that the objects contain a high degree of hydration. Amorphous calcium carbonate with high levels of hydration behaved as a liquid in computer models (14). Furthermore, low image contrast in TEM was observed for a polymer-induced liquid precursor phase (31), as well as in tetrahydrofuran–water mixtures which underwent liquid–liquid phase separation (32). Importantly, the ion activity product derived from the titration curve at all times remained significantly below the solubility of ACC as reported by Brečević and Nielsen (33) (see Fig. 8A). This also contrasts with the earlier assignment of the solubility to different forms of ACC, which—although having similar ion activity products—were not corrected for the influence of ionic strength (17, 34). The fact that we still observe an amorphous phase, and considering the above discussion, we propose that the observed objects are vitrified droplets of a DLP, rich in calcium carbonate that forms from the solution through a liquid–liquid phase separation process. We note, however, that our TEM data cannot provide information surrounding the dynamical behavior of ions in the observed objects. Low-dose selected area electron diffraction (LDSAED) was used to assess the differences in short range order between the background solution after nucleation and the DLP (at 0.96 tσ max). This analysis revealed broad rings indicating the absence of any long-range order in the DLP (Fig. 4D) and representing a d-spacing larger than that of the background solution (Fig. 4E), in line with an increased ion density within the droplets (20).
Fig. 4.
(A and B) Cryo-TEM image of the DLP in titration experiments in supersaturated solution conditions at (A) 0.92 tσ max and (B) 0.96 tσ max showing objects with diameters of ∼320 and ∼420 nm, respectively (white arrows). (Scale bars: A and B, 500 nm.) C shows a line scan through the upper object in B (indicated in B by the black dashed line). The black dashed lines in C indicate the object boundaries, while the blue line indicates the mean intensity value of the dilute background solution. The low contrast related to the maximum intensity in the line scan indicates a high degree of hydration. (D) Low-dose selected area electron diffraction (LDSAED) shows the amorphous nature of the objects in B. (Scale bar: 2 nm−1.) The Inset shows the integrated radial average profile over the diffraction pattern in D, with the large peak reflecting the ring closest to the center. (E) Bar plots indicating the d-spacing of the background solution of the DLP at 0.96 tσ max (red), and of the submicrometer-sized DLP at 0.96 tσ max (blue) of n = 5 samples with corresponding error bars (SD of the distribution). Statistical analysis (via a Welch–Aspin generalized T test; SI Appendix, section 2.7) shows a significant difference between the DLP and its background solution by the indicated P value. (F) Mean size ± SD for the DLP particles in cryo-TEM (blue) and the DLS size distribution at 0.96 tσ max (green). DLS distributions correspond to the first decay in the correlation function recorded at 0.96 tσ max (Fig. 3B).
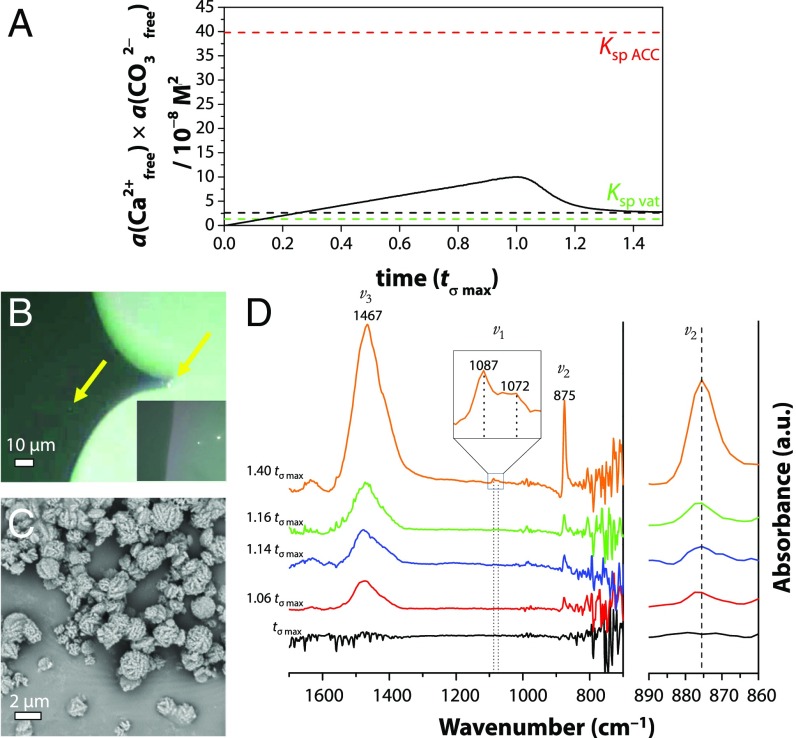
Fig. 8.
(A) Free ion product development vs. normalized time (black solid line) during a typical titration experiment. The black dashed line indicates the solubility product Ksp, compared with the reported solubility product of ACC (Ksp ACC) (33) and vaterite (Ksp vat) (56). (B) POM indicating micrometer-sized entities at 1.03 tσ max (yellow arrows), which show birefringence when the surrounding solution (dark gray) retracts (Inset). (C) SEM at 1.03 tσ max showing a typical spherical–framboidal vaterite morphology. (D) In situ ATR-FTIR spectra from tσ max to 1.40 tσ max showing typical vibrations of vaterite at 875 cm−1 (CO32− ν2 out of plane bend), 1,087/1,072 cm−1 (CO32− ν1 symmetric stretch), and 1,467 cm−1 (CO32−, ν3 asymmetric bond stretch) (57) gradually increasing in time. The Top Inset shows an enlargement of the ν1 peak at 1.40 tσ max, while the spectrum on the far Right displays the magnified ν2 spectral region.
Simulations at high calcium and carbonate concentrations support the experimental observations. From initially free ions in water at 0.57 M, a Ca2+ and CO32− ion-rich liquid domain formed over 40 ns of MD simulation. The spherical-like nanoparticle (with diameter ∼3.0 nm; Fig. 5A) which emerged was in equilibrium with a lean aqueous solution containing free ions, ion pairs, and occasional larger associates (SI Appendix, Figs. S18 and S19). This is in line with predictions from lattice-gas simulations of liquid–liquid phase separation (14). While the initial ion concentrations here were much higher than in experiments, this was chosen to reduce any barrier to nucleation. At still higher concentrations (1.1 and 1.7 M), cylindrical ionic networks spanned the periodic simulation cells (Fig. 5B and SI Appendix, section 3.3.1). This transition is explained by a crossover in the minimum surface energy between a sphere and percolating cylinder at limited system sizes, as would be expected for a liquid phase. The concentrations of free ions in lean solution at equilibrium (SI Appendix, Table S2) were comparable to those found from solutions at relatively low concentrations, and calcium concentrations [c(Ca2+) = 1–2 mM] were less than that proposed for the limit of solution stability at 300 K (15), further supporting the proposed phase separation mechanism.
Fig. 5.
(A and B) Snapshots taken from simulations demonstrating the existence of a DLP in CaCO3 solutions at initial concentrations of (A) 0.57 M and (B) 1.1 M. Averages were measured from the final 5 ns of simulation. Calcium and carbonate are shown as purple and yellow, respectively, and a van der Waals surface (from ion atom centers) is highlighted. In B, a 16-Å slice through a large cylindrical cluster is taken, which intersected the simulation cell boundaries. Water molecules are represented by the blue circles. (C) Cluster coordination probabilities for Ca2+ to bind to NCa–C carbons with corresponding SD at 1.1 M. (D) Probability density for Ca–C bond lifetimes (distance cutoff: 4.2 Å) at 1.1 M, with data smoothed using a running average. (E) Mass density, ρ, of ions (red) and water (blue) in the DLP as a function of distance from the center of mass at 1.1 M with regression curves fitted (bandwidth: 0.6 nm). (F) Coordination probability map generated from interpolated data. Ca2+ coordination numbers in the first coordination shell to carbonate oxygen atoms, Ca2+ coordination, and water, Ca2+ solvation, are plotted with the distance of calcium from the center of mass highlighted by the map color on the right (scale in nanometers). (G) Calculated TEM image at 1.7 M. Bottom to Top: a schematic of the supercell used in the calculation, showing orientation of the DLP with respect to the incident electrons; a selected region of the calculated TEM image; smoothed line scans taken from the image as shown by the blue and black curves.
From our analyses, the structure and dynamic properties of dense liquid CaCO3 at all concentrations were consistent and comparable to a viscous fluid (SI Appendix, section 3.4). Ca2+ in the DLP was found to bind preferentially to two carbonates (∼45%, Fig. 5C; see SI Appendix, section 3.3.2, for details); an increase in three-coordinate Ca2+ was observed compared with ionic associates in lean solution, but not enough (35%) to condense and rigidify the dense liquid. Our coordination levels were in reasonable agreement with those found in the high pH simulations of Demichelis et al. (18) and for dense liquid nanoparticles simulated by Wallace et al. (14), where the average coordination in the largest clusters was around 2.8. Further analysis showed that ion coordination was relatively high in the core of the DLP, while a gradual decrease was observed away from the core in a wide and diffuse interfacial region (Fig. 5 E and F, and SI Appendix, section 3.3.2). Ion diffusion coefficients, Dion, varied as a function of distance from the center of the dense liquid toward the interfacial region and were 10−8 to 10−6 cm2/s (SI Appendix, section 3.4): at least two orders of magnitude higher than Dion in ACC with a 1:1 CaCO3:H2O stoichiometry (35). The dynamic nature of ion coordination was confirmed by short Ca–C coordination lifetimes (Fig. 5D and SI Appendix, section 3.3.2). In the core of the dense phase, the water was relatively tightly bound and on average a high level of hydration was found (4–7 H2O/CaCO3; SI Appendix, section 3.3.3).
TEM images for these dense phases (Fig. 5G) were calculated using a multislice algorithm (SI Appendix, section 1.12) and based on the method by Rullgård et al. (36). These were in good agreement with the experimental cryo-TEM data showing 85 ± 5% vs. ∼93% transmission compared with the low-density background solution, respectively (see Figs. 4C and 5G, noting that the size of the simulated system limits the defocus values that can be used; SI Appendix, section 3.5.1). This agrees with our cryo-TEM observations which gave no evidence for clusters >1.1 nm within and surrounding the DLP phase (SI Appendix, Fig. S10).
To substantiate the estimated levels of hydration in the DLP in our simulations, experimental cryo-electron micrographs of the DLP droplets were compared with those of solid ACC. Since our vitreous ice layers have a thickness of ∼130 nm (37), which is smaller than the measured lateral diameter of a DLP droplet (Fig. 4 A and B), we propose that the observed DLP droplets are oblate structures that fit the thickness of the ice layer. We therefore compared these with spherical ACC particles (mineralized and analyzed in situ according to ref. 38), having a diameter approximately equal to the ice layer thickness. Analysis of such images showed that the contrast of an ACC particle relative to the background solution and the carbon support film (i.e., independent of imaging conditions) was significantly higher than that of the DLP (≈3.5 times, as demonstrated in Fig. 6).
Fig. 6.
(A) Cryo-TEM image showing a line scan (red box) through one of the two ACC particles in the direction of the red arrow. The width of the line scan is taken as ∼0.5 times the observed particle diameter. (B) Intensity vs. distance of the line scan in A, where the boundaries of the ACC particle are indicated by the two black dashed lines. The intensity difference with the mean intensity of the background solution (dark blue line) is given by the indicated black arrow and value. (C) Cryo-TEM image of Fig. 4B with indicated line scan (light blue box) through a DLP particle in the direction of the blue arrow. The width of the line scan is taken as ∼0.5 times the observed DLP diameter. (D) Intensity vs. distance of the line scan in C, where the DLP droplet boundaries are indicated by the two black dashed lines. The intensity difference with the mean intensity of the background solution (dark blue line) is given by the indicated arrow and value. (Scale bars: A, 100 nm; B, 500 nm.)
To obtain quantitative information on differences in hydration level between the DLP and ACC from the cryo-TEM experiments, we compared electron transmission properties of ACC with varying hydration in TEM simulations. As a primary step, ACC was produced in MD simulations by relaxing random distributions of ions (300 CaCO3 units) and a varying number of water molecules (CaCO3·n H2O, where n = 0 – 7; SI Appendix, section 1.12.4). Radial distribution functions confirmed an amorphous arrangement of ions and the final configuration was then used in TEM image simulations. Supercells were created to ensure the sample depth was set approximately equal to that of the experimental TEM analysis (i.e., 130 nm).
Fig. 7A shows the simulated electron intensities measured at the detector for ACC, as informed by calculating mean intensities of a number of line scans from simulated TEM images in the region of the bulk phases. The mean intensities show that the contrast is greatest for ACC with low water content. Experimentally obtained relative mean values for ACC intensities were close to those for simulated CaCO3·1H2O (67% vs. 76 ± 4%). As both the samples in simulation and experiment are approximately equal in depth, the difference in relative intensities is most likely due to the difference in the defocus parameters adopted (the chosen defocus did not affect the assignment of DLP vs. ACC in the experiments; SI Appendix, section 3.5.1).
Fig. 7.
(A) Electron transmission intensities measured for bulk ACC with varying levels of hydration; and (B) comparison of mass densities of ACC and DLP in simulations. (A) Mean electron intensities measured at the detector in TEM simulations for bulk ACC with a range of hydration levels, n (i.e., CaCO3·nH2O) are given by black data points. The data were averaged using a number of line scans, and errors shown in black are 1 SD of the sampled distribution. The blue and red lines are the mean intensities measured for bulk water and DLP (with SD in the blue shaded area) using the same input parameters. The mean intensity of low concentration CaCO3 solution was the same as that for pure water within statistical uncertainties. The experimental mean intensity for the DLP was ∼135 (i.e., ∼93% of the background solution; Fig. 4C) and for ACC ∼100 (i.e., 67% relative to the background solution; Fig. 6B), and we note the difference in the microscope parameters in experiments compared with TEM simulations. (B) Calculated mass densities from simulations of bulk ACC with n water molecules per calcium carbonate (i.e., CaCO3·nH2O), where the blue data show the ionic mass density in ACC and the red data provide the total mass density (i.e., ions and water). The shaded blue and red areas provide the ionic and total mass densities in the core region of the DLP observed in high concentration simulations (Fig. 5E and SI Appendix, Fig. S21).
Within uncertainties, the electron intensity measured for the DLP in simulations is in good agreement with ACC containing 5–7 H2O/CaCO3 (Fig. 7A), that is, distinctly different from ACC with CaCO3:1H2O. The experimentally determined TEM electron intensity for the DLP also falls within this range; hence, these data show that it is possible to quantitatively differentiate between low hydration amorphous solids and dense liquids using TEM. We can compare the mass density of the DLP from simulations (ρ = 970–1,500 kg⋅m–3; Figs. 5E and 7B) to the mass densities of bulk ACC with varying levels of hydration (Fig. 7B). Both the total mass and ionic mass densities of the DLP are consistent with ACC containing 4–6 H2O/CaCO3. Combined, these results allow us to place bounds on the hydration level in the DLP as 4–7 H2O/CaCO3, which is consistent with the results from structural analyses in SI Appendix, section 3.3.3.
Formation of Vaterite.
Following the prenucleation stage and formation of the DLP, at ∼0.96 tσ max an increase in the amount of NaOH required to maintain a constant pH of 9.75 (due to release of H+ in solution) marked the nucleation and growth of the first solid CaCO3. This increase reflects the withdrawal of carbonate ions from the buffer equilibrium while its binding behavior implies that growth of CaCO3 occurs via a net transfer of ions from solution onto the growing CaCO3 according to the below (SI Appendix, section 2.5):
Simultaneously, at 0.96 tσ max, polarized optical microscopy (POM) showed objects with diameters of 1–3 µm that did not show birefringence when viewed through crossed polarizers (i.e., the material showed optically isotropic behavior; SI Appendix, Fig. S7), but these observations did not give any indication about the liquid or solid nature of the objects.
From 1.03 tσ max onward, the particles displayed birefringence during or after drying of the surrounding solution, implying a rapid transformation of the disordered precursor to one of the crystalline forms of CaCO3 (Fig. 8B). SEM demonstrated that these birefringent particles had a corrugated spherical morphology characteristic of vaterite (39) (Fig. 8C and SI Appendix, Fig. S8). This identification was confirmed by in situ attenuated total reflection–Fourier transform infrared spectroscopy (ATR-FTIR) (Fig. 8D), which showed the growth over time of vibrational peaks characteristic of vaterite at 875 cm−1, 1,072 cm−1, and 1,087 cm−1 (SI Appendix, Fig. S8). In contrast to the report of Gebauer et al. (17), no experimental evidence was obtained that indicated the formation of solid ACC. ATR-FTIR did not show characteristic peaks associated with ACC, nor did the SEM results demonstrate a typical solid, spherical morphology. Indeed, the ion activity product derived from the titration curve exhibited a good resemblance to the solubility product of vaterite (Fig. 7A, dotted line). We note that we do not observe a shift in the carbonate ν2 band from 863 cm−1 (ACC) toward 873 cm−1 (vaterite), which would indicate that vaterite grows at the expense of ACC (40). This agrees with our data in Fig. 8A that we never surpass the solubility of ACC in our titration experiments.
Discussion
We present an extensive study of the nucleation of CaCO3 from a supersaturated solution that forms via liquid–liquid phase separation. Experiments and simulations agree that no clusters, or polymeric assemblies thereof, larger than 0.9 nm in size are stable before nucleation. Furthermore, they demonstrate that the bound calcium in solution is predominantly present in the form of ion pairs alongside a population of clusters stochastically formed from the association of ions/ion pairs, of which the abundance decays rapidly with increasing cluster size in accordance with CNT.
Our results are incongruent with the findings of Gebauer et al. (17). However, it is important to note that, after initially proposing a narrow size distribution for PNCs based on AUC experiments, it was later realized that the sharp peaks in the AUC traces reflected the average value for all species in equilibrium on the timescale of the experiment (>8 h), rather than a distribution of cluster sizes (21). Particle sizes were determined according to the Stokes–Einstein equation or by using the sedimentation coefficients and the densities of ACC and ikaite, after fitting with a discrete species model. However, considering that Stokes–Einstein breaks down for systems where the solute size approaches that of the solvent (41), and that DOLLOPs are likely to have a much lower density than any phase of reference, we remain skeptical about the inference of particle size from the AUC data. Moreover, to date, analysis of AUC data has not accounted for the impact on cluster size distribution that must arise in the concentration gradient caused by the centrifugation process. Hence, the interpretation of the small associates found here as thermodynamically stable prenucleation clusters hinges on the proposed binding model for cluster formation in which the equilibrium binding energy for every ion pair is equal (17) and negative by about 20 kJ/mol (18). Based on ratios of species concentrations in our simulations, we find that the binding constant, , for ion pairing is entirely consistent with earlier measurements (i.e., ∼104) (18, 42). The formation of (CaCO3)2 in a single step from two ion pairs, on the other hand, suggests that is reduced by orders of magnitude. While small system sizes limit statistical accuracy and activities are not included, the large difference in values raises doubts about the assumptions which underlie the model.
Wolf et al. (43) and Pouget et al. (20) both suggested the presence of PNCs in an outgassing supersaturated Ca(HCO3)2 solution—the “Kitano method” (44)—using mass spectrometry and cryo-TEM in combination with AUC, respectively. However, the injection in the vacuum system of a mass spectrometer will drive the outgassing of the solution and the resulting increase in supersaturation will promote the formation of clusters with larger diameters, similar to what has been observed in simulations at high concentration (18, 45, 46). Moreover, the defocus conditions that Pouget et al. applied for HRTEM imaging on the same electron microscope, are of the order of microns. The corresponding contrast transfer function (CTF) in this case (Materials and Methods and SI Appendix, section 1.9) indicates a direct interpretable resolution substantially larger than 1 nm, and we thus conclude that these data cannot prove the existence of 0.6-nm clusters, as was indicated in the original publication. Since, as indicated previously, it is now realized that also the AUC data do not unambiguously prove the presence of clusters with a defined particle size, we therefore conclude that neither of these reports provide solid evidence supporting the formation of prenucleation clusters.
Our results also run counter to the conclusions from a study where CaCO3 was nucleated in the presence of a silica precursor, in which nanometer-sized objects observed by cryo-TEM and DLS in solution were attributed to PNCs (26). These results can be explained by the presence of silica primary particles, as demonstrated recently (47). In fact, it is not possible to discriminate between primary particles of silica and the proposed PNCs based on the data presented in that study (26).
At higher supersaturation, we provide evidence for the formation of objects consistent with a dense liquid before the growth of solid mineral phases, which has recently been proposed to feature in a multistep CaCO3 mineralization pathway (6, 14). Amorphous CaCO3 is commonly considered to have the formula CaCO3·1 H2O, and to our knowledge the highest water content reported for ACC is ∼1.4 H2O/CaCO3 (48), which is still clearly distinct from the 4–7 H2O/CaCO3 we suggest for the DLP. Recently, Nielsen et al. (49) investigated CaCO3 nucleation with the use of in situ liquid phase TEM and observed that the dissolution behavior of amorphous particles under the electron beam showed extreme qualitative differences and that dissolution rates differed by more than an order of magnitude. They tentatively related these differences to either solid or liquid-like behavior of the particles (where liquid-like particles dissolve faster). It is important to note, however, that these observed differences in dissolution rate will also depend on other factors such as the difference in particle size, thickness of the imaged liquid layer, and applied electron dose rate. In any case, the apparent difference in electron-scattering intensities between these particles showing different dissolution rates is significantly lower compared with the difference we observe between the ACC and the DLP, and suggests a significantly lower degree of hydration for any of the amorphous phases reported by Nielsen compared with the DLP observed here.
In contrast to the scenarios proposed previously for other systems (11, 14), we conclude that liquid–liquid separation in the studied system happens via an activated process. Our total calcium and carbonate concentrations of ∼1 mM at tσ max are well below the spinodal limit reported by Zou et al. (15), although we note that their solutions were not prepared identically. Moreover, it is unlikely that the slow addition of Ca2+ ions allows the system to cross the spinodal line before the appearance of the DLP. Thus, liquid–liquid separation in our experiment is more likely to involve nucleation and growth of the DLP within the binodal regime. Our DLS data in Fig. 2D fits the growth of phase-separated domains both through coalescence by Brownian collisions and through Ostwald ripening (50). The light-scattering data do not allow us to distinguish between either of the two mechanisms for liquid–liquid phase separation; however, we note that we do not observe coarsening behavior displaying power-law regimes of the form tα with α ≠ 1/3 as is often associated with late postseparation processes in spinodal decomposition in light-scattering data (51–53) (for details, see SI Appendix, section 2.7.2). Moreover, our simulations predict a noticeable free-energy barrier to the nucleation of dense liquid clusters at relatively low supersaturation (SI Appendix, section 3.3.1). We therefore propose that the formation of the ∼200-nm liquid droplets occurs through density fluctuations that subsequently ripen/coalesce to form larger (sub)micrometer-sized objects, from which eventually vaterite nucleates.
In summary, our work provides a comprehensive reevaluation of the nucleation mechanism for CaCO3 in controlled dilute solutions (as presented in Fig. 9). Although the nucleation process depends critically on many parameters, such as temperature, pH, and composition, we conclude that nucleation can be described by the concepts of CNT. While the mechanism of growth involves intermediate phases, the fundamental concepts of classical nucleation still hold, as for the recently reported cases of calcium phosphate (24) and iron oxide (54) nucleation.
Fig. 9.
Schematic demonstrating the development of CaCO3 structure during the titration experiment in dilute calcium carbonate solutions. In the prenucleation stage, predominantly CaCO30 and CaHCO3+ ion pairs exist alongside free ions in solution. After a critical concentration at ∼0.90 tσ max, a liquid–liquid phase separation leads to the formation of a dense liquid phase (DLP) and a lean ionic solution of free ions and ion pairs. At the nucleation point (∼0.96 tσ max), the DLP reacts with free Ca2+ and free CO32− under macroscopic release of H+ and after ∼tσ max converts to vaterite, until after ∼1.30 tσ max equilibrium has been reached.
Materials and Methods
Titration Experiments.
In the titration experiment, a 10 mM CaCl2 solution was slowly added into a 10 mM carbonate buffer at 20 ± 1 °C and pH 9.75 (SI Appendix, section 1.1–1.4). This pH was selected since it reflects a high binding tendency of calcium with carbonate species due to the high fraction of carbonate ions in the carbonate buffer (17). The free Ca2+ concentration [c(Ca2+free)] was monitored using a Ca2+-ISE, and the amount of NaOH added to maintain a constant pH was registered. In addition, we measured the free Na+ concentration [c(Na+free)] using a Na+-ISE (SI Appendix, section 1.3).
To analyze solution species, samples were extracted from the titration experiment at regular time intervals. In the prenucleation stage, DLS was used to detect nanometer-sized objects in solution (SI Appendix, section 1.5). In addition, cryo-TEM was used to investigate the presence of clusters, as was done in calcium phosphate experiments (24). To this end, the samples were vitrified by plunge freezing (SI Appendix, section 1.9). For imaging, we used a Titan Krios microscope, which offers high resolution, detector sensitivity, and detector size (4,000 × 4,000 pixels CCD). Imaging contrast was optimized by applying a nominal defocus of −0.5 µm. This defocus value resulted in a CTF that allowed the direct interpretation of dark contrast objects ≥0.9 nm (25).
Formed CaCO3 after the prenucleation stage was observed in (polarized) light microscopy, SEM, and cryo-TEM (FEI Tecnai G2 operated at 200 kV and equipped with a LaB6 filament). Analysis was performed using in situ ATR-FTIR, DLS, and electron diffraction.
Simulations.
MD at 298 K and 1 atm was used to investigate the speciation of calcium (bi)carbonate in solution (see SI Appendix, section 1.10, for full details). Configurations were prepared to achieve an initial pH of 9.9 by setting the CO32−/HCO3− ratio determined by the Henderson–Hasselbalch equation and using a pKa of 10.328 for HCO3− ⇄ CO32− + H+. Subsequently, Ca2+ was added to neutralize the total charge in the system, generating total Ca2+ concentrations of 20–30 mM (SI Appendix, Table S1, provides the initial system compositions). Two different initial arrangements of the ions were used: in the first type of simulation (cluster system), ions were inserted into a box of water as a single, low-energy cluster with an average ionic coordination consistent with DOLLOP, as taken from extensive random structure searches (45), and allowed to relax. In the second type (random system), ions were randomly introduced into a volume of water and equilibrated. The 20-ns trajectories were generated with averages calculated in 2-ns windows at equilibrium. The total number of ions and water molecules was the same in both the cluster and random systems.
Random systems were also prepared for simulations at high initial free Ca2+ concentrations [c(Ca2+free)] of 0.57, 1.1, and 1.7 M (SI Appendix, Table S2). These simulations contained only carbonate anions; otherwise, they were prepared following the methods used for lower concentration simulations. Simulations were performed at 298 K and 1 atm for 60 ns, with the final 5-ns window used to analyze equilibrium states. TEM simulations were performed using a multislice algorithm for the system at 1.7 M initially and bulk amorphous phases with varying degrees of hydration. For full details, see SI Appendix, section 1.12.
The force field of Demichelis et al. (18) was used to model the interactions between atoms. This is an adaptation of earlier force fields and has been shown to accurately reproduce the properties of bulk phases and, crucially, the free energies of solvation for ions in water (18, 42, 55). Clusters were defined according to a geometric criterion where the distance between Ca and C (of carbonate and bicarbonate) was within 4.2 Å: slightly larger than the minimum in Ca–C radial distribution functions for low-density amorphous CaCO3 clusters.
Supplementary Material
Acknowledgments
Experimental work was performed at the Eindhoven University of Technology. The computational part of this study was performed at the Centre for Scientific Computing and Department of Chemistry (University of Warwick). Computational resources were provided by the Scientific Computing Research Technology Platform (Warwick University), the MidPlus Regional e-Infrastructure Centre (Grant EP/K000128/1), and ARCHER, the UK national supercomputing service. The work of P.J.M.S. and N.A.J.M.S. is supported by a VICI grant of the Netherlands Organization for Scientific Research. The work of A.R.F. and P.M.R. was supported under Engineering and Physical Sciences Research Council Grant EP/I001514/1, and A.R.F. acknowledges support from the University of Sheffield under a Doctoral Prize Fellowship. The work of J.J.D.Y. was supported by the US Department of Energy, Office of Basic Energy Sciences, Division of Materials Science and Engineering at the Pacific Northwest National Laboratory (PNNL). PNNL is operated by Battelle for the US Department of Energy under Contract DE-AC05-76RL01830. This work is dedicated to the memory of P.M.R., who sadly passed away on March 23, 2017.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1700342114/-/DCSupplemental.
References
- 1.Gibbs JW. On the equilibrium of heterogeneous substances. Am J Sci. 1878;16:441–458. [Google Scholar]
- 2.Volmer M, Weber A. Keimbildung in übersättigten Gebilden. Z Phys Chem. 1926;119:277–301. [Google Scholar]
- 3.Petsev DN, Chen K, Gliko O, Vekilov PG. Diffusion-limited kinetics of the solution-solid phase transition of molecular substances. Proc Natl Acad Sci USA. 2003;100:792–796. doi: 10.1073/pnas.0333065100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Giuffre AJ, Hamm LM, Han N, De Yoreo JJ, Dove PM. Polysaccharide chemistry regulates kinetics of calcite nucleation through competition of interfacial energies. Proc Natl Acad Sci USA. 2013;110:9261–9266. doi: 10.1073/pnas.1222162110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Smeets PJM, Cho KR, Kempen RGE, Sommerdijk NAJM, De Yoreo JJ. Calcium carbonate nucleation driven by ion binding in a biomimetic matrix revealed by in situ electron microscopy. Nat Mater. 2015;14:394–399. doi: 10.1038/nmat4193. [DOI] [PubMed] [Google Scholar]
- 6.De Yoreo JJ, et al. CRYSTAL GROWTH. Crystallization by particle attachment in synthetic, biogenic, and geologic environments. Science. 2015;349:aaa6760. doi: 10.1126/science.aaa6760. [DOI] [PubMed] [Google Scholar]
- 7.Lowenstam HA, Weiner S. On Biomineralization. Oxford Univ Press; Oxford: 1989. [Google Scholar]
- 8.Grotzinger JP, James NP. Carbonate Sedimentation and Diagenesis in the Evolving Precambrian World. SEPM; Tulsa, OK: 2000. pp. 75–90. [Google Scholar]
- 9.Dey A, de With G, Sommerdijk NA. In situ techniques in biomimetic mineralization studies of calcium carbonate. Chem Soc Rev. 2010;39:397–409. doi: 10.1039/b811842f. [DOI] [PubMed] [Google Scholar]
- 10.Gong YUT, et al. Phase transitions in biogenic amorphous calcium carbonate. Proc Natl Acad Sci USA. 2012;109:6088–6093. doi: 10.1073/pnas.1118085109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Faatz M, Grohn F, Wegner G. Amorphous calcium carbonate: Synthesis and potential intermediate in biomineralization. Adv Mater. 2004;16:996–1000. [Google Scholar]
- 12.Wolf SE, Leiterer J, Kappl M, Emmerling F, Tremel W. Early homogenous amorphous precursor stages of calcium carbonate and subsequent crystal growth in levitated droplets. J Am Chem Soc. 2008;130:12342–12347. doi: 10.1021/ja800984y. [DOI] [PubMed] [Google Scholar]
- 13.Bewernitz MA, Gebauer D, Long J, Colfen H, Gower LB. A metastable liquid precursor phase of calcium carbonate and its interactions with polyaspartate. Faraday Discuss. 2012;159:291–312. [Google Scholar]
- 14.Wallace AF, et al. Microscopic evidence for liquid-liquid separation in supersaturated CaCO3 solutions. Science. 2013;341:885–889. doi: 10.1126/science.1230915. [DOI] [PubMed] [Google Scholar]
- 15.Zou Z, et al. On the phase diagram of calcium carbonate solutions. Adv Mater Interfaces. 2017;4:1600076. [Google Scholar]
- 16.Cölfen H, Antonietti M. Mesocrystals and Nonclassical Crystallization. Wiley; New York: 2008. [Google Scholar]
- 17.Gebauer D, Völkel A, Cölfen H. Stable prenucleation calcium carbonate clusters. Science. 2008;322:1819–1822. doi: 10.1126/science.1164271. [DOI] [PubMed] [Google Scholar]
- 18.Demichelis R, Raiteri P, Gale JD, Quigley D, Gebauer D. Stable prenucleation mineral clusters are liquid-like ionic polymers. Nat Commun. 2011;2:590. doi: 10.1038/ncomms1604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gebauer D, Kellermeier M, Gale JD, Bergström L, Cölfen H. Pre-nucleation clusters as solute precursors in crystallisation. Chem Soc Rev. 2014;43:2348–2371. doi: 10.1039/c3cs60451a. [DOI] [PubMed] [Google Scholar]
- 20.Pouget EM, et al. The initial stages of template-controlled CaCO3 formation revealed by cryo-TEM. Science. 2009;323:1455–1458. doi: 10.1126/science.1169434. [DOI] [PubMed] [Google Scholar]
- 21. Anonymous (2013) General discussion. Farad Discuss 159:139–180.
- 22.Hu Q, et al. The thermodynamics of calcite nucleation at organic interfaces: Classical vs. non-classical pathways. Faraday Discuss. 2012;159:509–523. [Google Scholar]
- 23.Lamer VK, Dinegar RH. Theory, production and mechanism of formation of monodispersed hydrosols. J Am Chem Soc. 1950;72:4847–4854. [Google Scholar]
- 24.Habraken WJEM, et al. Ion-association complexes unite classical and non-classical theories for the biomimetic nucleation of calcium phosphate. Nat Commun. 2013;4:1507. doi: 10.1038/ncomms2490. [DOI] [PubMed] [Google Scholar]
- 25.Friedrich H, Frederik PM, de With G, Sommerdijk NAJM. Imaging of self-assembled structures: Interpretation of TEM and cryo-TEM images. Angew Chem Int Ed Engl. 2010;49:7850–7858. doi: 10.1002/anie.201001493. [DOI] [PubMed] [Google Scholar]
- 26.Kellermeier M, et al. Colloidal stabilization of calcium carbonate prenucleation clusters with silica. Adv Funct Mater. 2012;22:4301–4311. [Google Scholar]
- 27.Siggia ED. Late stages of spinodal decomposition in binary mixtures. Phys Rev A. 1979;20:595–605. [Google Scholar]
- 28.Lifshitz IM, Slyozov VV. The kinetics of precipitation from supersaturated solid solutions. J Phys Chem Solids. 1961;19:35–50. [Google Scholar]
- 29.Ostwald W. Studien über die Bildung und Umwandlung fester Körper. Z Phys Chem. 1897;22:289–330. [Google Scholar]
- 30.Pouget EM, et al. The development of morphology and structure in hexagonal vaterite. J Am Chem Soc. 2010;132:11560–11565. doi: 10.1021/ja102439r. [DOI] [PubMed] [Google Scholar]
- 31.Cantaert B, et al. Think positive: Phase separation enables a positively charged additive to induce dramatic changes in calcium carbonate morphology. Adv Funct Mater. 2012;22:907–915. [Google Scholar]
- 32.Denkova AG, Bomans PHH, Coppens MO, Sommerdijk NAJM, Mendes E. Complex morphologies of self-assembled block copolymer micelles in binary solvent mixtures: The role of solvent-solvent correlations. Soft Matter. 2011;7:6622–6628. [Google Scholar]
- 33.Brečević L, Nielsen AE. Solubility of amorphous calcium carbonate. J Cryst Growth. 1989;98:504–510. [Google Scholar]
- 34.Gebauer D, et al. Proto-calcite and proto-vaterite in amorphous calcium carbonates. Angew Chem Int Ed Engl. 2010;49:8889–8891. doi: 10.1002/anie.201003220. [DOI] [PubMed] [Google Scholar]
- 35.Bushuev YG, Finney AR, Rodger PM. Stability and structure of hydrated amorphous calcium carbonate. Cryst Growth Des. 2015;15:5269–5279. [Google Scholar]
- 36.Rullgård H, Öfverstedt LG, Masich S, Daneholt B, Öktem O. Simulation of transmission electron microscope images of biological specimens. J Microsc. 2011;243:234–256. doi: 10.1111/j.1365-2818.2011.03497.x. [DOI] [PubMed] [Google Scholar]
- 37.van de Put MWP, et al. Graphene oxide single sheets as substrates for high resolution cryoTEM. Soft Matter. 2015;11:1265–1270. doi: 10.1039/c4sm02587c. [DOI] [PubMed] [Google Scholar]
- 38.Nudelman F, Sonmezler E, Bomans PHH, de With G, Sommerdijk NAJM. Stabilization of amorphous calcium carbonate by controlling its particle size. Nanoscale. 2010;2:2436–2439. doi: 10.1039/c0nr00432d. [DOI] [PubMed] [Google Scholar]
- 39.Njegić-Dzakula B, Falini G, Brecević L, Skoko Z, Kralj D. Effects of initial supersaturation on spontaneous precipitation of calcium carbonate in the presence of charged poly-l-amino acids. J Colloid Interface Sci. 2010;343:553–563. doi: 10.1016/j.jcis.2009.12.010. [DOI] [PubMed] [Google Scholar]
- 40.Farhadi-Khouzani M, Chevrier DM, Zhang P, Hedin N, Gebauer D. Water as the key to proto-aragonite amorphous CaCO3. Angew Chem Int Ed Engl. 2016;55:8117–8120. doi: 10.1002/anie.201603176. [DOI] [PubMed] [Google Scholar]
- 41.Schultz SG, Solomon AK. Determination of the effective hydrodynamic radii of small molecules by viscometry. J Gen Physiol. 1961;44:1189–1199. doi: 10.1085/jgp.44.6.1189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Raiteri P, Gale JD. Water is the key to nonclassical nucleation of amorphous calcium carbonate. J Am Chem Soc. 2010;132:17623–17634. doi: 10.1021/ja108508k. [DOI] [PubMed] [Google Scholar]
- 43.Wolf SE, et al. Carbonate-coordinated metal complexes precede the formation of liquid amorphous mineral emulsions of divalent metal carbonates. Nanoscale. 2011;3:1158–1165. doi: 10.1039/c0nr00761g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kitano Y. The behavior of various inorganic ions in the separation of calcium carbonate from a bicarbonate solution. Bull Chem Soc Jpn. 1962;35:1973–1980. [Google Scholar]
- 45.Finney AR, Rodger PM. Probing the structure and stability of calcium carbonate pre-nucleation clusters. Faraday Discuss. 2012;159:47–60. [Google Scholar]
- 46.Tribello GA, Bruneval F, Liew C, Parrinello M. A molecular dynamics study of the early stages of calcium carbonate growth. J Phys Chem B. 2009;113:11680–11687. doi: 10.1021/jp902606x. [DOI] [PubMed] [Google Scholar]
- 47.Carcouët CCMC, et al. Nucleation and growth of monodisperse silica nanoparticles. Nano Lett. 2014;14:1433–1438. doi: 10.1021/nl404550d. [DOI] [PubMed] [Google Scholar]
- 48.Ihli J, et al. Dehydration and crystallization of amorphous calcium carbonate in solution and in air. Nat Commun. 2014;5:3169. doi: 10.1038/ncomms4169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Nielsen MH, Aloni S, De Yoreo JJ. In situ TEM imaging of CaCO3 nucleation reveals coexistence of direct and indirect pathways. Science. 2014;345:1158–1162. doi: 10.1126/science.1254051. [DOI] [PubMed] [Google Scholar]
- 50.Wong N-C, Knobler CM. Light-scattering studies of phase separation in isobutyric acid + water mixtures: Hydrodynamic effects. Phys Rev A. 1981;24:3205–3211. [Google Scholar]
- 51.Rouw PW, Woutersen ATJM, Ackerson BJ, De Kruif CG. Adhesive hard sphere dispersions: V. Observation of spinodal decomposition in a colloidal dispersion. Physica A. 1989;156:876–898. [Google Scholar]
- 52.Bhat S, Tuinier R, Schurtenberger P. Spinodal decomposition in a food colloid-biopolymer mixture: Evidence for a linear regime. J Phys Condens Matter. 2006;18:L339–L346. doi: 10.1088/0953-8984/18/26/L01. [DOI] [PubMed] [Google Scholar]
- 53.Roux D. Spinodal decomposition in microemulsions. J Phys France. 1986;47:733–738. [Google Scholar]
- 54.Baumgartner J, et al. Nucleation and growth of magnetite from solution. Nat Mater. 2013;12:310–314. doi: 10.1038/nmat3558. [DOI] [PubMed] [Google Scholar]
- 55.Raiteri P, Gale JD, Quigley D, Rodger PM. Derivation of an accurate force-field for simulating the growth of calcium carbonate from aqueous solution: A new model for the calcite-water interface. J Phys Chem C. 2010;114:5997–6010. [Google Scholar]
- 56.Plummer LN, Busenberg E. The solubilities of calcite, aragonite and vaterite in CO2-H2O solutions between 0 and 90°C, and an evaluation of the aqueous model for the system CaCO3-CO2-H2O. Geochim Cosmochim Acta. 1982;46:1011–1040. [Google Scholar]
- 57.Chu DH, et al. CO2 mineralization into different polymorphs of CaCO3 using an aqueous-CO2 system. RSC Adv. 2013;3:21722–21729. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.