Significance
Quantitative understanding of the ultrafast energy transfer between fluorescent nanoemitters and the environment is essential in nanophotonics and optoelectronics and beneficial to many industrial applications. For nanoemitters like single or colloidal dye molecules or quantum dots, their fluorescence decay near a metallic substrate can be described by a noninteracting single-dipole picture. In this work, we find a dominant fluorescent decay channel in a 2D molecular aggregate as a result of the strong and coherent dipole–dipole interaction mediated by a metallic substrate. This unique mechanism leads to an ultrafast fluorescent decay and 10-times greater energy dissipation rate than expected. Our finding opens up a unique way to manipulate energy transfer and to develop light-energy devices on the molecular level.
Keywords: molecular aggregate, fluorescence, nonradiative decay, dipole–dipole interaction, surface plasmon
Abstract
Two-dimensional molecular aggregate (2DMA), a thin sheet of strongly interacting dipole molecules self-assembled at close distance on an ordered lattice, is a fascinating fluorescent material. It is distinctively different from the conventional (single or colloidal) dye molecules and quantum dots. In this paper, we verify that when a 2DMA is placed at a nanometric distance from a metallic substrate, the strong and coherent interaction between the dipoles inside the 2DMA dominates its fluorescent decay at a picosecond timescale. Our streak-camera lifetime measurement and interacting lattice–dipole calculation reveal that the metal-mediated dipole–dipole interaction shortens the fluorescent lifetime to about one-half and increases the energy dissipation rate by 10 times that expected from the noninteracting single-dipole picture. Our finding can enrich our understanding of nanoscale energy transfer in molecular excitonic systems and may designate a unique direction for developing fast and efficient optoelectronic devices.
How a fluorescent nanoemitter releases its energy to the environment is a longstanding research topic in nanoscale light-energy collection and conversion (1–4). In the past decades, there have been considerable investigations on the fluorescence enhancement and quenching of a nanoemitter influenced by a structured environment (5–8). It is known that in a lossless medium, the emitter can decay radiatively by emitting photons or nonradiatively by generating molecular vibrations (9–11). The typical fluorescence lifetime due to these two dissipation channels is of the order of nanoseconds (12, 13). By contrast, in the proximity of a lossy medium such as a metallic substrate, the emitter can also decay nonradiatively through transferring energy into collective electron oscillations. The strength of this dissipation channel usually dominates over that of the above two channels and results in a significantly shortened fluorescence lifetime down to tens of picoseconds (14, 15).
So far, most of the nanoemitters studied are single dye molecule (DM), single quantum dot (QD), or colloids of randomly dispersed DMs or QDs (5, 6, 16). In such systems, each emitter can be well described by a single dipole which interacts exclusively with the environment. Owing to the sparsity and randomness of the dipole distribution, interaction between different dipoles at different locations is considered negligible in earlier works (17). Strikingly, however, the so-called molecular aggregate (MA) belongs to a unique class of nanoemitters that behave rather distinctively from the above. Each MA can be envisioned as a collection of self-assembled dipoles arranged at a close distance ( nm) on an ordered molecular lattice (18–20). The primary interaction between the molecular dipoles within a MA is the Coulombic dipole–dipole interaction, as opposed to the photonic radiation–absorption interaction. The Coulomb interaction is intrinsically coherent (no random processes are involved). As a consequence, the energy levels in the MA undergo an overall reorganization to form a blue-shifted H band or a red-shifted J band, producing the so-called H aggregate or J aggregate, respectively (21, 22). The fascinating MAs can exhibit strong exciton–photon coupling (23–28) and superradiance (29, 30) and have been used to demonstrate fundamentally important phenomena, such as Rabi splitting (31–33) and room-temperature Bose–Einstein condensation (34, 35). They have also been applied to design various devices, such as organic light-emitting diodes (36), solar cells (37), and light-harvesting organic antennas (38, 39).
In this work, we identify the dominant role of metal-mediated dipole–dipole interaction in controlling the ultrafast quenching and energy dissipation of a two-dimensional molecular aggregate (2DMA) placed near a metallic substrate. Through a series of delicate molecular-level fabrication and picosecond-timescale measurement, we have observed a greatly shortened fluorescence lifetime down to only 5 ps or less. This observation can be interpreted only by our interacting lattice–dipole model, as opposed to the conventional single-dipole model where the internal interaction is completely ignored. Based on the interacting-dipole model, we are able to demonstrate that the amplitude and phase of this interaction between the dipoles are strongly affected by a metallic substrate at a precisely controlled nanometric distance from the 2DMA. The metal-mediated dipole–dipole interaction in the 2DMA leads to at least 10 times greater energy dissipation rate than that commonly expected from the single-dipole picture. Our finding can enrich our understanding of nanoscale energy transfer in molecular excitonic systems and can provide useful insight into many other 2D excitonic materials that have attracted intense research interest in recent years (40, 41).
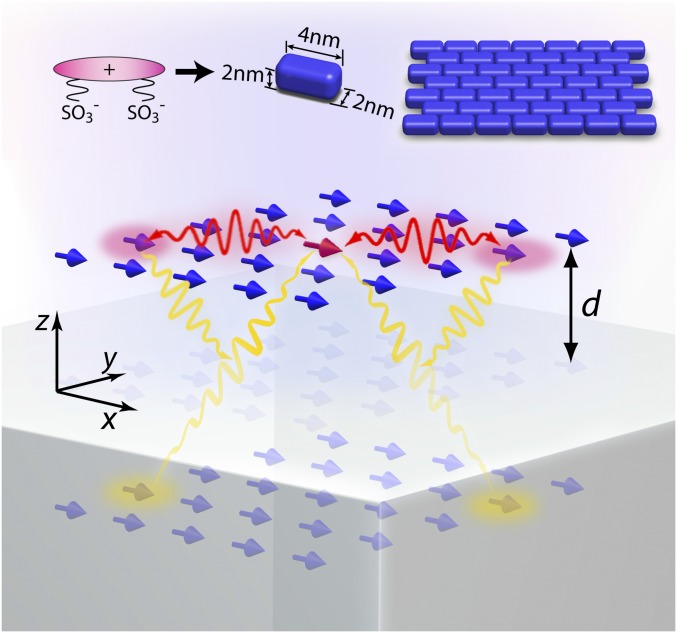
We conceptually illustrate our system in Fig. 1. A 2D dipole array representing a monolayer J aggregate is positioned near a silver substrate at a distance . Due to self-assembly, a group of dipoles ( in total) automatically forms a brickstone lattice (18) and is polarized along the long axis of the molecules (chosen to be ). The dynamics of this interacting-dipole system are described by coupled equations (42),
| [1] |
in which and label the sites where the dipoles situate. is the polarizability of the monomer that contains a monomer resonance frequency (detailed form below). is the dipole moment that relates to under a total electric field E by . is an incident electric field and is the interaction tensor. In this system, a nonretarded Coulombic form of suffices (43),
| [2] |
where a crucial coefficient due to the substrate is
| [3] |
Here and are the permittivities of dielectric and metal in the upper and lower half space, respectively. The first term of Eq. 2 represents the interaction between two real dipoles inside the dielectric; the factor removes the unphysical self-interaction. is the displacement vector between the two real dipoles and ; is its magnitude. The second term represents the interaction between a real dipole in the dielectric and an image dipole in the metal. The coefficient determines the amplitude and phase of an image dipole relative to its corresponding real dipole (43). takes account of an additional distance between a real dipole and an image dipole. As is known, the first term in gives rise to the formation of the red-shifted J band from the monomer resonance frequency. It does not include any effect from a dissipative substrate. On the contrary, the second term takes account of the dissipative motion of electrons in the metal by . Once the metal is placed within a distance of several nanometers to the 2DMA, this term dominates the nonradiative decay. In this sense, the metal mediation to the dipole–dipole interaction acts upon every pair of dipoles inside the 2DMA, accompanying the J-band formation.
Fig. 1.
Schematics of the model system and the fabricated sample structure. The 2D molecular aggregate is placed above the metal surface at a distance . The aggregate has a brickstone lattice. The molecules (dipoles) are all oriented along the same direction. The interactions lie between real and image dipoles.
As a comparison, we may attempt to follow the conventional picture and consider the entire 2DMA as a single dipole of an effective polarizability resonant at the free-space J-band frequency (44). Here the effective and the monomer are related by , where is a “normalization” constant. Then the dynamic equation becomes
| [4] |
where is the effective single-dipole moment, and G takes care of only the interaction between the effective single dipole as a whole and its image dipole,
| [5] |
In this picture, the internal dipole–dipole interaction inside the 2DMA, mediated by the metallic substrate, has been completely ignored. As shown below, because of this missing nonradiative decay channel encapsulated in the metal-mediated dipole–dipole interaction, the conventional picture leads to a large discrepancy between the theoretical prediction and the experimental result.
Materials and Methods
To accurately characterize the complex system of 2DMA on a metal surface, we need to choose a 2DMA which has a stable structure and a strong radiation power. It is known that the J aggregate of dye, 5,5’,6,6’-tetrachloro-1,1’-diethy1-3,3’-di(4-sulfobuty1)-benzimidazolocarbocyanine (TDBC), is a superior MA of coupled transition dipoles (18, 19). It shows a very intense, narrow, and redshifted J band with respect to the monomer band and is chemically compatible with various nanofabrication techniques. Bridging single molecules and large-size crystals, TDBC aggregate has been considered as an ideal mesoscopic material for making excitonic devices (45).
Molecular Multilayer Growth.
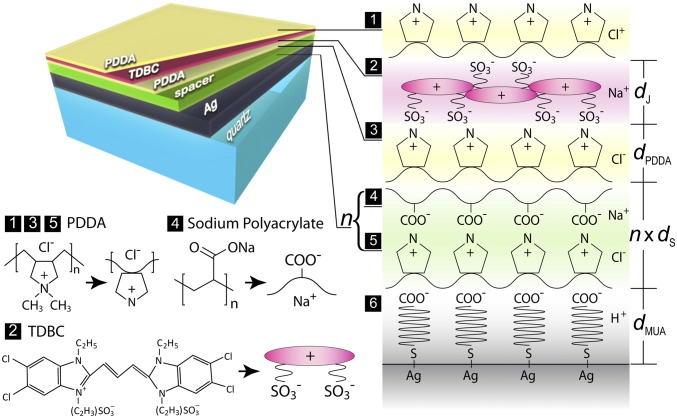
Our experiment requires deposition of a well-ordered molecular monolayer on a high-quality metal surface and a precise control of the spacer thickness. We achieve this by molecular layer-by-layer (LBL) adsorption (45, 46) (schematically shown in Fig. 2). The LBL technique has been well known for its reliability in making molecular-level devices (36, 45, 47–49). Our substrate is prepared by evaporating 100-nm-thick Ag at a rate of 0.8 Å/s on a well-cleaned ultraflat (5 Å roughness) quartz plate. The fresh-made substrate is then immersed into a 0.1-M 11-mercaptoundecanoic (11-MUA) acid aqueous solution to conformally coat a monolayer of decanoic acid. The Ag with the decanoic acid group on top carries negative charges and is able to adsorb poly(diallyldimethylammonium) chloride (PDDA) (a cationic polyelectrolyte). The anionic polyelectrolyte sodium polyacrylate (PolyArc) is then adsorbed onto the positively charged surface of PDDA. layers of PDDA and PolyArc, denoted by (PDDA/PolyArc)n, can be subsequently adsorbed. It provides a spacer of precisely controlled thickness at a molecular level (refer to the labeling “4” and “5” in Fig. 2). Finally, TDBC anionic cyanine molecules can strongly adhere to the positively charged PDDA and form a J-aggregate monolayer. We thus make a (PDDA/TDBC/PDDA) assembly on top of the spacer with the thickness . The overall molecular multilayer structure can be written as MUA-(PDDA/PolyArc)n-(PDDA/TDBC/PDDA) from the bottom to the top.
Fig. 2.
Schematics of the grown molecular multilayer structure. The layers are formed one by one by the adsorption between positively and negatively charged molecules. From the bottom to the top, it consists of 100 nm Ag, a MUA bonding layer, a (PDDA/PolyArc)n spacer layer, and a (PDDA/TDBC/PDDA) cyanine layer encapsulated in PDDA.
Morphology Characterization.
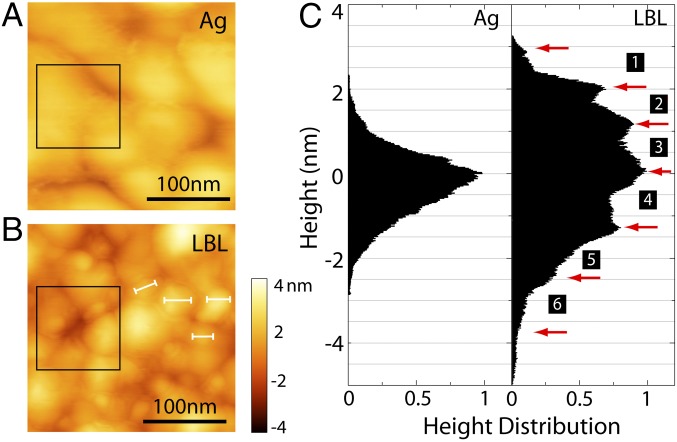
The LBL thin films grown on the Ag surface possess a morphology as layered materials bearing nanometric thickness variation (45). The topography can be verified by atomic force microscopy (AFM), which also determines the thickness of each layer. Fig. 3 shows the AFM (CypherAFM) scanned surface morphology with and without coated molecules. The 100-nm Ag by electron-beam evaporation on quartz has about 50–100 nm grain size (Fig. 3A). The square-root roughness is around 1.9 nm. After completing the molecule deposition as shown in Fig. 2, the surface morphology changes. In Fig. 3B, we can observe the lumped regions with clear boundaries, which are J-aggregate domains (18, 19). The domain size (labeled with white lines) is about 20–30 nm. It is known that each TDBC monomer has the in-plane dimension of 1–3 nm (50), so the total number of individual molecules in each J-aggregate domain is about 40–60, which is consistent with the literature (51). Histograms of height distribution on the sample can be obtained. We randomly select a 100-nm 100-nm area on a bare-Ag sample (shown in the black box in Fig. 3A). The histogram (marked with “Ag” in Fig. 3C) shows a Gaussian-like distribution. To see the multilayer feature of the LBL sample, we select an area near the sample edge where the molecular layers are porous. In this area, different numbers of molecular layers are randomly exposed under the AFM tip. They cause statistically discrete height variation. A histogram of the AFM counts over this area then exhibits discrete steps (marked with numbers in Fig. 3C). The jump between every two peaks corresponds to the thickness of one molecular layer (45). According to this measurement we can obtain the thickness of each layer from the top to the bottom to be around 1.0 nm, 0.9 nm, 1.2 nm, 1.3 nm, 1.2 nm, and 1.5 nm, respectively. Hence one spacer layer () is around 2.5 nm thick, the 11-MUA layer () is around 1.5 nm thick, and the PDDA () is around 1.2 nm thick. To systematically study the effect of distance between TDBC and Ag on the fluorescence behavior, we fabricate a series of samples with numbers of spacer layers (n = 1–6). This provides a fine-tuned distance from 5.2 nm to 17.7 nm.
Fig. 3.
Morphologic characterization of the LBL structure of MUA-(PDDA/PolyArc)-(PDDA/TDBC/PDDA). (A) AFM image for bare 100-nm Ag on quartz. (B) AFM image for a molecular multilayer on Ag. The size of the scanning area is 0.25 m 0.25 m. The white bars indicate the typical size of molecular aggregate domains. (C) The statistical height distribution in the areas marked by the black boxes in A and B. The red arrows indicate the discrete steps labeled with numbers. Each number corresponds to a layer labeled in Fig. 2.
Our LBL technique guarantees excellent conformity between Ag and PDDA/TDBC molecular layers throughout the major area of the sample. This ensured conformity is the most critical to the optical measurement. The about 2-nm roughness of Ag over 50–100 nm grain area merely induces a slow topography variation to the entire stack. It does not affect our observation of fluorescence lifetime and photoluminescence intensity of 2DMA.
Results and Discussion
Fluorescence Lifetime and Photoluminescence Measurement.
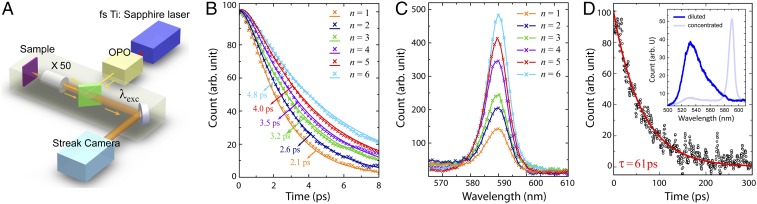
The fluorescence lifetime of the J aggregate is measured by a picosecond streak-camera setup as shown in Fig. 4A. The excitation light is carried out with an optical parametric oscillator (Spectra Physics; Inspire HF 100) pumped by a mode-locked Ti:sapphire oscillator. The laser pulse width is about 200 fs and the repetition rate is 80 MHz. The light is guided into a Zeiss inverted microscope (Axiovert 200) and focused onto the sample by a Zeiss 50× objective. The emission signal is detected in the reflection configuration, and the signal passing through a bandpass filter with a bandwidth of 30 meV is collected by a synchroscan Hamamatsu streak camera (C10910-02), whose overall time resolution is 2 ps. The transmissivity of the optical system is carefully calibrated to evaluate the absolute power level at the focusing plane. The laser pulse width is measured by a home-built autocorrelator at the focus throughout the scanning range. The incident wavelength is chosen at 585 nm for on-resonance excitation of TDBC. For each sample, the measurement is repeated several times in different areas of samples and the final result is the average of multiple measurements. In Fig. 4B, the measured time-resolved fluorescent intensities of the molecular structures with one to six spacer layers are shown by the marks of different colors. The exponential fitting (solid lines in the same color) assisted with a convolution algorithm (52) indicates the increase of lifetime with the increasing distance . The overall lifetime is extremely short and only several picoseconds.
Fig. 4.
Lifetime and photoluminescence measurement for the molecular multilayer structures of MUA-(PDDA/PolyArc)n-(PDDA/TDBC/PDDA) with , and sparsely distributed TDBC monomers. (A) Picosecond streak-camera setup for the fluorescence lifetime measurement. (B) Time-resolved photon counts (marks) and exponential-fitting curves (solid lines). (C) Measured photoluminescence intensity. The structures with different numbers of spacer layers from 1 to 6 are shown in different colors. (D) Time-resolved photon counts (circles) for sparse TDBC monomers on an Ag surface with nm SiO2 spacer and the exponential fitting curve (solid line). Inset shows the measured photoluminescence intensity of diluted TDBC monomer solution, in comparison with that of concentrated TDBC J-aggregate solution.
We also measured the photoluminescence (PL) spectrum (Horiba Fluorolog-3) for different spacer thickness , as shown in Fig. 4C. The result displays a trend that the fluorescence power increases with . It agrees with our expectation that when the fluorescence material is brought away from a lossy medium, the nonradiative decay usually drops.
As an important reference, we performed the same measurement for sparsely distributed TDBC monomers near an Ag surface. In this situation, the monomer lifetime must be well described by the noninteracting single-dipole model following Eqs. 4 and 5. We use an extremely dilute TDBC solution with the concentration of M so that only TDBC monomers exist. We drop cast only 1 L of such solution onto a sample, which has been precoated with 100 nm Ag and 5 nm SiO2 as a spacer. The intermolecular distance can be estimated to be over 10 nm, at which the Coulombic dipole–dipole interaction can be completely ignored and the single-dipole model must be valid. The observed PL spectrum clearly shows the 530-nm monomer peak as opposed to the 590-nm J-aggregate peak (Fig. 4D, Inset).
The fluorescence lifetime measurement on the monomer sample follows the same scheme as in Fig. 4A. But the excitation wavelength is changed to 460 nm. To select the emitted photons around the monomer peak only, we use a bandpass filter of nm. We observe a long lifetime of about 61 ps, as exponentially fitted in Fig. 4D. This number is consistent with the single-dipole model calculation.
Theoretical Analysis and Comparison with Experiment.
Our theoretical analysis for the fluorescent behaviors is based on our interacting lattice–dipole model. Each TDBC monomer is treated as a dipole with the Lorentzian polarizability (46),
| [6] |
where gives the experimentally observed monomer resonance wavelength around 530 nm, and gives its free-space fluorescence lifetime about 260 ps (53), which is strongly limited by the nonradiative vibration levels (19). is the oscillator strength. With a brickstone pattern, can be chosen such that the resonance wavelength of the J aggregate can be fitted to the experimentally observed value around 590 nm (18, 19). In the absence of an incident field, we can summarize Eqs. 1 and 2 into a matrix eigenvalue problem,
| [7] |
where is a column vector and is an matrix determined by Eq. 2. The eigenfrequencies solved from Eq. 7 are generally complex valued, . The imaginary part gives the lifetime of the mode from the nonradiative decay. The lattice–dipole mode profile can be obtained by the eigenstates of . The majority of the solutions are the so-called dark modes, which cannot be excited by incoming light. We are interested only in the so-called bright mode. It can be easily identified, as it necessarily has the least phase variation over the J-aggregate domain.
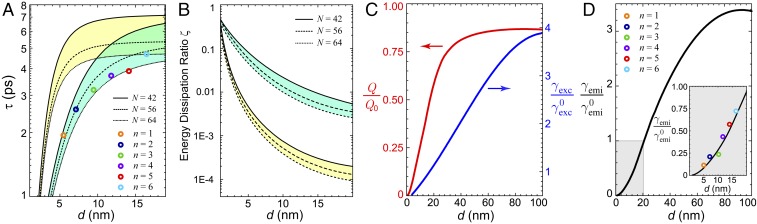
The calculated lifetime of the bright mode as a function of the distance is plotted in Fig. 5A. The three curves spanning the green region correspond to a variable total dipole number . The colored circles are the experimental results from Fig. 4B. Our theoretical calculation matches the trend of the experimental results very well. For comparison, we plot in yellow the lifetime calculated from the conventional single-dipole model (refer to Eqs. 4 and 5). Apparently, the trend in yellow deviates significantly from the measurement. In other words, the actual lifetime of the J aggregate is much shorter than expected from the single-dipole picture. This means that the major dissipation channel lies in the metal-mediated dipole–dipole interaction.
Fig. 5.
Theoretical analysis of the fluorescence behavior of the J aggregate on the Ag surface with different numbers of spacer layers. (A) Calculated lifetime based on the single-dipole model (yellow region) and the lattice–dipole model (green region) as a function of distance from the substrate. In the calculation, the total number of dipoles in the array is set to be 42, 56, and 64 for both models and is shown in the solid, dashed, and dotted lines, respectively. The measured lifetime from Fig. 4A is plotted with circles. Only the lattice–dipole model agrees with the measurement. (B) Calculated energy dissipation rate based on the single-dipole model (yellow region) and the lattice–dipole model (green region) as a function of distance from the substrate. (C) Calculated normalized excitation rate (in red) and radiation rate (in blue) as a function of . (D) Calculated emission rate as a function of . Inset zooms in the near-surface region ( nm). For comparison, the measured photoluminescence intensity imported from Fig. 4C is also displayed (circles).
We are also able to analyze the energy dissipation and fluorescent properties in great detail. At a close distance to the metal surface, the emissive energy of 2DMA mostly goes into the Drude loss (electron–phonon collision) inside the metal. We can define an energy dissipation ratio as the energy flux toward the metal vs. the total energy flux in all directions, , where S is the energy flux density calculated using the retarded formula of dipole radiation (43), is a closed surface surrounding the dipole lattice, and is the integration area beneath the 2DMA but above the substrate. Fig. 5B shows as a function of with our lattice–dipole model, in comparison with the conventional single-dipole model. The energy dissipation rate of the former is about 10 times greater than that of the latter. This means that in reality much more emissive energy from 2DMA than one would expect is transferred to the lossy metal.
The fluorescence process involves excitation and radiation (5–7). The abilities of excitation and radiation can be represented by the emission rate and the quantum yield defined as , where and are the radiative decay rate and total decay rate, respectively. So the emission rate can be written as . The dipoles above a metallic substrate are excited by the addition of incident field and reflected field from the substrate . The normalized excitation rate can be expressed as
| [8] |
where and are the reflection coefficients of the silver substrate and a reference quartz substrate, respectively. The quantum yield can be calculated by the ratio of time-averaged energy flux toward the upper space vs. the total energy flux toward the whole space and so can be expressed as
| [9] |
where is the part of facing the upper half-space. To normalize , we choose a bare quartz without Ag as the substrate to calculate .
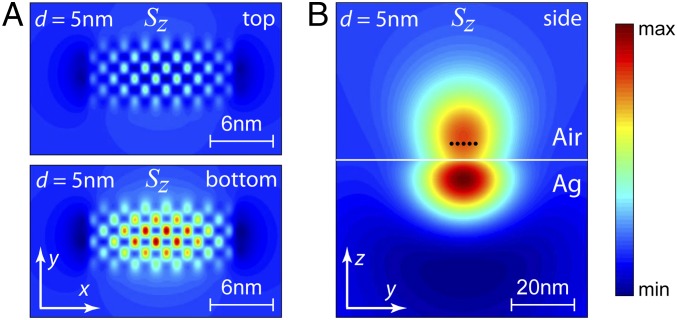
Fig. 5C shows the normalized quantum yield and excitation rate as a function of . We can see that increases with increasing . It reaches a saturation value when approaches about 50 nm. Fig. 5D shows the emission rate of the 2DMA. It is strongly suppressed as is smaller than 20 nm. Fig. 5D, Inset gives a zoom-in of the curve for the short distance (the shaded region). The colored circles indicate the PL data from Fig. 4C after an appropriate normalization to quartz samples. Our theoretical calculation matches the experimental results reasonably well. This further proves that the interacting lattice–dipole model successfully describes the 2DMA near a metallic substrate. Moreover, we have calculated the energy flux density of a 6-by-7 dipole lattice, as an example. Fig. 6A shows the amplitude distribution of the forward and backward energy flux density along viewed from the top and bottom, respectively. The backward energy flux density, which dissipates into the metal, is much stronger than the forward one. The color map clearly exhibits a brickstone lattice pattern, where the amplitude is stronger in the center and weaker on the edge. It displays detailed structures that cannot be obtained from an effective single dipole. Fig. 6B shows the distribution of viewed from the side. It also suggests that the major portion of energy flows into the metal region.
Fig. 6.
Distribution of the energy flux density of the system. (A) Top view and Bottom view of the distribution on the dipole lattice. The viewing plane () is located at 5 nm above (Top) and below (Bottom) from the dipole plane. Here is chosen as 5 nm. (B) Lateral views of the distribution on the dipole lattice. The viewing plane () is located 30 nm away from the edge of the dipole lattice.
Conclusion
We have investigated the fluorescent behaviors of 2D molecular aggregates at different distances from a metallic substrate, by measuring the lifetime and photoluminescence intensity. Our study shows that when the molecular aggregates are close to the metal surface, the dipole–dipole interaction mediated by the metal plays a dominant role in the nonradiative decay. It leads to an ultrafast fluorescent decay and ultrastrong energy dissipation. The studies of coupled systems of molecular aggregate and metal can deepen our understanding of the interaction between nanoemitters and nanostructures. Our findings provide guidelines to design and optimize fast and efficient molecular optoelectronic devices.
Acknowledgments
Q.H. thanks Tresback Jason in the Center for Nanoscale Systems at Harvard University for his help on AFM characterization. D.J. thanks Steven Kooi in the Institute for Soldier Nanotechnologies at Massachusetts Institute of Technology (MIT), Cambridge, MA for his help on photoluminescence measurement. N.X.F., Q.H., D.J., and S.H.N. acknowledge financial support by the National Science Foundation (NSF) (Grant CMMI-1120724) and Air Force Office of Scientific Research (AFOSR) Multidisciplinary Research Program of the University Research Initiative (MURI) (Award FA9550-12-1-0488). N.X.F. and S.H.N. are also supported by the Cooperative Agreement between the Masdar Institute of Science and Technology (Masdar Institute), Abu Dhabi, United Arab Emirates and MIT, Reference 2/MI/MI/CP/11/07633/GEN/G/00. X.Z., J.X., and X.L. acknowledge financial support from AFOSR MURI (Award FA9550-12-1-0488), “Light-Material Interactions in Energy Conversion” Energy Frontier Research Center funded by the US Department of Energy, Office of Science, Office of Basic Energy Sciences (Award DE-AC02-05CH11231) (for fluorescence lifetime measurement), and the King Abdullah University of Science and Technology Office of Sponsored Research (OSR) (Award OSR-2016-CRG5-2950-03). Y.L. acknowledges the financial support of the NSF under Grant DMR-1654192 and the support of the 3M Non-Tenured Faculty Award.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
References
- 1.Andrew P, Barnes WL. Forster energy transfer in an optical microcavity. Science. 2000;290:785–788. doi: 10.1126/science.290.5492.785. [DOI] [PubMed] [Google Scholar]
- 2.Herek JL, Wohlleben W, Cogdell RJ, Zeidler D, Motzkus M. Quantum control of energy flow in light harvesting. Nature. 2002;417:533–535. doi: 10.1038/417533a. [DOI] [PubMed] [Google Scholar]
- 3.Coles DM, et al. Polariton-mediated energy transfer between organic dyes in a strongly coupled optical microcavity. Nat Mater. 2014;13:712–719. doi: 10.1038/nmat3950. [DOI] [PubMed] [Google Scholar]
- 4.Rabouw FT, Hartog SA, Senden T, Meijerink A. Photonic effects on the Forster resonance energy transfer efficiency. Nat Commun. 2014;5:1–6. doi: 10.1038/ncomms4610. [DOI] [PubMed] [Google Scholar]
- 5.Dulkeith E, Morteani AC, Niedereichholz T, Klar TA, Eeldmann J. Fluorescence quenching of dye molecules near gold nanoparticles: Radiative and nonradiative effects. Phys Rev Lett. 2002;89:203002. doi: 10.1103/PhysRevLett.89.203002. [DOI] [PubMed] [Google Scholar]
- 6.Anger P, Bharadwaj P, Novotny L. Enhancement and quenching of single-molecule fluorescence. Phys Rev Lett. 2006;96:113002. doi: 10.1103/PhysRevLett.96.113002. [DOI] [PubMed] [Google Scholar]
- 7.Kinkhabwala A. Large single-molecule fluorescence enhancements produced by a bowtie nanoantenna. Nat Photon. 2009;3:654–657. [Google Scholar]
- 8.Alexander W, et al. Distinctive signature of indium gallium nitride quantum dot lasing in microdisk cavities. Proc Natl Acad Sci USA. 2014;111:14042–14046. doi: 10.1073/pnas.1415464111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chance RR, Prock A, Sibey R. Molecular fluorescence and energy transfer near interfaces. In: Prigogine I, Rice SA, editors. Advances in Chemical Physics. Vol 37 Wiley, Hoboken; NJ: 1978. [Google Scholar]
- 10.Novotny L. Single molecule fluorescence in inhomogeneous environments. Appl Phys Lett. 1996;69:3806–3808. [Google Scholar]
- 11.Kasha M. Energy transfer mechanisms and molecular exciton model for molecular aggregates. Radiat Res. 1963;20:55–70. [PubMed] [Google Scholar]
- 12.Amerongen HV, Valkunas L, Grondelle RV. Photosoynthetic Excitons. World Scientific; Singapore: 2000. [Google Scholar]
- 13.Gersten J, Nitzan A. Spectroscopic properties of molecules interacting with small dielectric particles. J Chem Phys. 1981;75:1139–1152. [Google Scholar]
- 14.Chance RR, Prock A, Sibey R. Lifetime of an excited molecule near a metal mirror: Energy transfer in the eu3+/silver system. J Chem Phys. 1974;60:2184–2185. [Google Scholar]
- 15.Lakowicz JR. Radiative decay engineering 5: Metal-enhanced fluorescence and plasmon emission. Anal Biochem. 2005;337:171–194. doi: 10.1016/j.ab.2004.11.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Moreau A, et al. Controlled-reflectance surfaces with film-coupled colloidal nanoantennas. Nature. 2012;492:86–90. doi: 10.1038/nature11615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Stuart RH, Hall DG. Enhanced dipole-dipole interaction between elementary radiators near a surface. Phys Rev Lett. 1998;80:5663–5666. [Google Scholar]
- 18.Kobayashi T. J-Aggregates. World Scientific; Singapore: 1996. [Google Scholar]
- 19.Saikin SK, Eisfeld A, Valleau S, Aspuru-Guzik A. Photonics meets excitonics: Natural and artificial molecular aggregates. Nanophotonics. 2013;2:21–38. [Google Scholar]
- 20.Arias DH, et al. Thermally-limited exciton delocalization in superradiant molecular aggregates. J Phys Chem B. 2013;171:4553–4559. doi: 10.1021/jp3086717. [DOI] [PubMed] [Google Scholar]
- 21.Eisfeld A, Briggs JS. The j- and h-bands of organic dye aggregates. Chem Phys. 2006;324:376–384. [Google Scholar]
- 22.Spano FC. The spectral signatures of frenkel polarons in h- and j-aggregates. Acc Chem Res. 2009;43:429–439. doi: 10.1021/ar900233v. [DOI] [PubMed] [Google Scholar]
- 23.Lidzey DG, et al. Strong exciton-photon coupling in an organic semiconductor microcavity. Nature. 1998;395:53–55. [Google Scholar]
- 24.Zheng YB, et al. Dynamic tuning of plasmon-exciton coupling in arrays of nanodisk-j-aggregate complexes. Adv Mater. 2010;22:3603–3607. doi: 10.1002/adma.201000251. [DOI] [PubMed] [Google Scholar]
- 25.Fofang NT, Grady NK, Fan Z, Govorov AO, Halas NJ. Plexciton dynamics: Exciton-plasmon coupling in a j-aggregate-au nanoshell complex provides a mechanism for nonlinearity. Nano Lett. 2011;11:1556–1560. doi: 10.1021/nl104352j. [DOI] [PubMed] [Google Scholar]
- 26.Zhang J, Fu Y, Chowdhury MH, Lakowicz JR. Enhanced Förster resonance energy transfer on single metal particle. 2. Dependence on donor-acceptor separation distance, particle size, and distance from metal surface. J Phys Chem C. 2007;111:11784–11792. doi: 10.1021/jp067887r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Dintinger J, Klein S, Bustos F, Barnes WL, Ebbesen TW. Strong coupling between surface plasmon-polaritons and organic molecules in subwavelength hole arrays. Phys Rev B. 2005;71:035424. [Google Scholar]
- 28.Hobson PA, et al. Strong exciton-photon coupling in a low-q all-metal mirror microcavity. Appl Phys Lett. 2002;81:3519–3521. [Google Scholar]
- 29.Meinardi F, Cerminara M, Sassella A, Bonifacio R, Tubino R. Superradiance in molecular h aggregates. Phys Rev Lett. 2003;91:247401. doi: 10.1103/PhysRevLett.91.247401. [DOI] [PubMed] [Google Scholar]
- 30.Fidder H, Knoester J, Wiersma DA. Superradiant emission and optical dephasing in j-aggregates. Chem Phys Lett. 1990;171:529–536. [Google Scholar]
- 31.Lidzey DG, et al. Room temperature polariton emission from strongly coupled organic semiconductor microcavities. Phys Rev Lett. 1999;82:3316–3319. [Google Scholar]
- 32.Bellessa J, Bonnand C, Plenet JC, Mugnier J. Strong coupling between surface plasmons and excitons in an organic semiconductor. Phys Rev Lett. 2004;93:036404. doi: 10.1103/PhysRevLett.93.036404. [DOI] [PubMed] [Google Scholar]
- 33.Vasa P, et al. Real-time observation of ultrafast rabi oscillations between excitons and plasmons in metal nanostructures with j-aggregates. Nat Photon. 2013;7:128–132. [Google Scholar]
- 34.Klaers J, Schmitt J, Vewinger F, Weitz M. Bose-Einstein condensation of photons in an optical microcavity. Nature. 2010;468:545–548. doi: 10.1038/nature09567. [DOI] [PubMed] [Google Scholar]
- 35.Plumhof JD, Stoferle T, Mai L, Scherf U, Mahrt RF. Room-temperature Bose-Einstein condensation of cavity exciton-polaritons in a polymer. Nat Mater. 2013;13:247–252. doi: 10.1038/nmat3825. [DOI] [PubMed] [Google Scholar]
- 36.Tischler JR, Bradley MS, Bulovic V, Song JH, Nurmikko A. Strong coupling in a microcavity led. Phys Rev Lett. 2005;95:036401. doi: 10.1103/PhysRevLett.95.036401. [DOI] [PubMed] [Google Scholar]
- 37.Wurfel U, Thorwart M, Weber E. Quantum Efficiency in Complex Systems. Academic, Cambridge; MA: 2011. [Google Scholar]
- 38.Savolainen J, et al. Controlling the efficiency of an artificial light-harvesting complex. Proc Natl Acad Sci USA. 2008;105:7641–7646. doi: 10.1073/pnas.0711927105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hildner R, Brinks D, Nieder JB, Cogdell RJ, Hulst NF. Quantum coherent energy transfer over varying pathways in single light-harvesting complexes. Proc Natl Acad Sci USA. 2013;340:1448–1451. doi: 10.1126/science.1235820. [DOI] [PubMed] [Google Scholar]
- 40.Amani M, et al. Near-unity photoluminescence quantum yield in mos2. Science. 2015;350:1064–1068. doi: 10.1126/science.aad2114. [DOI] [PubMed] [Google Scholar]
- 41.Sie EJ, et al. Valley-selective optical stark effect in monolayer ws2. Nat Mater. 2015;14:290–294. doi: 10.1038/nmat4156. [DOI] [PubMed] [Google Scholar]
- 42.Philpott MR, Sherman PG. Excitons and polaritons in monomolecular layers. Phys Rev B. 1975;12:5381–5394. [Google Scholar]
- 43.Novotny L, Hecht B. Principles of Nano-Optics. Cambridge Univ Press; Cambridge, UK: 2006. [Google Scholar]
- 44.Ellenbogen T, Crozier KB. Exciton-polariton emission from organic semiconductor optical waveguides. Phys Rev B. 2011;84:161304. [Google Scholar]
- 45.Jonathan RT, et al. Solid state cavity qed: Strong coupling in organic thin films. Org Electron. 2007;8:94–113. [Google Scholar]
- 46.Fukumotoa H, Yonezawab Y. Layer-by-layer self-assembly of polyelectrolyte and water soluble cyanine dye. Thin Solid Films. 1998;327–329:748–751. [Google Scholar]
- 47.Stockton WB, Rubner MF. Molecular-level processing of conjugated polymers. 4. Layer-by-layer manipulation of polyaniline via hydrogen-bonding interactions. Macromolecules. 1997;30:2717–2725. [Google Scholar]
- 48.Decher G. Fuzzy nanoassemblies: Toward layered polymeric multicomposites. Science. 1997;277:1232–1237. [Google Scholar]
- 49.Ariga K, Lvov Y, Kunitake T. Assembling alternate dye-polyion molecular films by electrostatic layer-by-layer adsorption. J Am Chem Soc. 1997;119:2224–2231. [Google Scholar]
- 50.Valleau S, Saikin SK, Yung MH, Guzik AA. Exciton transport in thin-film cyanine dye j-aggregates. J Chem Phys. 2012;137:034109. doi: 10.1063/1.4732122. [DOI] [PubMed] [Google Scholar]
- 51.Moll J, Daehne S, Durranta JR, Wiersma DA. Optical dynamics of excitons in j aggregates of a carbocyanine dye. J Chem Phys. 1995;102:6362–6370. [Google Scholar]
- 52.Lakowicz JR. Topics in Fluorescence Spectroscopy, Biochemical Applications. Vol 3 Kluwer Academic; Boston: 2002. [Google Scholar]
- 53.Kemnitz K, Yoshihara K, Tani T. Short and excitation-independent fluorescence lifetimes of j-aggregates adsorbed on AgBr and SiO2. J Chem Phys. 1990;94:3099–3104. [Google Scholar]