North–south polarization of European electricity consumption under future warming

Significance

We statistically analyze 2006–2012 high-frequency temperature and electricity load data from 35 European countries to compute climate change impacts on electricity demand until 2100. Extrapolating countries’ load responses to temperature beyond currently experienced climate, we find a future polarization of both peak load and electricity consumption in Europe. Specifically, while total European consumption remains constant under future warming, we project significant increases in the south, decreases in the north, and a shift of seasonal peak load from winter to summer for 19 countries. This changing spatial and temporal pattern of consumption and peak load has important implications for the build-out of transmission infrastructure, the construction of peak-generating capacity, and the design of energy-efficiency policy and storage capacity.

Abstract

There is growing empirical evidence that anthropogenic climate change will substantially affect the electric sector. Impacts will stem both from the supply side—through the mitigation of greenhouse gases—and from the demand side—through adaptive responses to a changing environment. Here we provide evidence of a polarization of both peak load and overall electricity consumption under future warming for the world’s third-largest electricity market—the 35 countries of Europe. We statistically estimate country-level dose–response functions between daily peak/total electricity load and ambient temperature for the period 2006–2012. After removing the impact of nontemperature confounders and normalizing the residual load data for each country, we estimate a common dose–response function, which we use to compute national electricity loads for temperatures that lie outside each country’s currently observed temperature range. To this end, we impose end-of-century climate on today’s European economies following three different greenhouse-gas concentration trajectories, ranging from ambitious climate-change mitigation—in line with the Paris agreement—to unabated climate change. We find significant increases in average daily peak load and overall electricity consumption in southern and western Europe (∼3 to ∼7% for Portugal and Spain) and significant decreases in northern Europe (∼−6 to ∼−2% for Sweden and Norway). While the projected effect on European total consumption is nearly zero, the significant polarization and seasonal shifts in peak demand and consumption have important ramifications for the location of costly peak-generating capacity, transmission infrastructure, and the design of energy-efficiency policy and storage capacity.

Changes in the Earth’s climate stemming from greenhouse-gas emissions (1) will impact natural and human systems worldwide (2, 3). The energy sector uniquely connects to anthropogenic climate change, as it plays an important role in both mitigation and adaptation (4–8). To meet the long-run mitigation targets agreed to at the 21st United Nations Climate Change Conference in Paris in 2015, the energy sector must undergo a fundamental transformation toward low- and zero-carbon sources of energy (9, 10). Electricity is anticipated to be a key to decarbonizing the transport sector and it will play a much larger role in space and water heating (9). At the same time, the power sector itself is highly climate-sensitive—on both the supply side and the demand side. Energy supply depends on the availability of water to cool power generators and is potentially affected by changing flow regimes for run-of-river hydropower (11). Further, higher temperatures reduce transmission capacity of high-voltage power lines (12), lower the efficiency of some fossil-fuel-powered generators, and depress yields of certain crops used for bioenergy (13). On the demand side, short-term human responses to weather shocks and long-term adaptation to changing climatic conditions will alter energy consumption patterns in the residential (14), commercial (15), agricultural, and industrial sectors (6, 16). Adaptation to hotter temperatures will be driven by thermal stress on humans, which has been shown to negatively impact human health (17, 18), social interactions (19), and economic output (20, 21). Human mortality rates increase during heat waves (22), whereas heat stress depresses labor productivity (23, 24). Adaptation responses to offset these negative impacts of climate change will influence electricity consumption and load patterns. While demand for space heating is expected to decrease in response to less-frequent cold days, increased adoption and operation of air conditioning due to growing demand for space cooling during hot days will put upward pressure on electricity consumption as well as daily and seasonal peak loads (14, 18, 25–29).

Previous empirical work on the relationship between temperature and electricity consumption primarily focused on the United States (e.g., refs. 30–32) or single European countries (e.g., refs. 33 and 34). Furthermore, most prior studies examined total consumption impacts, whereas recent results suggest that the effects on peak load (i.e., the highest load observed in a day/month/year) may be substantially larger and costlier (32). This study uses observed hourly electricity data across 35 European countries—which are connected by the world’s largest synchronous electrical grid—to estimate how climate change impacts the intensity of peak-load events and overall electricity consumption.

The novelty of this study is threefold. First, it examines the future of Europe’s electricity consumption patterns under climate change. Second, we use dose–response functions estimated at the country level to remove the influence of nontemperature confounders on peak load/consumption. Based on the normalized residual load data (in which the influence of nontemperature confounders has been removed), we then calibrate a common response function of load and temperature that allows us to project electricity consumption/peak load beyond each country’s currently experienced temperature range. That is, unlike other studies, we derive the relation of consumption/peak load to temperature by combining actually observed responses from all European countries covered by our data sample.

This is important, as we find that, for instance, Scandinavian countries display monotonically decreasing temperature response functions—current summers are not sufficiently warm to, for example, warrant air conditioning. To project what a hotter future may look like, we use the temperature responses of other European countries. This technique implies that if end-of-century summer temperatures in Sweden resemble summer temperatures of present-day Northern Italy, then Swedish electricity demand and peak load will increase in accordance with the rise in temperature. Thus, our approach incorporates a spatial dimension for extrapolation, rather than solely relying upon temporal extrapolation of national data beyond the frame of experience. In the case of Scandinavian countries, relying solely on temporal extrapolation of national data would result in projecting monotonically decreasing temperature response functions—even at high temperatures. Thus, electricity consumption would be assumed to continuously decline as temperatures rise.

Finally, our statistical methods flexibly control for the impacts of important confounders, such as economic growth and other socioeconomic trends. Hence, we provide a framework that allows us to construct a counterfactual world with climate change scenarios imposed on present-day Europe. The effects we detect demonstrate the importance of incorporating anticipated higher electricity consumption and peak load (in western and southern Europe) due to climate change for planning and policy purposes.

Specifically, we statistically estimate the relationship between daily electricity consumption/peak load and temperature at the country level for 35 European countries using data for the years 2006–2012 and controlling flexibly for low-frequency trends and weekday and seasonal fixed effects. We use these country-level estimates to remove the effect of the confounders and calculate residual load, which contains only the temperature component of load and a constant for each country. Based on the normalized residual load for all countries and years, we then estimate a common dose–response function. We use this estimated common response function to project counterfactual electricity loads under different climate-change scenarios at the country level. The considered climate scenarios correspond to the Representative Concentration Pathways (RCPs, ref. 35) and range from ambitious climate change mitigation in line with the Paris agreement (RCP-2.6) to unabated climate change (RCP-8.5). It is important to note that our computations should not be interpreted as point forecasts of a most likely overall energy future since they do not incorporate, for example, demographic changes. Rather, they should be interpreted as simulations of climate-change impacts on a high-frequency indicator important to human welfare—electricity load—for the world’s largest economy (if one adds the countries together).

We compute a time series of population-weighted daily maximum and daily average temperature for each of the 35 European countries for the years 2006–2012 (observational data) and 2013–2099 (projected values under different scenarios of climate-change mitigation). Population projections, which we use exclusively for within-country temperature weighting, correspond to the “middle-of-the-road” Shared Socio-economic Pathway (SSP-2, ref. 36). All temperature and population data come from the climate dataset of the Intersectoral Impact Model Intercomparison Project (ISI-MIP, ref. 37) covering bias-corrected (38) data on a horizontal grid of 0.5° resolution. The European Network of Transmission Systems Operators for Electricity (39) provides data on electricity load consumption (i.e., hourly load values per country) for the period 2006–2012. A detailed description of all data can be found in Methods, and a list of all countries is provided in SI Appendix, Table S1.

Results

Temperature Responsiveness of Electricity Load.

First, we analyze the relationship between daily peak load/daily electricity consumption and daily maximum/daily average temperature using 2006–2012 data. We define daily peak load/daily electricity consumption as the maximum/sum of the 24 hourly load values reported for a day. The 2006–2012 sample period is determined by the availability of observational data on both daily temperature and hourly load values. We build a regression model of country-level-aggregated daily consumption and peak load vs. daily maximum and daily average temperature, which controls for weekdays, seasons, and large-scale economic events and models the temperature response flexibly (Methods). We conduct the analysis at the country level—as opposed to smaller geographical units—because high-frequency load data are currently only available for all countries in Europe at this level of aggregation. The country-level analysis is appropriate, as there is significant heterogeneity in temperature response across countries. A pooled, panel-style model, for example, would average out this heterogeneity in temperature response, which is one of the main findings of this paper. Similarly, aggregating smaller countries into larger regions would introduce arbitrariness, lose information, and sacrifice statistical power.

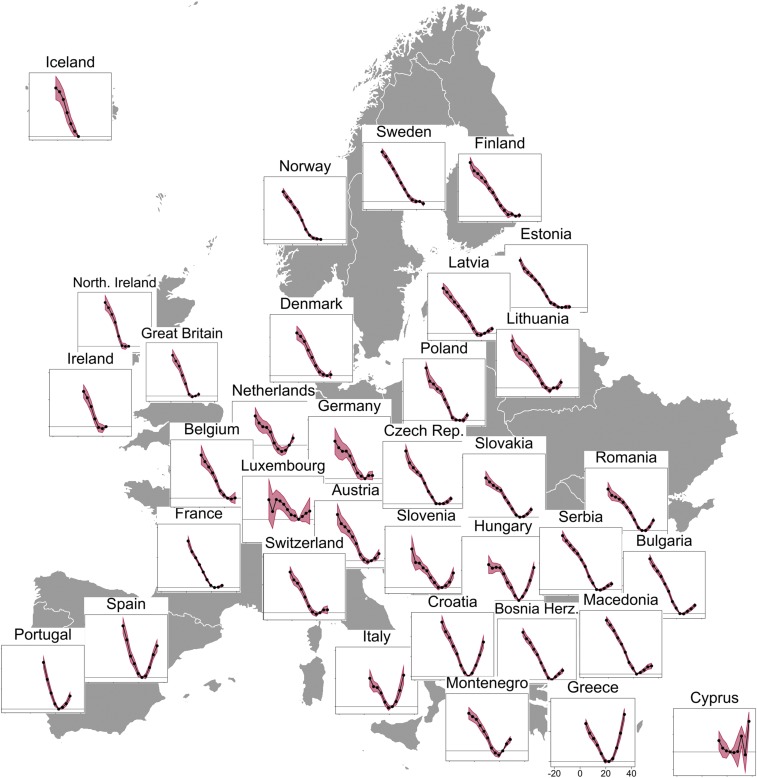
We find that most countries’ response functions display similar functional forms: load values are smallest for daily maximum temperatures of ∼22 °C (71.6 °F, daily average temperatures of 16 °C/60.8 °F) and increase monotonically in lower and higher temperatures, where there is data coverage. While we identify an asymmetric U-shape in southern European countries such as Greece and Italy, we can only estimate the country-level response function for the lower portion of the temperature spectrum in northern Europe due to data coverage (Fig. 1 and SI Appendix, Figs. S1–S4).

Fig. 1.

Similar temperature responses of daily peak load across countries. Response of daily peak load (y axes, in gigawatts; see SI Appendix, Fig. S1, for a comprehensive overview of each country’s axes scaling) to daily maximum temperature (x axes, between −20 °C and +40 °C) based on observational data for the years 2006–2012. Black dots represent the effect of replacing a day of daily maximum temperature in the omitted category (21 °C–24 °C) with a day of the relevant maximum temperature (see Methods for details). Pink shaded areas denote 95%-confidence band based on Newey–West standard error. Regression functions of all countries display similar characteristics with minimal peak load values at ∼22 °C (71.6 °F) that increase monotonically in lower and higher temperatures, where data coverage is sufficient. Refer to SI Appendix, Fig. S1, for a detailed depiction of all country panels including axes titling and scaling.

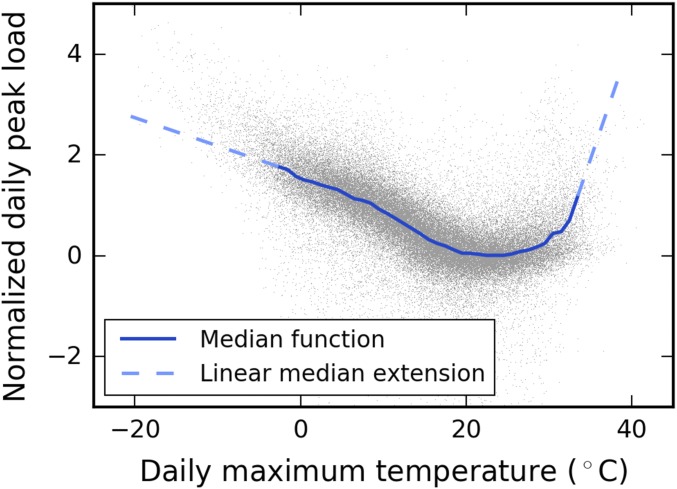
However, if Hamburg’s climate by the end of the century will resemble that of Rome’s current climate, one would expect increased adoption of air conditioners and hence a positively sloped—and possibly steeper—response curve at higher temperatures. To account for this response, we must extrapolate a country’s temperature response beyond the temperature range that it currently experiences. To this end, we combine normalized and population-weighted consumption/peak load data from all countries. We remove the impact of nontemperature confounders using the country-level regression coefficients. We then compute the median response for each 1 °C-temperature bin (Fig. 2 and SI Appendix, Fig. S5 A–C) and use the characteristics of this common response curve to extrapolate at the country level. This approach, discussed in detail in Methods, implies that we estimate future electricity load by country—particularly on hot days—using patterns observed in other European countries—specifically, countries that already experience very warm temperatures (compare SI Appendix, Fig. S5D). Put differently, we assume similar adaptation behavior to hot temperatures throughout Europe. We apply this common dose–response function to projected daily temperature data for the years 2013–2099. The resulting peak load and daily consumption values lie well within the range of our data sample for 2006–2012 (Fig. 3 and SI Appendix, Figs. S6–S8).

Fig. 2.

Common response function. Observational daily peak load and daily maximum temperature data (2006–2012) of all countries are combined taking national population size into account (gray dots). Load values have been adjusted based on the country-level regression coefficients to remove the influence of nontemperature confounders and the resulting residual load data have been normalized to allow for comparison across countries (${\widehat{L}}_{c,d}^{\text{norm}}$; see Methods for details). We obtain the response function by linking the medians of 1 °C bins (thick blue line). The first and last bin each comprises at least 20,000 data points; we linearly extend the median function for temperatures beyond these bins (dashed blue lines).

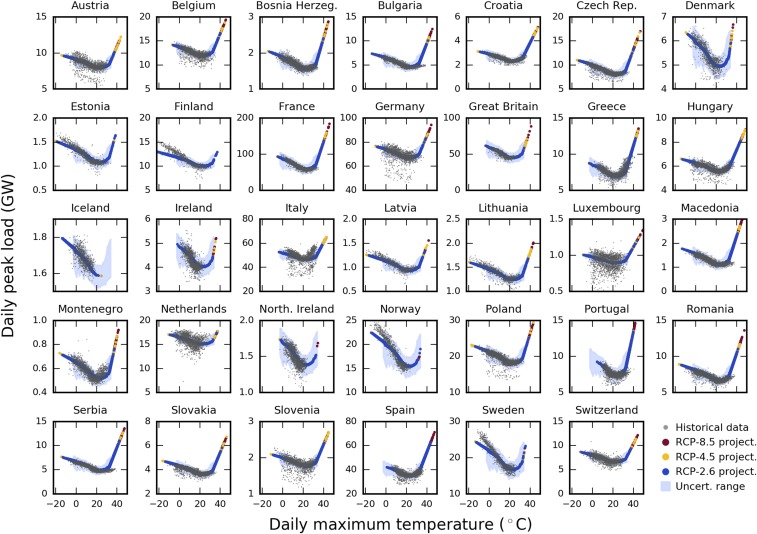
Fig. 3.

Estimated daily peak load values for projected daily maximum temperatures in 2013–2099 under three warming scenarios. Estimated peak load values for the years 2013–2099 under three different RCPs (blue, yellow, and red dots) lie well within the range of observational data (${\widehat{L}}_{c,d},$ gray dots). Blue shaded areas denote the uncertainty range (see Methods for details).

North–South Polarization Under Future Warming.

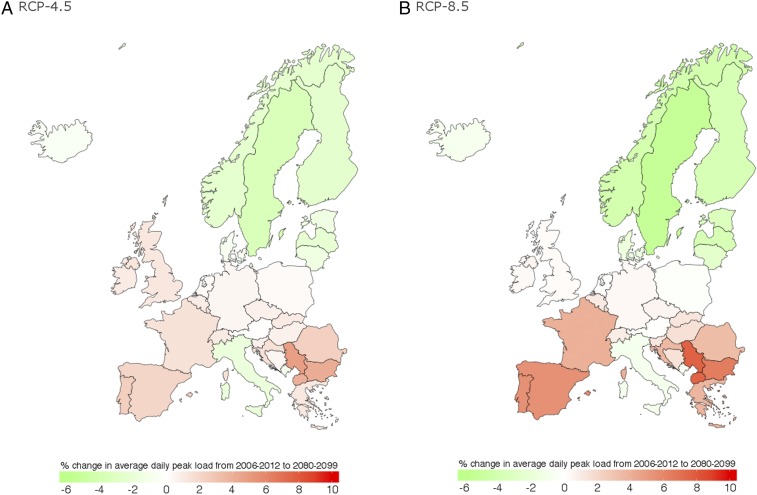
When comparing future peak loads to observed values in the past, our analysis shows a significant north–south polarization across Europe (Fig. 4 and SI Appendix, Fig. S9). While average daily peak load decreases in northern Europe—countries with present-day winter peaks—it increases in southern and western Europe (with the exception of Italy)—countries with current summer peaks. The percentage change in Central European countries is generally slightly positive, indicating a small increase in average daily peak load. The polarization is most pronounced by the end of this century and for a scenario of unabated climate change (RCP-8.5) but still holds for earlier periods and for a scenario of significant climate change mitigation (RCP-4.5; Table 1 and SI Appendix, Table S2). Even in the case of very ambitious climate change mitigation (RCP-2.6) the polarization pattern persists.

Fig. 4.

Percentage change in average daily peak load from 2006–2012 to 2080–2099 for projected daily maximum temperatures under mitigated (A) and unmitigated (B) climate change. While daily peak load decreases in northern European countries, it increases in southern and western European countries. This trend is most pronounced for a scenario of unabated climate change (RCP-8.5, B) but still holds for a scenario of mitigated climate change (RCP-4.5, A). Table 1 provides data on all countries and the three RCPs, as well as on different planning horizons until 2100.

Table 1.

Percentage change in average daily peak load by country relative to 2006–2012 for daily maximum temperatures under RCP-2.6, RCP-4.5, and RCP-8.5

Country	2020–2039			2040–2059			2060–2079			2080–2099
	RCP-2.6	RCP-4.5	RCP-8.5	RCP-2.6	RCP-4.5	RCP-8.5	RCP-2.6	RCP-4.5	RCP-8.5	RCP-2.6	RCP-4.5	RCP-8.5
Austria	−0.001	0.195	0.122	0.268	0.074	0.011	0.173	−0.058	−0.045	0.084	0.076	−0.106
Belgium	0.953	1.091	1.190	1.200	1.068	1.097	1.098	0.883	0.988	1.073	0.938	1.029
Bosnia–Herzegovina	−0.164	0.418	0.204	0.238	0.360	0.240	0.219	0.221	0.858	−0.086	0.449	1.457
Bulgaria	1.914	3.452	2.610	2.732	3.348	3.071	2.918	3.294	5.103	2.645	4.185	6.535
Croatia	0.093	1.269	0.947	0.806	1.184	1.256	0.797	1.100	2.478	0.370	1.500	3.615
Czech Republic	0.474	0.819	0.909	1.013	0.632	0.692	0.766	0.543	0.652	0.670	0.782	0.563
Denmark	−0.737	−0.657	−0.275	−0.246	−0.752	−0.785	−0.504	−1.008	−1.164	−0.421	−0.694	−1.731
Estonia	−1.490	−1.531	−1.117	−1.082	−1.806	−1.910	−1.263	−1.971	−2.346	−1.306	−1.458	−3.345
Finland	−2.544	−2.637	−2.419	−2.369	−2.727	−2.840	−2.363	−2.884	−3.141	−2.412	−2.573	−3.855
France	1.256	1.806	1.993	2.023	2.217	2.025	1.622	1.547	2.194	1.448	1.453	4.005
Germany	0.448	0.548	0.614	0.641	0.496	0.486	0.549	0.381	0.407	0.531	0.475	0.385
Great Britain	1.334	1.585	1.759	1.956	1.305	1.322	1.658	0.980	0.819	1.824	1.188	0.213
Greece	−1.193	0.239	−1.021	−0.601	0.385	0.196	−0.723	0.771	1.988	−0.920	1.156	3.727
Hungary	0.029	0.702	0.657	0.395	0.503	0.689	0.418	0.619	1.100	0.182	0.740	1.594
Iceland	−0.563	−0.527	−0.214	−0.544	−0.439	−0.621	−0.319	−0.595	−0.630	−0.218	−0.543	−0.793
Ireland	1.126	1.338	1.354	1.472	1.084	1.072	1.315	0.944	0.736	1.386	0.998	0.335
Italy	−2.121	−1.866	−1.931	−1.801	−1.793	−1.909	−2.001	−1.934	−1.501	−2.040	−1.796	−0.921
Latvia	−2.467	−2.445	−2.086	−2.013	−2.702	−2.696	−2.237	−2.803	−3.118	−2.266	−2.324	−3.864
Lithuania	−1.693	−1.632	−1.303	−1.288	−1.836	−1.806	−1.493	−1.883	−2.121	−1.540	−1.476	−2.628
Luxembourg	1.191	1.316	1.379	1.360	1.288	1.340	1.300	1.150	1.294	1.264	1.228	1.421
Macedonia	1.633	3.170	2.028	2.547	3.104	3.098	2.513	3.286	5.368	2.229	3.992	7.625
Montenegro	−1.191	−0.886	−1.051	−0.827	−0.928	−1.202	−0.882	−1.220	−0.937	−1.089	−0.914	−0.575
Netherlands	0.287	0.352	0.430	0.482	0.249	0.224	0.417	0.133	0.053	0.418	0.281	−0.151
Northern Ireland	1.462	1.650	1.753	1.822	1.391	1.403	1.676	1.247	0.996	1.820	1.318	0.570
Norway	−2.531	−2.440	−1.917	−2.088	−2.578	−2.677	−2.168	−2.960	−3.250	−1.989	−2.477	−4.209
Poland	0.027	0.190	0.425	0.437	0.033	0.078	0.249	−0.017	−0.049	0.131	0.281	−0.253
Portugal	1.978	2.274	1.853	2.263	2.627	2.837	1.758	2.671	3.591	1.645	2.453	5.568
Romania	1.089	2.107	1.983	1.762	1.996	1.882	1.758	2.095	2.832	1.419	2.385	3.416
Serbia	2.770	4.535	3.800	3.773	4.335	4.290	3.843	4.244	6.013	3.290	4.884	7.732
Slovakia	0.559	1.084	1.158	1.046	0.827	0.978	0.937	0.861	1.125	0.713	1.056	1.320
Slovenia	0.356	0.743	0.616	0.675	0.683	0.653	0.602	0.560	0.951	0.480	0.712	1.251
Spain	1.485	1.376	1.276	1.662	2.009	2.169	1.350	2.044	3.472	1.255	2.078	5.572
Sweden	−3.623	−3.571	−3.086	−3.034	−3.674	−3.818	−3.247	−4.081	−4.381	−3.236	−3.522	−5.378
Switzerland	1.197	1.339	1.316	1.519	1.256	1.018	1.356	0.874	0.850	1.269	1.029	0.962

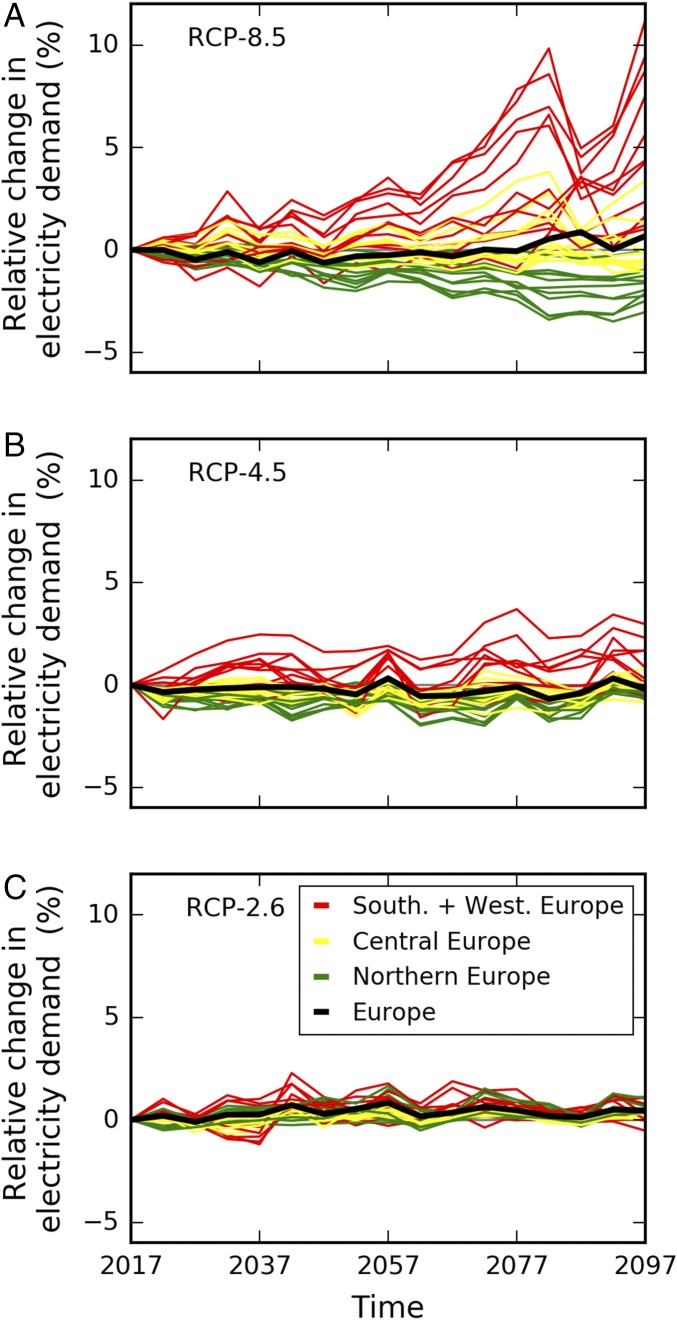
Regarding the change in average daily electricity demand from the near-term (2015–2019) to the more long-term future (different 5-year periods between 2020 and 2099), we find a similar polarization pattern for RCP-8.5 and RCP-4.5 (Fig. 5 A and B, Table 2, and SI Appendix, Fig. S10 A and B and Table S3). There is no clear trend for a scenario of very ambitious climate-change mitigation (RCP-2.6; Fig. 5C and SI Appendix, Fig. S10C). The percentage change in total European electricity demand fluctuates around zero in all scenarios but begins to increase slightly during the last two decades of the 21st century under RCP-8.5.

Fig. 5.

Percentage change in daily electricity demand (5-year average) compared with 2015–2019 average for projected daily maximum temperatures under different scenarios of climate change mitigation. Five-year average electricity demand values are denoted by the year in the middle of the respective time interval on the x axis. (A) Under a scenario of unabated climate change (RCP-8.5), daily electricity demand decreases in northern Europe and increases in countries in southern and western Europe. Total European electricity demand increases in the last two decades of the century relative to 2015–2019. (B) For a scenario of mitigated climate change (RCP-4.5), the trend observed in A is present but less pronounced. (C) For a scenario of very ambitious climate change mitigation that keeps global temperature increase below 2 °C (RCP-2.6), there is no clear trend. Table 2 provides data on all countries, RCPs, and 5-year periods until 2100.

Table 2.

Percentage change in average daily electricity consumption by country relative to 2015–2019 for daily maximum temperatures under RCP-2.6, RCP-4.5, and RCP-8.5

Country	RCP-2.6				RCP-4.5				RCP-8.5
	2035–2039	2055–2059	2075–2079	2095–2099	2035–2039	2055–2059	2075–2079	2095–2099	2035–2039	2055–2059	2075–2079	2095–2099
Austria	0.118	0.774	0.346	0.370	−0.461	−0.359	−0.532	−0.336	−0.532	−0.275	−0.249	−0.785
Belgium	0.153	0.536	0.278	0.370	−0.352	0.030	−0.259	−0.384	−0.647	−0.467	−0.946	−0.537
Bosnia–Herzegovina	−0.240	0.633	0.306	0.122	−0.115	0.371	−0.119	−0.049	0.114	0.763	1.943	2.356
Bulgaria	−1.062	0.178	0.804	0.078	0.718	0.914	1.191	1.688	0.456	1.665	5.748	7.525
Croatia	−0.063	0.822	0.727	0.244	1.275	1.562	0.648	0.840	1.056	2.276	4.215	4.367
Czech Republic	−0.017	0.974	0.359	0.385	−0.834	−0.428	−0.549	−0.461	−0.559	−0.315	−0.239	−1.041
Denmark	0.149	0.821	0.376	0.485	−0.694	−0.588	−0.445	−0.617	−0.467	−0.536	−1.108	−1.260
Estonia	0.526	1.496	0.802	0.720	−0.532	−0.665	−0.645	−0.532	−0.956	−1.540	−2.474	−3.036
Finland	0.603	0.987	0.751	0.656	0.050	−0.003	−0.128	−0.038	−0.526	−1.031	−1.578	−1.958
France	1.022	1.774	0.975	1.078	−0.026	1.304	−0.267	−0.693	−1.785	−1.087	−0.903	1.640
Germany	0.054	0.505	0.185	0.288	−0.442	−0.228	−0.332	−0.337	−0.483	−0.329	−0.646	−0.610
Great Britain	−0.021	0.303	0.172	0.354	−0.603	−0.765	−0.559	−0.643	−1.086	−0.929	−1.875	−1.618
Greece	−0.816	−0.293	0.270	−0.530	2.458	1.900	3.695	2.961	1.107	2.989	6.352	8.761
Hungary	−0.233	0.119	0.323	0.007	0.366	0.264	0.132	0.275	0.723	1.125	1.775	1.342
Iceland	−0.206	−0.134	−0.024	0.230	−0.022	−0.043	−0.010	0.062	0.252	−0.198	−0.009	−0.069
Ireland	0.057	−0.023	0.063	0.035	−0.138	−0.562	−0.212	−0.317	−0.737	−0.602	−1.190	−1.041
Italy	−0.003	0.283	−0.001	0.056	0.032	0.180	0.098	0.042	0.052	0.236	0.761	1.014
Latvia	0.227	1.219	0.477	0.488	−0.583	−0.549	−0.597	−0.368	−0.675	−0.991	−1.759	−2.250
Lithuania	−0.012	0.809	0.202	0.211	−0.528	−0.368	−0.463	−0.169	−0.397	−0.597	−1.081	−1.532
Luxembourg	0.075	0.306	0.148	0.201	−0.239	0.090	−0.247	−0.181	−0.417	−0.221	−0.467	−0.118
Macedonia	−1.191	0.434	0.626	−0.047	1.517	1.382	2.426	2.292	0.306	2.756	7.827	11.223
Montenegro	−0.352	0.700	0.197	0.105	−0.719	−0.088	−0.679	−0.481	−0.166	0.091	0.900	1.208
Netherlands	−0.012	0.185	0.099	0.095	−0.240	−0.226	−0.245	−0.208	−0.218	−0.230	−0.525	−0.498
Northern Ireland	0.067	−0.002	0.086	0.097	−0.208	−0.567	−0.239	−0.280	−0.615	−0.524	−1.129	−0.959
Norway	0.423	1.142	0.809	1.120	−0.711	−0.799	−0.566	−0.491	−0.628	−1.103	−2.016	−2.123
Poland	−0.145	0.698	0.253	0.126	−0.582	−0.276	−0.336	−0.206	−0.272	−0.337	−0.505	−1.133
Portugal	0.790	1.089	0.786	0.538	1.006	1.686	1.034	0.078	−0.155	1.353	1.886	4.267
Romania	−0.538	0.268	0.761	0.017	0.302	0.234	0.379	0.807	0.730	1.291	3.365	3.374
Serbia	−0.648	1.390	1.494	0.784	1.220	1.555	1.048	1.668	0.985	3.524	7.237	9.460
Slovakia	−0.282	0.492	0.292	0.023	−0.231	−0.060	−0.281	−0.155	0.253	0.518	0.868	−0.171
Slovenia	0.062	0.450	0.237	0.192	0.161	0.261	−0.058	0.075	0.015	0.376	0.817	0.615
Spain	0.676	1.008	0.695	0.017	0.834	1.702	0.850	0.289	0.156	1.287	2.794	5.634
Sweden	0.635	1.653	0.960	1.041	−0.856	−0.770	−0.690	−0.721	−0.785	−1.067	−2.199	−2.493
Switzerland	0.062	0.701	0.239	0.287	−0.929	−0.640	−1.116	−0.867	−1.019	−0.694	−1.131	−1.032

Discussion

Complementary to previous studies, which focused exclusively on the role of prices and income on future electricity demand, we quantify the impact of a factor thought to be stationary until recently—climate. The effects we detect are due to temperature changes in response to anthropogenic carbon emissions only. To isolate this effect, infrastructure, technology, and socioeconomic factors such as population and economic structure are held constant in this study. Future planning studies will need to incorporate how changes in population, income, or industrial structure—as well as an enhanced integration of the European grid (“Europeanization”) or other technological developments—will affect both generation and consumption. Recent work suggests that population changes significantly drive electricity consumption, with growing populations leading to higher consumption (40). In terms of economic growth, adoption of air conditioners is thought to be increasing in income and decreasing in unit costs, as well as in the expected price of electricity (41). It is particularly difficult to forecast changes in efficiency, cost, and adoption of new technologies (e.g., heat pumps) across sectors—a topic we leave for future work. Finally, strengthening existing policies and designing new policies to address climate change mitigation and adaptation will significantly affect energy markets across the European Union.

Our results remain qualitatively true for three different carbon emission scenarios (RCP-2.6, RCP-4.5, and RCP-8.5), suggesting that the qualitative results will remain valid also for other climate models. Climatic differences between various carbon-concentration scenarios (RCPs) are small until the year 2050 due to inertia in the climate system. Consequently, also the differences in electricity demand that we report here are rather small across different scenarios until 2050.

A central assumption of this study is that warmer European countries can be surrogates for the future of cooler European countries. That is, our analysis assumes that as climate zones shift north so does the temperature response. This assumption is empirically supported by our finding that—within the current temperature range—the relationship between the normalized electricity load and ambient temperature has the same functional form for all examined European countries (Fig. 2). However, cultural, economic, and other differences across Europe might hinder this assumed adaptation to warmer temperatures. For example, if Swedes have a much higher (or lower) heat tolerance and consequent use of air conditioning, we would overestimate (or underestimate) the temperature response. In addition to differences in heat tolerance, other variation might arise from differences in income, work practice (e.g., common working hours, siesta times, and holiday distribution), the economic structure (e.g., outdoor vs. indoor sectors or degree of sector electrification), and the prevalence of alternative energy sources.

Increased demand for cooling is considered to be one of the main drivers of the social costs of carbon (42)—an important figure used in federal rulemaking in the United States. Here we show that for Europe as a whole electricity consumption is projected to remain flat under future warming. However, this result does not imply that there are no damages from climate change for the electricity sector. Rather, we observe a shift in demand from the north, which has a much higher share of renewables in electricity consumption (35.8% in Sweden and 44.8% in Norway), to the south (Italy 17.6%, Spain 15.2%, and Greece 10%, ref. 43). In contrast to recent analyses for the United States (32), we further do not find a uniform rise in daily peak load across all regions. Instead, we find an increase in southern and western Europe and a decrease in the north. Additionally, we observe a change in the temporal load profile of many European countries with annual peak load—the highest load value of the year—shifting from winter to summer. In our dataset, 30 of the 35 countries currently experience annual peaks in winter. With warmer winters and hotter summers, it is an empirical question as to whether the annual peak will shift seasons. Using the residual (temperature-driven) simulation results for the 2080–2099 period under RCP-8.5, we find that 19 of these 30 countries will experience annual peak demand in summer instead of winter (SI Appendix, Table S4).

The spatial redistribution of consumption across the continent, the decreases in present-day winter peaks in the north, and the increases in future summer peaks in the south may require costly investments in transmission infrastructure, storage, and generating capacity. An additional challenge arises due to the temporal redistribution of annual peak load from winter to summer in many countries. This seasonal shift has ramifications for the types of generating capacity which can be dispatched to meet peak demand. It also has strong implications for future (interseasonal) storage requirements—particularly if a larger share of the electricity is produced by renewable sources.

From an economic perspective, the most significant redistributive effects will come from changes in the intensity of peaks across the continent. Currently, the northern European countries experience annual peak load in winter due to electric heating and lighting demand (44). In southern Europe, the pattern is opposite: peak demand generally occurs in summer, which is consistent with high cooling demand. Generally, the entire energy system—generation and transmission capacity—is designed to meet peak demand on the highest load day of the year. Regulators build in capacity reserve margins to meet unexpectedly high peak loads. To meet these unexpectedly high loads, electricity generators run so-called peaker plants. These peaker plants are rarely used, relatively inefficient, high-pollutant plants with short ramp-up times and high marginal costs of generation. In the United States, the cost of the additional capacity necessary to operate a single extra air-conditioning unit of 1 kW is estimated to be approximately $1,220, which reduces to $455 per kW after accounting for separate discounting of air conditioning and power plant (45, 46). Additional investment is required because these peaker plants must be placed in the direct vicinity of load centers. Overall, significant investments in peaker plants or storage of renewable power will be necessary to meet higher peak demand in southern and western Europe.

Given the high marginal cost of power at these peak periods electricity prices will likely increase in the long run. The temporal pattern of how these costs will be passed through to consumers depends on the local regulatory structure. The worst-case scenario in our computations predicts a maximum increase in average daily peak load between 5% and 7% for Portugal and Spain, which are among the economies with the largest predicted increases by the end of century. This increase is equivalent to an average 0.1% per year growth, which can be offset by very modest improvements in energy efficiency or market-based regulations. The forecasting horizon here is significantly larger than the planning horizon of energy systems planners; the period 2020–2039 is more in line with the planning horizon. In this more proximate period, Spain and Portugal’s predicted increases are between 1.2% and 2.8%—again, relatively small levels of increase.

In conclusion, our analysis suggests that the impacts of climate change on electricity load for the EU-35 overall are neutral, yet demand redistributes spatially from the north to the south and, in many countries, temporally from winter to summer. The magnitude of the increase in the south allows the additional costs to be offset by carefully crafted policies. We speculate that the main burden of the climate-induced electricity effect will rest on the planners of transmission infrastructure and peak-generating and storage capacity.

Methods

For 35 European countries (see SI Appendix, Table S1 for a list of countries) we compute population-weighted daily maximum and daily average temperature time series for the years 2006–2099. All temperature and population data come from the ISI-MIP (37) climate dataset covering data on a grid of 0.5°-by-0.5° resolution. To assign grid cells to countries, we construct a mask using spatial information provided by the Global Administrative Areas initiative (47).

Population-Weighted Temperature Time Series.

We spatially aggregate the gridded daily maximum and daily average temperature data to the country level using population-density weights: for each grid cell $g$ that geographically belongs to a country $c$ we multiply the daily maximum (or daily average) temperature value $T_{g,c,d}$ as given by the data by the population value $P_{g,c}$ for the respective year. Summing over all grid cells and dividing by the total population of country $c$ yields the population-weighted daily maximum (or daily average) temperature value $T_{c,d}$ on day $d$:

$$T_{c,d}=\frac{{\displaystyle {\sum }_g{T}_{g,c,d}\cdot P_{g,c}}}{{\displaystyle {\sum }_g{P}_{g,c}}}.$$

Temperature Data.

For the historical period (2006–2012) we use daily maximum and daily average temperature data from the WFDEI meteorological forcing dataset (48), which applies the WATCH forcing data methodology to ERA-interim reanalysis data (49). With regard to temperature projections (from 2013 on) we use time series of daily maximum and daily average near-surface temperature corresponding to different RCPs (RCP-2.6, RCP-4.5, and RCP-8.5, ref. 35). These data originate from the Princeton Earth System Model of the Geophysical Fluid Dynamics Laboratory (GFDL-ESM2M, ref. 50), which is one of the global climate models of the fifth phase of the Coupled Model Intercomparison Project (CMIP-5, ref. 51) with a median warming sensitivity (1). The temperature data include a bias-correction technique (38) to ensure long-term statistical agreement of the projected values with historical observations from the WATCH database.

Population Data.

Historical population data come from the United Nations World Population Prospects (UNWPP, ref. 52), and population projections (from 2010 on) correspond to the second SSP (SSP-2, ref. 36). These population data are used exclusively to translate gridded temperature data into population-weighted national temperature time series. Our analysis does not consider the influence of population trends on electricity demand and peak load.

Electricity Load Data.

Data on electricity consumption—hourly load values per country—originate from the European Network of Transmission Systems Operators for Electricity (39). For 21 countries, the database covers the entire period 2006–2012. For two, three, one, and eight countries, data are only available from 2007, 2008, 2009, and 2010 on, respectively. Within these periods, data points are occasionally missing for several hours or days. If data are missing for 1 h or more, we excluded the whole day from the analysis to avoid distortions. Cyprus (99.72% data points missing), Iceland (39.9%), Montenegro (5.61%), and Great Britain (2.62%) have the scarcest data density. Cyprus is excluded from the second part of the analysis because of data scarcity. A comprehensive list of all countries and their respective load data coverage is given in SI Appendix, Table S1. The results are robust to restricting the sample period to years where we have coverage for all countries.

Regression Model.

For each country c, the independent variable is population-weighted daily maximum or daily average temperature ($T_{c,d}$ in degrees Celsius) for the period 2006–2012. The dependent variable is national daily peak load or national daily electricity consumption ($L_{c,d}$ in gigawatts or gigawatt hours, respectively). To place the fewest restrictions on the functional form of the dose–response function(s), we sort the independent variable into discrete bins, ${\text{Bin}}_i$, of 3 °C width (in total $N_c$ bins). To ensure sufficient data coverage, we select the first and last bin such that at least 2% of all data points lie below its upper or above its lower boundary, respectively. The main result of the regression is robust against variations of the specific number of data points present in the first and last bin (SI Appendix, Fig. S11). Following a commonly applied approach (3), we then regress the dependent variable on dummy variables $B_i$ representing the bins:

$$B_i\left(T_{c,d}\right)=\{\begin{array}{cc}1& if\hspace{0.17em}{T}_{c,d}\in {\text{Bin}}_i\\ 0& if\hspace{0.17em}{T}_{c,d}\notin {\text{Bin}}_i\end{array}.$$

This discretization allows us to flexibly model the nonlinear relation between temperature and electricity load without relying on, for example, splines that might unnecessarily distort the data (53). As is standard in the impacts literature, we apply Chebyshev polynomials, $C_{j,d}$, of degree $j=0,\dots ,6$ to capture the influence of other influencing factors that operate on lower frequencies than electricity demand, such as macroeconomic activity (32, 54–56). Recursively, the Chebyshev polynomials are given by

$$C_{j,d}=2d\cdot C_{j-1,d}-C_{j-2,d}\hspace{1em}\text{for}\hspace{0.17em}j\ge 2,$$

with $C_{0,d}=1$ and $C_{1,d}=d$. Polynomials up to the order six are sufficient to obtain robust results (compare SI Appendix, Figs. S12 and S13). Furthermore, dummy variables $W_{k,d}$ and $S_{l,d}$ control for weekdays and seasons, respectively. The regression model thus reads

$$L_{c,d}={\displaystyle \sum _{i=0}^{N_c-1}{\alpha }_{i,c}{B}_i\left(T_{c,d}\right)}+{\displaystyle \sum _{\text{j}=0}^6{\beta }_{j,c}{C}_{j,d}}+{\displaystyle \sum _{\text{k}=0}^6{\gamma }_{k,c}{W}_{k,d}}+{\displaystyle \sum _{\text{l}=0}^3{\delta }_{\text{l},c}{S}_{\text{l},d}+{\mathrm{\Omega }}_c+{\mathit{ϵ}}_{c,d}},$$

where ${\alpha }_{i,c},\hspace{0.17em}{\beta }_{j,c},\hspace{0.17em}{\gamma }_{k,c},\hspace{0.17em}\text{and}\hspace{0.17em}{\delta }_{\text{l},c}$ are the regression coefficients, ${\mathrm{\Omega }}_c$ describes a country-specific constant, and ${\mathit{ϵ}}_{c,d}$ denotes the stochastic error term. We compute a 95%-confidence band using the Newey–West standard error, which is robust against autocorrelations of time-ordered data (here, up to 15 days). The procedure described above is equivalent to estimating dose–response functions separately by country.

Response Function.

We derive a common dose–response function for all countries by combining the national observational temperature and load data (Fig. 2 and SI Appendix, Fig. S5). Concerning the load data, only the parameter related to the temperature variable and the constant are considered:

$${\widehat{L}}_{c,d}=L_{c,d}-{\displaystyle \sum _{j=0}^6{\beta }_{j,c}{C}_{j,d}}-{\displaystyle \sum _{k=0}^6{\gamma }_{k,c}{W}_{k,d}}-{\displaystyle \sum _{l=0}^3{\delta }_{l,c}{S}_{l,d}}={\displaystyle \sum _{\text{i}=0}^{{\text{N}}_{\text{c}}-1}{\alpha }_{i,c}{B}_i\left(T_{c,d}\right)+{\mathrm{\Omega }}_c+{\mathit{ϵ}}_{c,d}}.$$

To render these residual load data comparable across countries, we normalize as follows:

$${\widehat{L}}_{c,d}^{\text{norm}}=\frac{{\widehat{L}}_{c,d}-{\widehat{L}}_{c,d}\left(T_{{\text{fix}}_1}\right)}{{\widehat{L}}_{c,d}\left(T_{{\text{fix}}_2}\right)-{\widehat{L}}_{c,d}\left(T_{{\text{fix}}_1}\right)},$$

where ${\widehat{L}}_{c,d}\left(T_{{\text{fix}}_{\lambda }}\right)$ with $\lambda =\mathrm{1,2}$ denotes the mean of all load values ${\widehat{L}}_{c,d}$ at temperatures $T_{c,d}\in \left[T_{{\text{fix}}_{\lambda }}\pm 0.5°\text{C}\right]$. We choose temperatures $T_{{\text{fix}}_1}$ and $T_{{\text{fix}}_2}$ such that for each country the associated load values are as far apart as possible, while the respective temperature bins still carry a sufficient number of data points to obtain a robust result. For daily maximum temperatures, we choose $T_{{\text{fix}}_1}=20\hspace{0.17em}°\text{C}$ and $T_{{\text{fix}}_2}=8\hspace{0.17em}°\text{C};$ for daily average temperatures, we set $T_{{\text{fix}}_1}=14\hspace{0.17em}°\text{C}$ and $T_{{\text{fix}}_2}=4\hspace{0.17em}°\text{C}$. We weight the data according to the countries’ populations, with the least populated country, Luxembourg, serving as the “population unit.” Note that no scaling is applied to the x axis. We then bin these data into discrete temperature intervals of 1 °C width, with the first and last bin comprising at least 20,000 data points to ensure sufficient data coverage. The main results presented in this study do not depend on the specific choice of bin width (SI Appendix, Fig. S14). For each bin, we compute the median, as well as the 5th and 95th percentiles. We then obtain the response function by linearly linking the medians of two neighboring bins (Fig. 2). Analogously, the uncertainty range is obtained by linking the 5th and 95th percentile values, respectively. For temperatures that are lower (higher) than the first (last) bin, we linearly extend the line given by the first (last) two bins. We chose this linear extrapolation for temperatures outside the range currently sufficiently covered by the data because we consider it to be a balance between the complexity of the functional form of the extrapolation and the quality of the representation of the existing data (i.e., how well the fit can represent the existing data). In other words, on the one hand the data do not justify assuming that peak load and electricity consumption are constant for temperatures above or below the observed values. Thus, such an assumption would be very strong. On the other hand, the sparseness of data for high and low extreme temperatures inhibits detecting functional forms more complex than the linear approach—for instance higher-order polynomials. Note that the projected values ${\widehat{L}}_{c,d}^{\text{proj}}={\widehat{L}}_{c,d}^{\text{proj},\text{norm}}\left({\widehat{L}}_{c,d}\left(T_{{\text{fix}}_2}\right)-{\widehat{L}}_{c,d}\left(T_{{\text{fix}}_1}\right)\right)+{\widehat{L}}_{c,d}\left(T_{{\text{fix}}_1}\right)$ are compared with the residual load data ${\widehat{L}}_{c,d}$ (in Figs. 3–5, Tables 1 and 2, and SI Appendix, Figs. S6–S10 and Tables S2 and S3). We excluded Cyprus from this part of the analysis due to its scarce data density (compare SI Appendix, Table S1).