On a square-root transformation of the odds ratio for a common outcome

To the Editor

It is well known that for a common outcome, the magnitude of an odds ratio (OR) relating an exposure to that outcome can substantially exceed the corresponding risk ratio (RR) when analyzing cohort data. When an outcome is rare (10% is often used as a cut-off) the OR closely approximates the RR and is often interpreted as a RR. But when the outcome is common, if the OR is interpreted as a RR, it can vastly exaggerate the RR, and is never optimal to use. Because logistic regression is often the tool of choice for multivariate control, the reporting of OR’s, even when the outcome is common, is routine. Although numerous methods have been developed to estimate RR’s for a common outcome while still allowing for covariate control,^1,2 these methods continue to be used infrequently.² The practice reporting of OR’s for common outcomes remains frequent in the biomedical literature. The intuitive understanding of the magnitude of the OR in such settings is more difficult. This letter proposes a simple transformation of an OR for a common outcome that, in the vast majority of settings, yields a quantity that is far closer to the RR. The purpose of this letter is not to suggest that the methods for estimating RR’s for common outcomes should not be used; rather it is intended to assist in the interpretation of OR’s for common outcomes when they are in fact reported in papers.

The proposed transformation is a simple one: it is to simply take the square root of the OR estimate. Thus, as a somewhat better approximation to the RR, an OR of 2 becomes 1.41, an OR of 4 becomes 2, and OR of 9 becomes 3, and so on. I will provide brief motivation for this transformation, and then discuss some properties related to its performance as a quantity that more closely approximates the RR.

First, consider a setting in which the outcome probability for the exposed is some quantity w above 0.5 and the outcome probability for the unexposed is that same quantity w below 0.5 so that the probability for the exposed and unexposed are p₁ = 0.5 + w and p₀ = 0.5 − w respectively. We then have RR = p₁/p₀ = (0.5 + w)/(0.5 − w) and $OR=\frac{p_1(1-p_0)}{(1-p_1)p_0}=\frac{{(0.5+w)}^2}{{(0.5-w)}^2}$. In this case, the OR is exactly the square of the RR and taking the square root recovers the RR. It turns out that this same transformation works surprisingly well for most values of the outcome probabilities when the outcome is common.

Let us begin with a causative exposure so that p₁ > p₀. Suppose first that both p₀ and p₁ are between 0.2 and 0.8. In this case the OR can be inflated by a factor as large as 400% (e.g. with p₀ = 0.2, p₁ = 0.8, we have RR = 4 but OR = 16); however, it can be shown (see the eAppendix for mathematical proofs of all claims) that the most sqrt(OR) can be inflated above RR is by a factor of 25% (e.g. with p₀ = .5, p₁ = 0.8, we have RR = 1.6 and sqrt(OR) = 2). With outcomes probabilities p₀ and p₁ between 0.2 and 0.8, the square root of the OR will be at most 25% away from the RR.

If instead, both p₀ and p₁ are between 0.1 and 0.9, the OR can be inflated by a factor as large as 900% (e.g. with p₀ = 0.1, p₁ = 0.9, we have RR = 9 but OR = 81), but the square root of the odds can be inflated at most by a factor of 67% for the RR (e.g. with p₀ = 0.5, p₁ = 0.9, we have RR = 1.8 and sqrt(OR) = 3). The square root transformation reduces the inflation dramatically, and, as above, when the risk for exposed and unexposed average to 0.5, the transformation negates the bias exactly. More substantial inflation can occur when the outcome probabilities exceed 0.9, but the square root transformation will still provide an improvement as an approximation to the RR.

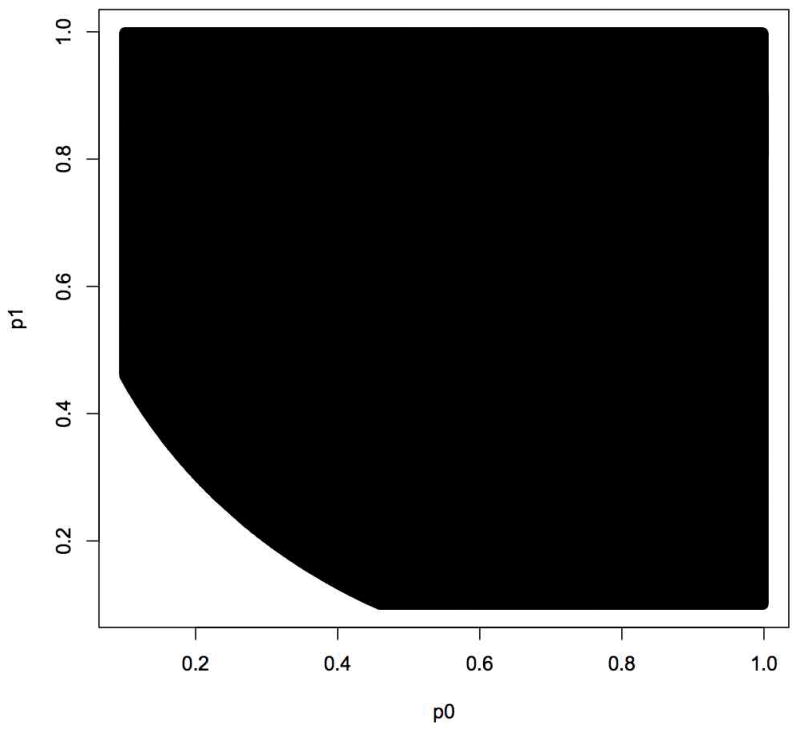
The square root transformation will in fact always de ate the OR towards the RR. It can in, some circumstances, over-deflate so that sqrt(OR) is less than RR (for example, with p₀ = 0.3, p₁ = 0.5, RR = 1.67 and sqrt(OR) = 1.52) but, once again with p₀ and p₁ between 0.2 and 0.8, the maximum deflation will be by a factor of 1/1.25-fold (i.e. a 20% reduction), and with p₀ and p₁ between 0.1 and 0.9, the maximum deflation will be a factor of 1/1.67-fold i.e. a 40% reduction. Even in these circumstances in which the sqrt(OR) is deflated beyond the RR, the factor by which sqrt(OR) is deflated beyond the RR will, in the vast majority of settings, be smaller than the factor by which OR is inflated above RR. The values of the outcome probabilities for which this is so when both probabilities are above 0.1 is plotted in Figure 1 as the black area. When both outcomes probabilities are above 0.1, the factor of inflation for the OR exceeds the factor of deflation for the sqrt(OR) for about 93% of possible outcome probabilities. When both probabilities are above 0.2, this is so for 99% of the possible outcome probabilities. When both probabilities are above 0.25, it is always the case. Analogous statements to all claims above also hold for protective exposures with p₁ < p₀.

Figure 1.

Ratio scales are sometimes converted into excess relative risk measure for the purposes of obtaining measures of public health significance.^3,4 For these purposes it is not the ratio of the RR to the OR or sqrt(OR) that matters, but the differences between these quantities. Once again the square root transformation is superior in the vast majority of settings. It always deflates the OR towards the RR; it can sometimes over-deflate, but, even then, in the vast majority of cases the absolute difference |sqrt(OR) − RR| is smaller the absolute difference |OR−RR|. For causative exposures, when both probabilities are between 0.2 and 0.8, the absolute difference for OR can be as large as 12, but for sqrt(OR) only as large as 0.55; when both outcome probabilities are between 0.1 and 0.9, the absolute difference for OR can be as large as 72, but only as large as 2.43 for sqrt(OR). For causative exposures, the square root transformation has a smaller absolute difference 95% of the time if both outcomes probabilities are above 0.1, and 99% of the time if both outcome probabilities are above 0.2. For protective exposures, with p₁ < p₀ the square root transformation has a smaller absolute difference 90% of the time if both outcomes probabilities are above 0.1, and 98% of the time if both outcome probabilities are above 0.2.

Again, the square transformation is much closer to the RR in almost all scenarios, and provides a somewhat reasonable approximation to the RR. As a rule of thumb, one might suggest that when the prevalence of the outcome is above 20%, the square root approximation is preferable. The transformation may thus be of use with randomized trial, cohort, or cross-sectional data, or with case-control data with cumulative sampling. Case-control studies with incidence density sampling, however, provide a direct estimate of the incidence rate ratio³ and further discussion of rate ratios and proportional hazards models is given in the eAppendix. The transformation proposed here may also be of interest in the interpretation of the results of meta-analyses. In meta-analyses, approximate conversions are typically made between standardized effect sizes and log odds ratios.^5,6 The approximations employed effectively assume common outcome probabilities and do not perform well when the outcome probabilities are very small or very large.⁷ The conversions that are used in meta-analyses are thus applicable precisely when the outcome is common and effectively deliver OR’s assuming a common outcome; conversion of these to approximate RR’s could once again be obtained by applying the square-root transformation. Again, the purpose of this letter is not displace methods that estimate RR’s for common outcomes, but rather to aid the interpretation of OR estimates for common outcomes already reported in the literature.