Spatiochromatic Interactions between Individual Cone Photoreceptors in the Human Retina

Abstract

A remarkable feature of human vision is that the retina and brain have evolved circuitry to extract useful spatial and spectral information from signals originating in a photoreceptor mosaic with trichromatic constituents that vary widely in their relative numbers and local spatial configurations. A critical early transformation applied to cone signals is horizontal-cell-mediated lateral inhibition, which imparts a spatially antagonistic surround to individual cone receptive fields, a signature inherited by downstream neurons and implicated in color signaling. In the peripheral retina, the functional connectivity of cone inputs to the circuitry that mediates lateral inhibition is not cone-type specific, but whether these wiring schemes are maintained closer to the fovea remains unsettled, in part because central retinal anatomy is not easily amenable to direct physiological assessment. Here, we demonstrate how the precise topography of the long (L)-, middle (M)-, and short (S)-wavelength-sensitive cones in the human parafovea (1.5° eccentricity) shapes perceptual sensitivity. We used adaptive optics microstimulation to measure psychophysical detection thresholds from individual cones with spectral types that had been classified independently by absorptance imaging. Measured against chromatic adapting backgrounds, the sensitivities of L and M cones were, on average, receptor-type specific, but individual cone thresholds varied systematically with the number of preferentially activated cones in the immediate neighborhood. The spatial and spectral patterns of these interactions suggest that interneurons mediating lateral inhibition in the central retina, likely horizontal cells, establish functional connections with L and M cones indiscriminately, implying that the cone-selective circuitry supporting red–green color vision emerges after the first retinal synapse.

SIGNIFICANCE STATEMENT We present evidence for spatially antagonistic interactions between individual, spectrally typed cones in the central retina of human observers using adaptive optics. Using chromatic adapting fields to modulate the relative steady-state activity of long (L)- and middle (M)-wavelength-sensitive cones, we found that single-cone detection thresholds varied predictably with the spectral demographics of the surrounding cones. The spatial scale and spectral pattern of these photoreceptor interactions were consistent with lateral inhibition mediated by retinal horizontal cells that receive nonselective input from L and M cones. These results demonstrate a clear link between the neural architecture of the visual system inputs—cone photoreceptors—and visual perception and have implications for the neural locus of the cone-specific circuitry supporting color vision.

Introduction

In sensory circuits, the receptors forming the first tier of neurons are often the first to be well understood, whereas the second tier can be more difficult to study, even though they remain central to understanding how the circuit functions. A prime example of such a challenge is found in the retina. Cone photoreceptors have been characterized extensively (Baylor et al., 1987; Schnapf et al., 1990), whereas examination of the signals that they pass to horizontal cells has led to different conceptions about how cone signals are transformed before they reach retinal ganglion cells for transmission to the brain. Because horizontal cells are positioned to mediate spatial antagonism in the outer retina (Baylor et al., 1971; Verweij et al., 2003; Packer et al., 2010), they can be involved in coding two kinds of signals via surround inhibition: spatial contrast and, in trichromatic primates, spectral information (Thoreson and Mangel, 2012). Although spatial opponency is a hallmark of many retinal ganglion cell types, the functional connectivity that endows neurons in the midget ganglion cell pathway with spectral opponency has been variously inferred from electrophysiological recordings, ranging from receptive fields featuring spectrally cone-type-pure organization (Wiesel and Hubel, 1966; Reid and Shapley, 1992; Martin et al., 2001; Reid and Shapley, 2002) to those with a mixed spectral composition (De Monasterio and Gouras, 1975; Lennie et al., 1991; Diller et al., 2004; Buzás et al., 2006; Crook et al., 2011).

In none of the studies mentioned above were the set of cones providing the signals known. Given the variation in cone ratios and arrangement among retinae (Roorda and Williams, 1999; Hofer et al., 2005b; Sabesan et al., 2015), the variable outcomes could have arisen from the specific local spectral topography of the cone mosaic stimulated in each instance or from heterogeneity in the wiring schemes deployed within a single class of neurons. Moreover, with conventional in vivo techniques, small eye motions and the normally imperfect ocular optics lead to unknown spatiotemporal patterns of photons impinging on the photoreceptors, adding more uncertainty to how the circuit is being driven. Multielectrode array studies have been able to resolve individual cone inputs to ganglion cells (Field et al., 2010; Li et al., 2014; Freeman et al., 2015), but the results have thus far been confined to the peripheral retina. To overcome these issues in probing how cone signals interact in the central retina, we used adaptive optics (AO) microstimulation (Harmening et al., 2014) coupled with high-speed retinal tracking to measure detection thresholds for stimuli delivered to parafoveal cones. The spectral types of the cones had been identified independently by absorptance imaging (Sabesan et al., 2015). By examining the link between the spectral topography of the cone mosaic and the detection sensitivity of single receptors, we demonstrate that a functional signature of early retinal circuitry—spatial antagonism—emerges when vision is tested at the elementary scale of individual cones.

Materials and Methods

AO imaging and cone-resolved retinal densitometry.

We used a multiwavelength AO scanning laser ophthalmoscope (AOSLO) for structural and functional characterization of the trichromatic cone mosaic in two male subjects with normal color vision. All procedures were approved by the Institutional Review Board at the University of California–Berkeley and adhered to the tenets of the Declaration of Helsinki. Informed consent was obtained from each subject at enrollment. Before imaging, cycloplegia and mydriasis were induced via instillation of 1.0% tropicamide ophthalmic solution.

Detailed descriptions of using AOSLO for visual psychophysics and retinal imaging have been reported previously (Roorda et al., 2002; Tuten et al., 2012). Briefly, broadband light from a supercontinuum source (SuperK Extreme; NKT Photonics) was long- and band-pass filtered sequentially to produce three independent narrowband input channels, one in the infrared (IR; λ = 842 ± 11 nm) for retinal imaging and wavefront sensing and two stimulation channels positioned in the green (λ = 543 ± 11 nm) and red (λ = 710 ± 12.5 nm) portions of the visible spectrum. High-speed acousto-optic modulators (AOMs) were used to control stimulus intensity with 8-bit resolution. The relative vergences of the 3 input channels were adjusted to account for the longitudinal chromatic aberration of the human eye before being recombined and raster scanned across a 1.2° square patch of retina. Wavefront measurement and correction were achieved by a Shack–Hartmann wavefront sensor and a 144-actuator deformable mirror (Multi-DM; Boston Micromachines), respectively. Light collection optics were designed to separate light emerging from the eye into three corresponding output channels, each equipped with a photomultiplier tube positioned behind a confocal pinhole to permit simultaneous multiwavelength imaging. Transverse chromatic aberration (TCA) was computed by comparing the relative shifts in retinal structure observed in these images (Harmening et al., 2012); stimuli were delivered with these TCA shifts corrected.

The approach to identifying L, M, and S cones using retinal densitometry was described in detail previously (Sabesan et al., 2015): the absorptance scatter plots, the relative numbers of L, M, and S cones, and the classification error estimates for the same subjects (S1 and S2) can be found in that study. Densitometric assignment confidence values for each tested L and M cone were estimated using the Gaussian mixture model clustering analyses described previously (Roorda and Williams, 1999; Hofer et al., 2005b; Sabesan et al., 2015). Briefly, for each cone in the mosaic, the change in reflectance intensity after an L-cone-selective bleach was plotted in Cartesian coordinates against the reflectance change obtained after a bleach targeting M cones. Each data point was converted into a polar angle and compiled into histograms, which were fit with the sum of two 1D Gaussians; the point of intersection of the component Gaussians delineates the spectral clusters. For a given polar angle, the densitometric confidence value was determined by the ratio of the component Gaussian to the summed Gaussian. Therefore, cones with a polar angle at the intersection of the component functions will feature a 50% assignment probability. The average probability of cone assignments for the specific cones tested in our experiments was 96.8% and 95.6% for subjects S1 and S2, respectively.

Psychophysical procedures and analyses.

For each subject, a contiguous array of cones located within the cone mosaic classified by AOSLO densitometry was selected for increment threshold testing using AO microstimulation (Harmening et al., 2014). In retinal coordinates, the tested cones were located on the horizontal meridian ∼1.5° temporal to the foveal center in both subjects. Thresholds were measured under conditions akin to the Stiles' two-color cone-isolating paradigm (Stiles, 1959). In this approach, chromatic backgrounds were used to elevate the steady-state activity of one class of cones, thereby reducing their sensitivity to a monochromatic test flash. The subject's task was to detect a nominally 0.45 arcmin square stimulus (λ = 710 nm for biasing detection toward L cones; λ = 543 nm for M-cone-biased stimulation) presented for 125 μs against a background comprising three elements: (1) the dim, IR imaging raster (842 nm), (2) low light leak through the stimulus channel (due to imperfect extinction of the AOM), and (3) a steady adapting background field with a spectral composition that was chosen to suppress the sensitivity of the nontargeted cone classes (see Fig. 1A,D; λ_peak = 470 nm for M cone adaptation; λ_peak = 710 nm for L cone adaptation). For M and L cone adaptation, the cumulative luminances of the adapting backgrounds were 30 and 60 cd/m², respectively. Photopigment isomerizations induced by the background were computed for each receptor class using the Psychtoolbox routine RetIrradianceToIsoRecSec (Brainard, 1997). The M-cone-adapting field produced 5.34 (L), 5.50 (M), and 5.35 (S) log isomerizations cone⁻¹ s⁻¹; for L-directed adaptation, these values were 5.62, 5.44, and 2.22 log isomerizations cone⁻¹ s⁻¹, respectively. Therefore, in addition to reducing their sensitivity to flashes of fixed intensity, the chromatic backgrounds produced more activity in cones belonging to the class targeted for adaptation (0.17 log units, or ∼1.5×).

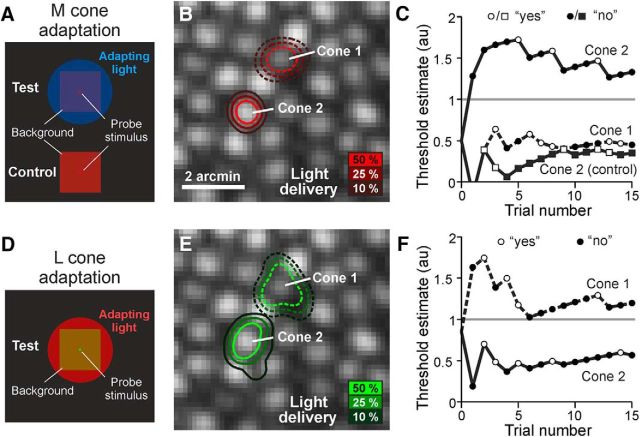
Figure 1.

Measuring photoreceptor increment thresholds against chromatic adapting fields. A, Schematic of subject's view during microstimulation. A 470 nm adapting light selectively reduced the sensitivity of M and S cones to the cone-sized test probe (710 nm) flashed on the 1.2° imaging background. Stimulus is not to scale. B, Stimulus light delivery distribution for two targeted cone photoreceptors plotted on the cone-resolved AOSLO image. The contour lines (Cone 1 = dashed; Cone 2 = solid) indicate the stimulus light intensity accumulated over 15-trial staircases, incorporating a diffraction blur of the 3 × 3 pixel stimulus (0.45 arcmin) and errors in delivery location. C, Threshold staircases for Cones 1 and 2. Final threshold estimate for Cone 2 exceeded the light intensity limit (gray horizontal line), indicating a cone unable to detect the signal at maximum intensity. Cone 1 remained sensitive to the stimulus, a likely L cone. Control trials, in which the blue adapting light was turned off and Cone 2 regained sensitivity, confirmed that the previously elevated threshold was due to the adapting field, making this likely an M cone. Threshold estimates are in arbitrary units (au); see Materials and Methods. D–F, A 710 nm L-cone-adapting light reduced sensitivity of Cone 1 to a 543 nm test probe, biasing detection toward the previously insensitive Cone 2; data are otherwise displayed as in A–C.

Targeted cones were selected manually in a high-magnification view of the retina in the imaging and stimulus delivery software interface (Yang et al., 2010). A total of 108 and 105 photoreceptors were selected for testing under the M and L cone adaptation paradigms, respectively; 92 were tested under both conditions. Real-time retinal tracking permitted stimulus delivery to the cone of interest with cellular-scale precision (Arathorn et al., 2007). The delivery error across all trials (n = 10,992) was 0.20 arcmin (∼1 μm). This corresponds to ∼20% of the cone inner segment diameter at our test eccentricity (∼1.5°), confirming that most of the delivered light from the trials (∼80%) was confined to a single targeted cone (Harmening et al., 2014).

In each set of trials, up to three cones were selected for testing. After adapting to the background light for 3–5 min, cone thresholds were measured using randomly interleaved, 15-trial adaptive QUEST staircases guided by a yes–no response paradigm (Watson and Pelli, 1983; King-Smith et al., 1994). Detection thresholds, defined as the intensity at which the subject detects the stimulus 50% of the time, were expressed on a linearized scale of arbitrary units, with a value of 0 indicating the presence of the background alone and a value of 1.0 corresponding to the upper limit of stimulus modulation. Note that the QUEST algorithm uses priors about the underlying psychometric function governing detection. In instances where the maximum intensity stimulus was detected <50% of the time, threshold estimates were thus produced that exceeded the maximum deliverable light intensity. All threshold measurements were repeated at least twice. As a control, a subset of cones exhibiting high thresholds under our test conditions were remeasured with the adapting background switched off. A recovery of sensitivity supported the interpretation that elevated thresholds were induced by adaptation and not due to underlying cone dysfunction or insufficient light delivery. Under the stimulus conditions available, S cone sensitivity was >2 log units below M or L cone sensitivity. Therefore, S cones were unlikely to provide a measurable threshold (cone thresholds were expected to be >1). TCA was measured before and after each block of trials (Harmening et al., 2012) and a bite bar was used to prevent shifts in subject position during testing. Blocks of data for which TCA shifted by more than 1/2 of a cone diameter (∼4 pixels; 3 μm on the retina) were excluded from subsequent analyses. The median TCA shift across all trial blocks was 0.84 pixels; just three blocks (7.6%) had TCA shifts between 3 and 4 pixels.

Estimating the effects of optical blur and cone coupling.

A model of light capture was constructed to examine the effect of uncontrolled stimulus blur on detection across the trichromatic mosaic. The 2D Gaussian light-collecting apertures representing individual cones were placed at the cone locations observed in the AOSLO image. The size of each aperture, defined as the full width at half-maximum, was set to be 50% of the inner segment diameter at the test eccentricity (Hirsch and Curcio, 1989; MacLeod et al., 1992) and its light capture efficiency (i.e., the peak height of the Gaussian) was scaled by the expected cone contrast for each spectral type given the chromatic content of the background and stimulus (Cole and Hine, 1992). A spatiotemporal representation of the 3-by-3 pixel stimulus was then generated via convolution with a diffraction-limited point spread function and a 2D Gaussian with SD matched to the observed tracking error in stimulus delivery across all trials (0.20 arcmin). This stimulus representation was centered on each cone in the weighted model array, with the integrated element-wise product of the cone and stimulus matrices representing the effective retinal light capture by the entire mosaic for stimuli centered on that photoreceptor.

Predicted thresholds attributed to each cone in the model array were computed based on the simplifying assumption that, across this small patch of retina, a fixed number of photopigment isomerizations, summed from all cones in the array, must be triggered to reach threshold. Therefore, the predicted cone threshold map is the inverse of the effective light capture map; the product of the two remains constant across the array. To quantify the effect that optical defocus or uncorrected aberration might have in explaining the results, optical defocus in diopters (D) was introduced to the stimulus representation until the differences between the observed and simulated threshold topographical maps, quantified as their root mean squared error, were minimized.

We note here the following assumptions implicit to the light capture model: (1) each cone has the same inner segment diameter, (2) each cone has a sensitivity governed by its endogenous photopigment and is otherwise independent of its neighbors, (3) each cone has an equivalent input weight onto downstream circuitry, and (4) all cone outputs are summed linearly across the entire mosaic. No additional assumptions are made about downstream signal processing. This model can be considered conservative in that it deliberately overemphasizes the contributions of the photons landing on adjacent cones (due to optical blur) to the visual response. For instance, the model pools every absorbed photon linearly despite the fact that the photoresponse of cones is nonlinear for a given state of adaptation (Valeton and van Norren, 1983; Schnapf et al., 1990). In addition, the area of linear spatial summation only encompasses ∼20 cones in the central retina, with psychophysical and ideal observer analyses both confirming that light falling outside this zone is less effective at triggering detection (Inui et al., 1981; Davila and Geisler, 1991; Dalimier and Dainty, 2010). Therefore, a more elaborate model of detection would downplay the effect of the scant light falling onto more distant receptors when the stimulus is blurred, in turn pushing the amount of defocus required to explain the topographical pattern of sensitivities that we observed even higher. For these reasons, our model is conservative at estimating the amount of blur required to explain our results. Finally, although this model does not attempt to capture all of the physiological complexities involved in the processing of cone signals by postreceptoral circuitry (Li et al., 2014; Freeman et al., 2015), a similar implementation nonetheless accounts for the sensitivity gradient observed with AO-corrected microstimuli delivered on and between cones in the parafovea (Harmening et al., 2014).

To examine how gap junctional cone coupling might influence cone thresholds, we estimated the change in membrane voltage that would occur in one cone under steady-state current injection in neighboring cones of a network model (Detwiler and Hodgkin, 1979). We calculated values for cones embedded in both a hexagonal and a square array because there is evidence that cones may be coupled to all or to only a few of their surrounding neighbors (Tsukamoto et al., 1992; DeVries et al., 2002; Hornstein et al., 2004). The first step was to calculate the space constant λ, given the cone coupling resistance (r_s), cone input resistance (r_m), and effective cone spacing D as follows:

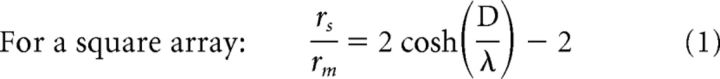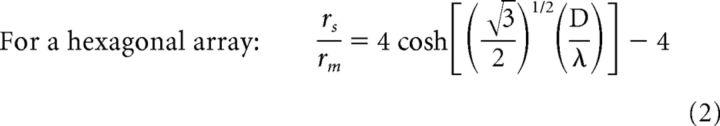For each array type, we solved for λ in units of cone spacing D as follows:

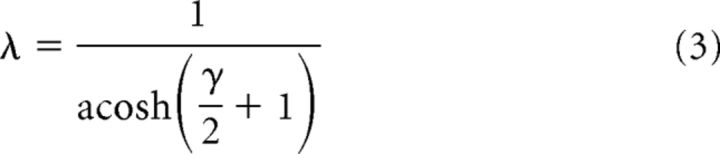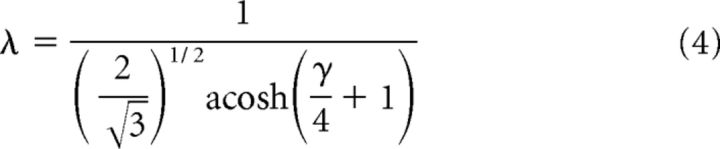where γ = r_s/r_m. In primate cones, r_m is likely to be fairly consistent at ∼100 MΩ, whereas cone coupling conductance (1/r_s) occurs over a wide range (averaging 650 pS). We accommodated this range by computing λ over cone conductances of 400–2400 pS, values reported by Hornstein et al. (2004). For the square array, this yielded a λ of 0.3–0.57, whereas for the hexagonal array, λ was 0.35–0.7. Space constants of <1 suggest that current flow through gap junctions mostly affects cones that are immediate neighbors. Equation 3 was used by prior studies to estimate λ (DeVries et al., 2002; Hornstein et al., 2004).

The second step was to estimate the membrane voltage change for cones with the different values of λ at varying radial distances (r) from a modulated cone as follows:

where i₀ is the injected current at r = 0, and K₀ is the zeroth-order modified Bessel function of the second kind. This formula follows equation 10 in Detwiler and Hodgkin (1979), a continuous-sheet model approximation that they showed slightly overestimates the spread of potential in adjacent cones compared with the network model for values where λ < 1. Because our adapting light is a steady-state condition, the values calculated from Equation 5 provide a percentage change in membrane voltage for cones at various distances r in the network when the background light is turned on at the cone where r = 0. For a cone situated in a network of n surrounding cones of the opposite type (the same type would produce no effect), the total change in voltage (ΔV) would be the following:

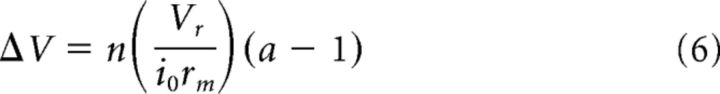where a is the relative activity level in opposite-type cones expected for the adapting background light (∼1.5 in our stimulus conditions; see above). Assuming that the incremental sensitivity of cone photoreceptors adheres to the Weber–Fechner law of adaptation (Schnapf et al., 1990), the effect of electrical coupling on cone thresholds was assumed to be proportional to the relative voltage changes estimated across the range of receptor configurations.

Cone neighborhood analyses.

The influence of local spectral demographics on individual cone sensitivities was first explored by examining the relationship between L and M cone thresholds and the number of directly adjacent, preferentially activated (M/S or L) photoreceptors. For each adaptation condition, the relationship between threshold and local receptor configuration was assessed for data combined from both subjects using linear regression. Preliminary analyses confirmed the slopes of the threshold versus neighborhood fits were statistically indistinguishable between subjects for each adaptation condition (p = 0.687 for L cones; p = 0.647 for M cones). Because our goal was to examine the relative changes in threshold as a function of neighborhood demographics, we minimized any potential differences in overall sensitivity between observers (e.g., due to differences in detection criterion for the yes–no task or variation in preretinal screening of the ocular media) by applying vertical shifts to bring the mean sensitivities of cones in the most common receptor configuration (n = 3 opposite-type neighbors) into alignment before fitting. Data were combined in this fashion for all subsequent neighborhood analyses, with plot axes labeled “Relative threshold” to indicate this normalization.

The relationship between cone threshold and neighborhood was then evaluated more quantitatively and across greater spatial scales by deriving two metrics of local mosaic demographics that incorporated known features of primate H1 and H2 horizontal cells (Dacey et al., 1996; Dacey et al., 2000). The contributions of individual L, M, and S cones to each of the indices described below were computed from their Gaussian-weighted proximities to the cone of interest as follows:

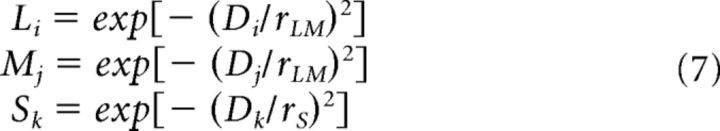where i–k are indices independently identifying L, M, and S cones, respectively; D is the distance to the cone of interest; and r_LM and r_S are the radii of the spatial weighting functions for the two indices, respectively. Specifically, these weighting function radii were defined as the distance from the peak of the weighting function to the point where it reached 37% (i.e., 1/e) of its maximum height (Croner and Kaplan, 1995).

The first neighborhood metric, which we term the H1 opponency index, is inspired by H1 horizontal cells that pool L and M cone signals linearly while avoiding S cone input altogether (Dacey et al., 1996; Dacey et al., 2000). For an L cone in the mosaic, denoted i', the H1 index is calculated as follows:

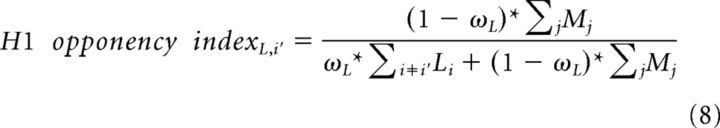where ω_L is the synaptic input weight of L cones to H1 horizontal cells. This metric reflects the proportion of M cones within the local population of L and M cones, thereby representing the fractional drive of M cones to the local H1 network. To calculate the H1 index for an M cone, the summed M cone term in the numerator is exchanged for its L cone counterpart.

Physiological recordings from H2 horizontal cells suggest that these interneurons are driven prominently by S cones. The S-cone input to these cells is approximately equivalent to the summed drive of L and M cones (Dacey et al., 1996) despite comprising only a small fraction of the overall cone population (Curcio et al., 1991; Hofer et al., 2005b). Therefore, if S cones exert any influence on the sensitivity of nearby L and M cones, then one might expect these interactions to occur at a spatial scale similar to H2 horizontal cell anatomy. This hypothesis was assessed by comparing the thresholds of individual L and M cones to a metric representing their spatially weighted proximity to all S cones in the mosaic. For an individual L cone in the mosaic, denoted i', the S cone proximity index is as follows:

where S_k is computed using Eq. 7 and depends solely on the radius, r_S, of the spatial weighting function.

The H1 and S cone proximity weighting function radii (r_LM and r_S, respectively) that best explained the variance observed in L and M cone thresholds were determined independently using nonlinear least-squares fitting. In cases in which both the H1 and S cone proximity indices captured a significant amount of the threshold variance for a particular dataset, multiple regression was used to examine the significance of these predictors operating together in a nested model. A role for spectrally biased connectivity into the H1 network was examined by allowing the H1 index cone weighting parameter (ω_L) to vary freely and testing whether it explained more variance than a restricted model in which the L and M cone weights were constrained to be equal. In all cases, model performance was evaluated using the F test, with p < 0.05 considered statistically significant. All model fitting and statistical analyses were performed using MATLAB (The MathWorks). The spatial scales at which these neighborhood indices best accounted for our data were compared with histological measurements obtained from camera lucida drawings of Golgi-filled human H1 and H2 horizontal cell dendritic fields taken at a similar eccentricity (0.5 mm ≈ 1.6°) (Kolb et al., 1992).

Results

Single-cone sensitivity within the trichromatic cone mosaic

To investigate the effect of local circuitry on a cone's threshold, we took advantage of the nearly random arrangement of L-, M-, and S-wavelength-sensitive cones in the human retina, a consequence of which is that cones of one spectral class will be surrounded by varying numbers of opposite-type receptors (Hofer et al., 2005b). By elevating steady-state activity preferentially in one subset of cones (L or M) with chromatic adapting fields, the degree to which cone signals influence each other at the single-cell scale could be inferred from the relationship between cone thresholds and the local spectral topography. Two-color increment threshold testing is a classic psychophysical method for biasing detection toward spectrally distinct mechanisms in the human visual system (Stiles, 1949, 1959), possibly including the three cone subtypes (Wald, 1964). Before using this approach to probe how signals from individual cones in the central retina might interfere with each other perceptually, we first examined the extent to which its efficacy at isolating cone types is maintained at the cellular level. Figure 1 shows an example of a pair of cones, tested on the same day, in which the perceptual threshold derived from each cone was measured under L- and M-cone-adapting conditions. When M cones were adapted (Fig. 1A–C), Cone 1 exhibited a threshold that fell within the modulation range of the stimulation channel, indicating that it was likely an L cone, whereas the threshold for Cone 2 was >1, exceeding the modulation limit of the stimulation source, making it likely an M cone. When the blue adapting light was turned off, Cone 2 was retested and found to have a threshold within the stimulus range; this control condition eliminates the possibility that Cone 2 was an S cone or possibly dysfunctional. The same pair was then tested under L-cone-adapting conditions (Fig. 1D–F). Here, the threshold behavior was reversed, with Cone 1 now having a threshold >1 and Cone 2 readily measured. These data are consistent with the cone identities made under M cone adaptation. Of a total of 121 tested cones, 92 cones were examined under both adapting scenarios. From those, 58 cones (63%) had thresholds within the modulation range after adapting to one background and fell above the modulation limit (i.e., >1) when measured against the other background, similar to the cones shown in Figure 1. This suggests that cone-targeted microstimulation coupled with differential chromatic adaptation can reveal spectral specificity on the cellular scale, potentially enabling a cone-by-cone functional mapping of the trichromatic mosaic.

To verify independently the psychophysically determined cone identities, we made threshold maps over contiguous portions of the mosaic (Fig. 2A,B,D,E) and compared them with maps generated by absorptance imaging (Fig. 2C,F). Such a comparison requires creating a criterion for converting the threshold values to a spectral type. To do so, the L and M thresholds were compiled into histograms for each adaptation condition (Fig. 2G,H) and a criterion was calculated that maximized the agreement between the densitometric classification and the threshold distribution using Cohen's κ coefficient, a statistic of agreement for categorical data (Cohen, 1968). Cones with thresholds below the criterion were classified as belonging to the ostensibly unadapted class, whereas those with thresholds exceeding the criterion would be classified as belonging to the adapted subset or as S cones (given that stimulus conditions did not permit sufficient light delivery for S cones to register sensitivity). For both L- and M-cone-adapting conditions, we found that individual cone thresholds generally agreed with predictions based on the action spectra of the photopigments that they housed—77% of cones behaved according to type (163/213; Cohen's κ = 0.46; p < 0.001). To rule out misclassification during absorptance imaging as a source of error in our functional assignments of cone type (see Materials and Methods), we examined the effect of excluding cones with densitometric assignment probabilities below a confidence value on the observed agreement between the objective and psychophysical classification approaches (Fig. 2I). The agreement between classifications was relatively unchanged over almost the entire range of densitometric confidence values, suggesting that agreement was robust in the face of densitometric errors. Together, these data demonstrate that psychophysical performance linked to specific cone types can be probed readily on an individual photoreceptor basis.

Figure 2.

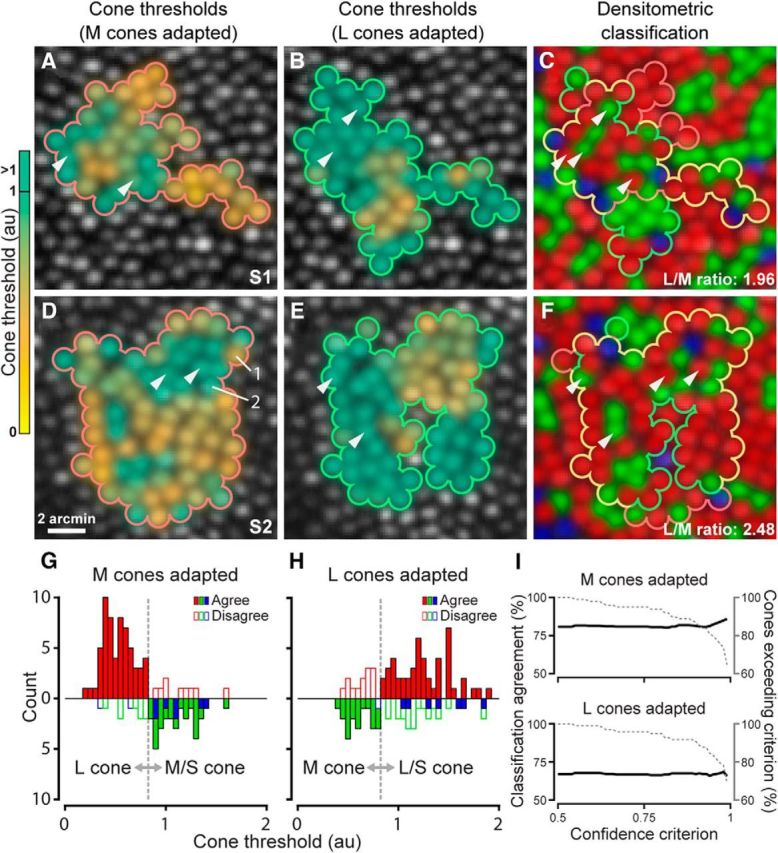
Cone threshold maps are spectral-type specific but less punctate than the cone mosaic topography. A, Threshold maps for cones tested under M cone adaptation in Subject 1. Color code indicates the average threshold of each cone. White arrowheads mark example L cones surrounded by three or more M/S cones (cf. A,C); these cones exhibited higher-than-average thresholds. B, Cone array tested during L cone adaptation. White arrowheads mark example M cones with high thresholds that had at least four spectrally unlike neighboring cones. C, L (red), M (green), and S (blue) cone photoreceptor mosaic for Subject 1 (eccentricity = 1.5°) classified by densitometry. Cones tested in A and B during M (710 nm test) or L cone adaptation (543 nm test) are outlined in red and green, respectively, and in yellow for both conditions. D–F, Cone threshold and densitometry data for Subject 2; otherwise as in A–C. Cones 1 and 2 from Figure 1 are shown in D. Scale bar applies to all maps. G, H, Histograms of cone thresholds collected against M- or L-cone adapting backgrounds; subject data are combined. Densitometric identities are plotted up for L cones and down for M/S cones. A classification criterion (gray dashed line) delineated cones belonging to the classes differentiated by the perceptual task (see text). Filled color bars are cones behaving according to their spectral type; white filled bars are cones performing against type. I, Cone classification agreement as a function of densitometry assignment confidence for M (top) and L cone adaptation (bottom). Black lines show the percentage agreement computed for cones with densitometry assignment confidence (see Materials and Methods) that equaled or exceeded the abscissa value (dashed line represents percentage exceeding confidence criterion).

Spatial and spectral patterns of cone interactions

As evident in Figure 2, the cell-by-cell specificity of sensitivity across the mosaic was less pronounced than would be expected if detection were governed solely by the spectral sensitivity of each targeted cone; if this were the case, then one would predict little threshold variability within each cone class. Instead, we observed substantial within-class variability during both L and M cone adaptation (Fig. 2G,H), including a number of receptors exhibiting wholesale deviations from predictions based on their spectral identities determined from absorptance imaging. Errors in densitometric assignments have already been ruled out as a primary cause of the spectral disagreement (Fig. 2I), suggesting that variability in thresholds for a given spectral type arises from another source.

Under adapting conditions in which steady-state activity is elevated preferentially for one spectral type, sensitivity of a cone may depend on the feedback inhibition from cones in its immediate surroundings. To test the hypothesis that the threshold measured in a given cone might be influenced by the spectral makeup of its neighborhood, threshold data for all cones in the class less sensitive to the background (L or M) were binned according to the number of directly adjacent preferentially activated cones (M/S or L, depending on the conditions). We found that the sensitivity of cones belonging to the same spectral class varied systematically with the number of opposite-type (i.e., activated) neighbors in their immediate vicinity. The magnitude of this effect was similar across the two test conditions (Fig. 3; L cones: slope = 0.10; r² = 0.23; p < 0.001; M cones: slope = 0.09; r² = 0.14; p = 0.023). For instance, measured against a long-wavelength background, an M cone surrounded by six L cones was more likely to have a higher threshold than an M cone situated in a more homogeneous patch of retina. This neighborhood effect appears to raise thresholds in a subset of cones in a predictable fashion and thus increases the variability in thresholds obtained from each cone population.

Figure 3.

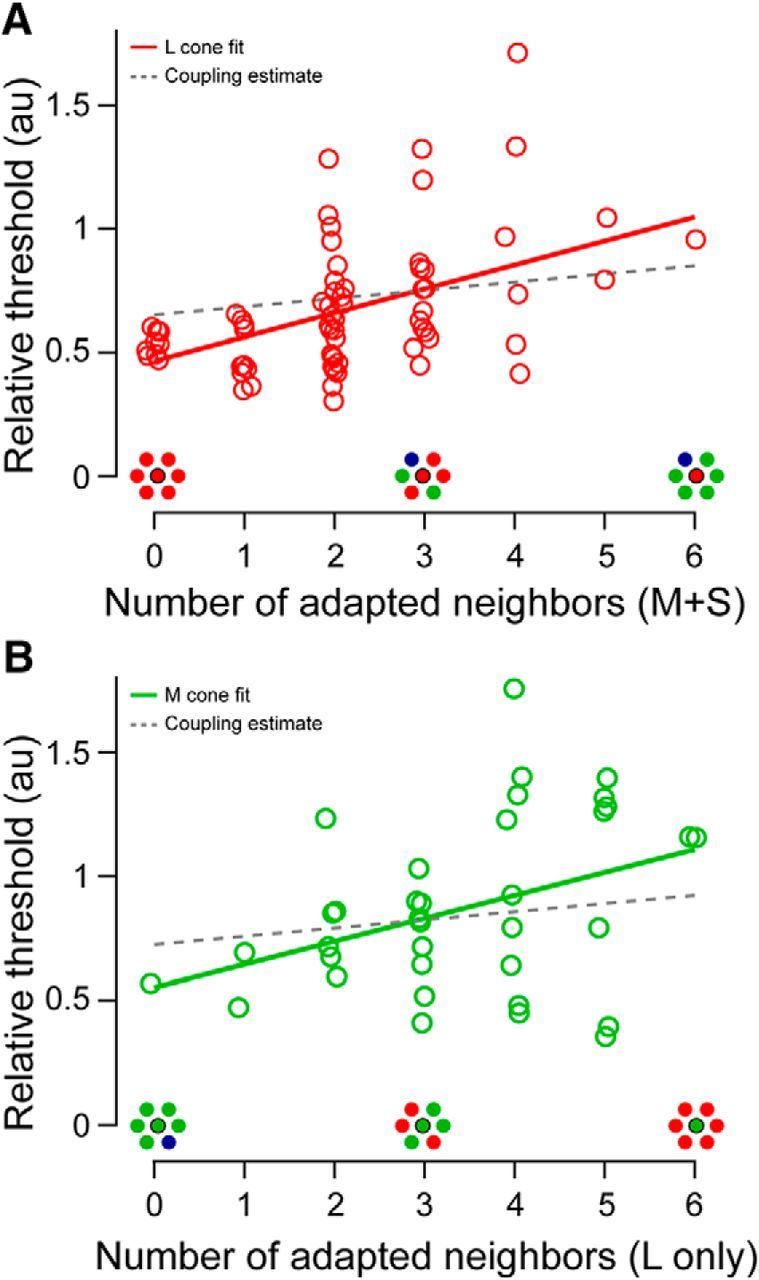
Relationship between cone thresholds and spectral demographics of neighboring cones. A, L cone thresholds measured against a short-wavelength background increase with each additional preferentially activated (M or S) neighboring cone. Data from S1 and S2 are combined as described in the text. Solid line is a linear regression to the data (slope = 0.10; r² = 0.23; p < 0.001). Dashed line is the maximum estimated neighborhood effect resulting from electrical coupling between all adjacent cones (coupling slope = 0.033, corresponding to a 3.3% increase in baseline activity per opposite-type neighbor; see Materials and Methods). B, M cone threshold data analyzed as in A measured against a long-wavelength background. Thresholds also increased as the cone neighborhood became more spectrally opponent (slope = 0.09; r² = 0.14; p = 0.023).

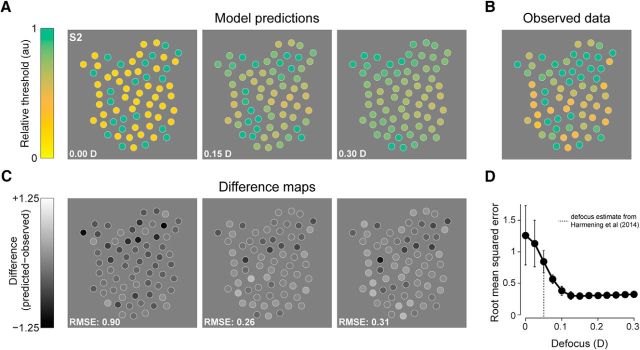
We considered two mechanisms that might explain this effect, but found that both can be ruled out. First, we investigated whether uncorrected defocus in our stimulation light could account for the systematic rise in threshold. If the stimulus light was distributed across multiple rather than single receptors, then the threshold attributed to the targeted cone would depend on the average sensitivity of its local neighborhood. An optical model of light capture in the cone mosaic, developed previously to account for the spatial grain of achromatic sensitivity in the parafovea (Harmening et al., 2014), confirmed that the observed threshold elevation would be governed only in small part by the spatial spread in our stimulus (Fig. 4). Undetected stimulus spread equivalent to 0.15 D of defocus was required to minimize the error between the observed and predicted data (Fig. 4D). This value is threefold higher than that estimated from an independent psychophysical experiment performed on the same stimulation platform and with the same subjects (Harmening et al., 2014). In confocal imaging systems, axial and lateral resolution degrades quickly with increasing defocus, compromising image quality. Because retinal videos were monitored continuously and recorded during stimulus presentation, a blur of that magnitude is unlikely to have occurred during our experiments.

Figure 4.

Residual stimulus blur does not account for cone detection variability. A, 2D sensitivity maps predicted by a model of light capture in the cone mosaic of Subject 2 (see Materials and Methods) computed using the expected sensitivities of the three cone classes during M cone adaptation. The defocus values indicated in each panel (given in diopters, D) are those incorporated into the stimulus to estimate the effects of poor spatial control of our test probe. Spatial variation in thresholds becomes smaller with increasingly blurred stimuli. B, Measured thresholds from Figure 2D are replotted here for comparison with the model predictions. C, Difference plots for the maps in A and B. Darker spots correspond to cones with sensitivity that is lower than the model prediction. Root mean squared errors (RMSEs) are computed from the difference maps to assess model performance. D, Average RMSE from the four datasets shown in Figure 2 (2 subjects × 2 adaptation conditions) plotted as a function of stimulus defocus in diopters. Error bars = ±1 SD. The RMSE asymptotes near 0.15 D, ∼3 times higher than previous estimates of residual defocus for AO stimulation (0.05 diopters; dashed line; Harmening et al., 2014), suggesting that threshold variation cannot be attributed solely to optical defocus.

Second, cones coupled by gap junctions may underpin a neighborhood effect (Hsu et al., 2000). Against chromatic backgrounds, thresholds would be altered only if the surrounding cones were of the opposite type than the targeted cone. We estimated the magnitude of this effect based on cone coupling data recorded in macaque retina (Hornstein et al., 2004) using a network model (Detwiler and Hodgkin, 1979). The electrotonic space constant of this network falls between 0.3 and 0.7 cone spacings (see Materials and Methods), suggesting that only the nearest cones would affect threshold substantially, as was found previously (DeVries et al., 2002; Hornstein et al., 2004). For a fully connected hexagonal array, this range of space constants yielded voltage changes in neighboring cones that were 3.2–6.6% of the voltage shift due to the adapting light directly (Eq. 5). In the limit at which all 6 adjacent cones are coupled to the test cone and belonged to the class driven ∼1.5× more strongly by the background (as in our data; see Materials and Methods), the activity of the central cone would be increased by, at most, 20%. This is akin to increasing the effective background intensity by the same factor. The corresponding increase in cone threshold would be governed by the Weber–Fechner relationship (ΔI/I = constant), leading to thresholds for a cone surrounded by six adapted cones to be 20% higher than a cone situated in a homogenous patch. With fewer adapted, coupled cones in the surround, the effect would be smaller. Therefore, gap junctional coupling could account for only a small fraction of the ∼100% threshold increase across the photoreceptor configurations as plotted in Figure 3.

If this neighborhood effect has a postreceptoral origin, then the most likely mediators are horizontal cells, retinal interneurons known to convey spatially antagonistic signals to cones. Primate retina contains two types of horizontal cells: H1 cells, which receive equivalent functional input from L and M cones while avoiding S cones, and H2 cells, which receive strong input from the sparsely distributed S cones as well as modest input from L and M cones (Dacey et al., 1996; Dacey et al., 2000). Because each cone in the receptor mosaic synapses onto multiple H1 and H2 cells (Wässle et al., 2000), the elevated steady-state activity created by the prolonged adapting field in one subset of cones (Normann and Perlman, 1979; Schnapf et al., 1990) may spread through one or both of these horizontal cell networks to suppress the sensitivity of nearby receptors driven less strongly by the adapting wavelength.

To examine this potential role for horizontal cells, we developed two metrics of cone neighborhood spectral demographics that incorporated known features of H1 and H2 cells (Fig. 5A; see Materials and Methods). These indices were computed for each cone in our subjects' mosaics using the actual cone maps, taking into account the distribution of receptor configurations encountered (Fig. 3). Figure 5B illustrates the effect of changing the spatial weighting function radius on the relationship between cone thresholds and the H1 and S cone proximity indices. Both L and M cone data (measured against short- and long-wavelength adapting fields, respectively) were best explained by H1 indices computed across a short spatial dimension—a scale essentially restricted to the test cone and its immediate neighbors (Fig. 5B, top left). The optimal H1 weighting function radius was 4.91 μm for L cones (r² = 0.24; F = 11.0; p < 0.001) and 7.78 μm for M cones (r² = 0.17; F = 3.73; p = 0.035). This scale is consistent with the trends observed in Figure 3 and is within a few micrometers of the dendritic field dimensions of human H1 cells (∼9 μm radius) at the eccentricity tested here (Fig. 5C; Kolb et al., 1992). For comparison, the average spacing between cones at this eccentricity was ∼5.8 μm (1.16 arcmin, assuming 60 arcmin = 300 μm). Allowing the relative weights of L and M cones into the H1 index to vary freely did not outperform a model in which individual L and M cone input weights were constrained to be equal (L cone data: F = 0.384, p = 0.538; M cone data: F = 2.08, p = 0.159). Enlarging the H1-weighting function radius (Fig. 5B, top right) increases the contribution of more distant cones to the computed index until, eventually, enough receptors are included that the indices for L and M cones coalesce around abscissa values that reflect the subject's global L:M ratio. As a result, the H1 opponency index explains less threshold variance when used over larger spatial scales.

Figure 5.

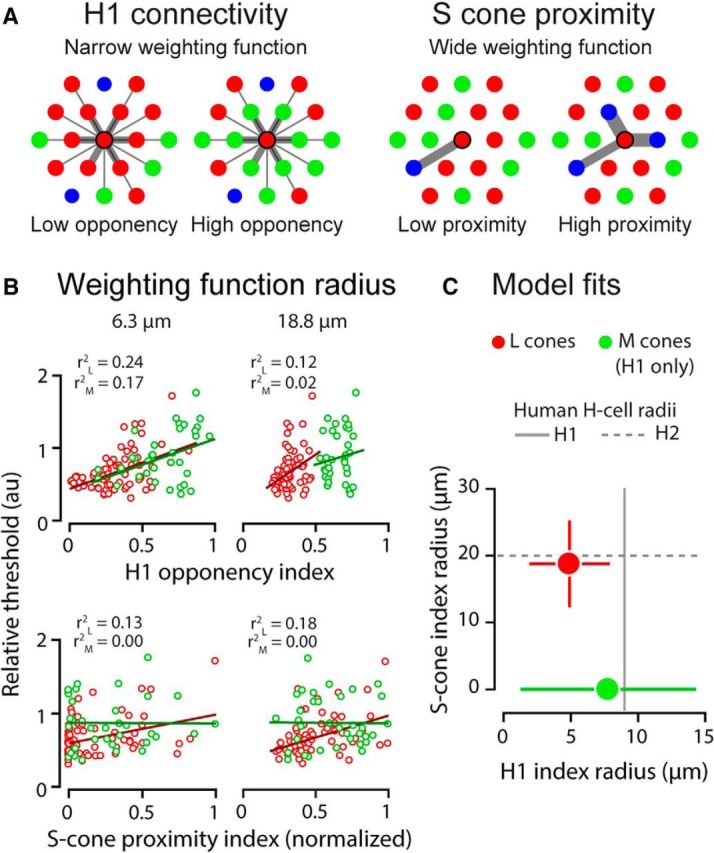
Preferentially activated neighbors influence single-cone thresholds at a spatial scale consistent with human horizontal cell anatomy. A, Schema of H1 and S cone proximity indices. In these examples, the neighborhood indices are computed for the central L cone in each cluster. Each neighboring cone's contribution to the index is weighted by its proximity to the central cone (width of connectivity lines). For model details, see Materials and Methods. B, L and M cone thresholds plotted as a function of H1 and S-cone proximity indices computed independently for two example radii. Data and regression fits in red are for L cones, those in green are for M cones. C, Optimal H1 and S cone proximity weighting function radii for L and M cone threshold data (red and green circles, respectively). M cone marker is placed at y = 0 because S cone proximity had no effect on thresholds obtained against a long wavelength background. Error bars represent the 95% confidence intervals of the fitted parameters. These radii closely match human H1 and H2 horizontal cell dendritic field dimensions (solid and dashed gray lines, respectively) measured histologically at the same eccentricity (Kolb et al., 1992).

We also examined the effect of S cone proximity alone on L and M cone thresholds. For L cones measured against a 470 nm background, thresholds were best predicted by an S cone proximity index computed using a radius of 18.8 μm (Fig. 5B, bottom right; r² = 0.18; F = 8.82; p < 0.001), a scale similar to the morphology of H2 horizontal cells that receive robust S cone input (Fig. 5C; Kolb et al., 1992). In contrast, S cone proximity exerted no influence on M cone thresholds obtained against a 710 nm background (Fig. 5B, bottom; optimal radius: 34.4 μm; r² = 0.002; F = 0.04; p = 0.964), a predictable outcome given that S cones were not activated by the stimulating or background wavelengths (Stockman et al., 1999).

Finally, because each L cone in the mosaic is connected to both the H1 and H2 cell networks, it is possible the lateral interactions that we observed could be best explained by both circuits operating interdependently at distinct spatial scales. With this in mind, we used multiple regression to examine the relative effects of the H1 and S cone proximity indices on L cone thresholds. Incorporating the H1 and S cone proximity indices into a multiple regression model accounts for 23% more of the variance in L cone thresholds. Nested model testing confirmed that including the S cone term improves model performance relative to the H1 term alone (r² = 0.294; F = 4.31; p = 0.042). Together, these results suggest that cone thresholds are influenced by activity in neighboring cones and that this influence can be mediated by both H1 and H2 cells.

Discussion

Color vision in humans hinges on two key features of the visual system. First, a trichromatic array of photoreceptors samples the retinal image, transducing incident photons into neural signals. Next, the chromatic information encoded in the cone signals is extracted by neural machinery capable of monitoring the relative activity of the three receptor types (Solomon and Lennie, 2007). We used AO microstimulation (Fig. 1) to examine the link between detection thresholds and the cellular topography of the L, M, and S cones in the human parafovea, obtaining maps of single-cone sensitivity that not only reflect the peak spectral sensitivity of the underlying mosaic of cone pigments, but also reveal cellular scale spatial interactions that could have implications for the postreceptoral circuitry involved in color signaling. Our results build upon recent work in which single-cone stimulation is used to elucidate how the cellular architecture of the photoreceptor mosaic shapes vision (Harmening et al., 2014; Bruce et al., 2015; Sabesan et al., 2016; Sincich et al., 2016).

Relatively little was known about the packing arrangement of the three primate cone types until the advent of AO densitometry (Roorda and Williams, 1999; Hofer et al., 2005b). Although the primary findings from these studies—that L and M cones exist in varying proportions and degrees of random arrangement among color-normal subjects—were consistent with observations obtained using either in vitro (Mollon and Bowmaker, 1992) or indirect (Rushton and Baker, 1964; Cicerone and Nerger, 1989; Carroll et al., 2000) methods, the densitometric technique has yet to be corroborated at the cellular scale. Such an effort is needed because the photoreceptor topographies yielded by this approach undergird a number of theories related to color vision, ranging from hypotheses about the principles guiding cone mosaic development (Deeb, 2006; Knoblauch et al., 2006) to models of how the visual system constructs spatiochromatic percepts from the ambiguous outputs of individual cones (Hofer et al., 2005a; Brainard et al., 2008; Sabesan et al., 2016).

The good agreement between our single-cone psychophysical assignments of spectral type and their biophysical counterparts provides the first independent validation of AO densitometry undertaken at the cellular level. Measured against chromatic backgrounds, single-cone thresholds for L and M photoreceptors (as defined by densitometry) shifted, on average, in predictable directions (Fig. 2G,H). Nevertheless, the agreement that we observed between the two classification approaches was not perfect, a result that could be attributed to a number of factors. For instance, densitometric misclassifications would place an upper limit on the agreement between the two techniques. The assignment uncertainty estimated in previous densitometry studies hovers around 5% (Hofer et al., 2005b; Sabesan et al., 2015). It has been suggested this error arises primarily from optical blur and cone reflectance variability during absorptance imaging. This error may result in a mosaic with artificially clumped patches of like-type cones (Hofer et al., 2005b). If errors of this sort were influencing our data, then one might expect that cones performing against densitometric type would feature low assignment probabilities and be situated in spectrally homogenous clusters. Our data are inconsistent with both of these predictions: excluding low-confidence cones failed to improve classification agreement (Fig. 2I) and functionally idiosyncratic cones tended to reside in spectrally opponent cone neighborhoods (Fig. 3).

Instead, our results suggest that a cone's sensitivity to briefly flashed stimuli depends not only on its endogenous photopigment, but also on the steady-state activity in nearby receptors. For both L and M cones, thresholds were elevated systematically with the addition of each opposite-type neighbor with a baseline activity that was increased by the chromatic background (Fig. 3). The neighborhood effects that we measured exceeded the elevation estimated by a model of light spread in our AO-corrected stimulus (Fig. 4; Harmening et al., 2014), consistent with previous demonstrations that the resolution achievable with AO is sufficient to probe vision at the scale of single cones (Makous et al., 2006; Sincich et al., 2009; Rossi and Roorda, 2010; Ratnam et al., 2017).

Having ruled out an exclusively optical explanation, our results point toward a neural basis for the photoreceptor interactions that we observed. The relationship evident in Figure 3 demonstrates that sensitivity under conditions in which steady-state activity is biased toward either L or M cones is governed by the local L–M ratio, implying that the neural mediator of these interactions assimilates L and M cone signals indiscriminately. Horizontal cells, a first-order source of lateral inhibition, fulfill this criterion, with anatomical and physiological evidence suggesting that they contact all L and M cones residing within their dendritic fields (Wässle et al., 1989; Dacey et al., 1996; Dacey et al., 2000). Accordingly, we created spatially weighted metrics of cone neighborhood demographics that incorporated known properties of peripheral H1 and H2 cells. The spatial scales at which these opponency indices best accounted for the threshold data were close to the dimensions of horizontal cell dendritic fields in the human parafovea (Fig. 5).

Although this finding supports a role for horizontal cells in mediating the interactions that we observed, it is worth considering a few alternative routes for the lateral spread of steady-state photoreceptor activity. First, individual primate L and M cones couple capriciously with some, but not all, of their adjacent neighbors via gap junctions (Hornstein et al., 2004). Gap junction-mediated signal transfer is confined to the central cone and its immediate neighbors (DeVries et al., 2002). However, the neighborhood effect was too large to be explained by gap junction coupling between cones because we estimated that the voltage spread would shift thresholds by, at most, only a few percentage points for each coupled cone under our stimulus conditions. Moreover, the suppressive influence of S cone proximity on L cone thresholds (operating at a scale spanning multiple cones and consistent with the anatomy of H2 cells) could not be mediated by gap junctions because S cones are not electrically coupled with L or M cones (Hornstein et al., 2004). Second, it is also possible that lateral inhibition occurring in the inner retina, mediated by amacrine cells, could account for our data. Like horizontal cells, amacrine cells do not appear to distinguish between L and M cones (Calkins and Sterling, 1996), but recent histochemical and physiological evidence suggests that these interneurons may play less of a role in shaping cone-driven signals in the central retina than was thought previously (Sinha et al., 2017).

Our results suggest that adapting signals pool spatially across neighboring parafoveal cones and thus have implications for mechanisms of sensitivity regulation in the retina. Previous investigations have shown that adaptational processes operate at multiple spatial and temporal scales, as well as at different stages of the visual pathway (Hood, 1998; Dunn et al., 2007). Rapid cone-driven adaptation appears to be highly localized, likely confined to individual photoreceptors (MacLeod et al., 1992; Lee et al., 1999). Conversely, over a longer time course (>10 s), a second mechanism of sensitivity regulation appears to be present (Hayhoe et al., 1992), one that would be engaged by our prolonged adapting field to yield an inhibitory effect. Analysis of in vitro physiological recordings suggests that horizontal cells are capable of mediating this type of slow, spatially expansive feedback (van Hateren, 2007; Zhang et al., 2011).

Pooling across a modest number of photoreceptors would reduce noise and improve the fidelity of the adapting signal (Rieke and Rudd, 2009), but it is not clear what the cost of averaging across cone classes would be for color vision. Indiscriminate mixing of signals from adjacent L and M cones could reduce chromatic discrimination by effectively reducing the differences in their spectral sensitivities (Hsu et al., 2000; Hornstein et al., 2004), though this effect might be mitigated by the clumpy arrangement of the trichromatic cone mosaic (Hofer et al., 2005b). Spectral blurring across these small spatial scales would be consistent with the relatively lower spatial resolution of the chromatic pathways (Mullen, 1985; Sekiguchi et al., 1993). Such a scheme is also compatible with the recent finding that tiny monochromatic flashes presented to individual parafoveal cones in mixed neighborhoods predominately elicited achromatic percepts, whereas stimuli delivered to clusters of like-type cones tended to produce hue senstations (Sabesan et al., 2016).

Our visual world is rich with spectral information, but if hues are to be finely discriminated, then cone-specific circuitry must exist at some stage of the visual system. In the S cone pathway, cone-selective wiring emerges in the retina, where short-wavelength receptor signals are transmitted predominantly through a retinogeniculate circuit implicated in blue–yellow color vision (Mariani, 1984; Dacey and Lee, 1994; Dacey et al., 1996; Martin et al., 1997; Chichilnisky and Baylor, 1999; Field et al., 2007; Crook et al., 2009). Whether the L and M cone signals that underlie red–green color vision are similarly partitioned in the central retinal circuitry has remained a less tractable problem, with recordings from downstream neurons yielding equivocal results (Reid and Shapley, 1992, 2002; Diller et al., 2004; Buzás et al., 2006). Our results are consistent with the interpretation that parafoveal L and M cones feed into the surround-forming circuitry indiscriminately, similar to the wiring patterns observed in peripheral ganglion cells (Field et al., 2010), thereby shifting the burden of separating L and M cone signals to higher visual areas, which may achieve this feat using the statistics of L and M cone responses to natural stimuli (Wachtler et al., 2007; Brainard et al., 2008; Benson et al., 2014).