Sample size, statistical power, and false conclusions in infant looking-time research

Abstract

Infant research is hard. It is difficult, expensive, and time consuming to identify, recruit and test infants. As a result, ours is a field of small sample sizes. Many studies using infant looking time as a measure have samples of 8 to 12 infants per cell, and studies with more than 24 infants per cell are uncommon. This paper examines the effect of such sample sizes on statistical power and the conclusions drawn from infant looking time research. An examination of the state of the current literature suggests that most published looking time studies have low power, which leads in the long run to an increase in both false positive and false negative results. Three data sets with large samples (>30 infants) were used to simulate experiments with smaller sample sizes; 1000 random subsamples of 8, 12, 16, 20, and 24 infants from the overall samples were selected, making it possible to examine the systematic effect of sample size on the results. This approach revealed that despite clear results with the original large samples, the results with smaller subsamples were highly variable, yielding both false positive and false negative outcomes. Finally, a number of emerging possible solutions are discussed.

There has been much discussion in the scientific literature broadly, and increasingly in the psychological literature in particular, about whether or not there exists a replication crisis in science (Crandall & Sherman, 2016; Open Science Collaboration, 2015; Pashler & Harris, 2012; Stroebe & Strack, 2014). Although it is debated whether the problem has arisen to the level of a crisis, one outcome of this discussion is an increased awareness of the effect of conventional scientific practices on the conclusions we draw from our studies. One area that has received attention is the effect of less-than-optimal sample sizes on false positive and false negative conclusions (Button et al., 2013; Fraley & Vazire, 2014; Schweizer & Furley, 2016; Vadillo, Konstantinidis, & Shanks, 2015). This is particularly an issue in fields or areas of inquiry in which subject populations are difficult to identify or recruit, or in which the testing of individual subjects is time consuming and expensive. Research involving infants as participants fits these criteria, and thus it is important to carefully consider how sample sizes are established and whether our current conventions should be adjusted.

There have been discussions and debate about the issue of sample sizes in science broadly, and how decisions about sample size contribute to statistical power (see, e.g., Desmond & Glover, 2002). Button et al. (2013), for example, examined the effect of low powered studies on the field of neuroscience. They argue for changes in research practices to deal with low power, arguing that this is important for drawing strong conclusions from studies. Low power not only reduces the sensitivity to detect true differences, it also increases the likelihood of observing a false positive result (as a result of the bias to publish significant effects). Thus, studies with low power not only create the problem of having difficulty interpreting nonsignificant small effects, but also increase the proportion of studies in which a spurious effect is taken to reflect the truth.

That is, it is not often recognized that sample size—and statistical power—directly relate to the likelihood of making both Type 1 and Type 2 errors. By convention, we select our Type 1 error rate (e.g., the likelihood of concluding falsely that a difference exists) as 5%—or p = .05. We select our Type 2 error rate (e.g., the likelihood of failing to detect a true difference) as 20%–or power of .80. However, we rarely consider how factors, such as sample size, influence these rates. Moreover, although our estimates of power appear to be independent of our Type 1 error rate, in reality p values are much more variable (and less reliable) with low power (Halsey, Curran-Everett, Vowler, & Drummond, 2015), and p-values get smaller with increased sample size (Motulsky, 2015).

It would be unproductive to insist that all studies have very large sample sizes. Power and p-value depends both on the size of the effect and the sample size. If the true effect is large, a smaller sample would provide sufficient power to detect that effect. Moreover, power analyses are imperfect and requiring large samples may make it impossible for some research to be conducted at all (Bacchetti, 2013). More controversial is the possibility that extremely large samples may yield many statistically significant but very small effects that are not meaningful (Quinlan, 2013). Thus, it is important to not only consider the sample size, but also the effect size.

It is also to point out that studies with small sample sizes (and lower power) can be an important part of scientific discovery, and it is critical that we not abandon or reject all studies with low power. But, it is clear that researchers must carefully consider the implications of target sample sizes, both for the time and expense of conducting research and for the conclusions that can be drawn from the study once the target sample has been obtained. The bottom line message here is that it is important that a field not depend exclusively on studies with small samples, and that research with small samples be considered in the context of a larger body of research.

The discussion of small samples and underpowered studies is particularly relevant to the study of infant development. Infant research is hard. Many variables can affect our measurement and our conclusions—we must identify and use reliable and valid measures, develop sensitive measurement procedures, train and maintain well trained experimenters. Problems in any of these will influence our measurement and may cause us to draw an incorrect conclusion. Another source of difficulty is the ability to recruit adequate samples of infant subjects. Ain other areas of research with specialized populations or expensive and highly technical methods, it can be difficult, time consuming, and expensive to identify, recruit, and test a large number of infant research participants. As a result, researchers examining infant development often opt for testing as few infants as possible per cell or condition. In this demonstration, I focus on studies with infants using looking time as the dependent measure. I focus on these studies because they are widely used across many areas of infant development, they have been in use for decades (and thus standards and conventions are well established), and because of the relative ease of use, these methods are likely to continue to be a primary way of assessing infant development. To be clear, the specific conclusions drawn here about power levels and conventional sample size can only be directly applied to research using these methods; but the general conclusions about the relations between power, sample size, and conclusions can be applied to other methods.

Standards and conventions have evolved such that most published research using infant looking time is conducted with 8 to 24 infants per cell (see later section). However, it is not clear that these sample sizes were chosen on the basis of formal power analyses, nor it is clear that these sample sizes provide sufficient power to test the hypotheses under study. It might seem that only large and robust effects would be significant in studies with low power, and so we should have even more confidence in results from such studies (see Friston, 2012). However, given the bias to publish significant results and not non-significant results, low power actually increases the proportion of false positive results across the field (see later section).

The goal of this paper is to evaluate sample sizes in infant research by undertaking a careful consideration of looking time research. In this context, I will delineate the effect of those sample sizes on effect sizes, statistical power, and the incidence of false positive and false negative conclusions in the literature. Several caveats must be made. First, the goal is not to advocate only for very large samples—this would eliminate much of the important work in infant development, and would mean that only some researchers could contribute to this field (and there is some concern about over-powered studies, see Friston, 2012; Quinlan, 2013). Rather, this paper is intended to inspire discussion within labs, among researchers, and across the field about the consequences of the decisions we make, how to best decide on what samples we should use, and about alternative approaches to data collection and analysis.

Second, although for simplicity I focus here on a relatively narrow set of studies from a methodological standpoint (i.e., only studies that measured infant looking time), the message here is not only about how to improve research using this method. Instead, the present discussion about these issues in a very well constrained problem provides a model for thinking about sample size, statistical power, and conclusions more broadly.

Finally, the goal is to provide a starting point for changing conventions, and for setting standards for reporting and interpreting results. The bottom line is that we should be considering not only p-values, but also effect sizes and power when drawing conclusions from our research (Fraley & Vazire, 2014).

The paper includes three sections. The first section is a discussion of the influence of sample size on statistical power in infant research. This is not a mathematical discussion of power, or a discussion of different ways to calculate power—there are other good sources for that information (J. Cohen, 1992; Halsey et al., 2015; Krzywinski & Altman, 2013). Rather, this section focuses on broader conceptual issues, discussing how low powered studies might impact the field of infant development in non-obvious ways. The second section is a description of the state of the field with respect to power and samples size in infant looking-time studies. In this section, 70 papers are reviewed, examining the power and sample size for a single effect reported in each paper (typically the first or main statistical test reported for the first experiment in the paper). The goal of this description is to demonstrate that sample sizes in this field are determined by convention rather than by formal estimates of power. Although the main conclusion from this section is that infant looking time studies have low power, the goal is not to cast doubt on the conclusions from this body of work. Indeed, the assumption is that many reported studies provide an accurate understanding of infants’ development. Rather, the goal is to describe common practices in the field as a starting point for a discussion of how the field might evolve in beneficial ways, and ways that would allow more confidence about the reproducibility of reported findings as well as in the conclusions we draw from our reported results.

In the final section, three example data sets are explored to establish the influence of sample size on the conclusions that are drawn from a given study. All three data sets were collect in my lab and are relatively large for this field (> 30 infants per cell). The large numbers of infants included in these data sets provide the opportunity to examine how the results would vary as a function of sample size. Specifically, by randomly drawing subsamples of different sizes from these larger samples, we simulate experiments with smaller samples, and can directly see what effect the sample size would have on the conclusions that could be drawn.

Sample size and infant research

Our understanding of infant development was dramatically altered by the development of looking time measures by Robert Fantz in the 1950s and 1960s (Fantz, 1958, 1963, 1964). Adapting methods developed for use with chimpanzees, Fantz demonstrated that young infants’ looking behavior is systematically related to sensory and cognitive factors. Fantz’s first studies demonstrated that infants prefer to look at patterned stimuli than at unpatterned stimuli (Fantz, 1958, 1963), and that early preferences were for stimuli that resembled human faces (Fantz & Nevis, 1967). Although these revelations seem modest now, this early worked opened the door for the study of cognitive and perceptual abilities in infants, and led the way to the current state of the field in which we use looking time to draw conclusions about infants’ perception of emotions (Peltola, Leppänen, Palokangas, & Hietanen, 2008; Young-Browne, Rosenfeld, & Horowitz, 1977), theory of mind (Onishi & Baillargeon, 2005), understanding of physical relations (Muentener & Carey, 2010; Spelke, Breinlinger, Macomber, & Jacobson, 1992), categorization (Oakes & Ribar, 2005), word learning (Graf Estes, Evans, Alibali, & Saffran, 2007), and much, much more.

Despite the advances that have allowed us to dig deeper into infants’ developing abilities, there are many challenges to conducting infant work. In addition to the problem of working with uncooperative subjects who have few motor or voluntary abilities (e.g., we can’t ask them to fill out a questionnaire or complete a task on a computer), infant researchers must identify a pool of potential research participants, effectively recruit participants from that pool, and maintain a lab with trained personnel to conduct the studies. Each of these tasks is time consuming, expensive, and difficult. Few infant researchers feel awash with data. Many researchers struggle to test enough infants to meet their goals at critical career points, such a completing a dissertation, conducting a body of work substantial enough to be awarded tenure, or making sufficient progress on a grant-funded project to be awarded a renewal.

An informal poll of the members of the International Congress for Infant Studies (via the listserv) in September 2016 revealed a significant amount of variability in the rate at which infant researchers can collect data. Some researchers indicated that it was impossible for them to recruit infant research participants and they had given up on testing infants altogether. Other labs reported being quite productive, testing 20 to 40 infants per week. However, to test large numbers of infants, a lab will simultaneously test infants of different ages and conduct several studies—often a lab is conducting 10 or more studies simultaneously. Indeed, although one lab indicated that a single experiment could be completed in a month, the most productive labs generally indicated that takes at least 3 and often 6 months to complete a single experiment. Many researchers reported that they could test 10 infants (or fewer) in a given week (typically by recruiting multiple ages at once). These researchers feel lucky if they can accumulate data from 300 to 400 infants in a year, divided among many different studies. Even when the acquisition rate is low, labs are running several studies simultaneously and testing infants of several different ages. Given attrition, pilot testing, and other factors, this means that it may take many months to complete a single experiment even when sample sizes are low. Indeed, some researchers indicated that data collection for a single experiment can take a year or more. Because many papers include the data from multiple experiments, researchers must often collect data for over a year to complete the data collection for a single paper.

As a result of these difficulties, we are a field that values effects observed with relatively small samples. In 2014, Wally Dixon conducted a survey of researchers in child development, asking them to endorse papers published since 1960 that were important, revolutionary, fascinating, or controversial. He published in SRCD Developments (the newsletter of the Society for Research in Child Development), a series of articles reporting these results in a series of the “Twenty most _________ studies in child psychology” lists— the 20 most important, revolutionary, fascinating, and controversial studies. Several infant looking time studies appeared on these lists, in particular Baillargeon (1987), Baillargeon et al. (1985), Hamlin et al. (2007), Onishi and Baillargeon (2005), Saffran et al. (1996), and Wynn (1992). Clearly this is not an exhaustive list of all infant looking time studies, and many other studies have had a significant impact on the field. However, given that these papers were identified as controversial, fascinating, important, and/or revolutionary, these studies have clearly had a significant impact. The sample sizes in these studies ranged from 12 per cell (Baillargeon, 1987; Hamlin et al., 2007) to 24 per cell (Saffran et al., 1996). These papers were published in top journals, have been widely cited, and have been the source of considerable discussion and debate in the field.

These studies illustrate the range of sample sizes of highly visible, influential studies of infant looking. If the field has relied on rules of thumb and convention to determine sample sizes, researchers will rely on studies like those in the previous paragraph to provide a standard for target sample sizes. Indeed, as described in the review of the recent literature described in the next section, these are the samples sizes that are most commonly used in infant looking studies.

However, relying on convention and rules of thumb—rather than formal power analyses—to determine sample sizes can result in studies with low power. It is well understood that this may be a problem for detecting a true effect—that is, lower power by definition means lower likelihood that a real effect will be statistically significant. Counterintuitively, however, low power also decreases the likelihood that significant effects are true effects (Button et al., 2013). In other words, the proportion of published results with significant effects that reflect true effects will be lower if we decrease the probability that studies with true effects are significant. To make this more concrete imagine that 200 studies are conducted. Let’s further assume that in 100 of these studies the null hypothesis is true and in the other 100 the null hypothesis is false. With the conventional alpha of .05, 5% of the 100 studies in which the null hypothesis is true will yield a significant effect (i.e., a false positive). However, consider what happens if we have only 0.2 power for the 100 studies in which the null hypothesis is false. In this case, we expect a significant effect. With 0.2 power, only 20 of the 100 studies will yield a significant result (i.e., a true positive). Further, given publication biases, we expect that only the studies with significant effects would be published, the 5 false positives and the 20 true positives. Thus, of the 25 published studies with significant effects, 5 of 25 (20%) would be false positives, which is far higher than the 5% rate one might expect with an alpha of .05. Moreover, because our hypothetical studies had low power, 80 studies were conducted that led to false negatives, and the published literature misrepresents the status of real and potentially important effects.

Of course this is an extreme example, and (as will be clear later) power is usually higher than 0.2. However, the conclusion remains the same: p-values are not independent of power (Halsey et al., 2015), and p-values should not be considered without also considering the sample size (Royall, 1986). Of course, power analyses are not without controversy (see McShane & Böckenholt, 2014 and; Muthén & Muthén, 2009 for alternative ways to calcuate and determine power and sample size), making it even more difficult to know how to evaluate a body of literature. However, it is important to characterize a research area using standard methods to examine the power and effect sizes in a collection of studies. This will allow us to better understand the scope of the problem. This was the goal of the next section.

Power and sample size

Why do we care about sample sizes? Given that the highly influential studies described above yielded positive results with samples that ranged from 12 to 24 infants per cell, why is it a problem to use samples of this size? One might conclude that the nature of infant research, only large effects can be reliably detected, and therefore 12 to 24 infants per cell is a sufficient convention. Indeed, studies—such as the classic important studies referenced earlier—with such sample sizes have made significant and key contributions to the field. Moreover, error in measurement and experimental design also contribute to false conclusions in infant research. Investigators must carefully consider how the reliability and validity of their measurement, as well as other factors in their experimental design or procedure, make them more or less confident in their conclusions.

But sample size can have powerful effects on outcomes and is subject to conventions. As will become clear in the following paragraphs, conventional sample sizes have yielded many published infant looking time studies with low power, potentially inflating the publication of false positive results. Indeed, it is possible that some controversies in the field—for example about infants’ developing numerical abilities (L. B. Cohen & Marks, 2002; McCrink & Wynn, 2004; Simon, Hespos, & Rochat, 1995; Wynn, 1992)—reflect at least in part the use of small samples combined with a bias to publish positive findings. We may observe fewer conflicting results if power was routinely considered as a factor in evaluating work, especially when considering a body of research. To be clear, there may be cases when a study with a relatively small sample makes an important contribution to the literature. What I am advocating here is considering the consequences for the field when most studies have small samples, and adjusting our conventions accordingly.

The focus here is on infant looking time studies and as a result the conclusions about specific samples sizes can only be applied to studies using those methods. However, the issues discussed here likely can be applied broadly to studies with infants using a variety of methods, and the examples and methods presented here may provide a model for evaluating other approaches. For the purposes of the present discussion, I focused on a constrained set of methods, measures, and procedures. Different methods, measures, and subject populations yield different levels of variability, there will be variation in effect sizes and sample size requirements as a function of what method is used or what measures are analyzed. For these reasons, the evaluation presented here focused narrowly on infant looking time studies.

The general point is that statistical power is critically important for interpreting the results of empirical studies. Higher power is not only important for sufficient sensitivity to detect true effects, higher power also is associated with more accurate estimates of effect sizes and lower probability of false positive results (Fraley & Vazire, 2014). However, behavioral scientists often lack a clear understanding about the importance of statistical power for interpreting their findings (Vankov, Bowers, & Munafò, 2014), or even what sample sizes are required to obtain sufficient power (Bakker, Hartgerink, Wicherts, & van der Maas, 2016). Moreover, it is tempting to conclude that when a field is restricted to small sample sizes, our science is more likely to report only large effects. However, the bias to publish only significant results means that the published literature likely over-estimates effect sizes, and the reported effects in published papers may be twice the true effect sizes (Brand, Bradley, Best, & Stoica, 2008; Lane & Dunlap, 1978; Open Science Collaboration, 2015).

Despite the possibility that publication practices and biases may create inaccuracies in our understanding of phenomena, the problem of low power may be pervasive in science. Recent reviews suggest that many published studies have low power in neuroscience (Button et al., 2013) and psychology (Fraley & Vazire, 2014). Given the difficulty of recruiting infant subjects, it would not be surprising if the conventional sample sizes in infant looking time studies often yield relatively low power. However, this topic has not been discussed much in the context of infant looking time studies.

Table 1 lists all 70 articles using looking time studies published in the years 2013 to 2015 in a collection of psychology journals that publish large numbers of articles focusing on infants. The articles were published in Child Development (N = 11), Cognition (N = 3), Cognitive Development (N = 3), Developmental Psychology (10), Developmental Science (4), Frontiers in Psychology (N = 3), Infancy (N = 7), Infant Behavior and Development (N = 13), Journal of Cognition and Development (N = 3), and Journal of Experimental Child Psychology (N = 13). Although there are other journals in which the kind of data evaluated here might be reported, I focused on journals that commonly publish this type of work. These papers were scrutinized by experts in infant research in the peer review process, and we can have confidence that the methods reported have “passed muster” by a broad set of experts from our peer group. Thus, although this is not an exhaustive list of all looking time studies published during these 3 years, I selected all the studies published in the journals listed above that met the criteria listed in the following paragraphs (I sincerely apologize if I inadvertently omitted from this list any papers published in the listed journals that did meet those criteria). Thus, this sample will provide a good indication of standard, accepted practices in the field.

Table 1.

Citation	N per cell	Statistical test	Calculated effect size	Observed Power	50% effect size	Sample size needed given effect size	Sample needed for 50% effect
Althaus & Plunkett (2015)	29	t(28) = 4.037, p < 0.001	0.76	0.98	0.38	16	57
Bahrick et al. (2013)	16	t(15) = 5.26, p< .0001	1.32	0.99	0.66	7	21
Bahrick et al. (2015)	16	t(15) = 3.27, p = .005	0.82	0.87	0.41	14	49
Baker, J.M., et al. (2014)*	28	t(27) = 2.474, p = .02	0.49	0.70	0.24	35	139
Baker, R.K. et al. (2014)	24	F(1, 88) = 6.56, p = .012	0.07	0.43	0.03	108	120
Bardi et al. (2014)	12	t(11) = 2.768, p<.05	0.79	0.70	0.40	15	52
Benavides-Varela & Mehler (2015)	22	t(21) = 2.123, p < .05	0.45	0.52	0.23	41	151
Bidet-Ildei et al. (2014)	12	Z= 1.96; p<.05	1.37	0.99	0.69
Biro et al. (2014)	12	t(22) = 2.54, p = .019	1.08	0.72	0.54	15	55
Bremner et al. (2013)	12	F(1,10) = 10.95, p < .008	0.52	0.91	0.26	11	26
Brower & Wilcox (2013)	10	t(18) = −0.58, p = .58	0.26	0.09	0.13	234	930
Cantrell et al. (2015)	20	t(19) = 3.05 p = .007	0.68	0.82	0.34	19	70
Casasola & Park (2013)	16	F(1, 15) = 5.38, p < .05	0.26	0.49	0.13	26	56
Cashon et al. (2013)	23	t(22) = 3.44, p	0.72	0.91	0.36	18	63
Coubart et al. (2014)	16	F(1, 12) = 12.8, p = .004	0.52	0.97	0.26	11	26
Esteve-Gibert et al. (2015)	24	F(1, 20) = 7.262, p = .014	0.27	0.31	0.13	25	56
Ferry et al. (2015)	11	t(10) = 3.577, p = .005	1.07	0.89	0.54	9	24
Flom et al. (2014)*	20	t(19) = 2.5, p = .02	0.56	0.66	0.28	28	103
Frick & Möhring (2013)	20	F(1, 36) = 6.94, p < .05	0.16	0.27	0.08	14	26
Frick & Wang (2014))	7	t(13) = 2.82, p = .01	1.45	0.70	0.73	9	31
Gazes et al. (2015)	32	F(1,28) = 10.21, p = .003	0.27	0.84	0.13	25	56
Graf Estes & Hay (2015)*	16	t(15) = 2.28, p = .038	0.57	0.57	0.29	27	96
Gustafsson et al. (2015)	30	F(1,29) = 4.588, p = 0.041	0.14	0.32	0.07	52	108
Henderson & Scott (2015)*	16	t(15) = 2.20, p < 0.05	0.55	0.54	0.28	28	103
Hernik & Csibra (2015)	16	t(15) = 2.65, p = .018	0.66	0.69	0.33	21	75
Heron-Delaney et al. (2013)	18	t(17) = 2.44, p = .025	0.58	0.64	0.29	26	96
Hillairet de Boisferon et al. (2014)	23	t(22) = 2.89, p < .01	0.60	0.78	0.30	24	90
Hillairet de Boisferon et al. (2015)	18	t(17) = 2.29, p < .05	0.54	0.58	0.27	29	110
Hock et al. (2015)	15	t(14) = 2.84, p<.02	0.73	0.75	0.37	17	60
Imura et al. (2015)	19	t(18) = 4.39, p = 0.0004	1.01	0.98	0.51	10	33
Kampis et al. (2013)	22	F(1,21) = 7.03, p= 0.015	0.25	0.61	0.13	27	56
Kavsek & Marks (2015)	16	F(1, 15) = 55.13, p ≤ .001	0.79	1.00	0.39	5	16
Kwon et al. (2014)	36	t(35) = 4.32, p < .001	0.72	0.99	0.36	18	63
Lee et al. (2015)	23	t(21) = 2.60, p = 0.02	0.55	0.71	0.28	28	103
Lewkowicz (2013)	35	F(1, 67) = 4.30, p < .05	0.06	0.09	0.03	126	257
Lewkowicz et al. (2015)*	24	t(23) = 0.52, p = .30	0.11	0.08	0.06	651	2183
Libertus et al. (2014)	16	t(15)= 2.7, p < .02	0.67	0.71	0.34	20	70
Liu et al. (2015)*	11	t(10) = 3.16, p =	0.95	0.81	0.48	11	37
Longh et al. (2015)	15	F(1, 14) = 6.015, p < .028	0.30	0.58	0.15	22	48
Loucks & Sommerville (2013)	13	t(12) = 2.38, p = .035	0.66	0.59	0.33	21	75
Mackenzie et al. (2014)	16	t(15) = 3.56, p = .003	0.89	0.91	0.45	12	41
Matatyaho-Bullaro et al. (2014)	12	t(11) = 6.44, p < .001	1.94	1.00	0.97	5	11
May & Werker (2014)*	24	F(1, 22) = 10.67, p < .01	0.33	0.87	0.16	19	45
Moher & Feigenson (2013)	18	F(1,16) = 21.996, p < .001	0.58	1.00	0.29	9	23
Novack et al. (2013)*	16	t(15)=3.50, p<.003	0.88	0.91	0.44	13	43
Oakes & Kovack-Lesh (2013)	12	t(11)=2.06, p=.06	0.59	0.46	0.30	25	90
Otsuka et al. (2013)	12	t(11) = 3.04, p < .01	0.88	0.79	0.44	13	43
Ozturk et al. (2013)	12	t(11) = 2.77, p < .02	0.80	0.71	0.40	15	52
Park & Casasola (2015)	15	F(1, 32) = 20.86, p < .001	0.39	0.80	0.20	16	35
Perone & Spencer (2014)*	39	t(38) = 3.50, p < .001	0.56	0.93	0.28	28	103
Pruden et al. (2013)*	23	t(22) = 3.12, p < .05	0.65	0.84	0.33	21	75
Quinn & Liben (2014)	12	t(11) = 5.14, p =	1.48	0.99	0.74	6	17
Rigney & Wang (2013)	18	F(1, 17)=10.83, p<.004	0.39	0.87	0.19	16	37
Robson et al. (2014)*	24	t(23) = −2.305, p = .031	0.47	0.60	0.24	38	139
Sanefuji (2014)	12	t(10) = 2.79, p = .019	0.84	0.75	0.42	14	47
Sato et al. (2013)	14	t(13) = 3.04, p < 0.01	0.81	0.80	0.41	15	49
Skerry & Spelke (2014)	32	F(1,31) = 8.524, p = 0.006	0.27	0.84	0.13	25	56
Slone & Johnson (2015)	20	t(19) = 2.76, p < .05	0.62	0.75	0.31	23	84
Soley & Sebastián-Gallás (2015)	32	t(31) = 2.42, p = .02	0.42	0.63	0.21	47	180
Starr et al. (2013)	20	t(19) = 3.50, p < .005	0.78	0.91	0.39	15	54
Takashima et al. (2014)	13	t(12) = 2.46, p < .05	0.68	0.62	0.34	19	70
Tham et al. (2015)	12	t(10) = 2.342, p = .041	0.71	0.61	0.35	18	67
Träuble & Bätz (2014)*	15	t(14) = ?4.09, p < .001	1.06	0.97	0.53	10	30
Tsuruhara et al. (2014)	12	t(11) = 3.94, p < .01	1.14	0.95	0.57	9	27
Turati et al. (2013)	17	F(1,14) = 5.489; p = 0.034	0.28	0.58	0.14	24	52
Vukatana et al. (2015)	35	F(2, 68) = 3.27, p = .044	0.09	0.19	0.04	83	192
Woods & Wilcox (2013)	15	F(1, 14)= 7.57, p =.02	0.35	0.71	0.18	18	39
Yamashita et al. (2014)*	12	t(11) = 4.55, p = .0008	1.31	0.98	0.66	7	21
Zieber et al. (2014)*	16	t(15) = 2.54, p = .02	0.64	0.67	0.32	22	79
Zieber et al. (2015)	11	t(10) = 2.71, p < .03	0.81	0.63	0.41	15	49

The goal was to narrow the range of variability to allow us to evaluate the effect of sample size on a well-defined, constrained set of studies. Thus, the articles in this list were selected using the following inclusion criteria. First, because it is plausible that sample size requirements and effect sizes change with the age of the subjects, I included papers only if the infants tested were younger than 18 months. Second, the method involved must have involved observer-recorded looking time. Although I included studies that used a wide range of methods used to record looking time—e.g., online recording by one or more observer, offline coding in real time, frame-by-frame coding from recordings of the session—in all of the papers included here the dependent measure was related to looking time (e.g., the duration of looking, the proportion of looking, or difference in looking). Other measures—such as reaction time, number of looks, etc.—may have different levels of variability, and therefore the sample size requirements may be different. In addition, I excluded studies in which an eye tracker was used. In these studies, eye gaze is recorded quite differently than when coded by a human observer, and the scale of measurement is often quite different (e.g., millisecond level recording with eye trackers as compared to tenths of second recordings by human observers). Moreover, eye tracking procedures often involve more trials, finer spatial resolution, and other factors that change both the nature of the measure and the variability observed. Factors such as the validity and reliability of looking time measures may also differ when looking time is coded by human observers versus automatically by an eye-tracker. Future work may examine the effects of power and sample size in eye-tracking studies. In all the studies evaluated here, infants’ a priori preference, changes in preferences (after familiarization), or response to novelty was assessed. These procedures have been widely used in the field.

There were several other inclusion criteria. Only work that examined development in typically developing, healthy, full-term infants was included. In addition, papers were excluded if their main focus was individual differences or if they tested infants longitudinally. In these instances, the hypotheses were quite different from the studies listed in Table 1, making it difficult to know how power and effect size would compare. It would be extremely useful for a future investigation to examine such studies. Finally, only a single statistical test was evaluated in each study. For many studies, multiple experiments were reported. In this case, only information about the first experiment reported was included. Often this experiment reported the main finding of the study. In 3 papers, the first experiment reported was a control condition or included adults as participants. In these cases, I included the information about the second reported experiment.

For the present purposes, I selected a single statistical test that was key for the conclusions of the paper. Typically, this was the first reported test that evaluated infants’ responding on the test trials. However, if there were multiple analyses, the statistical test associated with the largest effect size was selected. This decision was made to bias the sample toward larger effects, which will favor smaller samples. In two cases a non-significant effect is included because that effect was critical for the conclusions of the paper. The specific test used is listed in Table 1. The distribution of group or cell samples sizes is presented in Figure 1. This histogram indicates the frequency of each sample size across the 70 studies.

Figure 1.

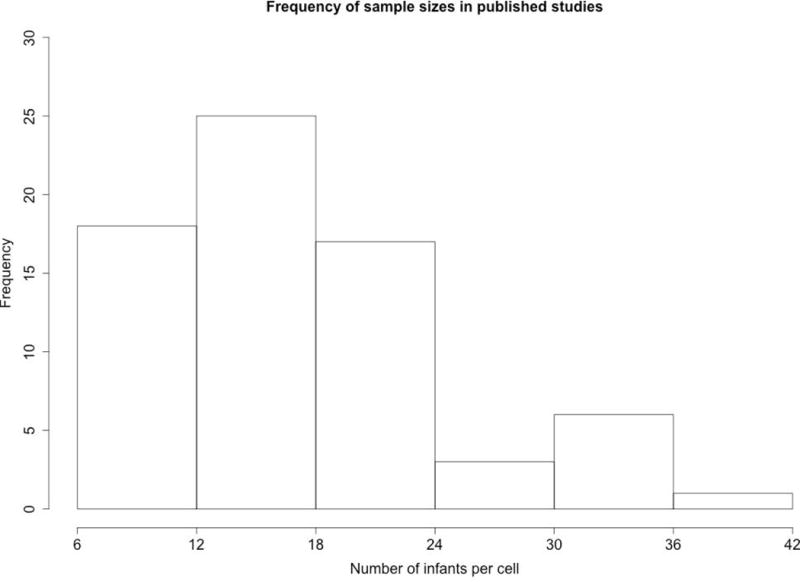
Several things are immediately apparent. First, the data in Table 1 show that only 4 of the experiments had 10 or fewer subjects per cell; in three of these experiments conclusions were drawn by comparing two groups of infants (14 to 20 infants total). Ironically, such between-subjects comparisons typically require larger sample sizes to achieve the same power as within-subjects comparisons (Bramwell, Bittnerjr, & Morrissey, 1992; Charness, Gneezy, & Kuhn, 2012), and thus these studies probably should have had larger sample sizes. Just 11 (15%) of the experiments had 25 or more infants per cell. The vast majority of the experiments had between 11 and 24 infants per cell.

Why have we adopted the convention of testing 11 to 24 infants per cell in this type of study? One possibility is that the controversial, fascinating, important, and revolutionary studies described earlier used similar sample sizes, and thus a convention was established because of these influential studies. It is also possible that these sample sizes reflect sufficient power to detect the kinds of effects typically observed in infant research—so the convention is not based on an arbitrary decision, but actually reflects the kind of power needed to detect the true effects that exist. Indeed, in the original studies and most of the studies listed in Table 1, significant effects were observed with these sample sizes. But, conclusions about sample size and power must be drawn carefully when relying solely on published findings. The widespread bias to publish only significant effects makes it much more difficult to determine what the true effect s is, and therefore whether the power in these studies was sufficient. It is commonly understood that the bias to publish significant effects creates a file drawer problem, in which non-significant findings are not reported. When studies have low power, it is likely that there are more such file drawer studies, making it even less likely that the significant finding reflects a true effect. To be clear, assuming the absence of p-hacking (or engaging in practies that inflate the p-value, see Head, Holman, Lanfear, Kahn, & Jennions, 2015; Lakens, 2015; Ulrich & Miller, 2015), many published findings must reflect true effects. The problem is that the level of power influences our confidence about whether a particular finding reflects a true effect. Thus, if the convention in a field is to conduct low powered studies, it becomes less clear what proportion of published findings reflect true effects.

This discussion raises an interesting paradox regarding the pressures of difficult-to-obtained subject populations on conducting studies with low power. If in fact running studies with small sample sizes is more likely to yield non-publishable, file-drawer results, researchers may get more bang for their buck if they ran fewer studies with larger sample sizes. To be clear, I am not advocating for a complete rejection of studies with small samples sizes—there may be some cases and some study populations where small samples sizes are the only option. However, it may be that our reliance on small sample sizes in general has actually created a more difficult situation for researchers who have limited access to infants. That is, by creating a culture in which small sample sizes are widely accepted, researchers who have difficulty recruiting infants may fall into the trap of testing many underpowered studies that become “file drawer” studies; these researchers may have more success in general if our conventional sample size yielded studies with higher power. Changing our convention to expect larger samples sizes in general would obviously mean that it take longer to collect the data for a single study. However, these better powered studies may be more likely to yield interpretable (and publishable) findings, reducing the number of file drawer studies.

To address the question of whether our conventional sample sizes provide sufficient power, I calculated the observed effect size in each study using the approach described by Lakens (2013). Although effect size was reported in many studies, Lakens’s method was used to calculate the effect size for all the statistics listed here to ensure that effect size was calculated in the same way for all experiments. A handful of calculated effect sizes differed from those reported in the published papers (indicated by an * in the table), perhaps reflecting a different method for calculating effect sizes, an error in calculation, or a typo. The incidence of these inconsistencies suggests that editors and reviewers often are satisfied with the presence of effect sizes, and do not doublecheck the effect sizes (note that there has recently been a discussion of the prevalence of errors in statistical reporting more broadly, Nuijten, Hartgerink, Assen, Epskamp, & Wicherts, 2015). The development of a tool like statcheck (Epskamp & Nuijten, 2016, a package for R that operates like spellcheck, except for statistical reporting, but does not evaluate effect size) that could detect such errors would be a significant benefit to the field.

Figure 2 provides a histogram of the frequency of the calculated Cohen’s d scores for the 49 t tests reported in Table 1. We chose to plot only Cohen’s d because they were more numerous than the η_p² reported for F tests. To make sure that the data included in the following figures and discussion were comparable, my evaluation focused only on t tests, as they were the most frequent statistic sampled from the studies (many studies reported both ANOVAs and t tests, but main conclusions were drawn from t tests comparing infant’s looking at two tests, or comparing infant’s preference to chance). Recall that, by convention, Cohen’s d of .2 is a small effect, .5 is a medium effect, and .8 is a large effect (J. Cohen, 1992). Sawilowsky (2009) further suggested that d scores of 1.2 and 2 be considered very large and huge effect sizes respectively. These effect sizes indicate that the means differ by at least 1.2 standard deviations, and indeed are quite large.

Figure 2.

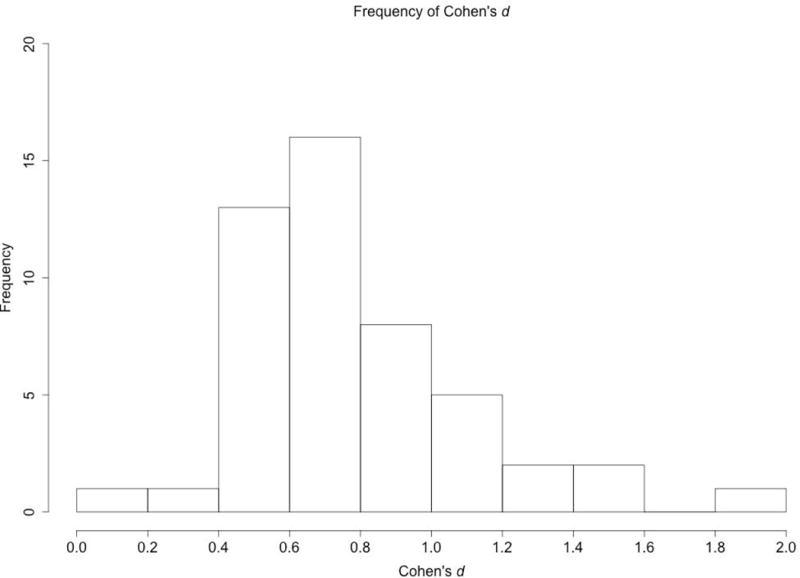
Figure 2 shows that 28 of the 49 effect sizes (57%) falling between .4 and .8, and thus fall the medium category, with. Fourteen effect sizes (29%) were between .8 and 1.2 (large), and only 5 effect sizes (10%) were very large or huge. The 2 small effect sizes were the two cases in which the t test did not reveal a significant difference, and conclusions were drawn based on a null finding. Thus, these data suggest that the impression that ours is a field of large effect sizes is incorrect. Moreover, given that effects sizes are typically overestimated in studies with small sample sizes (Hedges & Vevea, 1996; Lane & Dunlap, 1978), the data presented here suggests that research evaluating infants looking times is (at best) mainly a field of medium estimated effect sizes, and is likely a field in which actual effect sizes are often small.

What does this mean about the conclusions that we can draw from the reported results? After all, these t tests were significant. Perhaps this means that the sample sizes used provided sufficient power to detect those effects, assuming the effect sizes were an accurate estimate of the true effect size (which is likely a generous assumption). To test this possibility, I used G*Power to determine the sample size need to achieve the conventional power level of .80 (assuming alpha = .05) using the estimated effect sizes listed in Table 1. In addition, because observed effect sizes are often twice as large as true effect sizes when small sample sizes are used (Lane & Dunlap, 1978; Open Science Collaboration, 2015), Table 1 also includes effect sizes that are 50% of the observed effect size, as well as the sample sizes need to achieve .80 power for these reduced effect sizes.

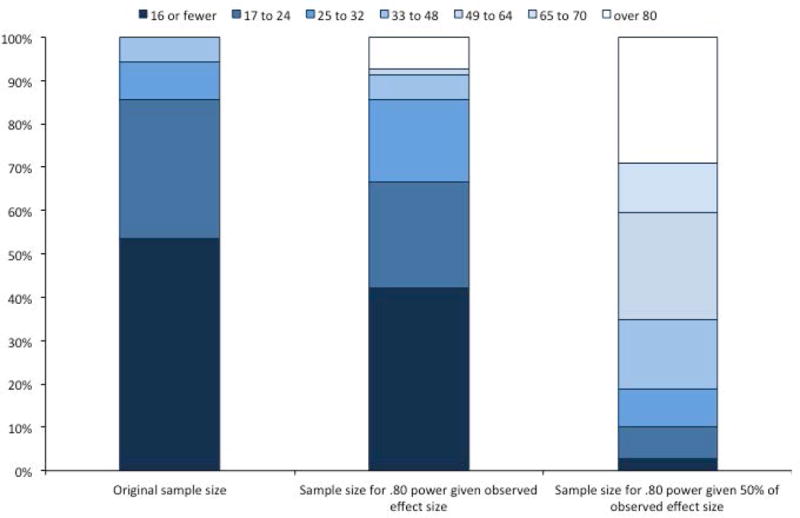
Figure 3 presents the distribution of sample sizes in the original studies (A), the sample sizes required to achieve .80 power to detect the calculated effect sizes (B), and the sample sizes required to achieve .80 power to detect 50% of those calculated effect sizes (C). It is immediately clear that the three distributions are quite different. Most published studies included 24 or fewer infants per cell (over 80%). However, the histogram in Figure 3B shows that these sample sizes would have provided sufficient power to detect 67% of the observed effect sizes. The samples used in the published studies were rarely large enough to achieve .80 power given the reduced effect sizes (e.g., if the true effect sizes were 50% of those observed in the published studies). Moreover, although few of the original studies had sample sizes of over 32, these larger samples were required to achieve .80 power for detecting a significant effect in the vast majority (81%) of cases if we assume the reduced effect sizes. Thus, assuming that the reported effect sizes are approximately twice the size of the true effect (Lane & Dunlap, 1978; Open Science Collaboration, 2015), it is clear that studies using infant looking time generally have low power.

Figure 3.

What is the takeaway message from this analysis? Given that the reported studies tend to have low power, it seems that in this area of research, like many areas of psychological research, has relied on convention and rules of thumb to determine sample sizes. It is tempting to argue that this is not a problem because we are a field of large effects—that is, our sample sizes give us the sensitivity to detect relatively large effects. However, inspection of Table 1 shows that even when experiments yield relatively large effects (greater than .60), the studies often still have low power. Clearly the likelihood that a true positive effect is observed decreases with decreased power (see Krzywinski & Altman, 2013 for a nice description). However, because p-values vary more in low powered studies (Halsey et al., 2015), decreased power may be problematic for conclusions from both positive and null findings. The particular effect of sample size on effect size and power is further explored in the final section through the examination of three different data sets collected in my lab.

An exploration of 3 datasets

One challenge with analyses based on published studies is that they necessarily reflect the biases of the publication process (e.g., the strong tendency to focus on significant effects). Moreover, one cannot easily explore the effects of sample sizes in published studies because many other factors may covary with sample size. This section therefore examines the relationship between power and sample size in three relatively large datasets, using a Monte Carlo approach in which experiments with smaller sample sizes were simulated by selecting random subsets of the subjects from these actual experiments.

I selected three studies with relatively large samples sizes; 33 in the first set (published in Kwon, Luck, & Oakes, 2014, Experiment 2), and 32 in the other two sets (Experiment Action and Experiment Sound, both unpublished). The relevant details of each study will be described below. Importantly, because these are real datasets, the true effect size is unknown. But, because the sample sizes are relatively large (in the context of most infant research with looking time as the dependent measure), it is possible to simulate the effects with a variety of sample sizes smaller than the original sample.

The first experiment was a paired preference study with 6-month-old infants; the data represent their preferences on two types of trials. Experiments Action and Sound were habituation experiments with 10-month-old infants; the data represent their looking time to familiar and novel test items following a habituation sequence. All data reported were from infants who met the relevant inclusion criteria (e.g., completed all 6 trials in the Kwon e al. experiment; met the habituation criterion in Experiments Action and Sound). All infants were healthy, full term, and had no history of vision problems. No infants were statistical outliers (e.g., all responding was within 3 SD of the mean).

To demonstrate the effect of sample size in these experiments, 1000 subsamples of 8, 12, 16, 20, and 24 infants were drawn without replacement from the full dataset using the samp function in R (yielding 5000 subsamples in total for each experiment). These sample sizes were selected to be representative of the sample sizes used in the published literature. As seen in Figure 1, most studies have sample sizes between 6 and 24 infants per cell. The goal here was to examine the mean response and t values across the subsamples of a given size, making it possible to determine how variations in sample size could influence the outcome of the experiment. The simulated sample sizes were based on the typical range of values from the meta-analysis described earlier, and the sample sizes selected for these simulations approximate those that are typically used in the recent literature. By varying the sample size systematically within this range (8 to 24 infants per cell) it is possible to see how power and p-values change over this range (e.g., is the change linear).

Example 1

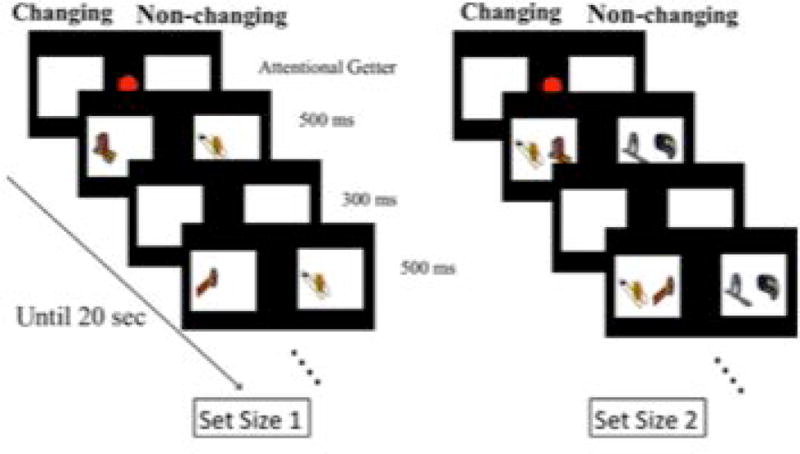
Kwon et al. (2014) reported the results of a simultaneous streams change detection task with 33 6-month-old infants (Experiment 2). Infants were presented with 6 trials, in which a changing stream was paired with a non-changing stream (see Figure 4). On each trial, infants’ preference for the changing stream was assessed by measuring how long they looked to each stream. A change preference score was calculated by dividing the amount of time infants looked at the changing stream by their total looking (e.g., the changing and non-changing streams combined). If infants significantly preferred the changing stream, their preference score would be significantly greater than chance, or .50 (i.e., equal looking to the two streams). We tested infants’ preference for the changing stream when each stream contained only a single item (set size 1; left side of Figure 4 and when each stream contained two items (set size 2; right side of Figure 4s).

Figure 4.

Statistical analyses of the entire group of infants showed that infants significantly preferred the changing stream at set size 1, t(32) = 3.07, p = .004, d = .54 (see Figure 5), but they failed to prefer the changing stream at set size 2, t(32) = −.34, p = .84, d = .06. We are assuming that the preference is a true effect at set size 1 and a null (or negligible) effect at set size 2, and these assumptions are based on two sources of evidence. First, several previous studies have found significant effects at set size 1 but not at set size 2 in 6-month-old infants using variants of this procedure (Oakes, Baumgartner, Barrett, Messenger, & Luck, 2013; Ross-Sheehy, Oakes, & Luck, 2003). Second, we conducted a Bayes factor analysis (Rouder, Speckman, Sun, Morey, & Iverson, 2009) which indicated that the data from set size 1 were 8.9 times more likely to arise from a true effect than to arise from a null effect, and the data from set size 2 were 5.1 times more likely to arise from a null effect than from a true effect. Thus, we are justified in assuming that the data from this experiment reflect a true effect at set size 1 and a null or negligible effect at set size 2.

Figure 5.

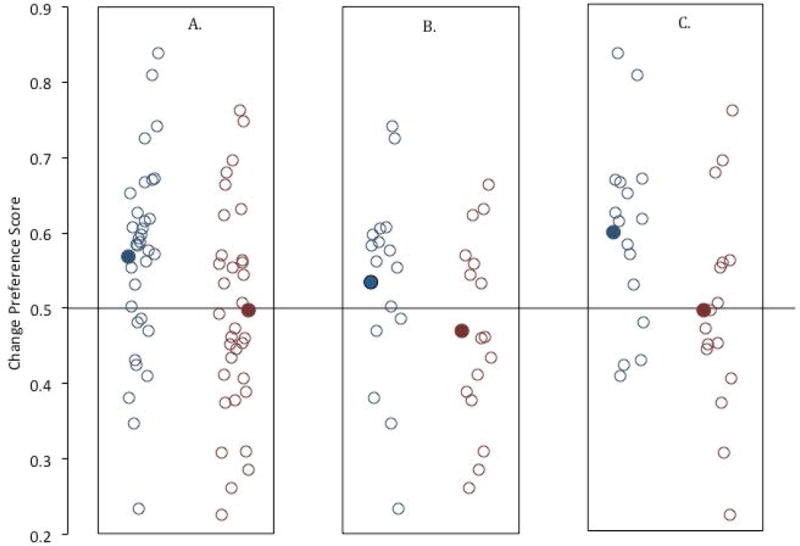
The estimates of the sample size needed to have 80% power given these effect sizes (assuming alpha = .05) is 18 for set size 1. Although infants as a group preferred the changing side at set size 1 (the blue circles) but not at set size 2 (the red circles), it is also clear that there was significant variability in infants’ responding (the individual circles in the graph). Moreover, one infant appears to be an outlier at set size 1; his or her mean responding was .233, which is 2.62 SDs below the mean. However, our standard exclusion criterion is for values that are 3 SD from the mean, and deciding whether and how to exclude outliers after having looked at the results can significantly affect the probability of Type 1 error (Bakker & Wicherts, 2014a, 2014b). Therefore, we did not exclude this infant from our analyses.

As a first step, we extracted from this sample of 33 infants two non-overlapping subsamples of 16 infants to simulate what might happen in experiments with a sample size of only 16 infants. The results from these two subsamples presented in Figures 5B and 5C. Note that we would have drawn different conclusions if we had sampled only one of these two sets of infants. Specifically, for the first sample of 16 infants, the t test comparing mean preference score at set size 1 was not significant, t (15) = 1.07, p = .30, d = .268 (excluding the potential outlier infant changed the t test to t (14) = 1.99, p = .07, d = .52). The t test comparing the infants’ mean change preference score for set size 2 trials to chance was not significant, t (15) = −.07, p = .94, d = .02. Thus, from this sample, the results are ambiguous at best, and do not provide clear evidence that infants prefer the changing stream. For the second sample, the t test comparing infants’ set size 1 preference scores to chance was significant, t (15) = 3.22, p = .006, d = .81, indicating that they did prefer the changing stream. Their preference for the changing stream at set size 2 was not significant, t(15) = −.07, p = .94, d = .02. If we had tested only the first sample of infants, we would have concluded that we had no evidence that infants significantly preferred a change at set size 1—despite the fact that most of the infants in that sample had change preference scores above .50.

Of course, it’s possible that these two subsamples are not representative of what would typically occur with a sample size of 16 in this experiment. The first subsample described may have been particularly non-representative, and the results may have been non-representative of subsamples of 16 infants in general. To test this possibility, we examined the effect of sample size more systematically using the Monte Carlo approach described earlier. For each of five different sample sizes (N = 8, N = 12, N = 16, N = 20, and N = 24), 1000 experiments were simulated by randomly sampling (without replacement) from the larger sample of 33 infants. The result was 5000 subsamples of infants, and each subsample contained the data from 8, 12, 16, 20, or 24 infants. For each subsample, the mean change preference scores for both set sizes, as well as the t and p values when comparing each mean score to chance, were calculated. The distributions of mean change preference scores for set size 1 and set size 2 are presented in Figure 6. Each simulated experiment is represented in the figure as an individual diamond (one representing the mean change preference score for set size 1 and another representing the mean change preference score for set size 2). Importantly, when selecting infants to include in a subsample, their change preference scores for both types of trials were selected. Thus, the mean change preference scores for set size 1 and set size 2 presented in Figure 6 represent the change preferences from the same subsamples; any differences between the scores do not reflect differences in the samples selected, but rather reflect differences in how those same subsets of infants responded on the two types of trials.

Figure 6.

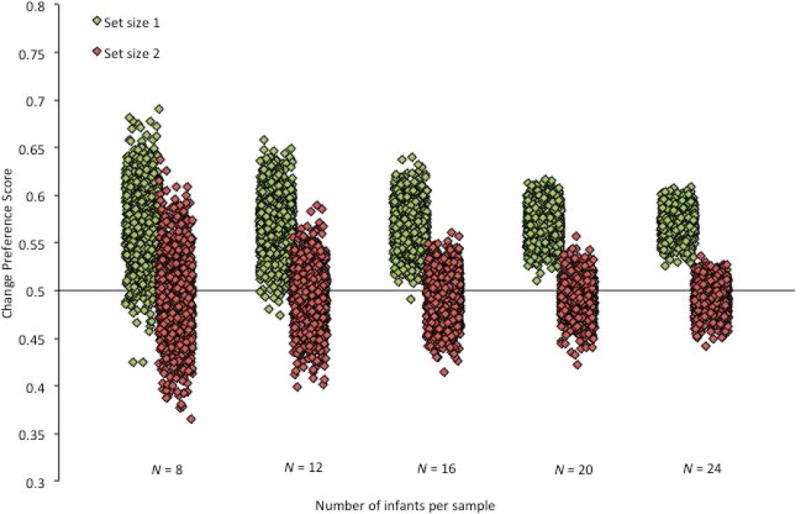
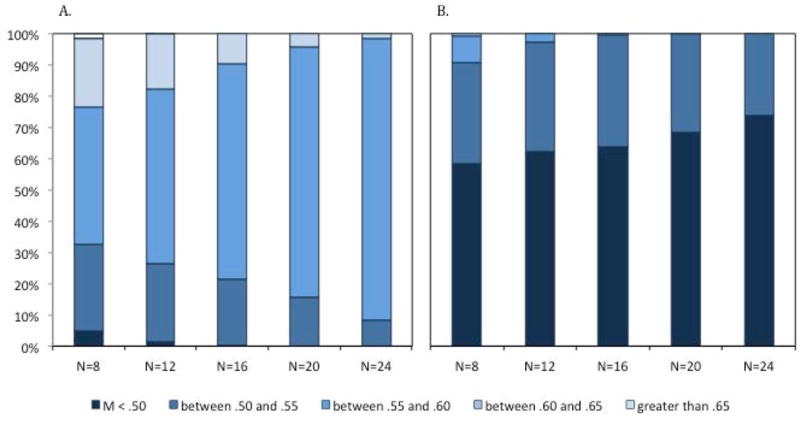
This visualization illustrates that the size of the sample has a significant impact on the distributions of the mean change preference for the samples. The distribution of the means for the simulated experiments with 8 infants has a larger spread than the distribution of means for the simulated experiments with larger numbers of infants—for both the positive outcome (set size 1) and the negative outcome (set size 2). This is further illustrated in Figure 7, which presents the proportion of subsamples with means in particular ranges. Note that many subsamples of 16 or fewer infants yielded mean change preferences scores that are below .55 at set size 1 (33% of the subsamples of 8 infants, 26% of the subsamples of 12, and 22% of the subsamples of 16 infants) and above .55 at set size 2 (9% of the subsamples of 8 infants and 3% of the subsamples of 12 infants). If one of these subsamples had been the sample reported in the paper, we may have concluded that infants failed to detect a change at set size 1 and/or did detect a change at set size 2. Of course, this may be a legitimate conclusion for individual infants, but what is clear from the subsamples that included at least 20 infants, the group of infants as a whole did not show this pattern of responding.

Figure 7.

The issue is further illustrated by the distribution of p-values when comparing the mean change preference scores for each subsample to chance (.50). This distribution is presented in Figures 8 and 9. In Figure 8, it is clear that the distribution of the p-values changes as the sample size increases. In Figure 9, it is clear that this is particularly true for set size 1. Interestingly, as the sample size decreases, the proportion of p-values that are less than .05 decreases for set size 1 and increases for set size 2, confirming that low powered studies both decrease true positives and increase false positives.

Figure 8.

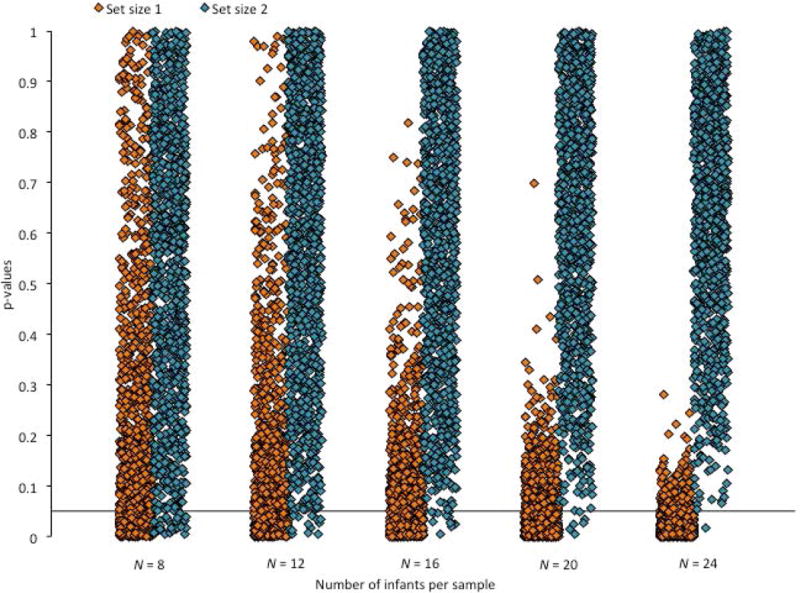
Figure 9.

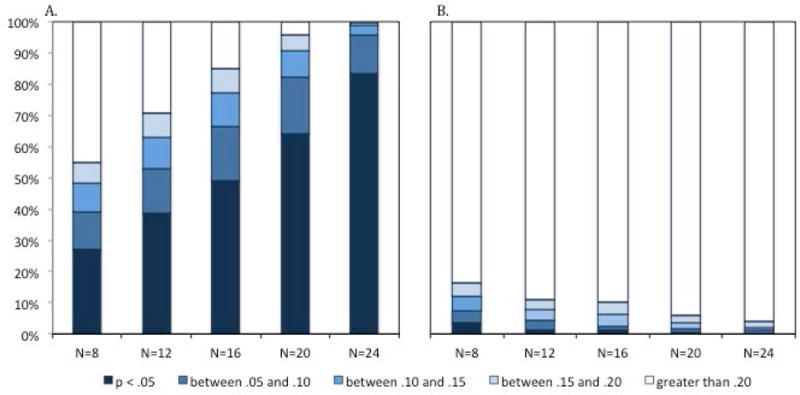
The take-home message is clear. If our study had included one of these randomly selected sets of 8, 12, or 16 infants in the actual experiment (rather than the entire group of infants), there is a non-trivial chance we would have concluded that we have no evidence of change detection at set size 1 or that we have evidence of change detection at set size 2. In other words, by having a sample size that is too small, we increase the likelihood of a study with ambiguous or false results. Considering again the problem of researchers whose abilities to recruit infants is limited. The data presented here suggests that collecting the data from a single study with 24 infants would be more likely to yield interpretable results than collecting the data from two studies with 12 infants each.

Examples 2 and 3

To confirm that these observations were not specific to a single study, sample, procedure, and/or dependent measure, we took this same approach in evaluating two unpublished datasets from my lab. These second and third samples are two experiments that were conducted using the same audio-visual stimuli in habituation procedures using the switch design. In each experiment, 32 10-month-old infants were habituated to two multimodal dynamic events; infants saw these events until they reached a habituation criterion of a 50% decrement of their initial looking to the events. Following habituation, infants were tested with one of the two familiar events and a switched event, in which the features of the two events were combined in a new way. The two experiments only differed in the ways the features were combined; in the first Experiment infants’ attention to the Action was observed and in the second infants’ attention to the Sound was observed. Therefore, in the following discussion I will refer to them as Experiment Action and Experiment Sound.

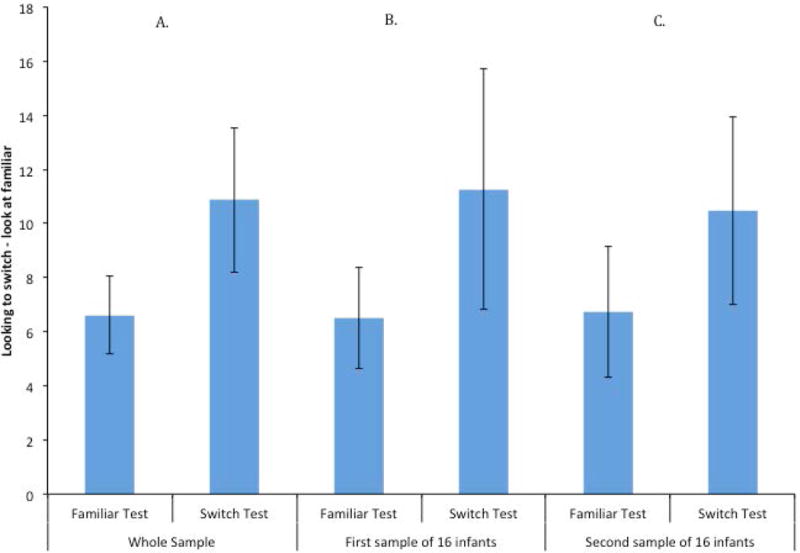
Mean looking times for test events in Experiment Action are presented in Figure 10; the results from the whole sample is presented in Figure 10A, and the results of two non-overlapping subsamples of 16 infants are presented in Figures 10B and 10C. Statistical analyses of the whole sample revealed that this groups of infants significantly increased their looking to the novel stimulus compared to the familiar, t (31) = 3.36, p = .002, d = .59. The Bayes factor indicated that the data were 17.1 times more likely to come from a true difference than to come from a null effect, so we can be quite confident that these data reflect a real increase in looking. The first of the two subsamples of 16 infants showed ambiguous results; their increase to the novel event was marginally significant, t (15) = 2.09, p = .054, d = .522. The second subsample of 16 infants significantly increased their looking to the switch test, t (15) = 3.19, p = .006, d = .797.

Figure 10.

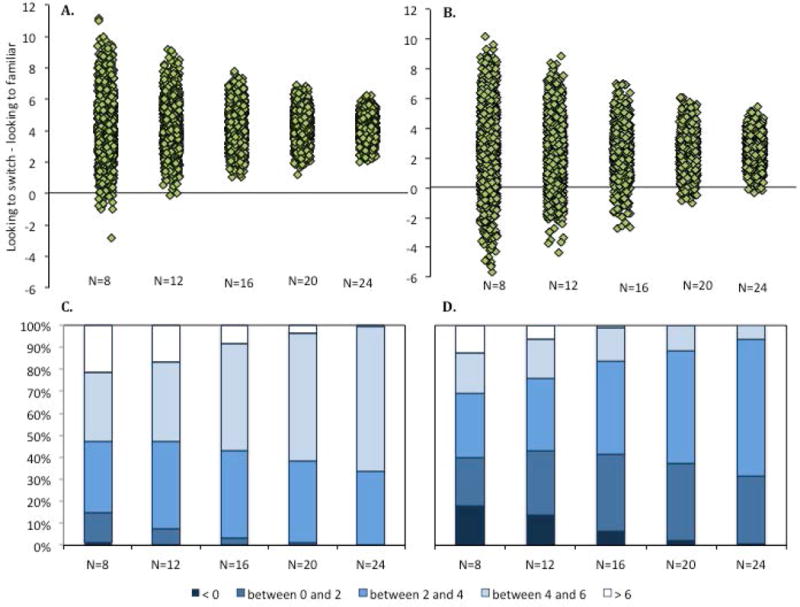
The distributions of the mean difference scores (looking at switch – looking at familiar) obtained from the 1000 simulated experiments with subsamples of 8, 12, 16, 20, and 24 infants are presented in Figure 11A. Again, these distributions differed as a function of sample size. The number of subsamples with means near the center increased as the number of infants in the subsamples increase. This is even clearer when looking at the distributions in Figure 11C. For the larger subsamples of infants, the mean difference between the switch and the test item is rarely less than 2 s (only 1% of the subsamples of 20 infants), whereas this occurred with some frequency with smaller subsamples (e.g., 14% of the subsamples of 8 infants had difference scores less than 2 s). Moreover, over 99% of the subsamples of 24 infants and 97% of the subsamples of 20 infants had difference scores of greater than 4 s.

Figure 11.

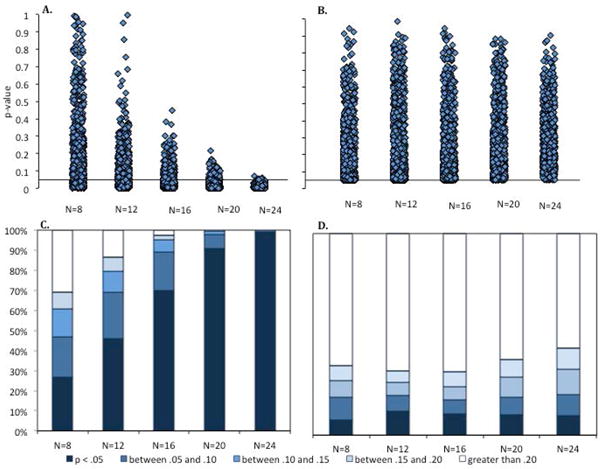
The results of the t tests comparing infants’ responding to the two tests confirmed the impression that larger sample sizes consistently more accurately represent the group of infants as a whole. The distribution of p-values from those t tests are presented in two forms in Figure 12. In Figure 12A, it is clear that although the p-values for larger subsamples rarely was over p = .05, there were many instances of larger p-values with subsamples of fewer infants. This is confirmed in the alternative way of visualizing these distributions in Figure 12C.

Figure 12.

Experiment Sound was similar to the Experiment Action, except that the particular combination of features used differed. In this case, as illustrated in Figure 13, the group as a whole failed to significantly dishabituate to the switch event relative to the familiar event, t (31) = 1.46, p = .15, d = .26. The Bayes factor analysis favored the null hypothesis by a factor of 2.0, so it is likely that either the null hypothesis is true or the actual effect is quite small.

Figure 13.

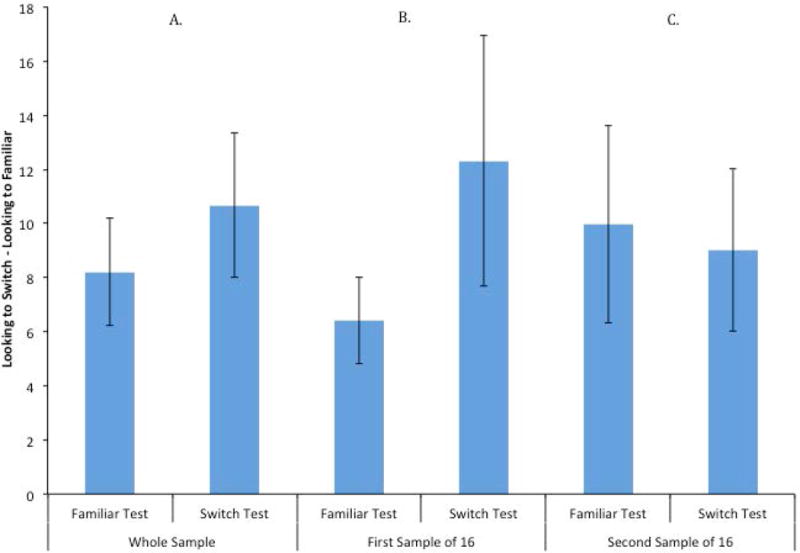
Two simulated experiments with non-overlapping subsamples of 16 infants showed different patterns. The first subsamples of 16 infants significantly dishabituated to the novel item, t (15) = 2.21, p = .018, d = .666. The second subsample of 16 infants as a group failed to respond differently to the familiar and switch tests, t (15) = .42, p = .68, d = .10, and actually looked slightly less to the switch than to the novel test event. Once again, we would have drawn very different conclusions from these two subsamples. If we had tested only the 16 infants in the first subsample, we would have concluded that infants do dishabituate to the switch event, and they learned the association embodied by the habituation events. The null finding in the second sample of 16 infants casts doubt on this conclusion. The question is which of these findings more closely resembles the “true” effect?

The distribution of dishabituation scores to the switch from the simulations is revealing. Figure 11B shows how the distribution of difference scores changes with sample size. Note the differences in the distributions for Experiment Action and Experiment Sound. Although the two non-overlapping samples depicted in Figure 13 suggests that there may be some significant dishabituation, the distributions of the simulations presented in Figure 11D reveal that this significant dishabituation was rare. Moreover, large differences in looking to the switch and familiar test trials were more frequent in the subsamples of fewer infants than in the subsamples of more infants.

This observation is corroborated by the distributions of t values and the p-values. The distribution of p-values is presented in Figure 12. The effect of the size of the subsample is much subtler here than in the previous experiment. Across all subsample sizes, few subsamples yielded significant results (8% of subsamples of 8 infants, 12% of subsamples of 12 infants, and 10% of subsamples of 16, 20, and 24 infants. Regardless of subsample size, more than 55% of the subsamples yielded p-values greater than .20.

Conclusions

This paper has described the state of the field with respect to sample size in studies of infant looking time. The conclusions should be considered in light of several facts. First, the target sample sizes were based on an evaluation of all the published studies recording infants’ looking time in the top journals that publish much of this work. Second, the conclusions about specific sample sizes are only directly applicable to infant looking time studies—work that involves more trials, different dependent measures, automatic observation, etc., may yield different amounts of variability and effect sizes. Thus, although the conclusions about the importance of power and sample size are generally true, the specific sample and effect sizes reported here are representative only of this subset of the literature. Third, as is true for many areas of science, samples sizes appear to have been determined in large part by rule of thumb and convention. Unfortunately because data collection with infants is difficult, expensive, and time consuming, this has meant that many reported studies have relatively low power.

The problem of low power and relatively small sample sizes is not unique to this area of research. There has been significant debate about the effect of sample size on research, whether increasing sample sizes without making other changes will be effective, and about how best to calculate power. However, the simulations shown here are revealing. They show how the studies run in my lab would have differed if we had collected data from subsamples of different sizes. This is an important demonstration. For each of these studies, we could have had a target of only 16 infants per cell, and we would have stopped collecting data after just the first 16 infants tested. Note, moreover, that in the two positive cases, the effect sizes were medium—between .5 and .6. Thus, although when smaller subsamples showed significant differences, the effect sizes observed clearly over-estimated the true effect size. Thus, by using smaller sample sizes, the outcomes in many cases would have been different from the ones we ultimately observed. To be clear, the subsamples did yield the same results as was observed from the full sample more frequently than any other outcome—and most outcomes that differed only differed by a small amount. However, in these examples smaller samples would have increased the likelihood of observing ambiguous results—or even results that led to a very clear but different conclusion than the conclusion drawn from the full sample. Thus, by adopting the convention of using relatively small sample sizes in our work, we as a field are increasing the chances that the outcome of any single study is difficult to interpret or not representative of the most likely outcome from the study.

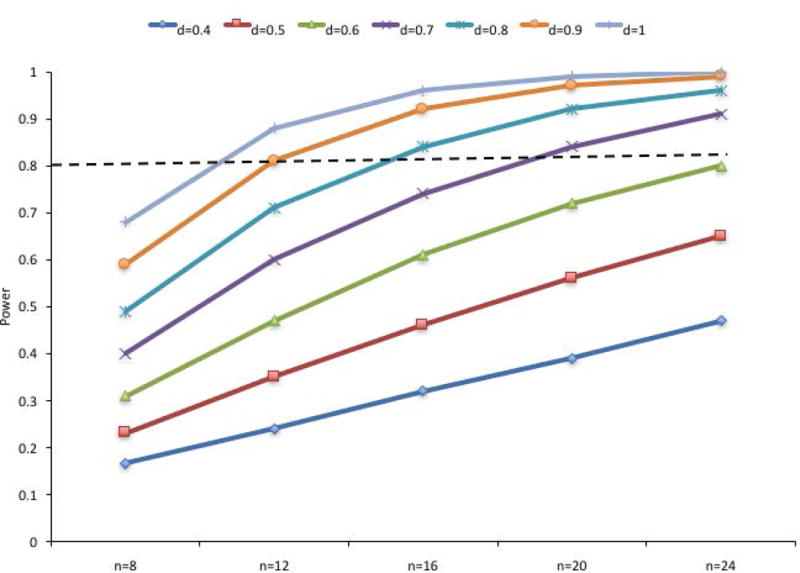
So what do we do? One obvious solution is to increase sample sizes. Of course, given how difficult it is to identify, recruit, and test infant research participants, it is unlikely that all infant looking time studies will involve very large samples. Moreover, it is not clear that all studies should have very large samples Indeed, it has been argued that for some areas of science, sample sizes should be determined by considering cost efficiency in addition to power (Bacchetti, Simon, Mcculloch, & Segal, 2009; Miller & Ulrich, 2016). It is not cleart, however, hat radical changes need to be made to the standard sample size in infant looking time studies to address the power problem, in general. Figure 14 illustrates the change in the power to observe effects of different sizes (these are Cohen’s d for paired comparison 2-tailed t tests, alpha = .05). Note that although samples sizes of 8 provide insufficient power to detect any of the effect sizes depicted, samples of 20 or 24 infants will provide sufficient power for effect sizes of approximately .60 and higher. Thus, it is not clear that the field needs to adopt a convention of testing hundreds of infants per cell, but we may have more consistent results if we relied on sample sizes of 20 to 32 per cell, rather than 12 to 24 infants per cell.

Figure 14.

Moreover, the cost of consistently relying on small sample sizes and low powered studies may be too high. For researchers who have difficulty collecting data from infants, spending the time to collect the data for a single study with 24 or 32 infants is likely to consistently yield more interpretable, replicable results than spending that same time collecting the data for 2 studies each with 12 or 16 infants—and collecting the data from 48 infants in one study will clearly yield more precise results than 4 samples of 12. Given the data presented here, it seems likely that by having larger target sample sizes, researchers may actually end up with fewer file drawer studies, and their efforts may yield more published products in the long run.

Increasing sample sizes is not the only solution, however, and other approaches to this general problem may be fruitful. A compromise might be found in the use of careful sequential hypothesis analyses (Lakens, 2014). In this approach, researchers identify a target final sample size (e.g., 48 infants), but conduct a test of their hypothesis at some interim point in data collection (e.g., 24 infants). By adopting a clear stopping rule and an approach that adjusts for the increase in Type 1 error, this method may allow researchers to efficiently conduct high-powered studies even with difficult samples such as infant subjects. Importantly, these designs depend on planned interim data analysis, as flexible, undisclosed interim data analysis and stopping rules may lead to an increase in the publication of false positive results (see Simmons, Nelson, & Simonsohn, 2011). The point is that by adopting ethical, transparent means of “peeking” at the data (see Sagarin, Ambler, & Lee, 2014, for a suggestion), researchers may more effectively and efficiently obtain the samples sizes required to have sufficient power to draw strong conclusions from their results.

There are other solution to the problem of small sample sizes, as described by Tressoldi and Giofré (2015). The use of Bayes factors instead of p-values has been increasingly described as one solution. The Bayes factor can be used to indicate the relative likelihood of the observed results arising from the null versus alternative hypotheses (Jarosz & Wiley, 2014; Rouder et al., 2009; Wagenmakers et al., 2015). It may be possible to combine this approach with sequential hypothesis testing (Schönbrodt, Wagenmakers, Zehetleitner, & Perugini, 2015). Others have argued abandoning traditional testing altogether, with some suggesting that estimation statistics may be a reasonable alternative to traditional t tests (Claridge-Chang & Assam, 2016). Others have explored the value of p-curving, or the evaluation of the distribution of p-values across a set of experiments (Lakens & Evers, 2014; Simonsohn, Nelson, & Simmons, 2014a, 2014b). This may be one way researchers can look at the data across a collection of relatively small sample studies to assess their value. Other alternatives are to conduct resampling analyses to evaluate the replicability of an observed result, for example using a Jackknife approach (Ang, 1998), or permutation analyses (Berry, Johnston, & Mielke, 2011; Huo, Heyvaert, Van Den Noortgate, & Onghena, 2014). For such approaches to be successful, authors, editors, and reviewers need to be open to other ways of evaluating data, and using other approaches as the basis of our conclusions about those data. However, adopting new approaches may be critical for increasing our confidence about the conclusions we can draw from any particular finding, and as a result what conclusions we draw in general about our work. Although I have focused here on a narrow slice of infant research, these issues are important across methods, measures and questions.

Future work will make specific recommendations about how to address the issue of small sample sizes in infant looking time studies, or any subarea of infant development. Here I have illustrated an issue that we as a field need to address. In addition, by describing some of the approaches that are being considered in other areas of research, the hope is that infant researchers will expand the set of tools they use to evaluate their research to help draw the strongest conclusions from whatever sample sizes programs of research can support.

Appendix A

Papers listed in Table 1