Recent divergences in stratospheric water vapor measurements by frost point hygrometers and the Aura Microwave Limb Sounder

Abstract

Balloon-borne frost point hygrometers (FPs) and the Aura Microwave Limb Sounder (MLS) provide high-quality vertical profile measurements of water vapor in the upper troposphere and lower stratosphere (UTLS). A previous comparison of stratospheric water vapor measurements by FPs and MLS over three sites - Boulder, Colorado (40.0° N); Hilo, Hawaii (19.7° N); and Lauder, New Zealand (45.0° S) - from August 2004 through December 2012 not only demonstrated agreement better than 1% between 68 and 26 hPa but also exposed statistically significant biases of 2 to 10% at 83 and 100 hPa (Hurst et al., 2014). A simple linear regression analysis of the FP-MLS differences revealed no significant long-term drifts between the two instruments. Here we extend the drift comparison to mid-2015 and add two FP sites - Lindenberg, Germany (52.2° N), and San José, Costa Rica (10.0° N) - that employ FPs of different manufacture and calibration for their water vapor soundings. The extended comparison period reveals that stratospheric FP and MLS measurements over four of the five sites have diverged at rates of 0.03 to 0.07 ppmv year⁻¹ (0.6 to 1.5% year⁻¹) from ~2010 to mid-2015. These rates are similar in magnitude to the 30-year (1980–2010) average growth rate of stratospheric water vapor (~ 1% year⁻¹) measured by FPs over Boulder (Hurst et al., 2011). By mid-2015, the FP–MLS differences at some sites were large enough to exceed the combined accuracy estimates of the FP and MLS measurements.

1 Introduction

Water vapor in the Earth’s atmosphere influences the radiation budget by strongly attenuating outgoing long-wave radiation. Though the lower troposphere holds the vast majority of atmospheric water vapor, abundance changes in the relatively dry upper troposphere and lower stratosphere (UTLS) can significantly impact global surface temperatures and climate (Forster and Shine, 2002; Solomon et al., 2010). Satellite-based remote sensors have greatly enhanced our ability to monitor UTLS water vapor on a near-global scale. However, because of the limited operational lifetimes of satellite sensors, an analysis of trends over decadal or longer scales requires the merging of measurements by different instruments. Efforts to combine UTLS water vapor data sets from different satellites have demonstrated the need to reduce measurement biases between instruments before trend analyses are performed (Davis et al., 2016; Hegglin et al., 2014; Froidevaux et al., 2015). The necessity of adjusting data sets before they are merged imposes an additional source of uncertainty on any determination of long-term trends.

Balloon-borne frost point hygrometers (FPs) provide vertical profile measurements of water vapor at high resolution from the surface to the middle stratosphere (~ 28 km). Measurement programs with FPs typically focus on the UTLS for the purpose of long-term climate monitoring and/or studies of processes that influence humidity in the upper atmosphere (e.g., cloud microphysical processes that regulate dehydration). Though FP data sets are spatially and temporally sparse compared to those produced by satellite sensors, long-term records of UTLS water vapor – like the 36-year record over Boulder, Colorado – are invaluable for determining long-term trends (Oltmans and Hofmann, 1995; Oltmans et al., 2000; Rosenlof et al., 2001; Scherer et al., 2008; Hurst et al., 2011) and for validating satellite-based remote sensors like the Aura Microwave Limb Sounder (MLS; Vömel et al., 2007a; Hurst et al., 2014).

Nearly every day since August 2004 the Aura MLS has provided ~ 3500 near-global vertical profile measurements of water vapor from the UT well into the mesosphere, and it continues to do so today. Stratospheric water vapor measurements by the MLS and NOAA frost point hygrometers (FPHs) were recently compared to evaluate biases and temporal drifts between them during the period August 2004 through December 2012 (Hurst et al., 2014). Measurements over three UTLS water vapor monitoring sites of the Global Monitoring Division of NOAA’s Earth System Research Laboratory were compared: Boulder, Colorado; Hilo, Hawaii; and Lauder, New Zealand. Statistically significant FPH–MLS biases ranging from −0.10 (−2.2%) to −0.46 ppmv (−10.3%) were reported at 100 hPa over all three sites and at 83 hPa over Boulder and Hilo. Higher in the stratosphere, at the six MLS retrieval pressures from 68 to 26 hPa, the average FPH–MLS agreement was better than 0.04 ppmv (0.8%). FPH–MLS differences at each of the three sites were also analyzed for temporal drifts using weighted linear regression fits to the full records. With a few minor exceptions the linear trends in FPH–MLS differences through the end of 2012 were not statistically different from zero (Hurst et al., 2014).

Here we present an updated comparison of stratospheric water vapor measurements by FPs and the MLS for the period August 2004 through June 2015. Data from two different types of FPs are used: the NOAA FPH (Mastenbrook and Oltmans, 1983; Hall et al., 2016) and the cryogenic frost point hygrometer (CFH) (Vömel et al., 2007b; Vömel et al., 2016). The balloon-borne measurements are compared to MLS profiles obtained during overpasses of Boulder, Hilo, Lauder and two additional FP sounding sites: Lindenberg, Germany, and San José, Costa Rica (Table 1). Note that the Hilo and Lauder FP soundings were performed exclusively with the NOAA FPH, the Lindenberg and San José profiles are solely from the CFH, and the Boulder record combines soundings by both FP types. Though both FP types use the same measurement principle, they are built from different parts, are independently calibrated and have subtle yet important differences in their software and frost control logic. Data from the two FP types are also independently processed and quality assured.

Table 1.

Frost point hygrometer site information and coincident MLS profile statistics.

	Site	Altitude	Latitude	Longitude	Comparison	FP	FP	MLS Profiles	MLS Profiles
Site	Code	(m a.s.l.)	(° N)	(° E)	Start datea	Type	Profilesb	v3.3c	v4.2d
Lindenberg	LIN	112	52.21	14.12	2006.66	CFH	132	801	787
Boulder	BLD	1743	39.95	−105.20	2004.67	FPH/CFH	144/31	1000	990
Hilo	HIH	10	19.72	−155.05	2010.94	FPH	51	275	276
San José	SJC	1075	9.98	−84.13	2005.52	CFH	158	788	858
Lauder	LDR	370	−45.04	169.68	2004.65	FPH	117	463	458

^aDecimal date of first FP profile after the 2004.59 start of MLS data reporting

^bNumber of FP profiles with at least one coincident MLS profile

^cNumber of MLS version 3.3 profiles coincident with the FP profiles

^dNumber of MLS version 4.2 profiles coincident with the FP profiles.

FP profiles at each site are independently compared to MLS version 3.3 (v3.3) and the latest v4.2 water vapor retrievals using the same analysis methods. MLS v3.3 water vapor was retrieved until 30 June 2015, after which only v4.2 data are available. MLS v4.2 retrievals feature an improved cloud detection methodology, use more spectral channels and include an improved forward model for greater accuracy (Livesey et al., 2015). Unless otherwise noted, the values presented in the text and figures pertain to the comparison conducted with MLS v3.3 retrievals. Tables presenting results based on MLS v3.3 and v4.2 are so specified. We consider it essential to evaluate both MLS versions because many papers have been written using v3.3 retrievals and many more will be published using v4.2 retrievals. All water vapor mixing ratios are reported as mole fractions (µmol mol⁻¹ dry air) in units of parts per million by volume (ppmv).

2 Methods

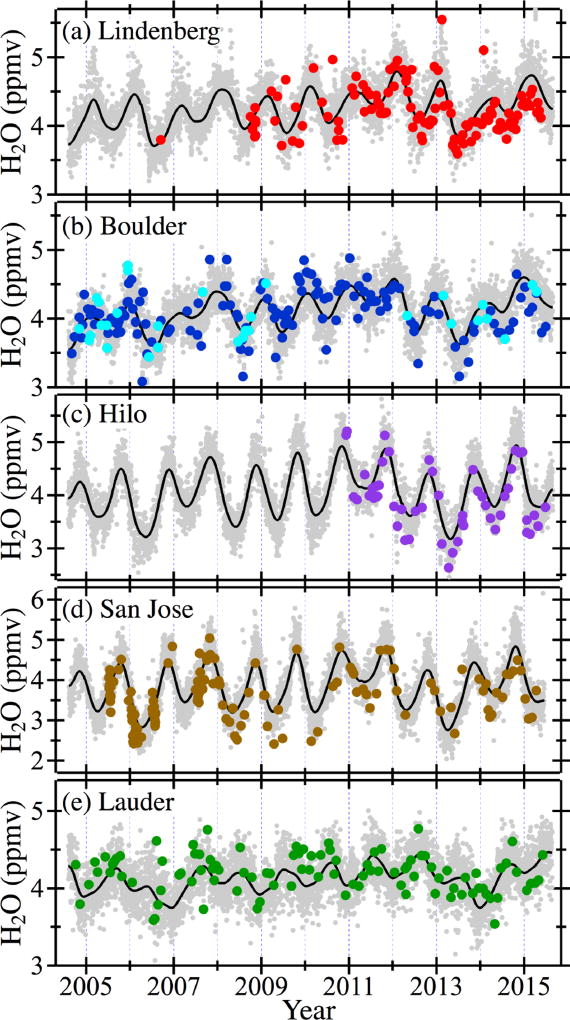
Evaluations of biases and drifts in coincident FP and MLS measurements of water vapor require that their profiles are matched in space and time. The same spatial criteria presented as “coincidence criteria set #1” in Hurst et al. (2014), within ±2° latitude and ±8° longitude, were employed to identify MLS profiles proximate to the five FP sounding sites. The spatially coincident MLS retrievals are plotted as time series along with the FP mixing ratios at 68 hPa over each site (Fig. 1). Note in Fig. 1 that, towards the end of each record, many of the markers representing FP mixing ratios reside near the lower limits of the MLS data envelope.

Figure 1.

Daily average MLS version 3.3 overpass retrievals (gray markers, smoothed black curves) and in situ frost point hygrometer (FP) data at 68 hPa for individual soundings at each site (filled circles). Data from two types of FPs are shown: NOAA FPH at Boulder (dark blue), Hilo and Lauder, and CFH at Lindenberg, Boulder (cyan) and San Jose. Note the emerging biases between FP and MLS mixing ratios at all five sites towards the ends of their records.

For this work a criterion of ±18 h was used to identify temporally coincident MLS and FP profiles. This enabled MLS profiles to be compared with 94–100% of the FP soundings at each site. Employing the spatial and temporal criteria together, an average of 4–6 spatiotemporally coincident MLS overpass profiles were identified per FP sounding at each of the 5 sites (Table 1). As in Hurst et al. (2014) the multiple MLS profiles coincident with each FP flight were distilled into a single “median” coincident profile composed of the median MLS mixing ratio at each pressure level. Our choice to use median rather than mean mixing ratios reduces the potential for any anomalous MLS retrievals to skew the values used for this comparison.

Before FP-MLS differences were computed, each FP profile was convolved with the MLS averaging kernels to degrade its high vertical resolution to the ~ 3 km resolution of lower-stratospheric MLS retrievals and place the FP mixing ratio “retrievals” on the MLS pressure grid (Read et al., 2007; Lambert et al., 2007). Each convolution employed a forward model, operating in log(P)–log(H₂O) space, that ingests both the FP profile and an a priori profile (Read et al., 2007). We used the MLS median profiles as a priori profiles because they produce convolved profiles equivalent to those generated using the actual MLS a priori profiles (Hurst et al., 2014). FP profiles were independently convolved with the MLS v3.3 and v4.2 averaging kernels for eight MLS retrieval pressure levels: 100, 83, 68, 56, 46, 38, 32 and 26 hPa. FP mixing ratios were not retrieved at pressures < 26 hPa because the averaging kernels require data above the typical maximum altitude of high-quality FP measurements. Although convolved FP retrievals at pressures > 100 hPa are feasible, the coincidence criteria applied to FP and MLS retrievals at pressure levels 100–26 hPa produced very noisy comparison results at > 100 hPa, presumably due to the much greater variability of water vapor at pressures > 100 hPa, especially in the tropics. Applying more stringent coincidence criteria to improve the spatiotemporal matching of FP and MLS data below 100 hPa severely reduces the number of coincident profiles at each site and diminishes the value of the statistics generated by this type of comparison.

FP–MLS differences were calculated for each FP sounding by subtracting the MLS median coincident profile from the convolved FP profile. Statistical outliers were identified independently for each site and pressure level by evaluating the residuals of FP–MLS differences from smoothed time series of the differences. Points with absolute residuals exceeding twice the mean absolute residual were flagged as outliers and excluded from further study. Approximately 10% of the FP–MLS differences were flagged as outliers.

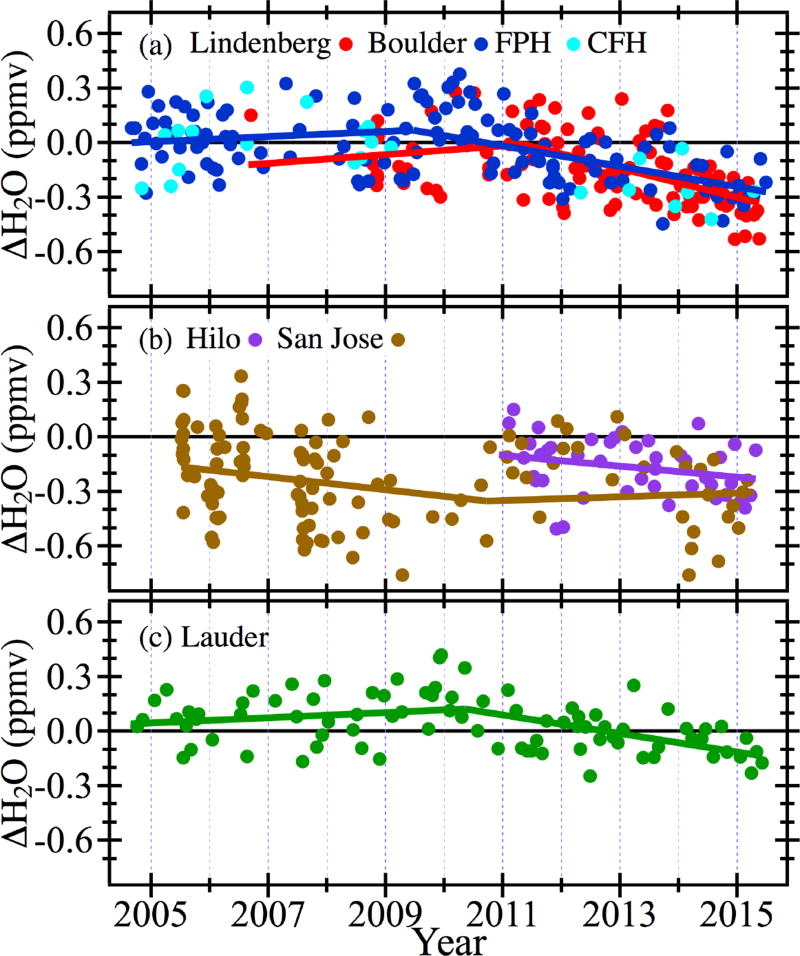
For some sites the records of FP–MLS differences at 68 hPa visually exhibit time-dependent changes in trends (Fig. 2). Many of the time series at other pressure levels over the sites (not shown) also show these same characteristics. Intuitively, full-record linear trend analyses of these time series of differences would greatly misrepresent the data. Instead, the time-dependent changes in these records indicate they should be evaluated for a statistically significant “change-point”, the point where the mean of the time series first undergoes a structural pattern change. Such an analysis was performed on each time series of FP–MLS differences using the two-phase regression model described by Lund and Reeves (2002). The model considers every data point to be a potential undocumented changepoint and calculates an F-statistic for each. The F-statistic is a quantitative assessment of how much the sum of squared residuals is reduced when the time series is fit in two periods (separated by the change-point) instead of one period. The maximum in the time series of F-statistics, F_max, identifies the most probable change-point in the time series.

Figure 2.

Differences between FP mixing ratios and spatiotemporally coincident MLS v3.3 water vapor retrievals at 68 hPa over the five FP sounding sites. In the top panel (a) dark blue and cyan markers for Boulder depict soundings made with the NOAA FPH and the CFH, respectively. Lines show the trends in FPH–MLS differences in two distinct periods separated by a changepoint, except for Hilo where the shorter FP records show no indications of statistically significant changepoints.

The two-phase regression model was first applied to time series of smoothed FP-MLS differences at each site to look for conformity between the detected changepoints. Except for Hilo, nearly all of the changepoints identified for the eight pressure levels above each site were within ±1 year of the mean changepoint for the site. This intra-site consistency facilitated the recognition of any non-conforming changepoints found when the model was applied to time series of unsmoothed FP-MLS differences. When an anomalous changepoint was detected in the unsmoothed differences, the time series of F-statistics was examined for a secondary maximum nearer in time to the consensus changepoint for that site. The value of the F-statistic at the secondary maximum was typically only slightly less than F _max, so the more conforming changepoint of the secondary maximum was used instead of the anomalous changepoint.

The dates and confidence levels of the changepoints for each time series of FP-MLS differences (except at Hilo) are presented in Table 2. For Hilo the analysis found no discernsable maxima (F_max) in the time series of F-statistics, probably because the record only began at the end of 2010, after the changepoints that were determined for most other sites. Visually the time series of differences at Hilo depict decreasing trends from the start of the record (Fig. 2b).

Table 2.

Changepoint dates and their confidence levels, MLS version 3.3.

	Lindenberg		Boulder		San José		Lauder
Pressure	Changepoint	CLa	Changepoint	CL	Changepoint	CL	Changepoint	CL
(hPa)	(year)	(%)	(year)	(%)	(year)	(%)	(year)	(%)
26	2011.4	83	2009.1	> 99	2008.9	66	2010.4	> 99
32	2011.1	>99	2009.0	> 99	2010.8	45	2010.7	99
38	2011.3	>99	2009.5	> 99	2009.3	48	2010.7	> 99
46	2011.6	92	2009.5	> 99	2008.9	71	2010.6	> 99
56	2011.9	94	2009.3	> 99	2010.1	> 99	2010.6	> 99
68	2011.4	99	2009.5	> 99	2010.7	> 99	2010.4	> 99
83	2011.4	80	2009.3	> 99	2010.6	> 99	2010.7	93
100	2011.7	40	2009.1	> 99	2009.1	73	2011.1	94
Meanb	2011.5		2009.3		2009.8		2010.6
SD	0.3		0.2		0.9		0.2

^aConfidence levels for the listed changepoint dates, with > 99 indicating a value between 99 and 100%.

^bMean and standard deviation of the changepoint dates for each site.

The confidence level of each changepoint was calculated using the 90th, 95th and 99th percentiles of the F _max distribution as a function of n (time series length) presented in Table 1 of Lund and Reeves (2002). Confidence levels for F-statistic values between the 90th and 99th percentiles and for values below the 90th percentile were interpolated and extrapolated, respectively, using a quadratic fit to the n-dependent percentiles. Confidence levels for F-statistic values above the 99th percentile are reported as > 99% (Table 2). Of the 32 changepoints identified for Lindenberg, Boulder, San José and Lauder, the confidence levels of 24 are ≥90% and all but 4 are > 68%, substantiating the need to break each time series into two separate intervals (periods 1 and 2) for trend analysis. The mean and standard deviation of the 8 changepoints for each site are also presented in Table 2. Dissimilarities between the mean changepoints for the four sites are probably due in part to the disparate lengths and data populations of the FP records prior to their changepoints.

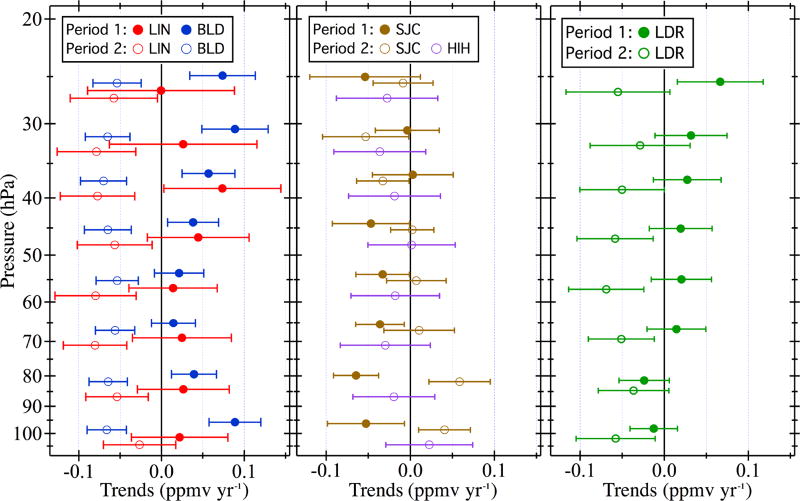
Changepoints with high confidence levels were successfully identified in the time series of FP-MLS differences using piecewise linear regression, so this same analysis method was also used to evaluate trends in the differences. Piecewise continuous linear regression fits (i.e., perfectly connected at the changepoint) were employed instead of non-continuous fits because there is no evidence of step jumps in FP-MLS differences at the changepoints. The absence of step jumps is confirmed by the lack of statistically significant (2σ) differences between 1-year averages of FP-MLS before and after the changepoints. The piecewise continuous linear fits included statistical weights (reciprocals of the squared uncertainties of the FP-MLS differences) determined from the combined uncertainties (in quadrature) of the FP and MLS mixing ratios. Each MLS uncertainty was computed as the product of the standard error (σ/√ n) of the median MLS mixing ratio and the Student t value for 95% confidence. FP uncertainties were estimated (95% confidence) as 5% of the FP mixing ratios (see Sect. 5). Trends for periods 1 and 2 are presented with their uncertainties in Table 3 and Fig. 3. Trend uncertainties were computed as the products of the fit slope uncertainties and the Student t values for 95% confidence. Fits of the Hilo differences were performed using weighted linear regression over the full-record period (decimal dates 2010.95–2015.5). The resulting period 2 trends and their uncertainties are included in Table 3 and Fig. 3.

Table 3.

Linear regression slopes of FP–MLS v3.3 differences. Slopes are presented with their 95% confidence intervals. Periods 1 and 2 refer to the intervals before and including the changepoint (Table 2) and immediately after the changepoint to 30 June 2015, respectively. Values in boldface type are statistically different from zero with 95% confidence.

MLS		Lindenberg	Boulder	Hilo	San José	Lauder
Pressure	Period	(ppmv year−1)	(ppmv year−1)	(ppmv year−1)	(ppmv year−1)	(ppmv year−1)
26	1	−0.001 ±0.089	0.074± 0.040		−0.054 ±0.066	0.066± 0.051
32	1	0.026 ±0.089	0.089± 0.040		−0.004 ±0.038	0.032± 0.043
38	1	0.073 ±0.071	0.057± 0.032		0.003 ±0.048	0.027± 0.040
46	1	0.044 ±0.061	0.038± 0.031		−0.047 ±0.046	0.019± 0.037
56	1	0.014 ±0.053	0.021± 0.030		−0.033 ±0.032	0.020± 0.036
68	1	0.024 ±0.060	0.014± 0.027		−0.036 ±0.029	0.014± 0.035
83	1	0.026 ±0.056	0.039± 0.027		−0.065 ±0.027	−0.024± 0.030
100	1	0.022 ±0.058	0.089± 0.031		−0.053 ±0.046	−0.013± 0.028
26	2	−0.058 ±0.053	−0.054± 0.029	−0.028 ±0.060	−0.009 ±0.036	−0.055± 0.062
32	2	−0.079 ±0.048	−0.065± 0.027	−0.036 ±0.055	−0.053 ±0.051	−0.029± 0.059
38	2	−0.077 ±0.045	−0.070± 0.028	−0.019 ±0.055	−0.033 ±0.031	−0.050± 0.050
46	2	−0.057 ±0.045	−0.065± 0.028	0.001 ±0.052	0.002 ±0.026	−0.058± 0.045
56	2	−0.080 ±0.049	−0.054± 0.025	−0.018 ±0.053	0.007 ±0.035	−0.069± 0.045
68	2	−0.081 ±0.038	−0.056± 0.024	−0.030 ±0.053	0.011 ±0.042	−0.051± 0.039
83	2	−0.054 ±0.038	−0.065± 0.023	−0.020 ±0.049	0.059 ±0.036	−0.036± 0.042
100	2	−0.027 ±0.044	−0.066± 0.024	0.023 ±0.052	0.041 ±0.031	−0.058± 0.047

Figure 3.

Trends in FP–MLS differences for the pre- and post-changepoint periods at eight stratospheric pressure levels (100–26 hPa) over the five FP sounding sites. Markers for each pressure level are slightly offset in pressure for clarity. Horizontal error bars depict the 95% confidence intervals of the trends. Only period 2 trends are shown for Hilo because the shorter records show no indications of statistically significant changepoints.

For FP-MLS differences computed using MLS v4.2 retrievals the changepoints and confidence levels (Table 4) are very similar to those for v3.3 (Table 2). Mean changepoints for each of the four sites are different by ≤ 0.3 year from those calculated in the v3.3 analysis. Many of the trends determined from weighted, piecewise continuous linear regression fits to the FP–MLS v4.2 differences (Table 5) are also very similar to those for the v3.3 retrievals (Table 3).

Table 4.

Changepoint dates and their confidence levels, MLS version 4.2.

	Lindenberg		Boulder		San José		Lauder
Pressure	Changepoint	CLa	Changepoint	CL	Changepoint	CL	Changepoint	CL
(hPa)	(year)	(%)	(year)	(%)	(year)	(%)	(year)	(%)
26	2011.4	96	2009.1	>99	2008.9	69	2010.6	> 99
32	2011.4	99	2009.0	>99	2010.8	39	2010.7	> 99
38	2011.3	>99	2010.0	>99	2010.8	76	2010.7	> 99
46	2011.7	92	2009.6	>99	2009.5	86	2010.6	> 99
56	2011.6	87	2009.3	>99	2010.1	96	2010.6	> 99
68	2011.4	>99	2009.5	>99	2010.6	> 99	2011.1	> 99
83	2011.4	83	2010.2	>99	2010.9	> 99	2010.7	97
100	2011.4	73	2009.1	>99	2009.1	78	2010.7	> 99
Meanb	2011.4		2009.5		2010.1		2010.7
SD	0.1		0.4		0.8		0.2

^aConfidence levels for the listed changepoint dates, with >99 indicating a value between 99 and 100%

^bMean and standard deviation of the listed changepoint dates for each site.

Table 5.

Linear regression slopes of FP–MLS v4.2 differences. Slopes are presented with their 95% confidence intervals. Periods 1 and 2 refer to the intervals before and including the changepoint (Table 4) and immediately after the changepoint to 30 June 2015, respectively. Values in boldface type are statistically different from zero with 95% confidence.

MLS		Lindenberg	Boulder	Hilo	San José	Lauder
Pressure	Period	(ppmv year−1)	(ppmv year−1)	(ppmv year−1)	(ppmv year−1)	(ppmv year−1)
26	1	0.007 ±0.089	0.077± 0.041		−0.054 ±0.065	0.053± 0.047
32	1	0.026 ±0.082	0.081± 0.040		−0.015 ±0.038	0.026± 0.043
38	1	0.076 ±0.071	0.052± 0.029		0.009 ±0.034	0.033± 0.040
46	1	0.046 ±0.061	0.038± 0.030		−0.013 ±0.039	0.011± 0.038
56	1	0.023 ±0.059	0.022± 0.030		−0.026 ±0.033	0.017± 0.035
68	1	0.032 ±0.059	0.018± 0.027		−0.019 ±0.031	0.005± 0.029
83	1	0.030 ±0.058	0.029± 0.024		−0.028 ±0.025	−0.017± 0.030
100	1	0.064 ±0.066	0.079± 0.030		−0.037 ±0.047	−0.023± 0.030
26	2	−0.062 ±0.053	−0.056± 0.030	−0.015 ±0.070	−0.011 ±0.035	−0.044± 0.063
32	2	−0.079 ±0.051	−0.064± 0.027	−0.032 ±0.057	−0.029 ±0.051	−0.024± 0.060
38	2	−0.071 ±0.045	−0.082± 0.031	−0.014 ±0.055	−0.055 ±0.047	−0.059± 0.050
46	2	−0.054 ±0.046	−0.063± 0.029	−0.005 ±0.052	−0.007 ±0.031	−0.060± 0.045
56	2	−0.065 ±0.044	−0.055± 0.026	−0.030 ±0.055	−0.002 ±0.036	−0.075± 0.043
68	2	−0.079 ±0.039	−0.054± 0.024	−0.038 ±0.053	−0.013 ±0.042	−0.064± 0.047
83	2	−0.058 ±0.038	−0.083± 0.028	−0.059 ±0.052	0.043 ±0.041	−0.025± 0.045
100	2	−0.037 ±0.039	−0.077± 0.023	−0.001 ±0.050	0.022 ±0.031	−0.064± 0.041

3 Results for MLS v3.3

In the remainder of this work we report stratospheric averages of trends and changes in FP–MLS differences. These are computed as weighted averages over the eight pressure levels above each site. Weights are the reciprocals of squared trend uncertainties (95% confidence), yielding uncertainties with 95% confidence. Unless otherwise noted, averages reported in relative units (%) are based on the mean stratospheric water vapor mixing ratio of 4.4 ppmv from 100 to 26 hPa.

Almost all of the period 1 trends in FP-MLS differences over Lindenberg, Boulder and Lauder are positive, but for each of Lindenberg and Lauder these trends are statistically different from zero (95% confidence) at only one pressure level (Table 3). For Boulder, period 1 trends at six pressure levels are statistically significant, yielding a stratospheric average trend of 0.047 ±0.011 ppmv year⁻¹ (Table 6). The period 1 stratosphere-averaged trend over Boulder translates to a mean change of 0.22 ± 0.05 ppmv (5.0 ± 1.2%) in FP-MLS differences over ~ 4.6 years (August 2004 to mid-2009). Stratosphere-averaged period 1 changes at Lindenberg and Lauder were smaller: 0.14 ± 0.11 and 0.06 ± 0.08 ppmv, respectively (Table 6). Period 1 trends at seven of the eight pressure levels above San José are negative, yielding a stratosphere-averaged change of −0.17 ± 0.06 ppmv (−3.8 ± 1.3%) in FP-MLS differences from 2005.5 to ~2009.9.

Table 6.

Stratospheric average trends and changes in FP–MLS differences. Weighted averages of trends and changes in FP–MLS differences at all eight pressure levels (100–26 hPa) over each site. Stratospheric averages are presented with their 95% confidence limits. All values were computed using the regression slopes and their uncertainties in Tables 3 and 5. Values in boldface type are significantly different from zero with 95% confidence.

		Period 1		Period 2		Full record
	MLS	Trend	Change	Trend	Change	Change
Site	Version	(ppmv year−1)	(ppmv)	(ppmv year−1)	(ppmv)	(ppmv)
Lindenberg	3.3	0.029 ±0.023	0.14 ±0.11	−0.064± 0.016	−0.25± 0.06	−0.11± 0.13
Lindenberg	4.2	0.039 ±0.023	0.19 ±0.11	−0.062± 0.015	−0.25± 0.06	−0.07± 0.13
Boulder	3.3	0.047 ±0.011	0.22 ±0.05	−0.062± 0.009	−0.38± 0.06	−0.16± 0.08
Boulder	4.2	0.044 ±0.011	0.22 ±0.05	−0.066± 0.010	−0.40± 0.06	−0.18± 0.08
Hilo	3.3			−0.015± 0.019	−0.07± 0.09
Hilo	4.2			−0.025± 0.019	−0.11± 0.09
San José	3.3	−0.039 ±0.013	−0.17 ±0.06	0.006± 0.012	0.04± 0.07	−0.12± 0.09
San José	4.2	−0.020 ±0.012	−0.10 ±0.06	−0.002± 0.013	−0.02± 0.07	−0.11± 0.09
Lauder	3.3	0.009 ±0.013	0.06 ±0.08	−0.052± 0.017	−0.25± 0.08	−0.19± 0.11
Lauder	4.2	0.006 ±0.012	0.04 ±0.07	−0.054± 0.017	−0.26± 0.08	−0.21± 0.11

All but 4 of the 24 period 2 trends at Lindenberg, Boulder and Lauder are negative and statistically significant (Table 3, Fig. 3). Stratosphere-averaged trends are −0.064 ±0.016, −0.062 ± 0.009 and −0.052 ±0.017 ppmv year⁻¹, respectively (Table 6), demonstrating relatively consistent rates of change (−1.2 to −1.5% year⁻¹) in the FP-MLS differences. These mean trends translate to stratosphere-averaged changes of −0.25 ppmv (−5.8%), −0.38 ppmv (−8.7%) and −0.25 ppmv (−5.7%) over the period 2 lengths of roughly 4.0, 6.2 and 5.1 years, respectively. This is compelling evidence that FP–MLS differences at these three extratropical sites changed significantly during the 4– 6 years prior to mid-2015.

All but one of the period 2 trends at Hilo are negative, but none are statistically significant due to the shorter FP measurement record. The stratosphere-averaged trend in FP–MLS differences at Hilo, −0.015 ±0.019 ppmv year⁻¹, also lacks statistical significance (95% confidence). Period 2 trends at San José are split between positive and negative, with two of each being statistically different from zero (Table 3). The resulting stratosphere-averaged period 2 trend for San José is small and not statistically different from zero.

Changes in FP–MLS differences over the entire comparison period are calculated by summing the changes for periods 1 and 2 at each pressure level. For Lindenberg, Boulder and Lauder the stratosphere-averaged full-record changes are −0.11±0.13, −0.16±0.08 and −0.19±0.11 ppmv, respectively (Table 6). Uncertainties in the full-record changes were calculated from the combined (in quadrature) uncertainties of the period 1 and 2 changes at each of the eight pressure levels, not from the stratospheric averages in Table 6. Remarkably the stratosphere-averaged full-record change of −0.12 ±0.09 ppmv at San José is similar to those at the other sites despite the period 1 changes at San José being mostly negative.

4 Results for MLS v4.2

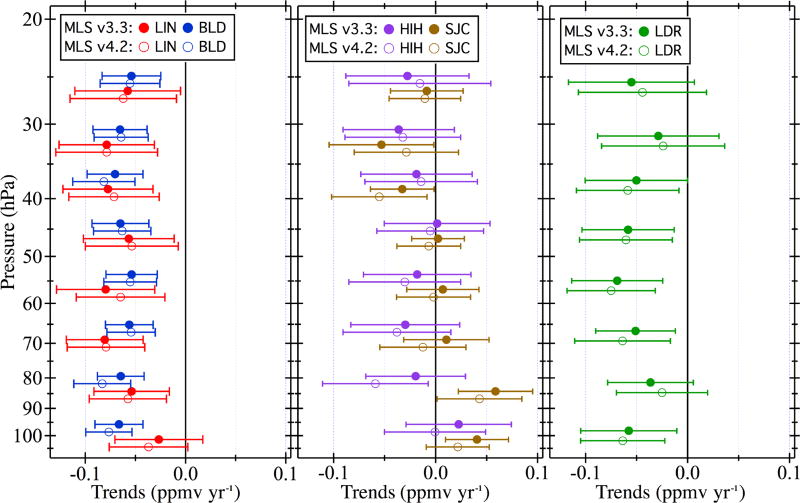
Trends in FP–MLS v4.2 differences (Table 5) are, for the most part, very similar to those determined for v3.3 (Table 3). Period 2 trends calculated using v3.3 and v4.2 retrievals (Fig. 4) demonstrate that the choice of MLS version makes little difference to the results. An exception is at Hilo, where the switch from v3.3 to v4.2 strengthens the negative period 2 trends at 83 and 100 hPa, and intensifies the stratosphere-averaged trend from −0.015 ±0.019 to −0.025 ± 0.019 ppmv year⁻¹. Interestingly the choice of MLS retrieval version also makes a significant difference in the period 1 trends at San José, with v3.3 yielding a stronger stratosphere-averaged trend of −0.039 ± 0.013 ppmv year⁻¹ than v4.2 (−0.020±0.012 ppmv year⁻¹). The choice of MLS version makes very little difference to the stratosphere-average period 2 trends at San José even though v4.2 reduces the number of pressure levels with significant trends from four to two.

Figure 4.

Period 2 trends in FP–MLS differences using MLS v3.3 (filled circles) and v4.2 (open circles) retrievals at eight stratospheric pressure levels (100–26 hPa) over the five FP sounding sites. Markers for each pressure level are slightly offset in pressure for clarity. Horizontal error bars depict the 95% confidence intervals of the trends.

5 Discussion

The magnitudes of statistically significant stratosphere-averaged trends in FP-MLS differences (−0.6 to −1.5% year⁻¹) from ~2010 to mid-2015 are similar in magnitude to the ~ 1% year⁻¹ average stratospheric water vapor increase reported from FP measurements over Boulder during 1980–2010 (Hurst et al., 2011). Negative trends in FP-MLS differences imply that MLS measurements have biased high, that FP measurements have biased low or that some combination of both has occurred over the last 4–6 years. Given these scenarios, an increasing trend in stratospheric water vapor would be exaggerated by MLS measurements that have biased high and underestimated or undetected by FP measurements that have biased low. For a decreasing water vapor trend the effects of these temporally changing biases would be reversed.

Here we assess the recent changes in FP–MLS differences in relation to the estimated accuracies of stratospheric water vapor measurements by the MLS and FPs. Accuracy estimates for MLS v3.3 and v4.2 retrievals are identical and range from 4 to 8% (0.18 to 0.32 ppmv) over the pressure levels of interest (Livesey et al., 2013; Livesey et al., 2015). Vömel et al. (2007a) assessed the stratospheric measurement uncertainties of the CFH and estimated the accuracy to be < 10% (< 0.5 ppmv), but a recent reassessment lowers the uncertainty estimate (1σ) to < 5% (Vömel et al., 2016). A recent evaluation of the NOAA FPH (Hall et al., 2016) demonstrates that the stratospheric measurement uncertainties (2σ ) are <6% (<0.3 ppmv). Employing 3 and 5% as 1σ and 2σ accuracy estimates for the FPs, the combined (in quadrature) accuracy estimates of FP and MLS measurements of stratospheric water vapor at the eight retrieval pressures range from 5.0 to 8.5% (0.23 to 0.34 ppmv) and 6.4 to 9.4% (0.29 to 0.40 ppmv), respectively. From here forward the combined accuracy estimates for FPs and MLS based on FP measurement uncertainties of 3 and 5% are denoted ACC_FP3 and ACC_FP5, respectively.

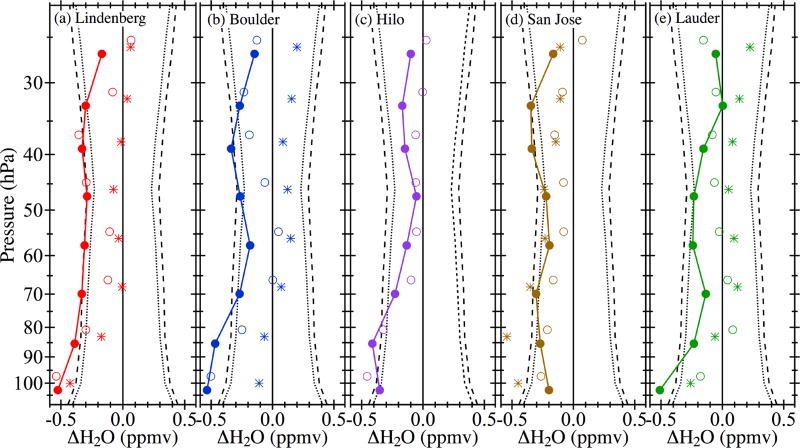
Figure 5 displays the values of FP–MLS differences (v3.3) at the start of each record, at the changepoint and at the end of each record for the eight pressure levels, as determined by the piecewise linear fits described above. By the end of the comparison period in mid-2015, 18 of the 40 differences exceeded the ACC_FP3 and another 5 were within 0.05 ppmv of the ACC_FP3. End point differences surpassed the more conservative ACC_FP5 estimates for 11 site–pressure level combinations, and another 5 were within 0.05 ppmv of the ACC_FP5. Six of the end point differences exceeding the ACC_FP5 were at 100 and 83 hPa, pressure levels for which FP–MLS biases of up to 10% have already been reported (Hurst et al., 2014).

Figure 5.

FP–MLS v3.3 differences at the starting points (open circles), changepoints (asterisks) and ending points (filled circles) of the time series as defined by piecewise continuous linear fits. Colored vertical curves join the ending points to serve as visual guides. Black vertical curves depict the combined accuracy estimates for FP and MLS measurements of stratospheric water vapor based on FP accuracy values of 3% (dotted) and 5% (dashed). Note that many of the ending point values lie near or outside the combined accuracy estimates. For Hilo only the starting and ending point differences are presented because no significant changepoints were detected in the shorter records.

By mid-2015 the FP–MLS differences at seven pressure levels over Lindenberg exceeded the ACC_FP5 (Fig. 5). However, the starting point differences for four of these seven levels also exceeded or nearly exceeded the ACC_FP5 (Fig. 5), indicating that the large differences in mid-2015 resulted from the continuation of long-term biases rather than recent drifts. At the other three pressure levels over Lindenberg the end point differences exceeded ACC_FP5 because of large decreases in FP–MLS differences during period 2. At Boulder, six and four end point differences exceeded or were within 0.05 ppmv of the ACC_FP3 and ACC_FP5, respectively, with all but one (100 hPa) caused by strong negative period 2 trends. At Lauder and San José, one and three end point differences exceeded or were within 0.05 ppmv of the ACC_FP5, respectively, all of which resulted from strong declines. At Hilo the starting point and end point differences at 100 and 83 hPa exceeded or were within 0.05 ppmv of the ACC_FP5, consistent with the long-term biases already reported for these pressure levels (Hurst et al., 2014).

Very similar results were obtained when MLS v4.2 retrievals were employed (not shown). By mid-2015, 44 and 25% of the FP–MLS differences (both MLS versions) exceeded the ACC_FP3 and ACC_FP5, respectively. Likewise, 57 and 40% of the end point differences exceeded or were within 0.05 ppmv of the ACC_FP3 and ACC_FP5 estimates, respectively. If the recent divergences between FPs and MLS continue, they will inevitably push FP–MLS differences at most pressure levels to exceed the combined accuracy estimates of the two instruments.

It is intriguing that the period 2 trends at the three extratropical sites are similar to one another but disparate from those at tropical San José. The differences at Hilo have also drifted downward since late 2010, but the FPH record is too short to permit the detection of statistically significant trends. We deliberately compared MLS retrievals with five different records of in situ, balloon-borne measurements compiled using two independent FPs with different manufacturers, calibration, frost control parameters and data processing. Our finding of similar divergences (not step changes) in FP and MLS measurements over the three extratropical sites suggests a positive drift in MLS retrievals over these locations, primarily because it is highly unlikely that the two different types of FPs are drifting at similar rates at the three sites. We plan to continue closely comparing MLS and FP measurements over these five sites to ascertain if they continue to diverge, settle into a stable bias or start to reconverge.

The causes of the recent divergences in stratospheric water vapor measurements by FPs and MLS at Lindenberg, Boulder and Lauder are currently unknown. The MLS team is actively exploring multiple avenues in their investigation of possible instrumental behaviors that might lead to water vapor measurement drifts of the magnitudes documented here. For example, the relationship between the MLS “standard” O₃ product, measured in the 240 GHz region and shown to be very stable (Hubert et al., 2016), and a secondary MLS O₃ product obtained from the same 190 GHz spectral region used for the water vapor measurements is being closely examined. At this stage it is premature to offer conclusions from these studies.

Given the known sensitivities of MLS retrievals to atmospheric temperature changes, an annual drift of 1% in water vapor retrievals would require a steep temperature trend of 2.5 K year⁻¹ that is not observed in the temperature retrievals of MLS or other instruments. Such a temperature trend would also manifest itself as drifts in the MLS retrievals of other atmospheric constituents, like ozone, that are absent from the measurement records. Frost point hygrometers are stable over a wide range of atmospheric temperatures (−80 to 30 °C) because their electronics are well insulated and their measurements are independent of atmospheric temperatures. It is therefore highly unlikely that atmospheric temperature changes are driving the observed drifts in MLS retrievals or FP measurements of water vapor.

6 Conclusions

Recent, significant divergences in stratospheric water vapor measurements by balloon-borne frost point hygrometers and the Aura Microwave Limb Sounder are reported for four globally distributed FP sites: Lindenberg, Germany; Boulder, Colorado; Hilo, Hawaii; and Lauder, New Zealand. These sites employ two types of FPs with different manufacturers, calibration, frost control parameters and data processing. The rates of divergence from ~ 2010 to mid-2015 range from 0.03 to 0.07 ppmv year⁻¹ (0.6 to 1.5% year⁻¹), similar in magnitude to the ~ 1% year⁻¹ average growth rate of stratospheric water vapor observed over Boulder during 1980–2010 (Hurst et al., 2011). By mid-2015, the FP-MLS differences at some sites were large enough to exceed the 5–8% (1 σ) combined accuracy estimates of the FP and MLS measurements.

These divergences should prompt serious discussions about our future capabilities to monitor UTLS water vapor around the globe. Currently there is no comprehensive, long-term plan for a monitoring program that even approaches the 3500 near-global profiles per day by MLS (Müller et al., 2016). A third-generation Stratospheric Aerosol and Gas Experiment (SAGE III) spectrometer is ready to be deployed in late 2016 on the International Space Station, where it will provide an average of 32 vertical profiles of UTLS water vapor each day. Ultimately, when Aura MLS fails, there will be an immediate 99% reduction in the spatiotemporal density of measurements because there is no plan to replace MLS with a satellite sensor of similar capabilities. For this reason Müller et al. (2016) have proposed the creation of a large network of FPs covering the globe and funded in a committed way that would make the network sustainable for many decades. Towards this goal, a network of 20–30 globally distributed FP sounding sites is in development as part of the Global Climate Observing System (GCOS) Reference Upper Air Network (GRUAN; Bodeker et al., 2016). However, even with a FP network of 100 sites performing weekly soundings the spatiotemporal density of UTLS water vapor measurements would be only 0.4% of what MLS is currently providing.

7 Data availability

NOAA FPH data for Boulder, Hilo and Lauder are available via anonymous ftp at ftp://ftp.cmdl.noaa.gov/data/ozwv/WaterVapor. FP data for all five sites will be made available through the GCOS Reference Upper Air Network (http://www.gruan.org) and the Network for the Detection of Atmospheric Composition Change (http://www.ndsc.ncep.noaa.gov). MLS version 3.3 data for overpasses of the five FP sites are available at the Aura Validation Data Center (http://avdc.gsfc.nasa.gov/pub/data/satellite/Aura/MLS/V03/L2GPOVP/H2O). For version MLS 4.2 overpass data please substitute “V04” for “V03 ” in the URL.