Single-Arm Phase II Survival Trial Design Under the Proportional Hazards Model

Abstract

For designing single-arm phase II trials with time-to-event endpoints, a sample size formula is derived for the modified one-sample log-rank test under the proportional hazards model. The derived formula enables new methods for designing trials that allow a flexible choice of the underlying survival distribution. Simulation results showed that the proposed formula provides an accurate estimation of sample size. The sample size calculation has been implemented in an R function for the purpose of trial design.

1 Introduction

A time-to-event endpoint, such as event-free survival or overall survival, is often the primary endpoint for cancer clinical trials. In pediatric oncology, single-arm phase II trials with time-to-event endpoints are often conducted with limited numbers of patients. Various statistical methods have been proposed for designing randomized phase III trials with time-to-event endpoints (e.g., by George and Desu, 1977; Lachin, 1981; Rubenstein et al., 1981; Schoenfeld, 1983; Lakatos, 1988; Barthel et al. 2006; and many others). However, the literature on designing single-arm phase II trials with time-to-event endpoints is relatively scarce. The current practice for designing such trials is limited to using a parametric maximum likelihood test under the exponential model or a naive approach based on dichotomizing the event time at a landmark time point (Owzar and Jung, 2008). Trial design under the exponential model may not be reliable and the naive approach is inefficient.

Recently, Kwak and Jung (2014) proposed a two-stage phase II survival trial design using the one-sample log-rank test (OSLRT) (Breslow, 1975; Woolson, 1981; and Finkelstein et al., 2003). However, simulation results showed that Kwak and Jung’s design is conservative and underpowered. To correct the power and conservativeness of the OSLRT, Wu (2015) proposed a modified one-sample log-rank test (MOSLRT) for single-arm phase II survival trial designs. The MOSLRT preserves the type I error well and provides adequate power for trial design for a class of common parametric survival distributions. However, all the parametric survival distributions make strong assumptions about the shape of the hazard functions and are difficult to validate for historical data. In this paper, formulae for the number of events and sample size are derived under the proportional hazards model. The derived formula for the number of events is an analog version of the Schoenfeld formula for a two-arm randomized phase III trial using the two-sample log-rank test (Schoenfeld, 1983). Trial design based on the proposed sample size formula offers great flexibility in choosing of the underlying survival distribution, which could be a parametric survival distribution, a non-parametric Kaplan-Meier curve, or a spline version of the survival distribution (Kooperberg and Stone, 1992; Bantis et al., 2012; Anderson et al., 2013).

The rest of the paper is organized as follows. The MOSLRT is introduced in section 2. The formulae for the number of events and sample size are derived in section 3. Parameter setting for trial design is discussed in section 4. Simulations are conducted to study the performance of the proposed methods in section 5. An example is given in section 6 to illustrate the single-arm phase II survival trial designs. Concluding remarks are made in section 7.

2 Test Statistics

Let S₀(t) denote the survival function under the null hypothesis that is chosen for a single-arm phase II trial design. Let S(t) denote the survival function of the experimental treatment. Consider the following proportional hazards model:

$$S\left(t\right)={\left[S_0\left(t\right)\right]}^{\delta },$$ (1)

where δ(> 0) is the hazard ratio. The hypothesis of improvement in survival with the experimental treatment is

$$H_0:\delta \ge 1\text{vs}.H_1:\delta <1.$$ (2)

Testing this hypothesis is equivalent to testing the difference between the survival distributions with the experimental treatment and under the null hypothesis. Thus, the OSLRT can be used. However, the OSLRT is conservative, as shown by Kwak and Jung (2014); Sun et al. (2010); and Wu (2015). Recently, Wu (2015) proposed a MOSLRT that preserves the type I error well and provides adequate power for study design. To introduce the MOSLRT, assume that during the accrual phase of the trial, n subjects are enrolled in the study. Let T_i and C_i denote the event time and censoring time, respectively, of the i^th subject. We assume that the event time T_i and censoring time C_i are independent and that {T_i, C_i, i = 1, …, n} are independent and identically distributed. Then, the observed event time and event indicator are X_i = T_i ∧C_i and Δ_i = I(T_i ≤ C_i), respectively, for the i^th subject. On the basis of the observed data {X_i, Δ_i, i = 1,…, n}, we define $O={\displaystyle {\sum }_{i=1}^n{\mathrm{\Delta }}_i}$ as the observed number of events and $E={\displaystyle {\sum }_{i=1}^n{\mathrm{\Lambda }}_0\left(X_i\right)}$ as the expected number of events (asymptotically), where Λ₀(t) = − log S₀(t) is the cumulative hazard function under the null hypothesis. Then, the MOSLRT is defined by

$$L=\frac{O-E}{\sqrt{\left(O+E\right)/2}}.$$

To study the asymptotic distribution, we formulate it using counting-process notation. Specifically, let N_i(t) = Δ_iI{X_i ≤ t} and Y_i(t) = I{X_i ≥ t} be the failure and at-risk processes, respectively, then

$$O={\displaystyle \sum _{i=1}^n{\displaystyle {\int }_0^{\infty }d{N}_i\left(t\right)},E={\displaystyle \sum _{i=1}^n{\displaystyle {\int }_0^{\infty }{Y}_i\left(t\right)d{\mathrm{\Lambda }}_0\left(t\right).}}}$$

Thus, the counting-process formulation of the MOSLRT is given by $L=W/\widehat{\sigma }$, where

$$W=n^{-1/2}{\displaystyle \sum _{i=1}^n{\displaystyle {\int }_0^{\infty }\left\{d{N}_i\left(t\right)-Y_i\left(t\right)d{\mathrm{\Lambda }}_0\left(t\right)\right\},}}$$

and

$${\widehat{\sigma }}^2=n^{-1}{\displaystyle \sum _{i=1}^n{\displaystyle {\int }_0^{\infty }\left\{d{N}_i\left(t\right)+Y_i\left(t\right)d{\mathrm{\Lambda }}_0\left(t\right)\right\}/2.}}$$

Under the null hypothesis H₀, by the strong law of large numbers, $n^{-1}O\to E_{H_0}\left(\mathrm{\Delta }\right)$ and $n^{-1}{\displaystyle {\sum }_{i=1}^n{\displaystyle {\int }_0^{\infty }{Y}_i\left(t\right)d{\mathrm{\Lambda }}_0\left(t\right)\to {\displaystyle {\int }_0^{\infty }G\left(t\right)S_0\left(t\right)d{\mathrm{\Lambda }}_0\left(t\right)=E_{H_0}\left\{{\mathrm{\Lambda }}_0\left(X\right)\right\}}}}$, where G(t) is the survival distribution of the censoring time C. Then, ${\widehat{\sigma }}^2\to {\displaystyle {\int }_0^{\infty }G\left(t\right)S_0\left(t\right)d{\mathrm{\Lambda }}_0\left(t\right)={\text{Var}}_{H_0}}\left(W\right)$, and $E_{H_0}\left(W\right)=0$ (Wu, 2015). Therefore, by the counting process central limit theorem (Fleming and Harrington, 1991), L is asymptotically standard normal distributed. Hence, we reject the null hypothesis H₀ with one-sided type I error α if $L=W/\widehat{\sigma }<-z_{1-\alpha }$, where z_1−α is the 100(1 − α) percentile of the standard normal distribution.

3 Sample Size Formulae

Traditionally, sample size is often derived under the fixed alternative. However, when the asymptotic distribution of the test statistics is difficult to derive under the fixed alternative, contiguous alternatives (Lin et al., 1999) can also be considered by assuming that the alternative value of the testing parameter decreases to the null value at the rate of n^−1/2, where n is the sample size. For example, under the proportional hazard model, the null hypothesis of interest is H₀ : γ = 0 and the fixed alternative hypothesis of interest is H₁ : γ = γ₁, where γ = − log(δ) is the negative hazard ratio and γ₁ > 0. The contiguous alternatives of interest are $H_{1n}:\gamma ={\gamma }_{1n}=b/\sqrt{n}$, which converges to the null hypothesis H₀ : γ = 0 as sample size n goes to infinity. Here, we will first derive a formula for the number of events under the contiguous alternatives. The proportional hazard model (1) is equivalent to λ(t) = e^−γλ₀(t), where λ₀(t) and λ(t) are the hazard functions under the null hypothesis and the experimental treatment, and γ = − log(δ) > 0. To derive the formula, we consider a sequence of contiguous alternatives $H_{1n}:\gamma ={\gamma }_{1n}=b/\sqrt{n}$, where b < ∞. Under the H_1n, as shown in Appendix 1, $L=W/\widehat{\sigma }$ is approximately normal distributed with mean

$$\mu =-b{p}_0^{1/2}=n^{1/2}\log \left(\delta \right)p_0^{1/2},$$

and unit variance, where $p_0=E_{H_0}\left(\mathrm{\Delta }\right)$ is the probability of failure under the null hypothesis, which can be shown as

$$p_0={\displaystyle {\int }_0^{\infty }G\left(t\right)S_0\left(t\right)d{\mathrm{\Lambda }}_0\left(t\right)}.$$

Therefore, the study power 1 − β under the contiguous alternatives H_1n satisfies the following:

$$1-\beta =P\left(L<-z_{1-\alpha }|H_{1n}\right)=P\left(L-\mu <-\mu -z_{1-\alpha }|H_{1n}\right)\simeq \mathrm{\Phi }\left(-n^{1/2}\log \left(\delta \right)p_0^{1/2}-z_{1-\alpha }\right).$$

Thus, d = np₀, the expected number of events under the null hypothesis, satisfies the equation

$$z_{1-\beta }=-d^{1/2}\log \left(\delta \right)-z_{1-\alpha }.$$

Solving for d, we obtain

$$d=\frac{{\left(z_{1-\alpha }+z_{1-\beta }\right)}^2}{{\left[\log \left(\delta \right)\right]}^2},$$ (3)

which gives the expected number of events under the null hypothesis. To calculate the sample size of the trial, let p₁ be the probability of failure under the alternative, which is given by

$$p_1={\displaystyle {\int }_0^{\infty }G\left(t\right)S_1\left(t\right)d{\mathrm{\Lambda }}_1\left(t\right),}$$

where S₁(t) = [S₀(t)]^δ and Λ₁(t) = δΛ₀(t). Then, the required sample size for the trial is given by d₁/p₁, where d₁ is the number of events under the alternative. However, we don’t know for the d₁, and we have only derived number of events d under the null hypothesis. The d/p₀ is the sample size under the null which underestimates the sample size required under the alternative, where p₀ is the probability of failure under the null. As d/p₁ > d₁/p₁, thus, d/p₁ overestimates the required sample size. Let P be the average probabilities of failure under the null and alternative, that is

$$P=\left(p_0+p_1\right)/2,$$

then, a reasonable estimate of the required sample size is n = d/P which can be calculated by

$$n=\frac{{\left(z_{1-\alpha }+z_{1-\beta }\right)}^2}{P{\left[\log \left(\delta \right)\right]}^2}.$$ (4)

For the purpose of comparison, the sample size formula for the MOSLRT under the fixed alternative H₁ (Wu, 2015) is also given as follows:

$$n=\frac{{\left(\overline{\sigma }{z}_{1-\alpha }+\sigma z_{1-\beta }\right)}^2}{{\omega }^2},$$ (5)

where ω = v₁ − v₀, ${\overline{\sigma }}^2=\left(v_1+v_0\right)/2$, and ${\sigma }^2=v_1-v_1^2+2v_{00}-v_0^2-2v_{01}+2v_0{v}_1$, with v₀, v₁, v₀₀, and v₀₁ being given by the following equations:

$$v_0={\displaystyle {\int }_0^{\infty }G\left(t\right)S_1\left(t\right)d{\mathrm{\Lambda }}_0\left(t\right),}$$

$$v_1={\displaystyle {\int }_0^{\infty }G\left(t\right)S_1\left(t\right)d{\mathrm{\Lambda }}_1\left(t\right),}$$

$$v_{00}={\displaystyle {\int }_0^{\infty }G\left(t\right)S_1\left(t\right){\mathrm{\Lambda }}_0\left(t\right)d{\mathrm{\Lambda }}_0\left(t\right),}$$

$$v_{01}={\displaystyle {\int }_0^{\infty }G\left(t\right)S_1\left(t\right){\mathrm{\Lambda }}_0\left(t\right)d{\mathrm{\Lambda }}_1\left(t\right).}$$

4 Parameter Setting for Trial Design

For trial design using sample size formula (4), we first consider one of the following common parametric survival distributions: Weibull, gamma, Gompertz, log-normal, or log-logistic. The design parameters of the underlying survival distribution S(t) under the null hypothesis can be set as follows. Let S(x) be the survival probability of S(t) at a landmark time point x, S₀(x) be the level of S(x) at which investigators are no longer interested in the experimental treatment, and S₁(x)(> S₀(x)) be the level of S(x) at which investigators consider the experimental treatment is promising. Then the hypothesis of (2) is equivalent to the following hypothesis:

$$H_0:S\left(x\right)\le S_0\left(x\right)vs.H_1:S\left(x\right)>S_0\left(x\right),$$

and the trial is powered at the alternative S(x) = S₁(x). Here, the shape parameter of the underlying survival distribution is assumed to be known from historical data. Thus, the scale parameter (Table 1) for each distribution can be determined by the value of S₀(x), which is given as follows:

1. Weibull $S_0\left(t\right)=e^{-{\mathrm{\lambda }}_0{t}^{\kappa }}$, with λ₀ = − log S₀(x)/x^κ,

2. Log-normal $S_0\left(t\right)=1-\mathrm{\Phi }\left(\frac{\log t-{\mu }_0}{\sigma }\right)$, with μ₀ = log(x) − σΦ⁻¹(1 − S₀(x)),

3. Gompertz $S_0\left(t\right)=e^{-\frac{{\theta }_0}{\gamma }\left(e^{\gamma t}-1\right)}$, with θ₀ = −γ log S₀(x)/(e^γx − 1),

4. Gamma S₀(t) = 1 − I_k(λ₀t), with ${\mathrm{\lambda }}_0=I_k^{-1}\left(1-S_0\left(x\right)\right)/x$,

5. Log-logistic S₀(t) = 1/(1 + λ₀t^p), with λ₀ = (1/S₀(x) − 1)/x^p.

The hazard ratio can be calculated by

$$\delta =\frac{\log S_1\left(x\right)}{\log S_0\left(x\right)},$$

and the survival distribution under the alternative is given by S₁(t) = [S₀(t)]^δ. To calculate the probabilities p₀ and p₁ for formula (4), we assume that subjects are recruited with a uniform distribution over the accrual period t_a and followed for a period of t_f and that no subject is lost to follow-up. Thus, the censoring distribution is a uniform distribution over [t_f, t_a + t_f]. That is, the censoring survival distribution G(t) = 1 if t ≤ t_f; = (t_a + t_f − t)/t_a if t_f ≤ t ≤ t_a + t_f; = 0 otherwise. Hence, the probabilities of failure p₀ and p₁ can be calculated by the following integration:

$$p_i=1-\frac{1}{t_a}{\displaystyle {\int }_{t_f}^{t_a+t_f}{S}_i\left(t\right)dt,i=0,1}$$

where S₁(t) = [S₀(t)]^δ. If S₀(t) is a spline version of the survival distribution, then p_i can also be calculated by numerical integration. If S₀(t) is a Kaplan-Meier curve, then p_i can be calculated numerically using Simpson’s rule as follows:

$$p_i=1-\frac{1}{6}\left\{S_i\left(t_f\right)+4S_i\left(0.5t_a+t_f\right)+S_i\left(t_a+t_f\right)\right\},i=0,1.$$

The proposed sample size formula can also incorporate lost to follow-up in the sample size calculation. For example, let C₁ be the loss to follow-up time and C₂ be the administrative censoring time, then the overall censoring time is C = C₁ ∧ C₂, where C₁ and C₂ are independent. Thus, the overall censoring distribution is G(t) = P(C > t) = P(C₁ > t)P(C₂ > t) = G₁(t)G₂(t). It is often assumed that the loss to follow-up distribution is an exponential G₁(t) = e^−ηt, and administrative censoring distribution G₂(t) is uniform. Therefore the sample size formula (4) can be calculated by numerical integrations. For non-uniform accrual, once the accrual distribution is specified, the sample size can be calculated as well.

Table 1.

Various parametric distributions used for single-arm phase II trial designs.

	Surv. function	Density	Parameter		Cumu. hazard	Hazard
Dist.	S(t)	f(t)	Scale	Shape	Λ(t)	λ(t)
WB(λ, κ)	$e^{-\mathrm{\lambda }{t}^{\kappa }}$	$\kappa \mathrm{\lambda }{t}^{\kappa -1}{e}^{-\mathrm{\lambda }{t}^{\kappa -1}}$	λ	κ	λtκ	κλtκ−1
GM(λ, k)	1 − Ik (λt)	$\frac{\mathrm{\lambda }{t}^{k-1}{e}^{-\mathrm{\lambda }t}}{\Gamma \left(k\right)}$	λ	k	− log S(t)	$\frac{f\left(t\right)}{S\left(t\right)}$
LN(μ, σ2)	$1-\mathrm{\Phi }\left(\frac{\log t-\mu }{\sigma }\right)$	$\frac{1}{\sqrt{2\pi }\sigma t}{e}^{-\frac{\left(\log t-\mu \right)}{2{\sigma }^2}}$	μ	σ	− log S(t)	$\frac{f\left(t\right)}{S\left(t\right)}$
LG(λ, p)	$\frac{1}{1+\mathrm{\lambda }{t}^p}$	$\frac{p\mathrm{\lambda }{t}^{p-1}}{{\left(1+\mathrm{\lambda }{t}^p\right)}^2}$	λ	p	log(1 + λtp)	$\frac{p\mathrm{\lambda }{t}^{p-1}}{1+\mathrm{\lambda }{t}^p}$
GZ(θ, γ)	$e^{-\frac{\theta }{\gamma }\left(e^{\gamma t}-1\right)}$	$\theta e^{\gamma t}{e}^{-\frac{\theta }{\gamma }\left(e^{\gamma t}-1\right)}$	θ	γ	$\frac{\theta }{\gamma }\left(e^{\gamma t}-1\right)$	θeγt

Footnote: abbreviation Dist.: distribution; Surv.: survival; Cumu.: cumulative

5 Simulation studies

We first investigated whether formula (4) would give an accurate sample size estimation. We calculated sample sizes under various hazard ratios δ = 1.2⁻¹–2.0⁻¹, with powers of 80%, 85%, and 90% and a type I error of 5%. The accuracy was assessed by simulations performed under the Weibull distribution. The Weibull shape parameter κ was set to 0.5, 1 and 2 to reflect a decreasing, constant and increasing hazard function, and the median survival time under the null was set to m₀ = 1. We assumed that subjects were recruited with a uniform distribution over the accrual period t_a = 3 (years) and followed for t_f = 1 (year) and that no subject was lost to follow-up; that is, only administrative censoring was considered in the trial. Under these assumptions, the number of events and sample sizes were calculated, and empirical powers and type I errors were estimated based on 100,000 simulation runs (Table 2). All simulated empirical powers and type I errors were close to the nominal levels. Additional sample size calculations were conducted under the Weibull model for various combinations of accrual period t_a, follow-up time t_f and landmark time point x for survival probability S₀(x) under null which varies from 0.2 to 0.7 and a 10% increasing survival probability S₁(x) under alternative to mimic a variety of real trial design. Detail for the set up of the design parameters were given in Table 2. Simulations were conducted to estimate the empirical type I error and power for the corresponding sample size based on 100,000 runs. The empirical type I errors and powers were close to the nominal levels for all scenarios. Thus, the formula (4) did provide an accurate estimation of the sample size for trial design.

Table 2.

Number of events (d) and sample sizes (n) were calculated from formulae (3) and (4) for various of hazard ratios (δ) under the Weibull distribution, with nominal type I error of 0.05 and power of 80%, 85%, and 90%. The empirical type I errors $(\widehat{\alpha })$ and powers $(1-\widehat{\beta })$ were estimated based on 100,000 simulation runs.

Power	Design		κ = 0.5			κ = 1			κ = 2
	δ−1	d	n	$\widehat{\alpha }$	$1-\widehat{\beta }$	n	$\widehat{\alpha }$	$1-\widehat{\beta }$	n	$\widehat{\alpha }$	$1-\widehat{\beta }$
90%	1.2	258	415	0.051	0.904	338	0.051	0.901	285	0.049	0.902
	1.3	125	205	0.051	0.903	166	0.052	0.902	139	0.049	0.901
	1.4	76	128	0.052	0.904	103	0.051	0.904	85	0.049	0.900
	1.5	53	90	0.053	0.907	72	0.051	0.904	59	0.050	0.901
	1.6	39	68	0.052	0.905	54	0.052	0.902	44	0.049	0.900
	1.7	31	54	0.052	0.904	43	0.052	0.906	35	0.050	0.903
	1.8	25	45	0.055	0.908	36	0.052	0.908	29	0.049	0.905
	1.9	21	38	0.054	0.902	30	0.052	0.904	24	0.049	0.900
	2.0	18	33	0.054	0.903	26	0.053	0.903	21	0.050	0.903
85%	1.2	217	349	0.051	0.854	284	0.051	0.853	240	0.049	0.852
	1.3	105	172	0.051	0.854	140	0.051	0.856	116	0.049	0.852
	1.4	64	107	0.054	0.856	86	0.051	0.855	71	0.050	0.853
	1.5	44	75	0.053	0.855	60	0.052	0.856	49	0.049	0.853
	1.6	33	57	0.054	0.858	46	0.051	0.860	37	0.050	0.853
	1.7	26	46	0.053	0.861	36	0.052	0.856	29	0.049	0.854
	1.8	21	38	0.053	0.861	30	0.052	0.861	24	0.049	0.855
	1.9	18	32	0.054	0.858	26	0.052	0.865	20	0.050	0.851
	2.0	15	28	0.055	0.859	22	0.053	0.859	17	0.049	0.848
80%	1.2	186	300	0.052	0.806	244	0.051	0.805	206	0.050	0.806
	1.3	90	148	0.052	0.805	120	0.051	0.807	100	0.048	0.805
	1.4	55	92	0.051	0.806	74	0.052	0.807	61	0.049	0.803
	1.5	38	65	0.052	0.808	52	0.052	0.811	43	0.050	0.812
	1.6	28	49	0.055	0.809	39	0.052	0.810	32	0.048	0.808
	1.7	22	39	0.053	0.809	31	0.052	0.810	25	0.049	0.808
	1.8	18	33	0.054	0.818	26	0.053	0.818	21	0.049	0.815
	1.9	16	28	0.055	0.816	22	0.053	0.816	17	0.048	0.801
	2.0	13	24	0.056	0.813	19	0.053	0.814	15	0.048	0.809

Next, we conducted simulations to compare the sample size formulae (4) and (5). In simulations, the survival distributions were taken as Weibull, gamma, Gompertz, log-normal and log-logistic (Table 1). The parameters of the survival distribution under the null were set as follows: the shape parameter of each distribution was set to 0.5, 1, and 2; the survival probabilities at a landmark time point x = 2 under the null were set to S₀(x) = 0.2 – 0.7 and under the alternative were set to S₁(x) = 0.35 – 0.8, with same accrual and censoring distributions as before. Given a nominal type I error of 5% and power of 80%, the required sample sizes based on formulae (4) and (5) were calculated for each design scenario. For each calculated sample size, 100,000 random samples were generated from the corresponding distribution to estimate the empirical type I error and power (Tables 3 and 4). The simulation results showed that the empirical powers were close to the nominal level of 80% for all scenarios. Thus, sample size formulae (4) and (5) both gave an accurate estimation of sample size. The results also showed that the sample sizes calculated by formula (4) under the contiguous alternatives (Table 3) were almost identical to that calculated by formula (5) under the fixed alternative (Table 4). Furthermore, the MOSLRT controlled the type I error well when the survival probability under the null was low (S₀(x) < 0.5) and was slightly more liberal when the survival probability under the null (S₀(x) ≥ 0.5) was high.

Table 3.

Sample sizes (n) were calculated from formula (4) for various of accrual period (t_a), follow-up time (t_f), landmark time point (x), and survival probabilities under null and alternative for the Weibull distribution with nominal type I error of 0.05 and power of 80%. The empirical type I errors $(\widehat{\alpha })$ and powers $(1-\widehat{\beta })$ were estimated based on 100,000 simulation runs.

Design		κ = 0.5			κ = 1			κ = 2
(ta, tf, x)	S0(x), S1(x)	n	$\widehat{\alpha }$	$1-\widehat{\beta }$	n	$\widehat{\alpha }$	$1-\widehat{\beta }$	n	$\widehat{\alpha }$	$1-\widehat{\beta }$
(1,1,1)	0.2, 0.3	90	.050	.806	85	.050	.808	79	.050	.808
	0.3, 0.4	115	.052	.806	106	.052	.808	95	.050	.806
	0.4, 0.5	128	.052	.808	115	.052	.805	99	.050	.806
	0.5, 0.6	129	.053	.807	113	.053	.805	93	.052	.808
	0.6, 0.7	118	.054	.807	102	.053	.806	79	.052	.806
	0.7, 0.8	95	.055	.803	81	.055	.808	60	.054	.810
(1,2,1)	0.2, 0.3	83	.050	.807	76	.049	.804	73	.048	.801
	0.3, 0.4	103	.051	.809	90	.050	.807	83	.047	.803
	0.4, 0.5	111	.051	.806	93	.049	.808	80	.049	.800
	0.5, 0.6	109	.053	.806	86	.051	.807	69	.049	.807
	0.6, 0.7	97	.053	.806	73	.051	.808	52	.050	.808
	0.7, 0.8	77	.056	.808	55	.054	.808	35	.050	.819
(2,2,2)	0.2, 0.3	90	.051	.807	85	.050	.810	79	.050	.803
	0.3, 0.4	115	.050	.805	106	.051	.808	95	.050	.805
	0.4, 0.5	128	.052	.807	115	.052	.808	99	.050	.806
	0.5, 0.6	129	.053	.809	113	.053	.807	93	.051	.808
	0.6, 0.7	118	.054	.806	102	.054	.806	79	.053	.808
	0.7, 0.8	95	.054	.808	81	.055	.808	60	.054	.809
(3,2,1)	0.2, 0.3	80	.048	.808	75	.048	.807	73	.049	.803
	0.3, 0.4	97	.050	.806	86	.048	.806	83	.049	.805
	0.4, 0.5	104	.051	.811	86	.051	.806	80	.048	.806
	0.5, 0.6	100	.052	.807	78	.051	.809	67	.048	.802
	0.6, 0.7	88	.053	.807	63	.052	.807	49	.048	.803
	0.7, 0.8	69	.054	.813	46	.053	.814	31	.048	.812
(3,2,2)	0.2, 0.3	88	.051	.805	82	.050	.807	77	.049	.805
	0.3, 0.4	112	.052	.809	101	.051	.808	91	.050	.807
	0.4, 0.5	123	.052	.808	108	.051	.806	92	.050	.806
	0.5, 0.6	123	.052	.807	105	.052	.809	84	.050	.806
	0.6, 0.7	112	.054	.809	92	.054	.807	69	.050	.808
	0.7, 0.8	90	.054	.809	72	.055	.809	50	.053	.810
(3,3,2)	0.2, 0.3	84	.050	.807	78	.051	.808	74	.048	.804
	0.3, 0.4	105	.051	.804	93	.049	.808	84	.049	.804
	0.4, 0.5	115	.052	.809	97	.051	.808	83	.049	.807
	0.5, 0.6	113	.052	.807	91	.052	.807	72	.050	.807
	0.6, 0.7	101	.054	.806	78	.054	.809	56	.050	.808
	0.7, 0.8	81	.055	.808	60	.054	.809	38	.051	.810

Table 4.

Sample sizes (n) were calculated from formula (4) under the contiguous alternative for the Weibull, gamma, log-logistic, log-normal, and Gompertz distributions with nominal type I error of 0.05 and power of 80%. The corresponding empirical type I errors $(\widehat{\alpha })$ and powers $(1-\widehat{\beta })$ were estimated based on 100,000 simulation runs.

Distribution	Design	n	$\widehat{\alpha }$	$1-\widehat{\beta }$	n	$\widehat{\alpha }$	$1-\widehat{\beta }$	n	$\widehat{\alpha }$	$1-\widehat{\beta }$
WB(λ, κ)	S0(2) vs S1(2)	κ = 0.5			κ = 1			κ = 2
	0.2 vs 0.35	45	.052	.810	44	.051	.808	43	.050	.806
	0.2 vs 0.4	27	.052	.815	26	.052	.812	26	.050	.815
	0.3 vs 0.45	56	.053	.809	54	.053	.808	51	.051	.805
	0.5 vs 0.65	60	.054	.806	57	.054	.812	50	.052	.812
	0.6 vs 0.75	54	.055	.811	50	.056	.808	42	.053	.810
	0.7 vs 0.8	104	.055	.805	95	.054	.807	77	.055	.807
GM(γ, k)		k = 0.5			k = 1			k = 2
	0.2 vs 0.35	45	.052	.813	44	.050	.811	44	.050	.810
	0.2 vs 0.4	27	.053	.819	26	.052	.811	26	.050	.813
	0.3 vs 0.45	55	.052	.806	54	.052	.808	53	.050	.809
	0.5 vs 0.65	59	.055	.806	57	.055	.813	53	.054	.807
	0.6 vs 0.75	53	.056	.809	50	.056	.808	46	.054	.812
	0.7 vs 0.8	103	.056	.807	95	.056	.806	85	.055	.810
LG(λ, p)		p = 0.5			p = 1			p = 2
	0.2 vs 0.35	46	.050	.812	45	.051	.807	45	.051	.811
	0.2 vs 0.4	27	.052	.809	27	.052	.815	27	.051	.818
	0.3 vs 0.45	57	.052	.807	56	.053	.806	55	.052	.811
	0.5 vs 0.65	62	.054	.809	59	.056	.808	55	.053	.809
	0.6 vs 0.75	55	.056	.810	52	.056	.807	47	.055	.811
	0.7 vs 0.8	106	.054	.809	99	.055	.806	86	.055	.809
LN(μ, σ)		σ = 2			σ = 1			σ = 0.5
	0.2 vs 0.35	45	.051	.808	45	.052	.811	44	.050	.803
	0.2 vs 0.4	27	.052	.815	27	.051	.818	26	.050	.807
	0.3 vs 0.45	56	.053	.811	55	.052	.809	53	.052	.809
	0.5 vs 0.65	60	.054	.807	57	.054	.811	51	.051	.808
	0.6 vs 0.75	53	.056	.807	49	.057	.809	42	.054	.812
	0.7 vs 0.8	102	.057	.807	91	.054	.809	73	.055	.807
GZ(θ, γ)		γ = 0.5			γ = 1			γ = 2
	0.2 vs 0.35	43	.050	.807	43	.048	.809	44	.049	.808
	0.2 vs 0.4	25	.050	.808	25	.050	.807	25	.049	.800
	0.3 vs 0.45	51	.050	.806	50	.051	.805	50	.049	.806
	0.5 vs 0.65	50	.054	.807	46	.051	.810	42	.048	.804
	0.6 vs 0.75	43	.054	.812	37	.053	.809	32	.049	.809
	0.7 vs 0.8	80	.054	.809	65	.055	.808	51	.051	.800

Footnote: abbreviation WB: Weibull; GM: gamma; LG: log-logistic; LN: log-normal; GZ: Gompetz

6 Example

Between January 1974 and May 1984, the Mayo Clinic conducted a double-blind randomized trial on treating primary biliary cirrhosis of the liver (PBC), comparing the drug D-penicillamine (DPCA) with a placebo (Fleming and Harrington, 1991). PBC is a rare but fatal chronic liver disease of unknown cause, with a prevalence of approximately 50 cases per million in the population. The primary pathologic event appears to be the destruction of the interlobular bile ducts, which may be mediated by immunologic mechanisms. Of 158 patients treated with DPCA, 65 died. The median survival time was 9 years. Suppose an experimental treatment is now available and investigators wish to design a new trial using the Mayo Clinic patients treated with DPCA as the historical data with which to formulate the hypothesis. The survival distribution of the DPCA data is estimated by a Kaplan-Meier curve, a spline version of the survival distribution, which is fitted by using the R function oldlogspline, and the Weibull distribution, which is fitted by using the R function survreg with the estimated shape parameter κ = 1.22 (Figure 1). Both the spline and Weibull distributions are fitted well and are close to the Kaplan-Meier curve. The 5-year survival probability estimate from the Kaplan-Meier curve is 71%. Thus, for the trial design, S₀(5) = 71% is the 5-year survival probability at which investigators are no longer interested in the experimental treatment, and S₁(5) = 82% is the 5-year survival probability at which investigators consider the experimental treatment to be promising. Then, the hazard ratio is δ = log(0.82) / log(0.71) = 0.58. To calculate the sample size, we assume a uniform accrual with an accrual period t_a = 8 years and a follow-up period t_f = 3 years, with no patient being lost to follow-up. Thus, given a type I error of α = 5% and power of 1−β = 80%, the required sample sizes calculated using the R function SIZE (Appendix 2) are 63, 63, and 63 under the Weibull, spline and Kaplan-Meier curve, respectively. With a power of 90%, the required sample sizes are 88, 87 and 88 under the Weibull, spline and Kaplan-Meier curve, respectively. Sample size calculations under the spline distribution and Kaplan-Meier curve make no assumption regarding the underlying survival distribution. Thus, this approach takes advantage of possible misspecification by using a parametric survival distribution for the trial design.

Figure 1.

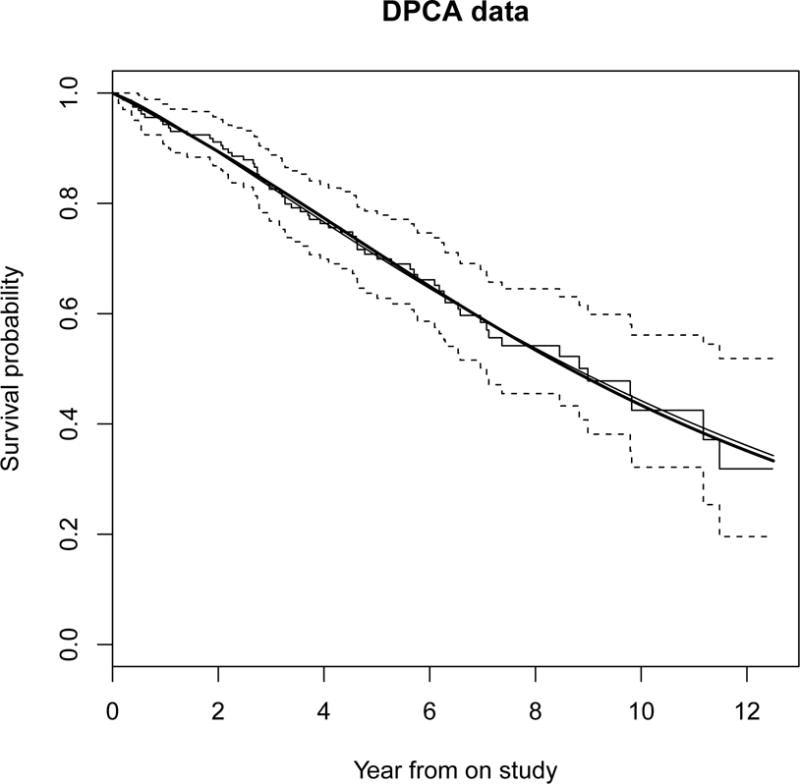
Step functions are the Kaplan-Meier survival curve and its 95% confidence boundaries. Solid and dark solid curves are the fitted Weibull and spline survival distributions, respectively.

7 Conclusion

In this paper, formulae for the number of events and sample size for a single-arm phase II survival trial are derived for the MOSLRT under the proportional hazards model. The new sample size formula is simple and easy to compute. The simulation results show that the proposed formula provides an accurate estimation of sample size for trial design. The sample size calculation using the new formula is extended to a class of flexible survival distributions, including a Kaplan-Meier curve or a spline version of the survival distribution, and has been implemented in the R function SIZE for trial design.

Table 5.

Sample sizes (n) were calculated from formula (5) under the fixed alternative for the Weibull, gamma, log-logistic, log-normal, and Gompertz distributions with nominal type I error of 0.05 and power of 80%. The empirical type I errors $(\widehat{\alpha })$ and powers $(1-\widehat{\beta })$ were estimated based on 100,000 simulation runs.

Distribution	Design	n	$\widehat{\alpha }$	$1-\widehat{\beta }$	n	$\widehat{\alpha }$	$1-\widehat{\beta }$	n	$\widehat{\alpha }$	$1-\widehat{\beta }$
WB(λ, κ)	S0(2) vs S1(2)	κ = 0.5			κ = 1			κ = 2
	0.2 vs 0.35	44	.051	.801	44	.051	.811	44	.049	.812
	0.2 vs 0.4	26	.051	.802	26	.051	.811	26	.052	.818
	0.3 vs 0.45	55	.053	.803	53	.051	.803	51	.050	.807
	0.5 vs 0.65	58	.054	.795	55	.052	.799	49	.053	.805
	0.6 vs 0.75	52	.056	.796	48	.056	.798	41	.055	.804
	0.7 vs 0.8	100	.055	.793	91	.055	.794	75	.055	.798
GM(γ, k)		k = 0.5			k = 1			k = 2
	0.2 vs 0.35	44	.051	.806	44	.051	.810	44	.051	.812
	0.2 vs 0.4	26	.051	.808	26	.051	.812	26	.051	.813
	0.3 vs 0.45	54	.053	.803	53	.053	.804	52	.051	.802
	0.5 vs 0.65	57	.054	.795	55	.054	.798	52	.054	.800
	0.6 vs 0.75	51	.056	.796	48	.055	.797	44	.055	.796
	0.7 vs 0.8	98	.055	.792	91	.056	.790	82	.054	.795
LG(λ, p)		p = 0.5			p = 1			p = 2
	0.2 vs 0.35	45	.053	.804	45	.052	.807	44	.051	.803
	0.2 vs 0.4	27	.053	.808	27	.053	.813	26	.052	.805
	0.3 vs 0.45	56	.053	.804	55	.053	.801	54	.052	.804
	0.5 vs 0.65	60	.056	.799	57	.054	.795	54	.054	.804
	0.6 vs 0.75	53	.056	.798	50	.056	.796	45	.055	.797
	0.7 vs 0.8	101	.055	.791	95	.055	.795	83	.054	.797
LN(μ, σ)		σ = 2			σ = 1			σ = 0.5
	0.2 vs 0.35	45	.052	.805	44	.051	.808	44	.050	.805
	0.2 vs 0.4	27	.053	.813	26	.051	.807	26	.051	.809
	0.3 vs 0.45	55	.052	.801	54	.054	.806	53	.051	.807
	0.5 vs 0.65	58	.055	.798	55	.053	.800	50	.052	.803
	0.6 vs 0.75	51	.056	.794	47	.056	.796	41	.052	.803
	0.7 vs 0.8	98	.057	.793	88	.055	.798	72	.054	.803
GZ(θ, γ)		γ = 0.5			γ = 1			γ = 2
	0.2 vs 0.35	43	,049	.810	43	.049	.809	45	.050	.816
	0.2 vs 0.4	26	.049	.818	26	.050	.821	27	.049	.824
	0.3 vs 0.45	51	.052	.804	50	.050	.810	51	.050	.811
	0.5 vs 0.65	50	.052	.808	46	.052	.811	44	.049	.820
	0.6 vs 0.75	42	.055	.805	37	.053	.811	33	.051	.819
	0.7 vs 0.8	77	.054	.797	64	.053	.802	53	.050	.814

Footnote: abbreviation WB: Weibull; GM: gamma; LG: log-logistic; LN: log-normal; GZ: Gompetz

Appendix 1: Derivation of the asymptotic distribution for the MOSLRT

The methods used to derive the asymptotic distribution of the MOSLRT under the contiguous alternative are similar to the derivation of the two-sample log-rank test (Fleming and Harrington, 1991).

Consider a sequence of contiguous alternatives H_1n : λ_1n(t) = e^−γ1nλ₀(t), where γ_1n is a sequence of positive constants satisfying n^1/2γ_1n = b < ∞. Then, the weighted one-sample log-rank score W is given by

$$W=n^{-1/2}{\displaystyle \sum _{i=1}^n{\displaystyle {\int }_0^{\infty }{w}_n\left(t\right)\left\{d{N}_i\left(t\right)-Y_i\left(t\right)d{\mathrm{\Lambda }}_0\left(t\right)\right\}}},$$

where w_n(t) is a weight function convergence to w(t) as n → ∞. If we further define a sequence of martingale by

$$M_i^{\left(n\right)}\left(t\right)=N_i\left(t\right)-{\displaystyle {\int }_0^t{Y}_i\left(u\right)e^{-{\gamma }_{1n}}d{\mathrm{\Lambda }}_0\left(u\right)}$$

and let

$$W_M=n^{-1/2}{\displaystyle \sum _{i=1}^n{\displaystyle {\int }_0^{\infty }{w}_n\left(t\right)d{M}_i^{\left(n\right)}\left(t\right),}}$$

$$W_D=n^{-1/2}{\displaystyle \sum _{i=1}^n{\displaystyle {\int }_0^{\infty }\left(e^{-{\gamma }_{1n}}-1\right)w_n\left(t\right)Y_i\left(t\right)d{\mathrm{\Lambda }}_0\left(t\right)},}$$

then we have

$$W=W_M+W_D.$$

It is easy to show that

$$W_M=n^{-1/2}{\displaystyle \sum _{i=1}^n{\displaystyle {\int }_0^{\infty }w\left(t\right)d{M}_i^{\left(n\right)}\left(t\right)+o_p\left(1\right)}}$$

and

$$W_D=-n^{1/2}{\gamma }_{1n}{\displaystyle {\int }_0^{\infty }w\left(t\right)\left\{n^{-1}{\displaystyle \sum _{i=1}^n{Y}_i\left(t\right)}\right\}}d{\mathrm{\Lambda }}_0\left(t\right)+o_p\left(1\right).$$

As

$$n^{1/2}{\gamma }_{1n}=b\text{and}{n}^{-1}{\displaystyle \sum _{i=1}^n{Y}_i\left(t\right)\to \mathrm{\pi }\left(t\right),}$$

where π(t) = P(X ≥ t), we have where

$$W_D\to -bV,$$

where

$$V={\displaystyle {\int }_0^{\infty }{w}^2\left(t\right)\mathrm{\pi }\left(t\right)d{\mathrm{\Lambda }}_0\left(t\right).}$$

Therefore,

$$W=n^{-1/2}{\displaystyle \sum _1^n{\displaystyle {\int }_0^{\infty }w\left(t\right)d{M}_i^{\left(n\right)}\left(t\right)-bV+o_p\left(1\right)}.}$$

By the martingale central limit theorem (Fleming and Harrington, 1991), W is approximate normal with mean −bV and variance V. When w(t) = 1, the variance V reduces to

$$p_0={\displaystyle {\int }_0^{\infty }\mathrm{\pi }\left(t\right)d{\mathrm{\Lambda }}_0\left(t\right)={\displaystyle {\int }_0^{\infty }G\left(t\right)S_0\left(t\right)d{\mathrm{\Lambda }}_0\left(t\right).}}$$

Hence,

$$W\to N\left(-b{p}_0,p_0\right).$$

By the dominated convergence theorem, ${\widehat{\sigma }}^2\to p_0={\displaystyle {\int }_0^{\infty }G\left(t\right)S_0\left(t\right)d{\mathrm{\Lambda }}_0\left(t\right)}$. Finally, by Slutsky’s theorem, it follows that

$$L=W/\widehat{\sigma }\to N\left(-b{p}_0^{1/2},1\right).$$

Appendix 2: R code for the sample size calculation under the Weibull distribution, spline distribution, and Kaplan-Meier curve

library (survival)
library (polspline)
time=c	(1.10,	12.33,	2.77,	5.27,	6.58,	9.82,	0.36,	11.59,	1.84,	11.18,	10.78,	0.61,
	6.29,	12.24,	3.70,	12.48,	6.18,	7.12,	6.54,	2.74,	3.93,	3.73,	8.99,	12.22,
	6.09,	11.96,	10.94,	11.48,	11.07,	3.21,	9.47,	5.01,	3.26,	0.19,	4.63,	10.16,
	6.96,	9.79,	11.10,	4.54,	0.54,	4.77,	7.37,	1.06,	10.72,	2.05,	10.55,	10.47,
	8.49,	8.45,	8.83,	7.08,	5.77,	6.44,	2.68,	9.14,	2.97,	6.27,	1.41,	5.57,
	9.03,	2.66,	8.41,	2.26,	2.84,	8.87,	8.07,	8.63,	8.49,	8.19,	3.55,	8.38,
	8.36,	8.21,	2.09,	7.86,	3.16,	7.84,	0.38,	6.78,	5.63,	2.95,	4.61,	7.38,
	7.05,	7.28,	7.24,	4.09,	7.07,	7.00,	7.00,	6.92,	4.32,	6.39,	6.86,	6.69,
	6.71,	6.38,	6.47,	6.48,	4.36,	6.22,	5.70,	6.18,	5.95,	2.48,	5.97,	5.94,
	5.95,	3.38,	0.92,	5.33,	5.54,	2.74,	0.95,	5.35,	5.29,	5.23,	5.16,	1.90,
	5.02,	4.96,	4.63,	3.93,	2.01,	4.88,	3.99,	4.85,	4.84,	2.02,	4.66,	4.42,
	4.66,	4.42,	0.49,	3.26,	4.30,	4.18,	3.96,	3.70,	4.06,	3.87,	0.11,	3.84,
	3.86,	3.38,	2.19,	3.73,	2.47,	3.57,	2.40,	1.46,	3.54,	3.48,	3.37,	3.16,
	2.57,	2.30)

status=c	(1,	0,	1,	1,	1,	1,	1	0,	1,	1,	0,	1,	1,	0,	1,	0,	1,	1,	1,	1,	1,	1,	1,	0,	1,	0,	0,	1,
	0,	1,	0,	1,	1,	1,	1	0,	1,	1,	0,	1,	1,	1,	1,	1,	0,	1,	0,	0,	0,	1,	1,	1,	1,	0,	1,	0,
	1,	1,	1,	0,	0,	1,	0	1,	1,	0,	0,	0,	0,	0,	1,	0,	0,	0,	1,	0,	1,	0,	1,	0,	1,	1,	1,	0,
	0,	0,	0,	1,	0,	0,	0	0,	1,	0,	0,	0,	0,	0,	0,	0,	0,	0,	1,	0,	0,	1,	0,	0,	0,	1,	1,	0,
	0,	1,	1,	0,	0,	0,	0	1,	0,	0,	1,	0,	0,	0,	0,	0,	0,	0,	0,	0,	0,	0,	1,	1,	0,	0,	0,	0,
	0,	0,	1,	0,	0,	0,	1	0,	0,	0,	0,	0,	0,	0,	0,	0,	0,	0)

dat=data.frame(time=time, status=status)
SIZE=function(delta, ta, tf, alpha, beta, data)
{
tau=tf+ta
z0=qnorm(1-alpha)
z1=qnorm(1-beta)
######### fit KM curve #############
surv=Surv(time, status)
fitKM<- survfit(surv ~ 1, data = dat)
p0<-c(1, summary(fitKM)$surv)	# KM survival probability ###
t0<-c(0, summary(fitKM)$time)	# ordered failure times ###
outKM<-data.frame(t0=t0,p0=p0)
KM<-function(t){
t0=outKM$t0; p0=outKM$p0; k=length(t0)
if (t>=t0[k] || t<0) {ans<-0}
for (i in 1:(k-1)){
if (t>=t0[i] & t<t0[i+1]) {S0=p0[i]}}
return(S0)}
######### fit Weibull curve ###########
fitWB=survreg(formula=surv~1, dist=“weibull”)
scale=as.numeric(exp(fitWB$coeff))
shape=1/fitWB$scale
WB=function(t){
kappa=shape; lambda0=1/scaleˆkappa
S0 = exp(-lambda0*tˆkappa); return(S0)}
######## fit spline curve ##########
fitSP=oldlogspline(time[status == 1], time[status == 0], lbound = 0)
SP=function(t) {S0=1-poldlogspline(t, fitSP); return(S0)}
####### sample size calculation #####
S0=function(t){WB(t)}
S1=function(t){WB(t)ˆdelta}
p0=1-integrate(S0, tf, tau)$value/ta
p1=1-integrate(S1, tf, tau)$value/ta
PWB=(p0+p1)/2
S0=function(t){SP(t)}
S1=function(t){SP(t)ˆdelta}
p0=1-integrate(S0, tf, tau)$value/ta
p1=1-integrate(S1, tf, tau)$value/ta
PSP=(p0+p1)/2
S0=function(t){KM(t)}
S1=function(t){KM(t)ˆdelta}
p0=1-(S0(tf)+4*S0(0.5*ta+tf)+S0(ta+tf))/6
p1=1-(S1(tf)+4*S1(0.5*ta+tf)+S1(ta+tf))/6
PKM=(p0+p1)/2
d0=(z0+z1)ˆ2/log(delta)ˆ2		# number of events formula (3)
nWB=ceiling(d0/PWB)		# sample size formula (4) under Weibull model
nSP=ceiling(d0/PSP)		# sample size formula (4) under spine curve
nKM=ceiling(d0/PKM)		# sample size formula (4) under KM curve
d=ceiling(d0)
ans=list(c(d=d, nWB=nWB, nSP=nSP, nKM=nKM))
return(ans)
}
#### 80% power ####
SIZE(delta=0.58, ta=8, tf=3, alpha=0.05, beta=0.2, data=dat)
d nWB nSP nKM
21 63 63 63
#### 90% power ####
SIZE(delta=0.58, ta=8, tf=3, alpha=0.05, beta=0.1, data=dat)
d nWB nSP nKM
29 88 87 88