Skip to main content
PMC home page
NASA Author Manuscripts logoLink to NASA Author Manuscripts
. Author manuscript; available in PMC: 2017 Sep 29.
Published in final edited form as: J Adv Model Earth Syst. 2016 Aug 27;8(3):1345–1357. doi: 10.1002/2016MS000630

Select strengths and biases of models in representing the Arctic winter boundary layer over sea ice: the Larcform 1 single column model intercomparison

Felix Pithan 1, Andrew Ackerman 2, Wayne M Angevine 3, Kerstin Hartung 4, Luisa Ickes 5, Maxwell Kelley 2, Brian Medeiros 6, Irina Sandu 7, Gert-Jan Steeneveld 8, HAM Sterk 8, Gunilla Svensson 4, Paul A Vaillancourt 9, Ayrton Zadra 9
PMCID: PMC5621046  NIHMSID: NIHMS903740  PMID: 28966718

Abstract

Weather and climate models struggle to represent lower tropospheric temperature and moisture profiles and surface fluxes in Arctic winter, partly because they lack or misrepresent physical processes that are specific to high latitudes. Observations have revealed two preferred states of the Arctic winter boundary layer. In the cloudy state, cloud liquid water limits surface radiative cooling, and temperature inversions are weak and elevated. In the radiatively clear state, strong surface radiative cooling leads to the build-up of surface-based temperature inversions. Many large-scale models lack the cloudy state, and some substantially underestimate inversion strength in the clear state. Here, the transformation from a moist to a cold dry air mass is modelled using an idealized Lagrangian perspective. The trajectory includes both boundary layer states, and the single-column experiment is the first Lagrangian Arctic air formation experiment (Larcform 1) organized within GEWEX GASS (Global atmospheric system studies). The intercomparison reproduces the typical biases of large-scale models: Some models lack the cloudy state of the boundary layer due to the representation of mixed-phase micro-physics or to the interaction between micro-and macrophysics. In some models, high emissivities of ice clouds or the lack of an insulating snow layer prevent the build-up of surface-based inversions in the radiatively clear state. Models substantially disagree on the amount of cloud liquid water in the cloudy state and on turbulent heat fluxes under clear skies. Observations of air mass transformations including both boundary layer states would allow for a tighter constraint of model behaviour.

1. Introduction

The Arctic receives very little solar radiation in winter, but continues to emit longwave radiation to space. This radiative deficit at the surface is counteracted by the release of sensible heat and latent heat of sea-ice formation from the ocean as well as advection of heat from lower latitudes. The dominance of low-level and surface radiative cooling leads to the formation of the Arctic temperature inversion, i.e. an atmospheric temperature structure where temperatures increase with height in the lower troposphere [e.g. Zhang et al., 2011]. This strongly stable stratification suppresses vertical mixing and gives rise to a positive lapse-rate feedback in a warming climate, which is a major contributor to the Arctic amplification of climate change [Manabe and Wetherald, 1975; Pithan and Mauritsen, 2014]. However, observations show that in Arctic winter, the surface at any given location is not always cooling radiatively, nor is the boundary layer always stably stratified [e.g. Sedlar et al., 2012]. Indeed, the Arctic winter boundary layer can be in either a cloudy or a radiatively clear state, with distinct surface fluxes and atmospheric profiles typical for each state [Stramler et al., 2011; Tjernström, 2012].

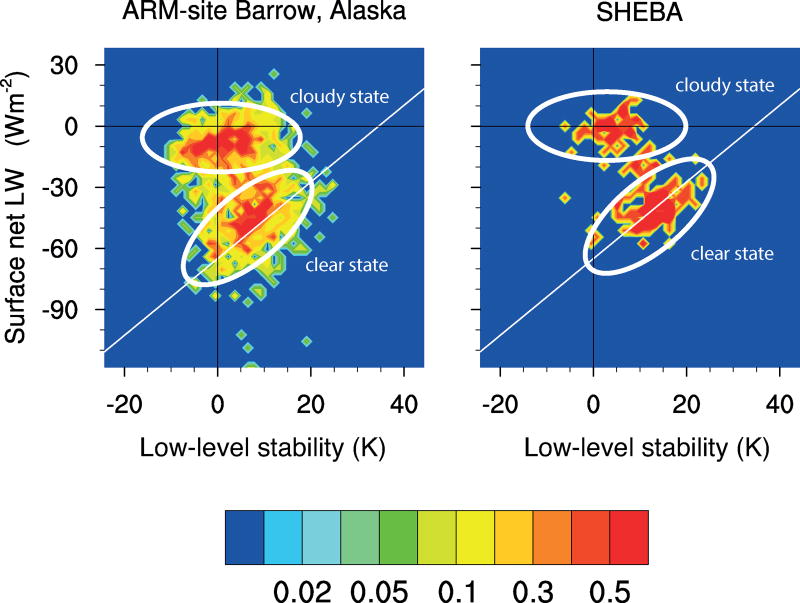
While the widespread existence of temperature inversions in the Arctic boundary layer and a relationship between cloud cover and near-surface temperature profiles were already reported by Sverdrup [1933], the existence of two discrete states of the Arctic wintertime boundary layer [Persson et al., 1999] was only recognized through observations made during the SHEBA campaign 1997/1998 [Persson et al., 2002]. Station measurements on an ice floe and regular balloon soundings revealed that Arctic wintertime boundary-layer states cluster around two typical situations [Stramler et al., 2011]: A cloudy state, during which the presence of liquid-containing, often mixed-phase low-level clouds inhibits surface radiative cooling, and a radiatively clear state, during which the surface cools radiatively under clear skies or pure ice clouds, which generally have a much lower emissivity than liquid-containing clouds (Figure 1).

Figure 1.

Figure 1

Open in a new tab

Bivariate pdf of low-level stability (defined as 850 hPa minus surface temperatures) and surface net longwave radiation defined positive downwards, NDJF 1997/1998 for SHEBA and NDJF 1990–1999 for the ARM site. Low-level stability is computed from individual soundings and surface radiation from the corresponding 6-hour average. Figure Source: Pithan et al. [2014]

To alleviate the substantial biases climate models display in the Arctic surface energy budget [Svensson and Karlsson, 2011] and low-level stability [Medeiros et al., 2011; Pithan et al., 2014], it is crucial to understand to what extent such biases are related to the representation of either of the typical boundary layer states or their frequency of occurence, and which processes or parametrizations in models have the greatest weight in causing these biases. Improving weather forecasts in polar regions equally requires understanding which physical processes cause present model deficiencies [Jung et al., 2016]. The present single-column model intercomparion uses a highly idealized framework to understand to what extent the participating climate, weather prediction and research models are able to reproduce the typical boundary layer states, and why they may fail to reproduce observed features of the Arctic winter boundary layer.

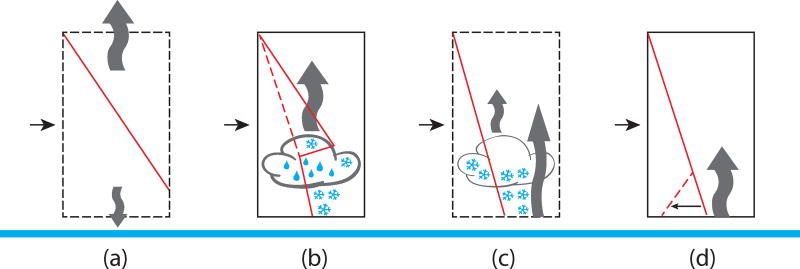
When relatively warm and moist air masses are advected over Arctic land or sea ice in winter (Figure 2a), radiative cooling triggers the formation of liquid-containing clouds, which force the boundary layer into its cloudy state (Figure 2b) [Curry, 1983; Stramler et al., 2011; Pithan et al., 2014]. Due to their high infrared emissivity, which is close to unity, liquid-containing clouds are associated with much larger rates of downwelling longwave radiation at the surface than clear skies or ice clouds [Morrison et al., 2012]. During the cloudy state, cloud-top radiative cooling keeps the boundary layer well-mixed or only weakly stable. Temperature and humidity inversions usually occur near the top of the cloud layer, with clouds frequently extending into the temperature inversion over the central Arctic ocean [Sedlar et al., 2012]. Surface sensible heat fluxes in the cloudy state are weak, and may be directed upwards, as the ocean below the sea ice remains much warmer than the near-surface atmosphere. The air mass loses heat through cloud-top radiative cooling and moisture through precipitation, ultimately making the environment too dry and cold for the mixed-phase cloud to persist, such that the boundary layer transitions to its radiatively clear state. In the clear state, surface radiative cooling on the order of 40Wm−2 [Stramler et al., 2011] leads to the build-up of surface-based temperature inversions (Figure 2d). The boundary layer is thus strongly stable and sensible heat fluxes are directed towards the surface. This air mass transformation has been described as the formation of continental polar air masses [Wexler, 1936; Curry, 1983]. It often originates near the downstream ends of the Atlantic and Pacific storm tracks [Woods et al., 2013].

Figure 2.

Figure 2

Open in a new tab

Sketch of Arctic air mass formation. Curved arrows represent radiative cooling, red lines are temperature profiles, which are driven towards the dashed lines by radiative cooling in the respective state. Full boxes mark quasi-steady states and dashed boxes unstable transition states Source: Pithan et al. [2014].

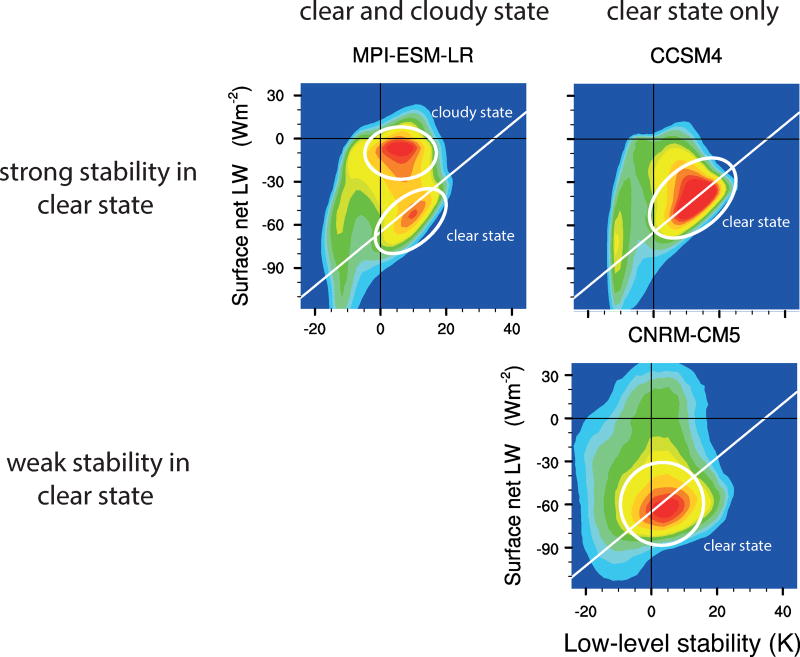
Comparing climate model output to satellite [Cesana et al., 2012] and in-situ observations [Pithan et al., 2014] reveals that many climate models lack the cloudy state of the Arctic winter boundary layer, and some models do not reproduce the strong low-level stability observed in the clear state. Examples for these biases are shown in Figure 3. Models in the rightmost column lack the cloudy state of the boundary layer, i.e. a second maximum in the pdf at low stability and weakly negative surface net longwave radiation. The CNRM-CM5 model at the bottom additionally has the radiatively clear state shifted to weaker stabilities at stronger longwave cooling rates than seen in observations (Figure 1).

Figure 3.

Figure 3

Open in a new tab

Bivariate PDFs as in Figure 1 using CMIP5 model output from the ocean domain north of 64° N. The models shown serve as examples for the three groups of models determined in Pithan et al. [2014]. White lines are included as visual reference indicating the observed relationship between stronger inversions and weaker surface cooling within the clear state.

The maintenance of the cloudy state at the low temperatures observed [Shupe et al., 2006; Morrison et al., 2012] poses a challenge to models, partly because theory predicts rapid freezing of supercooled water in the presence of ice particles. For a given temperature, the saturation vapour pressure over ice is lower than that over water surfaces, which can cause evaporation from water droplets and deposition of water molecules on ice particles [Wegener, 1911; Bergeron, 1935; Findeisen, 1938]. Observations show that layers of supercooled liquid often exist above the ice cloud such that supercooled droplets may not actually experience the presence of ice particles in the same air volume [Morrison et al., 2012]. However, large-scale models typically do not resolve this vertical structure. Much higher resolution large-eddy simulations (LES) have successfully been employed to study Arctic mixed-phase clouds, but show considerable inter-model spread with a strong sensitivity of model results to both ice number concentration and particle size distribution [Ovchinnikov et al., 2014]. The important role of cloud microphysics for the maintenance of Arctic mixed-phase stratocumulus clouds was also emphasized by Fridlind et al. [2012], who showed that consumption of ice nuclei by cloud processes can limit ice formation.

Past studies on the model representation of clear-sky Arctic boundary layers have largely focused on turbulent heat fluxes under stable stratification (e.g. Cuxart et al. [2006]; Beare et al. [2006]), but model results were also shown to be sensitive to radiation and surface coupling, especially at lower wind speeds [Sterk et al., 2013].

The present intercomparison aims to understand the main reasons for the two types of model biases found in the CMIP5 ensemble (Pithan et al. [2014], exemplified in Figure 3): The lack of a cloudy state and weak low-level stability despite strong surface radiative cooling. The experimental setup is based on earlier work by Wexler [1936]; Curry [1983] and Pithan et al. [2014]. It follows the formation of an Arctic air mass from an idealized Lagrangian perspective. Initial temperature and humidity profiles represent an air mass originating over open ocean, the lower boundary condition is a snow-covered sea-ice surface and models are run under polar night conditions, such that no solar radiation reaches the modelled column. In this setup, the atmospheric column cools radiatively. Clouds are formed, that precipitate and eventually glaciate, such that the column is transformed to a cold, dry state. The challenges to models are (1) to initially reach and maintain a radiatively opaque cloudy state with temperature profiles and surface fluxes resembling those observed in Arctic winter and (2) to qualitatively reproduce the observed fluxes and profiles of the radiatively clear boundary layer.

2. Experimental strategy, setup and participating models

2.1. Lagrangian vs. Eulerian frameworks in observations and modelling

Boundary-layer observations are generally taken in an Eulerian framework, which means that the observatory is fixed on the ground (or slowly moving in the case of ship- or ice-based observations such as SHEBA). Measured quantities can thus change because of external influences such as the diurnal or seasonal cycle, diabatic processes such as rain or radiation and because of advection, as synoptic weather patterns advect air from different sources past the measurement site. Single-column models can be run in an Eulerian framework by including advective tendencies in the model forcing.

As explained in the introduction, the state of the Arctic winter boundary layer strongly depends on the transformation of warm and moist air masses that are advected over sea ice or Arctic land. In a Eulerian modelling framework, this means that advective tendencies, i.e. the amount of heat and moisture being advected into the column, would largely dictate the boundary-layer state, giving a single-column model relatively little freedom to develop the biases that occur in free-running models.

We therefore choose a Lagrangian or air-mass following framework [Wexler, 1936; Curry, 1983; Pithan et al., 2014] , assuming that our model column follows a homogeneous air mass advected over a homogeneous Arctic sea ice surface. This setup allows models to freely develop their own state and biases over several days while retaining the simplicity of a single-column setup and has successfully been used in other intercomparison studies [Bretherton et al., 1999; van der Dussen et al., 2013]. As our frame of reference follows the moving air mass, advective tendencies are set to zero even though an observer at a ground station (i.e. in a Eulerian framework) would report substantial advection of heat and moisture as the modelled column is advected into an area that was previously dominated by cooler and dryer air.

2.2. Boundary and initial conditions

Models are initialized with analytical temperature and humidity profiles (Table 1) which represent typical air masses entering the Arctic in winter in an idealized way. A geostrophic wind of 5 ms−1 is prescribed throughout the troposphere to drive turbulent mixing. Surface conditions are initialized to a surface temperature of 250 K, a 1 m thick sea-ice layer and 0.1 m water equivalent of snow on top of the sea ice. The ocean underneath the sea ice is assumed to be at the freezing point of sea water. As the model column is supposed to follow the same air mass on its trajectory, advective tendencies are set to zero. The use of interactive surface temperatures does not follow the Lagrangian approach, but is justified by observations showing that the surface-atmosphere interaction has a much shorter timescale than that of air mass advection and transformation [Persson et al., 1999]. The run length was set to 20 days, which is beyond the typical residence time of air masses over Arcticsea ice [Woods and Caballero, 2016]. We therefore limit most analyses to the first 10 days, which also have temperatures that are more representative of Arctic ocean conditions. The model location is set to 80° N and the experiment is started on the 1st of January, such that insolation is zero throughout the run. Greenhouse gas concentrations are prescribed as in Table 2.

Table 1.

Initial profiles of temperature, humidity and geostrophic zonal wind ugeo (ms−1). The meridional geostrophic wind component is zero. p0 = 1013hPa, assumed lapse rate γ = 8 * 10−3 Km−1, gas constant for air R = 287 J kg−1K−1, gravitational acceleration g = 9.81 ms−2. Temperature profile based on Curry [1983].

Pressure (hPa) Temperature (K) Humidity ugeo (ms−1)
1013 T0 = 273 rh wrt water: 80 % 5
1013–600
T=T0(pp0)Rγg−1
 linear interpolation of rh 5
600 rh wrt water: 20 % 5
600–300
T=T0(pp0)Rγg−1
 rh wrt water: 20% 5
300-model top T = T300hPa q= 3 * 10−6kg kg−1 0
Open in a new tab

Table 2.

Greenhouse gas concentrations

GHG CO2 N2O CH4 CFC-11 CFC-12
volume mixing ratio 360 10−6 309.5 10−9 1693.6 10−9 252.8 10−12 466.2 10−12
Open in a new tab

2.3. Models participating in the intercomparison

In response to a call endorsed by the GASS steering group, the Larcform 1 experiment as described above was run using the single-column versions of climate and weather prediction models as well as research models. Some of the participating models use fixed rather than thermodynamically interactive sea ice thickness and two models do not represent snow on sea ice (see Table 3).

Table 3.

Models participating in the intercomparison. Physics schemes used in WRF are described in the text, prognostic: models with separate prognostic variables for cloud ice and liquid and parametrisation of freezing rates; f(T): phase partitioning as a function of temperature, p(T): temperature-dependent probability for total freezing of condensate at each timestep, ice: this model assumes all condensate to be ice for the present case, fixed ice: models with fixed ice thickness, no snow: models that do not represent snow on sea ice . z0m is the momentum roughness length.

Model documentation phase of condensate snow and ice z0m(m) contributor
CAM 5.3 Neale et al. [2010] prognostic interactive 5e-3 FP and BM
CMC-GDPS Bélair et al. [2009] f(T) interactive 1.6e-4 AZ
CMC-HRDPS Mailhot et al. [2006] prognostic interactive 1.6e-4 AZ
CMC-RDPS Mailhot et al. [2006] f(T) interactive 1.6e-4 AZ
EC-Earth V3 (IFS 36r4) ECMWF [2010] prognostic no snow, fixed ice 1e-3 KH
ECHAM 6.2 Stevens et al. [2013] prognostic interactive 1e-3 FP
ECHAM6.1.0-HAM2.2 Stevens et al. [2013] prognostic interactive 1e-3 LI
Lohmann et al. [2007]
ECMWF-IFS ECMWF [2010] prognostic no snow, fixed ice 1e-3 IS
GISS E2 Schmidt et al. [2014] P(T) fixed ice
νmu∗+0.018u∗2g
 AA
WRF 3.5.1 Skamarock et al. [2008] prognostic fixed ice 1e-3 HAMS and WA
WUR-D91 Duynkerke [1991] ice fixed ice 1e-1 GJS
Open in a new tab

The WRF 3.5.1 single-column model here uses the Mellor-Yamada-Janjic boundary-layer scheme [Janjic, 1994], the NOAH land surface model, the eta-similarity surface layer scheme, the RRTMG radiation package [Iacono et al., 2008] and the WRF single-moment five-class microphysics scheme [Hong et al., 2004]. The CAM-single column model constrains wind speeds to the prescribed geostrophic values. Sensitivity experiments with other models (not shown) suggest that such differences in wind speeds do not qualitatively alter the thermodynamical representation of both boundary-layer states.

Following the evaluation of these initial standard model runs (denoted std throughout the paper), additional sensitivity experiments were performed with individual models to discern causes for specific biases or model behaviours. These runs usually employ the same setup described here but use slight modifications of the respective models, which will be explained in context where such results are presented.

3. Results and discussion

As the present intercomparison is not based on an observational dataset nor includes an LES reference run, model results cannot be evaluated by directly comparing model output at a given time to the observational or high-resolution modelling ‘truth’. We instead use our understanding of the modelled air-mass transformation and its relation to the observed states of the Arctic winter boundary layer and focus our evaluation on whether or not, and why, models qualitatively reproduce the typical surface fluxes and atmospheric profiles of both boundary layer states. We mostly use the SHEBA dataset explained in the introduction as observational reference for the boundary-layer states. Since we compare a single air-mass following model experiment with analytical initial profiles to point observations of a whole season, models can at most be expected to qualitatively reproduce the typical observed boundary layer states. We therefore do not quantitatively interpret the lifetime of clouds, heat fluxes or other variables. We here give a brief overview of the results before focusing on the physical mechanisms that cause typical model biases.

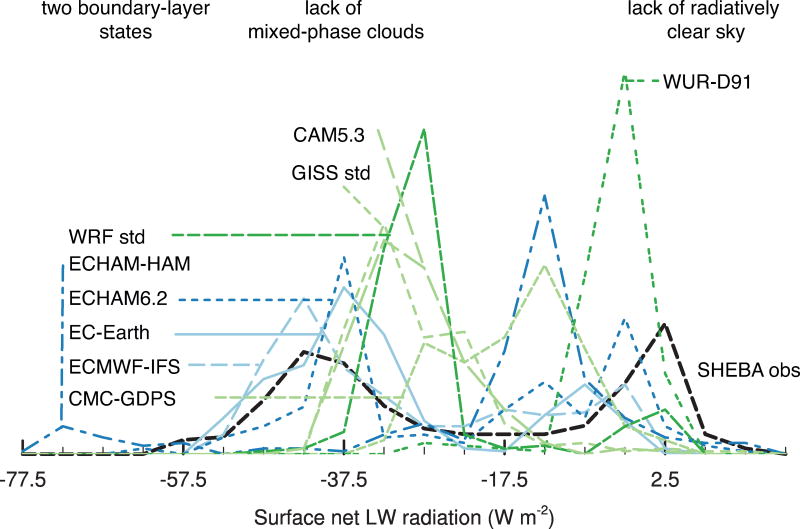
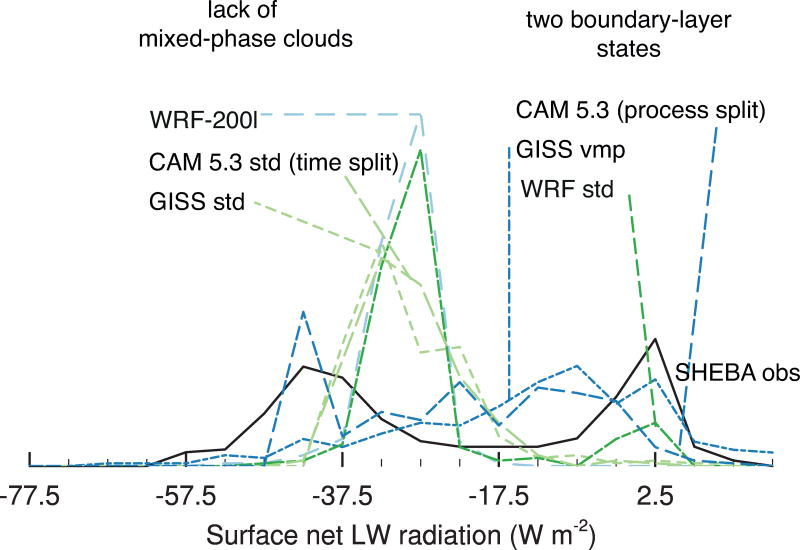
Most participating models generate a bimodal distribution of surface net longwave radiation in the experiment (Figure 4, all fluxes are positive downwards), indicating that they do represent the clear and cloudy state of the boundary layer. Models tend to have slightly less surface radiative cooling than observations in the clear state, and slightly more cooling in the cloudy state. CAM 5.3 and GISS std lack the cloudy state of the boundary layer and therefore have a unimodal distribution of surface net longwave radiation. The WUR-D91 model only displays the cloudy state of the boundary layer with weak rates of surface radiative cooling.

Figure 4.

Figure 4

Open in a new tab

PDF of hourly means of surface net longwave radiation in participating models for days one to ten and NDJF SHEBA observations. Each tickmark corresponds to the center of one bin.

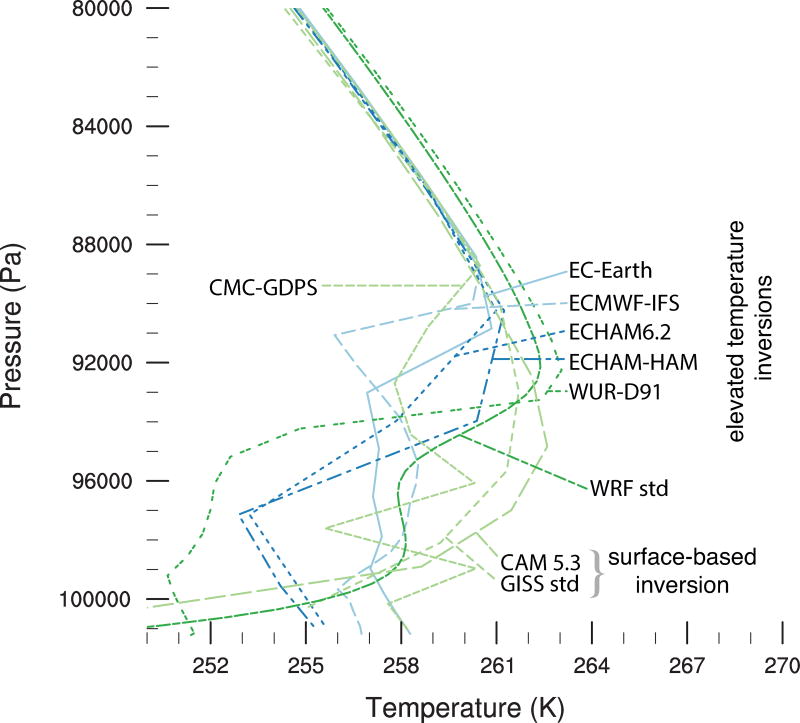
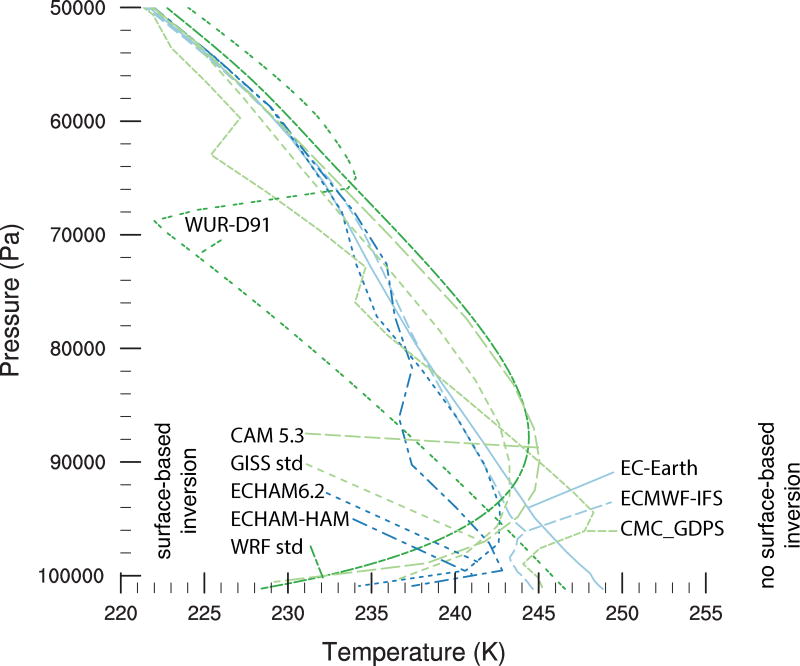
Not all models that represent both states in terms of net longwave radiation also reproduce the observed temperature profiles. Two days into the run, elevated inversions dominate the temperature profile in models that represent the cloudy state of the boundary layer (Figure 5), consistent with observations [Stramler et al., 2011]. The models lacking the cloudy state (CAM5.3 and GISS std) generate surface-based temperature inversions. A surface-based inversion has started to develop in WRF-std, while an elevated temperature inversion persists. The elevated inversion was generated by a mixed-phase cloud during the first day of the experiment and persists even though the cloud has vanished. This transition occurs at a later stage in other models. We do not focus on the transition in the present paper because observed transitions in a Eulerian framework can be caused by the advection of a different air mass rather than a state transition within the air mass, which makes it difficult to identify observational analogues. After ten days (Figure 6), surface-based inversions dominate the temperature profile in ECHAM6.2, ECHAM-HAM, GISS std, WRF std and CAM5.3 in line with observations of the radiatively clear boundary layer. WUR-D91, CMC (all versions, but only CMC-GDPS is shown here), EC-Earth and ECMWF-IFS do not form a surface-based temperature inversion but maintain a well-mixed or at least near-neutral profile near the surface.

Figure 5.

Figure 5

Open in a new tab

Temperature profiles averaged over one hour after two days.

Figure 6.

Figure 6

Open in a new tab

Temperature profiles averaged over one hour after ten days.

3.1. Existence or lack of the cloudy state

We here investigate in more detail why some models (CAM5.3, GISS std and a high vertical resolution version of WRF called WRF-2001) do not represent the cloudy state of the boundary layer and have virtually no cloud liquid water throughout the experiment. Pithan et al. [2014] showed that for most of the climate models investigated in that study, the lack of a cloudy state could be explained by mixed-phase cloud microphysics not allowing for cloud liquid water to exist at cold enough temperatures. However, this explanation did not hold up for CAM4, the predecessor of CAM5.3, which allowed cloud liquid water to exist down to −40 °C but still did not generate a cloudy state of the boundary layer. Caldwell [2012] reports that CAM5 underestimates cloud liquid water because of an issue in the coupling between cloud macro- and microphysics.

Different physical processes that are handled by individual parameterisations can be coupled in ‘time split’ or ‘process split’ mode in a general circulation model [Williamson, 2002]. In the time split mode, each process acts on the model state separately, and the model state is updated after the call to each individual parameterisation. A parameterisation therefore sees the atmospheric state as it was left by the preceding parameterisation. In process-split mode, in contrast, all parameterisations are given the same initial state from the last time step, their tendencies are accumulated and the model state is updated once per timestep using the sum of all individual tendencies. CAM uses the time-split mode to couple cloud macrophysics, cloud microphysics and radiation, called in this order [Neale et al., 2010]. In the CAM5.3 run for Larcform1, the cloud macrophysics generate considerable amounts of liquid water. However, all liquid water is converted into cloud ice by the flowing call to cloud microphysics. When radiation is called, it thus sees an atmospheric column that contains no liquid water, and radiative cooling occurs at the surface rather than at cloud top. The lack of radiative cooling at the cloud level also reduces the generation of cloud liquid water in the next time step.

Caldwell [2012] addressed this by implementing a substepping procedure into the cloud schemes, i.e. retaining the time-split coupling but shortening the coupling time step. Since that code was not available to us when running the intercomparison, we simply change the coupling of different processes in the CAM5.3 code such that cloud microphysics and macrophysics are process-split, i.e. they act on the same model state and their physical tendencies are summed up before updating the model. This leads to cloud liquid water persisting for several days at the beginning of the experiment, substantially reducing radiative cooling and preventing the build-up of a surface-based temperature inversion at this stage (not shown). The emergence of a cloudy state of the boundary layer in the modified model can also be seen in the PDF of surface net longwave radiation, which now includes a second peak (Figure 7). In our experiment, the lack of cloud liquid water and a cloudy state of the Arctic winter boundary layer in CAM (see also English et al. [2014]) is thus caused by the time-split coupling of different processes that does not allow the cloud liquid to adequately interact with radiation without the additional substepping suggested by Caldwell [2012].

Figure 7.

Figure 7

Open in a new tab

PDF of surface net longwave radiation in selected models (up to day ten) and NDJF SHEBA observations. Each tickmark corresponds to the center of one bin.

In GISS, cloud condensate can only be either liquid or ice at a given time and location, and a likelihood for supercooled water to freeze instantaneously is dependent on temperature [Schmidt et al., 2014]. This leads to a growing chance of entirely freezing a supercooled layer with time, and does not allow a persistent mixed phase cloud to form in our experiment. When running GISS with a virtual mixed-phase scheme that is designed to represent the effect of mixed-phase clouds (GISS vmp), liquid water appears in the column after about a day and leads to reduced surface radiative cooling consistent with observations of the cloudy Arctic boundary layer (Figure 7) as well as the establishment of an elevated temperature inversion during the cloudy state of the boundary layer (not shown). The GISS vmp scheme was only being developed during the intercomparison, but these results suggest it has the potential to substantially alleviate weaknesses of the GISS CMIP5 model reported by Pithan et al. [2014].

An unexpected resolution dependency occurs in WRF, which is run at different vertical resolutions (90 and 200 levels) to investigate the sensitivity of results to vertical resolution. The 90-level version is representative of an operational model, whereas 200 levels is a very high vertical resolution used for research purposes [Sterk et al., 2013]. While high vertical resolution is usually thought of as beneficial for the representation of mixed-phase clouds [Barrett, 2012], the high vertical resolution version WRF-200l lacks cloud liquid water and the corresponding cloudy state of the boundary layer, which lower vertical resolution version WRF-90l does generate (Figure 7). In the high vertical resolution version, the lowest model level, which is only 1.2 m thick, dries to the surface through frost deposition or negative water vapour flux before a cloud can be formed. As the air cools further, it becomes saturated with respect to ice, but does not reach saturation with respect to water, which prevents the generation of cloud liquid water. The deposition of water vapour at the surface is similar in the lower-resolution versions, but hardly has an effect on the much thicker surface layers containing substantially more water vapour in total (not shown). Very high vertical model resolutions can violate implicit assumptions in the design of parametrisations and thus be detrimental to model performance. In this case, we suggest that the very high vertical resolution would require a faster coupling between different atmospheric layers, such that surface fluxes could tap into a larger moisture reservoir than that of the first model level alone. This hypothesis could be tested by substantially decreasing the timestep, but further investigation of the issue is beyond the scope of the present paper.

3.2. Build-up of surface-based inversions under radiatively clear skies

ECHAM6.2, ECHAM-HAM, WRF-90l and CAM5.3 do represent the growing surface-based inversions observed under clear skies once strong surface radiative cooling is sustained for many hours and days. However, the CMC models sustain well-mixed layers even with little or no cloud liquid water being present, preventing the generation of strong stability and surface-based temperature inversions. EC-Earth and ECMWF-IFS also do not generate surface based inversions despite substantial surface radiative cooling.

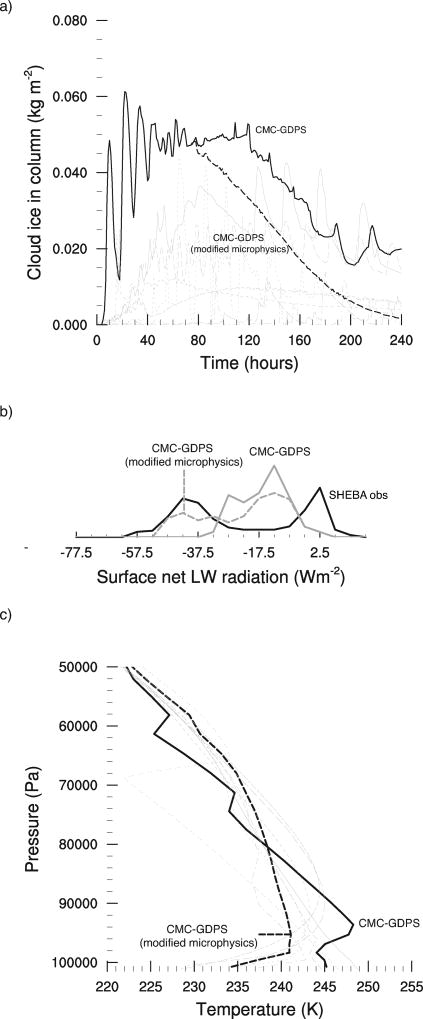
The sustained well-mixed layers in CMC models are likely caused by an exaggerated emissivity of ice clouds, caused by a combination of too small an effective radius for ice particles and an overestimated ice water path. In a sensitivity experiment with enhanced precipitation efficiency of ice clouds in the microphysics scheme (see Appendix A for details), CMC-GDPS does develop a surface-based inversion by day ten (Figure 8). While the standard model version has one of the highest ice water paths of the intercomparison, the modified microphysics lead to an almost complete removal of cloud ice by day ten, which corresponds to the lower end of the intermodel spread (Figure 8a). The reduced ice water path leads to stronger surface radiative cooling in the clear state (Figure 8b) and the development of a surface-based temperature inversion as expected for the radiatively clear state (Figure 8c).

Figure 8.

Figure 8

Open in a new tab

a) Vertically integrated ice water paths for the CMC-GDPS standard and modified versions and other models (gray). b) PDF of surface net longwave radiation for the CMC-GDPS standard and modified versions, and NDJF SHEBA observations. c) Vertical profiles of temperature after ten days, CMC-GDPS standard and modified versions and other models (gray).

WUR-D91 is an even more extreme example of high ice cloud emissivities, since it maintains a single well-mixed layer and surface heat fluxes corresponding to the cloudy state of the boundary layer throughout the experiment despite assuming by construction that all cloud condensate is frozen.

Temperature profiles and surface fluxes similar to those in models lacking a representation of snow on sea ice (ECMWF-IFS and EC-Earth) were obtained in a sensitivity experiment with no snow on sea ice in ECHAM6.2 (not shown). Snow has a much lower conductivity than ice and strongly reduces the upward heat flux from the ocean to the surface. We conclude that the lack of an insulating snowpack causes the absence of surface-based inversions in ECMWF-IFS and EC-Earth. This is consistent with Tjernström and Graversen [2009] reporting that the ERA-Interim reanalysis derived using the ECMWF model was lacking surface-based inversions in early winter at the SHEBA site despite the assimilation of local observations.

3.3. Turbulent heat flux, cloud liquid water and energy budget

In the radiatively clear boundary layer, observed downward sensible heat fluxes are typically on the order of 10 W m−2 [Stramler et al., 2011]. In the models lacking snow on sea ice in Larcform1, sensible heat fluxes in the clear state of the boundary layer [surface radiative cooling greater than 20 W m−2] are much smaller. Sensible heat fluxes still vary by a factor of five among the remaining models (Table 5). Larger downward heat fluxes under clear skies observed at SHEBA (Figure 8 of Stramler et al. [2011]) may be due to larger wind speeds at the SHEBA site [Persson et al., 2002] sustaining more mixing than in our experiment. The friction velocity varies much more between different models than between the clear and cloudy state in individual models (not shown).

Table 5.

Overview of turbulent heat fluxes (defined positive downwards) in the clear state, cloud liquid water in the cloudy state and net surface energy loss over the first ten days. Clear and cloudy state are partitioned at a surface net longwave radiation of - 20 Wm−2

Model hs (clear)
[Wm−2]		 clwvi (cloudy)
[kgm−2]		 net sfc energy loss
103[kJm−2]
EC-Earth 0.23 0.037 27.3
ECMWF-IFS 1.65 0.029 24.1
ECHAM6.2 5.12 0.16 17.5
ECHAM-HAM 8.02 0.39 15.5
CMC-GDPS 3.09 0.01 12.9
GISS std 5.79 - 18.3
WRF-90l 12.05 0.05 13.0
WUR-D91 - 0 6.3
CAM5.3 9.57 - 16.5
GISS vmp 3.97 0.04 8.2
CAM5.3 (process split) 9.70 0.02 13.0
Open in a new tab

Vertically integrated cloud liquid water in the cloudy state varies by an order of magnitude among models, which confirms that small amounts of liquid water are sufficient to sustain the cloudy state. Liquid water is absent in WUR-D91, where all condensate is assumed to be ice, and the cloudy state is maintained because of a high emissivity of ice clouds. Median observed liquid water paths for the SHEBA winter are at the lower end of model results, and the high end of model results exceeds the 95th percentile of observations [Shupe et al., 2006]. However, a more realistic setup where clouds are constrained to a realistic height, e.g. by subsidence, is required to determine if these models actually tend to overestimate LWP in Arctic mixed-phase clouds given realistic moisture advection.

The greatest accumulated surface energy deficit (defined as the sum of sensible, latent and radiative fluxes at the surface accumulated over time) over the first ten days of the experiment occurs in the models without an insulating snow layer. As before, we consider the first half of the experiment to obtain a roughly realistic weight between the clear and cloudy states. Leaving aside the WUR-D91 model, which lacks a radiatively clear boundary-layer state, accumulated energy loss varies by about 50 % among the remaining models. Changes to the GISS cloud and snow schemes roughly halve the accumulated surface energy loss, and making mixed-phase clouds appear in CAM5.3 reduces the energy loss by about 20 %. Note that the accumulated energy loss is largely balanced by latent heat release, i.e sea ice growth, in winter.

4. Conclusions

Running an idealized Lagrangian single-column experiment of Arctic air mass formation in a set of climate, operational forecast and research models, we reproduce and investigate the two main types of biases global models display in the Arctic wintertime boundary layer: (1) A lack of mixed-phase clouds and thereby of the cloudy state of the boundary layer and (2) weak low-level stability and a lack of surface-based temperature inversions despite strong surface radiative cooling in the radiatively clear state.

(1) Pithan et al. [2014] report that in many models, the lack of a cloudy state is related to a temperature-dependent diagnostic phase partitioning of cloud condensate, which causes total freezing at relatively warm temperatures. Sensitivity experiments with an improved representation of mixed-phase cloud properties in GISS for the present study confirm the crucial role of representing mixed-phase microphysics. All physics schemes using separate prognostic variables for cloud ice and cloud liquid water with explicitly computed freezing rates were able to qualitatively represent the cloudy state of the boundary layer in our study The global and regional versions of the CMC model do reproduce the cloudy state with a temperature-dependent diagnostic phase partitioning. CAM5.3 lacks the cloudy state of the boundary layer despite a sophisticated treatment of cloud microphysics because of the sequential/time-split coupling of cloud microphysics, cloud macrophysics and radiation [Williamson, 2002; Caldwell, 2012]. When cloud macro- and microphysics are called in parallel/process-split, the same physical schemes do reproduce mixed-phase clouds and the corresponding atmospheric profiles and surface fluxes.

(2) Weak low-level stability and a lack of surface-based temperature inversions occur in models that do not represent snow on sea ice or have high atmospheric emissivities and thereby maintain stronger downwelling longwave fluxes in the absence of cloud liquid water. The precipitation efficiency of ice clouds can control the development of surface-based temperature inversions in one model. Inter-model differences in turbulent fluxes in stably stratified conditions [Cuxart et al., 2006] are confirmed, but are of secondary importance for this airmass transformation case including cloud processes and surface coupling.

While our results suggest that models using a separate prognostic variable for cloud ice are generally able to represent mixed-phase clouds in Arctic winter and the associated boundary-layer state, the idealized experiment does not permit us to quantitatively constrain the occurrence of such clouds, the magnitude of turbulent heat fluxes or the liquid water path, which all vary considerably among models in the intercomparison. As a next step, we are going to develop a more realistic, observationally-based setup that allows to evaluate and improve the model representation of cloud lifetime, cloud properties and surface fluxes. Lagrangian observations of individual air masses undergoing the transition to Arctic air over sea ice are not available yet, but the upcoming Year of Polar Prediction [WWRP, 2014] may provide an opportunity to obtain such data.

Table 4.

Groups of models according to their representation of BL states

with cloudy state lacking a cloudy state
ECHAM6.2
ECHAM-HAM
strong stability in clear state WRF std WRF-200l
CAM5.3 (process split) CAM5.3 (std)
GISS vmp GISS std
CMC-GDPS (modified microphysics)
ECMWF-IFS
weak stability in clear state EC-Earth
CMC-GDPS (standard)
Open in a new tab

Key Points.

  • ○

    A Lagrangian-style single column model experiment can reproduce Arctic air mass formation

  • ○

    Model deficiencies are caused by mixed-phase microphysics, process interaction and surface representation

  • ○

    Lagrangian, i.e. air mass-following observations would allow for a tighter constraint on model behaviour

Acknowledgments

We gratefully acknowledge support from the GASS (Global atmospheric system studies) steering group. We thank the researchers involved in the collection of SHEBA and ARM data for making their datasets available, and the modelling groups, the Program for Climate Model Diagnosis and Intercomparison and the World Climate Research Program’s Working Group on Coupled Modelling for making available the CMIP5 multi-model data set. F.P. was funded by the ERC under Marie-Curie grant UACSURF (GAP-654492) for parts of this study. AA and MK were funded by the NASA MAP program. GJS acknowledges funding from NWO contract 863.10.010. MS acknowledges the support from NWO (The Dutch Science Foundation) with grant 829.09.005 (?Quantifying contributions of surface climate feedbacks to the Arctic amplification of greenhouse warming? in the Sustainable Earth program). BM was supported by the Regional and Global Climate Modeling Program of the U.S. Department of Energy’s Office of Science, Cooperative Agreement DE-FC02-97ER62402. NCAR is sponsored by the National Science Foundation. KH was supported by the Swedish e-Science Research Centre SeRC. Thanks to Bert Holtslag for comments on an earlier version of this manuscript, and to Thorsten Mauritsen for advice and support in the development of the case. We gratefully acknowledge the input and advice of two anonymous reviewers. Model results are available at https://doi.org/10.1594/PANGAEA.856770.

Appendix A. Sensitivity experiment for CMC microphysics

The CMC-GDPS model uses the microphysics scheme of Sundqvist [1978], in which the generation of precipitation (eq. 3.1a in Sundqvist [1978]) is a function of a conversion timescale c0f−1 and a threshold value (mrf) of cloud water above which precipitation formation becomes more efficient. In CMC-GDPS, this relationship is described by a freezing function [Mailhot et al., 1998]

fmr(T)=min(1.,1.33e−0.066(T−T0)2)for 250K≤T≤T0max(0.03,0.75(1.07+εy1+y))for T≤250K, (A1)

where y = x (1 + x (1 + 1.333x)), x = |T-232|/18, ε = sign (T–232), T0 = 273.15K. For the sensitivity test discussed in section 3.1, precipitation formation is accelerated by reducing both the conversion timescale and threshold value. The modified freezing function reads

fmr(T)=min(1.,1.33e−0.066(T−T0)2)for 230K≤T≤T00.001for T≤230K. (A2)

References

  1. Barrett A. Ph.D. thesis. University of Reading; 2012. Why can’t models simulate mixed-phase clouds correctly? [Google Scholar]
  2. Beare RJ, Macvean MK, Holtslag AA, Cuxart J, Esau I, Golaz J-C, Jimenez MA, Khairoutdinov M, Kosovic B, Lewellen D, et al. An intercomparison of large-eddy simulations of the stable boundary layer. Boundary-Layer Met. 2006;118(2):247–272. [Google Scholar]
  3. Bélair S, Roch M, Leduc A-M, Vaillancourt PA, Laroche S, Mailhot J. Medium-range quantitative precipitation forecasts from canada’s new 33-km deterministic global operational system. Weather and Forecasting. 2009;24(3):690–708. [Google Scholar]
  4. Bergeron T. Proc. 5th Assembly. UGGI; Lisbon: 1935. On the physics of clouds and precipitation; pp. 156–178. [Google Scholar]
  5. Bretherton CS, Krueger SK, Wyant MC, Bechtold P, van Meijgaard E, Stevens B, Teixeira J. A GCSS boundary layer model intercomparison study of the first ASTEX Lagrangian experiment. Boundary-Layer Met. 1999;93:341–380. [Google Scholar]
  6. Caldwell P. The case of disappearing condensate, presentation given at the 17th Annual CESM Workshop; 18–21 June 2012; Breckenridge, CO. 2012. available online at http://www.cesm.ucar.edu/working_groups/Atmosphere/Presentations/2012/caldwell.pdf. [Google Scholar]
  7. Cesana G, Kay J, Chepfer H, English J, de Boer G. Ubiquitous low-level liquid-containing Arctic clouds: New observations and climate model constraints from CALIPSO-GOCCP. Geophys. Res. Letters. 2012;39(20):L20, 804. [Google Scholar]
  8. Curry J. On the Formation of Continental Polar Air. J. Atmos. Sci. 1983;40:2278–2292. [Google Scholar]
  9. Cuxart J, Holtslag A, Beare R, Bazile E, Beljaars A, Cheng A, Conangla L, Ek M, Freedman F, Hamdi R, et al. Single-column model intercomparison for a stably stratified atmospheric boundary layer. Boundary-layer Met. 2006;118(2):273–303. [Google Scholar]
  10. van der Dussen JJ, de Roode SR, Ackerman AS, Blossey PN, Bretherton CS, Kurowski MJ, Lock AP, Neggers RAJ, Sandu I, Siebesma AP. The GASS/EUCLIPSE Model Intercomparison of the Stratocumulus Transition as Observed During ASTEX: LES results. Journal of Advances in Modeling Earth Systems. 2013;5:483–499. doi: 10.1002/jame.20033. [DOI] [Google Scholar]
  11. Duynkerke PG. Radiation fog: A comparison of model simulation with detailed observations. Monthly Weather Review. 1991;119(2):324–341. [Google Scholar]
  12. ECMWF . Tech. rep. ECMWF; 2010. Ifs documentation cy36r1 - part iv physical processes. [Google Scholar]
  13. English JM, Kay JE, Gettelman A, Liu X, Wang Y, Zhang Y, Chepfer H. Contributions of clouds, surface albedos, and mixed-phase ice nucleation schemes to arctic radiation biases in cam5. Journal of Climate. 2014;27(13):5174–5197. [Google Scholar]
  14. Findeisen W. Die kolloidmeteorologischen vorgänge bei der niederschlagsbildung. Meteor. Z. 1938;55:121–133. [Google Scholar]
  15. Fridlind AM, Van Diedenhoven B, Ackerman AS, Avramov A, Mrowiec A, Morrison H, Zuidema P, Shupe MD. A fire-ace/sheba case study of mixed-phase arctic boundary layer clouds: entrainment rate limitations on rapid primary ice nucleation processes. J. Atmos. Sci. 2012;69(1):365–389. [Google Scholar]
  16. Hong S-Y, Dudhia J, Chen S-H. A revised approach to ice microphysical processes for the bulk parameterization of clouds — and precipitation. Mon. Wea. Rev. 2004;132:103–120. [Google Scholar]
  17. Iacono MJ, Delamere JS, Mlawer EJ, Shephard MW, Clough SA, Collins WD. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008;113:D13103. [Google Scholar]
  18. Janjic ZI. The Step-Mountain Eta Coordinate Model: Further Developments of the Convection, Viscous Sublayer, and Turbulence Closure Schemes. Mon. Wea. Rev. 1994;122:927–945. [Google Scholar]
  19. Jung T, Gordon ND, Bauer P, Bromwich DH, Chevallier M, Day JJ, Dawson J, Doblas-Reyes F, Fairall C, Goessling HF, Holland M, Inoue J, Iversen T, Klebe S, Lemke P, Losch M, Makshtas A, Mills B, Nurmi P, Perovich DK, Reid P, Renfrew IA, Smith G, Svensson G, Tolstykh M, Yang Q. Advancing polar prediction capabilities on daily to seasonal time scales. Bull. Am. Met. Soc. 2016 doi: 10.1175/BAMS-D-14-00246.1. [DOI] [Google Scholar]
  20. Lohmann U, Stier P, Hoose C, Ferrachat S, Kloster S, Roeckner E, Zhang J. Cloud microphysics and aerosol indirect effects in the global climate model echam5-ham. Atmospheric Chemistry and Physics. 2007;7(13):3425–3446. [Google Scholar]
  21. Mailhot J, Bélair S, Benoit R, Bilodeau B, Delage Y, Fillion L, Garand L, Girard C, Tremblay A. Scientific Description of RPN Physics Library - Version 3.6 -, Recherche en prévision numerique, Atmospheric environment service. Dorval, Quebec, Canada: 1998. available online at http://collaboration.cmc.ec.gc.ca/science/rpn/physics/physic98.pdf. [Google Scholar]
  22. Mailhot J, Belair S, Lefaivre L, Bilodeau B, Desgagne M, Girard C, Glazer A, Leduc A-M, Méthot A, Patoine A, et al. The 15-km version of the canadian regional forecast system. Atmosphere-Ocean. 2006;44(2):133–149. [Google Scholar]
  23. Manabe S, Wetherald R. The effects of doubling the CO2 concentration on the climate of a general circulation model. J. Atmos. Sci. 1975;32:3–15. [Google Scholar]
  24. Medeiros B, Deser C, Tomas R, Kay J. Arctic inversion strength in climate models. J. Climate. 2011;24:4733–4740. [Google Scholar]
  25. Morrison H, de Boer G, Feingold G, Harrington J, Shupe M, Sulia K. Resilience of persistent Arctic mixed-phase clouds. Nat. Geosci. 2012;4:11–17. doi: 10.1038/ngeo1332. [DOI] [Google Scholar]
  26. Neale R, Chen C-C, Gettelman A, Lauritzen P, Park S, Williamson DL, Conley A, Garcia R, Kinnison D, Lamarque J-F, Marsh D, Mills M, Smith A, Tilmes S, Vitt F, Morrison H, Cameron-Smith P, Collins W, Iacono M, Easter R, Ghan S, Liu X, Rasch P, Taylor M. NCAR technical note TN-486+STR. NCAR; 2010. Description of the ncar community atmosphere model (cam 5.0 description of the ncar community atmosphere model (cam 5.0) [Google Scholar]
  27. Ovchinnikov M, Ackerman AS, Avramov A, Cheng A, Fan J, Fridlind AM, Ghan S, Harrington J, Hoose C, Korolev A, McFarquhar GM, Morrison H, Paukert M, Savre J, Shipway BJ, Shupe MD, Solomon A, Sulia K. Intercomparison of large-eddy simulations of arctic mixed-phase clouds: Importance of ice size distribution assumptions. Journal of Advances in Modeling Earth Systems. 2014;6(1):223–248. doi: 10.1002/2013MS000282. [DOI] [Google Scholar]
  28. Persson P, Uttal T, Intrieri J, Fairall C, Andreas E, Guest P. Third Symposium on Integrated Observing Systems. Am. Meteorol. Soc; Dallas, Tex: 1999. Observations of large thermal transitions during the arctic night from a suite of sensors at sheba. [Google Scholar]
  29. Persson P, Fairall C, Andreas E, Guest P, Perovich D. Measurements near the Atmospheric Surface Flux Group tower at SHEBA: Near-surface conditions and surface energy budget. J. Geophys. Res. 2002;107(10.1029) [Google Scholar]
  30. Pithan F, Mauritsen T. Arctic amplification dominated by temperature feedbacks in contemporary climate models. Nat. Geosci. 2014;7:181–184. doi: 10.1038/ngeo2071. [DOI] [Google Scholar]
  31. Pithan F, Medeiros B, Mauritsen T. Mixed-phase clouds cause climate model biases in arctic wintertime temperature inversions. Climate Dyn. 2014;43(1–2):289–303. [Google Scholar]
  32. Schmidt GA, Kelley M, Nazarenko L, Ruedy R, Russell GL, Aleinov I, Bauer M, Bauer SE, Bhat MK, Bleck R, et al. Configuration and assessment of the giss modele2 contributions to the cmip5 archive. Journal of Advances in Modeling Earth Systems. 2014;6(1):141–184. [Google Scholar]
  33. Sedlar J, Shupe MD, Tjernström M. On the relationship between thermodynamic structure and cloud top, and its climate significance in the arctic. J. Climate. 2012;25(7) [Google Scholar]
  34. Shupe MD, Matrosov SY, Uttal T. Arctic mixed-phase cloud properties derived from surface-based sensors at sheba. Journal of the Atmospheric Sciences. 2006;63(2):697–711. doi: 10.1175/JAS3659.1. [DOI] [Google Scholar]
  35. Skamarock W, Klemp J, Dudhia J, Gill D, Barker D, Duda M, Huang X, Wang W, Powers J. A Description of the Advanced Research WRF Version 3. Mesoscale and Microscale Meteorology Division, National Center for Atmospheric Research (NCAR); Boulder, CO, USA: 2008. [Google Scholar]
  36. Sterk H, Steeneveld G, Holtslag A. The role of snow-surface coupling, radiation, and turbulent mixing in modeling a stable boundary layer over arctic sea ice. J.Geophys. Res.: Atmos. 2013;118:1199–1217. [Google Scholar]
  37. Stevens B, Crueger T, Esch M, Giorgetta M, Mauritsen T, Rast S, Schmidt H, Bader J, Block K, Brokopf R, et al. The Atmospheric Component of the MPI-M Earth System Model: ECHAM6. J. Adv. Model. Earth Syst. 2013 doi: 10.1002/jame.20015. [DOI] [Google Scholar]
  38. Stramler K, Del Genio A, Rossow W. Synoptically driven Arctic winter states. J. Climate. 2011;24(6):1747–1762. [Google Scholar]
  39. Sundqvist H. A parameterization scheme for non-convective condensation including prediction of cloud water content. Q.J. Roy. Meteor. Soc. 1978;104:677–690. [Google Scholar]
  40. Svensson G, Karlsson J. On the Arctic Wintertime Climate in Global Climate Models. J. Climate. 2011;24(22):5757–5771. [Google Scholar]
  41. Sverdrup H. Meteorology, The Norwegian North Polar expedition with the Maud’ 1918–1925, scientific results, vol. II. Geophysical Institute; Bergen, Norway: 1933. [Google Scholar]
  42. Tjernström M. ECMWF GABLS workshop on diurnal cycles and the stable boundary layer, 7–10 November 2011. European Centre for Medium-Range Weather Forecasts; 2012. The Arctic Ocean boundary layer: Interactions with the sea-ice surface and clouds. [Google Scholar]
  43. Tjernström M, Graversen R. The vertical structure of the lower Arctic troposphere analysed from observations and the ERA-40 reanalysis. Q. J. Roy. Met. Soc. 2009;135(639):431–443. [Google Scholar]
  44. Wegener A. Thermodynamik der Atmosphäare. JA Barth; Leipzig, Germany: 1911. [Google Scholar]
  45. Wexler H. Cooling in the lower atmosphere and the structure of polar continental air. Mon. Wea. Rev. 1936;64:122–136. [Google Scholar]
  46. Williamson DL. Time-split versus process-split coupling of parameterizations and dynamical core. Monthly Weather Review. 2002;130(8):2024–2041. doi: 10.1175/1520-0493. [DOI] [Google Scholar]
  47. Woods C, Caballero R, Svensson G. Large-scale circulation associated with moisture intrusions into the arctic during winter. Geophys. Res. Lett. 2013;40(17):4717–4721. [Google Scholar]
  48. Woods C, Caballero R. The role of moist intrusions in winter Arctic warming and sea ice decline. J. Climate. 2016 doi: 10.1175/JCLI-D-15-0773.1. [DOI] [Google Scholar]
  49. WWRP. [last accessed 20th February 2014];WWRP Polar Prediction Project Year of Polar Prediction (YOPP) Implementation Plan. 2014 available online at http://polarprediction.net/en/documents/
  50. Zhang Y, Seidel D, Golaz J, Deser C, Tomas R. Climatological Characteristics of Arctic and Antarctic Surface-Based Inversions. J. Climate. 2011;24(19):5167–5186. [Google Scholar]

RESOURCES