Reference Correlations for the Thermal Conductivity of Liquid Bismuth, Cobalt, Germanium and Silicon

Abstract

The available experimental data for the thermal conductivity of liquid bismuth, cobalt, germanium and silicon have been critically examined with the intention of establishing thermal conductivity reference correlations. All experimental data have been categorized into primary and secondary data according to the quality of measurement specified by a series of criteria. The proposed standard reference correlations for the thermal conductivity of liquid bismuth, cobalt, germanium, and silicon are respectively characterized by uncertainties of 10, 15, 16 and 9.5% at the 95% confidence level.

1. Introduction

The last two decades there is an increasing use of mathematical models to simulate a variety of processes involving liquid metals such as ‘cast to shape,’ primary and secondary metal production, powder production by spray forming, and welding. Depending on what aspect of the process is modeled, a need for viscosity or thermal conductivity data of relevant alloys exists. Historically there are wide discrepancies in the viscosity and thermal conductivity data reported for the metallic elements and alloys.¹ For example there is a spread of about 400% in the reported values for the viscosity of molten aluminum and about 100% for the viscosity of molten iron.^{1, 2} Such discrepancies prompted the need to review the values in the literature. Thus, following the need for reference values of the density, viscosity and thermal conductivity of liquid metals, a project was initiated by the International Association for Transport Properties, IATP (former Subcommittee on Transport Properties of the International Union of Pure and Applied Chemistry, IUPAC) in 2006 to evaluate critically the density, the viscosity, and the thermal conductivity of selected liquid metals. Thus

• in 2006 reference values for the density and the viscosity of liquid aluminum and iron were published,² as a result of a project supported by IUPAC.

• Following this, in 2010, values for the density and viscosity for liquid copper and tin were proposed.³ That work had also been supported by IUPAC.

• In 2012, the work was continued and reference correlations of the density and viscosity of liquid bismuth, nickel, lead, silver, and antimony were proposed,⁴ to be concluded with liquid cadmium, cobalt, gallium, indium, mercury, silicon, thallium, and zinc,⁵ and the eutectic alloys Al+Si, Pb+Bi, and Pb+Sn.⁶

For the remaining liquid metals in the periodic table very limited information is available in literature.

In 2017 the investigation was extended to reference correlations for the thermal conductivity of liquid metals. Thus, reference correlations were proposed for liquid copper, gallium, indium, iron, lead, nickel, and tin.⁷ The present work concludes this investigation on thermal conductivity for the liquid metals bismuth, cobalt, germanium, and silicon. As previously, these are based on critically-assessed measurements of the thermal conductivity. Values of the thermal conductivity calculated via the Wiedermann-Franz law, from the measurement of the electrical conductivity, were not considered here. Although the Wiedermann-Franz law⁸ was first published in 1853, its basis is a simple theory of one mechanism of thermal conduction in a specific group of solid metals. Thus, its application to the liquid phase of a wider group of metals is of uncertain pedigree.^9–11

In 1970 Touloukian et al.¹² published a review of thermal-conductivity data, and reference values for the thermal conductivity of some liquid metals and bismuth. Following this, in 1996, Mills et al.¹³ also proposed reference equations for some liquid metals, and among them a new reference correlation for the thermal conductivity of liquid bismuth. For liquid cobalt, germanium, and silicon, only a single value at the melting point was given. Thus, reference correlations for the other three melts are long overdue especially because since 1996, as it will be discussed later on, new more accurate measurements have emerged. These data, together with a critical assessment of measurement methodology and the objective assignment of statistical weights to be attached to results, allow us to make improved proposals for reference correlations

2. Experimental Techniques

Molten metals are highly reactive at high temperature. Hence, it is difficult to find an appropriate container for the materials during the measurement of thermophysical properties. Moreover, convection induced by a non-uniform temperature field in molten metals at high temperatures is exceedingly difficult to avoid completely, so that the measurement of thermal conductivity is generally contaminated by convective flows of heat.

A large number of techniques, both steady-state and transient, have been employed to measure the thermal conductivity of molten bismuth, cobalt, germanium, and silicon. Transient methods employed were the transient hot wire, the laser flash, the electromagnetic levitation, the temperature wave, and the hot-disk technique, while steady-state methods employed include the guarded heat flow and the concentric-cylinder technique. These methods and their major characteristics were presented in our previous paper,⁷ and therefore here only the main issues confronted by each method will be mentioned. The main problems faced by the transient and steady-state techniques are

• the electrical insulation of the sensor’s wires from the conducting metal and the numerical description of this effect on the calculations (mainly in the transient hot-wire technique),

• avoiding the presence of buoyancy-driven convective flow within the sample (mainly in the guarded heat flow, laser flash and the electromagnetic-levitation techniques)

• suppressing Marangoni convective effects (mainly in the electromagnetic-levitation technique)

• suppressing buoyancy and thermocapillary forces contributing to convection (mainly in the temperature-wave technique)

• the lack of high quality standard reference values for molten metal which are required in techniques in need of calibration (mainly in the transient hot-disk technique).

Moreover, among the set of techniques, the laser flash and the temperature-wave technique directly measure the thermal diffusivity, α (m² s⁻¹), of the sample and not the thermal conductivity, λ (W m⁻¹ K⁻¹). The two are related through the equation

$$\alpha =\frac{\lambda }{\rho C_P},$$ (1)

where ρ (kg m⁻³) is the density of the melt, and C_P (J kg⁻¹ K⁻¹) its isobaric heat capacity. For the liquid metals considered here, density and the heat capacity are readily available in the literature (e.g., Ref. ¹⁴), so that the conversion we have performed is straightforward, although it introduces a small additional uncertainty in the thermal conductivity values.

3. Data Compilation

The analysis that is described here is applied to the best available experimental data for the thermal conductivity of the molten metals. Thus, a prerequisite to the analysis is a critical assessment of the experimental data. For this purpose, two categories of experimental data are defined: primary data, employed in the development of the correlation, and secondary data, used simply for comparison purposes. According to the recommendation adopted by the Subcommittee on Transport Properties (now known as The International Association for Transport Properties) of the International Union of Pure and Applied Chemistry, the primary data are identified by a well-established set of criteria.⁷ These criteria have been successfully employed to establish standard reference values for the viscosity and thermal conductivity of fluids over wide ranges of conditions, with uncertainties in the range of 1%. However, in many cases, such a narrow definition unacceptably limits the thermodynamic states for which data can be represented. Consequently, within the primary data set, it is also necessary to include results that extend over a wide range of conditions, albeit with a poorer accuracy, provided they are consistent with other more accurate data or with theory. In all cases, the accuracy claimed for the final recommended data must reflect the estimated uncertainty in the primary information.

Tables 1 to 4 present the datasets found for the measurement of the density of liquid bismuth, cobalt, germanium, and silicon, respectively. In these tables, the purity of the sample, the technique employed, and the uncertainty quoted, are also presented. Furthermore, the form in which the data are presented and the temperature range covered are also noted. As already discussed in Section 2, the datasets have been classified into primary and secondary sets. More specifically, following the brief presentation of the various techniques employed for the measurement of the thermal conductivity of the liquid metals, in the following subsections a discussion will be presented for each liquid metal.

TABLE 1.

Data sets considered for the thermal conductivity of liquid bismuth at 0.1 MPa

First author	Publ. year	Puritya (mass %)	Technique employedb	Uncertainty quoted (%)	No. of data	Temp. Range (K)	Form of datac
Previous reference correlation/values
Mills13	1996	-		-	-	545–1100	E
Touloukian12	1970	99.997		10	6	544–1000	P
Primary data
Kondo15	2017	99.99	Laser flash (TD)	-	3	571–673	D
Savchenko16	2013	99.99	Laser flash (TD)	4.5	10	545–1000	D
Magomedov17	1972	-	Guarded heat flow	6	14	561–958	D
Krestovnikov18	1968	HP	Guarded heat flow	8	9	698–1110	D
Dutchak19	1967	-	Guarded heat flow	-	7	573–870	D
Pashaev20	1961	-	Guarded heat flow	5	4	554–625	D
Nikolsky21	1959	-	Guarded heat flow	-	26	625–945	D
Secondary data
Nagai22	2006	99.999	Hot disk (Normal gravity)	-	6	585–1104	D
Nagai22	2006	99.999	Hot disk (Microgravity)	-	6	585–1105	D
Veinik23	1989	-	na	20	1	567	P
Filippov24	1973	-	Temperature wave (TD)	-	7	563–1045	D
Powell25	1958	-	Guarded heat flow	-	6	573–823	P
Konno26	1920	-	Guarded heat flow	-	5	571–857	P

^aHP = High Purity grade

^bTD = thermal diffusivity measurement; na = not available

^cD = diagram, E = equation, P = tabulated experimental data

TABLE 4.

Data sets considered for the thermal conductivity of liquid silicon 0.1 MPa

First author	Publ. year	Puritya (mass %)	Technique employedb	Uncertainty quoted (%)	No. of data	Temp. Range (K)	Form of datac
Previous reference correlation/values
Mills13	1996	-		-	1	1687	P
Primary data
Kobatake37	2010	-	Electromagnetic levitation	7	10	1702–1945	P
Magomedov38	2008	-	Guarded heat flow - Concentric cylinders	6	5	1708–1803	D
Nishi31	2003	-	Laser flash (TD)	7.7	6	1684–1705	D
Yamasue32	2002	HP	Transient hot wire	5	3	1700–1724	P
Takasuka33	1995	-	Laser flash (TD)	-	13	1694–1785	D
Yamamoto39	1991	-	Laser flash (TD)	2	7	1692–1724	D
Secondary data
Inatomi40	2007	99.9999	Electromagnetic levitation	20	22	1700–1958	D
Nagai41	2000	99.9999	Hot disk (Normal gravity)	3.2	5	1688–1723	D
Nagai41	2000	99.9999	Hot disk (Microgravity)	3.2	3	1688–1713	D

^aHP = High Purity grade

^bTD = thermal diffusivity measurement

^cD = diagram, P = tabulated experimental data

3.1. Data for bismuth

Twelve investigators reported thermal conductivity measurements for liquid bismuth (see Table 1). We note that three of them^{15, 16, 24} employed instruments that measure thermal diffusivity, but they also quote thermal conductivity. The twelve investigators are also depicted in Fig. 1, together with the 6 reference values proposed in 1970 by Touloukian et al.¹² and the reference equation proposed by Mills et al.¹³ in 1996. The measurements of Savchenko et al.¹⁶ performed at 2013 in a laser-flash instrument with a 4.5% uncertainty were considered as primary data, as they have already been included in the previous derivation of thermal conductivity reference correlations for indium, lead and tin.⁷ For the same reason, the guarded heat-flow measurements of Magomedov and Pashaev,¹⁷ Dutchak and Panasyuk,¹⁹ and Nikolsky et al. ²¹ were also included in the primary data set. The measurements of Krestovnikov et al.¹⁸ performed in a concentric-cylinders instrument with 8% uncertainty were also included in the primary data set. The guarded heat-flow measurements of Pashaev²⁰ with 5 % uncertainty were also included in the primary dataset, even though in the previous derivation of thermal conductivity reference correlations for gallium and tin⁷ they deviated considerably. Finally, the very recent laser-flash measurements of Kondo et al.¹⁵ were also part of the primary data set.

FIG. 1.

Measurements of the thermal conductivity of liquid bismuth as a function of the temperature. Kondo et al.¹⁵ (◆), Savchenko et al.¹⁶ (●), Magomedov and Pashaev¹⁷ (△), Krestovnikov et al.¹⁸ (⌖), Dutchak and Panasyuk¹⁹ (■), Pashaev²⁰ (⬙), Nikolsky et al.²¹ (+), Nagai et al.²²: Microgravity (◒) Normal gravity (◓), Veinik et al.²³ (x), Filippov²⁴ (- -), Powell and Tye²⁵ (▲), and Konno²⁶ (◇). Previous reference correlation of Mills et al.¹³ (—), and reference values of Touloukian et al.¹² ( ) are also shown. (····) melting point.

The hot-disk measurements of Nagai et al.²² were not included in the primary data set as they deviate considerably (see Fig. 1) from all other measurements (as also in the case of silicon). The measurements of Filippov²⁴ also seem always to differ from all other measurements (see Fig. 1); so was the case also in our previous publication.⁷ The older measurements of Powell and Tye,²⁵ and Konno,²⁶ seemed not to follow the trend of all other measurements. The single measurement of Veinik et al.²³ with a 20% uncertainty near the melting temperature, was not included because very little information on the technique employed was supplied.

3.2. Data for cobalt

Only 4 investigators reported thermal conductivity measurements for liquid cobalt, as shown in Table 2 and depicted in Fig. 2. We note that two of them^{28, 29} employed instruments that measure thermal diffusivity, but they also quote thermal conductivity. Based on lack of a large body of experimental data, in 1996 Mills et al.¹³ proposed a single reference value for the thermal conductivity of liquid cobalt at its melting point, based on the value of Ostrovskii et al.³⁰ Since 1996, however, two more sets have been reported. Fukuyama et al.²⁷ in 2017 and Nishi et al.²⁸ in 2003, one employing the electromagnetic levitation technique and the other using a laser-flash instrument to measure the thermal diffusivity of cobalt. Employing values for the heat capacity¹⁴ and the density,⁵ the thermal conductivity can easily be obtained. Previous measurements by the group of Fukuyama of the thermal conductivity of liquid copper,⁴² nickel,⁴³ and iron,⁴⁴ and by Nishi of the thermal conductivity of liquid nickel,²⁸ have already been employed in our recent reference correlation for the thermal conductivity of these metals.⁷ Thus these two sets formed the primary data sets. The older measurements of Zinovyev et al.²⁹ and Ostrovskii et al.³⁰ were considered as secondary data.

TABLE 2.

Data sets considered for the thermal conductivity of liquid cobalt at 0.1 MPa

First author	Publ. year	Purity (mass %)	Technique employeda	Uncertainty quoted (%)	No. of data	Temp. Range (K)	Form of datab
Previous reference correlation/values
Mills13	1996			-	1	1769	P
Primary data
Fukuyama27	2015	-	Electromagnetic levitation	-	17	1782–1903	D
Nishi28	2003	99.999	Laser flash (TD)	2.2	13	1768–1838	D
Secondary data
Zinovyev29	1986	99.95	Temperature wave (TD)	7	5	1768–1844	D
Ostrovskii30	1980	-	na	-	1	1769	P

^aTD = thermal diffusivity measurement; na = not available

^bD = diagram, P = tabulated experimental data

FIG. 2.

Measurements of the thermal conductivity of liquid cobalt as a function of the temperature. Fukuyama et al.²⁷ (○), Nishi et al.²⁸ (●), Zinovyev et al.²⁹ (- -), and Ostrovskii³⁰ (◇). Previous reference value of Mills et al.¹³ (−) is also shown. (····) melting point.

3.3. Data for germanium

As in the case of cobalt, Mills et al.¹³ proposed only a single reference value for the thermal conductivity of liquid germanium at its melting point, probably based on the measurements of Taylor et al.³⁴ Since then, 3 more sets of measurements have been published (see Table 3 and Fig. 3). The measurements of Nishi et al.³¹ and Takasuka et al.³³ have been performed in laser-flash instruments, while the measurements of Yamasue et al.³² have been performed in a transient hot-wire instrument. Measurements from the first two investigators have successfully been employed in developing reference correlations of liquid metals in our previous publication⁷ whereas in the same paper the measurements of Yamasue et al.⁹ were considered secondary data since they were much lower than all other measurements. Here, measurement from all three groups were part of the primary data set. The measurements of Taylor et al.³⁴ and Crouch et al.,³⁵ performed in laser-flash instruments, probably in the same laboratory, were also included in the primary data set, although their values were slightly lower than the results of other measurements.

TABLE 3.

Data sets considered for the thermal conductivity of liquid germanium at 0.1 MPa

First author	Publ. year	Puritya (mass %)	Technique employedb	Uncertainty quoted (%)	No. of data	Temp. Range (K)	Form of datac
Previous reference correlation/values
Mills13	1996	-		-	1	1212	P
Primary data
Nishi31	2003	-	Laser flash (TD)	2.2	19	1218–1399	D
Yamasue32	2002	99.99	Transient hot wire	5.9	5	1273–1473	P
Takasuka33	1995	-	Laser flash (TD)	-	69	1201–1329	D
Taylor34	1985	-	Laser flash (TD)	-	12	1218–1296	D
Crouch35	1982	-	Laser flash (TD)	-	3	1243–1283	P
Secondary data
Filippov24	1973	-	Temperature wave (TD)		2	1212–1601	D
Glazov36	1971	HP	Guarded heat flow - Concentric cylinders	10	7	1221–1409	D
Glazov36	1971	HP	Guarded heat-flow	10	7	1326–1468	D

^aHP = High Purity grade

^bTD = thermal diffusivity measurement

^cD = diagram, P = tabulated experimental data

FIG. 3.

Measurements of the thermal conductivity of liquid germanium as a function of the temperature. Nishi et al.³¹ (○), Yamasue et al.³² (●), Takasuka et al.³³ (+), Taylor et al.³⁴ (△), Crouch et al.³⁵ (▲), Filippov²⁴ (- -), and Glazov et al.³⁶: Concentric cylinders (□) Guarded heat flow (■). Previous reference value of Mills et al.¹³ (−) is also shown. (····) melting point.

As discussed previously, the measurements of Filippov²⁴ were not considered as primary data. Furthermore the measurements of Glazov et al.³⁶ performed in 1971 in a concentric-cylinder instrument, as well as in a guarded heat-flow apparatus with a 10% uncertainty, were considered as secondary data, as their values were 50% lower than everybody else (see Fig. 3). This was quite worrying because they employed two different instruments. Nevertheless, no explanation was found.

We should note here that from the eight investigators in Table 3, five employed instruments that measure the thermal diffusivity: Nishi et al.³¹ and Filippov²⁴ gave also thermal conductivity values, but to convert the values of Takasuka et al.,³³ Taylor et al.³⁴ and Crouch et al,³⁵ we employed literature values for the heat capacity³³ and the density.⁴⁵

3.4. Data for silicon

In the same way as for cobalt and germanium, Mills et al.¹³ in 1996 proposed only a single reference value for the thermal conductivity of liquid silicon at its melting point. Eight investigators, as shown in Table 4 and depicted in Fig. 4, have since reported measurements of the thermal conductivity of liquid silicon. From these Nagai et al.⁴¹ was not included in the primary data set for reasons outlined in the discussion of the bismuth data sets. The results of Inatomi et al.⁴⁰ have also been excluded because they claim a 20% uncertainty. All the rest of the measurements were considered to form the primary data set, because the results of the authors have been employed successfully in developing reference correlations in our previous work.⁷ We did not consider the 2007 measurements of Kobatake et al.,⁴⁶ since in 2010 they publish new measurements³⁷ with lower uncertainty.

FIG. 4.

Measurements of the thermal conductivity of liquid silicon as a function of the temperature. Kobatake et al.³⁷ (⌖), Magomedov and Gadjiev³⁸ (□), Nishi et al.³¹ (▲), Yamasue et al.³² (○), Takasuka et al.³³ (◆), Yamamoto et al.³⁹ (x), Inatomi et al.⁴⁰ (△), and Nagai et al.⁴¹: Microgravity (◒) Normal gravity (◓). Previous reference value of Mills et al.¹³ (−) is also shown. (····) melting point.

Finally, we note here that from the nine investigators in Table 4, three employed instruments that measure the thermal diffusivity: Nishi et al.³¹ quoted also thermal conductivity values, but to convert the values of Takasuka et al.,³³ and Yamamoto et al.,³⁹ we employed literature values⁴⁷ for the heat capacity and the density.

4. Thermal Conductivity Reference Correlation

The primary thermal conductivity data for liquid metals, shown in Tables 1–4, were employed in a linear regression analysis to represent the thermal conductivity at 0.1 MPa as a function of the temperature. Nothing other than a linear representation can be justified given the scatter of the data. Since the quoted uncertainties of all works were of similar magnitude, the data were weighted only according to the number of points. The following equation was obtained for the thermal conductivity, λ (W m⁻¹ K⁻¹), as a function of the absolute temperature, T (K),

$$\lambda =c_0+c_1(T-T_{\text{mp}}).$$ (2)

The coefficients c₀ (W m⁻¹ K⁻¹), c₁ (W m⁻¹ K⁻²), as well as the melting temperature T_mp (K), are shown for each liquid metal in Table 5. In the same table, the percentage deviation (2σ) of each equation at the 95% confidence level is also shown.

TABLE 5.

Temperature range, coefficients, and deviations at the 95% confidence level of Eq. (2).

	Trange (K)	c0 (W m−1 K−1)	c1 (W m−1 K−2)	Tmp (K)	Deviation (2σ) (%)
Bismuth	545 – 1110	13.199 39	0.011 47	544.55 (Ref. 4)	10
Cobalt	1769 – 1903	29.493 59	0.087 81	1768.15 (Ref. 5)	15
Germanium	1212 – 1473	45.552 52	0.024 09	1210.4 (Ref. 48)	16
Silicon	1690 – 1945	54.702 18	0.001 53	1687.0 (Ref. 5)	9.5

Figures 5–8 show the primary data and their percentage deviations from the above equation for each liquid metal. The dashed vertical line shows the melting point for each metal. In all cases, the deviations from Eq. (2) are broadly consistent with the quoted uncertainty of each investigator. These reference thermal conductivity correlations can be considered to represent the data well and the overall uncertainty is commensurate with the authors’ claim.

FIG. 5.

Percentage deviations of experimental thermal-conductivity values of bismuth, from those calculated by Eq. (2), as a function of the temperature. Kondo et al.¹⁵ (◆), Savchenko et al.¹⁶ (●), Magomedov and Pashaev¹⁷ (△ ), Krestovnikov et al.¹⁸ (⌖), Dutchak and Panasyuk¹⁹ (■), Pashaev²⁰ (⬙), and Nikolsky et al.²¹ (+). Previous reference correlation of Mills et al.¹³ (—), and reference values of Touloukian et al.¹² ( ) are also shown. (····) melting point.

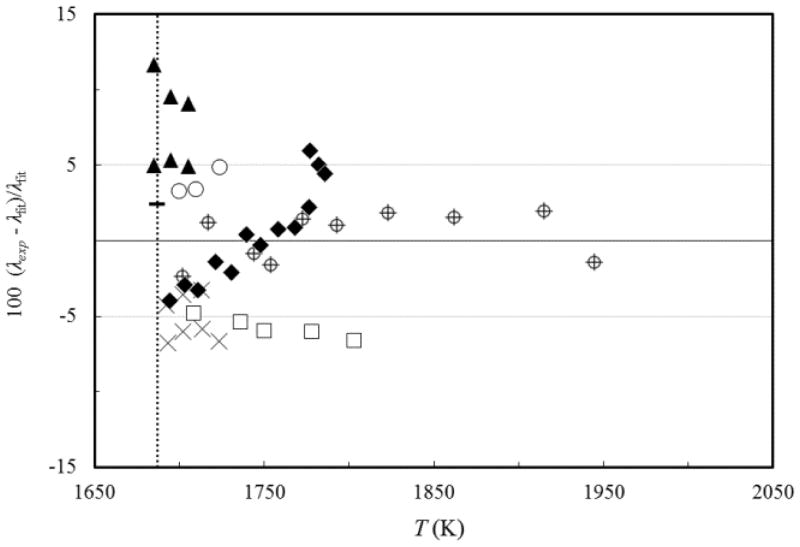
FIG. 8.

Percentage deviations of experimental thermal-conductivity values of silicon, from those calculated by Eq. (2), as a function of the temperature. Kobatake et al.³⁷ (⌖), Magomedov and Gadjiev³⁸ (□), Nishi et al.³¹ (▲), Yamasue et al.³² (○), Takasuka et al.³³ (◆), and Yamamoto et al.³⁹ (x). Previous reference value of Mills et al.¹³ (−) is also shown. (····) melting point.

Finally, in Table 6, thermal-conductivity values calculated with the use of Eq. (2) are shown for each metal.

TABLE 6.

Recommended values for the thermal conductivity of liquid bismuth, cobalt, germanium and silicon.

Temperature (K)	Bismuth	Cobalt	Germanium	Silicon
	λ (W m−1 K−1)
550	13.26
600	13.84
650	14.41
700	14.98
750	15.56
800	16.13
850	16.70
900	17.28
950	17.85
1000	18.42
1050	19.00
1100	19.57
1150	20.14
1200
1250			46.51
1300			47.71
1350			48.92
1400			50.12
1450			51.32
1500			52.53
1550
1600
1650
1700				54.72
1750				54.80
1800		32.29		54.88
1850		36.68		54.95
1900		41.07		55.03
1950		45.46		55.10
2000				55.18
2050				55.26

5. Conclusions

The available experimental data for the thermal conductivity of liquid bismuth, cobalt, germanium and silicon have been critically examined with the intention of establishing a thermal-conductivity reference correlation. All experimental data have been categorized into primary and secondary data according to the quality of measurement, the technique employed and the presentation of the data, as specified by a series of criteria. The proposed standard reference correlations for liquid bismuth, cobalt, germanium and silicon, respectively, are characterized by deviations of 10%, 15%, 16%, and 9.5% at the 95% confidence level.

FIG. 6.

Percentage deviations of experimental thermal-conductivity values of cobalt, from those calculated by Eq. (2), as a function of the temperature. Fukuyama et al.²⁷ (○), and Nishi et al.²⁸ (●). Previous reference value of Mills et al.¹³ (−) is also shown. (····) melting point.

FIG. 7.

Percentage deviations of experimental thermal-conductivity values of germanium, from those calculated by Eq. (2), as a function of the temperature. Nishi et al.³¹ (○), Yamasue et al.³² (●), Takasuka et al.³³ (+), Taylor et al.³⁴ (△), and Crouch et al.³⁵ (▲). Previous reference value of Mills et al.¹³ (−) is also shown. (····) melting point.