An improved electronic determination of the Boltzmann constant by Johnson noise thermometry

Abstract

Recent measurements using acoustic gas thermometry have determined the value of the Boltzmann constant, k, with a relative uncertainty less than 1 × 10⁻⁶. These results have been supported by a measurement with a relative uncertainty of 1.9 × 10⁻⁶ made with dielectric-constant gas thermometry. Together, the measurements meet the requirements of the International Committee for Weights and Measures and enable them to proceed with the redefinition of the kelvin in 2018. In further support, we provide a new determination of k using a purely electronic approach, Johnson noise thermometry, in which the thermal noise power generated by a sensing resistor immersed in a triple-point-of-water cell is compared to the noise power of a quantum-accurate pseudo-random noise waveform of nominally equal noise power. The experimental setup differs from that of the 2015 determination in several respects: a 100 Ω resistor is used as the thermal noise source, identical thin coaxial cables made of solid beryllium–copper conductors and foam dielectrics are used to connect the thermal and quantum-accurate noise sources to the correlator so as to minimize the temperature and frequency sensitivity of the impedances in the connecting leads, and no trimming capacitors or inductors are inserted into the connecting leads. The combination of reduced uncertainty due to spectral mismatches in the connecting leads and reduced statistical uncertainty due to a longer integration period of 100 d results in an improved determination of k = 1.380 649 7(37) × 10⁻²³ J K⁻¹ with a relative standard uncertainty of 2.7 × 10⁻⁶ and a relative offset of 0.89 × 10⁻⁶ from the CODATA 2014 recommended value. The most significant terms in the uncertainty budget, the statistical uncertainty and the spectral-mismatch uncertainty, are uncorrelated with the corresponding uncertainties in the 2015 measurements.

1. Introduction

According to the resolution of the 25th Conférence General des Poids et Mesures, the unit of thermodynamic temperature, the kelvin, will be redefined in 2018 with the introduction of the ‘New SI’, by fixing the value of the Boltzmann constant, k [1]. To ensure that there are no significant unknown systematic effects on the value of k determined by any single technique, the Consultative Committee for Thermometry (CCT) of the International Committee for Weights and Measures requires that the kelvin redefinition should proceed when the next CODATA adjustment assigns a value of k with a relative uncertainty below 1 × 10⁻⁶, supported by at least one determination from a second technique reporting a relative uncertainty below 3 × 10⁻⁶ [2]. Two determinations by acoustic gas thermometry have already achieved relative uncertainties less than 1 × 10⁻⁶, so the current CODATA-recommended value of k has met the first requirement [3–5]. To meet the second requirement, at least three different research groups have been pursuing determinations of k with a relative uncertainty less than 3 × 10⁻⁶ using dielectric-constant gas thermometry (DCGT) [6, 7], Doppler broadening thermometry [8, 9], and Johnson noise thermometry (JNT) [10–12]. The second target has now been met by PTB, who recently reported a determination by DCGT with a relative uncertainty of 1.9 × 10⁻⁶ [13]. Thus, the redefinition of the kelvin can proceed. This paper reports a second Boltzmann constant determination meeting the second target, carried out at NIM by the joint NIST/NIM/MSL JNT team. This second result, which is purely electronic and distinctly different from the gas thermometry determinations, provides additional assurance that any unknown systematic errors in any of the determinations must be small.

JNT infers the thermodynamic temperature from measurements of voltage or current noise caused by the thermal motion of electrons in conductors [14–16]. As a purely electronic approach, it is an appealing alternative to the various forms of primary gas thermometry and has attracted a lot of interest. In 2015, we published a determination of the Boltzmann constant with a relative uncertainty of 3.9 × 10⁻⁶ by JNT, in which the thermal voltage noise generated by a 200 Ω resistor immersed in a triple-point-of-water (TPW) cell was compared to a synthesized pseudo-noise voltage generated by a quantum-accurate voltage noise source (QVNS) [12]. In the measurement, the frequency-response mismatch between the two sets of connecting leads between the two noise sources and the measurement circuit (correlator) was a key factor in the two largest contributions to the measurement uncertainty. Firstly, the frequency-response mismatch causes a bias in the measurement that rapidly increases with frequency, and therefore limits the bandwidth and the statistical uncertainty, which is the largest uncertainty term. Secondly, it is necessary to correct the spectral-mismatch bias using an even-order polynomial function of frequency, and there is some uncertainty due to imperfect knowledge of the selected model. For any given model that is insufficiently complex to perfectly model the spectral data, we expect the statistical uncertainty to decrease with increasing bandwidth, and the biasing effect of the spectral mismatches to increase with increasing bandwidth, and therefore some compromise between the two uncertainty terms is necessary. Coakley et al developed a cross-validation method to select the best model for any particular bandwidth, and to quantify the uncertainty in a way that accounted for both random measurement error and model ambiguity. They also selected the fitting bandwidth according to an uncertainty minimization criterion. Since the selected fitting bandwidth was a function of random data, an additional component of uncertainty was also quantified to account for imperfect performance of the bandwidth selection method [17].

In this paper, we report a new determination of k by JNT following major changes to the connecting leads between the noise sources and the correlator. Section 2 briefly describes the experimental principles and notes that the experiment measures the ratio of two important fundamental physical constants, k/h, where h is the Planck constant. Section 3 discusses the improvements to the measurement system and the rationale behind them. Improvements have been made to the switching and preamplifier circuits, and more importantly to the connecting leads between the noise sources and the switching circuits. This is followed by a description of the experimental results and an uncertainty analysis in section 4. Finally, the results are summarized and a brief discussion concludes the paper.

2. Experiment principles

For temperatures near 300 K and frequencies below 1 GHz, the mean square voltage of Johnson noise is described by Nyquist’s law with a relative error of less than 1 × 10⁻⁹,

$$\overline{V_{\mathrm{T}}^2}=4\mathit{kTR}\mathrm{\Delta }f,$$ (1)

where T is the temperature, R is the resistance of the sensor, and Δf is the bandwidth over which the noise is measured [14]. In principle, k can be determined by directly measuring the fluctuating voltage noise power across a sensing resistor at a known temperature. However, since the noise signal is extremely small, random, and distributed over very large bandwidths, it is a challenge to define the system bandwidth, amplify the noise signal, and accumulate the very large amount of data over very long periods while ensuring that the sensing resistance, the bath temperature, the measurement electronics, and the low electromagnetic interference (EMI) environment remain stable.

To realize k determination, we adopt the QVNS-calibrated JNT pioneered by NIST [10], in which several breakthrough technologies were adopted to overcome the above challenges. With a switched-input correlator, we can accurately define the source impedance by a four-wire connection, eliminate uncorrelated noise in the lead wires and preamplifiers by cross-correlation, and eliminate the effect of amplifier gain drifts by frequently switching between the thermal noise source and QVNS [18]. With the fast and accurate analogue-to-digital converters (ADCs), we can process digital data in the frequency domain, where bandwidths can be defined accurately [19]. Most importantly, with the QVNS, we can synthesize quantum-accurate pseudo-noise waveforms as reference noise voltage signals to calibrate the gain and frequency response of the amplifier [20, 21].

To determine k, the sensing resistor of the thermal noise source is immersed in the well of a TPW cell so that it produces thermal noise with the power spectral density given by Nyquist’s law (1):

$$S_{\mathrm{R}}=4k{T}_{\text{TPW}}{X}_{\mathrm{R}}{R}_{\mathrm{K}},$$ (2)

where T_TPW is the temperature of the TPW and the sensing resistance is expressed as the ratio X_R in units of the von Klitzing resistance R_K ≡ h/e² [22] (where e is the charge of the electron, and h is Planck’s constant). The QVNS produces a pseudo-random noise voltage comprising a random-phase frequency comb with calculable average power spectral density:

$$S_{\mathrm{Q}-\text{calc}}=D^2{N}_{\mathrm{J}}^2{f}_{s}M/K_{\mathrm{J}}^2,$$ (3)

where K_J ≡ 2e/h, is the Josephson constant, f_s is a clock frequency, M is the bit length of the digital code for the synthesized noise waveform, D is a pre-selected amplitude-related parameter in the algorithm that generates the digital code, and N_J is the total number of Josephson junctions in the two identical subarrays within the QVNS circuit [10]. The value of S_Q-calc is set to closely match the value of S_R, so that the effects of nonlinearity and gain variations in the electronics are the same for both noise signals [23, 24]. The contribution of these non-ideal response features to the measurement uncertainty is greatly reduced by calculating the ratio S_R/S_Q for the alternate cross-correlator measurements of the noise power spectra [12].

If the 1990 conventional electrical units V₉₀ and Ω₉₀, where K_J-90 = 483 597.9 GHz/V₉₀ and R_K-90 = 25 812.807/Ω₉₀ [25], are used to determine voltage and resistance from the Josephson and quantum Hall effects, the value of the Boltzmann constant, expressed in terms of the 1990 conventional electrical units, is

$$k_{90}=\frac{\langle S_{\mathrm{R}}\rangle }{\langle S_{\mathrm{Q}}\rangle }\times \frac{S_{\mathrm{Q}-\text{calc}}}{4T_{\text{TPW}}R},$$ (4)

where 〈S_R〉/〈S_Q〉 is the ratio of the average-measured spectral densities. With JNT, 〈S_R〉/〈S_Q〉 is the ratio of the noise powers measured over identical bandwidths. According to the analysis in CODATA-98 [26],

$$\frac{k}{h}=\frac{k_{90}}{h_{90}},$$ (5)

and the Boltzmann constant k can be determined by

$$k=\frac{\langle S_{\mathrm{R}}\rangle }{\langle S_{\mathrm{Q}}\rangle }\times \frac{S_{\mathrm{Q}-\text{calc}}}{4T_{\text{TPW}}R}\times \frac{h}{h_{90}},$$ (6)

where the CODATA-recommended value is used for h = 6.62 6 070 040(81) × 10⁻³⁴ J s [27], and the exact value is used for h₉₀ = 4/[(K_J-90)²R_K-90] = 6.626 068 854… × 10⁻³⁴ J s.

3. Changes to the thermometer

Subsequent to our 2015 JNT determination, additional numerical experiments were carried out to investigate frequency-dependent models of the power spectral-ratio spectrum. The additional analysis suggested the frequency response of one or both sets of connecting leads between each of the two noise sources and the correlator was changing during the measurements. This conclusion was supported by measurements showing that both the capacitance and inductance of the leads changed with temperature and frequency, thus making problematic the close matching of the frequency response of the two sets of leads. These observations then led to a detailed study of the design, engineering, and modelling of the connecting leads, and to several major changes to the configuration of the connecting leads. In addition, changes were made to reduce spectral aberrations associated with dielectric losses in the input circuits. This section outlines changes made to the experimental setup to enable a better match of the frequency responses to the two noise sources. Full details of the changes made and the rationale behind them are given in [28].

3.1. The matching conditions

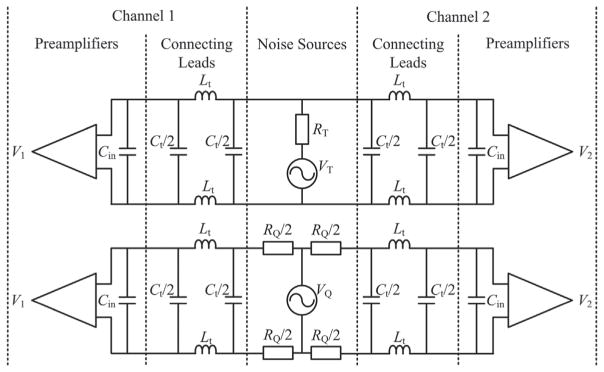
SPICE simulations of the JNT measurement show that the connecting leads from the noise sources to the correlator circuits are sufficiently short that time delays can be neglected and lumped-parameter models are sufficient to model the frequency response of the connecting leads. Indeed, differences between π-section, T-section, and transmission-line models of the connecting leads are practically non-existent at frequencies below 1 MHz. Figure 1 shows a simplified schematic diagram of the noise sources, connecting leads, and preamplifier inputs of the noise thermometer, where a single π-section is used to model the lead wires. One of the complicating factors in the matching of the frequency response to the two noise sources is that the thermal noise source has an impedance given by the sensing resistance, while the QVNS has practically zero output resistance. For this reason, four resistors with resistance of R_Q/2 in figure 1 are included on the QVNS chip as an aid to matching the frequency responses. Note that the QVNS resistors are held at 4.2 K to minimize the uncorrelated noise they produce. Analysis of several models, including that of figure 1, shows that the responses are matched under two conditions: (i) R_Q = 2R_T, where R_T is the sensing resistance of the thermal source, and (ii) the two sets of lead wires between the noise sources and the preamplifiers are identical.

Figure 1.

A simplified model of the input sections of the noise thermometer.

There are also concerns about the insertion of trimming inductors and capacitors to match the frequency responses of the connecting leads, as we did in the previous measurements. We choose to remove the trimming components in the current measurements for two reasons. Firstly, a weak f₂ dependence in the measured power spectral-ratio spectrum is expected due to the correlation of amplifier noise currents to thermal noise arising from cable resistance in the thermal measurement, but not in the QVNS measurements [10, 12], and therefore the measured power spectral-ratio spectrum should not be flat. Secondly, trials with SPICE models reveal that incorrectly placed trimming components match the low-frequency behaviour at the expense of a more complex mismatch at higher frequencies.

3.2. Impedance definitions for the connecting leads

Measurements of the connecting leads used in the 2015 measurement showed that the inductance and capacitance of the lead wires changed with both frequency and temperature. These effects were a particular problem with the leads to the QVNS since they must be partially immersed in liquid helium. The changes were attributed to dimensional changes in the assembly due to thermal expansion of both the conductors and dielectrics, as well as to changes in the dielectric constant of the insulation materials.

Similar impedance definition problems occur in ac electrical metrology, where, to define the impedance of a standard artefact (resistor, capacitor, and inductor) properly, it is necessary to define the distribution of the electric and magnetic fields about the artefact [29], and this is done by converting a network of wires and components into a coaxial network. Each conductor in the elemental circuit becomes the central conductor in a coaxial component, while the outer conductor is a part of a single low-potential conducting surface that surrounds every component and connecting lead. This ensures that there is practically zero electric field outside the surface.

Where there are nodes in a network, such an arrangement naturally leads to ground loops in the low-potential surface. To eliminate this problem, each section of a coaxial cable is fitted with a coaxial (common-mode) choke that forces the current in the outer conductor to be equal and opposite to the current in the inner conductor. In this way, there can be no magnetic field outside the shield.

Since there are no electric or magnetic fields outside any part of a coaxial network, the behaviour of the resulting network is independent of the placement of any of the components or cables. An additional benefit arises from the reciprocity principle: since the network does not generate any electric or magnetic fields outside the shield, it is also immune to electric and magnetic fields generated outside the shield, i.e. it is insensitive to electromagnetic interference.

The coaxial scheme is applied to the JNT probes as shown schematically in figure 2. In the figure, the solid black rectangles adjacent to each coaxial cable represent the high-permeability toroidal cores used for the coaxial chokes. The noise sources are connected to the switch circuit by multiple coaxial cables connected in series using connectors which are fixed at the interfaces of probe heads and the switch box. To keep the system as close to coaxial as practicable, the inner and outer conductors of a coaxial cable are connected to individual pins of a LEMO connector. The sections of cables from the probe heads to the switch box are further surrounded by a metallic shield. The coaxial chokes are mounted inside the switch unit at the inputs to the switch. Since the chokes act only on common-mode signals (the total current of the inner and outer leads of the coaxial cable), they have no effect on the measurement of differential-mode noise signals (the voltage between the pair of inner conductors that are connected to the preamplifier). Note that one of the chokes is unnecessary, but in the interest of preserving symmetry, all leads have been made with identical lengths of coaxial cable with one end terminated by a choke. The chokes are small high-permeability nano-crystalline toroidal cores through which 20 turns of the coaxial cable are wound. The chokes must have sufficient inductance to ensure that the common-mode impedance is much greater than the resistance of the outer conductors, and hence force the inner and outer currents to be equalized. The permeability of the nano-crystalline cores does fall with frequency, but they are only necessary at low frequencies. At high frequencies, the mutual inductance of the two conductors in the coaxial cable is sufficient to equalize the currents.

Figure 2.

Schematic showing the coaxial leads connecting each noise source, where JJ stands for Josephson junction subarray. Note that all coaxial cables are ‘shorted’ at both ends and then connected to the ground of the switch circuit. The solid black rectangles adjacent to each coaxial cable represent the high-permeability toroidal cores used for the coaxial chokes.

With the coaxial input networks, a potential problem arises in the definition of the sensing resistance. Because a coaxial choke acts as a 1:1 transformer, and voltages generated by currents flowing in the shield are reflected into the central conductors, the resistance of a coaxial component is the sum of the resistance of the central conductor and the resistance of the shield around it. Thus, there is a difference between the four-terminal resistance of the noise source measured by the resistance bridge and the four-pair coaxial resistance that generates the noise. For both the thermal noise source and QVNS, the ‘electrical short’ formed by the connection between the four shields contributes additional correlated noise to the total cross-correlated noise power. Fortunately, the error is very small and can be neglected. For both the QVNS and the thermal noise source, the four-terminal resistance of the connection between the shields is found to be about 1.5 μΩ, and thus the relative error in the resistance definitions is only 1.5 × 10⁻⁸.

Further analysis of the 2015 measurements suggests that the frequency responses of the connecting leads were changing during the measurements [17], a conclusion supported by direct measurements of the cables. Figure 3(a) shows the strong temperature and frequency dependencies of the inductance of the coaxial cables used for the connecting leads in the 2015 experiment. The effects were eventually traced to the skin effect [30]. At low frequencies, the current in a conductor is distributed uniformly across the conductor, while at high frequencies, the current travels very near the surface of the conductor. The change in the distribution of the current in the inner and outer conductors results in a change of about 25% in the cable inductance between the lowest and highest frequencies. The effect is sensitive to temperature because the skin effect depends on the conductivity of the conductors. To minimize these effects, the connecting leads are replaced with very thin (0.86 mm outside diameter) coaxial cables with solid inner and outer beryllium–copper conductors and PTFE foam dielectrics. This ensures a match of about 1% for the cable inductances, as shown in figure 3(b). The match could be further improved by cooling sections of the leads to the thermal noise source so that they have the same average temperature as the leads to the QVNS.

Figure 3.

Temperature and frequency dependencies of the stray inductances of the connecting leads for the (a) 2015 and (b) 2017 measurements.

3.3. Maximizing bandwidth

Consideration is also given to maximizing the bandwidth of the connecting leads, and this requires that the source impedances be matched to the characteristic impedance of the coaxial cables. In a differential measurement configuration using 50 Ω cables, this requires R_Q = 2R_T = 100 Ω. Unfortunately, such a low source resistance would seriously compromise the signal-to-noise ratio, and significantly increase the statistical uncertainty. However, reducing the sensing resistance to 100 Ω is deemed tolerable in that it would yield some flattening of the frequency response and a modest increase in the bandwidth. In the current measurement, two Ni–Cr alloy foil resistors with a total nominal resistance of 100 Ω are used as the thermal noise source. To meet the matching condition, four resistors with nominal resistance of 100 Ω are placed on a chip in each of the four QVNS output leads.

3.4. Reduced dielectric loss

Finally, an additional improvement is desired that will reduce spectral aberrations due to dielectric losses that originate in the dielectric shunt capacitances within the input circuit. Ideally, if the switch and preamplifier printed circuit boards (PCBs) are symmetric with respect to the noise sources, then the stray capacitance with the PCB dielectric will be the same and their contributions to the frequency response will be identical for both noise sources. However, the dielectric loss in the capacitance will generate Johnson noise and a noise-current term directly proportional to the frequency and the dielectric loss tangent, tanδ [10, 31]. Since noise currents generate a correlated signal in the thermal noise source, but not in the QVNS, there may be a small unwanted error, linear in frequency, in the measured power spectral ratio. In the current experiment, we replace the switch and input of the preamplifier PCBs, previously made of FR4 fibreglass, with PCBs made of Teflon, so that tanδ should be reduced, by perhaps an order of magnitude.

4. Measurement result and uncertainty analysis

4.1. Experiment

To determine the Boltzmann constant, it is necessary to closely match the noise power and the statistical distributions of the noise for the two noise sources. For the measurements reported here, the QVNS is programmed to synthesize a pseudo-random noise waveform with an average power spectral density S_Q-calc = 1.50847524 × 10⁻¹⁸ V²/Hz. The waveform comprises a series of odd harmonic tones with identical amplitudes and random relative phases at multiples of the 90 Hz pattern repetition frequency up to 9 MHz. The time-domain synthesized voltage waveform closely resembles that of the white Gaussian-distributed thermal noise of the 100 Ω sensing resistor of the thermal noise source.

For each noise source, the ADCs sample the noise signal with a sampling frequency of 4 MHz for a period of 1 s. The software calculates the fast Fourier transform (FFT) of the data and then the cross-correlated noise power spectra with 2 MHz bandwidth and 1 Hz resolution. After 100 such spectra are accumulated, the data are saved. Then the relays switch the system to measure the signal from the other noise source. The 200 s period required to measure signals from the two sources constitutes one ‘chop’. The JNT system alternatively measures the two noise signals in this way over an integration period of about 20 h, limited by the capacity of the batteries for the ADCs and the maintenance period of the TPW cell in the ice bath. The resistance of the sensing resistor is measured before and after each day’s measurement using a dc resistance bridge. To reduce statistical uncertainty, this process is repeated over 120 d to yield a total integration period of about 100 d.

4.2. Measurement results

In total, 43 752 chops of data are accumulated. The real part of the cross-correlation of the thermal spectrum is reduced in resolution by summing 180 neighbouring FFT bins to yield a spectrum with the same 180 Hz resolution as the QVNS spectrum. The thermal and QVNS cross-spectra are then averaged and the power spectral-ratio spectrum S_R/S_Q is calculated. Figure 4 shows that the resulting noise power ratio decreases monotonically with increasing frequency. This result is very different from the 2015 measurement result, where trimming components in the connecting leads were used to ensure the noise power ratio spectrum was flat within 0.01% up to about 800 kHz [12].

Figure 4.

The ratio of the thermal and QVNS cross-correlation spectra resulting from 120 measurements with 43 752 chops of data accumulated

As discussed in [12], there are two small factors that cause the deviation of the power spectral-ratio spectrum from a perfectly flat frequency response. Firstly, because the impedances of the two noise sources and the connecting leads could not be perfectly matched, there will be small differences in the frequency responses to the two noise sources. These effects can be modelled by an even-order polynomial function of frequency based on a low-frequency lumped-parameter model of the connecting leads, similar to figure 1. Secondly, the two noise sources respond differently to capacitively induced noise currents originating in the preamplifier and the cable resistances. For the thermal source, the noise currents flowing through the sensing resistor lead to extra undesirable correlated noise power. For the QVNS, these errors are absent because the superconducting Josephson junction circuit has practically zero impedance. The resulting errors are expected to have a f₂ dependence [32, 33], and thus are also accounted for by the least-squares fitting of the ratio spectrum, so long as the power spectral-ratio model includes a term in f₂ [10].

4.3. Data analysis

Neglecting the effects of dielectric loss, the power spectralratio spectrum is modelled by

$$\frac{S_{\mathrm{R}}}{S_{\mathrm{Q}}}=a_0+a_2{f}^2+a_4{f}^4+a_6{f}^6+\dots ,$$ (7)

where a₀ is the desired low-frequency limiting value of the power spectral density ratio required for the determination of k in equation (6), and the coefficients a₂, a₄, a₆, … represent the effects of the various error terms. The even-order polynomial model for the power spectral-ratio is a consequence of the use of lumped-parameter models for the input networks. Whatever their complexity, the models predict a low-pass frequency response with the squared magnitude described by the inverse of the even-order polynomials. For the model of figure 1, the frequency responses are sixth-order low-pass responses. In the low frequency limit, the expression for the power spectral-ratio is the ratio of the responses from the QVNS and thermal noise networks, which can be expanded using the binomial theorem into a power series in frequency with only even-order terms, as shown in equation (7).

Figure 5 summarizes the results of determinations of a₀ by the method of least-squares fitting as a function of the bandwidth selected and the complexity of the power spectral-ratio model with frequency-dependent terms included up to the second, fourth, sixth, eighth, and tenth order in equation (7). The values of a₀ are plotted with respect to a_0,calc, the value determined from the current CODATA-recommended value of k, the weighted average of the measured sensing resistance R, and the TPW temperature T_TPW. The plot shows that at low frequencies, the results from the different models are consistent with one another up to about 400 kHz. Above about 400 kHz, the second-order fit diverges, and above about 700 kHz the results for the other models also begin to diverge.

Figure 5.

Plot of the estimate of a₀ versus bandwidth and the order of the least-squares fit.

A five-fold cross-validation procedure is performed to analyse the data with polynomial models with orders ranging from 2 to 14 [17]. In this procedure, we randomly split observed spectral data from 120 runs of the experiment into five equally sized subsets. Data from each run appear in just one of the five subsets. From these subsets, we form training and validation data sets, and select the order of the model determined from the training data which is most consistent with the validation data according to a mean-square deviation criterion. Based on 20 000 splits, we determine the model selection fractions. Given that a dth-order model is valid and d is known, asymptotic theory (see [34] for more details) predicts a sampling distribution for the estimate of a₀. The standard deviation of this sampling distribution is the statistical uncertainty of the estimate. To account for the effect of imperfect knowledge of the model on results, we form a mixture of the sampling distributions from the candidate models weighted by their associated model selection fractions determined by cross-validation. We estimate the uncertainty of the estimated a₀ as the standard deviation σ̂_tot of the mixture model distribution, where

$${\widehat{\sigma }}_{\text{tot}}^2={\stackrel{\sim }{\sigma }}_{\alpha }^2+{\stackrel{\sim }{\sigma }}_{\beta }^2,$$ (8)

with

$${\stackrel{\sim }{\sigma }}_{\alpha }^2=\sum _d\widehat{p}(d){\widehat{\sigma }}_{{\widehat{a}}_0(d),\text{ran}}^2,$$ (9)

and

$${\stackrel{\sim }{\sigma }}_{\beta }^2=\sum _d\widehat{p}(d){\left({\widehat{a}}_0(d)-{\widehat{\overline{a}}}_0\right)}^2.$$ (10)

Above, â₀(d) is the estimate of a₀ associated with a d-thorder model, ${\widehat{\sigma }}_{{\widehat{a}}_0(d),\text{ran}}^2$ is the predicted variance of the estimate according to asymptotic theory, p̂(d) is the estimated model selection fraction for the dth-order model, and ā̂ = Σ_d p̂(d)â₀(d). We stress that both σ̃_α and σ̃_β are affected by imperfect knowledge of the ratio spectrum model. Hence, σ̃_α can be regarded as an uncertainty component that accounts for the joint effect of random measurement errors and a particular model’s ambiguity. In contrast, σ̃_β can be regarded as an uncertainty component that accounts for another model’s ambiguity effect.

The results of the cross-validation analysis for bandwidths of 10 kHz to different upper cut-off frequencies f_max are plotted in figure 6. We select the optimum f_max by minimizing σ̂_tot on a grid in frequency space with a resolution of 6.25 kHz. Our grid search yields a minimum value of σ̂_tot,* = 2.58 × 10⁻⁶ with values for σ̃_α = 2.53 × 10⁻⁶ and σ̃_β = 0.50 × 10⁻⁶ for a d = 2 model when f_max = 368.75 kHz. For this selected model and fitting bandwidth, the estimated value of a₀ − a_0,calc is 0.89 × 10⁻⁶ and the associated statistical uncertainty ${\widehat{\sigma }}_{{\widehat{a}}_0(d),\text{ran}}^2$ is 2.37 × 10⁻⁶. We estimate a component of uncertainty due to spectral model ambiguity as

Figure 6.

(a) Estimated order of the polynomial model d, (b) estimated relative standard uncertainty of a₀, and (c) estimated offset a₀ − a_0,calc and approximate 68% coverage interval.

$${\widehat{\sigma }}_{\text{model}1}=\sqrt{{\widehat{\sigma }}_{\text{tot},\ast }^2-{\widehat{\sigma }}_{{\widehat{a}}_0(d),\text{ran}}^2,}$$ (11)

which yields a value of 1.02 × 10⁻⁶. Note that in general, for any fitting bandwidth, we can define a component of uncertainty due to all model ambiguity effects as equation (11), provided that ${\widehat{\sigma }}_{\text{tot}}\ge {\widehat{\sigma }}_{{\widehat{a}}_0(d),\text{ran}}^2$. For the 128 fitting bandwidths considered in our analysis, this inequality is satisfied for 124 cases.

There are two minor competing concerns about the selection of f_max. On the one hand, because we choose f_max by doing the cross-validations at a high resolution of 6.5 kHz, we do not expect to find the global minimum of σ̂_tot,*. On the other hand, since the uncertainty estimates at the candidate fitting bandwidths are functions of random data, they are realizations of random variables. We expect that noise fluctuations could artificially deflate the reported value of σ̂_tot,*. To get some insight into these two effects, we split our 6.25 kHz grid into two 12.5 kHz grids. The difference in the selected uncertainties for the two 12.5 kHz grids is 0.06 × 10⁻⁶. We also fit a local regression model (LOCFIT) [35, 36] to the uncertainty data on the 6.5 kHz grid, and predicted values on a 0.01 kHz grid. The minimum values on the 0.01 kHz grid are 2.57 × 10⁻⁶ and 2.67 × 10⁻⁶ for two plausible, but different, implementations of LOCFIT. These results suggest that noise fluctuations and grid discreteness affect results at about the 0.1 × 10⁻⁶ level.

Since the uncertainty estimates are realizations of random variables, the selected f_max is a realization of a random variable. Hence, following [17], we determine an additional component of uncertainty, σ̂_fmax, that accounts for uncertainty associated with the imperfect performance of our selection method due to random effects as well as possible systematic effects, including frequency-dependent physical effects. We set this component to the estimated standard deviation of the estimates of a₀ that correspond to fitting bandwidths that yield the m lowest values of σ̂_tot. For about 10 percent of all fitting bandwidths on the grid, the value of m = 13 and the uncertainty σ̂_fmax is 0.57 × 10⁻⁶.

One notable feature of the analysis is that despite the improvements to the connecting leads, there appears to be no significant increase in the selected bandwidth. For example, for the d = 4 model, the minimum uncertainty was realized with a 575 kHz bandwidth in the 2015 measurement, while in the current measurement, the maximum bandwidth where d = 4 is selected is 525 kHz. This result is a consequence of the reduction in random uncertainty: to achieve a corresponding reduction in the systematic uncertainty, the bandwidth must also decrease. Also, because the uncertainty falls with $f_{max}^{-1/2}$ and systematic effects increase approximately concomitantly with $f_{max}^{d+2}$, very substantial improvements in the spectral mismatch are required to achieve even modest reductions in the prediction uncertainty. For the same reason, the systematic uncertainty should also be a small fraction of the random uncertainty, as it is in the current measurements.

There are several qualitative improvements in the data, compared to the 2015 data. Firstly, the consistency of the a₀ estimates at low frequencies, within ±3 × 10⁻⁶ below 400 kHz, enables the d = 2 model to work at a higher bandwidth than before. This is positive support for the changes made. Secondly, all the models with d ≤ 4 now give estimates of a₀ (see figure 5) that are consistent within ±10 × 10⁻⁶ up to about 1 MHz, without the significant divergent behaviour observed in the 2015 data. This is also positive support for the changes made. Thirdly, the steps in the plot of the selected model order versus the bandwidth in figure 6(a) are also more clearly monotonic than was observed in the 2015 data. As the bandwidth increases and the spectral mismatch effects increase, the model that best fits the data should steadily become more complex. Fourthly, almost all the estimates of a₀ up to 900 kHz in figure 6(c) lie within ±1σ of the expected value, which is also more consistent than observed in the 2015 data. Finally, the stability analysis finds no evidence for a time dependence of the measurement result, as was observed for the 2015 data [17].

4.4. Uncertainty budget

All the factors that contributed to the total uncertainty were analysed in detail in the 2015 determination [12]. In the present measurement, the power spectral density S_Q of the synthesized quantum voltage waveform, the temperature of the TPW, and some of the contributions to the uncertainty in the ratio of the power spectral densities S_R/S_Q and the resistance of the thermal sensor are unchanged. Below, we will only focus on differences from the previous analysis. Besides the prediction uncertainty of the cross-validation, decomposed as the statistical uncertainty and spectral model ambiguity, two other terms are reconsidered.

One of the uncertainty terms in the 2015 determination was possible spectral aberrations and thermal noise due to dielectric losses. Dielectric losses in the capacitances generated a correlated noise-current term directly proportional to frequency and tanδ in the thermal noise source, but not in the QVNS source, and thus introduced a small term, linear in frequency, in the measured power spectral-ratio (equation (7)) [10]. Circuit modelling suggested that neglecting this term could result in a standard uncertainty of no more than 1 × 10⁻⁶ in the 2015 measurements. By replacing the switch and preamplifier PCBs, previously made of FR4 fibreglass, with PCBs made of Teflon, the loss angle has been reduced by perhaps an order of magnitude, and thus the errors in a₀ determined with models neglecting the linear term are expected to be less than 0.2 × 10⁻⁶.

The other uncertainty term reconsidered here is the resistance relaxation (drift) effect in the metal foil sensing resistor that dominates the uncertainty of the resistance value. After the resistor is immersed in a TPW cell, the resistance exhibits exponential relaxation due to the differential thermal expansion strain in the foil. In both the 2015 and present determinations, we measure the resistance value with a precision dc resistance bridge and compare it with a standard resistor before and after each individual measurement. By checking the resistance values, we have found that the averaged relative drift for each noise measurement is less than 0.05 × 10⁻⁶, and therefore, the uncertainty of 0.5 × 10⁻⁶ to account for the relaxation effect in the 2015 determination was indeed overestimated. For the current determination, we estimate a relative standard uncertainty of 0.1 × 10⁻⁶.

4.5. Final result

With the best estimate of S_R/S_Q, the calculated value of the noise power spectral density S_{Q_calc}, the carefully calibrated value of the resistance R with traceability to the quantum Josephson voltage standard and the quantum Hall resistance, the temperature T that is traceable to the current definition of the kelvin, and the CODATA 2014 recommended value of h, the present measurement determines that k = 1.380 6497(37) × 10⁻²³ J K⁻¹, with a relative combined standard uncertainty of 2.7 × 10⁻⁶. Table 1 summarizes the contributions of all the various sources of uncertainty in the determination. For comparison, the uncertainty budget for the 2015 determination is also listed. The most significant terms for the two determinations should be considered uncorrelated, because the data for each are unique, both measurements use different matching and sensing resistor circuits, and the statistical uncertainty of the ratio measurement and the ambiguity associated with the spectral mismatch model are derived independently.

Table 1.

Uncertainty budget for determination of k by JNT. All uncertainties are expressed as relative uncertainties in parts per million. The uncertainty budget for the 2015 determination is given for comparison.

Component	Term	Relative uncertainty		Correlation
		2015	2017
Ratio of the power spectral densities, SR/SQ	Statistical	3.2	2.37	0
	Model ambiguity	1.8	1.02	0
	Bandwidth ambiguity	NA	0.57	0
	Dielectric losses	1.0	0.2	0
	EMI	0.4	0.4	0
	Nonlinearity	0.1	0.1	1
	Total μr (SR/SQ)	3.8	2.68
QVNS waveform SQ	Frequency reference	<0.001	<0.001	1
	Quantization effects	0.1	0.1	1
	Total (fSQ)	0.11	0.11
TPW temperature T	Reference standard TPW cell	0.29	0.29	1
	Temperature measurement	0.04	0.04	1
	Hydrostatic pressure correction	0.08	0.08	1
	Immersion effects	0.18	0.18	1
	Total μr (TW)	0.35	0.35
Resistance R	Ratio measurement	0.05	0.05	0
	Transfer standard	0.1	0.1	1
	Ac–dc difference	0.1	0.1	1
	Relaxation effect	0.5	0.1	1
	Thermoelectric effect	0.1	0.1	1
	Total μr (R)	0.53	0.21
	Total (kB)	3.9	2.7

5. Conclusion

We report a new and improved determination of the Boltzmann constant by JNT: k = 1.380 649 7(37) × 10⁻²³ J K⁻¹ with a relative combined standard uncertainty of 2.7 × 10⁻⁶. The value is 0.89 × 10⁻⁶ higher than the CODATA 2014 value assigned to the Boltzmann constant. The purely electronic measurement of k, with traceability to quantum electrical standards, provides strong assurance that there are no major systematic errors affecting the recent k determinations by primary gas thermometry [4, 5, 13].

Several changes were made to the noise thermometer to reduce systematic errors. Firstly, the connecting leads between the noise sources and the correlator adopted a coaxial arrangement to better define the inductance and capacitance of the leads. Secondly, to minimize the effects of different temperatures on the cable impedances, a very thin coaxial cable with solid beryllium–copper conductors and a foam dielectric was used. Thirdly, better matching of the frequency response for the two noise sources was achieved by using identical-length coaxial cables. No additional trimming inductors or capacitors were used. The sensing resistance was also reduced from 200 Ω to 100 Ω to improve the impedance match with the 50 Ω cables and to further flatten the frequency response of the connecting leads. Possible effects due to noise currents induced by dielectric loss in stray capacitance associated with the switch and preamplifier were substantially reduced by replacing the FR4 fibreglass PCBs with Teflon composite PCBs.

Although the changes did not yield an increase in the bandwidth of the thermometer, the results of analyses of the power spectral-ratio models are much more consistent with one another, yielding a significant reduction in uncertainty due to spectral mismatches. In combination with a three-fold increase of the integration period from 33 d to 100 d, the new determination yielded a relative uncertainty below 3 × 10⁻⁶, therefore meeting the CCT’s second requirement for proceeding with the redefinition of the kelvin.