Abstract
Computed tomography (CT) is widely used for dose planning in the radiotherapy of prostate cancer. However, CT has low tissue contrast, thus making manual contouring difficult. In contrast, magnetic resonance (MR) image provides high tissue contrast and is thus ideal for manual contouring. If MR image can be registered to CT image of the same patient, the contouring accuracy of CT could be substantially improved, which could eventually lead to high treatment efficacy. In this paper, we propose a learning-based approach for multimodal image registration. First, to fill the appearance gap between modalities, a structured random forest with auto-context model is learnt to synthesize MRI from CT and vice versa. Then, MRI-to-CT registration is steered in a dual manner of registering images with same appearances, i.e., (1) registering the synthesized CT with CT, and (2) also registering MRI with the synthesized MRI. Next, a dual-core deformation fusion framework is developed to iteratively and effectively combine these two registration results. Experiments on pelvic CT and MR images have shown the improved registration performance by our proposed method, compared with the existing non-learning based registration methods.
1 Introduction
Prostate cancer is a common cancer worldwide. In clinical treatments, external beam radiation therapy (EBRT) is one of the most efficient methods. In EBRT, computed tomography (CT) is acquired for dose planning since it can provide electron density information. However, due to low tissue contrast, it is difficult to contour major pelvic organs from CT images, such as prostate, bladder and rectum. Also, the low contouring accuracy largely limits the efficacy of prostate cancer treatment. Nowadays, magnetic resonance (MR) image is often used together with CT in the EBRT. MR image provides high tissue contrast, which makes it ideal for manual organ contouring. Therefore, it is clinically desired to register the pelvic MR image to the CT image of the same patient for effective manual contouring.
However, there are two main challenges for accurate pelvic MRI-to-CT registration. The first one comes from local anatomical deformation. This is because CT and MRI of the same patient are always scanned at different time points, thus the positions, shapes and appearances of pelvic organs could change dramatically due to possible bladder filling and emptying, bowel gas and irregular rectal movement. This necessitates the use of non-rigid image registration to correct the local deformations.
The second challenge comes from the appearance dissimilarities between CT and MRI. For example, there are no obvious intensity differences among the regions of prostate, bladder and rectum in CT image. But, in MR image, the bladder has brighter intensity than the prostate and rectum, as shown in Fig. 1. Moreover, the texture patterns of prostate in MRI are much more complex. These appearance dissimilarities make it difficult to design a universal similarity metric for MRI-to-CT registration.
Fig. 1.
Pelvic CT and MRI. From left to right: CT, labeled CT, labeled MRI and MRI.
To date, many approaches have been developed for multimodal image registration. They fall into two categories [1]. The first category is using mutual information (MI) [2] as similarity metric for registration. However, MI is a global similarity metric, thus has limited power to capture local anatomical details. Although it is technically feasible to compute MI between local patches, the insufficient number of voxels in the patch makes the intensity distribution less robust to compute MI.
The second category is based on image synthesis for registration. In these methods, one modality (e.g., CT) is synthesized from the other modality (e.g., MRI) to reduce large appearance gap between different modalities. Afterwards, the multimodal image registration problem is simplified to unimodal image registration, where most existing methods can be applied. Currently, the synthesis process is often applied to synthesizing the image with simple appearance from the image with rich and complex appearance, i.e., synthesizing CT from MRI [3]. However, such complex-to-simple image synthesis offers limited benefit to the pelvic MRI-to-CT registration. This is because the alignment at soft tissues such as prostate can hardly get improved due to low image contrast in CT. To alleviate this issue, we argue that image synthesis should be performed in bi-directions, and also the estimated deformations from both synthesized modalities should be effectively combined to improve multimodal image registration.
In this paper, we propose a learning-based multimodal image registration method based on our novel bi-directional image synthesis. The contributions of our work can be summarized as follows:
To reduce the large appearance gap between MRI and CT, we propose to use structured random forest and auto-context model for bi-directional image synthesis, i.e., synthesizing MRI from CT and also synthesizing CT from MRI.
To fully utilize the complementary image information from both modalities, we propose a dual-core registration method to effectively estimate the deformation pathway from MRI to CT space, by iteratively fusing two deformation pathways: (a) from the synthesized CT of MRI to CT, and (b) from MRI to the synthesized MRI of CT. Experimental results show that the registration accuracy could be boosted under this dual-core registration framework.
2 Method
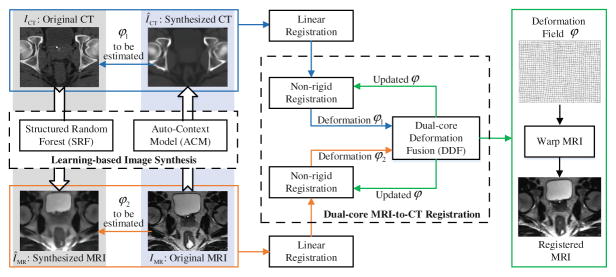
As shown in Fig. 2, the proposed multimodal image registration method consists of the following two major steps.
Fig. 2.
The framework of proposed learning-based MRI-to-CT image registration.
Learning-Based Image Synthesis
A learning-based image synthesis method is proposed to fill the appearance gap between CT and MRI. Since MRI synthesis is more challenging, our method will introduce in the context of CT-to-MRI synthesis. The same method can be applied to MRI-to-CT synthesis. In our method, a structured random forest is first used to predict the entire MRI patch from the corresponding CT patch. Then we further adopt an auto-context model [4] to iteratively refine the synthesized MRI. The details of this step are described in Sect. 2.1.
Dual-Core MRI-to-CT Image Registration
In the beginning of image registration, a synthesized MRI ÎMR is obtained from CT ICT, and also a synthesized CT ÎCT is obtained from MRI IMR. Then, the deformation between MRI and CT is estimated in two ways: (a) registering ÎCT to ICT, and (b) registering IMR to ÎMR, as shown in Fig. 2. Eventually, the MRI is warped to the CT space by following the iterative dual-core deformation fusion framework. The details of this step are described in Sect. 2.2.
2.1 Learning-Based Image Synthesis
Random Forest Regression
Random forest is a general machine learning technique, which can be used for non-linear regression. It can be used to regress MRI intensity from the corresponding CT patch. In the training of random forest, the input is N feature vectors X = [x1, x2, …, xN] and the corresponding N target MRI values y = [y1, y2, …, yN], where each x corresponds to appearance features extracted from a single CT patch, and each y is the MRI value corresponding to the center of the CT patch. Random forest consists of multiple binary decision trees, and each one is trained independently. For a given tree, the training is conducted by learning a set of split nodes to recursively partition the training set. Specifically, in each split node, for a feature indexed by k, its optimal threshold τ is found to best split the training set into left and right subsets SL and SR with consistent target MRI values. Mathematically, it is to maximize the variance reduction by a split:
| (1) |
| (2) |
where V(·) computes the variance of target MRI values in the training set, xk indicates the value of the k-th feature, and S indicates a training set. The same split operation is recursively conducted on SL and SR, until (a) the tree reaches the maximum tree depth, or (b) the number of training samples is too few to split. In the testing stage, given a testing sample with feature vector xnew, it is pushed to the root split node of each tree in the forest. Under the guidance of the split node (i.e., go left if , and go right otherwise), the testing sample will arrive at a leaf node of each tree, where the averaged target MRI values of training samples in that leaf is used as the prediction of the tree. The final output is the average of predictions from all trees.
Structured Random Forest (SRF)
In our MRI synthesis, structured random forest is adopted for prediction. The main difference between classic random forest and structured random forest is illustrated in Fig. 3. Instead of regressing a single MRI voxel intensity, the whole MRI intensity patch is concatenated as a vector and used as the regression target. Variance V(·) in Eq. (1) is then computed as the average variance across each dimension of the regression target vector. Through predicting a whole MRI patch, the neighborhood information can be preserved during patch-wise prediction and eventually will lead to better image synthesis performance, which is crucial for the subsequent registration. In the testing stage, the prediction is a vector, which can be constructed as a patch. The final prediction of each voxel is obtained by averaging values from all patches containing this voxel.
Fig. 3.
Classic random forest (top) and SRF (bottom).
Feature Extraction
In this paper, we extract Haar-like features [5] from CT patch to serve as appearance features for random forest. Specifically, a Haar-like feature describes (a) an average intensity within a sub-block, or (b) the average intensity difference between two sub-blocks, in the patch. To generate more Haar-like features, we randomly sample information within the patch. To capture both local and global appearances of the underlying voxel, Haar-like features are extracted from coarse, medium and fine resolutions, respectively.
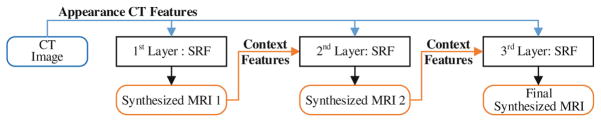
Auto-Context Model (ACM)
To incorporate the neighboring prediction results, an auto-context model [4] is adopted to iteratively refine the synthesized MRI. In this paper, we use three layers as illustrated in Fig. 4. In the first layer, appearance features (Haar-like features) from CT are extracted to train a SRF. Then, the trained forest can be used to provide an initial synthesized MRI. In the second layer, additional features (context features, also Haar-like features) are also extracted from the initial synthesized MRI to capture the information about neighborhood predictions. By combining the context features with appearance features, a second SRF can be trained. Similarly, with this new trained forest, the synthesized MRI and context features can be updated. This process iterates until reaching the maximum number of layers.
Fig. 4.
Iterative refinement of synthesized MRI by the auto-context model.
2.2 Dual-Core MRI-to-CT Image Registration
Intensity-based Non-rigid Registration
After CT and MRI are synthesized from MRI and CT, respectively, we can utilize the existing non-rigid registration methods to estimate the deformation (a) from synthesized CT to CT, and (b) from MRI to synthesized MRI. Here, we choose two popular methods for evaluation: (1) Diffeomorphic Demons (D. Demons) [6] and (2) Symmetric Normalization (SyN) [7].
Dual-Core Deformation Fusion (DDF) for MRI-to-CT Registration
Based on bi-directional image synthesis, both synthesized CT and MRI are utilized in registration. Let ICT, ÎCT, IMR and ÎMR denote the CT, synthesized CT, MRI and synthesized MRI, respectively. The goal is to estimate the deformation pathway φ from MRI to CT space. The objective function for MRI-to-CT non-rigid registration can be given as:
| (3) |
where ℳ is a dissimilarity metric, 𝒟 is an operator that deforms the image by deformation field φ, and ℛ is a regularization term to constrain the smoothness of φ.
To solve Eq. (3) and reuse the existing registration tools, we apply an alternative optimization method, by decomposing Eq. (3) into three steps:
| (4) |
| (5) |
| (6) |
The first and second steps (Eqs. (4) and (5)) are used to minimize the image difference (a) between CT modality pair and (b) between MRI modality pair, respectively. The third step (Eq. (6)) is used to ensure that the final deformation pathway φ is close to both separately estimated φ1 and φ2.
Both φ1 and φ2 can be solved by using either D. Demons or SyN, although the objective functions are slightly different in Eqs. (4) and (5). After fixing φ1 and φ2, the final deformation φ can be efficiently solved by letting the gradient of Eq. (6) equals to zero, which brings to . To approximate the optimal solution of Eq. (3), we alternate these three steps until convergence, as summarized in Algorithm 1.
In each iteration i, the tentatively deformed images and are used to estimate a next set of deformations and . The estimated deformations are then merged to form a combined deformation φi, which is used to update the currently estimated deformation φ = φ ∘ φi. Here, “∘” means deformation field composing. This procedure iterates until the incremental deformation φi is small enough.
Algorithm 1.
Alternating Optimization of Eq. (3) in the i-th iteration
| Result: φ – the final deformation field and approximated solution of Eq. (3) |
| i = 0; ; φ = 0; |
| do{ |
| i = i + 1; ; |
| ; φ = φ∘φi; ; |
| } while (||φi||2 > ε); |
3 Experiments
The experimental dataset consists of 20 pairs CT and MRI acquired from 20 prostate cancer patients. Three pelvic organs, including prostate, bladder and rectum, are manually labeled by physicians. We use them as the ground-truth. All the images are resampled and cropped to the same size (200*180*80) and resolution (1*1*1 mm3). The cropped image is sufficiently large to include prostate, bladder and rectum.
In the training step, the CT and MRI of the same patient are pre-aligned to train our image synthesis models and we use manual labels to guide accurate pre-alignment. Specifically, linear (FLIRT [8]) and non-linear (SyN [7]) registrations are first performed to register the CT and MRI of same patient. Then D. Demons [6] is applied to register the manual labels of prostate, bladder and rectum to refine the pre-alignment. Finally, all the subjects are linearly aligned to a common space. Note that, the well-aligned CT and MR image dataset are only used in image synthesis training step.
2-layer ACM and 10-fold cross validation (leave-2-out) are applied. For SRF, the input patch size is 15*15*15 and the target patch size is 3*3*3. We use 25 trees to synthesize MRI from CT, while 20 trees to synthesize CT from MRI. The reason of using more trees in the former case is because CT-to-MRI synthesis is more difficult.
Dice similarity coefficient (DSC), symmetric average surface distance (SASD) and Hausdorff distance (HAUS) between manual segmentations on CT and aligned MRI are used to measure the registration performance.
3.1 Registration Results
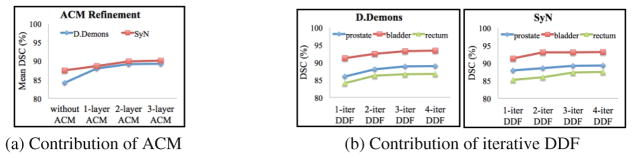
Figure 5 illustrates MRI-to-CT registration results from the whole dataset under different layers of ACM in image synthesis (Fig. 5-(a)) and different DDF iterations in image registration (Fig. 5-(b)). As shown in Fig. 5-(a), more layers of ACM lead to better registration accuracy due to better quality of synthesized images. The synthesized CT (S-CT) and synthesized MRI (S-MRI) are also visualized in Fig. 6. Figure 5-(b) demonstrates that the DDF framework improves registration performance of both D. Demons and SyN iteratively. In practice, we found that the use of 2-layer ACM in image synthesis and 3 iterations (3-iter) in DDF often leads to convergence, as shown in Fig. 5, the 3-layer ACM and 4-iter DDF do not have significant improvement.
Fig. 5.
Comparison of MRI-to-CT non-rigid registration results. (a) The mean DSC of prostate, bladder and rectum by different number of ACM layers in image synthesis. (b) Registration results of D. Demons (left) and SyN (right) with respect to different DDF iterations in Algorithm 1. Note that, 3-iter DDF is applied in (a), and 2-layer ACM is used in (b).
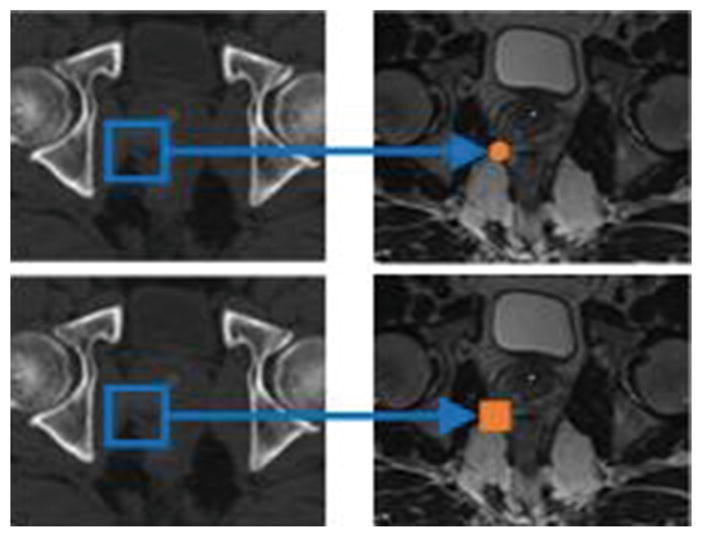
Fig. 6.
Demonstration of synthesized images and SyN registration results. (e) Result 1: direct registration of MRI to CT using MI; (f) Result 2: registration with our proposed method. Yellow contours: original CT labels of 3 organs. Red contours: warped MRI labels of 3 organs. (Color figure online)
Table 1 provides the mean and standard deviation of DSC for the three organs. It can be observed that, for D. Demons, which is not applicable for multimodal registration, can now work well by introducing the synthesized image. For SyN, using MI as similarity metric can get reasonable registration results on the original CT and MRI. However, better performance can be obtained using the synthesized image. This demonstrates that using synthesized image can enhance the performance of multimodal registration method. Moreover, the best performance is achieved under our dual-core deformation fusion algorithm as both demonstrated in Tables 1 and 2. The consistently higher DSC and lower SASD and HAUS by our proposed method demonstrate both its robustness and accuracy in multimodal image registration. Also, from those SyN-based registration results shown in Fig. 6, our proposed method can (a) better preserve structures during the registration than the direct registration of MRI to CT with MI, and (b) achieve more accurate results as shown by the overlaps of the label contours and indicated by arrows in the figure.
Table 1.
Comparison of DSC (%) values (with standard deviation of total 20 subjects) of three organs after non-rigid registration through original CT and MRI (CT & MRI), single-directional image synthesis (CT & S-CT, S-MRI & MRI), and our proposed bi-directional image synthesis under 3-iter DDF (Proposed).
| Method | Region | CT & MRI | CT & S-CT | S-MRI & MRI | Proposed |
|---|---|---|---|---|---|
| D. Demons | Prostate | N/A | 86.3 ± 5.0 | 87.4 ± 6.9 | 88.9 ± 4.3 |
| Bladder | N/A | 91.0 ± 1.1 | 91.5 ± 0.9 | 93.2 ± 0.5 | |
| Rectum | N/A | 84.2 ± 3.1 | 84.1 ± 6.2 | 86.6 ± 2.5 | |
| SyN (MI) | Prostate | 86.8 ± 3.5 | 87.9 ± 2.9 | 87.3 ± 3.4 | 89.2 ± 2.8 |
| Bladder | 90.4 ± 0.4 | 91.3 ± 0.5 | 91.5 ± 0.7 | 93.0 ± 0.3 | |
| Rectum | 83.7 ± 4.7 | 85.0 ± 4.2 | 85.2 ± 5.4 | 87.2 ± 3.2 |
Table 2.
Comparison of mean SASD(mm) and HAUS(mm) values (with standard deviation of total 20 subjects) of three pelvic organs after non-rigid registration based on single-directional image synthesis and our proposed bi-directional image synthesis under 3-iter DDF.
| Metric | Method | Single-directional | Bi-directional | |
|---|---|---|---|---|
| CT & S-CT | S-MRI & MRI | Proposed | ||
| SASD | D. Demons | 1.3 ± 0.7 | 1.7 ± 0.8 | 1.0 ± 0.6 |
| ANTs-SyN | 1.4 ± 0.8 | 1.3 ± 0.7 | 1.1 ± 0.7 | |
| HAUS | D. Demons | 8.9 ± 2.7 | 8.6 ± 3.0 | 6.7 ± 2.3 |
| ANTs-SyN | 7.6 ± 2.7 | 7.2 ± 2.0 | 6.7 ± 1.9 | |
4 Conclusion
In this paper, we propose a learning-based multimodal registration method to register pelvic MR and CT images for facilitating prostate cancer radiation therapy. To reduce the appearance gap between two modalities, the structured random forest and auto-context model are used to synthesize CT from MRI, and also synthesize MRI from CT. Furthermore, we propose the dual-core image registration method to drive the deformation pathway from MR image to CT image by fully utilizing the complementary information in multiple modalities. Experimental results show that our method has higher registration accuracy than the compared conventional methods.
References
- 1.Sotiras A, Davatzikos C, Paragios N. Deformable medical image registration: a survey. IEEE Trans Med Imaging. 2013;32(7):1153–1190. doi: 10.1109/TMI.2013.2265603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pluim JP, Maintz JA, Viergever MA. Mutual-information-based registration of medical images: a survey. IEEE Trans Med Imaging. 2003;22(8):986–1004. doi: 10.1109/TMI.2003.815867. [DOI] [PubMed] [Google Scholar]
- 3.Huynh T, et al. Estimating CT image from MRI data using structured random forest and auto-context model. IEEE Trans Med Imaging. 2015;35(1):174–183. doi: 10.1109/TMI.2015.2461533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tu Z, Bai X. Auto-context and its application to high-level vision tasks and 3d brain image segmentation. IEEE Trans Pattern Anal Mach Intell. 2010;32(10):1744–1757. doi: 10.1109/TPAMI.2009.186. [DOI] [PubMed] [Google Scholar]
- 5.Viola P, Jones MJ. Robust real-time face detection. Int J Comput Vision. 2004;57(2):137–154. [Google Scholar]
- 6.Vercauteren T, et al. Diffeomorphic demons: efficient non-parametric image registration. NeuroImage. 2009;45(1):S61–S72. doi: 10.1016/j.neuroimage.2008.10.040. [DOI] [PubMed] [Google Scholar]
- 7.Avants BB, et al. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med Image Anal. 2008;12(1):26–41. doi: 10.1016/j.media.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal. 2001;5(2):143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]