Engineered elastomer substrates for guided assembly of complex 3D mesostructures by spatially nonuniform compressive buckling

Abstract

Approaches capable of creating three-dimensional (3D) mesostructures in advanced materials (device-grade semiconductors, electroactive polymers etc.) are of increasing interest in modern materials research. A versatile set of approaches exploits transformation of planar precursors into 3D architectures through the action of compressive forces associated with release of prestrain in a supporting elastomer substrate. Although a diverse set of 3D structures can be realized in nearly any class of material in this way, all previously reported demonstrations lack the ability to vary the degree of compression imparted to different regions of the 2D precursor, thus constraining the diversity of 3D geometries. This paper presents a set of ideas in materials and mechanics in which elastomeric substrates with engineered distributions of thickness yield desired strain distributions for targeted control over resultant 3D mesostructures geometries. This approach is compatible with a broad range of advanced functional materials from device-grade semiconductors to commercially available thin films, over length scales from tens of microns to several millimeters. A wide range of 3D structures can be produced in this way, some of which have direct relevance to applications in tunable optics and stretchable electronics.

Graphical abstract

This work introduced approaches to assembly of complex 3D mesostructures via compressive buckling induced by elastomer substrates with spatially engineered distributions of strain. Systematic studies using combined theoretical modeling and experiment illustrate the key ideas and the compatibility of the approach with advanced electronic materials and planar semiconductor technologies, across length scales from sub-micron to several centimeters. Representative 3D structures with potential utility in tunable optics and stretchable electronics highlight some areas of application.

1. Introduction

3D mesostructures are of increasing attention^[1-5] due to extensive applications in micro- and nano- systems technologies, ranging from those in energy storage devices,^[6-9] to photonic and plasmonic nano-systems,^[10-14] micro-electronic circuits,^[15-20] biomedical tools,^[21-23] and optical/mechanical metamaterials.^{[12, 24-31]} Methods for forming interesting classes of 3D micro-/nano-scale architectures include those based on self-actuating materials,^[32-35] microcontact printing,^[36-37] bending/folding of thin films induced by residual stresses or capillary forces,^{[1, 5, 22, 38-41]} and additive manufacturing.^{[8, 18, 42-45]} Recently reported approaches utilize geometrical transformation of 2D precursor structures into 3D architectures by processes of compressive buckling induced by a prestrained elastomer support. Such methods are of interest due to their intrinsic compatibility with a broad range of advanced materials that exist naturally in 2D forms, their high-speed, parallel operation, and their applicability over characteristic length scales from nanometers to centimeters.^[46-50] A particularly attractive feature is in the quantitative agreement between analytical modeling of this process and experimental observation, and the associated capablity in using computation as a rigorous design tool for defining layouts of 2D precursor and spatial configurations of their bonding to the underlying elastomer that yield 3D structures of interest. An important limitation of past work in this area is that the compressive forces responsible for the 2D to 3D transformation process follow from relaxation of strains in a pre-stretched, uniform elastomer substrate. The spatially invariant magnitude of the resulting forces poses certain contraints on the range of 3D geometries that can be produced.^[46-50] Detailed studies exist on the buckling mechanics of the 2D precursors,^[49-57] but without significant attention to the mechanics of the substrates that provide the buckling force. Here, we present a versatile scheme that enables precise spatial control over these forces through a simple approach that involves engineered variations in the thickness of the elastomer substrates. The results, which include not only the essential concepts but also experimentally validated theoretical design tools, establish procedures for producing desired distributions of prestrain across the surface of the elastomer for spatially non-uniform buckling forces in the assembly of 3D mesostructures with previously unachievable levels of complexity. As with earlier and simpler embodiments, this basic approach is compatible with a broad range of advanced materials, from device-grade semiconductors, metals, to photo-patternable polymers, and commercially available thin films, across broad ranges of length scales. Demonstrations presented here include 3D structures consisting of photolithographically defined, microscale ribbons/membranes and laser-cut polymer sheets, in diverse structures such as those that resemble concave mirrors and suspended toroidal inductors.

2. Illustration of the design concept with engineered elastomer substrates

Figure 1a illustrates the general strategy that involves first bonding a 2D precursor to a pre-strained elastomer substrate. The sites for this bonding (red, Figure S1, Supporting Information) correspond to spatial modulations in surface chemistry selected to yield strong adhesion to the elastomer (Figure 1a). Release of the pre-strain causes the non-bonded regions (blue, Figure S1, Supporting Information) to buckle, with a combination of translational and torsional motions that culminate in the formation of a complext 3D mesotructure, as described previously.^[46-48] Detailed procedures to define selective bonding as well as the associated chemistry for micro-fabricated samples are discussed in Supplementary Text 1, and schematically in Figure S2 (Supporting Information). Here, the key difference is that the substrate includes spatial variations in thickness (Figure 1a), typically created using the casting and curing procedures of soft lithography, in registry with the structures and bonding sites associated with the 2D precursor. Here, forces uniformly applied to the edges of the substrate lead to spatial patterns of strain that correlate to the variations in thickness, with smaller strains in thicker regions. This response follows simply from scaling of the tensile stiffness S of the substrate with thickness, i.e., S = E(ε)*t*b, where E is the tangent modulus, t the thickness, and b the width. Upon release of the pre-strain, the degree of compressive buckling of the 2D precursor varies spatially in a corresponding manner, thereby leading to the formation of non-uniform 3D structures. Figure 1b shows a simple example that consists of a buckled ribbon of monocrystalline silicon (thickness = 1.5 μm, critical width = 80 μm) that extends across the interface between thin and thick regions (thickness ratio = 1:4, thickness of thin region = 0.4 mm) of an elastomer substrate. A thin layer of native oxide (∼ 3-5 nm) formed on the bonding sites (0.3 mm by 0.165 mm rounded rectangles, 1.7 mm apart) ensures strong adhesion to the activated (ultra-violet ozone exposure) surface the silicone elastomer upon contact. The non-bonding regions are passivated by a thin layer of polytetrafluoroethylene (PTFE) (see Experimental Section and Figure S3, Supporting Information, for details on fabrication). The periodicity (1.01 mm and 1.50 mm for the leftmost and the rightmost units, respectively) and amplitude (0.59 mm and 0.37 mm for the leftmost and the rightmost units, respectively) measured by placing the 3D structure under an optical microscope with calibration software (see Supplementary Text 2 for details) are different across the thin and thick regions of the substrate, with an abrupt change at the interface. These experimental values agree quantitatively with simulated results (periodicity = 0.975 mm and 1.474 mm for the leftmost and rightmost units respectively; amplitude = 0.564 mm and 0.358 mm for the leftmost and rightmost units respectively) extracted directly from finite element analysis (FEA, see Supplementary Text 3 for details), with maximum relative errors < 5% (Figure S4, Supporting Information). FEA simulations on strain distribution in the substrate (right frame, Figure 1b) indicate that under uniform, biaxial stretching of 70% at edges of the substrate, the strain value at the surface of the thin region (∼ 76%) is more than four times that of the thick region (∼ 17%). This effect leads to a greater degree of compressive buckling in the thin compared to the thick regions.

Figure 1. A general illustration of the process for 3D assembly by buckling induced by non-uniform distributions of strain and examples of resulting 3D mesostructures.

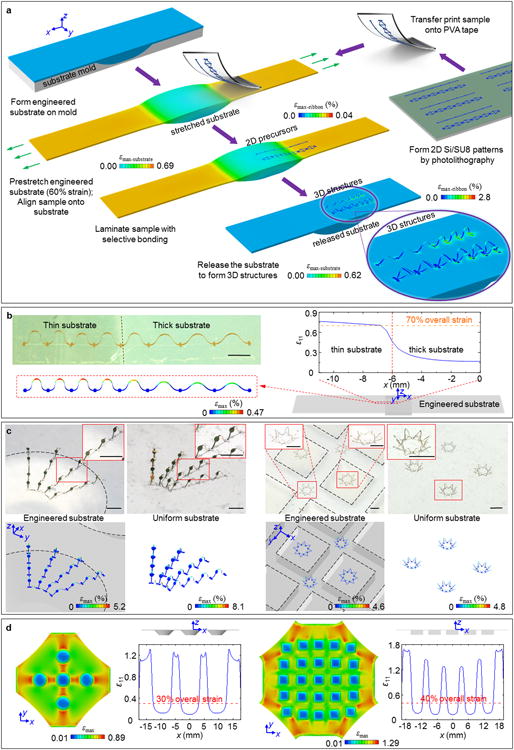
(a) Finite-element analysis (FEA) illustration of assembly of 3D structures via release of pre-stretched elastomer substrates with engineered variations in thickness. This example involves uniaxial strain in a strip of material with a thick region near the center. The magnified view highlights spatial variations in the amplitudes and periodicities of 3D structures that form as a result of buckling induced geometry transformations from 2D precursors. These variations follow from spatially non-uniform strains associated with thickness differences in elastomer substrate. Detailed fabrication procedures appear in Experimental Sections and Figure S3 and S5 (Supporting Information). (b) Optical image of a 3D strucure in a ribbon of monocrystalline silicon via use of a thickness engineered substrate (top left), corresponding FEA results (bottom left), and magnitude of the x-direction normal strain for an overall applied uniaxial strain of 70% (right). (c) Optical images of a radially-distributed, interconnected array of table structures (left) and a 2-by-2 array of eight-pointed star strucures (right) formed using engineered substrates. The dashed lines indicate outlines of boundaries between regions of different thickness across the substrates. The adjacent optical images show 3D structures formed using the same 2D precursors but using substrates with uniform thicknesses, and their corresponding FEA results (bottom). (d) FEA result showing a top view of the distribution of ε_max in each engineered substrate while stretched (with central part shown) in (c), as well as a side view in the unstretched state. Also shown is the magnitude of x-direction normal strain for given overall applied strains. In all cases, the colors in the FEA results indicate maximum principal strain ε_max distributions in the 3D structures and/or engineered substrates. Engineered substrates in (b) and (c) are shown with 30% translucency. Scale bars, 1000 μm.

This basic concept offers a straightforward route to realizing more complex strain distributions and thus highly sophisticated 3D structures. Figure 1c shows a radially-distributed, interconnected array of table-like platforms (left) and a collection of eight-pointed star-type structures (right), both made of bilayers of gold (40 nm thickness) and photodefinable epoxy (SU8, 5 μm thickness), formed using different types of engineered substrates (Figure 1d). Here, the bonding sites are deposited with a thin layer of silicon dioxide (∼40 nm) by electron beam evaporation to improve adhesion with the silicone substrate. The non-bonding regions are covered by a layer of photoresist (AZ5214, ∼1.3 μm) that is subsequently removed by acetone bath prior to initation of the buckling process (see Experimental Section and Figure S5, Supporting Information, for more details on fabrication). In both exmaples, the feature sizes (that is the widths of the ribbons) are as small as 30 μm. In case of the tables, the substrate involves a thickness variation in the form of an array of truncated cones (thickness of thin region = 0.2 mm, maximum thickness at each truncated cone = 2 mm, bottom diameter = 7.2 mm) to enable a radially gradient strain field that leads to the formation of tables with increasing tilt toward the periphery of the cones. The second engineered substrate features a square array, where adjacent eight-pointed stars are placed equidistantly on thick portion (squares, thickness = 2 mm, side length = 4.8 mm) and on thin portion (gaps between adjacent squares, thickness = 0.2 mm). The thin portion experiences significantly larger strains than the thick portion upon stretching, causing the stars on the former to fold more than those on the latter. On the contrary, the 3D structures of the same 2D precursors (Figure S6, Supporting Information) formed by uniform substrates, which are shown next to the engineered results in Figure 1c, display no such non-uniformity. Computed strain distributions along a selected central axis can be found in Figure 1d. FEA results of the 3D geometries that are displayed beneath the sample images in Figure 1b and 1c show excellent agreement, thereby providing reliable guidance for quantitative mechanical analysis and inverse design of 3D structures. Selective measurements of the period, out-of-plane displacement and in-plane size on structures in Figure 1c both experimentally and theoretically using the aforementioned techniques are presented in Figure S7 (Supporting Information), where discrepancy in any measurand from its modeling value is within 6%.

3. Numerical modeling of uniaxially stretched engineered substrates

Figure 2 illustrates the mechanics of strain engineering in a 2D model, for the case of uniaxial strain and thickness variations along the stretching direction. Figure 2a shows the overall layout of the engineered substrate, in which the top surface (Z = 0) is planar before stretching, and the bottom surface follows a curved path that defines the thickness variation. The length and width are 60 mm and 10 mm, respectively. The thicknesses of the two ends are t_max and t_min.

Figure 2. Modeling studies of the influence of various parameters on spatial distributions of strain in engineered substrates.

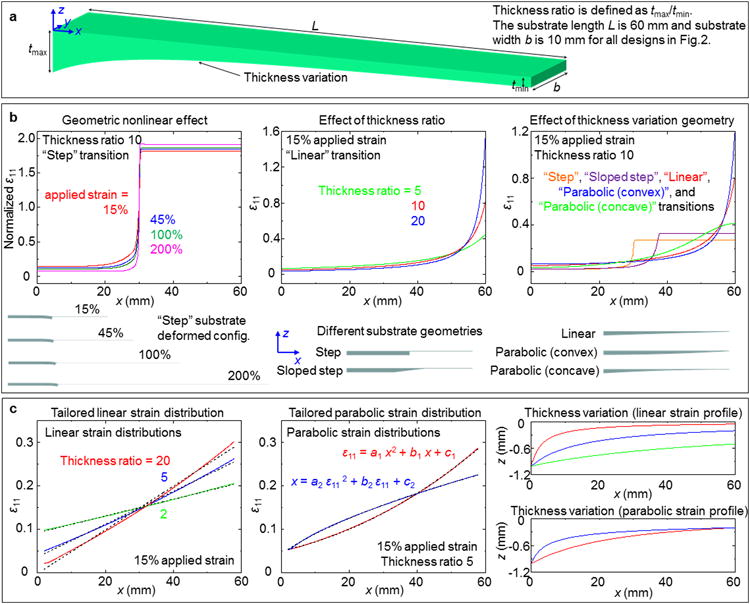
(a) Schematic illustration of engineered substrates with uni-directional variations in thickness. (b) Effect of geometric nonlinearity on strain distributions in a ‘step’ substrate at four different uniaxial levels of strain (left), effect of thickness ratios (5, 10 and 20) on strain distributions in ‘linear transition’ substrates at 15% applied strain (middle), and effect of substrate geometries (step, sloped step, linear, convex parabolic, and concave parabolic) on distributions of strain distributions at 15% applied (overall) strain (right). Side views of the corresponding engineered substrates in their unstrained states appear at the bottom bottom. (c) Inverse design results for linear (left) and parabolic (middle) distributions of strain enabled by optimized variations in thickness, with fitted lines shown in black dashes for comparison, and thickness as a function of position for each inverse design (right).

The overall applied strain, thickness ratio (t_max/t_min), and the geometry of the thickness variation are three key parameters that define the strain distributions. The geometric nonlinear effects under various applied strain levels appear in the left frame of Figure 2b, with the corresponding deformed substrate configurations at the bottom. The nonlinearity emerges from the fact that the thin portion of substrate becomes even thinner compared with the thick portion at higher strain levels. The result further increases the thickness ratio, and thereby, increases the difference in normalized strain levels. Generally, this effect is enhanced in substrates whose configurations vary significantly after stretching, e.g., the ‘sloped step’ and ‘concave parabolic’ patterns (Figure S8, Supporting Information).

The initial thickness ratio is critically important. The middle frame of Figure 2b shows the strain profiles (at 15% applied strain) for substrates that have linear variations in thickness (‘linear’) for cases with different thickness ratios. With a larger thickness ratio, the strain level is slightly lower at the thick portion and increases rapidly near the thin portion. The strain at the thin end (i.e., the maximum strain in the substrate) for a thickness ratio of 20 is 1.92 and 3.53 times larger than that for thickness ratios of 10 and 5, respectively, indicating an approximate linear scaling relationship between the maximum strain and the thickness ratio.

The right frame of Figure 2b illustrates the relationsihp between the geometry of the thickness transition and the resulting strain distribution. Studies include five different profiles with constant thickness ratios (10; t_max = 2 mm and t_min = 0.2 mm). The ‘step’ and ‘sloped step’ geometries feature the largest local strain gradient in regions that coincided with abrupt changes in thickness. Compared with the case of a ‘linear’ substrate, the ‘parabolic (convex)’ substrate has a relative smaller strain gradient near the left end, but a larger graident at the right end, consistent with the spatial gradient of the thickness. The same trend can be observed for the ‘parabolic (concave)’ substrate.

These and other modeling capabilities allow the selection of profiles in thickness to offer desired strain distributions under certain stretching levels. Figure 2c shows representative inverse design results (right frame of Figure 2c and Figure S9, Supporting Information) that yield linear (left) and parabolic (middle) strain distributions, respectively, under stretching level of 15%. An initial trial solution is determined by assuming a constant tangent modulus (i.e., assuming linear elastic behavior), where the thickness distribution is roughly inversely proportional to the target strain distribution. FEA then takes into account the local strain levels to refine the substrate geometry, which serves as an input to the model to update the strain-dependent tangent modulus. Repeated iteration of this process yields an optimized substrate geometry that renders the desired strain profile. The slope of the tailored linear strain profile can be adjusted by choosing different thickness ratios (left frame of Figure 2c). Two parabolic strain distributions can be also achieved following the same algorithm (middle frame of Figure 2c). The quality of the results can be defined by comparing the computed linear and parabolic strain profiles to best-fit lines and parabolas, as shown in black dashes in left and middle frames of Figure 2c. The functions for the fitted lines are ε₁₁ = 0.001931 x + 0.09189 (thickness ratio 2), ε₁₁ = 0.003787 x + 0.03587 (thickness ratio 5), and ε₁₁ = 0.005032 x - 0.002153 (thickness ratio 20); the functions for the fitted parabolas are ε₁₁ = 0.00004175 x² + 0.001645 x + 0.05046, and x = 751.4 ε₁₁² + 117 ε₁₁ - 6.457. These functions were adopted mainly to validate the inverse designs for achieving desired strain profiles in linear, parabolic or square-root relations. With this type of inverse design approach, many other forms of strain profiles are accessible at a wide range of applied strains.

4. Strain visualizations in biaxially stretched engineered substrates

These concepts in substrate strain engineering are readily extendable to 2D configurations. The left frame of Figure 3a demonstrates an engineered elastomer substrate with “chessboard” features of relief in the form of truncated circular cones. Other configurations render different strain fields at given stretching levels (right frame of Figure 3a). Geometrical nonlinearity in these unit cells appears as much larger stretching of the outer, thinner portion compared to the inner, thicker portion (Figure 3a and Figure S10, Supporting Information). With different types of surface features and their combinations (square, elliptical, diamond, and triangular, etc.), substrates of this tpye can yield a diverse range of strain distributions to meet requirements in 3D assembly, as described in subsequent sections.

Figure 3. Experimental and theoretical studies of spatial distributions of strain in several represenative engineered substrates.

(a) Schematic illustraiton of a ‘chessboard’ engineered substrate, with a magnified view of a unit cell in the lower right. Schematic top and side view illustrations and FEA results for different types of unit cells at 40% biaxial strain appear on the right. (b) Optical images of strain visualization studies on the ‘chessboard’ substrate shown in the left part of (a), at applied biaxial strains of 0, 40%, 60% and 80%. Magnified views of the regions with displacement markers are in the lower right. (c) Contour plots of different strain components (ε₂₂, ε₁₂, and ε_max) for the ‘chessboard’ substrate generated from experiments (left) and FEA (right). Colors in each contour plot display the magnitudes and directions of strain, where negative values in shear strain indicate a change in direction. Applied biaxial strains are 60% for all cases. (d) Optical images of three more substrates (see ‘elliptical’,‘diamond’ and ‘triangular’ arrays in Figure S12, Supporting Information, for details) stretched by 60% biaxial strain (top), and contour plots of ε₂₂ generated from experiments (bottom left) and FEA (bottom right). Scale bars, 2 cm.

Quantitative measurements of these strain fields serve to validate the FEA results (Figure 3b). Specifically, strain fields in the “chessboard” substrate (thickness of uniform region = 0.5 mm, maximum thickness of each truncated cone = 2.25 mm, bottom diameter = 7.35 mm) at 0, 40%, 60% and 80% biaxial stretching can be visualized by evaporating arrays of displacement markers (copper discs deposited via electron beam evaporation through a shadow mask: 80 nm thick, diameter = 0.6 mm, pitch = 1.875 mm) onto the substrate. A digital camera (Figure S11, Supporting Information) captures images that can be analyzed to yield contour plots of the strain distributions, illustrated here as overlays on the undeformed configurations. The results of Figure 3c (60% biaxial stretching) indicate that the experimental data agrees with FEA. Strain contour plots of three other engineered substrates appear in Figure 3d. Similar to the “chessboard” array, low strain levels occur within the thick substrate regions (where the surface features are located), with high strain levels in the thin regions between adjacent surface features. The undeformed configurations of the engineered substrates in Figure 3b and d appear in Figure S12 (Supporting Information). Additional results of strain field are in Figure S13 (Supporting Information). For all these cases, experimental and FEA strain contours match well, thereby illustrating the versatility of the approach and the utility of simulation tools.

Given a desired uniaxial or biaxial strain distribution, the design procedure starts by arranging the overall layout and spacing of unit cells (either thickened or thinned) in the engineered substrate to approach the desired strain profile. The geometries and thickness ratios of the unit cells with respect to the surrounding uniform substrates are then determined carefully to refine details to the designed strain profile. In some cases, special features such as through-holes and trenches can be used for generation of step-wise strain profiles.

5. 3D mesostructures enabled by engineered elastomer substrates

Engineered elastomer substrates allow control over gradual and dramatic geometrical changes in assembled 3D structures. Figure 4a and Figure S14 (Supporting Information) illustrates a series of gradually changing 3D ribbon structures (single-crystalline silicon, thickness = 1.5 μm) that have ribbon widths below 100 μm. 3D structures that have alternating buckled and flat sections can also be constructed, as demonstrated in Figure 4b with millimeter-scale ribbon structures (polyester, thickness = 50 μm). The corresponding cross-sectional views and strain distributions for each substrate appear in Figure 4c and Figure 4d respectively. The latter substrate (Figure 4b and d; thickness of thick island = 9 mm, thickness of thin region = 1 mm, depth of trench = 4 mm, width of trench = 1.5 mm) is designed such that the top surface experiences a step-wise strain distribution along x-axis, with almost zero strain in the thickened islands, resulting in effective strain isolations in the corresponding sections of the ribbon structures. 3D structures formed with the same 2D precursors (Figure S15, Supporting Information) on uniform substrates, appear in Figure S16 and S17 (Supporting Information) as a comparison. Additional complex array structures and corresponding FEA results, including arrays of pyramids (left, feature size = 150 μm) and radially oriented ribbons (right, feature size = 80 μm) in gold (40 nm) / SU8 (7 μm) bilayers appear in Figure 4e. For these mesostructures, the center unit experiences larger deformation than the surrounding counterparts, due to presence of an aligned hole (diameter = 1.2 mm) through the substrates (Figure 4f). In this case, the hole region (e.g. zero thickness) has zero stiffness, leading to large radial and circumfenrential deformations upon uniform biaxial stretching. The distribution of normal strain ε₁₁ along a horizontal line passing the center of hole (Figure 4f) displays a localized equivalent stretching strain (that is, the increase in hole diameter over the initial hole diameter). As a comparison, 3D structures formed with the same 2D precursors (Figure S18, Supporting Information) on uniform substrates are shown next to the engineered results in Figure 4e. Quantitative geometric comparison shows the relative differences between out-of-plane displacements and in-plane dimensions compared to modeling results are within 11% and 5% for the array of pyramids and the array of radially oriented ribbons, respectively (Figure S19, Supporting Information). Additional examples of 3D structures formed on uniform and engineered substrates appear in Figures S20-S23 (Supporting Information).

Figure 4. Various 3D structures enbabled by compressive buckling induced by spatially non-uniform strains in engineered substrates.

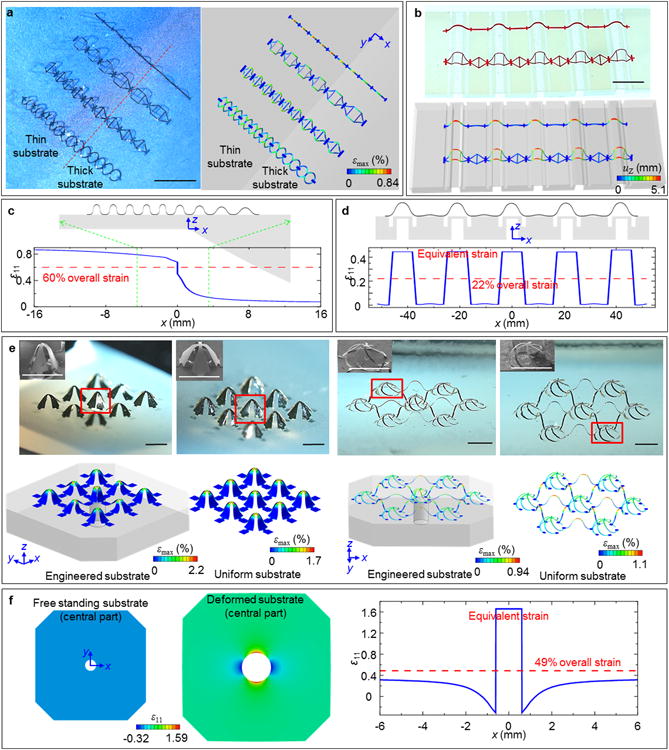
(a) Optical image of arrays of 3D ribbon structures made of silicon with a spatial gradient in key geometric features (left), and corresponding FEA results (right). (b) Optical image of related 3D structures made of thin films plastic with an abrupt change in key geometric features (left), and corresponding FEA results (right). (c) FEA results showing the side view of the structure shown in (a), and the magnitude of the x-direction normal strain for a 60% applied uniaxial strain. (d) FEA results showing the side view of the structure shown in (b), and the magnitude of x-direction normal strain for a 22% applied uniaxial strain. (e) Optical images of 3D structures made of bilayers of metal gold and photodefined patterns of epoxy (SU8) (top), and corresponding FEA results, including illustrations of the substrate geometries (bottom; only the central part of substrate is shown). The insets shows magnified SEM views of the regions identified with red boxes in each optical image. Experimental and FEA results of 3D structures formed using the same 2D precursors but with uniform substrates are on the right. (f) FEA results for the engineered substrates (only central part shown) before and after 49% biaxial stretching (left), and magnitude of normal strain ε₁₁ for a 49% applied biaxial strain (right). The colors indicate the maximum principal strains in the structures for (a) and (e), and the magnitude of out-of-plane displacements for (b). Engineered substrates in (a), (b) and (e) are shown with 30% translucency. Scale bars in (a), 500 μm. Scale bars in (b), 1 cm. Scale bars in (e), 1000 μm.

This strategy can yield 3D structures of many types, some of which ressemble practical device components such as concave mirrors and suspended inductors. Figure 5a shows an array of components that rotate to form a concave mirror (gold-coated polyimide, polyimide thickness = 50 μm), inspired by widely-used devices from geometrical optics. Here, the substrate is engineered with a central truncated cone (bottom radius = 10 mm, maximum thickness = 4.8 mm, thickness of remaining thin region = 0.8 mm) to enable controllable amount of rotation within each of the three loops of mirrors (rotational angles 4.7°, 13.9° and 27.3° inside-out, respectively), forming a relatively smooth and closed concave that is otherwise difficult to realize from previously reported techniques. 2D precursors and substrate geometries are displayed in Figure S24 (Supporting Information). The focal location of the structure, here defined as vertical distance between the centroid of region with the strongest reflected light (normalized intensity > 0.9) and the surface plane of the substrate, is simulated using optics ray tracing software (COMSOL Multiphysics, see Supplementary Text 4 for details) and found to change as a function of applied biaxial strain (blue curve, Figure 5a), suggesting its potential as a strain-tunable optical component. Analytically calculated, idealized focal locations from the fitted concave surface function z = f(x, y) (Figure S25, Supporting Information) for different levels of biaxial stretching (red curve, Figure 5a) agree well with the simulated values (blue curve, Figure 5a), proving the capability of this approach in creating approximately curved surfaces for various applications.

Figure 5. 3D structures with potential utility in tunable optics and stretchable electronics.

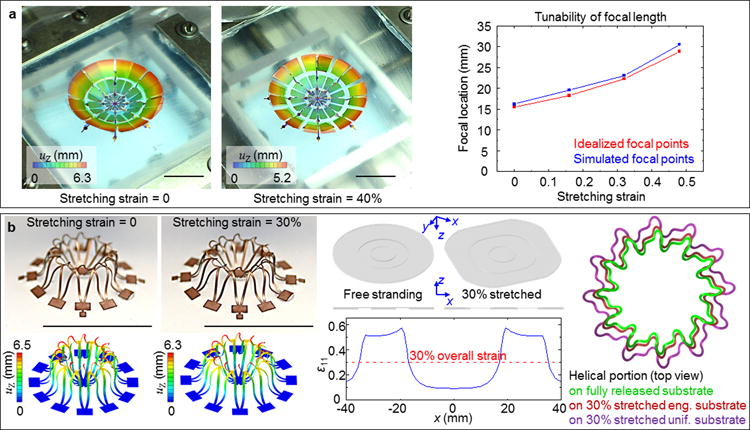
(a) A 3D concave mirror enabled by assembly using engineered substrates. The left two frames show overlaid experimental and FEA images of structure at 0 and 40% biaxial strain. The right frame shows change of simulated focal locations as a function of stretching levels, and comparison with ideal focal locations for the corresponding fitted concave surfaces. (b) A 3D helical coil elevated from the substrate. The left two frames show the experimental and FEA results of the structure at 0 and 30% strains. The middle frames show 3D and cross-sectional views of the substrate, as well as the magnitude of the x-direction normal strain for 30% applied biaxial strain. The right frame shows a top view of the helical coil upon 30% biaxial stretching, with and without the use of an engineered substrate. The colors in the FEA results indicate the magnitude of out-of-plane displacements. Engineered substrates in (b) are shown with 30% translucency. Scale bars, 1 cm.

Figure 5b demonstrates a 3D toroidal coil made of printed circuit board materials [polyimide film (25 μm) on copper foil (12 μm)] that is fully suspended from the substrate. The substrate in this case embraces a thickened center disc (3 mm in thickness) at which the 2D precursor is attached (Figure S26, Supporting Information), and a relatively thin surrounding region (1 mm in thickness) (Figure 5b). The thickness and area ratios of the two parts can be tuned such that during formation, the 3D coil only experiences ∼ 86% compression when a ∼ 300% biaxial compression is applied to the surrounding substrate. Due to this strain scaling effect, only ∼1/3 of the global strain will be sensed by the 3D coil upon biaxial stretching of the substrate, leading to small deformations of the coil geometry, and thereby, negligible changes in its inductive properties (Figure S27, Supporting Information). As a comparison, the same toroidal coil formed on uniform substrate experiences significantly larger deformations upon 30% biaxial stretching, as demonstrated in right frame of Figure 5b, and Figure S28 (Supporting Information). These and other features make this 3D structure valuable for applications such as epidermal electronics^[58-66], where parasitic impedance from substrate and motion-induced variance in electrical performances are undesired.

6. Conclusion

In summary, we report a viable approach to assembly of non-uniform 3D mesostructures through engineering of the underlying elastomer substrates. Guided by theoretical modeling, many sophisticated and useful structures can be deterministically constructed by precisely tailoring the substrates and 2D precursors. This approach is compatible with a broad set of materials at wide-ranging scales, as demonstrated in examples made of micron-scale semiconductors, metals, photo-patternable polymers, and millimeter-scale commercially available thin films. Furthermore, engineered substrates enable local concentration and/or isolation of strain under uniform external stretching, which becomes valuable in certain device designs where strain scaling is crucial. These and other features open up new opportunities for applications in areas including tunable optics and epidermal electronics. Future opportunities may follow in exploring approaches to combine the spatial variations of thickness and modulus in the elastomeric substrates towards finer manipulations of 3D assembly.

7. Experimental Section

Fabrication of engineered substrate began with formation of the mold by 3D printing [Stratasys^® Objet350 Connex3 printer; both rigid opaque (VeroWhitePlus-RGD835) and transparent (VeroClear-RGD810) printing materials can be used]. A thin layer of silicone mold release (Stoner^® S206) was applied to the mold surface before each use. Precursors to a low modulus, high elogation silicone material (Dragon Skin^® 10) were mixed and slowly poured onto the mold to fill all the surface cavities. After curing at room temperature for ∼ 10 hours, extra silicone on the edges was carefully trimmed by a razor blade to render a flat surface. This defined isolated, thick portions of the engineered substrate. Spin casting of a second layer of silicone precursors and room-temperature curing for another 10 hours defined thin portions of the engineered substrate that also connected the previously formed thick portions. Peeling the piece of cured elastomer away from mold completed the fabrication of the engineered substrate. Figures S29 and S30 (Supporting Information) present photographs of these experimental procedures and of 3D printed molds and elastomer substrates, respectively.

Fabrication of micron-scale, 3D single-crystalline silicon mesostructures began with photolithographic patterning of photoresist (AZ 5214E, MicroChemicals, thickness = 1.6 μm) on a SOI wafer (top silicon thickness = 1.5 μm) followed by reactive ion etching (RIE) to yield desired patterns in the top silicon layer. Immersion in hydrofluoric acid (HF, 49%) partially undercut the underlying silicon dioxide (SiO₂) layer. A spin-cast layer of PTFE (Teflon AF, Dupont, thickness = 700 nm) patterned by oxygen plasma etching on the non-bonding regions of the silicon served as an adhesion inhibitor to the elastomer substrate. A patterned layer of gold (thickness = 40 nm), which served the mask for this etching process, was later removed by wet etching (gold etchant TFA). Immersion in HF allowed complete removal of the SiO₂. Transferring the silicon structure onto a slab of polydimethylsiloxane (PDMS, Sylgard 184, 1:4) followed by retrieval with a water-soluble tape (polyvinyl alcohol, PVA) prepared the system for aligned lamination onto a pre-stretched elastomer substrate previously exposed to ultraviolet-induced ozone (UVOCS uv ozone cleaning system). Heating for 70 °C for 10 minutes to activate the surface bonding, washing away with warm water to remove the PVA, and slowly releasing the pre-strained elastomer to induce compressive buckling completed the assembly process. A schematic illustration appears in Figure S3 (Supporting Information).

Fabrication of micron-scale, 3D mesostructures of bilayers of gold and SU8 began with growth of 600 nm of SiO₂ on a silicon wafer by dry thermal oxidation. Photolithographic patterning of a negative photoresist (AZ nLof 2070, MicroChemicals, thickness = 7 μm), followed by electron beam evaporation of gold (thickness = 40 nm) and lift-off with acetone yielded a patterned gold layer on the SiO₂. A layer of SU8 (SU8 5, MicroChem, thickness = 7 μm) photolithographically patterned on top of gold defined the bilayer structure. Immersion in buffered oxide etchant (VWR International, 6:1) etched away the exposed SiO₂ and some of this material from the regions neard the edges of the patterns. Next, a photolithographically patterned layer of photoresist (AZ 5214E, MicroChemicals, thickness = 1.6 μm) defined openings to expose the SU8 at the locations of the bonding sites. The subsequent undercut etching of SiO₂ with HF, transfer printing onto a PVA tape, exposing to ozone, contacting a prestrained substrate, removing the photoresist by immersion in acetone and releasing the prestrain completed the process. A schematic illustration of these steps appears in Figure S5 (Supporting Information).

Fabrication of millimeter-scale, 3D mesostructures in plastic began by patterning commercially available films by laser cutting. Patterned application of a silicone adhesive (Dow Corning Flowable Sealant 734) using a masking element defined the bonding sites. A razor blade enabled removal of excess adhesive. Pressing the sample firmly onto the surface of a pre-strained elastomer and applying uniform downward force for ∼ 5 minutes yielded strong adhesion between the bonding sites and elastomer. Slowly releasing the pre-strain completed the assembly of 3D plastic mesostructures.

Experimental visualization of normal strain fields of engineered substrates began with formation of an array of metal dots (80 nm copper, diameter = 0.6 mm for each dot, pitch = 1.875 mm) by electron beam evaporation through a shadow mask. A digital camera captured images of the substrates at different levels of biaxial strain. Image processing software (PhotoModeler) allowed automated capture of the coordinate positions of the dots. Computations with MATLAB (version 2014b) defined the horizontal and vertical relative displacements between pairs of adjacent dots. Dividing these relative displacements by the initial distance between the dots yielded the normal strain values at each dot except those at the right-most column and top-most row of the array. Finally, the MATLAB function “contourf” generated contour plots of the strain fields.