Electrical access to critical coupling of circularly polarized waves in graphene chiral metamaterials

Electric control of coupling in hybrid graphene/metamaterial system enables strong selective modulation of light polarization.

Abstract

Active control of polarization states of electromagnetic waves is highly desirable because of its diverse applications in information processing, telecommunications, and spectroscopy. However, despite the recent advances using artificial materials, most active polarization control schemes require optical stimuli necessitating complex optical setups. We experimentally demonstrate an alternative—direct electrical tuning of the polarization state of terahertz waves. Combining a chiral metamaterial with a gated single-layer sheet of graphene, we show that transmission of a terahertz wave with one circular polarization can be electrically controlled without affecting that of the other circular polarization, leading to large-intensity modulation depths (>99%) with a low gate voltage. This effective control of polarization is made possible by the full accessibility of three coupling regimes, that is, underdamped, critically damped, and overdamped regimes by electrical control of the graphene properties.

INTRODUCTION

Controlling circular polarization states is important in modern photonics because it plays a pivotal role in the field of quantum computation and information (1, 2), optical communication of spin information (3), and circular dichroism (CD) spectroscopy (4, 5). Natural chiral materials composed of elements without any mirror symmetry have been widely used to manipulate the circular polarization states of light since the discovery of optical activity (OA) in a quartz crystal (6–8). However, naturally occurring chirality in the form of CD and OA is extremely weak, requiring a substantially long propagation length to observe chirality in naturally chiral media (9). Artificial structures called “chiral metamaterials” composed of subwavelength metallic building blocks have been proposed for enhancing CD (10–13) and OA (14–18), enabling various potential applications, such as broadband circular polarizers (19, 20) and wave plates (21–23).

In the terahertz (THz) regime, control over CD and OA is of great importance because macromolecules with ionic or polar constituents strongly absorb THz waves because of the presence of large-scale collective vibrational modes (24, 25), and biopolymers, such as proteins, DNA, and RNA, composed of chiral structures selectively absorb circularly polarized THz waves (26–28). Despite this importance of chirality at THz frequencies, active control of CD and OA has continued to remain challenging, mainly due to technical difficulties in manipulating THz waves and their polarization states. During the past few years, optical tuning of the CD and OA of chiral metamaterials has been demonstrated (29–31), which, however, requires elaborate experimental setups, such as pump lasers and appropriate optical components. For practical applications, an electrical approach for active control of the polarization state would be more attractive. Graphene, consisting of carbon atoms two-dimensionally arranged in a honeycomb lattice, has been studied extensively for the past decade because of its high carrier mobility and unique band structure with linear dispersion near the so-called Dirac point or charge-neutral point (CNP). Strong modulation of its THz properties can be achieved by electrically tuning the density of states available for intraband transitions. Efforts have been made to enhance graphene absorption in the THz regime by integrating graphene with metamaterials (32–38). Although a large number of works on graphene-based metamaterials have been reported, polarization modulation by simple electric gating remains largely unexplored.

Here, we demonstrate gate-controlled CD and OA in gated graphene integrated in a chiral metamaterial. As shown in Fig. 1A, the transmission of a right-handed circularly polarized (RCP) THz wave can be strongly modulated when a voltage is applied to the gate because of a critical transition followed by a change in the optical conductivity of graphene. On the other hand, the transmission of the other circular polarization remains very insensitive to the applied voltage. This selective control can be explained by the different radiation loss parameters of the chiral metamaterial for the two circular polarizations, leading to different transmission changes with applied gate voltage when graphene is incorporated into the metamaterial design. Furthermore, it is shown that the plane of linearly polarized waves can be electrically rotated while the linear polarization state maintains its linearity.

Fig. 1. Schematic views and device image of gate-controlled active graphene CDZM.

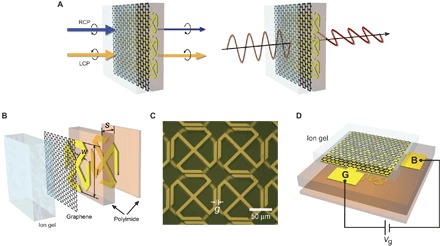
(A) CD and OA in graphene CDZM. CD: Transmissions for RCP and LCP waves are different to each other because of the different absorption between RCP and LCP waves (left). OA: The electric field vector of linearly polarized light rotates around the axis parallel to its propagation direction while passing the graphene CDZM (right). (B) Schematic rendering of a gate-controlled active graphene CDZM composed of a single-layer graphene deposited on the top layer of CDZM and subsequently covered by a layer of ion gel [thickness (t) = 20 μm]. The geometry parameters are given as l = 100 μm, w = 7 μm, and s = 10 μm. (C) Top-view microscopy image of the fabricated gate-controlled active graphene CDZM. The gap width between chiral metamolecules is given as g = 2 μm. (D) Schematic rendering of the fabricated graphene CDZM. B is a base connected to the ion gel, and G is a gate connected to the graphene layer.

RESULTS

To effectively control the polarization states of THz waves, we use a conjugated double Z metamaterial (CDZM), a bilayer chiral metamaterial structure that is morphologically transformed from a conventional conjugated gammadion shape (18), as shown in Fig. 1 (B and C). As shown in more detail later, in this metamaterial, the radiation loss for an RCP wave strongly depends on the gate voltage, in contrast to a small change in the radiation loss for a left-handed circularly polarized (LCP) wave. This feature is very useful for selective control of the response of the metamaterial for the two different circular polarizations. A graphene layer is directly attached to the top layer of the CDZM using a wet transfer method (39). Raman spectroscopy is performed to confirm the monolayer characteristics of transferred graphene when averaged over the overall area of the wafer (see fig. S1). During the synthesis and fabrication processes, chemical vapor deposition (CVD)–grown graphene easily becomes p-doped (40), which is also the case for our graphene samples. To control the conductivity of graphene via the gate voltage, we used an ion gel gate dielectric along with adequate electrodes for a large change in carrier concentration (Fig. 1C) (for details on the fabrication of the device, see Materials and Methods).

The fabricated graphene CDZM structures are characterized by THz time-domain spectroscopy (THz-TDS) (32). The transmission coefficients for the circularly polarized lights are obtained through linear polarization measurements with wire grid polarizers (see Materials and Methods). A voltage supply is connected to the electrode and the graphene layer to apply a gate voltage (Fig. 1D). Figure 2A shows the measured intensity transmission spectra for the RCP and LCP THz waves, T_RCP and T_LCP, through the graphene CDZM at four different gate voltages. For comparison, the intensity transmission spectra of a bare reference CDZM array are plotted in a black sold line (the transmission amplitude of the bare CDZM is about 20% for the RCP wave at the resonance frequency of 1.1 THz). The gate voltage relative to CNP ΔV = |V_g − V_CNP| determines the doping level of graphene. It is shown that T_RCP can be markedly reduced by increasing the applied voltage (ΔV < 1.8 V) but almost leaves T_LCP unchanged at the resonance frequency of 1.1 THz (Fig. 2B). However, further increasing the gate voltage beyond a critical voltage (ΔV > 1.8 V) leads to an increase in T_RCP. The maximum intensity modulation depth for the RCP wave, defined as a relative transmission of RCP change ΔT_RCP/T_RCP,CNP for graphene CDZM, is measured to be 99% at the resonance frequency of 1.1 THz.

Fig. 2. Gate-controlled circular transmission and CD.

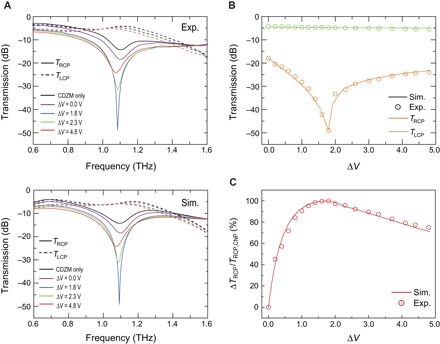
(A) Measured and simulated intensity of transmission spectra for RCP (T_RCP; solid line) and LCP (T_LCP; dashed line) waves are plotted for different gate voltages ΔV. (B) T_RCP (orange) and T_LCP (green) at the resonance frequency of 1.1 THz as a function of ΔV. Whereas T_LCP is almost unchanged, T_RCP can be markedly modified by the applied voltage. (C) Measured (scatters) and simulated (line) intensity modulation depth for ΔT_RCP/T_RCP,CNP plotted as a function of ΔV at the resonance frequency of 1.1 THz. The maximum modulation depth for T_RCP is measured to be 99%.

To clarify the mechanism of electrical control of one circular polarization observed in the experiments, we perform numerical simulations using both a FEM (finite element method) solver (CST Microwave Studio) and the FDTD (finite-difference time-domain) method (Lumerical FDTD Solutions). To numerically model the graphene layer in the simulations, we calculated the optical conductivity of graphene as a function of the Fermi levels using the Kubo formula (see Materials and Methods for more details) (41). For a better understanding of the gate-dependent modulation characteristics, measured T_RCP at the resonance frequency of 1.1 THz are plotted as a function of ΔV and compared with the simulation results. As clearly seen from the plot in Fig. 2 (B and C), the simulation results show an agreement with the measured data, where the Fermi level is related to the gate voltage by |E_F| = ℏv_F(πN)^1/2. Here, v_F is the Fermi velocity, N is the total carrier density given by $N={(n_0^2+{\mathrm{\alpha }}^2{\left|\mathrm{\Delta }V\right|}^2)}^{1/2}$, and α ≈ 8.0 × 10¹¹ cm⁻²V⁻¹ is the gate capacitance of the ion gel dielectric. For the intraband scattering time, we assume that τ = 31 fs and the value of the carrier density at the conductivity minimum is n₀ = 5.4 × 10¹⁰ cm². Relative changes in CD, Δ = |T_RCP − T_LCP|, are plotted in Fig. 3 as a function of the gate voltage from ΔV = 0.0 V to ΔV = 4.8 V. We experimentally achieve a very large modulation of CD of up to 45 dB (ΔV = 1.8 V) at 1.1 THz (Fig. 3B).

Fig. 3. Gate-controllable CD.

(A) Measured and simulated CD defined by the difference in transmission for RCP and LCP waves Δ = |T_RCP – T_LCP|. (B) CD Δ at the resonance frequency of 1.1 THz as a function of gate voltages ΔV.

Besides CD, OA can be electrically controlled via the gate voltage. With chiral media, pure optical rotation of a linear polarized wave with no ellipticity can be obtained at off-resonance frequencies (18, 44). The measured and simulated ellipticity η, defined as η = $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ sin⁻¹ [(|T_RCP|² − |T_LCP|²)/(|T_RCP|² + |T_LCP|²)], is plotted as a function of ΔV and frequency (Fig. 4A). At around 1.42 THz (purple dashed line), the transmission of the RCP and LCP waves are nearly identical (Fig. 2B), which implies that the ellipticity is very small (η ≈ 0). The ellipticity of the transmitted waves is less than 0.7° (2.1° in the experimental results) across the whole applied voltages at the frequency f_η≈0. The OA is characterized by the azimuthal rotation angle θ = $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ [arg(T_RCP) − arg(T_LCP)], as schematically illustrated in the inset of Fig. 4C. Figure 4B shows the measured and simulated azimuthal rotation angle θ through the graphene CDZM at three different gate voltages. We measured the azimuthal rotation angle θ to be as large as 40° at f_η≈0 = 1.42 THz in the case of ΔV = 0.0 V. This experimental result shows that the rotation angle per wavelength reaches values in greater than of 274°/λ. Here, the thickness of the sample is 31 μm. As shown in Fig. 4C, the rotation angle of the graphene CDZM can be tuned from 40° to 30° as the gate voltage increases from ΔV = 0.0 V to ΔV = 4.8 V, which means that the rotation modulation angle per wavelength reaches 72°/λ.

Fig. 4. Gate controllable OA.

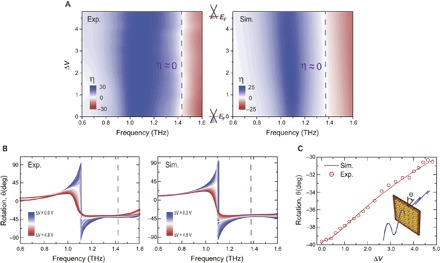
(A) Comparison between measured and simulated ellipticity η with different gate voltages ΔV. The dashed purple line represents the frequency of pure OA (η ≈ 0). (B) Measured and simulated azimuthal rotation angle θ with different ΔV. (C) Azimuthal rotation angle θ at the frequency for which f_η≈0 as a function of ΔV.

DISCUSSION

To explain the large modulation of CD, we use temporal coupled-mode theory (CMT) involving two resonant modes with two ports (42, 43). In our CMT model, as shown in Fig. 5A, the couplings between the two resonance modes (f₁ and f₂) and the incident/transmitted RCP waves are considered (see note S1). We note that the CMT model can be applied to RCP and LCP waves independently because there is no cross-coupling between them due to the C4 rotational symmetry of the structure. To quantitatively understand the coupling mechanism, we derive an analytical expression of transmission coefficients by taking account of the two resonances. Because there are three coupling channels between the incident and transmitted waves, that is, two via the resonance modes and one direct coupling, the complex transmission amplitude coefficient for RCP can be written as

$$t_{\mathrm{R}\mathrm{C}\mathrm{P}}=t_0+\frac{{\Gamma }_{1r}{e}^{i{\mathrm{\phi }}_1}}{i(f-f_1)-{\Gamma }_{1r}-{\Gamma }_{1i}}+\frac{{\Gamma }_{1r}{e}^{i{\mathrm{\phi }}_2}}{i(f-f_2)-{\Gamma }_{2r}-{\Gamma }_{2i}}$$ (1)

where Γ_1r, Γ_2r, Γ_1i, and Γ_2i are the radiation and intrinsic losses of the two resonances, respectively, f₁ and f₂ are the resonance frequencies, and φ₁ and φ₂ are the phase differences between the incident and transmitted waves mediated by the first and second resonances (35). Figure 5B shows that there is a clear transition in the phase of the RCP transmission coefficient at ΔV = 1.8 V. This abrupt transition suggests a presence of a critical coupling state that divides the excitation of the resonance modes into underdamped (ΔV < 1.8 V) and overdamped (ΔV > 1.8 V) regimes. In contrast to the reflective-type metasurface, which shows a critical transition in the phase of the reflected beam (35), our chiral metamaterial shows a critical transition for transmitted beams.

Fig. 5. Smith curves of T_RCP with different gate voltages.

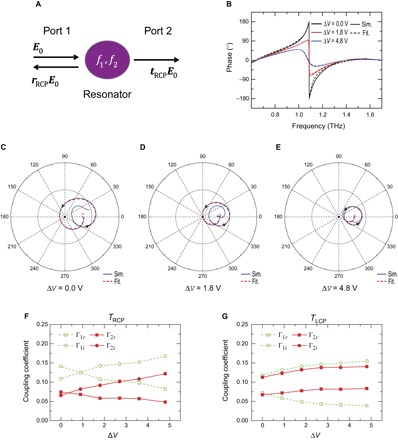
(A) Temporal coupled mode theory for two resonances, f₁ and f₂, with a two-port model. (B) Simulated (solid line) and fitted (dashed line) phases of RCP waves are plotted for three different gate voltages ΔV. Smith curves of the T_RCP for coupled mode theory of the two-port model representing (C) underdamping (ΔV < 1.8 V), (D) critical damping (ΔV = 1.8 V), and (E) overdamping (ΔV > 1.8 V) behavior. The radiation and intrinsic losses Γ_1r, Γ_1i, Γ_2r, and Γ_2i for (F) the RCP excitation and (G) the LCP excitation as a function of ΔV.

The transmission coefficients, fitted using Eq. 1, are plotted together with simulated transmission coefficients in the complex plane in Fig. 5 (C to E). This clearly shows that the transmission through the metamaterial can be classified as three different regimes around the critical coupling (ΔV = 1.8 V), where the Smith curve crosses the origin in the complex plane. In this fitting, the coupling coefficient (the loss parameters of the resonators), Γ_1r, Γ_2r, Γ_1i, and Γ_2i provide important information on the coupling mechanism. For the RCP excitation, as shown in Fig. 5F, the radiation losses (Γ_1r and Γ_2r) decrease as the gate voltage (ΔV) increases, implying that the resonance modes have a weaker coupling to free-space radiation. The curvature radius of the curve in the complex plane, determined by radiation losses Γ_1r and Γ_2r (see note S1 and table S1), decreases as the gate voltage increases, resulting in a limited phase angle range. On the other hand, for LCP excitation (Fig. 5G), the radiation loss for the second resonance (Γ_2r) increases as the gate voltage increases, leading to no critical transition. In both RCP and LCP excitations, the intrinsic losses increase as the gate voltage increases due to the increased optical conductivity of the graphene (see fig. S2).

The demonstrated active control of OA is associated with the phase change of two circularly polarized beams while transmitting the CDZM because the rotation angle is given as the phase difference. As can be expected by the Bohn-Kuhn model for a chiral medium (45), the OA becomes maximum at slightly off-resonance frequencies, where the CD becomes maximum (Fig. 2A). In our graphene CDZM, it is the change of loss parameters that controls the phase change by modifying the resonances. This is similar to the electrical control of the phase of linearly polarized light using a gate voltage in a metallic grating structure with graphene (46, 47). However, in this work, we change the phase of one circularly polarized light (LCP in our case) at an off-resonance frequency (1.42 THz) with a gate voltage to avoid significant losses at the resonance frequencies. This allows for the rotation of a linearly polarized beam with negligible losses (see fig. S3).

In conclusion, we have experimentally demonstrated an electrically tunable chiral metamaterial in which the transmission of the RCP wave can be markedly modified by varying the applied voltage without changing the transmission of the LCP. From the measurement, we validated that the graphene CDZM achieves a high-intensity modulation depth of up to 99% for the RCP wave at a small gate voltage while maintaining high transmission of the LCP wave up to 52%. As a result, a large CD value of up to 45 dB was achieved. In practice, all fabricated samples show a different performance from the designed one to a certain extent because of the imperfectness in fabrication process. Therefore, adding the active control would help to precisely locate the optimized operation point even after the sample is fabricated, while this post-optimization process would be impossible with passive devices. In addition, theoretical analysis based on the temporal CMT for two ports verifies that this gigantic active CD is attributed to a phase transition from an underdamped to an overdamped resonator by varying radiation losses in the metasurface resonators. Our work also highlights that a graphene CDZM structure can achieve an active modulation of the polarization rotation angle up to 10° with very small ellipticity. Note that the operating principles of graphene chiral metamaterials can be extended to other frequency ranges, from microwave to mid-infrared. In addition, because the designed CDZM structure is scalable, it can be applied with other active materials at microwave regime, such as diodes or varactors, and phase-change materials at infrared frequencies, such as VO₂ or Ge₃Sb₂Te₆, by changing the unit cell size. Benefitting from the electric control of polarization, the graphene CDZM concept may lead to various applications in THz technologies, such as an ultra-compact active polarization modulator for telecommunications and imaging devices and ultrasensitive sensors for identification of the chirality and structures of macromolecules or biomolecules.

MATERIALS AND METHODS

Sample fabrication

For the realization of the CDZM, we used and combined three fabrication techniques—conventional microelectromechanical systems process, CVD-grown graphene transfer, and ion gel transfer. First, to form a flexible substrate, a polyimide solution (PI-2610, HD MicroSystems) was spin-coated to a target thickness of 1 μm on a sacrificial silicon wafer, and the polyimide solution was fully cured in a subsequent two-step baking process in a convection oven and a furnace. As a first double Z metamaterial layer, a 100-nm-thick gold was deposited with a 10-nm-thick chromium adhesion layer on a negative photoresist (AZ nLOF 2035, MicroChemicals), which was patterned by photolithography. After the lift-off process, the first double Z metamaterial layer was defined. To separate the second double Z metamaterial layer from the first layer, the same polyimide curing process was repeated but with a different thickness of 10 μm. On top of a spacer, a second double Z metamaterial and a square ring-shaped graphene electrode were defined following the same process, which was used for the first layer. At the same time, a side-gate electrode was used beside the graphene electrode to simplify the fabrication process. This was a distinctive advantage based on the high-capacitance ion gel dielectric. Second, a commercial CVD-grown monolayer graphene on a copper film (Graphene Square) was transferred to the entire area covering the second double Z metamaterial (5 mm × 5 mm) and the surrounding graphene electrode. We used a conventional wet-based transfer method using a thermal release tape as a supporting layer. Third, as a gate dielectric, we used a 20-μm-thick ion gel using the cut-and-stick method. The ion gel solution was prepared by dissolving poly(vinylidene fluoride-co-hexafluoropropene) and 1-ethyl-3-methylimidazolium bis(trifluoromethanesulfonyl) amide in acetone with a weight ratio of 1:4:7. This solution was dried in a vacuum oven at a temperature of 70°C for 24 hours. The cured ion gel was cut with a razor blade and then transferred between two electrodes. Finally, the thin flexible graphene CDZM was peeled off from the silicon substrate and attached to a holed printed circuit board substrate.

THz-TDS measurements

To generate broadband THz waves, we used a low temperature–grown GaAs photoconductive antenna (iPCA, BATOP) as a THz emitter illuminated by a femtosecond Ti:sapphire laser (Mai Tai, Spectra-Physics) with a central wavelength of 800 nm and a repetition rate of 80 MHz. An electro-optic sampling method with a ZnTe crystal of 1-mm thickness was used to detect the transmitted THz signals in the time domain. The THz-TDS system has a usable bandwidth of 0.1 to 2.0 THz. Because the signal from the THz antenna was linearly polarized, the transmission amplitude for the linearly polarized waves was measured as t_xx, t_xy, t_yx, and t_yy by using four wire grid polarizers. Here, the first subscript indicates the polarization (x or y) of the transmitted wave, and the second subscript indicates the polarization of the incident wave. From these transmission amplitudes calculated in a linear basis, the RCP and LCP transmission amplitude, can be obtained as t_RCP = {(t_xx + t_yy) + i(t_xy + t_yx)}/2 and t_LCP = {(t_xx + t_yy) − i(t_xy + t_yx)}/2 (17).

Numerical modeling

Frequency-dependent material parameters (complex permittivity) of gold and those of polyimide and ion gel at THz frequencies were experimentally determined. The complex dielectric constants of gold for the frequency range of interest (0.1 to 2.5 THz) can be fitted by using the Drude model, with a plasma frequency of ω_p = 1.37 × 10¹⁶ rad/s and a collision frequency of γ = 4.07 × 10¹³ rad/s. The optical conductivity of graphene in the THz regime can be calculated as a function of E_F using the Kubo formula, which comprises only intraband contributions

$${\mathrm{\sigma }}_{\mathrm{intra}}(\mathrm{\omega })=\frac{e^2}{\mathrm{\pi }{\hslash }^2}\frac{i}{\mathrm{\omega }+i{\mathrm{\tau }}^{-1}}{\displaystyle {\int }_{\Delta }^{\infty }d\mathrm{ϵ}}\left(1+\frac{{\Delta }^2}{{\mathrm{ϵ}}^2}\right)[f(\mathrm{ϵ}-E_{\mathrm{F}})+f(\mathrm{ϵ}+E_{\mathrm{F}})]$$

Here, f(ϵ − E_F) is the Fermi distribution function with Fermi energy E_F, Γ describes the broadening of the interband transitions, τ is the momentum relaxation time due to intraband carrier scattering, and Δ is a half-bandgap energy from the tight-binding Hamiltonian near K points of the Brillouin zone (48).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/9/e1701377/DC1

fig. S1. Characterization of single-layer graphene by Raman spectroscopy.

fig. S2. Electric field distribution.

fig. S3. Transmission phase spectra.

note S1. Temporal CMT for two ports and two resonances.

table S1. Fitting parameters of temporal CMT.