Accurate Prediction of Retention in Hydrophilic Interaction Chromatography (HILIC) by Back Calculation of High Pressure Liquid Chromatography (HPLC) Gradient Profiles

Abstract

Gradient retention times are difficult to project from the underlying retention factor (k) vs. solvent composition (φ) relationships. A major reason for this difficulty is that gradients produced by HPLC pumps are imperfect – gradient delay, gradient dispersion, and solvent mis-proportioning are all difficult to account for in calculations. However, we recently showed that a gradient “back-calculation” methodology can measure these imperfections and take them into account. In RPLC, when the back-calculation methodology was used, error in projected gradient retention times is as low as could be expected based on repeatability in the k vs. φ relationships. HILIC, however, presents a new challenge: the selectivity of HILIC columns drift strongly over time. Retention is repeatable in short time, but selectivity frequently drifts over the course of weeks. In this study, we set out to understand if the issue of selectivity drift can be avoid by doing our experiments quickly, and if there any other factors that make it difficult to predict gradient retention times from isocratic k vs. φ relationships when gradient imperfections are taken into account with the back-calculation methodology. While in past reports, the accuracy of retention projections was >5%, the back-calculation methodology brought our error down to ~1%. This result was 6–43 times more accurate than projections made using ideal gradients and 3–5 times more accurate than the same retention projections made using offset gradients (i.e., gradients that only took gradient delay into account). Still, the error remained higher in our HILIC projections than in RPLC. Based on the shape of the back-calculated gradients, we suspect the higher error is a result of prominent gradient distortion caused by strong, preferential water uptake from the mobile phase into the stationary phase during the gradient – a factor our model did not properly take into account. It appears that, at least with the stationary phase we used, column distortion is an important factor to take into account in retention projection in HILIC that is not usually important in RPLC.

1. Introduction

Systematic metabolite identification in MS-based metabolomics has been a long-standing challenge due to the chemical diversity of metabolites and the lack of strict chemical structural rules such as in DNA and proteins [1]–[3]. Hydrophilic Interaction Liquid Chromatography (HILIC) combined with Mass Spectrometry (MS), has become a mainstay in the analysis of polar metabolites in complex mixtures [4]–[8]. However, in HILIC-MS, typically only mass spectral information is used to identify metabolites, while the chromatographic retention information is rarely used because HILIC is notoriously irreproducible. HILIC retention could be affected by many experimental factors including intentional factors such as mobile phase selection, column dimensions, flow rates, and temperature, and unintentional factors such as gradient delay, solvent mis-proportioning, gradient dispersion, column drift, and column age [9]–[12]. Unfortunately, mass spectral information alone is often insufficient to identify metabolites because of the inability to distinguish among isomeric compounds, or mass signals that are too weak to measure isotope patterns and/or fragmentation patterns, or the lack of reference compounds and the inability to perform de novo structure determination [13]. Chromatographic retention information could be very helpful in metabolite identification if the predictability of retention information could be improved under a range of practical experimental conditions [10].

Several methodologies have attempted to make retention information predictable across labs and experimental conditions [9], [14]–[19]. Linear Retention Indexing (LRI) is one of these methodologies and works by calculating an index score using the retention times of bracketing standards that elute before and after the metabolite of interest [17], [20]. LRI assumes that the metabolite will always elute at the same relative position between the two bracketing standards, which may only be true if experimental conditions are held constant. The prediction accuracy of LRI decreases significantly if experimental conditions are different from the ones where the LRIs were initially collected, especially in LC since the relative retention times heavily depend on solvent composition [21], [22]. For example, as shown in Fig. 1, ephedrine elutes between mannitol and Phe-Gly-Gly if the percentage of water in the mobile phase is less than 30%. However, when the percentage of water is greater than 30%, not only does ephedrine elute at a different position relative to the standards, it does not even elute between them anymore. Likewise, we would expect very poor prediction accuracy from LRI if we tried to predict ephedrine’s retention time at any other solvent composition than the one at which it was measured. The same is true for gradient elution, where the accuracy of LRI deteriorates as soon as the gradient slope, the flow rate, the column dimensions, or even the HPLC instrument is changed due to unintentional differences between the instruments.

Figure 1.

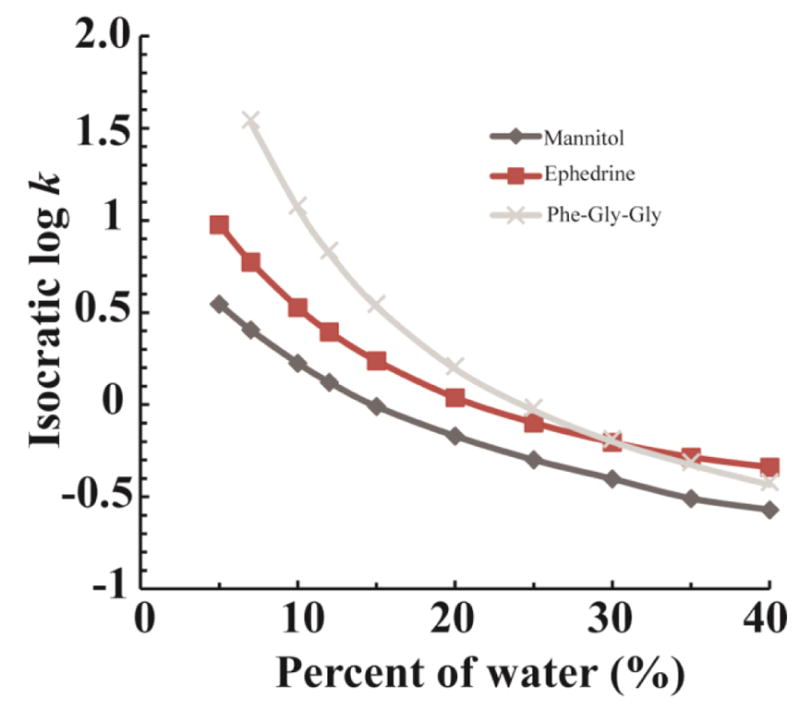
Retention factor (log k) vs. mobile phase water percentage (%) for three compounds: mannitol, ephedrine, and Phe-Gly-Gly. The log k of ephedrine is between mannitol and Phe-Gly-Gly when water percentage is less than 30%, but it elutes outside the two when the water percentage is greater than 30%.

A more accurate approach to predict gradient retention times is to measure the more fundamental relationships of retention factor (k) vs. solvent composition (φ) for each compound from a series of isocratic runs and then calculate, or “project”, their gradient retention times [16], [19], [23]. To project a gradient retention time from a k vs. φ relationship, the gradient may be considered as a series of short isocratic steps that together approximate the true gradient. This is shown in Eq. (1), where t_R is the gradient retention time, t_c is the time that a solute is under the influence of a particular time slice of the gradient as it moves through the column, k_φ is the retention factor at the solvent composition of the current gradient slice, and n is the smallest integer that makes the inequality true:

$$t_R={\mathrm{\sum }}_{i=1}^n\delta t_c=\delta {\mathrm{\sum }}_{i=1}^{n}1+\frac{1}{k_{\phi }}$$ (1)

Unfortunately, this approach is also usually inaccurate because the calculation relies on precise knowledge of the gradient, and the gradient actually produced by an LC instrument is always different from the ideal gradient it was programmed to produce [9], [10].

Retention projection with back calculation is a relatively new methodology that accounts for the effective shape of the gradient actually produced by an HPLC instrument. Instead of assuming the gradient is ideal or directly measuring the gradient, which is time consuming and can be quite difficult to measure precisely, this methodology back-calculates the effective gradient that must have been produced by the HPLC instrument to give the retention times measured for a set of back-calculation standards [9], [10], [22], [24], [25]. In short, it solves for the effective gradient by iteratively making changes to an assumed gradient until the projected retention times of the back-calculation standards match their measured retention times (see Fig. 2). It then uses the back-calculated gradient to project the retention times of other compounds with known k vs. φ relationships.

Figure 2.

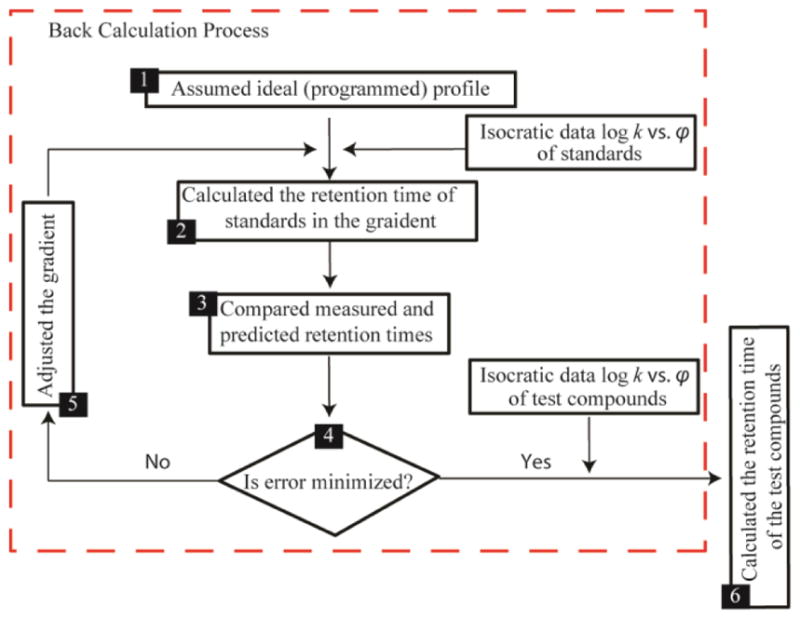
Flow chart of the retention projection methodology with back-calculation. Retention projection starts by assuming the gradient produced the LC instrument is ideal. Then the gradient is adjusted iteratively until the difference between the projected retention times and their experimental retention times are minimized. This back-calculated gradient is then used to project the retention times of other compounds with known k vs. φ relationships.

Retention projection with back-calculation has been applied in reversed phase liquid chromatography (RPLC) to give uniquely low prediction errors, for example, only ± 2.8 s in 20 min solvent gradient at 100 μL/min flow rate [9], [10]. Using this approach, the error in our retention projections was virtually the same as our experimental error, suggesting that the approach takes into account virtually all significant factors controlling retention. In a seven-lab study, retention projections were found to be 22-fold more accurate than LRIs under a range of experimental conditions [25]. Even under conditions ideal for accurate LRIs, retention projections were twice as accurate because they took into account the gradient non-idealities produced by each lab’s LC instrument [25]. This suggests it is possible to create retention databases useful for metabolite identification.

However, this approach to retention projection using the back-calculation methodology has not been extended to HILIC, yet. In previous studies using gradient retention projection from isocratic runs in HILIC where the back-calculation methodology was not used, the prediction accuracy was much worse than in RPLC [9], [14], [15], [21]. For example, Tyteca et al. predicted gradient retention times in HILIC and found the prediction error was 3.7% to 9.5%, which is roughly 30-fold less accurate than retention projections in RPLC using back-calculation [14]. A later publication by Tyteca et al. reported an improvement in the average prediction error to ~ 3% [15]. They attributed the improved accuracy to their use of a better equation to describe k vs. φ relationships, but it was probably also caused by their use of shallower gradients than in their previous work. Retention projections are generally more accurate in shallower gradients because the gradients more closely resemble the isocratic conditions in which the k vs. φ relationships were measured. Gika et al. also projected gradient retention times in HILIC and found prediction errors that were considerably more accurate, up to 0.4% [18]. However, their high accuracy mainly resulted from measuring their k vs. φ relationships in gradients instead of isocratic runs, and then predicting their gradient retention times in gradients similar to ones used to measure their k vs. φ relationships.

In this paper, we extend the back-calculation methodology to HILIC to (a) determine the level of retention projection accuracy achievable once gradient non-idealities are taken into account and (b) to determine if there are any additional factors that must be modeled in order to achieve a similar accuracy in HILIC as in RPLC. Since reproducibility in HILIC is a well-known issue [26]–[28], we measured both isocratic and gradient retention times within five days.

2. Material and methods

2.1 Selection of 23 compounds

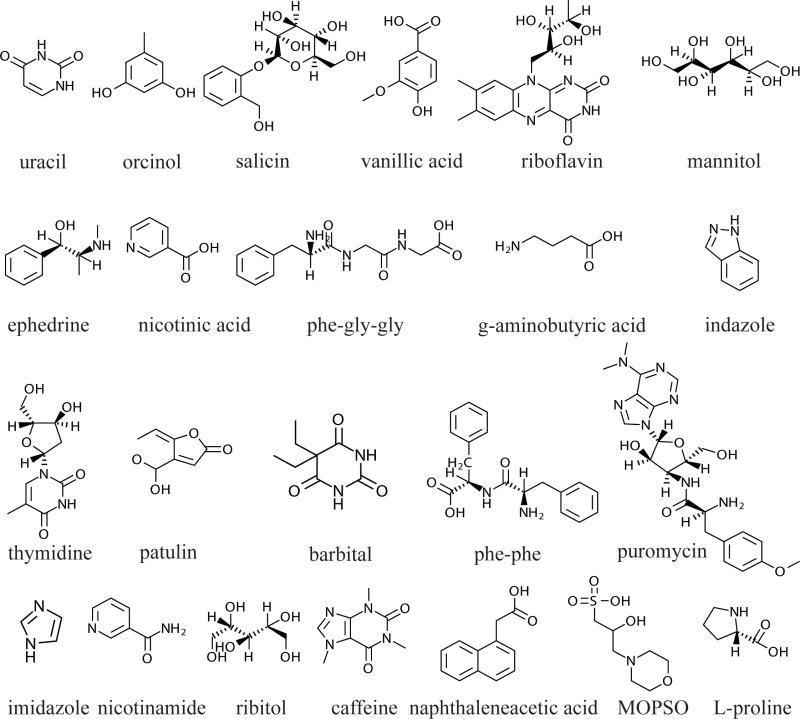
23 compounds out of 200 that we tested were selected (Fig. 3). They were selected to be chemically diverse, have different masses, retention times, and a range of pK_as. Some are hydrogen-bond donors and some are hydrogen-bond acceptors. 100 mM stock solutions of each compound were prepared in 1:1 water: acetonitrile. Stock solutions were then mixed and diluted in acetonitrile to a final injection concentration of 100 μM. All chemicals and solvents were purchased from Sigma-AldrichR (St. Louis, MO), Alfa AesarR (Ward Hill, MA), or TCI America (Portland, OR).

Figure 3.

Chemical structures of the 23 compounds that were used in the study. These chemicals were selected because they are chemically diverse, and elute over a wide range of retention, and can be distinguished easily by mass.

2.2 Mobile phase preparation

Mobile phase A was acetonitrile: water (95: 5 by volume) with 20 mM ammonium acetate, which contains 10 mM ammonium acetate and 10 mM acetic acid which was used to adjusted the pH to 4.7.Mobile phase B was water with 20 mM ammonium acetate (same as it in mobile phase A). To ensure a consistent pH in our mobile phase buffer from batch to batch, we measured components (ammonium acetate, acetic acid, acetonitrile, and water) gravimetrically with ±0.001 g accuracy. We made a stock buffer solution first: 1 L of 2 M stock buffer was made by adding 77.080 g ammonium acetate and 60.800 g acetic acid to 1000.000 g distilled deionized water. Then 1 L of mobile phase A was made (95: 5 acetonitrile: water) by adding 10 mL stock buffer (2 M) to 746.909 g acetonitrile and 40.000 g distilled deionized water, while 1 L of mobile phase B was made by adding 10 mL stock buffer (2 M) to 990.000 g distilled deionized water. The final concentration of buffer in mobile phase A and B was 20 mM.

2.3 Equipment and software

A HPLC-MS system that has a DIONEX Ultimate 3000 (HPG-3400 RS) pump and a Bruker Amazon SL ion trap MS (Bremen, Germany) was used. Back-calculation software was written in-house in Java 1.6 (Oracle, Redwood Shores, CA), which contains the Java OpenGL (JOGL) binding library version 2.0-rc11 (JogAmp, http://jogamp.org), the Unidata netCDF library version 4.2 (UnidataR, Boulder, CO), the Savitzky-Golay filter library version 1.2 by Marcin RzeŸnicki (http://code.google.com/p/savitzky-golay-filter/), the jmzML library, and the jmzReader library.

2.4 Chromatographic conditions

A Waters Acquity UPLC BEH HILIC column (2.1 mm × 100 mm, 1.7 μm particle size) was used in this study. To avoid the effect of temperature fluctuation on retention, the column temperature was held at 35.0 °C by a thermostatted circulating water bath (Exacal Circulating Bath EX-200DD) and an eluent pre-heater (Thermo Scientific Pre-Column heater 2 μL) in front of column. The injection volume was 5 μL in all runs.

2.5 Measurement of column repeatability

The repeatability of the column was measured by running a mixture of the 23 compounds in an isocratic run at 5% mobile phase B for 60 minutes at a 0.2 mL/min flow rate. More isocratic runs were performed 12, 24, 36, 48, 60, and 72 h later. RSD (relative standard deviation) was then calculated for each compound’s retention time in these 6 isocratic runs. We found the RSDs ranged from 0.06% to 0.3% in retention time and 1.6% in k, which is similar to RPLC where 1% RSD in k is typical [9].

2.6 Measurement of isocratic data

After measuring repeatability, we measured the isocratic k vs. φ relationships of the 23 compounds at 10 isocratic solvent compositions (5%, 7%, 10%, 12%, 15%, 20%, 25%, 30%, 35% and 40% of mobile phase B) for 60 minutes at 0.2 mL/min flow rate over three replicates. To ensure system and column equilibration, we ran 12 mL (30 times the column dead volume) of eluent through the column before each isocratic run. According to the Eq. (3), where t_R is the retention time and t₀ is the column dead time:

$$logk=log\frac{t_R-t_0}{t_o}$$ (3)

To avoid the influences of the instrument dead time (t_I) on the prediction accuracy, the equation is modified to:

$$logk=log\frac{(t_R-t_I)-(t_0-t_I)}{t_o-t_I}$$ (4)

The log k of each compound at each solvent composition was calculated by Eq. (5), where:

$$logk=log\frac{t_R-t_I}{t_o-t_I}$$ (5)

Both t_I and t₀ were measured using our dead time marker, n-hexadecylbenzamide. To measure t_I we replaced the column with a narrow bore PEEK tube (1 m length with 50 μM inner diameter).

2.7 Measurement of gradient delay volume

The gradient delay volume is the solvent volume contained from the solvent proportioner to the column entrance. The gradient delay volume was measured using a 5 min gradient run at 0.2 mL/min. Solvent A was water, solvent B was water mixed with 0.1% acetone, and acetone was monitored by a UV absorbance detector at 265 nm. The gradient delay volume was measured to be 0.56 mL for our instrument.

2.8 Measurement of gradient retention times

We measured retention times in nine different gradients with three gradient slopes (3.5% mobile phase B/min, 1.75% mobile phase B/min, and 0.875% mobile phase B/min) starting from 5% mobile phase B, at three flow rates (0.2 mL/min, 0.4 mL/min, and 0.8 mL/min). The column was equilibrated before each gradient run using 12 mL of starting solvent, as when isocratic data was measured. Each gradient was held at 40% mobile phase B at the end to clear the column. In this way, both isocratic data and gradient data were measured using the same LC-MS instrument within 3 days without pause.

3. Results and discussion

The back-calculation methodology was applied to (a) study the retention projection accuracy when accounting for gradient non-idealities and (b) determine any additional factors that need to be modeled besides gradient imperfections to achieve a similar accuracy in HILIC as in RPLC. Of the 23 chemically diverse compounds we selected, 10 were used as “back-calculation standards” to calculate the actual gradients produced by our instrument and the other 13 were used as “test compounds” to probe the accuracy of our retention projections. Their isocratic k vs. φ relationships and subsequently retention times in nine gradients were measured. We then attempted to project the gradient retention times of the 13 test compounds based on their k vs. φ relationships and obtained gradient profiles by three different approaches: (1) we assumed the gradient profiles were ideal in our retention projection calculations (“ideal gradient”), (2) we assumed the gradient profiles were ideal, but simply delayed to account for the gradient delay volume we measured independently for our HPLC system (“offset gradient”), and (3) we back-calculated the effective gradient profiles from the retention times of the 10 back-calculation standards (“back-calculated gradient”). Last, we tested the prediction accuracy in each case by comparing the projected retention times of the 13 test compounds to their measured retention times.

3.1 Selection of the back-calculation standards

Out of the 23 compounds, we selected back-calculation standards based on their retention times to be evenly spaced and together, to cover a wide range of the gradient. The retention time of each standard offers information about a short section of the gradient, so it is important that the standards elute over a wide range of retention times so that there is enough information to back-calculate the entire gradient. For example, in Table 1 (retention times of the 23 compounds in a 10 min gradient), 10 compounds were used as back-calculation standards (orcinol, uracil, salicin, vanillic acid, riboflavin, mannitol, ephedrine, nicotinic acid, Phe-Gly-Gly, and γ-amino butyric acid) and 13 compounds were used as test compounds (indazole, thymidine, puromycin, patulin, barbital, phe-phe, imidazole, nicotinamide, ribitol, caffeine, naphthalene acetic acid, 3-morpholino-2-hydroxypropanesulfonic acid (MOPSO), and L-proline). With these selections, the retention times of the back-calculation standards were evenly spaced and covered the entire 10 min gradient, while the retention times of the test compounds were scattered in between the back-calculation standards.

Table 1.

An Example of 10 min Gradient Run

	Name	Retention time (min)	m/z
1	Orcinol	1.6438	123
2	Barbital	1.6726	183
3	Patulin	1.6835	193
4	Indazole	1.688	119
5	Caffeine	1.9957	195
6	Uracil	2.1969	111
7	Thymidine	2.3877	241
8	Nicotinamide	2.416	123
9	Imidazole	2.8904	69
10	Salicin	3.0352	285
11	Ribitol	3.8874	151
12	MOPSO	3.9721	226
13	Naphthalene Acetic Acid	4.2291	185
14	Vanillic Acid	4.2749	167
15	Puromycin	4.7923	472
16	Riboflavin	5.2287	377
17	Mannitol	5.8291	182
18	Phe-Phe	6.7509	313
19	Ephedrine	7.0336	166
20	Nicotinic Acid	7.4984	123
21	Phe-Gly-Gly	8.4105	278
22	L-proline	8.9657	115
23	γ-amino butyric acid	9.6717	103

3.2 Isocratic data (log k vs. φ) of 23 compounds

Fig. 4 shows the log k vs. φ relationships of the 10 back-calculation standards and the 13 test compounds. Retention factors ranged from 1.2 to 2 within the mobile phase B percentage range of 5% to 40%. As is characteristic of HILIC, the retention factor of most compounds becomes smaller with the increasing percentage of water. However, of these 23 compounds, the log k of three test compounds (indazole, patulin, and barbital) did not change appreciably with solvent composition (their log k was around −1.0) because they were very poorly retained. Despite their poor retention, their retention factors were still different and repeatable and, as is often the case for compounds like these, their retention times are different enough to be identifying characteristics. Therefore, these three compounds were kept in our analysis.

Figure 4.

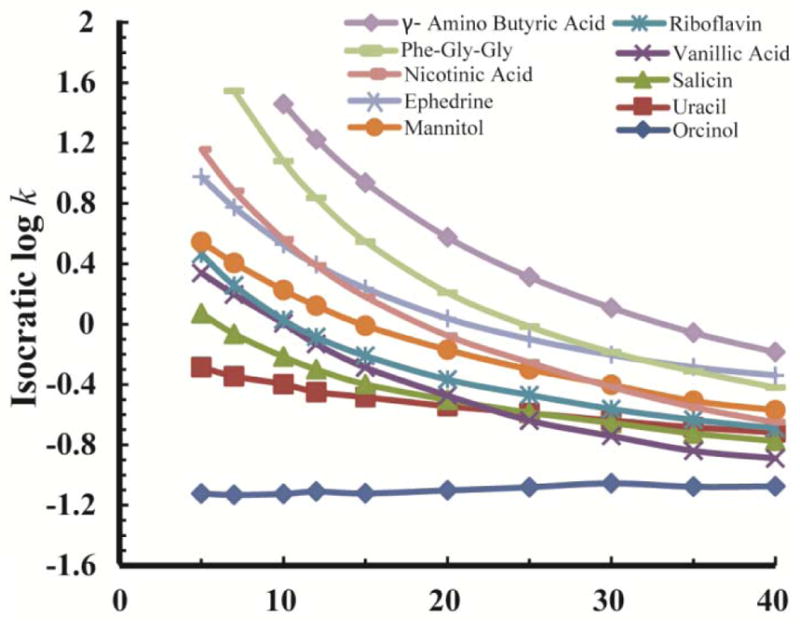
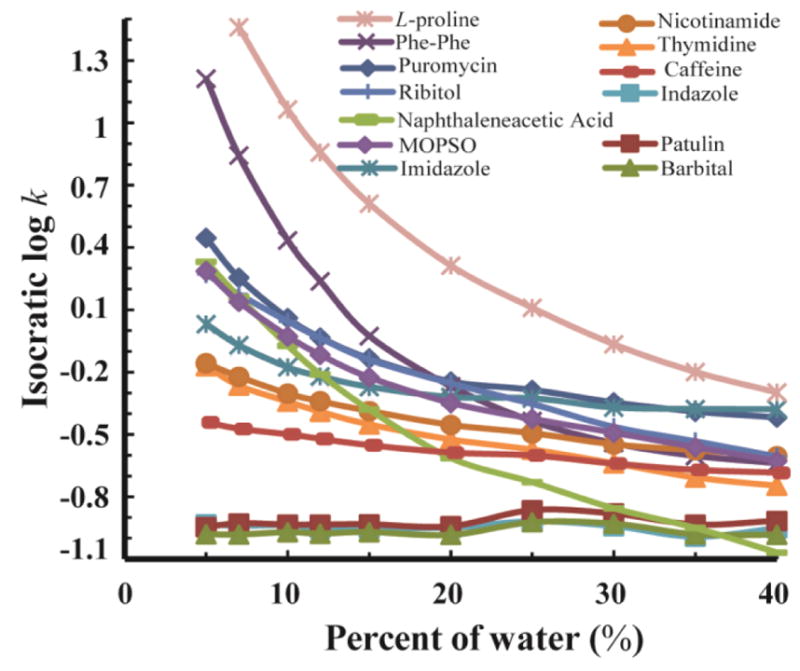
Isocratic data (log k vs. φ) measured for the 10 back-calculation standards (top) and the 13 test compounds (bottom). See section 2.6 for details.

3.3 The three types of gradient profiles: ideal, offset, and back-calculated

The accuracy of the gradient profile is key to the accuracy of projected retention times since it is used in their calculation. In this paper, we used three types of gradient profiles to project retention times: “ideal”, “offset”, and “back-calculated”. Fig. 5 shows an example of the three types of gradient profiles representing a gradient with a slope of 3.5% mobile phase B/min (starting from 5% mobile phase B) at a flow rate of 0.2 mL/min. The black dotted line in Fig. 5 is the ideal gradient that was programmed into the LC instrument. However, in reality, the gradient that was delivered to the inlet of the column was imperfect since it took time for the mobile phase to get from the solvent proportioner to the inlet of the column. This gradient delay is taken into account in the offset gradient (green line), which is the ideal gradient offset by the gradient delay (see section 2.6 for more details about measurements of the gradient delay). Though the offset gradient accounts for the biggest source of non-idealities in the gradient, it does not account for other sources of gradient non-ideality including solvent mis-proportioning and gradient dispersion. The red line is the back-calculated gradient, which could potentially account for all these factors: gradient delay, solvent mis-proportioning, and gradient dispersion. This is because the back-calculated gradients take whatever shape is necessary to minimize the retention time differences between measured and calculated retention times of the 10 back-calculation standards, thus characterizing the actual gradient experienced by the test compounds.

Figure 5.

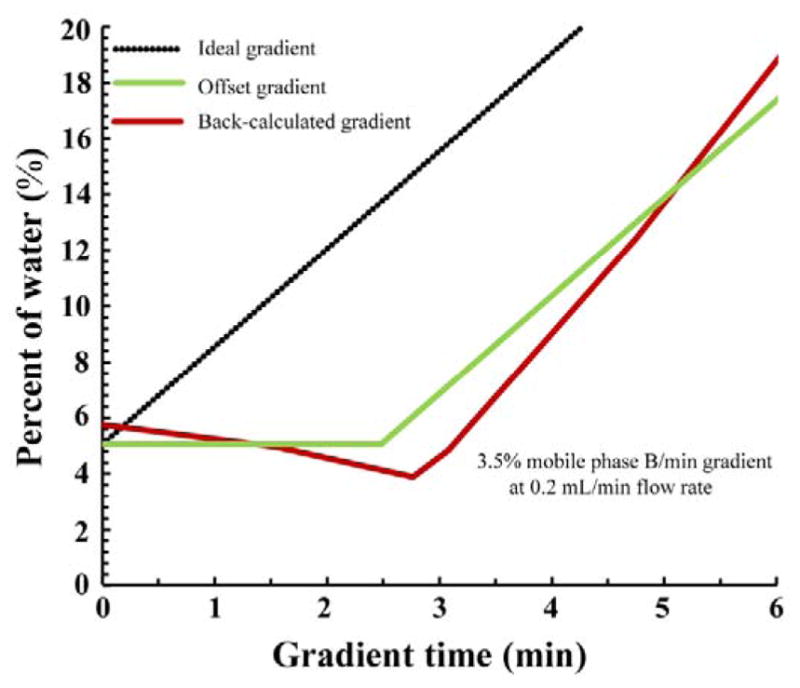
Example of the three types of gradient profiles: ideal, offset, and back-calculated gradient profiles in a gradient slope of 3.5% mobile phase B/min (started from 5%) at a flow rate of 0.2 mL/min. Mobile phase B: water with 20 mM ammonium acetate (pH 4.7). See section 2.8 for details.

Looking closer at these three gradient profiles in Fig. 5, the ideal gradient is the most distinct. It showed the mobile phase B fraction begin increasing right at time 0 at a rate of 3.5% mobile phase B/min, while the offset and back-calculated gradient profiles displayed a ~2.5 min delay before the onset of the gradient, which reflects the gradient delay of the LC system we used. Then, after the delay time, the two gradient profiles started increasing. Comparing just the offset and back-calculated gradients, there are a few more differences. First, the back-calculated gradient appears to be about 0.3 min more delayed than the offset gradient. Yet even though the back-calculated gradient is more delayed than the offset gradient, it reaches a steeper gradient slope and eventually catches up with the offset gradient (discussed below). Second, there appears to be a slight decline in mobile phase B fraction during the gradient delay of the back-calculated gradient. We believed this decline is just an artifact of the back-calculation process – there is not enough information from the back-calculation standards (i.e. retention times) to calculate the true mobile phase compositions in that region of the gradient profile.

In the back-calculated profile, the longer gradient delay combined with a steeper gradient slope was unexpected. One possible explanation of this behavior could be distortion of the gradient within the column (“column distortion”), caused by partitioning of water from the mobile phase into the stationary phase [26]–[28]. At the beginning of the gradient, the amount of water in the stationary phase is relatively small, and the water concentration in the stationary phase is at equilibrium with the water concentration in the mobile phase. As the amount of water in the mobile phase increases at the beginning of the gradient, it preferentially partitions into the stationary phase and lower water concentration in the mobile phase. This would appear as an extended gradient delay (2.5 to 2.8 min). As the water fraction in the mobile phase continues to increase, eventually the stationary phase becomes saturated and the mobile phase composition starts to recover (2.8 to 3.1 min). We then see a much steeper slope as the effect of the stationary phase on the mobile phase composition becomes insignificant (i.e., it catches up). After it catches up at ~5.2 min, we expected the slope in the back-calculated gradient would match the delayed gradient. However, from 5.2 min to 6 min, the water fraction appeared to increase even higher than the offset gradient. That would not happen in reality, rather, it is an artifact of the back-calculation process – there is only one retention time in that range and the algorithm does not have enough information to converge on the true mobile phase composition.

3.4 The effects of gradient shape and flow rate on the back-calculated gradient profiles

Gradient steepness and flow rate played an important role in the degree of gradient distortion in the back-calculated gradients. To analyze this influence, we tested three gradient slopes (3.5% mobile phase B/min, 1.75% mobile phase B/min, and 0.875% mobile phase B/min) starting from 5% of mobile phase B and three flow rates (0.2 mL/min, 0.4 mL/min, and 0.8 mL/min). In total, we back-calculated nine gradients (as shown in Supplementary Fig. 1).

To quantify the distortion in the back-calculated gradients, a metric was defined as “distortion delay”, which represents the maximum distance in time between the offset gradient and the back-calculated gradient. For example, gradient distortion causes the back-calculated gradient to lag behind the offset gradient (Fig. 5), but the delay between the two is greatest at the point where the offset gradient begins to rise. At that point, the distortion delay can be seen to be ~0.7 min.

We found that a slower flow rate caused the back-calculated gradient to have a greater distortion delay and a stronger influence on the shape of the back-calculated gradient (Supplementary Fig. 1). For example, as showed in Supplementary Fig. 1, at the same gradient slope of 3.5% mobile phase B/min, a slower flow rate of 0.2 mL/min gave a 0.44 min distortion delay while a faster flow rate of 0.4 mL/min caused a smaller distortion delay of 0.21 min, and an even faster flow rate of 0.8 mL/min caused the smallest distortion delay of 0.04 min. This observation suggests that the distortion delay is caused by column distortion, which is mitigated at faster flow rates since a greater volume of mobile phase passes through the column in a given amount of time, thereby the percentage of up taken water on the carried mobile phase is smaller, thereby lessening the effect of water uptake by the stationary phase on the mobile. We saw a similar effect when comparing gradient slopes. For example, at the flow rate 0.2 mL/min, we compared the back-calculated gradients in three gradients with slopes of 3.5% mobile phase B/min, 1.75% mobile phase B/min, and 0.875% mobile phase B/min. We found that the steepest gradient (3.5% mobile phase B/min) showed the greatest distortion delay and had the strongest influence on the shape of the back-calculated gradient.

3.5 Comparison of retention projection error using the three types of gradient profiles

Last, we tested the retention projection accuracy using the three types of gradient profiles (ideal, offset, and back-calculated), the three gradient shapes (3.5% mobile phase B/min, 1.75% mobile phase B/min, and 0.875% mobile phase B/min), and the three flow rates (0.2 mL/min, 0.4 mL/min, and 0.8 mL/min). We describe our overall prediction error in terms of the RMS (Root Mean Square) error of the 13 test compounds. As an example, Table 2 shows the individual projection errors of the 13 test compounds and the overall RMS error in one of the gradients (3.5% mobile phase B/min gradient, 0.2 mL/min flow rate) using each of the three types of gradient profiles. In this case, the overall prediction error was greatest, at ±71.5 s (28.97%), when using the ideal gradient, while the overall prediction error was considerably less, at ±7.2 s (2.25%), when using the offset gradient. The back-calculated gradient gave the smallest overall prediction error, at ±2.5 s (1.04%).

Table 2.

Retention Projection Error When Using the Three Types of Gradients

	tR, experimenta	tideal -tRb	tdelayed -tRc	tback-calculated -tRd
indazole	101.952	0.708	0.558	−0.108
thymidine	144.072	8.19	0.768	2.184
puromycin	307.344	106.458	19.656	0.42
patulin	101.496	0.516	0.426	−0.462
barbital	100.776	0.45	0.33	−0.396
phe-phe	419.502	157.488	14.448	0.582
imidazole	174.6	18.138	1.152	2.976
nicotinamide	145.938	7.062	0.954	1.524
ribitol	236.292	44.916	3.024	1.272
caffeine	120.084	1.53	0.312	−0.132
naphthalene acetic acid	254.1	70.704	0.324	−5.532
MOPSO	241.272	57.216	2.91	1.248
L-proline	530.232	140.028	−7.17	5.598
Overall prediction error e (s)		±71.51	±7.17	±2.51
Overall prediction error f (%)		±28.98	±2.26	±1.04

3.5% mobile phase B/min (started at 5%) at flow rate 0.2 mL/min, mobile phase B: water with 20 mM ammonium acetate (pH 4.7)

^athe experimental retention time (s) in the gradient

^bthe retention time differences (s) between the experimental retention time and the projected retention time, calculated using the ideal gradient profile (dotted line in Fig. 5), t_{ideal gradient} -t_{R, Experiment}

^cthe retention time differences (s) between the experimental retention time and the projected retention time, calculating using the delayed gradient profile (green line in Fig. 5), t_{ielayed gradient} -t_{R, Experiment}

^dthe retention time differences (s) between the experimental retention time and the projected retention time, calculating using the back-calculated gradient profile (red line in Fig. 5), t_{back-calculated gradient} -t_{R, Experiment}

^eOverall prediction error is defined as the RMS (root-mean-square) error of the test compounds. $\text{RMS}(\sqrt{\frac{1}{n}(x_1^2+x_2^2+x_3^2\dots +x_n^2)})$, x means the prediction error of each test compound

^f $\text{Prediction}\text{error}(\%)=(\sqrt{\frac{1}{n}(y_1^2+y_2^2+y_3^2\dots +y_n^2)})$, y means the prediction error (%) of each test compound

Table 3, 4, and 5 show the overall prediction errors when using the ideal, offset, and back-calculated gradient profiles in nine gradients with three gradient slopes and three flow rates. In Table 3, which shows retention projection errors using the ideal gradient profiles, the overall prediction error ranged from ±12 s to ±71 s (6.36% to 28.97%) in the nine gradients. In Table 4, which shows retention projection errors using the offset gradient profiles, the overall prediction error was 3–10 times more accurate, ranging from ±3.0 s to ±7.2 s (1.54% to 2.73%). This prediction accuracy is similar, if not more accurate than a report that, until now, showed the most accurate retention projections in HILIC. They also used an offset gradient profile [15]. In Table 5, which shows retention projection errors using the back-calculated gradient profiles, the prediction error was the smallest of all, ranging from ±0.62 s to ±2.5 s (0.53% to 1.83%), which was 6–43 times more accurate than when using the ideal gradient profiles and roughly threefold more accurate than when using the offset gradient profiles. This improved accuracy was a result of the fact that the back-calculation methodology accounts not just for gradient delay, but also for gradient distortion, solvent mis-proportioning, and gradient dispersion. In addition, based on the uniquely strong distortion in the back-calculated profiles obtained here (compared to those obtained in prior publications dealing with RPLC), we suspect that column distortion is unusually pronounced in this HILIC system. The back-calculation methodology may also be accommodating this column distortion to some degree, even though it could not properly take it into account.

Table 3.

The Overall Prediction Error (s) of 13 Test Compounds When Using Ideal Gradients

Overall Prediction Error (s)
Flow Rate	0.2 mL/min	0.4 mL/min	0.8 mL/min
Gradient Slope
3.5%/min g	± 71 e (28.97% f)	± 30 (18.37%)	± 14 (12.57%)
1.75%/min h	± 64 (19.27%)	± 28 (12.27%)	± 13 (8.17%)
0.875%/min i	± 62 (15.22%)	± 26 (9.05%)	± 12 (6.36%)

^eOverall prediction error is defined as the RMS (root mean square) error of the test compounds. $\text{RMS}(\sqrt{\frac{1}{n}(x_1^2+x_2^2+x_3^2\dots +x_n^2)})$, x means the prediction error of each test compound

^f $\text{Prediction}\text{error}(\%)=(\sqrt{\frac{1}{n}(y_1^2+y_2^2+y_3^2\dots +y_n^2)})$, y means the prediction error (%) of each test compound

^g3.5%/min is the gradient slope of 3.5% mobile phase B/min, mobile phase B: water with 20 mM ammonium acetate (pH 4.7)

^h1.75%/min is the gradient slope of 1.75% mobile phase B/min, mobile phase B: water with 20 mM ammonium acetate (pH 4.7)

ⁱ0.875%/min is the gradient slope of 0.875% mobile phase B/min, mobile phase B: water with 20 mM ammonium acetate (pH 4.7)

Table 4.

The Overall Prediction Error (s) of 13 Test Compounds When Using Offset Gradients

Overall Prediction Error (s)
Flow Rate	0.2 mL/min	0.4 mL/min	0.8 mL/min
Gradient Slope
3.5%/min g	± 7.2e (2.25% f)	± 3.3 (1.63%)	± 3.0 (2.73%)
1.75%/min h	± 6.3 (1.63%)	± 4.2 (1.65%)	± 3.9 (2.67%)
0.875%/min i	± 7.0 (1.56%)	± 4.4 (1.54%)	± 4.4 (2.62%)

^eOverall prediction error is defined as the RMS (root mean square) error of the test compounds. $\text{RMS}(\sqrt{\frac{1}{n}(x_1^2+x_2^2+x_3^2\dots +x_n^2)})$, x means the prediction error of each test compound

^f $\text{Prediction}\text{error}(\%)=(\sqrt{\frac{1}{n}(y_1^2+y_2^2+y_3^2\dots +y_n^2)})$, y means the prediction error (%) of each test compound

^g3.5%/min is the gradient slope of 3.5% mobile phase B/min, mobile phase B: water with 20 mM ammonium acetate (pH 4.7)

^h1.75%/min is the gradient slope of 1.75% mobile phase B/min, mobile phase B: water with 20 mM ammonium acetate (pH 4.7)

ⁱ0.875%/min is the gradient slope of 0.875% mobile phase B/min, mobile phase B: water with 20 mM ammonium acetate (pH 4.7)

Table 5.

The Overall Prediction Error (s) of 13 Test Compounds When Using Back-Calculated Gradients

Overall Prediction Error (s)
Flow Rate	0.2 mL/min	0.4 mL/min	0.8 mL/min
Gradient Slope
3.5%/min g	± 2.5e (1.04% f)	± 1.01 (0.74%)	± 0.62 (1.15%)
1.75%/min h	± 2.34 (0.77%)	± 0.64 (0.53%)	± 1.2 (1.52%)
0.875%/min i	± 1.89 (0.68%)	± 1.38 (0.59%)	± 2.7 (1.83%)

^eOverall prediction error is defined as the RMS (root mean square) error of the test compounds. $\text{RMS}(\sqrt{\frac{1}{n}(x_1^2+x_2^2+x_3^2\dots +x_n^2)})$, x means the prediction error of each test compound

^f $\text{Prediction}\text{error}(\%)=(\sqrt{\frac{1}{n}(y_1^2+y_2^2+y_3^2\dots +y_n^2)})$, y means the prediction error (%) of each test compound

^g3.5%/min is the gradient slope of 3.5% mobile phase B/min, mobile phase B: water with 20 mM ammonium acetate (pH 4.7)

^h1.75%/min is the gradient slope of 1.75% mobile phase B/min, mobile phase B: water with 20 mM ammonium acetate (pH 4.7)

ⁱ0.875%/min is the gradient slope of 0.875% mobile phase B/min, mobile phase B: water with 20 mM ammonium acetate (pH 4.7)

4. Conclusions

In this paper, we applied the back-calculation methodology in HILIC to (a) determine the retention projection accuracy when gradient non-idealities were taken into account and (b) determine what additional factors must be considered in HILIC when projecting gradient retention times from k vs. φ relationships. Known sources of error were either avoided or accounted: column drift, which is especially pronounced in HILIC, was avoided by collecting all retention data (both isocratic and gradient) within a week. Gradient non-idealities (gradient delay, gradient dispersion, and solvent mis-proportioning) were taken into account by back-calculating the effective gradient using the gradient retention times of a set of standards. This is the first time that the retention projection with back-calculation has been applied to HILIC, and it enabled uniquely accurate projections of gradient retention times for compounds with known k vs. φ relationships. Prediction errors were ~1% (from 0.62 s to 2.5 s), which was 6–43 times more accurate than when gradients were assumed to be ideal and 3–5 times more accurate than when only gradient delay was taken into account. To the best of our knowledge, this is the most accurate gradient retention prediction in HILIC and approximately 5-fold more accurate than previous reports [14], [15], [18].

However, the prediction error in HILIC (~1%) was still significantly worse than previously reported in RPLC (0.3%) using the same back-calculation methodology [7], [9], [10]. Our observations suggest that this is a result of strong water uptake into the stationary phase from the mobile phase during the gradient (i.e., “column distortion”) [11], [12], [26], [28]. Unlike RPLC, the gradients we back-calculated showed strong gradient delay beyond that caused by the instrument itself, followed by a steep recovery, which is characteristic of column distortion [11], [12], [28]. Therefore, at least with the HILIC stationary phase we used (Waters BEH HILIC, 1.8 μm particle size), it appears that column distortion is a significant factor to consider when projecting retention times that is less important in RPLC.

Supplementary Material

2

Retention times of 23 compounds, including the 10 back-calculation standards and the 13 test compounds. Back-calculation standards are highlighted in blue. Mobile phase A: acetonitrile/water (95/5) with 20 mM ammonium acetate (pH 4.7). Mobile phase B: water with 20 mM ammonium acetate (pH 4.7). The 10 min gradient was from 5% to 40% mobile phase B, the flow rate was 0.2 mL/min, and the temperature was 35°C. Column: Water Acquity UPLC BEH HILIC column (2.1 mm × 100 mm) with 1.7 μm particle size.

Highlights.

• First application of the methodology “retention projection with back calculation to HILIC.

• Performance of the most accurate gradient retention projection methodology in HILIC.

• Suggest column distortion can be a significant factor to consider when projecting retention times in HILIC.

• Investigation of effects of flow rate and gradient slop on gradient retention projection accuracy in HILIC.

• Comparison of the gradient retention projection accuracies when using ideal, offset, and back calculated gradients in HILIC.